1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 56, № 3, 2022

Теоретические основы химической технологии, 2022, T. 56, № 3, стр. 337-344

Новый класс точных решений уравнений Обербека‒Буссинеска, описывающих несжимаемую жидкость

В. В. Привалова a, b, *, Е. Ю. Просвиряков a, b, **

a Институт машиноведения УрО РАН
Екатеринбург, Россия

b Уральский федеральный университет имени первого Президента России Б.Н. Ельцина
Екатеринбург, Россия

* E-mail: valentprival@gmail.com
** E-mail: evgen_pros@mail.ru

Поступила в редакцию 11.02.2020
После доработки 08.11.2021
Принята к публикации 15.02.2022

Полный текст (PDF)

Аннотация

Построен новый класс точных решений уравнений Обербека–Буссинеска для несжимаемых сред с учетом массовых сил, тепловых источников (стоков) и джоулевой диссипации. Выражения для скоростей представляют собой квадратичные формы относительно двух координат, обобщающие класс решений Линя–Сидорова–Аристова. Температура, давление и поле массовых сил описываются формами четвертой степени. Рассмотрена возможность применения данного класса для конвективных течений в приближении Стокса и Озеена, а также продемонстрированы возможности нового класса для описания вращающихся жидких масс. На простом примере проиллюстрирована сложная структура поля скоростей для ползущего конвективного течения жидкости типа Куэтта в слое с проницаемой границей, движущейся неоднородно.

Ключевые слова: точные решения, конвекция, уравнения Обербека‒Буссинеска, приближение Стокса, приближение Озеена, вращающаяся жидкость, ползущее течение, застойная точка, противотечение, диссипативная функция

ВВЕДЕНИЕ

Многие технические устройства функционируют и технологические процессы реализуются при переменной температуре [1–6]. Неоднородное поле температуры в пространстве и во времени индуцирует конвективный перенос в жидкостях и газах [1, 7]. Описание конвекции в этом случае является очень сложной задачей, поскольку уравнения Обербека‒Буссинеска являются квадратично нелинейными [1, 7, 8]. К настоящему времени изучено много численных методов интегрирования уравнений Обербека‒Буссинеска, тем не менее не ослабевает интерес исследователей конвективных течений жидкости к точным решениям [9–16]. Построение точных решений уравнений Обербека‒Буссинеска осуществляется значительно сложнее, чем для уравнений Навье‒Стокса [11, 17–19]. Первым точным решением уравнений Обербека‒Буссинеска является одномерное течение Остроумова‒Бириха [20–23]. Многочисленные обобщения точного решения Остроумова–Бириха уравнений Обербека‒Буссинеска, описывающие однонаправленное течение жидкости и исследование устойчивости данного движения жидкости приведены в публикациях [22–27]. Слоистые и сдвиговые аналоги течения Остроумова‒Бириха рассмотрены в статьях [9, 13, 28–31]. Для течений, рассмотренных в этих работах, характерно однородное распределение скоростей относительно двух координат. Пространственно-неоднородные конвективные течения в точной постановке впервые рассмотрены в статьях [17, 32]. При построении точных решений, анонсированных в [17, 32] за основу брался класс точных решений, поле скоростей которого линейно зависит от части координат.

Полученные в статьях и монографиях точные решения для уравнений Обербека–Буссинеска принадлежат классу точных решений Линя–Сидорова–Аристова [33–35]. Поле скоростей в этом семействе точных решений линейно зависит от двух координат, а поля давления и температуры, как было показано в [17, 35] являются квадратичными формами.

В статьях [36, 37] недавно был предложен класс точных решений с нелинейной зависимостью от части координат для исследования изотермических и изобарических течений вязких несжимаемых жидкостей. Целью данной статьи является построение классов точных решений уравнений Обербека‒Буссинеска для поля скоростей, нелинейного относительно двух пространственных координат.

КЛАСС РЕШЕНИЙ КВАДРАТИЧНЫЙ ПО ДВУМ КООРДИНАТАМ

Для описания конвективного течения горизонтального слоя вязкой несжимаемой жидкости используем систему определяющих соотношений, включающих уравнение Навье‒Стокса в приближении Буссинеска, уравнение теплопроводности и уравнение несжимаемости. Векторная запись этих уравнений имеет следующий вид [1, 7, 38]:

(1)
${{{\mathbf{V}}}_{t}} + \left( {{\mathbf{V}},\nabla } \right){\mathbf{V}} = - \nabla P + \nu \Delta {\mathbf{V}} + {\mathbf{g}}\beta T,$
(2)
${{T}_{t}} + {\mathbf{V}} \cdot \nabla T = \chi \Delta T + Q,$
(3)
$\nabla \cdot {\mathbf{V}} = 0.$

Здесь ${\mathbf{V}}\left( {t,x,y,z} \right) = \left( {{{V}_{x}},{{V}_{y}},{{V}_{z}}} \right)$ ‒ вектор скорости и его проекции на оси декартовой системы координат; $P$ – отклонение давления от гидростатического, отнесенное к постоянной средней плотности жидкости $\rho $; ${\mathbf{g}}$ – вектор ускорения свободного падения; $\beta $ – температурный коэффициент объемного расширения жидкости; $T$ – отклонение от средней температуры; $Q$ – функция, определяющая тепловую (джоулевую) диссипацию, $\nu $, $\chi $ – коэффициенты кинематической вязкости и температуропроводности жидкости соответственно. Нижний индекс здесь обозначает дифференцирование по времени.

Далее запишем новый класс точных решений, обобщая известное семейство решений Линя‒Сидорова‒Аристова [17, 33–35, 39], в котором компоненты скорости линейно зависят от горизонтальных (продольных) координат, а функции давления и температуры представлены в виде квадратичной зависимости от тех же координат:

(4)
$\begin{gathered} {{V}_{x}} = {{U}_{0}} + {{U}_{1}}x + {{U}_{2}}y + {{U}_{3}}\frac{{{{x}^{2}}}}{2} + {{U}_{4}}xy + {{U}_{5}}\frac{{{{y}^{2}}}}{2}, \\ {{V}_{y}} = {{V}_{0}} + {{V}_{1}}x + {{V}_{2}}y + {{V}_{3}}\frac{{{{x}^{2}}}}{2} + {{V}_{4}}xy + {{V}_{5}}\frac{{{{y}^{2}}}}{2}, \\ {{V}_{z}} = {{W}_{0}} + {{W}_{1}}x + {{W}_{2}}y. \\ \end{gathered} $

Коэффициенты в выражениях (4) ${{U}_{i}}$, ${{V}_{i}}$ ($i = \overline {0;5} $), ${{W}_{j}}$ ($j = \overline {0;2} $) зависят от вертикальной (поперечной) координаты $z$ и времени $t$. Вид компоненты скорости ${{V}_{z}}$ обусловлен требованием выполнения уравнения несжимаемости, хотя в общем случае вертикальная скорость может являться нелинейной формой продольных координат с постоянными коэффициентами при степенях продольных координат выше первой [36].

Структура точного решения (4) для скоростей должна быть дополнена полиномиальным выражением для давления $P$ и температуры $T$. В статье [36] было показано, что степень многочлена для давления $P$ относительно горизонтальных координат не превосходит трех. Для температуры $T$ структура точного решения аналогична давлению.

Функция $Q$, определяющая энергию, рассеивающаюся в виде тепла благодаря молекулярной вязкости жидкости, в общем случае определяется следующим образом [7, 27]:

(5)
$\begin{gathered} Q = \frac{\nu }{{2{{c}_{p}}}}\left[ {{{{\left( {\frac{{\partial {{V}_{x}}}}{{\partial x}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{V}_{y}}}}{{\partial y}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{V}_{z}}}}{{\partial z}}} \right)}}^{2}} + } \right. \\ \left. { + \,\,{{{\left( {\frac{{\partial {{V}_{x}}}}{{\partial y}} + \frac{{\partial {{V}_{y}}}}{{\partial x}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{V}_{x}}}}{{\partial z}} + \frac{{\partial {{V}_{z}}}}{{\partial x}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{V}_{z}}}}{{\partial y}} + \frac{{\partial {{V}_{y}}}}{{\partial z}}} \right)}}^{2}}} \right]. \\ \end{gathered} $

Здесь ${{c}_{p}}$ ‒ коэффициент теплоемкости жидкости, вычисленный при постоянном давлении.

Вид решений для скоростей, давления и температуры (4) и функции источников и стоков $Q$ (5) подставляем в систему уравнений Обербека–Буссинеска (1)‒(3). Приравнивая выражения при одинаковых степенях координат $x$ и $y$, получим систему уравнений в частных производных, для определения коэффициентов полиномиальных выражений гидродинамических полей. Далее будут рассмотрены новые типы краевых задач для описания конвективных течений жидкости.

КЛАСС ТОЧНЫХ РЕШЕНИЙ ДЛЯ ПОЛЗУЩЕГО ТЕЧЕНИЯ ЖИДКОСТИ

При рассмотрении ползущего течения вязкой несжимаемой жидкости, пренебрегают конвективной производной $\left( {{\mathbf{V}},\nabla } \right){\mathbf{V}}$ в уравнении переноса момента импульса (1). Таким образом можно рассмотреть систему (1)–(3) в приближении Стокса, в которой часть уравнений значительно упрощается. Аналогично можно линеаризовать уравнение теплопроводности (2), пренебрегая членами второго порядка в слагаемом $\left( {{\mathbf{V}},\nabla } \right)T$. Следовательно, при рассмотрении такого приближения функция диссипации, определяющая внешние источники энергии, не может задаваться полиномом более высокой степени, чем диссипация, определяемая вязкостью жидкости.

Если в полученной после приближения Стокса и линеаризации уравнения теплопроводности системе (1)–(3), пренебречь массовыми силами, то поля давления, температуры и функция источников и стоков будут определяться полиномами третьей степени. Аналогичные рассуждения для поля температуры (4) справедливы при рассмотрении приближения Озеена [7] для системы уравнений (1)–(3), рассмотренного в статье [36].

КЛАСС ТОЧНЫХ РЕШЕНИЙ ДЛЯ КОНВЕКТИВНОГО ТЕЧЕНИЯ ВРАЩАЮЩЕЙСЯ ЖИДКОСТИ

Определяющее соотношение (1), описывающее конвективное течение вращающейся жидкости при отсутствии массовых сил и с учетом диссипативных сил можно записать в следующем виде:

(6)
$\frac{{\partial {\mathbf{V}}}}{{\partial t}} + {\mathbf{r}} \times \frac{{\partial {\mathbf{\Omega }}}}{{\partial t}} + 2{\mathbf{\Omega }} \times {\mathbf{V}} = - \nabla p + \nu \Delta {\mathbf{V}} + {\mathbf{g}}\beta T.$

Уравнение теплопроводности (2) и уравнение несжимаемости (3) остаются без изменений. Здесь ${\mathbf{r}} = \left( {x,y,z} \right)$ ‒ радиус-вектор, описывающий положение частицы жидкости; $p = P - \frac{1}{2}\left( {{\mathbf{\Omega }} \times {\mathbf{r}},{\mathbf{\Omega }} \times {\mathbf{r}}} \right)$ ‒ модифицированное давление; ${\mathbf{\Omega }}$ ‒ вектор, определяющий угловую скорость вращения жидкости ${\mathbf{\Omega }}\left( {t,x,y,z} \right) = \left( {{{\Omega }_{x}},{{\Omega }_{y}},{{\Omega }_{z}}} \right)$. Система уравнений (6) связывает силу Кориолиса, поле скоростей, градиентов давления и температуру. Компоненты вектора угловой скорости будем рассматривать в виде:

(7)
$\begin{gathered} {{\Omega }_{x}} = {{\Omega }_{1}}\left( {z,t} \right) + {{\Omega }_{{10}}}\left( {z,t} \right)x + {{\Omega }_{{01}}}\left( {z,t} \right)y, \\ {{\Omega }_{y}} = {{\Omega }_{2}}\left( {z,t} \right) + {{\Omega }_{{20}}}\left( {z,t} \right)x + {{\Omega }_{{02}}}\left( {z,t} \right)y, \\ {{\Omega }_{z}} = {{\Omega }_{3}}\left( {z,t} \right) + {{\Omega }_{{30}}}\left( {z,t} \right)x + {{\Omega }_{{03}}}\left( {z,t} \right)y. \\ \end{gathered} $

Использование представления (7) включает в себя приближение $f$-плоскости [1, 39] и $\beta $-плоскости [39, 40] при традиционном приближении вектора угловой скорости в случае использования одного параметра Кориолиса, для описания вращающихся слоев жидкости. Выражения (7) позволяют описывать вращающиеся жидкости посредством двух и трех параметров Кориолиса, что важно во многих задачах физико-химической и геофизической гидродинамики. Кроме того, формулы (7) приводят не к искусственному усложнению точных решений при переходе во вращающуюся систему координат. Они позволяют описывать очень сложные течения между бесконечными дисками, расположение которых согласуется с (7) и вращающихся с различными угловыми скоростями. Частный случай точного решения (4), (6), (7):

$\begin{gathered} {{V}_{x}} = {{U}_{0}} - \Omega y,\,\,\,\,{{V}_{y}} = {{V}_{0}} + {{\Omega }_{1}}x,\,\,\,\,{{V}_{z}} = 0, \\ P = {{P}_{0}} + {{P}_{1}}x + {{P}_{2}}y + \frac{{{{P}_{3}}}}{2}\left( {{{x}^{2}} + {{y}^{2}}} \right), \\ T = {{T}_{0}} + {{T}_{1}}x + {{T}_{2}}y + {{T}_{3}}\frac{{{{x}^{2}}}}{2} + {{T}_{4}}\frac{{{{y}^{2}}}}{2} \\ \end{gathered} $

был исследован в статье [40]. Было показано, что данное решение может описывать динамические равновесия вращающейся жидкости между двумя бесконечными дисками с учетом вязких и тепловых свойств жидкости.

КРАЕВАЯ ЗАДАЧА, ОПИСЫВАЮЩАЯ КОНВЕКТИВНОЕ ТЕЧЕНИЕ МАРАНГОНИ

Для иллюстрации предложенного класса решений (4) рассмотрим пример горизонтального течения бесконечного слоя (в плоскости $Oxy$) вязкой несжимаемой жидкости. Толщина слоя отсчитывается по оси $Oz$ и равна $h$. Нижнюю границу слоя жидкости, задаваемую уравнением плоскости $z = 0$, считаем абсолютно твердой. Сверху слой жидкости ограничен свободной поверхностью и определяется уравнением плоскости $z = h$. Коэффициенты ${{U}_{i}}$, ${{V}_{i}}$ ($i = \overline {1,5} $), ${{W}_{j}}$ ($j = \overline {0;2} $), ${{P}_{k}}$, ${{T}_{k}}$ ($k = \overline {3;14} $) полиномов ‒ функций решения (4) полагаем равными нулю. Таким образом, решение имеет вид [41]:

(8)
$\begin{gathered} {{V}_{x}} = {{U}_{0}},\,\,\,\,{{V}_{y}} = {{V}_{0}},\,\,\,\,{{V}_{z}} = 0, \\ P = {{P}_{0}} + {{P}_{1}}x + {{P}_{2}}y,\,\,\,\,T = {{T}_{0}} + {{T}_{1}}x + {{T}_{2}}y. \\ \end{gathered} $

В силу того, что все искомые функции зависят от поперечной координаты $z$, производные от функций по этой переменной в дальнейшем будем обозначать штрихом. Движение жидкости в краевой задаче полагаем установившимся, т.е. все искомые функции не зависят от времени. С учетом принятой структуры решения (13), выражение функции диссипации $Q$ (7) имеет вид:

(9)
$Q = {{Q}_{0}} = \frac{\nu }{{2{{c}_{p}}}}\left[ {{{{\left( {U_{0}^{'}} \right)}}^{2}} + {{{(V_{0}^{'})}}^{2}}} \right].$

Запишем систему уравнений (1) с учетом принятого вида решений (8) и функции диссипации (9) в порядке дальнейшего интегрирования [41]

(10)

Пусть на нижней границе слоя жидкости, определяемой уравнением плоскости $z = 0$, задано условие прилипания жидкости, а температуру считаем равной нулевому (отсчетному) значению. На верхней свободной поверхности слоя жидкости, определяемой уравнением плоскости $z = h$, задано условие термокапиллярной конвекции Марангони, постоянное (атмосферное) давление и продольные (горизонтальные) градиенты температуры. Физический смысл заданных горизонтальных градиентов температуры заключается в нагреве (охлаждении) верхней границы слоя жидкости. Отметим, что изменение поверхностного натяжения в данном случае вызвано именно изменением температуры жидкости. Граничные условия в этом случае имеют вид [9, 13]:

(11)
$\begin{gathered} {{V}_{x}}\left( 0 \right) = {{V}_{y}}\left( 0 \right) = 0,\,\,\,\,T\left( 0 \right) = 0, \\ \eta V_{x}^{'}\left( h \right) = - \sigma {{\left. {\frac{{\partial T{\kern 1pt} '}}{{\partial x}}} \right|}_{{z = h}}},\,\,\,\,\eta V_{y}^{'}\left( h \right) = - \sigma {{\left. {\frac{{\partial T{\kern 1pt} '}}{{\partial y}}} \right|}_{{z = h}}}, \\ P\left( h \right) = S,\,\,\,\,T\left( h \right) = Ax + By. \\ \end{gathered} $

С учетом принятого вида решений (8) граничные условия (11) преобразуются к виду:

(12)
$\begin{gathered} {{U}_{0}}\left( 0 \right) = {{V}_{0}}\left( 0 \right) = 0,\,\,\,\,{{T}_{0}}\left( 0 \right) = {{T}_{1}}\left( 0 \right) = {{T}_{2}}\left( 0 \right) = 0, \\ \eta U_{0}^{'}\left( h \right) = - \sigma {{T}_{1}}\left( h \right),\,\,\,\,\eta V_{0}^{'}\left( h \right) = - \sigma {{T}_{2}}\left( h \right), \\ {{P}_{0}}\left( h \right) = S,\,\,\,\,{{P}_{1}}\left( h \right) = {{P}_{2}}\left( h \right) = {{T}_{0}}\left( h \right) = 0, \\ {{T}_{1}}\left( h \right) = A,\,\,\,\,{{T}_{2}}\left( h \right) = B. \\ \end{gathered} $

Решение системы уравнений (10), удовлетворяющее граничным условиям (12) для поля скоростей, давления и температуры имеет вид, приведенный в статье [9], за исключением функций фонового давления ${{P}_{0}}$ и температуры ${{T}_{0}}$, которые за счет рассмотрения функции диссипации будут иметь вид:

(13)
$\begin{gathered} {{T}_{0}} = \left[ {\frac{{g\beta }}{{5040{{h}^{2}}\nu }}(82{{h}^{5}} + 82{{h}^{4}}z + 82{{h}^{3}}{{z}^{2}} - 58{{h}^{2}}{{z}^{3}} + } \right. \\ + \,\,5h{{z}^{4}} + 5{{z}^{5}}) - \left. {\frac{\sigma }{{12h\eta }}\left( {{{h}^{2}} + hz + {{z}^{2}}} \right)} \right]\left( {{{A}^{2}} + {{B}^{2}}} \right) \times \\ \times \,\,\frac{{z\left( {z - h} \right)}}{\chi } + \frac{{z\left( {z - h} \right)}}{{{{c}_{p}}\chi }}\left[ {\frac{{g\left( {11{{h}^{3}} - 9{{h}^{2}}z + h{{z}^{2}} + {{z}^{3}}} \right)\beta \sigma }}{{120h\eta }}} \right. - \\ - \,\,\frac{{\nu {{\sigma }^{2}}}}{{4{{\eta }^{2}}}} - \frac{{{{g}^{2}}{{\beta }^{2}}}}{{20160{{h}^{2}}\nu }}(215{{h}^{6}} - 345{{h}^{5}}z + 215{{h}^{4}}{{z}^{2}} + \\ \left. { + \,\,5{{h}^{3}}{{z}^{3}} - 51{{h}^{2}}{{z}^{4}} + 5h{{z}^{5}} + 5{{z}^{6}})} \right]\left( {{{A}^{2}} + {{B}^{2}}} \right), \\ {{P}_{0}} = \left[ {\frac{{g\beta }}{{336{{h}^{2}}\nu }}(183{{h}^{8}} - 328{{h}^{6}}{{z}^{2}} + 224{{h}^{3}}{{z}^{5}} - } \right. \\ \left. { - \,\,84{{h}^{2}}{{z}^{6}} + 5{{z}^{8}}} \right) - \left. {\frac{\sigma }{{h\eta }}\left( {3{{h}^{5}} - 5{{h}^{3}}{{z}^{2}} + 2{{z}^{5}}} \right)} \right] \times \\ \times \,\,\frac{{g\beta \left( {{{A}^{2}} + {{B}^{2}}} \right)}}{{120\chi }} + S + \frac{{g\beta \left( {{{A}^{2}} + {{B}^{2}}} \right)}}{{24\chi {{c}_{p}}}}{{\left( {h - z} \right)}^{2}} \times \\ \times \,\,\left[ {\frac{{g\left( {7{{h}^{4}} + 14{{h}^{3}}z - 12{{h}^{2}}{{z}^{2}} + 2h{{z}^{3}} + {{z}^{4}}} \right)\beta \sigma }}{{30h\eta }} - } \right. \\ - \,\,\frac{{\left( {h + 2z} \right)\nu {{\sigma }^{2}}}}{{{{\eta }^{2}}}} - \frac{{{{g}^{2}}{{\beta }^{2}}}}{{15120{{h}^{2}}\nu }} \times \\ \times \,\,\left( {305{{h}^{7}} + 610{{h}^{6}}z - 1020{{h}^{5}}{{z}^{2}} + 710{{h}^{4}}{{z}^{3}} - 80{{h}^{3}}{{z}^{4}}} \right. - \\ \left. {\left. { - \,\,114{{h}^{2}}{{z}^{5}} + 20h{{z}^{6}} + 10{{z}^{7}}} \right)} \right]. \\ \end{gathered} $

Таким образом, если в полученном решении краевой задачи (10), (12) не учитывать слагаемые, образованные учетом диссипативной функции, то получим точное решение, описывающее стационарное конвективное течение Бенара–Марангони при распределении градиента температуры на одной из границ, которое изучалось в статье [9].

Исследуем полученное решение для функции ${{T}_{0}}$, учитывающее диссипативную функцию. Для этого приведем функцию ${{T}_{0}}$ к безразмерному виду с характерным масштабом температуры $Ah$ и скорости $\frac{{{{c}_{p}}A{{h}^{2}}}}{\nu }$. Введя новую нормированную переменную $Z = \frac{z}{h}$, запишем функцию ${{T}_{0}}$ в безразмерном виде:

$\begin{gathered} {{T}_{0}} = \left( {1 + {{a}^{2}}} \right)\frac{{Z\left( {Z - 1} \right)}}{{12}} \times \\ \times \,\,\left[ {\frac{{{\text{Gr}}\Pr }}{{420}}\left( {82 + 82Z + 82{{Z}^{2}} - 58{{Z}^{3}} + 5{{Z}^{4}} + 5{{Z}^{5}}} \right) - } \right. \\ \left. { - \,\,Mg\left( {1 + Z + {{Z}^{2}}} \right)} \right]{\text{ + }}\left( {1 + {{a}^{2}}} \right)\frac{{Z\left( {Z - 1} \right)}}{{4{\text{Pe}}}} \times \\ \times \,\,\left[ {{\text{GrMg}}\frac{{{\text{Pr}}}}{{{\text{30}}}}\left( {11 - 9Z + {{Z}^{2}} + {{Z}^{3}}} \right) - {\text{M}}{{{\text{g}}}^{2}} - \frac{{{\text{G}}{{{\text{r}}}^{2}}{{{\Pr }}^{2}}}}{{{\text{5040}}}}} \right. \times \\ \left. { \times \,\,\left( {215 - 345Z + 215{{Z}^{2}} + 5{{Z}^{3}} - 51{{Z}^{4}} + 5{{Z}^{5}} + 5{{Z}^{6}}} \right)} \right]. \\ \end{gathered} $

Здесь ${\text{Gr}} = \frac{{g\beta {{h}^{4}}A}}{{{{\nu }^{2}}}}$, $\Pr = \frac{\nu }{\chi }$, $Mg = \frac{{A\sigma {{h}^{2}}}}{{\eta \chi }}$, ${\text{Pe}} = \frac{{A{{h}^{3}}{{c}_{p}}}}{{\chi \nu }}$ ‒ безразмерные числа подобия Грасгофа, Прандтля, Марангони и Пекле соответственно, $a = \frac{A}{B}$.

По условию рассматриваемой краевой задачи функция ${{T}_{0}}$ принимает нулевые значения на нижней и верхней поверхности слоя жидкости, т.е. при $Z = 0$ и $Z = 1$. Таким образом, исследование функции ${{T}_{0}}$, являющейся полиномом, сводим к исследованию нулевых точек на интервале $Z \in \left( {0;1} \right)$. Представим функцию ${{T}_{0}}$ в следующем виде:

${{T}_{0}} = \left( {1 + {{a}^{2}}} \right)\frac{{Z\left( {Z - 1} \right)}}{4}\left[ {\frac{1}{3}{{f}_{1}}\left( Z \right) + \frac{1}{{{\text{Pe}}}}{{f}_{2}}\left( Z \right)} \right].$

Здесь функции ${{f}_{1}}\left( Z \right)$ и ${{f}_{2}}\left( Z \right)$ являются полиномами:

$\begin{gathered} {{f}_{1}}\left( Z \right) = \frac{{{\text{Gr}}\Pr }}{{420}}\left[ {82\left( {1 + Z + {{Z}^{2}}} \right) - 58{{Z}^{3}} + 5\left( {{{Z}^{4}} + {{Z}^{5}}} \right)} \right] - \\ - \,\,Mg\left( {1 + Z + {{Z}^{2}}} \right), \\ {{f}_{2}}\left( Z \right) = {\text{GrMg}}\frac{{{\text{Pr}}}}{{{\text{30}}}}\left( {11 - 9Z + {{Z}^{2}} + {{Z}^{3}}} \right) - {\text{M}}{{{\text{g}}}^{2}} - \frac{{{\text{G}}{{{\text{r}}}^{2}}{{{\Pr }}^{2}}}}{{{\text{5040}}}} \times \\ \times \,\,\left( {215 - 345Z + 215{{Z}^{2}} + 5{{Z}^{3}} - 51{{Z}^{4}} + 5{{Z}^{5}} + 5{{Z}^{6}}} \right). \\ \end{gathered} $

Функция ${{f}_{1}}$ на интервале $\left( {0;1} \right)$ монотонна и может иметь одну нулевую точку при выполнении условия:

$\frac{{11\Pr }}{{70}} < \frac{{{\text{Mg}}}}{{{\text{Gr}}}} < \frac{{41\Pr }}{{210}}.$

Более одной точки стратификации на этом интервале функция ${{f}_{1}}$ иметь не может. Функция ${{f}_{2}}$ не имеет нулевых точек на интервале $Z \in \left( {0;1} \right)$. Таким образом, возможен такой подбор чисел подобия, при котором функция ${{T}_{0}}$ принимает нулевое значение внутри интервала $\left( {0;1} \right)$ (рис. 1).

Рис. 1.

Профиль функции ${{T}_{0}}$ при следующих значениях чисел подобия и параметрах обезразмеривания: ${\text{Gr}} = 1.783 \times {{10}^{4}}$, $\Pr = 6.993$, ${\text{Mg}} = 2.3163 \times {{10}^{4}}$, ${\text{Pe}} = 2.925 \times {{10}^{{10}}}$, $a = - 0.5$.

КРАЕВАЯ ЗАДАЧА, ОПИСЫВАЮЩАЯ КОНВЕКТИВНОЕ ПОЛЗУЩЕЕ ТЕЧЕНИЕ

Рассмотрим пример конвективного стационарного плоского движения вязкой несжимаемой жидкости при отсутствии массовых сил и диссипативной энергии в приближении Стокса. В приближении уравнение теплопроводности также будем рассматривать линеаризованным. Определяющие соотношения (1)‒(3) в этом случае сводятся к виду:

(13)
$\begin{gathered} \nu \Delta {\mathbf{V}} = P - {\mathbf{g}}\beta T,\,\,\,\,\Delta T = 0, \\ \nabla \cdot {\mathbf{V}} = 0. \\ \end{gathered} $

Рассматриваем движение жидкости в бесконечном горизонтальном слое. Нижняя и верхняя поверхности слоя жидкости параллельны оси $Ox$. Течение жидкости характеризуется следующими гидродинамическими полями:

(14)
$\begin{gathered} {{V}_{x}} = {{U}_{0}} + {{U}_{1}}x + {{U}_{3}}\frac{{{{x}^{2}}}}{2},\,\,\,\,{{V}_{z}} = {{W}_{0}} + {{W}_{1}}x, \\ P = {{P}_{0}} + {{P}_{1}}x + {{P}_{3}}\frac{{{{x}^{2}}}}{2} + {{P}_{6}}\frac{{{{x}^{3}}}}{{3!}}, \\ T = {{T}_{0}} + {{T}_{1}}x + {{T}_{3}}\frac{{{{x}^{2}}}}{2} + {{T}_{6}}\frac{{{{x}^{3}}}}{{3!}}. \\ \end{gathered} $

Нумерация коэффициентов в полиномах, задающих решения сохранена от вида решений (4) для общего случая. При таком выборе вида решений, система определяющих соотношений (13) преображается к виду:

(15)
$\begin{gathered} \nu \left( {\frac{{{{\partial }^{2}}{{V}_{x}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{V}_{x}}}}{{\partial {{z}^{2}}}}} \right) = \frac{{\partial P}}{{\partial x}}, \\ \nu \left( {\frac{{{{\partial }^{2}}{{V}_{z}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{V}_{z}}}}{{\partial {{z}^{2}}}}} \right) = \frac{{\partial P}}{{\partial z}} - g\beta T, \\ \frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}} = 0,\,\,\,\,\frac{{\partial {{V}_{x}}}}{{\partial x}} + \frac{{\partial {{V}_{z}}}}{{\partial z}} = 0. \\ \end{gathered} $

Подставляем вид решений (14) в спроецированную систему уравнений (15) (частные производные по $z$ сразу обозначим штрихом), получаем систему уравнений, записанную в порядке интегрирования:

(16)

Граничные условия на поверхностях слоя жидкости $z \in \left[ {0;h} \right]$ задаем в виде:

(17)
$\begin{gathered} {{V}_{x}}\left( {0;x} \right) = {{V}_{z}}\left( {0;x} \right) = 0, \\ T\left( {0;x} \right) = {{\Theta }_{1}}x + {{\Theta }_{3}}\frac{{{{x}^{2}}}}{2} + {{\Theta }_{6}}\frac{{{{x}^{3}}}}{{3!}}, \\ {{V}_{x}}\left( {h;x} \right) = {{A}_{0}} + {{A}_{1}}x + {{A}_{2}}\frac{{{{x}^{2}}}}{2},\,\,\,\,{{V}_{z}}\left( {h\,;x} \right) = 0, \\ T\left( {h;x} \right) = 0,\,\,\,\,P\left( {h;x} \right) = {{S}_{0}} + {{S}_{1}}x + {{S}_{3}}\frac{{{{x}^{2}}}}{2} + {{S}_{6}}\frac{{{{x}^{3}}}}{{3!}}. \\ \end{gathered} $

Отметим, что слой жидкости ограничен непроницаемой плоскостью $z = 0$, а верхняя граница $z = h$ является проницаемой. С учетом принятого вида решения (14) граничные условия (17) можно записать в следующем виде:

(18)
$\begin{gathered} {{U}_{0}}\left( 0 \right) = {{U}_{1}}\left( 0 \right) = {{U}_{3}}\left( 0 \right) = 0,\,\,\,\,{{W}_{0}}\left( 0 \right) = {{W}_{1}}\left( 0 \right) = 0, \\ {{T}_{0}}\left( 0 \right) = 0,\,\,\,\,{{T}_{1}}\left( 0 \right) = {{\Theta }_{1}},\,\,\,\,{{T}_{3}}\left( 0 \right) = {{\Theta }_{3}},\,\,\,\,{{T}_{6}}\left( 0 \right) = {{\Theta }_{6}}, \\ {{U}_{0}}\left( h \right) = {{A}_{0}},\,\,\,\,{{U}_{1}}\left( h \right) = {{A}_{1}},\,\,\,\,{{U}_{3}}\left( h \right) = {{A}_{3}}, \\ {{T}_{0}}\left( h \right) = {{T}_{1}}\left( h \right) = {{T}_{3}}\left( h \right) = {{T}_{6}}\left( h \right) = 0, \\ {{P}_{0}}\left( h \right) = {{S}_{0}},\,\,\,\,{{P}_{1}}\left( h \right) = {{S}_{1}},\,\,\,\,{{P}_{3}}\left( h \right) = {{S}_{3}},\,\,\,\,{{P}_{6}}\left( h \right) = {{S}_{6}}. \\ \end{gathered} $

Частное точное решение краевой задачи (16), (18) с учетом принятого вида решений (14) для поля скоростей имеет следующий вид:

$\begin{gathered} {{U}_{0}} = \frac{{z{{A}_{0}}}}{h} - \frac{{z{{A}_{3}}}}{{6h}}\left( {{{h}^{2}} - 3hz + 2{{z}^{2}}} \right) - \frac{{\left( {h - z} \right)z{{S}_{1}}}}{{2\nu }} - \\ - \,\,\frac{{z{{S}_{6}}}}{{12\nu }}\left( {{{h}^{3}} - 2h{{z}^{2}} + {{z}^{3}}} \right) - \frac{{gz\beta {{\Theta }_{1}}}}{{24h\nu }} \times \\ \times \,\,\left( { - 3{{h}^{3}} + 6{{h}^{2}}z - 4h{{z}^{2}} + {{z}^{3}}} \right) + \frac{{gz\beta {{\Theta }_{6}}}}{{720h\nu }} \times \\ \times \,\,\left( {20{{h}^{5}} - 15{{h}^{4}}z - 30{{h}^{3}}{{z}^{2}} + 40{{h}^{2}}{{z}^{3}} - 18h{{z}^{4}} + 3{{z}^{5}}} \right), \\ \end{gathered} $
$\begin{gathered} {{U}_{1}} = \frac{{z{{A}_{1}}}}{h} - \frac{{\left( {h - z} \right)z{{S}_{3}}}}{{2\nu }} - \\ - \,\,\frac{{gz\beta {{\Theta }_{3}}}}{{24h\nu }}\left( { - 3{{h}^{3}} + 6{{h}^{2}}z - 4h{{z}^{2}} + {{z}^{3}}} \right), \\ \end{gathered} $
$\begin{gathered} {{U}_{3}} = \frac{{z{{A}_{3}}}}{h} - \frac{{\left( {h - z} \right)z{{S}_{6}}}}{{2\nu }} - \frac{{gz\beta {{\Theta }_{6}}}}{{24h\nu }} \times \\ \times \,\,\left( { - 3{{h}^{3}} + 6{{h}^{2}}z - 4h{{z}^{2}} + {{z}^{3}}} \right), \\ \end{gathered} $
$\begin{gathered} {{W}_{0}} = - \frac{{{{z}^{2}}{{A}_{1}}}}{{2h}} + \frac{{\left( {3h - 2z} \right){{z}^{2}}{{S}_{3}}}}{{12\nu }} + \\ + \frac{{g{{z}^{2}}\beta {{\Theta }_{3}}}}{{240h\nu }}\left( { - 15{{h}^{3}} + 20{{h}^{2}}z - 10h{{z}^{2}} + 2{{z}^{3}}} \right), \\ \end{gathered} $
$\begin{gathered} {{W}_{1}} = - \frac{{{{z}^{2}}{{A}_{3}}}}{{2h}} + \frac{{\left( {3h - 2z} \right){{z}^{2}}{{S}_{6}}}}{{12\nu }} + \\ + \,\,\frac{{g{{z}^{2}}\beta {{\Theta }_{6}}}}{{240h\nu }}\left( { - 15{{h}^{3}} + 20{{h}^{2}}z - 10h{{z}^{2}} + 2{{z}^{3}}} \right). \\ \end{gathered} $

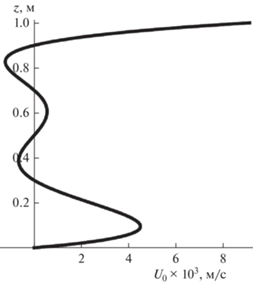
Исследование свойств компоненты скорости ${{U}_{0}}$ показало, что при определенном подборе начальных условий в слое жидкости возможно возникновение до четырех застойных точек. Профиль компоненты скорости ${{U}_{0}}$ в этом случае показан на рис. 2. Дальнейшее наложение остальных потоков для скорости ${{V}_{x}}$ приводит к сохранению числа нулевых значений скорости и к их уменьшению. Для всего потока жидкости, с учетом структуры выражений для скорости ${{V}_{x}}$, возможно существование двух нулевых значений удельной кинетической энергии.

Рис. 2.

Профиль функции ${{U}_{0}}$ при следующих значениях параметров граничных условий: $\beta = 1.82 \times {{10}^{{ - 4}}}$ 1/К, $\nu = {{10}^{{ - 6}}}$ м2/с, $h = 10$ м, ${{A}_{0}} = 0.0091$ м/с, ${{A}_{3}} = 4.4247$ 1/(м с), ${{S}_{1}} = 4.4414 \times {{10}^{{ - 6}}}$ м/с2, ${{S}_{6}} = - 9.0233 \times {{10}^{{ - 8}}}$ 1/(м с2), ${{\Theta }_{1}} = {{10}^{{ - 3}}}$ К/м, ${{\Theta }_{6}} = - 4.4853 \times {{10}^{{ - 7}}}$ К/м3.

ЗАКЛЮЧЕНИЕ

В статье предложен класс точных решений для системы уравнений Обербека‒Буссинеска. Поле скоростей нового класса решений является квадратичной формой относительно двух координат (горизонтальных) с коэффициентами, зависящими от третьей координаты (вертикальной) и времени. Показано, что для существования движения поля давления и температуры должны являться обобщенными многочленами четвертой степени относительно горизонтальных координат. Использование класса точных решений возможно при учете силовых полей со структурой аналогичной виду давления и температуры, включая тепловые источники и диссипацию энергии из-за тепловых превращений. Класс решений проиллюстрирован на двух примерах, показывающий влияние диссипации на структуру поля скоростей и на формирование противотечений в сильновязкой жидкости при неоднородном распределении скоростей на проницаемой границе слоя.

ОБОЗНАЧЕНИЯ

${{c}_{p}}$ теплоемкость жидкости, м2/(с2 К)
${\mathbf{g}} = \left( {0;0;g} \right)$ вектор ускорения свободного падения, м/с2
$h$ толщина слоя жидкости, м
$Ox$, $Oy$, $Oz$ оси декартовой системы координат
$P$ отклонение давления от гидростатического, отнесенное к постоянной средней плотности жидкости, м2/с2
${{P}_{0}}$, ${{P}_{1}}$, …, ${{P}_{{14}}}$ функции, определяющие структуру точного решения для давления $P$
$p$ модифицированное давление, м2/с2
$Q$ функция, определяющая тепловую (джоулевую) диссипацию, К/с
${\mathbf{r}} = \left( {x,y,z} \right)$ радиус-вектор, описывающий положение частицы жидкости, м
$T$ отклонение от средней температуры, К
${{U}_{0}}$, ${{U}_{1}}$, …, ${{U}_{5}}$ функции, определяющие структуру точного решения для скорости ${{V}_{x}}$
$\begin{gathered} {\mathbf{V}}\left( {t,x,y,z} \right) = \hfill \\ = \,\,\left( {{{V}_{x}},{{V}_{y}},{{V}_{z}}} \right) \hfill \\ \end{gathered} $ вектор скорости течения жидкости и его компоненты в декартовой системе координат, м/с
${{V}_{0}}$, ${{V}_{1}}$, …, ${{V}_{5}}$ функции, определяющие структуру точного решения для скорости ${{V}_{y}}$
${{W}_{0}}$, ${{W}_{1}}$, ${{W}_{2}}$ функции, определяющие структуру точного решения для скорости ${{V}_{z}}$
$\beta $ температурный коэффициент объемного расширения жидкости, 1/К
$\nu $ коэффициент кинематической вязкости жидкости, м2/с
$\chi $ коэффициент температуропроводности жидкости, м2/с
$\begin{gathered} {\mathbf{\Omega }}\left( {t,x,y,z} \right) = \hfill \\ = \,\,\left( {{{\Omega }_{x}},{{\Omega }_{y}},{{\Omega }_{z}}} \right) \hfill \\ \end{gathered} $ вектор, определяющий угловую скорость вращения жидкости и его компоненты в декартовой системе координат, 1/с
${{\Omega }_{1}}$, ${{\Omega }_{2}}$, ${{\Omega }_{3}}$, ${{\Omega }_{{10}}}$, ${{\Omega }_{{01}}}$, ${{\Omega }_{{20}}}$, ${{\Omega }_{{02}}}$, ${{\Omega }_{{30}}}$, ${{\Omega }_{{03}}}$ функции, определяющие структуру точного решения для угловой скорости вращения жидкости
${\text{Gr}}$ число Грасгофа
$Mg$ число Марангони
${\text{Pe}}$ число Пекле
$\Pr $ число Прандтля

ИНДЕКСЫ

$x$, $y$, $z$ координата, на ось которой записана проекция
$i$, $j$ номера компонентов

Список литературы

  1. Гершуни Г.З., Жуховицкий Е.М. Конвективная устойчивость несжимаемой жидкости. М.: Наука, 1972.

  2. Shtern V. Counterflows. Paradoxical Fluid Mechanics Phenomena. Cambridge: Cambridge University Press, 2012.

  3. Shtern V. Cellular Flows: Topological Metamorphoses in Fluid Mechanics. Cambridge: Cambridge University Press, 2018.

  4. Polyanin A.D., Kutepov A.M., Vyazmin A.V., Kazenin D.A. Hydrodynamics, Mass and Heat Transfer in Chemical Engineering. London: Taylor & Francis, 2002.

  5. Левич В.Г. Физико-химическая гидродинамика. М.: Гос. изд-во физико-мат. лит-ры, 1959.

  6. Shah R.K., London A.L. Laminar Flow Forced Convection in Ducts. Academic Press, 1978.

  7. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 6. Гидродинамика. 5-е изд. М.: Физматлит, 2006.

  8. Polyanin A.D., Zaitsev V.F. Handbook of Nonlinear Partial Differential Equations. Boca Raton: Chapman & Hall/CRC Press, 2012.

  9. Аристов С.Н., Просвиряков Е.Ю. О слоистых течениях плоской свободной конвекции // Нелинейная динамика. 2013. Т. 9. № 4. С. 651.

  10. Бурмашева Н.В., Просвиряков Е Ю. Термокапиллярная конвекция вертикально завихренной жидкости // Теорет. основы хим. технологии. 2020. Т. 54. № 1. С. 114

  11. Пухначёв В.В. Иерархия моделей в теории конвекции // Краевые задачи математической физики и смежные вопросы теории функций, Зап. научн. сем. ПОМИ. 2002. Т. 288. С. 152.

  12. Брацун Д.А., Вяткин В.А., Мухаматуллин А.Р. О точных нестационарных решениях уравнений вибрационной конвекции // Вычисл. мех. сплош. сред. 2017. Т. 10. № 4. С. 433.

  13. Аристов С.Н., Просвиряков Е.Ю., Спевак Л.Ф. Нестационарная слоистая тепловая и концентрационная конвекция Марангони вязкой несжимаемой жидкости // Вычисл. мех. сплош. сред. 2015. Т. 8. № 4. С. 445.

  14. Andreev V.K., Gaponenko Yu.A., Goncharova O.N., Pukhnachov V.V. Mathematical models of convection (De Gruyter Studies in Mathematical Physics). Berlin: De Gruyter, 2012.

  15. Goncharova O.N., Rezanova E.V. Example of an exact solution of the stationary problem of two-layer flows with evaporation at the interface // J. Appl. Mech. Tech. Phys. 2014. V. 55. № 2. P. 24. [Гончарова О.Н., Резанова Е.В. Пример точного решения стационарной задачи о двухслойных течениях с испарением на границе раздела // Прикл. мех. и теор. физ. 2014. № 2. С. 68.]

  16. Bekezhanova V.B., Goncharova O.N. Analysis of the exact solution for the evaporative convection problem and properties of the characteristic perturbations // International Journal of Thermal Sciences. 2018. V. 130. P. 323.

  17. Aristov S.N., Prosviryakov E.Y. A new class of exact solutions for three-dimensional thermal diffusion equations // Theor. Found. Chem. Eng. 2016. V. 50. № 3. P. 286. [Аристов С.Н., Просвиряков Е.Ю. Новый класс точных решений трехмерных уравнений термодиффузии // Теорет. основы хим. технологии. 2016.Т. 50. № 3. С. 294.]

  18. Андреев В.К. Решения Бириха уравнений конвекции и некоторые его обобщения. Препринт № 1‒10. Красноярск: ИВМ СО РАН, 2010.

  19. Рыжков И.И. Термодиффузия в смесях: уравнения, симметрии, решения и их устойчивость. Новосибирск : СО РАН, 2013.

  20. Ostroumov G.A. Free convection under the condition of the internal problem. NASA TM, 1958. [Остроумов Г.А. Свободная конвекция в условиях внутренней задачи. М.: Гос. изд_во техн._теорет. лит., 1952.]

  21. Birikh R.V. Thermocapillary convection in a horizontal layer, of liquid // J. Appl. Mech. Tech. Phys. 1966. № 7. P. 43. [Бирих Р.В. О термокапиллярной конвекции в горизонтальном слое жидкости // Прикл. мех. техн. физ. 1966. № 3. С. 69.]

  22. Ortiz-P’erez A.S., D’avalos-Orozco L.A. Convection in a horizontal fluid layer under an inclined temperature gradient // Phys. Fluids. 2011. V. 28. № 3. P. 084107.

  23. Smith M.K., Davis S.H. Instabilities of dynamic thermocapillary liquid layers. Pt. 1. Convective instabilities // J. Fluid Mech. 1983. V. 132. P. 119.

  24. Napolitano L.G. Plane Marangoni_Poiseuille flow of two immissible fluids // Acta Astronaut. 1980. V. 7. P. 461.

  25. Andreev V.K., Stepanova I.V. Unidirectional flows of binary mixtures within the framework of the Oberbeck–Boussinesq model // Fluid Dyn. 2016. V. 51. № 2. P. 136. [Андреев В.К., Степанова И.В. Однонаправленные течения бинарных смесей в модели Обербека‒Буссинеска // Известия Российской академии наук. Механика жидкости и газа. 2016. № 2. С. 13.]

  26. Андреев В.К., Бекежанова В.Б., Ефимова М.В., Рыжков И.И., Степанова И.В. Неклассические модели конвекции: точные решения и их устойчивость // Вычислительные технологии. 2009. Т. 14. № 6. С. 5.

  27. Betelin V.B., Galkin V.A., Dubovik A.O. On the control of layered flow of a viscous incompressible fluid within MHD // Doklady Mathematics. 2016. V. 94. № 2. P. 591. [Бетелин В.Б., Галкин В.А., Дубовик А.О. Об управляемом слоистом течении вязкой несжимаемой жидкости в модели магнитной гидродинамики // Докл. РАН. 2016. Т. 470. № 2. С. 150.]

  28. Aristov S.N., Prosviryakov E.Y., Spevak L.F. Unsteadystate Benard–Marangoni convection in layered viscous incompressible flows // Theor. Found. Chem. Eng. 2016. V. 50. № 2. P. 132.

  29. Privalova V. V., Prosviryakov E. Yu. The effect of tangential boundary stresses on the convective unidirectional flow of a viscous fluid layer under the lower boundary heating condition // Diagnostics, Resource and Mechanics of materials and structures. 2019. № 4. P. 44.

  30. Burmasheva N.V., Prosviryakov E.Yu. Unidirectional Thermocapillary Flows of a Viscous Incompressible Fluid with the Navier Boundary Condition // AIP Conference Proceedings. 2019. V. 2176. P. 030002.

  31. Burmasheva N.V., Prosviryakov E.Yu. Unidirectional Marangoni–Poiseuille Flows of a Viscous Incompressible Fluid with the Navier Boundary Condition // AIP Conference Proceedings. 2019. V. 2176. P. 030021.

  32. Aristov S.N., Prosviryakov E.Y. Nonuniform convective Couette flow // Fluid Dynamics. 2016. V. 51. № 5. P. 581. [Аристов С.Н., Просвиряков Е.Ю. Неоднородное конвективное течение Куэтта // Известия Российской академии наук. Механика жидкости и газа. 2016. № 5. С. 3.]

  33. Lin C.C. Note on a class of exact solutions in magnetohydrodynamics // Arch. Rational Mech. Anal. 1958. V. 1. P. 391.

  34. Sidorov A.F. Two classes of solutions of the fluid and gas mechanics equations and their connection to traveling wave theory // J. Appl. Mech. Tech. Phys. 1989. V. 30. № 2. P. 197. [Сидоров А.Ф. О двух классах решений уравнений механики жидкости и газа и их связи с теорией бегущих волн // Прикл. мех. и техн. физ. 1989. № 2. С. 34.]

  35. Аристов С.Н. Вихревые течения в тонких слоях жидкости. Автореф. … дис. докт. физ.-мат. наук. Владивосток, 1990.

  36. Prosviryakov E.Yu. New Class of Exact Solutions of Navier–Stokes Equations with Exponential Dependence of Velocity on Two Spatial Coordinates // Theor. Found. Chem. Eng. 2019. V. 53. № 1. P. 107. [Просвиряков Е.Ю. Новый класс точных решений уравнений Навье-Стокса со степенной зависимостью скоростей от двух пространственных координат // Теор. основы хим. технологии. 2019. Т. 53. № 1. С. 112.]

  37. Zubarev N.M., Prosviryakov E.Yu. Exact solutions for layered three-dimensional unsteady isobaric flows of a viscous incompressible fluid // Journal of Applied Mechanics and Technical Physics. 2019. V. 60. № 6. P. 1031. [Зубарев Н.М., Просвиряков Е.Ю. О точных решениях для слоистых трехмерных нестационарных изобарических течений вязкой несжимаемой жидкости // Прикл. мех. техн. физ. 2019. Т. 60. № 6 (358). С. 65.]

  38. Кутепов А.М., Полянин А.Д. и др. Химическая гидродинамика. М.: Бюро Квантум, 1996.

  39. Aristov S.N., Knyazev D.V., Polyanin A.D. Exact solutions of the Navier-Stokes equations with the linear dependence of velocity components on two space variables // Theor. Found. Chem. Eng. 2009. V. 43. № 5. P. 642. [Аристов С.Н., Князев Д.Е., Полянин А.Д. Точные решения уравнений Навье–Стокса с линейной зависимостью компонент скорости от двух пространственных переменных // Теорет. основы хим. технологии. 2009. Т. 43. № 5. С. 547.]

  40. Prosviryakov E. Yu. Dynamic equilibria of a nonisothermal fluid // Vestn. Samar. Gos. Tekhn. Univ., Ser. Fiz.-Mat. Nauki [J. Samara State Tech. Univ., Ser. Phys. Math. Sci.]. 2018. V. 22. № 4. P. 735.

  41. Privalova V. V., Prosviryakov E. Yu. Convective Couette-Type Flows Under Condition of Slip and Heating at the Lower Boundary // AIP Conference Proceedings. 2019. V. 2176. P. 030024.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал