Теоретические основы химической технологии, 2023, T. 57, № 2, стр. 166-176
Условие суспендирования для гладкостенного смесителя
И. В. Доманский a, b, *, А. И. Мильченко b, Ю. В. Саргаева b, С. А. Кубышкин b, Н. В. Воробьев-Десятовский b
a Санкт-Петербургский государственный технологический институт (технический университет)
Санкт-Петербург, Россия
b АО “ПОЛИМЕТАЛЛ ИНЖИНИРИНГ”
Санкт-Петербург, Россия
* E-mail: domanskij.iv@gmail.com
Поступила в редакцию 01.12.2020
После доработки 17.07.2021
Принята к публикации 22.07.2021
- EDN: SJAROU
- DOI: 10.31857/S0040357123010037
Аннотация
На основе известного допущения о преимущественном влиянии динамической скорости на отрыв частиц твердой фазы с днища, сформулировано условие суспендирования для гладкостенного смесителя. Подчеркнута важность опытного определения значения динамической скорости заданной промышленной суспензии. Показано, что при вычислении динамической скорости необходимо учитывать интенсивное тангенциальное течение перемешиваемой суспензии. Предложено уравнение для расчета минимальной частоты вращения мешалки, исключающей образование осадка на днище смесителя. Справедливость уравнения подтверждена экспериментально для смесителей лабораторного и промышленного масштабов при перемешивании систем Ж : Т.
ВВЕДЕНИЕ
Аппараты (смесители) с механическими перемешивающими устройствами (МПУ) для обработки систем Ж : Т относят к типовому и весьма распространенному виду технологического оборудования множества отраслей промышленности [1–9].
Чаще всего это смесители, которые оснащены соосными с емкостью типовыми МПУ и осевыми мешалками для создания циркуляции жидкости от привода (down-pumping) или к приводу (up-pumping). Корпусами таких аппаратов являются гладкостенные цилиндрические емкости (рис. 1а) или емкости с двумя или четырьмя радиальными отражательными перегородками (рис. 1б).
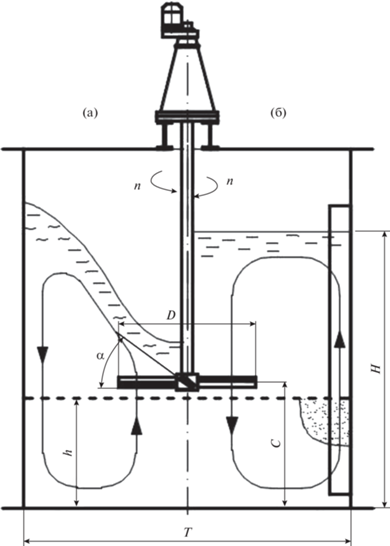
Рис. 1.
(а) Смеситель с типовым МПУ гладкостенный и с осевой мешалкой, обеспечивающей восходящий осевой закрученный поток суспензии; (б) Смеситель с типовым МПУ с отражательными перегородками и с осевой мешалкой, обеспечивающей нисходящий осевой закрученный поток суспензии.
В работах [10, 11] отмечается перспективность применения гладкостенных аппаратов с эксцентричным расположением вала мешалки и смесителей с планетарным МПУ различных модификаций.
К весьма перспективным гладкостенным аппаратам большого объема [12–14] относятся смесители с универсальным [15] восходящим потоком пульпы и прецессионным МПУ (ПМПУ, рис. 2), в котором крутящий момент от привода к мешалке передается посредством стандартной карданной муфты (шарнира Гука). При низкой частоте вращения шарнирный вал ПМПУ самоцентрируется [12] и смеситель эквивалентен аппарату с типовым МПУ (рис. 1а). С ростом же частоты, помимо вращательного движения вокруг собственной оси, шарнирный вал с мешалкой отклоняется от оси аппарата на угол Φ [13] и совершает дополнительное вращательное движение относительно оси корпуса смесителя (рис. 2) аналогично планетарным МПУ. Прецессионное механическое перемешивающее устройство не требует балансировки, а его вал нагружен лишь крутящим моментом и незначительной осевой силой. Такие ПМПУ отличаются относительно невысокой массой, простотой изготовления и обслуживания, а также надежностью при круглосуточной длительной эксплуатации в тяжелых климатических условиях [12–14].
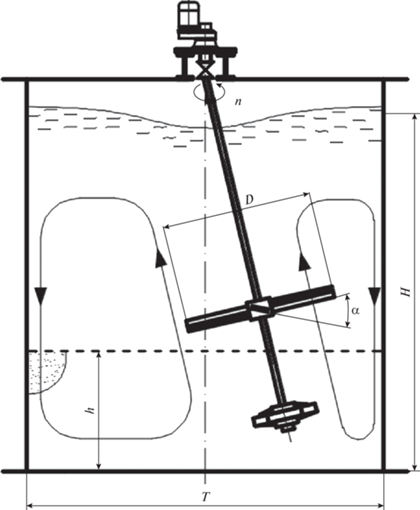
Рис. 2.
Гладкостенный смеситель с прецессионным МПУ осевой мешалки, обеспечивающей восходящий осевой закрученный поток пульпы.
Одним из основных условий эффективной работы смесителя при перемешивании суспензий является обеспечение практически полного взвешивания осадка твердой фазы с днища смесителя. В некоторых случаях эффективность проводимого в аппарате процесса зависит только от полноты взвешивания частиц твердой фазы [1–9]. Это, например, процесс извлечения целевого компонента из твердых частиц руды, в котором интенсивность массопереноса определяется диффузией в твердых частицах руды [16].
Основной задачей гидродинамического расчета таких смесителей является нахождение минимальной частоты вращения njs МПУ (частота суспендирования – impeller speed, when particles are “just suspended”), при которой происходит взвешивание всей загруженной твердой фазы. В настоящее время актуальность такой задачи существенно возросла в связи с необходимостью создания высокоэкономичных крупнотоннажных производств большой единичной мощности. Например, емкость реакторов, применяемых для выщелачивания золота, уже достигла 5000 м3 [17].
Знание важнейшего параметра процесса суспендирования njs позволяет обоснованно подойти к выбору типа смесителя для заданной конкретной суспензии.
Для нахождения njs при проектировании аппарата большого объема обычно применяется метод моделирования. В модельном аппарате, геометрически подобном проектируемому, проводится перемешивание суспензии, свойства которой близки промышленной, и опытным путем находится частота njs. Искомая же частота для промышленного смесителя njs вычисляется с помощью уравнения
Применение уравнения (1) для расчетов промышленных смесителей требует, кроме опытного определения частоты njs модельного аппарата, еще и проверенного практикой значения экспоненты x. К сожалению, эта характеристика смесителя, которая зависит от физических свойств компонентов суспензии и от коэффициента масштабирования T/TM, известна проектировщику в очень редких случаях.
Достаточно полное экспериментальное решение задачи расчета частоты суспендирования njs для аппарата с перегородками приведено в работе [18]. Предложенная в ней формула
(2)
${{n}_{{{\text{js}}}}} = S{{D}^{{ - 0.85}}}{{\left( {{{g\Delta \rho } \mathord{\left/ {\vphantom {{g\Delta \rho } {{{\rho }_{L}}}}} \right. \kern-0em} {{{\rho }_{L}}}}} \right)}^{{0.45}}}d_{{\text{p}}}^{{0.2}}{{X}^{{0.1}}}{{\nu }^{{0.1}}}$Механизм процесса суспендирования достаточно сложен. Даже для одиночной частицы сферической формы пока нет строгого теоретического решения. Лишь для частиц, диаметр которых меньше толщины ламинарного слоя можно рассчитать подъемную силу – силу Саффмана [21–23], величина которой определяется при наличии относительного движения фаз скоростью сдвига. Скорость сдвига определяет величину касательных напряжений τ0 и скорость диссипации энергии ε0 в пристенном слое жидкости. Для частиц, размер которых больше толщины ламинарного слоя, теоретическое решение отсутствует, но предлагаются упрощенные математические модели.
В работе [25] принято, что суспендирование частиц твердой фазы определяется величиной турбулентных пульсаций скоростей. Характеристикой величины турбулентных пульсаций является динамическая скорость ${{u}_{*}}$, величину которой для гладкостенных аппаратов большого объема предложено вычислять по формуле
в которой τ вычисляется при среднем значении окружной составляющей скорости в аппарате. На основе такого допущения предложена вероятностная модель суспендирования в гладкостенном смесителе, которая обеспечивает расчет интенсивности перемешивания, необходимой для предотвращения осаждения частиц на днище аппарата.В работах [27, 28] для аппаратов с перегородками предложено вычислять динамическую скорость по формуле Колмогорова [2, 28–30]
(4)
${{u}_{{*{\text{m}}}}} = {{\left( {\frac{{\nu {{\varepsilon }_{{\text{m}}}}}}{\rho }} \right)}^{{0.25}}},$В уравнении (4) принято
при известной величине коэффициента мощности NPВ результате теоретического анализа, представленного в [28], и обширного количества опытных данных, полученных для сосудов диаметром 0.30, 0.61, 1.0 м с отражательными перегородками и мешалками современных типов, предложено уравнение для расчета njs
(8)
$\begin{gathered} {{n}_{{{\text{js}}}}} = Z{{D}^{{ - 0.667}}}N_{{\text{P}}}^{{ - 0.33}}{{\left( {{{g{{\Delta \rho }}} \mathord{\left/ {\vphantom {{g{{\Delta \rho }}} {{{{{\rho }}}_{{\text{L}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{L}}}}}}} \right)}^{{0.5}}} \times \\ \times \,\,d_{{\text{p}}}^{{0.167}}X_{{\text{V}}}^{{0.154}}{{\left( {{C \mathord{\left/ {\vphantom {C D}} \right. \kern-0em} D}} \right)}^{{0.1}}}, \\ \end{gathered} $Уравнение (8) при приведении его к виду (1) позволяет найти x = 0.67, а это значит, что независимо от размеров смесителя необходимо обеспечивать εm = const.
Если в равенство (5) подставить формулу (4), то с учетом соотношений (6)–(8) нетрудно найти для аппарата с перегородками
(9)
$\begin{gathered} {{U}_{{{\text{js}}.{\text{m}}}}} = \\ = {{\left( {\frac{4}{\pi }\nu {{Z}^{3}}{{{\left( {{{g{{\Delta \rho }}} \mathord{\left/ {\vphantom {{g{{\Delta \rho }}} {{{{{\rho }}}_{{\text{L}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{L}}}}}}} \right)}}^{{1.5}}}d_{{\text{p}}}^{{0.5}}X_{{\text{V}}}^{{0.154}}{{{\left( {{C \mathord{\left/ {\vphantom {C D}} \right. \kern-0em} D}} \right)}}^{{0.1}}}\left( {{D \mathord{\left/ {\vphantom {D H}} \right. \kern-0em} H}} \right)} \right)}^{{0.25}}}. \\ \end{gathered} $Из уравнения (9) следует, что динамическая скорость Ujs.m зависит, в основном, от физических свойств компонентов пульпы и их объемной концентрации.
Необходимо отметить, что для смесителей с отражательными перегородками большого объема правило (5), которое с учетом (4) и (8) принимает вид εm = const, на практике не подтверждается.
С ростом объема смесителя обычно наблюдается значительное снижение удельной мощности, что доказывается опытом фирм изготовителей и практикой надежной эксплуатации аппаратов большого объема [6].
Так, согласно исследованиям [6], пилотный аппарат с объемом суспензии 50 л, предназначенный для изучения процесса выщелачивания и сорбции золота, потреблял 27 Вт при полной гомогенизации пульпы, то есть εm = 540 Вт/м3. Промышленный же аппарат объемом 2056 м3 потребляет всего лишь 37 кВт, то есть εm = P/V = 18 Вт/м3.
Таким образом, в настоящее время разработка методики расчета njs не завершена. Методика GMB [28] для смесителей с перегородками при εm = const не учитывает рост уровня турбулентности с ростом размера аппаратов. Методика, предложенная для гладкостенных аппаратов в [24–26], наоборот, не учитывает турбулентные пульсации, генерируемые мешалкой.
Отметим, что, если динамическая скорость – это единственный параметр, определяющий условие суспендирования заданной пульпы, то знание Ujs позволяет проектировать аппараты любого объема при создании в них требуемого уровня турбулентности.
Последующий анализ выполнен только для гладкостенных аппаратов с плоским днищем при условии, что динамическая скорость Ujs пульпы проектируемого смесителя предварительно найдена, например, экспериментально (см. ЭКСПЕРИМЕНТАЛЬНУЮ ЧАСТЬ).
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Для гладкостенного смесителя условие суспендирования частиц заданной твердой фазы, эквивалентный диаметр которых соизмерим или больше толщины ламинарного пристенного слоя, принимается зависящим от параметра Ujs. По аналогии с уравнением (5) далее принимается
Однако при вычислении динамической скорости ${{u}_{*}}$ следует учесть специфику рассматриваемых в статье гладкостенных смесителей, в которых наблюдается интенсивное вращательное течение пульпы.
Поскольку взвешиваемая частица находится на днище, то для вычисления динамической скорости ${{u}_{*}}$ далее используется аналогия процессов переноса импульса и теплоты в пристенном слое турбулентного потока.
В работе [31] показано, что интенсивность теплообмена между обечайкой лабораторного смесителя и перемешиваемой жидкостью характеризуется динамической скоростью в κ = 1.9–2.5 раза выше, чем вычислено по формуле (4)
(11)
${{u}_{{*1}}} = \kappa {{\left( {{{\nu {{\varepsilon }_{{\text{m}}}}} \mathord{\left/ {\vphantom {{\nu {{\varepsilon }_{{\text{m}}}}} \rho }} \right. \kern-0em} \rho }} \right)}^{{0.25}}},$При направленном течении пульпы вдоль стенки в турбулентном потоке также возникают пульсации скоростей, величина которых характеризуется динамической скоростью, вычисляемую по формуле (3). Эти пульсации приводит к дополнительной диссипации энергии в пристенном слое [32]
Аналогичный вариант суммарного воздействия двух источников турбулентности на интенсивность процессов переноса в пристенном слое успешно применен в исследовании теплообмена между стенкой вертикальной трубы и восходящим газожидкостным потоком [32]. В этом случае диссипация энергии в пристенном слое происходит за счет и относительного движения фаз и направленного течения газожидкостной смеси. Учет суммарного воздействия на теплообмен был выполнен путем сложения частных диссипаций. Такой подход позволил с достаточной точностью согласовать результаты экспериментальных и теоретических исследований [32].
Для вычисления диссипации энергии в пристенном слое гладкостенного смесителя пульпы далее применен аналогичный подход, позволивший получить
(14)
$\varepsilon = {{\varepsilon }_{1}} + {{\varepsilon }_{2}} = {{\kappa }^{4}}{{\varepsilon }_{{\text{m}}}} + \frac{{{{\tau }^{2}}}}{{\rho \nu }},$С учетом соотношений (11)–(14) условие суспендирования (10) можно представить в виде
Уравнение для расчета искомой частоты суспендирования njs нетрудно найти из условия (15), если выразить его слагаемые ${{u}_{{*1}}}$ и ${{u}_{{*2}}}$ через частоту njs и известные исходные данные:
физические свойства заданной промышленной пульпы (ρ, ν, φ) и динамическая скорость ее суспендирования Ujs;
основные размеры смесителя (T, H, D) и тип МПУ (коэффициент мощности NP).
Если в проектируемом аппарате предполагается применение такого МПУ, для которого неизвестен критерий мощности NP, то целесообразно провести измерения NP и Ujs на лабораторном аппарате, геометрически подобном проектируемому, при перемешивании заданной промышленной суспензии.
Введем в рассмотрение критерий удельной мощности процесса
С учетом формул (6), (7) и соотношения V = = 0.25πTе2H можно найти важную для расчетов связь
(17)
${{N}_{{\text{E}}}} = \frac{{4{{N}_{{\text{P}}}}\Gamma _{{\text{D}}}^{3}}}{{\pi {{\Gamma }_{{\text{H}}}}}}.$Комбинация параметров смесителя в виде правой части (17) часто встречается в дальнейшем и упрощает анализ получаемых результатов. Уравнение (11) [первое слагаемое уравнения (15)] с учетом (16) после подстановки в него n = njs нетрудно преобразовать к виду
(18)
${{u}_{{*1}}} = \kappa {{\left( {\nu {{N}_{{\text{E}}}}{{D}^{2}}n_{{{\text{js}}}}^{3}} \right)}^{{0.25}}}.$Аналогичную связь можно найти и для расчета составляющей ${{u}_{{*2}}}$. Для этого, прежде всего, необходимо установить зону наихудшего суспендирования на днище смесителя.
Как показывают наблюдения, в гладкостенном смесителе с плоским днищем даже небольшое снижение частоты вращения ниже частоты суспендирования njs, приводит к появлению осадка в периферийной зоне, где плоское днище сопрягается с обечайкой емкости (fillet). При этом первыми здесь выпадают в осадок самые крупные частицы. Можно принять, что касательное напряжение в этой части днища равно касательному напряжению τ0 на поверхности обечайки.
Далее приводятся соотношения, которые позволяют установить связь динамической скорости ${{u}_{{*2}}}$ с njs и исходными данными.
Крутящий момент M на валу мешалки [7] уравновешивается моментами сил трения на цилиндрической поверхности обечайки Мcyl и на поверхности днища Мbot. Момент, воспринимаемый обечайкой можно вычислить по уравнению [7]
где для типовых аппаратов со свободным уровнем пульпы(20)
${{\kappa }_{{{\text{cyl}}}}} = {{4{{\Gamma }_{{\text{H}}}}} \mathord{\left/ {\vphantom {{4{{\Gamma }_{{\text{H}}}}} {\left( {1 + 4{{\Gamma }_{{\text{H}}}}} \right)}}} \right. \kern-0em} {\left( {1 + 4{{\Gamma }_{{\text{H}}}}} \right)}},$(21)
${{\kappa }_{{{\text{cyl}}}}} = {{4{{\Gamma }_{{\text{H}}}}} \mathord{\left/ {\vphantom {{4{{\Gamma }_{{\text{H}}}}} {\left( {2 + 4{{\Gamma }_{{\text{H}}}}} \right)}}} \right. \kern-0em} {\left( {2 + 4{{\Gamma }_{{\text{H}}}}} \right)}}.$Усредненное по поверхности цилиндра значение касательного напряжения τ0 с учетом зависимости M = P/(2πn) и соотношения
можно рассчитать с учетом (7) по формуле(23)
${{{{\tau }}}_{0}} = \frac{{{{\kappa }_{{{\text{cyl}}}}}{{N}_{{\text{P}}}}\rho {{n}^{2}}{{D}^{5}}}}{{{{\pi }^{2}}{{T}^{2}}H}}.$Тогда уравнение (3) для расчета ${{u}_{{*2}}}$ с учетом (17) и при n = njs можно представить в следующей форме
(24)
${{u}_{{*2}}} = {{n}_{{{\text{js}}}}}D{{\left( {\frac{{{{\kappa }_{{{\text{cyl}}}}}{{N}_{{\text{E}}}}}}{{4\pi }}} \right)}^{{0.5}}}.$Условие суспендирования (15) после подстановки в него (18) и (24) и при n = njs можно представить в виде уравнения
(25)
${{\kappa }^{4}}{{N}_{{\text{E}}}}\eta _{{\text{D}}}^{{ - 1}}N_{{{\text{js}}}}^{3} + {{\left( {\frac{{{{\kappa }_{{{\text{cyl}}}}}}}{{4\pi }}} \right)}^{2}}N_{{\text{E}}}^{2}N_{{{\text{js}}}}^{4} = 1,$безразмерная частота суспендирования
безразмерный диаметр мешалкиПриближенное решение уравнения (25) относительно искомых Njs и njs для промышленного смесителя с погрешностью, не превышающей 1%, можно предложить в виде
(28)
${{N}_{{{\text{js}}}}} = {{\left( {{{{\left( {{{\kappa }^{4}}{{N}_{{\text{E}}}}\eta _{{\text{D}}}^{{ - 1}}} \right)}}^{{{8 \mathord{\left/ {\vphantom {8 7}} \right. \kern-0em} 7}}}} + {{{\left( {\frac{{{{\kappa }_{{{\text{cyl}}}}}{{N}_{{\text{E}}}}}}{{4\pi }}} \right)}}^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0em} 7}}}}} \right)}^{{{{ - 7} \mathord{\left/ {\vphantom {{ - 7} {24}}} \right. \kern-0em} {24}}}}}.$Уравнение (28) устанавливает в явном виде связь частоты njs и диаметра мешалки D и в полной мере замещает уравнение (1).
В качестве параметра, определяющего энергетическую составляющую эффективность смесителя, можно принять относительную удельную мощность
(29)
$\Psi = {{{{\varepsilon }_{{{\text{js}}.{\text{m}}}}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{{{\text{js}}.{\text{m}}}}}} {{{\varepsilon }_{{\text{m}}}}}}} \right. \kern-0em} {{{\varepsilon }_{{\text{m}}}}}},$Выражение для расчета Ψ с использованием исходных данных можно получить при решении системы уравнений (6), (7), (28), (29). После несложных преобразований с учетом (25)–(27) найдем искомую зависимость в виде
(31)
$\Psi = {{\left( {1 + {{{\left( {\frac{{{{\kappa }_{{{\text{cyl}}}}}}}{{4\pi }}} \right)}}^{3}}{{{\left( {\frac{{{{N}_{{\text{E}}}}\eta _{{\text{D}}}^{2}}}{{{{\kappa }^{8}}}}} \right)}}^{{{4 \mathord{\left/ {\vphantom {4 7}} \right. \kern-0em} 7}}}}} \right)}^{{{{ - 7} \mathord{\left/ {\vphantom {{ - 7} 8}} \right. \kern-0em} 8}}}}.$Итак, условие суспендирования (15) для гладкостенного аппарата позволило получить удобные для практического применения уравнения (28) и (31). Отметим, что Njs и Ψ зависят от двух безразмерных параметров: от параметра ηD, который согласно (27) определяется только исходными данными; от параметра NE, который согласно (17) зависит от выбора типа и размера мешалки. Уравнение (31) показывает, что с ростом NE уменьшается Ψ, то есть эффективность смесителя растет.
Достоверность уравнений (25), (28) и, соответственно, условия (15), необходимо подтвердить экспериментально.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Адекватность описания процесса суспендирования уравнениями (15), (28) можно подтвердить следующими тремя независимыми исследованиями.
В первую очередь необходимо заметить, что в диссертационной работе [33] приведены результаты обширного опытного исследования процесса перемешивания суспензий. Опыты, в том числе, проводились с различными типами осевых мешалок диаметром 160 мм в гладкостенном смесителе диаметром 0.39 м. Перемешивалась модельная суспензия: вода–стеклянные шарики при среднем диаметре частиц твердой фазы 120, 159 и 337 мкм и плотности 2500 кг/м3. Объемная доля твердой фазы принималась в диапазоне от 0.05 до 0.4. Клиренс в опытах составлял C = 0.33T; типы мешалок: A310, 45PBT4.
В работе [33] приведены значения njs и εm, которые позволяют по предложенным выше формулам (13), (14) с учетом (15) и (24) вычислить рассматриваемый здесь обобщенный параметр процесса суспендирования Ujs. На рис. 3 представлены частично результаты этих вычислений, которые подтверждают зависимость Ujs от диаметра частиц и объемной доли твердой фазы в пульпе, т.е. от заданных исходных свойств суспензии. Независимость же параметра Ujs от конструкции мешалки является здесь в определенной степени доказательством справедливости условия (10) или (15),
Рис. 3.
Зависимость Ujs от φ для гладкостенного смесителя с типовым МПУ при: 1 – dp = 159 мкм, мешалка 45РВТ4; 2 – dp = 159 мкм, мешалка А310; 3 – dp = = 337 мкм, мешалка 45РВТ4; 4 – dp = 337 мкм, мешалка А310.

Второй этап проверки условия (15) и уравнений (28) и (31) – собственные лабораторные испытания двух типов гладкостенных смесителей.
Экспериментальная установка состояла из трех стендов, отличающихся размером смесителей. Емкости смесителей представляли собою гладкостенные стеклянные сосуды с плоскими днищами. Для перемешивания суспензии применялись МПУ комбинированного типа, аналогичные применяемым в промышленных аппаратах гидрометаллургии благородных металлов, рис. 2. В работе проведены опыты как с типовым, так и с прецессирующим МПУ. Основная мешалка – стандартная трехлопастная с углом наклона лопастей к горизонту α = 24° [7, 8, 26] располагалась выше слоя осадка при клиренсе С = 0.4Т. Дополнительная мешалка – закрытая турбинная [7, 8] диаметром D = T/6 устанавливалась с клиренсом C = 0.1T и располагалась в осадке. Диаметры основных мешалок в опытах составляли: D = 0.1 и 0.11 м в смесителе с диаметром T = 0.29 м; D = 0.13 и 0.15 м при Т = 0.39 м; D = 0.18 и 0.20 м при Т = 0.52 м.
Перемешиваемая суспензия представляла собой смесь воды и твердой фазы в виде стеклянных шариков, средний диметр которых составлял 70 мкм, объемная доля частиц больше 110 мкм составляла 3%. Объемная доля твердой фазы в суспензии составляла φ = 0.093. Объемная доля частиц диаметром более 110 мкм составляла 2%. Плотность твердой фазы ρS = 2500 кг/м3. Плотность суспензии в опытах составляла ρ = 1140 кг/м3. Температура суспензии составляла 20 или 50°С, а кинематическая вязкость соответственно ν = 1 × × 10–6 м2/с и ν = 0.551 × 10–6 м2/с. Кинематическая вязкость суспензии вычислялась по формуле Эйнштейна
Значения ν составляли ν = 1.3 × 10–6 м2/с и ν = 0.71 × 10–6 м2/с, соответственно температуре пульпы.
Высота слоя суспензии в опытах Н = Т.
Измерение и методика обработки опытных данных. Для измерения крутящего момента на приводном валу применялась система “мотор–весы”. Привод устанавливался на подвижной платформе, ось вращения которой совмещена с осью смесителя. Натяжение нити, удерживающей платформу от вращения, измерялось с помощью электронных весов.
Частота вращения мешалки измерялась лазерным тахометром.
Измерение частоты вращения мешалки njs в момент взвешивания твердой фазы проводилось следующим образом.
Предварительно устанавливалась частота вращения мешалки n > njs, при которой происходило полное взвешивание твердой фазы. Далее с шагом 15 об/мин частота ступенчато уменьшалась и выдерживалась 5 мин с целью стабилизации поверхности образующегося осадка. По окончании выдержки фиксировались частота вращения, крутящий момент привода мешалки и высота слоя осадка около обечайки (fillet), рис. 1.
Опыт продолжался до момента, когда измеряемая высота осадка достигала отметки 0.1h0 (h0 – высота слоя осадка при n = 0). Поскольку сечение осадка в радиальном направлении имеет вид прямоугольного треугольника с основанием около 4h, то уровень 0.1h0 примерно соответствует взвешиванию 98% твердой фазы. При этом взвешиваются лишь те частицы, размер которых меньше 110 мкм.
Отметим, что уровень осадка вблизи обечайки по ее периметру носит волнообразный характер, но фиксировалось лишь среднее значение высоты.
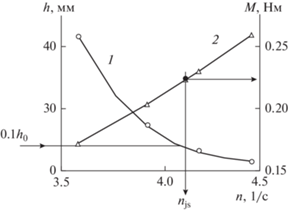
Пример обработки опытных данных приведен на рис. 4. Сначала методом интерполяции при h = = 0.1h0 находится njs. Далее, на основе опытной зависимости M(n) снова интерполяцией находился Mjs.
Минимальное значение мощности, достаточной для взвешивания частиц твердой фазы dp < 110 мкм, определяли по формуле Pjs = 2πMjsnjs, что позволяло вычислить NE по (17) и основные искомые величины ${{u}_{{*1}}}$ – по (18), ${{u}_{{*2}}}$ – по (24), Ujs – по (15). Поскольку величина ${{u}_{{*1}}}$ вычислена при n = njs, то для нахождения Ψ справедливо выражение
Результаты обработки опытных данных приведены на рис. 5.
Рис. 5.
Экспериментальная зависимость Ujs от NE при: 1 – температура суспензии 18°С, смеситель с типовым МПУ; 2 – температура суспензии 18°С, смеситель с прецессионным МПУ; 3 – температура суспензии 50°С, смеситель с типовым МПУ; 4 – температура суспензии 50°С, смеситель с прецессионным МПУ.
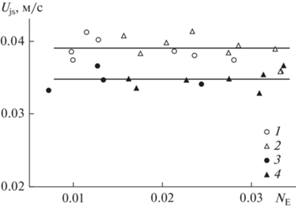
Данные, представленные на рис. 5, показывают, что все переменные параметры гладкостенных смесителей (T, D, NP) и характер движения мешалки (типовое МПУ или ПМПУ) не влияют на величину Ujs. Расслоение опытных точек связано лишь с изменением вязкости суспензии. Это подтверждает допустимость применения для описания процесса суспендирования условия (15).
В результате обработки опытных данных получено подтверждение, что величина Ψ зависит от NE и от ηD. Рост каждого из них приводит к снижению удельных затрат мощности. Отметим, что при одинаковых конструкциях мешалок смесители с ПМПУ энергоэкономнее, чем типовые, так как при более высоком NP обладают пониженной NJS. Однако это влияние в условиях проведенных лабораторных исследований укладывается в диапазон Ψ = 0.69–0.92. Более существенное снижение Ψ возможно лишь за счет роста ηD, то есть, соответственно, за счет увеличения размера смесителя.
Поэтому дополнительно к первым двум проверкам предлагаемого условия суспендирования (15) далее рассматриваются еще и третья–результаты масштабных промышленных испытаний гладкостенных смесителей.
Гладкостенный смеситель с ПМПУ. Собственный опыт проектирования и надежной эксплуатации таких нестандартных смесителей предлагается рассмотреть на примере анализа результатов проектирования и эксплуатации смесителя известнякового молока. Этот аппарат с объемом V = 238 м3 применяется для нейтрализации известняком серной кислоты, образующейся при автоклавном окислении пиритно-арсенопиритных золотосодержащих концентратов [12–14].
Поскольку в смесителе применяется комбинированное ПМПУ (рис. 2), для которого неизвестен критерий мощности, то для нахождения динамической скорости Ujs и критерия NP применялся смеситель, геометрически подобный проектируемому аппарату.
Свойства производственной суспензии и ее компонентов: ρL = 1000 кг/м3, ρS = 2710 кг/м3, φ = 0.165, ρ = 1283 кг/м3, ν = 1.57 × 10–6 м2/с, dp.m = 110 мкм, dp.max = 250 мкм.
Модельный аппарат. Размеры модельного смесителя: T = 0.3 м, D = 0.10 м, H = 0.3 м, (V = 0.021 м3). В отличие от выше описанной методики в данном опыте при нахождении njs не допускалось образование осадка. Результаты измерений: njs= 8.37 с–1, Pjs.M= 1.96 Вт.
Результаты расчетов по (7), (6), (32), (18), (24), (15) главных параметров: NP = 0.26, εm.М = 141 Вт/м3, ν = 1.57 × 10–6 м2/c, ${{u}_{{*1}}}$ = 0.046 м/с, ${{u}_{{*2}}}$ = 0.023 м/с, Ujs = 0.047 м/с. Дополнительно вычислено по (33) ΨM = 0.92.
Промышленный аппарат. Размеры смесителя: T = 7.0 м, D = 2.24 м, H = 6.2 м, (V = 238 м3). Принято, с учетом результатов модельных испытаний, NP = 0.26, Ujs = 0.047 м/с. По (26) с учетом (28) найдены njs = 41.2 мин–1, по (33) – Ψ = 0.22. В проекте было принято n = 49 мин–1 = 0.817 с–1, то есть n > njs, что на практике с запасом обеспечивало суспендирование известняка. Вычисления по (7), (18), (24), (15) позволяют найти: P = = 10е260 Вт, ${{u}_{{*1}}}$ = 0.038 м/с, ${{u}_{{*2}}}$ = 0.05 м/с, ${{u}_{*}}$ = = 0.053 м/с. Рост доли ${{u}_{{*2}}}$ в формирование Ujs по сравнению с модельным аппаратом и привел к снижению удельных затрат мощности Ψ.
Следует добавить, что смеситель укомплектован стандартной карданной муфтой ВК60 [34], цилиндрическим мотор-редуктором (частота вращения 49 мин–1, мощность 15 кВт [35]) и находится в круглогодичной надежной эксплуатации более 10 лет.
Аналогичные результаты достигнуты и при проектировании многих других прецессионных смесителей диаметром 5–12 м емкостью до 1250 м3 для решения иных производственных задач гидрометаллургии золота [12–14, 16].
Гладкостенный смеситель с типовым МПУ. Особенности расчета такого стандартного смесителя рассмотрены далее с использованием результатов промышленных испытаний, которые приведены в работе [36].
В аппарате изучался процесс гомогенизации водной суспензии магнетита и диоксида кремния, которая применяется в производстве железорудных окатышей. Поскольку обязательным условием гомогенизации является выполнение условия полного суспендирования, то далее приводится численная проверка применимости предложенного уравнения (28) для решения указанной в [36] задачи.
Модельный аппарат. Расчет динамической скорости суспендирования Ujs выполнен на основе испытаний модельного гладкостенного смесителя [36].
Размеры модельного смесителя: T = 1 м, D = 0.27 м, H = 0.78 м, (V = 0.61 м3).
Свойства модельной суспензии и ее компонентов: ρL = 1000 кг/м3, ρS.mag = 5000 кг/м3, ρS.sil = 2600 кг/м3, φ = 0.32 (содержание диоксида φsil = 0.016), ρ = = 2280 кг/м3, ν = 2.62 × 10–6 м2/с.
Результаты измерений при перемешивании гомогенной пульпы: njs.M= 4.25 с–1, Pjs.M= 61 Вт.
Результаты расчетов по (7), (6), (11) и (24) главных параметров модели: NP.M = 0.243, εm,М = 100 Вт/м3, ${{u}_{{*1}}}$ = 0.046 м/с, ${{u}_{{*2}}}$ = 0.025 м/с, ${{u}_{*}}$ = 0.047 м/с, ReM = 1.18 × 105. Дополнительно вычислено по (33) ΨМ = 0.91.
Промышленный аппарат. Свойства промышленной суспензии и ее компонентов незначительно отличаются от свойств модельной: ρL = 1000 кг/м3, ρS.mag = 5100 кг/м3, ρS.sil = 2600 кг/м3, φ = 0.32, ρ = = 2312 кг/м3, ν = 2.62 × 10–6 м2/с.
Размеры промышленного гладкостенного смесителя: T = 18.3 м, D = 5.9 м, H = 14.2 м, V = 3730 м3. При проведении испытаний на производстве [36] заданное высокое качество пульпы был получено при частоте njs= 0.313 с–1, при этом критерий Рейнольдса составил Re = 4.18 × 106.
Зависимость коэффициента мощности от числа Re и ГD для гладкостенных аппаратов с типовым МПУ при турбулентном режиме имеет вид [7]
где при высоких числах Re a = 0.08, b ~ 1.Согласно равенству (34) и с учетом NP.M = 0.243 нетрудно найти критерий мощности промышленного смесителя: NP.P = 0.153. Далее с учетом результатов модельных испытаний принято Ujs = = 0.047 м/с. По формуле (28) с учетом (26) найдено njs = 0.326 c–1, по (33) – Ψ = 0.22. По итогам испытаний рекомендовано принять n = 0.313 c–1, т.е. n ~ njs.
С учетом неполной идентичности модели и промышленного аппарата можно признать итоговый результат вполне удовлетворительным для предлагаемого метода расчета гладкостенных смесителей и с типовым МПУ.
Вычисления по (7) (18), (24), (15) позволяют найти: Pjs.P = 91.2 кВт, что значительно меньше установленной мощности имеющегося привода PP = 146 кВт; ${{u}_{{*1}}}$ = 0.0324 м/с, ${{u}_{{*2}}}$ = 0.0394 м/с, ${{u}_{*}}$ = 0.043 м/с. При этом εm = 24.4 Вт/м3, что в 4 раза меньше, чем для пилотной установки. Это связано с ростом доли ${{u}_{{*2}}}$ в формировании Ujs.
Таким образом, рассмотренные выше три проверки адекватности полученных уравнений (15), (25), (28), (31) реальным условиям процессов суспендирования в лабораторных и промышленных гладкостенных смесителях можно признать удовлетворительными.
Вместе с этим, приведенные два численных примера помогают оправдать повышенный интерес современных исследователей к углубленному изучению и применению в ряде отраслей промышленности перспективных гладкостенных смесителей с закрученным осевым потоком [7, 10, 11, 20, 36–39, 41].
ЗАКЛЮЧЕНИЕ
Сформулировано новое условие суспендирования (15), в котором динамическая скорость Ujs для гладкостенных смесителей учитывает влияние окружного течения перемешиваемой пульпы. На этой основе получено уравнение (28) для расчета частоты вращения мешалки (njs), достаточной для полного взвешивания заданной твердой фазы, а также уравнение (31) для оценки эффективности проектируемого смесителя. Анализ лабораторных опытных данных и условий суспендирования для двух действующих промышленных смесителей с рабочим объемом 238 и 3730 м3 различного исполнения и назначения подтвердил справедливость предложенных расчетных уравнений при эмпирическом коэффициенте пропорциональности κ = 2.5 в уравнении (11).
ОБОЗНАЧЕНИЯ
| a, b | показатели степени в уравнении (34) |
| C | клиренс, м |
| D | диаметр мешалки, м |
| dp | диаметр частицы, м |
| g | ускорение свободного падения, м/с2 |
| H | высота уровня пульпы, м |
| h | высота слоя осадка, м |
| M | крутящий момент, Н м |
| N | частота вращения привода, 1/с |
| P | мощность перемешивания, Вт |
| S | безразмерный параметр в уравнении (2) |
| T | диаметр емкости смесителя, м |
| U | динамическая скорость, м/с |
| ${{u}_{*}}$ | динамическая скорость, м/с |
| V | рабочий объем емкости смесителя, м3 |
| X | концентрация твердых частиц, кг ТЧ/кг ЖФ |
| X | показатель степени в уравнении (1) |
| Z | безразмерный параметр в уравнении (8) |
| α | угол наклона лопасти, ° |
| Δρ | разность плотности твердой и жидкой фазы, кг/м3 |
| ε | диссипация энергии, Вт/м3 |
| ηD | безразмерный диаметр мешалки |
| κ | коэффициент |
| ν | коэффициент кинематической вязкости, м2/с |
| ρ | плотность, кг/м3 |
| τ | касательное напряжение, Па |
| φ | объемная доля твердой фазы, об. % |
| Ψ | относительная удельная мощность |
| NE | критерий удельной мощности процесса |
| Njs | безразмерная частота суспендирования |
| NP | критерий мощности |
| Re | критерий Рейнольдса |
| ГD, ГH | геометрический симплекс |
ИНДЕКСЫ
Список литературы
Kraume M. Die Entwicklung der Ruhrtechnik von einer empirischen Kunst zur Wissenschaft // Chem. Ing. Techn. 2014. V. 86. № 12. P. 2051.
Nienow A.W. Stirring and stirred-tank reactors // Chem. Ing. Techn. 2014. V. 86. №12. P. 2063.
Atiemo-Obeng V.A., Penney V.R., Armenante P. Solid-Liquid Mixing // Handbook of industrial mixing: Science and Practice. Hoboken: Wiley–Interscience, 2004. P. 543.
Brown D.A.R., Etchells III A.W., Grenville R.K., Myers K.J., Gul N., Ozcan-Taskin, Atiemo-Obeng V.A., Armenante P.H., Penney W.R. Solid–Liquid Mixing // Advances in Industrial Mixing: A companion to the Handbook of Industrial Mixing. New Jersey: Wiley, 2016. P. 357.
Kraume M. Mischen und Ruhren. Grundlagen und modern Verfahren. Weinheim: Willey, VCH, 2003.
Beck H., Himmelsbach W. Handbuch der Rührtechnik: Grundlagen, Auswahlkriterien, Anwendung. Schopfheim: Ekato, 1990.
Брагинский Л.Н., Бегачев В.И., Барабаш В.М. Перемешивание в жидких средах. Физические основы и инженерные методы расчета. Л.: Химия, 1984.
Strek F. Michani a michaci zarizeni. Praha: SNTL, 1977.
Mishra P., Ein-Mozaffari F. Critical review of different aspects of liquid-solid mixing operations // Reviews in Chemical Engineering. 2020. V. 36. № 5. P. 555.
Cudak M., Domanski M., Szoplik J., Karcz J. An effect of the impeller eccentricity on the process characteristics in an agitated vessel – experimental and numerical modeling // Theor. Found. Chem. Eng. 2016. V. 50. № 6. P. 922.
Delaplace G., Bouvier L., Moreau A., Andre Ch. An arrangement of ideal reactors as a way to model homogenizing processes with a planetary mixer // AIChE J. 2011. V. 57. № 7. P. 1678.
Domanskii I.V., Mil’chenko A.I., Vorob’ev-Desyatovskii N.V. Large size agitators witch precession impeller for ore slurries – Study, design, tests // Chem. Eng. Sci. 2011. V. 66. P. 2277.
Mil’chenko A.I., Domanskii I.V., Vorob’ev-Desyatovskii N.V., Kubyshkin S.A. Design of Precession Impellers for Ore Pulp Agitation in Large-volume Agitators // Proc. 15th European Conferences on Mixing. Sankt-Petersburg, 2015. P. 234.
Domanskii I.V., Mil’chenko A.I., Sargaeva Y.V., Kubyshkin S.A., Vorob’ev-Desyatovskii N.V. Experience in design and robust operation of precession agitators of ore pulp for large-volume vessels // Theor. Found. Chem. Eng. 2017. V. 51. № 6. P. 1030.
Nienow A.W., Bujalski W. The versatility of up-pumping hydrofoil agitators // Chem. Eng. Res. Des. 2004. V. 82. № A9. P. 1073.
Вольдман Г.М., Зеликман А.Н. Теория гидрометаллургических процессов. М.: Интермет Инжиниринг, 2003.
Latva-Kokko M., Hirsi T., Ritasalo T., Tiihonen J. Improving the process performance of gold cyanide leaching reactors // The Southern African Institute of Mining and Metallurgy. World Gold Conference 2015.
Zwietering T.N. Suspension of solids in liquid by agitators // Chem. Eng. Sci. 1958. V. 8. P. 244.
Oldshue J.Y. Fluid mixing technology. N.Y.: Mc Graw-Hill, 1983.
Tamburini A., Cipollina A., Micale G., Scargiali F., Brucato A. Particle suspension in vortexing unbaffled stirred tanks // Ind. Eng. Chem. Res. 2016. V. 55. P. 7535.
Cleaver J.W., Yates B. Mechanism of detachment of colloidal particles from a flat substrate in turbulent flow // J. Colloid Interface Sci. 1973. V. 44. P. 464.
Boothroyd R.G. Flowing Gas–Solids Suspensions // Lecturer in Mechanical Engineering University of Birmingam. England, London, 1971. [Бусройд Р. Течение газа со взвешенными частицами. М.: Мир, 1975.]
Saffman P.G. The lift on a small sphere in a slow shear flow // J. Fluid. Mech. 1965. V. 22. P. 385.
Барабаш В.М., Брагинский Л.Н., Козлова Е.Г. Применение аппаратов с перемешивающими устройствами для перемешивания высококонцентрированных суспензий // Теорет. основы хим. технологии. 1990. Т. 24. №. 1. С. 63.
Барабаш В.М., Зеленский В.Е. Перемешивание суспензий // Теорет. основы хим. технологии. 1997. Т. 31. № 5. С. 465.
РД 26–01–90–85. Механические перемешивающие устройства. Метод расчета. Л.: ЛенНИИХИММАШ, 1987.
Baldi G., Conti R., Alaria E. Complete suspension of particles in mechanically agitated vessels // Chem. Eng. Sci. 1978. V. 33. P. 21.
Grenville R.K., Mak A.T.C., Brown D.A.R. Suspension of solid particles in vessels agitated by axial flow impellers // Chem. Eng. Res. Des. 2015. V. 100. P. 282.
Колмогоров А.Н. Локальная структура турбулентности в несжимаемой вязкой жидкости при очень больших числах Рейнольдса // Докл. АН СССР. Т. ХХХ. № 4. 1941. С. 299.
Calabrese R.V., Kresta S.M., Liu M. Recognizing the 21 Most influential contributions to mixing research // Chem. Eng. Prog. 2014. V. 110. № 1. P. 20.
Доманский И.В., Соколов В.Н. Обобщение различных случаев конвективного теплообмена с помощью полуэмпирической теории турбулентного теплообмена // Теорет. основы хим. технологии. 1968. Т. 2. С. 761.
Доманский И.В., Тишин В.Б., Соколов В.Н. Теплообмен при движении газо-жидкостных смесей в вертикальных трубах // Журн. прикл. химии. 1969. Т. 17. С. 851.
Wang S. Suspension of High Concentration Slurry in Agitated Vessels. A Thesis Submitted for the Degree of Master of Engineering. Melbourne: RMIT University, 2010.
ГОСТ 28300–2010. Валы карданные тягового привода тепловозов и дизель поездов. Общие технические условия. М.: Стандартинформ, 2011.
Getriebebau Nord 2004/G1000-4/2004. Hamburg, 2004
Wu J., Wang S., Nguen B., Daniel M., Ola E. Improved mixing in a magnetite iron ore tank via swirl flow: lab-scale and full-scale studies // Chem. Eng. Technol. 2016. V. 39. № 3. P. 505.
Wu B.J., Wang S., Nguen B., Connor T., Daniel M., Ola E. Gain improved tank slurry agitation via swirl flow technology // Eng. and Mining J. Apr.2016.
Assirelli M., Bujalski W., Eaglesham A., Nienow A.W. Macro- and micromixing studies in an unbaffled vessel agitated by a Rushton turbine // Chem. Eng. Sci. 2008. V. 63. P. 35.
Yoshida M., Shimada N., Kanno R., Matsuura S., Otake Y. Liquid flow and mixing in bottom regions of baffled and unbaffled vessels agitated by turbine-tipe impeller // Intern. J. Chem. Reactor Eng. 2014. V. 12. № 1. P. 629.
Лаптева Е.А., Фарахов Т.М. Математические модели и расчет тепломассообменных характеристик аппаратов. Казань: Отечество, 2013.
Stoian D. Enhancing energy efficiency and mass transfer in solid–liquid systems using mechanical mixing and cavitation. A Thesis Submitted in Fulfilment of the Requirements for the Degree of Doctor of Philosophy. RMIT University, 2017.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии