Теоретические основы химической технологии, 2023, T. 57, № 4, стр. 412-418
Цифровые двойники пористых структур аэрогелей с использованием клеточно-автоматного подхода и кривых Безье
И. В. Лебедев a, *, С. И. Иванов a, Р. Р. Сафаров a, Н. В. Меньшутина a
a Российский химико-технологический университет имени Д.И. Менделеева
Москва, Россия
* E-mail: chemcom@muctr.ru
Поступила в редакцию 31.05.2023
После доработки 05.06.2023
Принята к публикации 06.06.2023
- EDN: VIZFKX
- DOI: 10.31857/S004035712304005X
Аннотация
В статье предложена клеточно-автоматная модель на основе кривых Безье для создания цифровых двойников пористых наноструктур различной природы, разработанная с использованием клеточно-автоматного подхода. Проведены вычислительные эксперименты по созданию цифровых двойников полученных экспериментальных образцов аэрогелей на основе хитозана. Проведено сравнение структурных характеристик цифровых копий и экспериментальных образцов, на основе которых были сделаны выводы о корректной работе модели. Полученные цифровые двойники могут быть использованы для прогнозирования свойств пористых волокнистых материалов, в частности, аэрогелей на основе хитозана, что позволит частично заменить натурные эксперименты вычислительными и, следовательно, снизить затраты при разработке новых материалов с заданными свойствами.
ВВЕДЕНИЕ
В настоящее время современные методы математического и компьютерного моделирования получили широкое распространение в различных отраслях науки и промышленности, в частности, в химической технологии. Они позволяют с достаточной точностью прогнозировать ход и результаты различных процессов, тем самым уменьшая необходимое количество натурных экспериментов при проведении исследований, что в свою очередь существенно снижает затраты времени и ресурсов.
Сегодня используется множество подходов и методов моделирования, которые существенно различаются между собой по уровню (нано-, микро-, макро-) и масштабу задачи, допущениям, точности и быстроте расчетов. Одним из универсальных и простых в реализации подходов к моделированию является моделирование с использованием клеточных автоматов.
Клеточные автоматы (КА) – один из современных подходов к моделированию сложных гомогенных и гетерогенных динамических систем, который позволяет оптимизировать вычислительные процедуры и использовать технологии параллельных вычислений. КА могут отражать саму суть динамики различных систем и давать глубокое понимание сложных процессов, таких как многофазные потоки, химические реакции, биологические процессы в клетках, образование и размещение белков, активность нейронов, высвобождение активных фармацевтических ингредиентов, создание фармацевтических рецептур, социальной стратификации, музыкальных сочинений и многое другое.
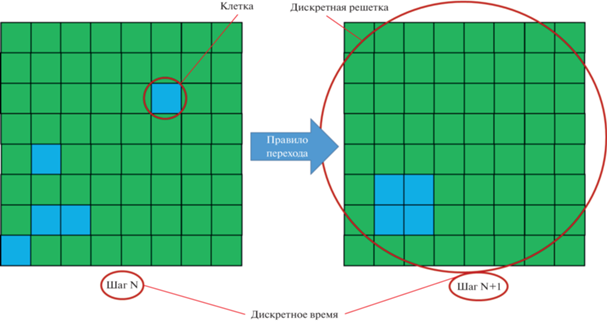
Клеточный автомат – дискретная модель, представляющая собой решетку произвольной размерности, каждая клетка которой в каждый момент времени может принимать одно из конечного множества состояний, и определено правило перехода клеток из одного состояния в другое.
Клеточные автоматы могут применяться для задач химической технологии: моделирования структуры и свойств материалов, химических реакций, процессов в аппаратах, логистики производства.
Процессы химической технологии, которые активно моделируются с помощью клеточных автоматов приведены в таблице 1.
Таблица 1.
Существующие применения КА в химической технологии
| № | Применение | Комментарии |
|---|---|---|
| 1 | Диффузия (массоперенос) [1] | Диффузия “газ в газе”, “газ в твердом”, “газ в жидкости”, “жидкость в жидкости” |
| 2 | Кристаллизация и вторичная кристаллизация [2] | В сочетании с диффузионными и теплообменными процессами кристаллизации и вторичной кристаллизацией неорганических материалов, полимеров, металлов |
| 3 | Растворение и эрозия [3] | Процессы растворения, вторичная кристаллизация, растворение лекарств, гранул, имплантов, эрозия полимеров. |
| 4 | Коррозия [4] | Процессы коррозии, коррозия в гальванических элементах, аккумуляторах, очистка воды с помощью электрофлотации |
| 5 | Адсорбция [5] | Процессы адсорбции, разделения, хроматографии, очистки газов, сверхкритических процессов для получения функциональных материалов |
| 6 | Гидратация [6, 7] | Процесс гидратации цемента |
| 7 | Химические реакции [8] | Каталитические реакции, реакционно-диффузионные процессы |
Клеточные автоматы все чаще используются для решения сложных мультимасштабных задач. В основном это связано с ростом доступных вычислительных мощностей и развитием технологий высокопроизводительных параллельных вычислений.
Среди причин для разработки подходов и моделей КА, можно выделить следующие четыре основных:
• Возможность использования КА в мультимасштабном моделировании (нано-, микро- и макромасштабах) имеет большое значение. В связи с этим КА-модели используются для описания химико-технологических процессов, структур материалов, тепло- и массопереноса и ряда других явлений, часто взаимосвязанных. КА – важный элемент при проектировании “цифровых двойников”. Их можно использовать для создания цифровых структур и проведения вычислительных экспериментов по прогнозированию их свойств.
• Легкое масштабирование моделей, построенных с использованием КА. В связи с тем, что для большинства цифровых структур существует линейная зависимость между количеством вычислительных ресурсов и требуемым временем расчета, увеличение пространственного и временного масштабов моделируемых систем может быть осуществлено просто путем подключения дополнительных вычислительных кластеров.
• Третья причина частично связана с первой и заключается в возможности объединения КА-моделей между собой и с моделями других классов. Гибридные модели на основе КА позволят изучать системы, в которых различные процессы могут иметь пространственные и временные масштабы, которые отличаются на целые порядки.
• Следующей причиной является то, что КА принадлежат к высокопроизводительным вычислительным инструментам, благодаря возможности эффективной реализации моделей КА с использованием различных технологий параллельных вычислений [9].
Возможности моделирования с использованием КА на микро- и мезомасштабах позволяют описать структуру, свойства материала и различные явления, а на макроуровне – процессы в оборудовании. Кроме того, возможно сочетание различных типов и размеров КА в одной модели, а также сочетание КА и других вычислительных методов [9].
Клеточный автомат состоит из набора простых (конечных) автоматов, называемых клетками. Клетки располагаются в ячейках регулярной пространственной решетки. Так как каждая клетка – конечный автомат, в каждый момент времени она может принимать одно из конечного множества состояний. Особенностью клеточного автомата является то, что в качестве входных сигналов каждая его клетка использует входные состояния соседних клеток. Таким образом, состояние клетки меняется в соответствии с состояниями соседних клеток. Клеточно-автоматные модели обладают следующими свойствами:
• Дискретностью пространства. Клеточный автомат состоит из регулярно упорядоченного набора клеток, которые образуют дискретную решетку произвольной размерности. Все клетки считаются одинаковыми.
• Дискретностью времени. Состояния клеток автомата определены в дискретные отрезки времени – итерации. Итеративный переход всех клеток клеточного автомата из одного состояния в другое называется эволюцией клеточного автомата.
• Дискретностью состояний. Множество возможных состояний клетки дискретно и конечно.
• Окрестностью – набором клеток, которые считаются соседними с рассматриваемой.
• Правилами перехода, по которым изменяется состояние каждой клетки на каждом шаге по времени в соответствии с ее окрестностью [10, 11].
Клеточно-автоматный подход основан на упрощении физических систем с их одновременной дискретизацией в пространстве и времени. Таким образом, моделируемая система представляется в виде массива клеток, взаимодействующих друг с другом. На рис. 1 представлен пример двухмерного клеточного автомата [9].
Масштабы отдельных клеток могут быть достаточно большими, чтобы не учитывать внутримолекулярные степени свободы и межмолекулярные взаимодействия, и в то же время остается возможным моделировать процессы, связанные с этими аспектами. КА-модели могут воспроизводить поведение довольно сложных систем, сохраняя при этом простоту правил перехода, поэтому они так интересны для решения задач химии и химической технологии, которые часто имеют крупный масштаб, но требуют учета микроскопических явлений [12].
В рамках данной работы клеточно-автоматный подход был использован для моделирования пористых наноструктур аэрогелей на основе хитозана.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
Аэрогели являются материалами, которые обладают рядом уникальных свойств таких, как высокая площадь удельной поверхности (200–2000 м2/г), высокая пористость (до 99.99%), малый размер пор (2–30 нм). Аэрогели могут быть получены на основе веществ, разрешенных к использованию в фармацевтической отрасли, и могут быть использованы в качестве матриц-носителей, в порах которых находятся активные фармацевтические ингредиенты (АФИ). Таким образом, внедрение лекарственных средств в аэрогели позволит получать фармацевтические композиции с улучшенными фармакокинетическими свойствами такими, как повышенная биодоступность, ускоренное или замедленное высвобождение, таргетная доставка. Это делает аэрогели перспективными системами доставки лекарственных средств, в том числе в мозг для терапии различных заболеваний.
Для получения аэрогелей используются технологии сверхкритических флюидов. На первом этапе получения аэрогелей используется золь-гель технология. После формирования геля проводится замена исходного растворителя, который находится внутри пористой структуры геля, на соответствующий растворитель, который должен растворяться в среде сверхкритического флюида. Как правило, это различные спирты (этиловый, изопропиловый). Заключительный шаг – сушка в среде сверхкритического флюида. В качестве сушильного агента для сверхкритической сушки, как правило, используется диоксид углерода. Он обладает сравнительно низкими параметрами, соответствующими сверхкритическому флюиду: его критическая температура – 31.1°С, давление 73.4 атм. Диоксид углерода отличается низкой ценой, он экологически безопасен, его использование соответствует всем принципам “зеленой” химии. Кроме того, при нормальных условиях диоксид углерода является газом – это позволяет легко удалять его после окончания процесса сверхкритической сушки. Благодаря развитой структуре и высокой пористости, аэрогели могут быть использованы для внедрения в них различных активных веществ, что представляет высокий интерес для современных фармацевтических разработок.
В данной работе были исследованы образцы аэрогелей на основе хитозана с различными структурными свойствами, которые могут быть использованы в дальнейшем как системы доставки лекарственных средств.
Поэтому важной задачей было построение модели аэрогельных частиц на основе хитозана с целью последующих исследований процессов адсорбции АФИ в аэрогельную матрицу и десорбции АФИ из нее в жидкой среде.
Среди моделей, которые используются для моделирования пористых структур широко распространены модели агрегации такие, как агрегация, ограниченная диффузией (diffusion-limited aggregation, DLA) [13] и кластер-кластерная агрегация, ограниченная диффузией (diffusion-limited cluster aggregation, DLCA) [14, 15].
Модели DLA и DLCA относятся к двум классам моделей агрегации–агрегация “частица–кластер” и агрегация “кластер–кластер” соответственно. Они могут быть модифицированы, позволяя изменять способ генерации таким образом, чтобы итоговая структура соответствовала конкретному материалу. Такие модели больше всего подходят для моделирования структур аэрогелей, образованных шарообразными глобулами (например, на основе диоксида кремния).
На основе модели DLCA была разработана программа расчета и визуализации структуры аэрогеля на основе хитозана, однако она не позволила с высокой степенью адекватности описать структуру аэрогелей на основе хитозана.
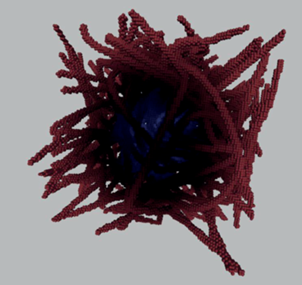
На рис. 2 представлена трехмерная цифровая копия структуры аэрогеля, полученная с помощью модели DLCA.
Рис. 2.
Пример трехмерной цифровой структуры аэрогеля на основе хитозана, полученной с помощью модели DLCA.
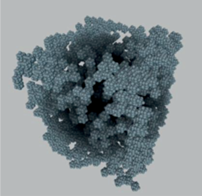
Это связано с тем, что главной особенностью структуры аэрогеля на основе хитозана является то, что она состоит из волокон, образующих единую сеть. Для таких волокнистых структур была разработана модель, в основе которой лежит использование кривых Безье.
Принцип работы модели состоит в том, что на поле генерации строятся кривые Безье, а волокна аэрогеля размещаются в месте их прохождения. Таким образом, модель позволяет получить структуру, состоящую из пересекающихся волокон, геометрия которых соответствует реальным.
В модели используется кривая Безье третьего порядка, которая строится в соответствии со следующим выражением:
(1)
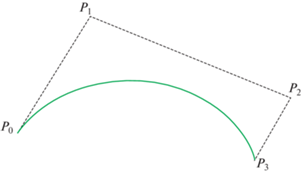
$\begin{gathered} B\left( t \right) = {{\left( {1 - t} \right)}^{3}}{{P}_{0}} + 3t{{\left( {1 - t} \right)}^{2}}{{P}_{1}} + \\ + \,\,3{{t}^{2}}\left( {1 - t} \right){{P}_{2}} + {{t}^{3}}{{P}_{3}},~\,\,\,\,t \in \left[ {0,1} \right], \\ \end{gathered} $Согласно (1) кривая строится по четырем опорным точкам. ${{P}_{0}}$ и ${{P}_{3}}$ – начало и конец кривой. ${{P}_{0}}$ выбирается в случайном месте на границе поля. ${{P}_{3}}$ выбираются в случайном месте поля и является центром пересечения нескольких волокон.$~~{{P}_{1}},{{P}_{2}}$ случайные точки на поле между ${{P}_{0}}$ и ${{P}_{3}}$. При этом кривая проходит через точки ${{P}_{0}}$ и ${{P}_{3}}$, но не проходит через точки ${{P}_{1}}$ и ${{P}_{2}}~$(рис. 3).
Разработанная клеточно-автоматная модель с использованием кривых Безье имеет следующие допущения:
– пространство, в котором производится моделирование, состоит из клеток одинакового размера, кубической формы;
– каждая клетка может иметь одно из 2 состояний: “материал” и “пустота”;
– соседними считаются клетки, имеющие общую грань;
– считается, что клетки имеют состояние “материал”, если лежат на пути прохождения кривой Безье;
На рис. 4 приведена трехмерная цифровая копия структуры аэрогеля, полученная с помощью модели на основе генерации кривых Безье.
В качестве входных параметров модель использует желаемые пористость аэрогеля и толщину волокна. Пористость и толщина волокна оцениваются в соответствии с экспериментальными данными.
Перед началом работы на поле в случайных клетках размещаются центры пересечения. После этого случайно выбираются опорные точки Р0, Р1, Р2 и Р3, при этом Р0 лежит на одной из граней поля, а Р3 – в одном из центров пересечения. Р1 и Р2 выбираются в случайных точках на поле. По этим опорным точкам в соответствии с формулой (1) строится кривая Безье. Все клетки, которые лежат на ней, переходят в состояние “волокно”. Далее толщина волокна увеличивается, пока не достигнет заданной. Расчет происходит до тех пор, пока в модели не будет не достигнута заданная пористость.
Модель на основе кривых Безье была использована далее при моделировании структур экспериментальных образцов аэрогелей на основе хитозана.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В рамках работы было получено 16 экспериментальных образцов аэрогелей на основе хитозана для которых были проведены аналитические исследования их структурных характеристик.
Структурные характеристики полученных аэрогелей были исследованы с помощью низкотемпературного адсорбционно-десорбционного анализа N2 (ASAP 2020MP, Micromeritics, Norcross, (Джорджия), США). Образцы предварительно сушили в вакууме при 50°С в течение 20 ч. Удельную поверхность определяли методом БЭТ. БДХ-анализ был использован для определения среднего диаметра пор частиц аэрогеля и распределения пор по размерам с использованием кривой десорбции.
Далее было сгенерировано 16 цифровых структур, которые соответствуют 16 экспериментальным образцам аэрогелей на основе хитозана. Были сгенерированы структуры размером 320 × 320 × 320 нм. Такой масштаб позволяет учитывать структурные свойства аэрогеля.
Для оценки соответствия цифровых структур и экспериментальных образцов было проведено сравнение удельной площади поверхности и кривых распределения пор по размерам.
В табл. 2 приведены удельные площади поверхности полученных цифровых структур и соответствующих им экспериментальных образцов.
Таблица 2.
Характеристики экспериментальных образцов аэрогелей на основе хитозана и соответствующих им цифровых структур
| № образца | Пористость, % | Sуд.эксп., м2/г | Sуд. расч., м2/г | Отклонение, % |
|---|---|---|---|---|
| 9 | 98 | 261 | 258 | 0 |
| 15 | 98 | 190 | 187 | 0 |
| 10 | 99 | 323 | 317 | 2 |
| 11 | 98 | 347 | 340 | 2 |
| 3 | 98 | 166 | 161 | 3 |
| 8 | 98 | 526 | 541 | 3 |
| 13 | 98 | 248 | 256 | 3 |
| 2 | 98 | 270 | 280 | 4 |
| 7 | 99 | 143 | 137 | 4 |
| 1 | 99 | 275 | 261 | 5 |
| 4 | 98 | 168 | 176 | 5 |
| 6 | 99 | 360 | 343 | 5 |
| 12 | 99 | 135 | 128 | 5 |
| 14 | 99 | 227 | 213 | 6 |
| 16 | 98 | 175 | 191 | 9 |
| 5 | 99 | 151 | 168 | 11 |
Как видно из табл. 2, отклонение расчетной удельной площади поверхности Sуд.расч. от экспериментальной Sуд.эксп. не превышает 11%, что говорит о соответствии данной характеристики у цифровых структур и экспериментальных образцов.
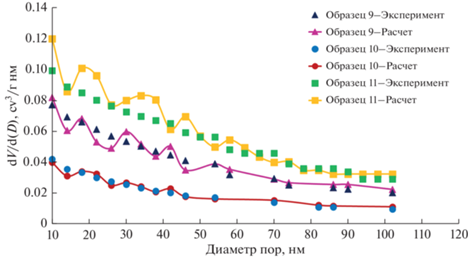
Далее было проведено сравнение кривых распределения пор по размерам. На рис. 6 показано сравнение экспериментальных образцов и соответствующих цифровых структур распределения пор по размерам для образцов 9–11.
Рис. 6.
Цифровые трехмерные структуры аэрогелей на основе хитозана, соответствующие образцам: (а) – образец 9, (б) – образец 10, (в) – образец 11.
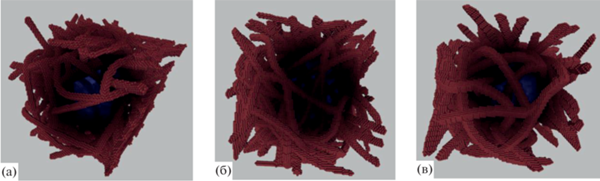
На рис. 7 представлены визуальные изображения цифровых трехмерных пористых структур, соответствующих экспериментальным образцам 9–11 аэрогелей на основе хитозана.
В представленных кривых распределения пор по размерам отклонение расчетных значений от экспериментальных не превышает 5%, что говорит о том, что кривые соответствуют друг другу. Так как структурные характеристики цифровых структур аэрогелей, удельная площадь поверхности и распределение пор по размерам, отклоняются от экспериментальных не более, чем нам 5%, можно сделать вывод о том, что сгенерированные цифровые структуры соответствуют экспериментальным.
ЗАКЛЮЧЕНИЕ
В данной работе предложена модель создания цифровых двойников волокнистых пористых структур, основанная на использовании клеточных автоматов и кривых Безье.
Были созданы цифровые структуры аэрогелей на основе хитозана. Полученные цифровые копии и экспериментальные структуры сравнивали по двум параметрам: распределению пор по размерам и удельной поверхности. Структурные характеристики цифровых структур – распределение пор по размерам и удельная поверхность соответствовали экспериментальным, из чего можно сделать вывод о соответствии цифровых копий экспериментальным образцам аэрогеля на основе хитозана.
Разработанная модель позволяет создавать цифровые двойники, соответствующие экспериментальным образцам нанопористых волокнистых структур, таких как аэрогели на основе хитозана. Данные цифровые двойники можно использовать в дальнейшем для прогнозирования различных свойств аэрогеля по его структуре, таких как адсорбция, десорбция, механические свойства и прочее. Это сократит количество необходимых экспериментальных исследований при разработке новых аэрогелей с заданными свойствами путем частичной замены натурных экспериментов вычислительными. Предложенная модель может быть реализована с использованием высокопроизводительных параллельных вычислений, что значительно повысит скорость расчетов.
Полученные цифровые структуры аэрогелей на основе хитозана будут использоваться для создания цифровых структур со встроенными активными фармацевтическими ингредиентами (АФИ). Эти цифровые структуры будут использоваться для прогнозирования высвобождения АФИ, что сократит количество необходимых экспериментов при создании новых препаратов с использованием аэрогелей на основе хитозана в качестве носителя.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации No 075-15-2020-792 (Уникальный идентификатор: RF–190220X0031).
ОБОЗНАЧЕНИЯ
| КА | клеточный автомат |
| АФИ | активный фармацевтический ингредиент |
| DLA | diffusion-limited aggregation, агрегация, ограниченная диффузией |
| DLCA | diffusion-limited cluster aggregation, кластер-кластерная агрегация, ограниченная диффузией |
| БЭТ | метод Брунауэра, Эммета, Теллера |
| БДХ | метод Баррета, Джойнера, Халенды |
| Sуд.эксп. | удельная площадь поверхности экспериментального образца, м2/г |
| Sуд.расч. | удельная площадь поверхности цифровой структуры, м2/г |
Список литературы
Svyetlichnyy D.S. A three-dimensional frontal cellular automaton model for simulation of microstructure evolution—initial microstructure module // Model. Simul. Mater. Sci. Eng. 2014. V. 22. № 8. P. 085001.
Krivovichev S.V. Algorithmic crystal chemistry: A cellular automata approach // Crystallogr. Rep. 2012. V. 57. № 1. P. 10–17.
Kimber J.A., Kazarian S.G., Štěpánek F. Microstructure-based mathematical modelling and spectroscopic imaging of tablet dissolution // Comput. Chem. Eng. 2011. V. 35. № 7. P. 1328–1339.
Pérez-Brokate C.F., di Caprio D., Féron D., De Lamare J., Chaussé A. 2014. Overview of Cellular Automaton Models for Corrosion. In Cellular Automata, ed J. Wąs, G.Ch. Sirakoulis, S. Bandini. 8751: 187–96. Cham: Springer International Publishing.
Gurikov P., Kolnoochenko A., Golubchikov M., Menshutina N., Smirnova I. A synchronous cellular automaton model of mass transport in porous media // Comput. Chem. Eng. 2016. V. 84. P. 446–457.
Brouwers H.J.H., de Korte A.C.J. Multi-cycle and multi-scale cellular automata for hydration simulation (of Portland-cement) // Comput. Mater. Sci. 2016. V. 111. P. 116–124.
Bullard J.W. 2008. A Determination of Hydration Mechanisms for Tricalcium Silicate Using a Kinetic Cellular Automaton Model // J. Am. Ceram. Soc. 2008. V. 91. № 7. P. 2088–2097.
Bonchev D., Thomas S., Apte A., Kier L.B. Cellular automata modelling of biomolecular networks dynamics // SAR QSAR Environ. Res. 2010. V. 21. № 1–2. P. 77–102.
Menshutina N., Kolnoochenko A., Lebedev A. Cellular Automata in Chemistry and Chemical Engineering // Annual Review of Chemical and Biomolecular Engineering. 2019. V. 10. P. 325–345.
Бандман О.Л. Клеточно-автоматные модели пространственной динамики // Системная информатика. 2006. Т. 10. С. 59–113.
Бандман О.Л. Метод построения клеточно-автоматных моделей процессов формирования устойчивых структур // Прикладная дискретная математика. 2010. № 4(10).
Lis M., Pintal L., Swiatek J., Cwiklik L. GPU-Based Massive Parallel Kawasaki Kinetics in the Dynamic Monte Carlo Simulations of Lipid Nanodomains // J. Chem. Theory Comput. 2012. V. 8(11). № 65. 4758 p.
Lee H.W., Im Y.-T. Cellular Automata Modeling of Grain Coarsening and Refinement during the Dynamic Recrystallization of Pure Copper // Mater. Trans. 2010. V. 51. № 10. P. 1614–1620.
Gandin Ch.-A., Rappaz M. A coupled finite element-cellular automaton model for the prediction of dendritic grain structures in solidification processes. Acta Metall. Mater. 1994. V. 42 № 7. P. 2233–2246.
Miller W., Succi S., Mansutti D. Lattice Boltzmann Model for Anisotropic Liquid-Solid Phase Transition // Phys. Rev. Lett. 2001. V. 86. № 16. P. 3578–3581.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии