Теоретические основы химической технологии, 2023, T. 57, № 4, стр. 419-426
Математическое моделирование течения двухфазных сред в сепараторах с криволинейными вставками
Р. И. Ибятов a, *, Ф. Г. Ахмадиев b, **
a Казанский государственный аграрный университет
Казань, Россия
b Казанский государственный архитектурно-строительный университет
Казань, Россия
* E-mail: r.ibjatov@mail.ru
** E-mail: Akhmadiev@kgasu.ru
Поступила в редакцию 22.04.2023
После доработки 26.04.2023
Принята к публикации 05.05.2023
- EDN: YZPCFU
- DOI: 10.31857/S0040357123040036
Аннотация
Рассмотрено течение двухфазной среды в жидкостных тарельчатых сепараторах с криволинейными вставками. Предложен алгоритм численного расчета величины зазора между соосными криволинейными вставками. Уравнения движения двухфазной среды, записанные в ортогональной системе координат, связанной с областью течения, решаются методом поверхностей равных расходов. Численные расчеты проведены для сепараторов с параболическими вставками. Расчеты показываю, что на входном участке происходит развитие течения от начального плоского профиля до параболического вида. При этом скорости потока вблизи стенок канала замедляются, а в центре области течения, наоборот, разгоняются. Поэтому, на начальном участке линии тока имеют искривления. На форму эпюры скоростей и кривизну линий тока существенно влияет скорость вращения вставок. При значительных скоростях вращения наблюдается асимметричность профиля скорости.
ВВЕДЕНИЕ
В химической, нефтехимической, пищевой и других областях промышленности широко используются процессы разделения гетерогенных жидкостных сред в тарельчатых сепараторах. В жидкостных сепараторах в качестве сепарирующих элементов применяются соосные совместно вращающиеся вставки. Пакет вставок разделяет жидкостную систему на тонкие слои, что обеспечивает уменьшения пути осаждения дисперсных частиц. Эффективность процесса разделения зависит от гидродинамической обстановки в пространстве между двумя соседними вставками. Поэтому исследование работы жидкостных сепараторов и разработка расчетных методик связаны с построением гидродинамической модели течения рабочей среды в пространстве между вставками.
В настоящее время в промышленности в основном используются сепараторы с коническими вставками. Вместе с тем, существуют аппараты, где в качестве сепарирующего элемента применяются вставки другой формы [1, 2]. У вставок двоякой кривизны, направление действия центробежной силы относительно касательной к образующей и расстояние между вставками по длине образующей являются переменными величинами, что влияет на скорость движущегося потока. Эти особенности применения сепараторов с криволинейными вставками могут быть использованы для интенсификации процесса разделения многофазных сред.
Известны большое количество статей и монографий, которые посвящены к изучению гидродинамики тарельчатых сепараторов с коническими вставками. Достаточно подробный анализ литературы имеется, например, в работах [1–8]. Однако, гидродинамическая обстановка при течении жидкостных сред между криволинейными вставками остается малоизученным [1–3]. Представляет интерес изучение течений рабочей среды между криволинейными вставками на входном участке, где происходит преобразование эпюры скорости к параболическому виду.
Целью данной работы является построение математической модели осесимметрического течение гетерогенной среды в пространстве между криволинейными вставками с учетом начального участка, соответствующих алгоритмов расчета и проведение вычислительного эксперимента.
ТЕОРЕТИЧЕСКИЙ АНАЛИЗ
Гетерогенная жидкостная среда подается с периферии криволинейных вставок и под действием перепада давления движется к центру аппарата. Для описания гидродинамики гетерогенных сред можно использовать методы механики многофазных сред [9]. Для тонкослойных осесимметричных течений двухфазных сред упрощенные уравнения сохранения массы и импульса в ортогональной системе координат ${{x}_{1}},\,{{x}_{2}},\,{{x}_{3}}$, связанной с областью течения, после оценки значимости слагаемых, могут быть записаны в виде [10–11]
Под действием центробежной силы частицы дисперсной фазы осаждаются к нижней поверхности верхней тарелки. При значительных концентрациях может образоваться тонкий слой осадка [12], который движется в обратном направлении к периферии вставки. Из-за осаждения дисперсных частиц изменится их средняя концентрация в потоке. Для учета изменения средней концентрации дисперсных частиц, при описании тонкослойных потоков, может быть использована квазигомогенная модель с переменными по продольной координате концентрацией ${{\alpha }_{2}}({{x}_{1}})$ и характеристиками $\rho ({{\alpha }_{2}}({{x}_{1}}))$, $\mu ({{\alpha }_{2}}({{x}_{1}}))$. Тогда уравнения сохранения массы и импульсов механики многофазных сред (1') в квазигомогенном приближении можно привести к виду
(1)
$\frac{{\partial ({{H}_{2}}{{H}_{3}}\rho U)}}{{\partial {{x}_{1}}}} + \frac{{\partial ({{H}_{1}}{{H}_{3}}\rho V)}}{{\partial {{x}_{2}}}} = 0,$(2)
$\begin{gathered} \rho \left( {\frac{U}{{{{H}_{1}}}}\frac{{\partial U}}{{\partial {{x}_{1}}}} + \frac{V}{{{{H}_{2}}}}\frac{{\partial U}}{{\partial {{x}_{2}}}} + \frac{{UV}}{{{{H}_{1}}{{H}_{2}}}}\frac{{\partial {{H}_{1}}}}{{\partial {{x}_{2}}}}} \right) = \\ = - \frac{1}{{{{H}_{1}}}}\frac{{\partial P}}{{\partial {{x}_{1}}}} + {{\tau }_{{12}}} + \rho {{F}_{1}}, \\ \end{gathered} $(3)
$ - \rho \frac{{{{U}^{2}}}}{{{{H}_{1}}{{H}_{2}}}}\frac{{\partial {{H}_{1}}}}{{\partial {{x}_{2}}}} = - \frac{1}{{{{H}_{2}}}}\frac{{\partial P}}{{\partial {{x}_{2}}}} + \rho {{F}_{2}},$Данная система уравнений должна решаться при следующих граничных и входных условиях
Граничное условие (4.1) записана с учетом наличия слоя осадка толщиной $\delta $, который скользить под действием центробежной силы к периферии тарелок со скоростью ${{U}_{\delta }}$.
Для решения задачи (1)–(4) применим метод поверхностей равных расходов, предложенный Л.П. Холпановым, В.Я. Шкадовым [13] и развитым в работах [10–12, 14] для моделирования течений гетерогенных сред. В работе [13] была показана, что данный подход позволяет моделировать напорные течения в трубах и каналах различной геометрической формы. В соответствии с этим методом вводится в поле течения рабочей среды линии тока, которые в условиях стационарности потока совпадают с поверхностями равных расходов. Поскольку течение осесимметричное, поверхности равных расходов вводятся как функции продольной координаты [10, 13]: ${{y}_{k}} = {{y}_{k}}({{x}_{1}}),$ $k = \overline {0,N + 1} $. Тогда компоненты скорости среды на введенных поверхностях тоже являются функциями координаты ${{x}_{1}}$: ${{U}_{k}} = U\left[ {{{x}_{1}},{{y}_{k}}\left( {{{x}_{1}}} \right)} \right],\,\,\,\,{{V}_{k}} = V\left[ {{{x}_{1}},{{y}_{k}}\left( {{{x}_{1}}} \right)} \right].$ Здесь поверхность ${{y}_{0}}$ совпадает с верхней вставкой или с поверхностью осажденной массы, а ${{y}_{{N + 1}}}$ – с поверхностью нижней вставки. Задачу о развитии течения рабочей среды между криволинейными вставками теперь можно свести к численному определению линии тока и полей скоростей на них. Зная скорости сплошной фазы на линиях тока можно вычислять траектории дисперсных частиц.
Запишем интегральные условия сохранения массы между линиями ${{y}_{{k - 1}}}$ и ${{y}_{k}}$
С учетом непроницаемости криволинейных вставок, продифференцируем данную зависимость
(5)
$\frac{d}{{d{{x}_{1}}}}\int\limits_{{{y}_{{k - 1}}}}^{{{y}_{k}}} {2\pi \,rU{{H}_{2}}d{{x}_{2}} = 0,\,\,\,\,k = \overline {1,N + 1} \,.} $Вычисление интеграла (5) можно провести по одной из формул численного интегрирования, например, по формуле трапеции и затем после дифференцирования полученную разностную формулу по координате ${{x}_{1}}$ получим:
(6)
$\frac{{d{{y}_{k}}}}{{d{{x}_{1}}}} = \frac{{d{{y}_{{k - 1}}}}}{{d{{x}_{1}}}} - \frac{{{{y}_{k}} - {{y}_{{k - 1}}}}}{{{{\Delta }_{k}}}}\frac{{d{{\Delta }_{k}}}}{{d{{x}_{1}}}},\,\,\,\,k = \overline {1,N + 1} \,{\text{,}}$Для функции скорости $U\left[ {{{x}_{1}},{{y}_{k}}\left( {{{x}_{1}}} \right)} \right]$ полный дифференциал равен
Выразим частную производную ${{{{\partial U} \mathord{\left/ {\vphantom {{\partial U} {\partial x}}} \right. \kern-0em} {\partial x}}}_{1}}$ через полный дифференциал
Запишем аналогичную формулу для давления
В этих формулах $\frac{{\partial U}}{{\partial {{y}_{k}}}}$ и $\frac{{\partial P}}{{\partial {{y}_{k}}}}$ означают значения производных $\frac{{\partial U}}{{\partial {{x}_{2}}}}$ и $\frac{{\partial P}}{{\partial {{x}_{2}}}}$ на линиях ${{x}_{2}} = {{y}_{k}}$.
На линиях тока имеют место зависимости [10, 13]
Тогда уравнение (2), записанное на введенных линиях тока, представляется в виде следующей системы обыкновенных дифференциальных уравнений
С учетом уравнения движения (3) окончательно получим систему уравнений
(7)
$\begin{gathered} \rho \frac{{{{U}_{k}}}}{{{{H}_{1}}}}\frac{{d{{U}_{k}}}}{{d{{x}_{1}}}} = - \frac{{dP}}{{{{H}_{1}}d{{x}_{1}}}} - \rho \frac{{{{U}_{k}}{{V}_{k}}}}{{{{H}_{1}}{{H}_{2}}}}\frac{{\partial {{H}_{1}}}}{{\partial {{x}_{2}}}} + \\ + \,\,\rho \left( {\frac{{U_{k}^{2}}}{{{{H}_{1}}{{H}_{2}}}}\frac{{\partial {{H}_{1}}}}{{\partial {{x}_{2}}}} + {{F}_{{2k}}}} \right)\frac{{{{H}_{2}}d{{y}_{k}}}}{{{{H}_{1}}d{{x}_{1}}}} + {{\tau }_{{12}}} + \rho {{F}_{{1k}}}, \\ k = \overline {1,N} . \\ \end{gathered} $Система уравнений (6)–(7) позволяет определить положения линий поверхностей равных расходов и поле скоростей на них, которая может быть решена одним из известных численных методов, например, методом Рунге–Кутты. Реализация численных расчетов для криволинейных областей сильно усложняется из-за вычислительных трудностей по сравнению с коническими областями.
В качестве примера для проведения численных расчетов по системе (6)–(7) рассмотрим криволинейный зазор, образованный двумя поверхностями вращения, которые заданы уравнениями
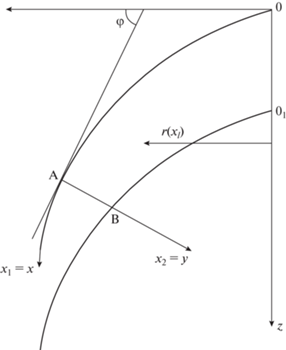
где параметр b = OO1 является заданным постоянным числом, r – величина определяющая расстояние любой точки зазора от оси вращения (радиус вращения). Необходимо определить зазор между криволинейными вставками.Обозначим через $({{x}_{1}},{{x}_{2}})$ оси ортогональной системы координат, связанных с поверхностью вращения. Пусть продольная координата ${{x}_{1}}$ совпадает с образующей верхней поверхности вращения (рис. 1). Тогда, как видно из рисунка, она показывает длину дуги ОА.
Длина дуги ${{x}_{1}}$ при заданном радиусе вращения r вычисляется по формуле
(10)
${{x}_{1}} = \int\limits_0^r {\sqrt {1 + ({{{{{df} \mathord{\left/ {\vphantom {{df} {dr)}}} \right. \kern-0em} {dr)}}}}^{2}}} } dr.$Нелинейная зависимость (10) является базовым уравнением для вычисления радиуса вращения $r$ по заданной координате ${{x}_{1}}$. В общем случае аналитически найти величину $r$ не представляется возможным. Эта величина входит во все уравнения (1)–(3). Поэтому необходимо построить алгоритм численного определения радиуса вращения $r$.
При заданной координате ${{x}_{A}}$ с помощью численного решения уравнения (10) можно определить радиус вращения данной точки ${{r}_{A}}$. Пусть кратчайшим расстоянием от точки ${{x}_{A}}$ до нижней тарелки является отрезок $d = AB$ (рис. 1). Величина данного отрезка, как расстояние между точками $A({{r}_{A}},\,{{z}_{A}})$ и $B(r,\,z)$, определяется с помощью формулы
(11)
$d(r) = \sqrt {{{{(r - {{r}_{A}})}}^{2}} + {{{\left( {f(r) + b - f({{r}_{A}})} \right)}}^{2}}} .$Потребуем выполнения условия минимума функции $d(r)$, которое записывается в виде равенства нулю первой производной. После дифференцирования зависимости (11) и выполнения несложных преобразований, для вычисления радиуса ${{r}_{B}} = r$ по известному значению ${{r}_{A}}$ получим следующее нелинейное уравнение
Таким образом, алгоритм численного расчета величины зазора между соосными криволинейными вставками, заданными уравнениями (8)–(9), будет следующим:
1. В верхней поверхности вращения выбирается произвольная точка ${{x}_{1}} = {{x}_{A}}$
2. По уравнению (10) вычисляется радиус вращения ${{r}_{A}}$.
3. Из уравнения (12) определяется радиус вращения ${{r}_{B}}$, который соответствует минимальному зазору между вставками в сечении ${{x}_{1}} = {{x}_{A}}$.
4. По найденным радиусам с помощью формулы (11) вычисляется искомое расстояние между криволинейными вставками.
В качестве реализации предложенного общего подхода определения величины зазора, рассмотрим вставки параболического вида, которые заданы уравнениями
Тогда радиус вращения $r$ для произвольной точки верхней вставки, заданной координатой ${{x}_{1}}$, вычисляется с помощью нелинейного уравнения
Не трудно заметить, что данный интеграл в квадратурах вычисляется только для значений параметра n, равных 1 и 2. Поэтому, в случае произвольного значения n, уравнение (15) решается численно.
Уравнение (12), позволяющее вычислить радиус вращения искомой точки ${{r}_{B}} = r$ по заданной координате ${{x}_{1}}$, для параболической вставки принимает вид
Расстояние между вставками по координате ${{x}_{1}} = {{x}_{A}}$ вычисляется по формуле
После определения величин зазора $h$ можно приступить к решению задачи (1)–(3) или системы уравнений (6)–(7). Уравнения движения (1)–(3), в ортогональной системе координат $({{x}_{1}} = x,\,\,{{x}_{2}} = y,\,\,{{x}_{3}} = \varphi )$ с коэффициентами Ляме ${{H}_{1}} = 1,\;{{H}_{2}} = 1,\;{{H}_{3}} = r$ для параболической вставки примут вид
(19)
$\rho \left( {U\frac{{\partial U}}{{\partial x}} + V\frac{{\partial U}}{{\partial y}}} \right) = - \frac{{\partial P}}{{\partial x}} + \frac{1}{r}\frac{\partial }{{\partial y}}\left( {r\mu \frac{{\partial U}}{{\partial y}}} \right) + \rho {{F}_{x}},$В дальнейшем перейдем к безразмерным переменным
(22)
$\begin{gathered} U\frac{{\partial U}}{{\partial x}} + V\frac{{\partial U}}{{\partial y}} = \\ = - \frac{{\partial P}}{{\partial x}} - \frac{{\cos \beta }}{{r\operatorname{Re} }}\frac{{\partial U}}{{\partial y}} + \frac{{{{\partial }^{2}}U}}{{\partial {{y}^{2}}}} + \frac{{{{{\operatorname{Re} }}^{2}}}}{{Fr}}r\sin \beta , \\ \end{gathered} $Здесь и далее $r = R - {{y\cos \beta } \mathord{\left/ {\vphantom {{y\cos \beta } {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}$ – безразмерный радиус. Виды граничных условий остаются без изменений.
Преобразуем систему уравнений (6). При дифференцировании соотношения ${{\Delta }_{k}}$ необходимо учитывать, что линии тока ${{y}_{k}}(x)$, соответственно радиусы ${{r}_{k}}(x)$, являются функциями продольной координаты ${{r}_{k}}(x) = R(x) - {{y}_{k}}(x){{\cos \beta } \mathord{\left/ {\vphantom {{\cos \beta } {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}$. После проведения операции дифференцирования и необходимых преобразований, данная система уравнений была приведена к виду
(24)
$\begin{gathered} \frac{{d{{y}_{k}}}}{{dx}} - {{S}_{k}}\frac{{d{{y}_{{k - 1}}}}}{{dx}} + {{I}_{k}}\frac{{d{{U}_{k}}}}{{dx}} + {{J}_{k}}\frac{{d{{U}_{{k - 1}}}}}{{dx}} + {{B}_{k}} = 0, \\ k = \overline {1,N + 1} \,{\text{,}} \\ \end{gathered} $Система уравнений движения (22) на линиях тока примет вид
Для удобства численного решения данная система уравнений была приведена к виду
(25)
$\frac{{d{{U}_{k}}}}{{dx}} + {{K}_{k}}\frac{{dP}}{{dx}} + {{L}_{k}}\frac{{d{{y}_{k}}}}{{dx}} = {{T}_{k}},\,\,\,\,\,k = \overline {1,N} \,{\text{,}}$В уравнениях (25) присутствуют частные производные по координате y. Для их вычисления сеточные решения представляются в виде разложения в ряд по полной системе базисных функций, удовлетворяющих граничным условиям
Построенная система (24), (25) состоит из ($2N + 1$) обыкновенных дифференциальных уравнений. Они достаточны для нахождения N значений линии тока и скоростей на каждом шаге численного решения. Одно уравнение освобождается для определения градиента давления.
Уравнения (24), (25) не разрешены относительно производных искомых величин. Для численного решения проведем необходимые преобразования. Из уравнений (25) выразим производные ${{d{{U}_{k}}} \mathord{\left/ {\vphantom {{d{{U}_{k}}} {dx}}} \right. \kern-0em} {dx}}$ и подставим в уравнения (24). Тогда получится уравнение
(26)
$\begin{gathered} \frac{{d{{y}_{k}}}}{{dx}} = \left( {{{S}_{k}}\frac{{d{{y}_{{k - 1}}}}}{{dx}} - {{J}_{k}}\frac{{d{{U}_{{k - 1}}}}}{{dx}}} \right. + \\ {{ + \,\,{{I}_{k}}{{K}_{k}}\left. {\frac{{dP}}{{dx}} - {{I}_{k}}{{T}_{k}} - {{B}_{k}}} \right)} \mathord{\left/ {\vphantom {{ + \,\,{{I}_{k}}{{K}_{k}}\left. {\frac{{dP}}{{dx}} - {{I}_{k}}{{T}_{k}} - {{B}_{k}}} \right)} {(1 - {{I}_{k}}{{L}_{k}})}}} \right. \kern-0em} {(1 - {{I}_{k}}{{L}_{k}})}}, \\ k = \overline {1,N + 1} \,{\text{.}} \\ \end{gathered} $Полученные уравнения подставим в уравнения (25). Тогда получится
(27)
$\begin{gathered} \frac{{d{{U}_{k}}}}{{dx}} = \frac{{{{L}_{k}}{{J}_{k}}}}{{1 - {{I}_{k}}{{L}_{k}}}}\frac{{d{{U}_{{k - 1}}}}}{{dx}} - \frac{{{{L}_{k}}{{S}_{k}}}}{{1 - {{I}_{k}}{{L}_{k}}}}\frac{{d{{y}_{{k - 1}}}}}{{dx}} - \\ - \,\,\left( {\frac{{{{L}_{k}}{{I}_{k}}{{K}_{k}}}}{{1 - {{I}_{k}}{{L}_{k}}}} + {{K}_{k}}} \right)\frac{{dP}}{{dx}} + \frac{{{{L}_{k}}({{I}_{k}}{{T}_{k}} + {{B}_{k}})}}{{1 - {{I}_{k}}{{L}_{k}}}} + {{T}_{k}}, \\ k = \overline {1,N} \,{\text{.}} \\ \end{gathered} $Искомые функции ${{d{{y}_{k}}} \mathord{\left/ {\vphantom {{d{{y}_{k}}} {dx}}} \right. \kern-0em} {dx}}$ и ${{d{{U}_{k}}} \mathord{\left/ {\vphantom {{d{{U}_{k}}} {dx}}} \right. \kern-0em} {dx}}$ представим в виде прогоночных соотношений
и подставим в уравнения (26), (27). После несложных преобразований, считая, что ${{\bar {Y}}_{k}},{{\hat {Y}}_{k}},{{\bar {W}}_{k}},{{\hat {W}}_{k}}$ известны, получим явные выражения прогоночных коэффициентов в виде следующих рекуррентных соотношений
Уравнение (26) с учетом граничных условий при $k = N + 1$ имеет вид
Отсюда для градиента давления получим формулу
(28)
$\frac{{dP}}{{dx}} = \frac{{{{S}_{{N + 1}}}{{{\bar {Y}}}_{N}} - {{J}_{{N + 1}}}{{{\bar {W}}}_{N}} - {{B}_{{N + 1}}}}}{{ - {{S}_{{N + 1}}}{{{\hat {Y}}}_{N}} + {{J}_{{N + 1}}}{{{\hat {W}}}_{N}}}}.$Итак, алгоритм вычислений правых частей системы обыкновенных дифференциальных уравнений первого порядка (26), (27) следующий. Для текущей координаты x определяются прогоночные коэффициенты и далее по формуле (28) находится градиент давления. После этого обратной прогонкой вычисляются значения правых частей дифференциальных уравнений (26), (27).
При проведении численных расчетов необходимо задать обоснованные входные (начальные) условия на линиях тока и значения продольной скорости на них. На основании принятого способа обезразмерования, продольным скоростям ${{U}_{k}}$ были заданы преимущественно единичные начальные условия. Местоположения и количество поверхностей равных расходов менялись в широком диапазоне.
РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ И ИХ ОБСУЖДЕНИЕ
Вычислительный эксперимент был проведен для вставок параболической и конической форм. На рисунках 2–5 показаны некоторые результаты численных расчетов для вставки параболической формы. Линии тока ${{y}_{k}}(x)$ были пронумерованы согласно направлению оси координат y (рис. 1), начиная от верхней вставки. Интересные результаты получены на входном участке. На начальном участке происходит развитие течения от начального плоского профиля до параболического вида (рис. 2). Поскольку криволинейная координатная линия x направлена от оси вращения (рис. 1), скорость течения имеет отрицательный знак. Скорости потока вблизи стенок канала замедляются (рис. 3, кривые 1 и 7), а в центре области течения, наоборот, разгоняются (рис.3, кривые 3, 4, 5). Из-за этого на начальном участке линии тока имеют искривления. Характерный вид поверхностей равных расходов показан на рис. 4. После формирования параболического профиля скорости наблюдается симметрическая картина течения (рис. 3 и 4). Крайние линии (рис. 3, кривые 1 и 7), а также линии 2 и 6, линии 3 и 5 попарно выходят к своим общим асимптотам. Максимальная скорость наблюдается в центре канала (рис. 3, кривая 4). Интенсивности изменения этих характеристик течения зависят от вязкости среды. При уменьшении вязкости и, следовательно, при увеличении число Re кривизна указанных линий уменьшается.
Рис. 2.
Эпюры скоростей при Re = 100, Fr = 4, L = 0.2 на сечениях по продольной координате: x = 0.15 – штрихпунктирная линия, x = 0.17 – разрывная линия, x = 0.19 – сплошная линия.
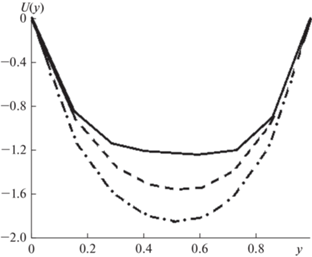
Рис. 3.
Изменения скоростей рабочей среды на линиях тока при значениях $\operatorname{Re} $ = 10, ${\text{Fr}}$ = 25, L = 0.2; цифры соответствуют номерам линий тока yk.
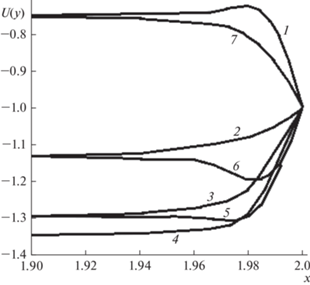
Рис. 4.
Изменения формы линии тока по длине канала при значениях $\operatorname{Re} $ = 10, ${\text{Fr}}$ = 25, L = 0.2; цифры соответствуют номерам линий тока yk.

Рис. 5.
Изменения формы линии тока по длине канала при значениях $\operatorname{Re} $ = 100, L = 0.2: ${\text{Fr}}$ = 4 – разрывная линия, ${\text{Fr}}$ = 0.44 – сплошная линия; цифры соответствуют номерам линий тока yk.
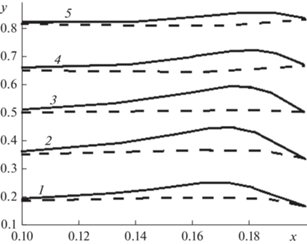
На форму эпюры скоростей и кривизну линий тока существенно влияет скорость вращения пакета вставок. На рис. 5 представлены линии тока для различных значений числа Fr при $\operatorname{Re} $ = 100. Центробежная сила действует против направления течения и тормозит движение рабочей среды. Поэтому, при значительных скоростях вращения вставок, скорость потока у верхней стенки канала замедляется. В результате замедления части потока наблюдается искривления линий равных расходов (рис. 5, сплошные линии). При этом растет асимметричность профиля скорости. Результаты расчетов качественно согласуются с данными работы [2]. Построенная математическая модель по расчету гидродинамической обстановки для несущей фазы является основой для определения траектории движения дисперсной фазы и, следовательно, расчета процесса разделения двухфазной среды в сепараторах.
ЗАКЛЮЧЕНИЕ
Построенная математическая модель позволяет проводить расчеты течения двухфазных сред в жидкостных тарельчатых сепараторах с криволинейными вставками. Расстояние между соседними вставками, которое является переменной величиной вдоль образующего тела вращения, вычисляется численно. Геометрическая форма вставок в уравнениях движения конкретизируется метрическими коэффициентами Ляме. Расчеты показали, что на начальном участке происходит развитие течения от начального плоского профиля до параболического вида. При увеличении скорости вращения растет асимметричность параболического профиля скорости. Использование криволинейных вставок позволяет увеличить эффективность разделения за счет увеличения воздействия центробежной силы на поток двухфазной среды и сокращения пути осаждения дисперсной фазы вследствие уменьшения расстояния между вставками.
ОБОЗНАЧЕНИЯ
| ${{F}_{1}},\,{{F}_{2}}$ | компоненты вектора массовых сил в направлении координат ${{x}_{1}}$ и ${{x}_{2}}$, м/с2 |
| ${{F}_{{12{{X}_{1}}}}},{{F}_{{12{{X}_{2}}}}}$ | компоненты вектора силы межфазного взаимодействия в направлении координат ${{x}_{1}}$ и ${{x}_{2}}$, кг/(м2 с2) |
| ${{H}_{i}}$ | коэффициенты Ляме |
| $h$ | расстояние между вставками, м |
| $P$ | давление, н/м2 |
| R | радиус вращения верхней вставки, м |
| $r$ | радиус вращения произвольной точки между вставками, м |
| $U,\,V$ | компоненты скорости в направлении координат ${{x}_{1}}$ и ${{x}_{2}}$, м/с |
| ${{\alpha }_{i}}$ | объемная концентрация $i$-ой фазы |
| $\beta $ | угол наклона касательной к верхней вставке, град |
| $\delta $ | толщина осадка, м |
| $\mu $ | динамическая вязкость смеси, Па с |
| $\rho $ | плотность двухфазной смеси, кг/м3 |
| ${{\rho }_{i}}$ | плотность i-ой фазы, кг/м3 |
| $\omega $ | скорость вращения, с–1 |
| ${\text{Fr}}$ | число Фруда |
| $\operatorname{Re} $ | число Рейнольдса |
ИНДЕКСЫ
Список литературы
Романков П.Г., Плюшкин С.А. Жидкостные сепараторы. Л.: Машиностроение. 1976. 256 с.
Семенов Е.В., Славянский А.А., Лебедева Н.Н. Особенности процесса центробежного разделения жидкостной системы в сепараторе со вставками двоякой кривизны // Химическое и нефтегазовое машиностроение. 2019. № 3. С. 3.
Жуков В.Г., Чесноков В.М. Давление в тонкослойном потоке жидкости тарельчатого центробежного сепаратора // Теорет. основы хим. технологии. 2016. Т. 50. № 6. С. 683.
Славянский А.А., Семенов Е.В., Грибкова В.А., Николаева Н.В. О кинетике потока жидкости в центробежном сепараторе // Хранение и переработка сельхозсырья. 2020. № 4. С. 166.
Семенов Е.В., Славянский А.А., Карамзин А.В. К расчету гидродинамических характеристик тарельчатого сепаратора // Хранение и переработка сельхозсырья. 2017. № 6. С. 39.
Торосян Д.С. К сепарированию высокодисперсных эмульсий тонкослойным центрифугированием // Журнал прикладной химии. 1994. № 12. С. 2704.
Карамзин А.В., Семенов Е.В. Количественный анализ процесса фракционирования тонкодисперсных частиц в центробежном сепараторе // Журнал прикладной химии. 2012. № 10. С. 1619.
Карпычев В.А., Семенов Е.В. Гидромеханические процессы технологической обработки молочных продуктов. М.: Легкая и пищевая промышленности. 1982. 240 с.
Нигматулин Р.И. Динамика многофазных сред. Ч. 1. М.: Наука, 1987.
Холпанов Л.П., Шкадов В.Я. Гидродинамика и тепломассообмен с поверхностью раздела. М.: Наука, 1990.
Ibyatov R.I., Kholpanov L.P., Akhmadiev F.G., Fazylzyanov R.R. Calculation of flow of heterogeneous media of non-newtonian behavior on permeable surfaces // J. Eng. Phys. Therm. 2003. V. 76. № 6. P. 1289. [Ибятов Р.И., Холпанов Л.П., Ахмадиев Ф.Г., Фазылзянов Р.Р. Расчет течения гетерогенных сред неньютоновского поведения по проницаемым поверхностям // Инж.-физ. журн. 2003. Т. 76. № 6. С. 80.]
Kholpanov L.P., Ibyatov R.I. Simulation of the hydrodynamics of multiphase heterogeneous media in a centrifugal field // Theor. Found. Chem. Eng. 2009. V. 43. № 5. P. 629. [Ибятов Р.И., Холпанов Л.П. Моделирование гидродинамики многофазных гетерогенных сред в центробежном поле// Теорет. основы хим. технологии. 2009. Т. 43. № 5. С. 534.]
Ibyatov R.I., Akhmadiev F.G., Kholpanov L.P. Flow of a multiphase medium over a permeable surface with formation of sediment // J. Eng. Phys. Therm. 2005. V. 78. № 2. P. 272. [Ибятов Р.И., Ахмадиев Ф.Г., Холпанов Л.П. Течение многофазной среды по проницаемой поверхности с образованием осадка // Инженерно-физический журн. 2005. Т. 78. № 2. С. 65.]
Kholpanov L.P., Ibyatov R.I. Calculation of the hydrodynamics of multiphase heterogeneous media in a centrifugal field // Heat Transfer Research. 2006. V. 37. № 4. P. 307.
Ibyatov R.I., Akhmadiev F.G., Kholpanov L.P., Bekbulatov I.G. Mathematical modeling of the flow of a multiphase heterogeneous medium in a permeable channel // Theor. Found. Chem. Eng. 2007. V. 41. № 5. P. 490. [Ибятов Р.И., Ахмадиев Ф.Г., Холпанов Л.П., Бекбулатов И.Г. Математическое моделирование течения многофазной гетерогенной среды по проницаемому каналу // Теорет. основы хим. технологии. 2007. Т. 41. № 5. С. 514.]
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии