1. На главную
  2. Электронные версии
  3. Теоретические основы химической технологии
  4. T. 57, № 5, 2023

Теоретические основы химической технологии, 2023, T. 57, № 5, стр. 524-531

Анализ процессов экстракционного и хроматографического разделения в каскаде смесительно-отстойных экстракторов

А. Е. Костанян a, *, А. А. Вошкин a

a Институт общей и неорганической химии им. Н.С. Курнакова РАН
Москва, Россия

* E-mail: kost@igic.ras.ru

Поступила в редакцию 17.07.2023
После доработки 25.07.2023
Принята к публикации 25.07.2023

Полный текст (PDF)

Аннотация

Каскад смесительно-отстойных экстракторов может работать как в режиме противоточной экстракции, так и в режиме хроматографии. При работе в режиме хроматографии органическая фаза не выводится из экстракторов, а циркулирует между смесительной и отстойной зонами в каждом аппарате. Настоящая работа посвящена теоретическому анализу процессов разделения в каскаде смесительно-отстойных экстракторов при работе каскада в режиме жидкость-жидкостной хроматографии и противоточной жидкостной экстракции. Рассмотрены обычные технологические схемы процессов хроматографического разделения и схемы с рециклом водной фазы. Показана перспективность применения в экстракционных технологиях принципов хроматографии для получения чистых и сверхчистых продуктов в промышленном масштабе.

Ключевые слова: математическое моделирование экстракционных процессов разделения, жидкостная экстракция, жидкость-жидкостная хроматография

ВВЕДЕНИЕ

Методы жидкостной экстракции, как и жидкостно-жидкостной хроматографии, часто применяются в аналитических целях для выделения из растворов и разделения компонентов смесей органических и неорганических соединений. Жидкостная экстракция широко используется в производствах химической, фармацевтической, гидрометаллургической и других отраслей промышленности для выделения из технологических растворов и очистки промежуточных и конечных продуктов. Жидкостно-жидкостная хроматография ввиду сравнительно малой производительности и сложности конструкции известных центробежных хроматографов пока не нашла заметного промышленного применения и используется в основном лишь для разделения и очистки фармацевтических продуктов в аналитических и препаративных масштабах [1–25]. Производительность применяемых в гидрометаллургии смесительно-отстойных экстракторов на несколько порядков превышает производительность хроматографических аппаратов. Хроматографические методы по сравнению с экстракцией более экономичны, они отличаются малым расходом органических растворителей и химических реагентов, простотой технологической схемы (можно разделять в одну стадию многокомпонентные смеси) и обеспечивают более высокую чистоту получаемых продуктов. Для применения жидкость-жидкостной хроматографии в промышленном масштабе можно использовать каскад смесительно-отстойных экстракторов в качестве экстракционно-хроматографической установки [26, 27]. В таких экстракторах для регулирования соотношения фаз в смесителе обычно имеется возможность рециркуляции одной из фаз между смесителем и отстойником. При работе каскада в режиме хроматографии неподвижная (в терминах хроматографии) органическая фаза не выводится из аппарата, а циркулирует между смесителем и отстойником. В процессах хроматографии, как правило, используется импульсный метод ввода пробы в хроматографическое устройство, что позволяет загружать в хроматограф лишь сравнительно небольшой объем разделяемой смеси компонентов. В жидкость-жидкостной хроматографии импульсный ввод большего объема разделяемого раствора компонентов может привести к нарушению гидродинамического режима работы аппарата с вытеснением неподвижной фазы и, как следствие, к ухудшению качества разделения. Следует отметить, что при загрузке в хроматографическое устройство малых объемов раствора смеси компонентов, как правило, получаются разбавленные фракции разделенных продуктов. В промышленных технологиях экономически целесообразно получать как можно более концентрированные фракции компонентов. Для достижения высокой производительности экстракционно-хроматографического процесса разделения и получения концентрированных фракций чистых продуктов необходимо загружать в установку большие объемы раствора разделяемых соединений, что можно обеспечить путем длительной загрузки. Такая установка должна иметь два резервуара для водной фазы: один с раствором подлежащих разделению компонентов, другой – с водной фазой элюента (с “чистой” подвижной фазой). При непрерывном режиме работы установки насос подвижной фазы периодически переключается с одного резервуара на другой. Подача в установку элюента и разделяемой смеси проводится с одинаковой объемной скоростью, что позволяет загружать большие объемы раствора компонентов без нарушения гидродинамического режима в аппарате.

Целью настоящей работы было проведение сравнительного теоретического анализа процессов разделения в каскаде смесительно-отстойных экстракторов, работающих в режиме противоточной экстракции и жидкость-жидкостной хроматографии.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОЦЕССОВ РАЗДЕЛЕНИЯ В КАСКАДЕ СМЕСИТЕЛЬНО-ОТСТОЙНЫХ ЭКСТРАКТОРОВ

Используя результаты наших предыдущих исследований [26, 28–30], математическую модель процессов хроматографического разделения в каскаде смесительно-отстойных экстракторов можно представить следующими уравнениями:

t > ts

(1)
$\begin{gathered} {{X}_{{1N}}}\left( t \right) = {{e}^{{ - aN\left( {t - {{t}_{s}}} \right)}}} \times \\ \times \,\,\mathop \sum \limits_1^N \left\{ {\frac{{{{{[aN\left( {t - {{t}_{s}}} \right)]}}^{{N - i + 1}}}}}{{\left( {N - i + 1} \right)!}}\left[ {1 - {{e}^{{ - aN{{t}_{s}}}}}\mathop \sum \limits_1^i \frac{{{{{(aN{{t}_{s}})}}^{{i - 1}}}}}{{\left( {i - 1} \right)!}}} \right]} \right\}~, \\ \end{gathered} $

t > ts + tin

(2)
$\begin{gathered} {{X}_{{2N}}}\left( t \right) = {{e}^{{ - aN\left( {t - {{t}_{{{\text{in}}}}} - {{t}_{s}}} \right)}}}\mathop \sum \limits_1^N \left\{ {\frac{{{{{[aN\left( {t - {{t}_{{in}}} - {{t}_{s}}} \right)]}}^{{N - i + 1}}}}}{{\left( {N - i + 1} \right)!}}} \right. \\ \times \,\,\left. {\left[ {1 - {{e}^{{ - aN{{t}_{s}}}}}\mathop \sum \limits_1^i \frac{{{{{(aN{{t}_{s}})}}^{{i - 1}}}}}{{\left( {i - 1} \right)!}}} \right]} \right\}~, \\ \end{gathered} $
(3)
$a = \frac{1}{{1 - S + S{{K}_{D}}}}~.~$

Уравнение (1) описывает изменение концентрации компонента с коэффициентом распределения KD в потоке водной фазы на выходе из каскада экстракторов при периодическом режиме процесса разделения (при одной загрузке разделяемого раствора компонентов). Уравнение (2) описывает изменение концентрации после повторной загрузки раствора компонентов через промежуток времени τin (tin). Таким образом, для моделирования непрерывного процесса, когда раствор компонентов подается в каскад в полу-непрерывном режиме через постоянные интервалы времени tin в течение определенного времени ts (τs), можно использовать уравнения (1) и (2), которые описывают выходные профили концентраций после двух последовательных загрузок раствор компонентов.

В уравнениях (1)–(3) приняты следующие обозначения:

KD = y/x – коэффициент равновесного распределения; x – концентрация в водной фазе, y – концентрация в органической фазе; N – число экстракторов в каскаде; XN = xN/xs – безразмерная концентрация компонента в водной фазе на выходе из установки (в последней ступени каскада); xs – концентрация компонента в исходном растворе; t = τF/Vc – безразмерное время; ts = τsF/Vc – безразмерное время загрузки раствора компонентов (длительность периодов загрузки раствора); tin = τinF/Vc – безразмерный интервал времени между загрузками; F – объемный расход “чистой” водной (подвижной) фазы в периоды ее подачи в каскад и раствора компонентов в периоды его загрузки в каскад; Vc – объем каскада экстракторов; S – доля объема, занимаемая органической (неподвижной) фазой в экстракторах; τs – время (длительность) периодов загрузки раствора компонентов в установку; τin – интервал времени между последовательными загрузками раствора компонентов в установку; τ – время.

При выводе уравнений (1), (2) приняты следующие допущения:

1. В каждой ступени каскада достигается равновесное распределение компонентов между органической и водной фазами, т.е. число теоретических тарелок, определяющих качество разделения, равно количеству экстракторов в каскаде (N).

2. Коэффициент распределения не зависит от концентрации (KD = const, прямая изотерма экстракции).

Для моделирования непрерывного процесса разделения в каскаде экстракторов, работающих в режиме хроматографии, необходимо определить оптимальный интервал между последовательными загрузками раствора компонентов в установку, обеспечивающий максимальную производительность и минимальный расход растворителя. Этот интервал определяется разделением соседних выходных концентрационных профилей от двух последовательных загрузок и может быть рассчитан по формуле:

$\begin{gathered} {{t}_{{{\text{in}}}}} = \frac{3}{{\sqrt {12N} }}\left( {\frac{1}{{{{a}_{l}}}}\sqrt {12 + Na_{l}^{2}t_{s}^{2}} + ~\,\,\frac{1}{{{{a}_{h}}}}\sqrt {12 + Na_{h}^{2}t_{s}^{2}} } \right) - \\ - \,\,{1 \mathord{\left/ {\vphantom {1 {{{a}_{l}}}}} \right. \kern-0em} {{{a}_{l}}}} + {1 \mathord{\left/ {\vphantom {1 {{{a}_{h}}}}} \right. \kern-0em} {{{a}_{h}}}}, \\ \end{gathered} $
где индексом h обозначен параметр а для компонента разделяемой смеси с максимальным коэффициентом распределения, а индексом l – параметр а для компонента смеси с минимальным коэффициентом распределения. Указанные параметры рассчитываются по формуле (3). Другим временным параметром, влияющим на процесс разделения является длительность периодов загрузки раствора компонентов в установку ts (τs): с увеличением продолжительности загрузки растет производительность процесса и концентрация компонентов в отобранных фракциях, но при этом снижается чистота получаемых продуктов.

Концентрация, чистота и выход продуктов хроматографического разделения при заданных параметрах процесса зависит также от времени отбора отдельных фракций: начало отбора – t1 (τ1) и окончание отбора – t2 (τ2). С уменьшением интервала отбора повышается концентрация и чистота, но снижается выход. Эти важные характеристики процессов разделения можно рассчитать следующим образом:

Количество компонента с коэффициентом распределения KDm во фракции (Qf), собранной за интервал времени τ1 – τ2 (в безразмерных единицах времени: t1 – t2):

(5)
$\begin{gathered} {{Q}_{f}} = F{\kern 1pt} \mathop \smallint \limits_{{{\tau }_{1}}}^{{{\tau }_{2}}} {{x}_{{Nm}}}\left( \tau \right)d\tau = F{{x}_{{sm}}}\int\limits_{{{\tau }_{1}}}^{{{\tau }_{2}}} {{{X}_{{Nm}}}\left( t \right)} \frac{{d\tau }}{{{{V}_{c}}}}{{V}_{c}} = \\ = {{V}_{c}}{{x}_{{sm}}}{\kern 1pt} \mathop \smallint \limits_{{{t}_{1}}}^{{{t}_{2}}} {{X}_{{Nm}}}\left( t \right)dt. \\ \end{gathered} $

Концентрация этого компонента (xf) во фракции:

(6)
$\begin{gathered} {{x}_{f}} = \frac{{{{Q}_{f}}}}{{F\left( {{{\tau }_{1}} - {{\tau }_{2}}} \right)}} = \frac{{{{V}_{c}}{{x}_{{sm}}}~}}{{F\left( {{{\tau }_{1}} - {{\tau }_{2}}} \right)}}\mathop \smallint \limits_{{{t}_{1}}}^{{{t}_{2}}} {{X}_{{Nm}}}\left( t \right)dt = \\ = \frac{{{{x}_{{sm}}}}}{{{{t}_{2}} - {{t}_{1}}}}\mathop \smallint \limits_{{{t}_{1}}}^{{{t}_{2}}} {{X}_{{Nm}}}\left( t \right)dt. \\ \end{gathered} $

Или в безразмерных (нормированных) единицах концентрации и времени:

(7)
${{X}_{f}} = \frac{{{{x}_{f}}}}{{{{x}_{{sm}}}}} = \frac{1}{{{{t}_{2}} - {{t}_{1}}}}\mathop \smallint \limits_{{{t}_{1}}}^{{{t}_{2}}} {{X}_{{Nm}}}\left( t \right)dt.$

Выход (степень извлечения) компонента:

(8)
$Y = {{\mathop \smallint \limits_{{{t}_{1}}}^{{{t}_{2}}} {{X}_{{Nm}}}\left( t \right)dt} \mathord{\left/ {\vphantom {{\mathop \smallint \limits_{{{t}_{1}}}^{{{t}_{2}}} {{X}_{{Nm}}}\left( t \right)dt} {\mathop \smallint \limits_0^\infty {{X}_{{Nm}}}\left( t \right)dt}}} \right. \kern-0em} {\mathop \smallint \limits_0^\infty {{X}_{{Nm}}}\left( t \right)dt}} = \frac{1}{{{{t}_{s}}}}~\mathop \smallint \limits_{{{t}_{1}}}^{{{t}_{2}}} {{X}_{{Nm}}}\left( t \right)dt.~$

Чистота компонента:

(9)
$Pu = \frac{{{{q}_{m}}}}{{{{q}_{1}} + {{q}_{2}} + \ldots {{q}_{m}} + {{q}_{{m + 1}}} + \ldots {{q}_{n}}}} \times ~100\% ,$
$\begin{gathered} {{q}_{1}} = {{x}_{{s1}}}\mathop \smallint \limits_{{{t}_{1}}}^{{{t}_{2}}} {{X}_{{N1}}}\left( t \right)dt;\,\,\,\,{{q}_{2}} = {{x}_{{s2}}}\mathop \smallint \limits_{{{t}_{1}}}^{{{t}_{2}}} {{X}_{{N2}}}\left( t \right)dt;~ \\ ~{{q}_{m}} = {{x}_{{sm}}}\mathop \smallint \limits_{{{t}_{1}}}^{{{t}_{2}}} {{X}_{{Nm}}}\left( t \right)dt;~ \\ \end{gathered} $
где: xs1, xs2, xsm – концентрации компонентов с коэффициентами распределения KD1, KD2, KDm в исходном растворе; XN1(t), XN2(t), XNm(t) рассчитываются по уравнению (1).

Математическую модель процессов разделения в каскаде смесительно-отстойных экстракторов в режиме противоточной экстракции можно представить уравнениями [31]:

(10)
${{X}_{N}} = \frac{{{{x}_{N}}}}{{{{x}_{s}}}} = \frac{{{{f}^{N}} - {{f}^{{N + 1}}}}}{{1 - {{f}^{{N + 1}}}}}~,$
${{v}_{y}}{{y}_{1}} = {{v}_{x}}\left( {{{x}_{s}} - {{x}_{N}}} \right)$
или
(11)
${{Y}_{1}} = \frac{{{{y}_{1}}}}{{{{x}_{s}}}} = \frac{{{{v}_{x}}}}{{{{v}_{y}}}}\left( {1 - {{X}_{N}}} \right)~,$
где: $f = \frac{{{{v}_{x}}}}{{{{v}_{y}}m}}~~$ – фактор экстракции; vx – объемная скорость потока водной фазы (исходного раствора (разделяемых компонентов); vy – объемная скорость потока органической фазы (фазы экстрагента); Y1= y1/xs – безразмерная концентрация компонента в органической фазе (в экстракте) на выходе из установки (в первой ступени каскада); xs – концентрация компонента в исходном водном растворе.

В отличие от хроматографии, где фракции разделенных компонентов выводятся из каскада экстракторов с одной (водной) фазой, при работе каскада в режиме противоточной экстракции один из компонентов (или одна группа компонентов) выводится с органической фазой (фазой экстракта), а второй компонент (или группа компонентов) – с водной фазой (фазой экстракта). Концентрации компонентов в выходных потоках фаз определяются формулами (10) и (11). Выходы компонентов при этом составляют:

в фазе рафината:

(12)
${{Y}_{x}} = {{X}_{N}}$
в фазе экстракта:

(13)
${{Y}_{y}} = {\text{ }}1 - {{X}_{N}}.$

Чистота компонента:

в фазе рафината:

(14)
$\begin{gathered} P{{u}_{x}} = \frac{{{{x}_{{N1}}}}}{{{{x}_{{N2}}} + {{x}_{{N1}}}}}~ \times 100\% = \\ = \frac{{{{x}_{{s1}}}{{X}_{{N1}}}}}{{{{x}_{{s2}}}{{X}_{{N2}}} + {{x}_{{s1}}}{{X}_{{N1}}}}} \times 100\% ~ \\ \end{gathered} $

в фазе экстракта:

(15)
$P{{u}_{y}} = \frac{{{{y}_{{12}}}}}{{{{y}_{{11}}} + {{y}_{{12}}}}}~\,\, \times 100\% = \frac{{{{x}_{{s2}}}{{Y}_{{12}}}}}{{{{x}_{{s2}}}{{Y}_{{12}}} + {{x}_{{s1}}}{{Y}_{{11}}}}} \times 100\% ~.~$

В формулах (14) и (15) с нижним индексом 1, 2 и 11, 12 обозначены концентрации компонентов 1 и 2 в фазах рафината и экстракта. Принято, что первый компонент выходит из каскада преимущественно в фазе рафината, а второй – преимущественно в фазе экстракта.

АНАЛИЗ ПРОЦЕССОВ РАЗДЕЛЕНИЯ В КАСКАДЕ СМЕСИТЕЛЬНО-ОТСТОЙНЫХ ЭКСТРАКТОРОВ

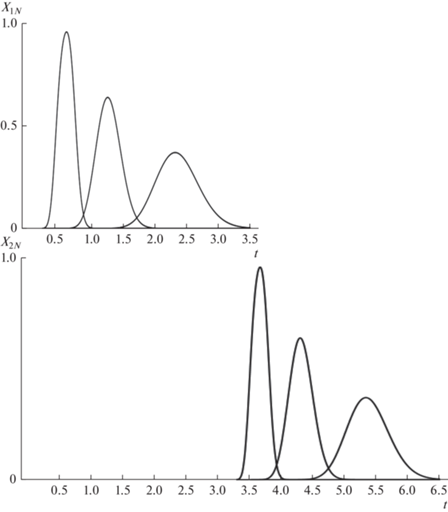
На рис. 1 и рис. 2 приведены результаты моделирования периодического (одна загрузка раствора разделяемых компонентов) и непрерывного (полунепрерывная загрузка раствора компонентов) процессов хроматографического разделения трехкомпонентной смеси (KD1= 0.4, KD2= 1.2, KD3= 2.5) в каскаде из 50 смесительно-отстойных экстракторов в условиях длительной загрузки раствора компонентов ts = 0.3 (30% объема каскада заполняется раствором компонентов). Для периодического процесса выходные профили концентраций рассчитывались по уравнению (1). Для моделирования непрерывного процесса достаточно рассчитать выходные профили концентраций после первой и второй загрузок раствора компонентов. Эти профили рассчитаны по уравнениям (1)–(4).

Рис. 1.

Моделирование периодического процесса хроматографического разделения трехкомпонентной смеси (KD1= = 0.4, KD2= 1.2, KD3= 2.5) в каскаде из 50 смесительно-отстойных экстракторов в условиях длительной загрузки раствора компонентов ts = 0.3 и при S = 0.8. Выходные профили концентраций рассчитаны по уравнению (1).

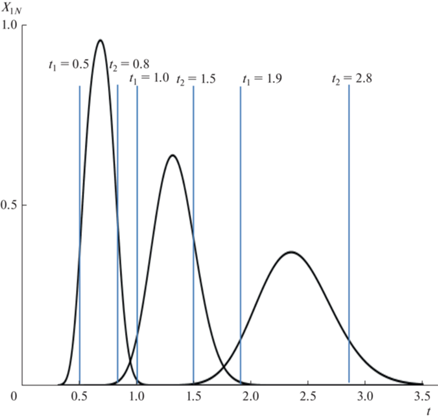
Рис. 2.

Моделирование непрерывного процессов хроматографического разделения трехкомпонентной смеси (KD1= = 0.4, KD2= 1.2, KD3= 2.5). Параметры процесса: N = 50; ts = 0.3; S = 0.8. Выходные профили концентраций рассчитаны по уравнениям (1)–(4).

Как отмечалось выше, от выбора интервала отбора фракций компонентов зависят концентрация, чистота и выход (количество) получаемых продуктов. Эти количественные показатели процесса разделения для выбранных интервалов отбора фракций компонентов можно рассчитать по формулам (7)–(9). Так, при отборе первой фракции в интервале t1 = 0.5 – t2 = 0.8, второй фракции в интервале t1 = 1 – t2 = 1.5 и третей фракции в интервале t1 = 1.9 – t2 = 2.8 расчет по формулам (7)–(9) приводит к следующим результатам:

Первая фракция (компонент KD1= 0.4):

средняя концентрация в отобранной фракции, Xf = 0.79; выход, Y = 79.3%; чистота, Pu = 99.92%.

Вторая фракция (компонент KD2= 1.2):

средняя концентрация в отобранной фракции, Xf = 0.47; выход, Y = 78.4%; чистота, Pu = 99.64%.

Последняя фракция (компонент KD3 = 2.5):

средняя концентрация в отобранной фракции, Xf = 0.278; выход, Y = 83.3%; чистота, Pu = 99.71%.

При расчете чистоты компонентов в отбираемых фракциях по формуле (9) принято, что концентрация всех компонентов в исходном растворе одинакова, т.е. xs1 = xs2 = xs3.

Таким образом, при работе каскада экстракторов в режиме хроматографии можно в одной операции разделить все компоненты смеси с выходом Y = 78.4–83.3% и чистотой получаемых продуктов Pu = 99.64–99.92%. При этом получаются не очень сильно разбавленные (достаточно концентрированные) растворы продуктов. Так в первой фракции концентрация компонента KD1 достигает 79% от его содержания в исходном растворе.

При работе рассматриваемого каскада экстракторов в режиме противоточной экстракции расчеты по формулам (10)–(15) при одинаковых потоках водной и органической фаз (vx = vy) показывают, что в чистом виде можно выделить лишь первый компонент смеси в фазе рафината с выходом Yx = 60% и концентрацией Xf = 0.60. Остальная часть этого компонента в смеси с вторым и третьим компонентом выводится из каскада с фазой экстракта. Следует отметить, что практически такой же результат может быть достигнут и при использовании каскада с меньшим числом аппаратов (N = 10–20). Однако во всех случаях в режиме экстракции нельзя разделить все три компонента. В отличие от экстракции увеличение количества ступеней каскада в режиме хроматографии может существенно улучшить показатели процесса разделения. Так, при N = 100 (рис. 3) при отборе первой фракции в интервале t1 = 0.5 – t2 = = 0.85, второй фракции в интервале t1 = 1 – t2 = 1.5 и третей фракции в интервале t1 = 1.9 – t2 = 2.7 будут получены продукты чистотой Pu = 99.99% и с концентрацией и выходом: в первой фракции (компонент KD1= 0.4): средняя концентрация, Xf = 0.80, выход, Y = 92.9%; во второй фракции (компонент KD2= 1.2): средняя концентрация, Xf = 0.53, выход, Y = 87.8%; в последней фракции (компонент KD3 = 2.5):

Рис. 3.

Моделирование периодического процесса хроматографического разделения трехкомпонентной смеси (KD1= 0.4, KD2= 1.2, KD3= 2.5) в каскаде из 100 смесительно-отстойных экстракторов в условиях длительной загрузки раствора компонентов ts = 0.3 и при S = 0.8. Выходные профили концентраций рассчитаны по уравнению (1).

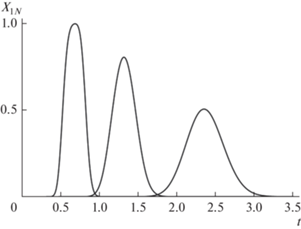
средняя концентрация, Xf = 0.34, выход, Y = 89.4%.

При расчете чистоты компонентов в отбираемых фракциях по формуле (9) как и выше принято xs1 = xs2 = xs3.

Очевидно, что, суживая интервал отбора, можно добиться 100% чистоты продуктов, поэтому хроматография может быть использована для получения сверхчистых веществ.

В режиме хроматографии кроме увеличения количества ступеней в каскаде улучшить показатели процесса разделения можно также за счет повторного прокачивания загруженного раствора компонентов через каскад, т.е. при работе установки в режиме рециркуляционной хроматографии. На рис. 4 приведены результаты моделирования периодического процесса хроматографического разделения трехкомпонентной смеси (KD1= 0.2, KD2= 0.6, KD3 = 1.2) в каскаде из 50 смесительно-отстойных экстракторов, работающих в режиме рециркуляционной хроматографии, после двух проходов загруженного раствора компонентов. Выходные профили концентраций рассчитывались: после первого прохода – по уравнению (1), после второго – по уравнению (16).

$t \geqslant \left( {n - 1} \right)b + {{t}_{s}}$
$\begin{gathered} X\left( {2,t} \right) = {{e}^{{ - aN\left( {t - b - {{t}_{s}}} \right)}}} \times \\ \times \,\,\mathop \sum \limits_1^{2N} \left\{ {\frac{{{{{\left[ {aN\left( {t - b - {{t}_{s}}} \right)} \right]}}^{{2N - i + 1}}}}}{{\left( {2N - i + 1} \right)!}}\left[ {1 - {{e}^{{ - aN{{t}_{s}}}}}\mathop \sum \limits_1^i \frac{{{{{\left( {aN{{t}_{s}}} \right)}}^{{i - 1}}}}}{{\left( {i - 1} \right)!}}} \right]} \right\}~, \\ \end{gathered} $
Рис. 4.

Результаты моделирования периодического процесса разделения трехкомпонентной смеси (KD1 = 0.2, KD2= 0.6, KD3= 1.2) в каскаде из 50 смесительно-отстойных экстракторов, работающих в режиме рециркуляционной хроматографии, после двух проходов загруженного раствора компонентов. Параметры процесса: N = 50; ts = 0.2; S = 0.8. Выходные профили концентраций рассчитывались: после первого прохода – по уравнению (1), после второго – по уравнению (16)

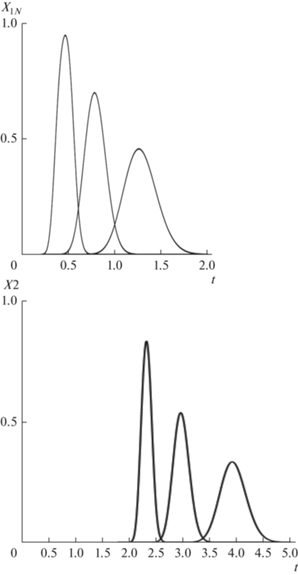
где b = Vr/Vc – соотношение объемов трубопровода рецикла Vr и каскада Vc.

Уравнение (16) получено на основе допущения о движении потока в трубопроводе рецикла в режиме идеального вытеснения, что оправдано при использовании длинного трубопровода малого диаметра.

Расчеты показывают, что качество разделения в каскаде из 50 смесительно-отстойных экстракторов, работающих в режиме рециркуляционной хроматографии, практически соответствуют результатам, которые могут быть достигнуты в каскаде из 100 экстракторов, работающих в режиме обычной хроматографии. Следует отметить, что рециркуляционную схему целесообразно применять при разделении компонентов с малыми величинами коэффициентов распределения (KD = = 0.1–1.5). Для разделения компонентов с большими величинами коэффициентов распределения необходимо использовать очень длинные трубопроводы рецикла, обеспечивающие разделение концентрационных профилей соседних циклов.

ЗАКЛЮЧЕНИЕ

Результаты проведенного теоретического анализа процессов разделения в каскаде смесительно-отстойных экстракторов в режиме жидкость-жидкостной хроматографии и противоточной жидкостной экстракции подтверждают перспективность применения в экстракционных технологиях принципов хроматографии для получения чистых и сверхчистых продуктов в промышленном масштабе. При работе каскада экстракторов в режиме хроматографии можно в одной операции разделить все компоненты смеси с высоким выходом и чистотой получаемых продуктов. Для разделения многокомпонентных смесей можно использовать как простые технологические схемы, так и схемы с рециклом водной фазы. В последнем случае за счет повторного прокачивания загруженного раствора компонентов через каскад можно вдвое сократить число аппаратов в каскаде, необходимое для достижения заданного качества разделения.

Временными параметрами, влияющими на такие важные показатели процесса хроматографического разделения как, концентрация, чистота и выход продуктов, являются длительность периодов загрузки раствора компонентов в установку и интервалы отбора фракций компонентов. В работе приведены зависимости, необходимые для моделирования рассматриваемых процессов и определения их оптимальных параметров.

Исследование выполнено за счет гранта Российского научного фонда № 23-29-00162, https://rscf.ru/project/23-29-00162/

Список литературы

  1. Berthod A., Maryutina T., Spivakov B., Shpigun O., Sutherland I.A. Countercurrent chromatography in analytical chemistry (IUPAC technical report) // PureAppl. Chem. 2009. V. 81. P. 355.

  2. Jerz G., Winterhalter P. The 10th International Conference on Countercurrent Chromatography held at Technische Universität Braunschweig, Braunschweig, Germany, August 1–3, 2018 // J. Chromatogr. A. 2020. V. 1617. Article number 460698.

  3. Friesen J.B., McAlpine J.B., Chen S.-N., Pauli G.F. The 9th International Countercurrent Chromatography Conference held at Dominican University, Chicago, USA, August 1–3, 2016 // J. Chromatogr. A. 2017. V. 1520. P. 1.

  4. Ignatova S., Sutherland I. The 8th International Conference on Counter-current Chromatography held at Brunel University, London, UK, July 23–25, 2014 // J. Chromatography A. 2015. V. 1425. P. 1.

  5. Conway W.D. Counter-current chromatography: Simple process and confusing terminology // J. Chromatogr. A. 2011. V. 1218. P. 6015.

  6. Morley R., Minceva M. Operating mode and parameter selection in liquid–liquid chromatography // J. Chromatogr. A. 2020. V. 1617. Article number 460479.

  7. Ito Y. Golden rules and pitfalls in selecting optimum conditions for high-speed counter-current chromatography // J. Chromatogr. A. 2005. V. 1065. P. 145.

  8. Guilois-Dubois S., Guyot S., Poupard P. Preparative isolation of apple flavan-3-ols monomers and oligomers using pH-zone-refining centrifugal partition chromatography combined with reversed-phase liquid chromatography // J. Chromatogr. A. 2021. V. 1653. Article number 462382.

  9. Li H., Zhang F., Jin Q., Zhu T. Preparative separation and purification of Cyclosporin D from fungus Hypoxylon Spp. by improved closed-loop recycling counter-current chromatography // J. Chromatogr. A. 2021. V. 1649. Article number 462221.

  10. He J.M., Huang J., Wu W.L., Mu Q. Unlimited recycling counter-current chromatography for the preparative separation of natural products: naph- thaquinones as examples // J. Chromatogr. A. 2020. V. 1626. Article number 461368.

  11. Peng A., Hewitson P., Sutherland I., Chen L., Ignatova S. How changes in column geometry and packing ratio can increase sample load and throughput by a factor of fifty in counter-current chromatography // J. Chromatogr. A. 2018. V. 1580. P.120.

  12. Roehrer S., Minceva M. Evaluation of interapparatus separation method transferability in countercurrent chromatography and centrifugal partition chromatography // Separations 2019. V. 6. P. 36.

  13. Wang F., Li R., Long L., Tian X., Xiao Z., Zhang S., Yin H. A three‑phase solvent system in high‑speed counter‑current chromatographic for the separation and purification of bioactive constituents from Acanthus ilicifolius // Chromatographia. 2015. V. 78. P. 1401.

  14. Luan G., Wang H., Lv H., Hu N., Suo Y. Wang X. Separation and purification of five flavone glucosides and one lignan from Caragana korshinskii kom. by the combination of HSCCC and semi‑preparative RPLC // Chromatographia. 2016. V. 79. P. 823.

  15. Liu H., Gong C., Liao Z., Chen T., Li Y. Isolation and purification of three analogues from Clematis akebioides by molecularly imprinted solid‑phase extraction and HSCCC // Chromatographia. 2017. V. 80. P. 1651.

  16. Zhu L.-W., Xie B.-Y., Liu S.-Z., Wu Y.-H., Zhang G.-G., Qiu Y.-K. Development of an on‑line two‑dimensional normal phase liquid chromatography system for analysis of weakly polar samples // Chromatographia. 2023. V. 86. P. 285.

  17. Lin L., Huang L., Ke Y., Xu X., Huang L. Study on quality control of tenofovir disoproxil fumarate enantiomers by high‑performance liquid chromatography–mass spectrometry // Chromatographia. 2023. V. 86. P. 213.

  18. Wang L., Hu C., Zhang J., Gong P., Zhang H., Zhao S. Identification of five flavonoid compounds from the remaining ginger powder purified by using high‑speed counter‑current chromatography and their bioactivity // Food Anal. Methods. 2022. V. 15 P. 485.

  19. Belova V.V. The prospects for using recirculation–countercurrent chromatography for separating multicomponent mixtures // Theor. Found. of Chem. Eng., 2021. V. 55. № 5. P. 1091.

  20. Barker P.E., Knoechelmann A., Ganetsos G. Simulated counter-current moving column chromatography used in the continuous separation of carbohydrate mixtures // Chromatographia. 1990. V. 29. № 3/4. P. 161.

  21. Nyiredy S. Botz L. Medium-pressure solid-liquid extraction: a new preparative method based on the principle of counter-current // Chromatographia Supplement. 2003. V. 57. P. 291.

  22. Ito Y., Clary R., Witten J.J., Zeng Y. Vortex counter-current chromatography: performance of a new preparative column // Chromatographia. 2012. V. 75. P. 1091.

  23. Belova V.V. On rare metal separation by counter-current extraction in chromatography mode // Russ. J. Inorg. Chem. 2016. V. 61. № 12. P. 1601.

  24. Gu D.Y., Yang Y., Zhong J., Aisa H.A., Zhang T.Y. High-speed counter-current chromatography combined with column chromatography for isolation of methyllycaconitine from Delphinium pseudocyanthum // Chromatographia. 2007. V. 66. P. 949.

  25. Hou W., Liu C., Li S., Niu H., Liu Z., Zhang Y., Jin Y., Li X. Efficient combination of ionic‑liquid‑based ultrasound‑assisted extraction, complex chromatography, and molecular docking for screening of acetylcholinesterase inhibitors from Ganoderma atrum // J. Food Meas. Charact. 2023. V. 17. P. 1228.

  26. Костанян А.Е., Милевский Н.А., Вошкин А.А. Анализ процессов экстракционно-хроматографического разделения в каскаде смесительно-отстойных экстракторов // Теорет. основы хим. технологии. 2021. Т. 55. № 5. С. 559.

  27. Костанян А.Е., Иванов В.К., Вошкин А.А. Теоретический анализ периодических процессов экстракционно-хроматографического разделения в замкнутом каскаде аппаратов // ДАН. Химия, науки о материалах. 2021. Т. 499. № 1. С. 53.

  28. Kostanyan A.E. Simple equations to simulate closed-loop recycling liquid–liquid chromatography: ideal and non-ideal recycling models // J.Chromatogr. A. 2015. V. 1423. P. 71.

  29. Kostanyan A.A., Voshkin A.A., Belova V.V. Analytical, Preparative, and Industrial-Scale Separation of Substances by Methods of Countercurrent Liquid-Liquid Chromatography // Molecules. 2020. V. 25. Article number 6020.

  30. Костанян А.Е., Вошкин А.А. Математическое моделирование процессов разделения методами жидкость-жидкостной хроматографии // Теорет. основы хим. технологии. 2023. Т. 57. № 1. С. 3.

  31. Айнштейн В.Г., Захаров М.К., Носов Г.А., Захаренко В.В., Зиновкина Т.В., Таран А.Л., Костанян А.Е. Общий курс процессов и аппаратов химической технологии. Учебник в 2 кн.: Физматкнига. Москва.: Логос, 2006.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Теоретические основы химической технологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал