Высокомолекулярные соединения (серия А), 2020, T. 62, № 2, стр. 146-155
КИНЕТИЧЕСКАЯ МОДЕЛЬ СТРУКТУРНОЙ РЕЛАКСАЦИИ В ПЛЕНКЕ ДИБЛОК-СОПОЛИМЕРА
Д. А. Филатов a, Е. Н. Говорун b, *, Я. В. Кудрявцев c
a Институт элементоорганических соединений имени А.Н. Несмеянова Российской академии наук
119991 Москва, ул. Вавилова, 28, Россия
b Московский государственный университет имени М.В. Ломоносова. Физический факультет
119991 Москва, Ленинские горы, 1-2, Россия
c Институт нефтехимического синтеза им. А.В. Топчиева Российской академии наук
119991 Москва, Ленинский пр., 29, Россия
* E-mail: govorun@polly.phys.msu.ru
Поступила в редакцию 16.07.2019
После доработки 10.08.2019
Принята к публикации 04.09.2019
Аннотация
Разработана релаксационная модель “созревания” структуры при отжиге микрофазно расслоенной полимерной пленки. Выведены уравнения, описывающие появление и аннигиляцию дефектов в кинетически контролируемом режиме и основанные на экспериментальных данных об эволюции гексагональной структуры. С их помощью проанализированы законы изменения масштаба бездефектных областей со временем. Обнаружено, что доминирование процесса аннигиляции дефектов при их тройном контакте приводит к степенной зависимости ориентационной корреляционной длины ξor ~ t1/4, экспериментально наблюдаемой при высокой температуре отжига. Более подробный анализ эволюции двух типов дефектов (дислокаций и дисклинаций) показывает, что такая зависимость может выполняться и в модели, учитывающей аннигиляцию пар и четверок дисклинаций при условии влияния дислокаций на этот процесс. Полученные результаты демонстрируют возможности макрокинетических моделей для описания структурных перестроек в пленках блок-сополимеров.
ВВЕДЕНИЕ
Микрофазное расслоение в пленках диблок-сополимеров и возможность быстрой и управляемой релаксации их структуры активно исследуются в течение двух последних десятилетий [1–17]. Целью подобных работ является получение образцов со строго периодическим расположением доменов нанометрового размера на как можно большем пространственном масштабе. Используя такие образцы в качестве наношаблонов, можно изготавливать покрытия, обладающие большим потенциалом практического применения и уже используемые для создания супергидрофобных поверхностей, молекулярных сенсоров и прозрачных электродов [18–20].
Локальная сегрегация блоков макромолекулы при нагревании образца выше температуры стеклования протекает достаточно быстро. В дальнейшем в пленке происходит так называемое “созревание фаз” – увеличение пространственного размера ξ областей (“зерен”) с бездефектной микрофазно расслоенной структурой. При отжиге образца в вакууме изменение величины ξ как правило асимптотически описывается степенным законом ξ ~ ktα, где коэффициент k определяется характерным временем изменения размера области и зависит от температуры, а показатель степени α отражает механизм процесса [1].
Размер области ξ оценивают различными способами. С. Harrison c cоавторами [3] проанализировали различные виды структурных перестроек горизонтально ориентированных цилиндров в пленке диблок-сополимера полистирол–полиизопрен по данным растровой электронной микроскопии и в пленке ПС – чередующийся сополимер этилена и пропилена по данным атомно-силовой микроскопии. По интенсивности затухания корреляционной функции ориентации цилиндрических доменов определяли ориентационную корреляционную длину ξor и характерное расстояние между дефектами ξ = 1/ρ1/2, где ρ – поверхностная плотность дисклинаций типа +1/2 в пленке. Обе эти величины симбатно изменялись во времени и при высокой температуре отжига описывались степенной функцией ξor, ξ ~ tα (α = 0.25 ± 0.03). При меньшей температуре отжига зависимость размера области от времени нельзя было описать степенной функцией, что объясняли близостью к температуре стеклования полимерных блоков.
Для пленок диблок-сополимера ПС–ПММА (Mn ≈ 67 кг/моль, 30 мас. % ПММА) C.T. Black и соавт. в работе [4] изучали упорядочение системы вертикально ориентированных цилиндров из блоков ПММА диаметром 20 нм в матрице ПС при 165°С. В качестве корреляционной длины ξ0 было введено расстояние, соответствующее последнему различимому пику в спектре (гистограмме) расстояний между цилиндрами. Таким cпособом удалось проследить за процессом увеличения бездефектных областей вплоть до масштаба ~400 нм. Зависимость ξ0 от времени также была близка к степенной: ξ0 ~ tα с показателем α = = 0.28 ± 0.04.
Сопоставление поведения пленок диблок-сополимера ПС–ПММА (Mn ≈ 64 кг/моль, 34 мас. % ПММА) для горизонтальной и вертикальной ориентации цилиндров, соответствующей разным типам взаимодействия с подложкой, показало, что и для горизонтальной ориентации при 180–210°С наблюдаемое значение показателя α близко к 1/4 [5].
Механизм созревания структуры варьируется от системы к системе, что отражается на значении показателя α. Для пленок диблок-сополимера ПС–ПММА cо структурой ламелей, ориентированных перпендикулярно подложке, величина α заметно меньше и зависит от ММ полимера [5]: α ≈ 0.14 и 0.02 при Mn ≈ 32 и 46 кг/моль соответственно.
Для пленок со слоем гексагонально упакованных сферических доменов из блоков полиизопрена в матрице ПС показатели степени α во временнόй зависимости ориентационной корреляционной длины ξor и корреляционной длины ξ, рассчитанной из концентрации дефектов, составили ≈1/4 и 1/5 [6].
Первые теоретические модели созревания фаз были предложены для металлических сплавов в терминах диффузионной теории, описывающей движение искривленной межфазной границы [21]. В предположении, что полная площадь межфазной поверхности обратно пропорциональна среднему значению ее кривизны, предсказано, что характерный размер доменов асимптотически растет со временем как t1/2.
Двумерная задача о созревании фаз в двухкомпонентной системе, переходящей путем спинодального распада от однородного состояния к ламеллярной структуре, изучалась аналитически и с помощью численных расчетов [22, 23]. На основе разложения свободной энергии по малому параметру порядка в рамках теории Гинзбурга–Ландау с учетом гидродинамических эффектов было предсказано, что в случае малой вязкости характерный размер структуры изменялся ∼lnt, что в двойных логарифмических координатах ближе всего к показателю степени α = 0.3 [23].
Поведение системы дефектов в двумерной системе, характеризующейся векторным параметром порядка, проанализировано в работах [24, 25]. Эволюцию параметра порядка при “замораживании” системы до нулевой температуры описывали уравнением Ланжевена без учета теплового шума. Положение дефектов отождествляли с точками, где параметр порядка обращается в ноль. Предсказано, что зависимость среднего расстояния между дефектами от времени имеет вид (t/lnt)1/2 [25].
Ранее эта зависимость была найдена аналитически для похожей модели [26] релаксации дефектов в пленках ЖК-смектиков, где для оценки принимали, что свободная энергия дефекта и сила трения между двумя сближающимися дефектами пропорциональны логарифму размера дефекта. Заметим, что в двойном логарифмическом масштабе зависимость вида (t/lnt)1/2 соответствует значению показателя степени α несколько выше 0.5. В работе [26] также предполагали, что временная зависимость среднего расстояния между дефектами в пленке и зависимость расстояния Δr между двумя сближающимися дефектами от времени до момента их аннигиляции имеют одинаковый вид. Такое же допущение для описания сближения трех или четырех дефектов приводит к оценке Δr ~ t1/4, что согласуется с экспериментально наблюдаемой временной зависимостью корреляционной длины [3].
Непосредственный анализ изображений пленки [3] показывает, что при укрупнении бездефектных областей существенную роль играет аннигиляция в тройках и четверках дисклинаций. В этих случаях пара дисклинаций аннигилирует в непосредственной близости от третьей дисклинации (или от другой их пары), которая поглощает энергетически невыгодные дислокации, образующиеся в процессе сближения дисклинаций.
Такая картина процесса не противоречит результатам компьютерного моделирования пленки диблок-сополимера со структурой горизонтально ориентированных цилиндров [27]. Оценки показывают, что избыточная свободная энергия, связанная с наличием дефекта, равна 2–7 kBT для дислокаций и 5–20 kBT для дисклинаций, а аннигиляция пары дефектов требует преодоления нескольких энергетических барьеров.
Заметим, однако, что средний размер “зерен” и его зависимость от времени при отжиге не имеют прямого отношения к зависимости расстояния между сближающимися дефектами в паре или квадруполе от времени до их аннигиляции. В связи с этим использование такого предположения из скейлинговых соображений в теоретических оценках работ [3] и [26] представляется некорректным. При сближении двух дисклинаций одновременно растет расстояние между дисклинациями в других парах, а среднее расстояние между дефектами вообще не меняется при их движении в отсутствие аннигиляции.
В настоящей работе сделана попытка корректного теоретического анализа имеющихся экспериментальных данных. Мы формулируем и анализируем две кинетические модели поведения поверхностной плотности дефектов в системе горизонтальных цилиндрических мицелл, которая в эксперименте в большинстве случаев демонстрирует универсальную степенную зависимость от времени с показателем степени α ≈ 0.25. Для расчета изменения количества дефектов и среднего расстояния между ними используются упрощенная модель аннигиляции дисклинаций при их тройных и четверных контактах и более детальная модель, описывающая поведение как дисклинаций, так и дислокаций в предположении, что парная аннигиляция дисклинаций контролируется присутствием дислокаций.
МОДЕЛЬ
Дефекты микроструктуры в пленке диблок-сополимера, образующего цилиндры, ориентированные вдоль подложки, можно разделить на элементарные дислокации и дисклинации (поворотные дислокации), как и при описании дефектов в кристаллах [28]. Различные типы дефектов в расположении системы горизонтально ориентированных цилиндров на поверхности пленки диблок-сополимера схематически изображены ниже.

(1 – дисклинация типа +1/2, 2 – дисклинация типа –1/2, 3 – дислокация).
Согласно экспериментальным данным работы [3], поверхностная плотность дисклинаций типов +1/2 и –1/2 примерно одинакова, а временные зависимости ориентационной корреляционной длины и среднего расстояния между дисклинациями, рассчитанного по их поверхностной плотности, симбатны. Это позволяет рассматривать изменение ориентационной корреляционной длины со временем в терминах поверхностной плотности дефектов.
Обозначим через ndl и ndc поверхностную плотность дислокаций и суммарную поверхностную плотность дисклинаций cоответственно. Будем предполагать, что процесс аннигиляции дефектов является кинетически контролируемым, т.е. вероятность контакта пары дефектов пропорциональна произведению их поверхностных плотностей. Тогда степенной асимптотический закон роста корреляционной длины со временем ξor ~ t1/4 должен соответствовать механизму аннигиляции дисклинаций при их тройном взаимодействии, который описывается кинетическим уравнением
Его решение с начальным условием ndс(0) = ndс0 имеет вид
а зависимость размера “зерна” (бездефектной области) $\xi = {1 \mathord{\left/ {\vphantom {1 {n_{{dc}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} \right. \kern-0em} {n_{{dc}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}$ от времени задается выражением ${{\xi }^{4}}(t) = {{\xi }^{4}}(0) + {{a}_{3}}t$. Следовательно, при ${{\xi (t)} \mathord{\left/ {\vphantom {{\xi (t)} {\xi (0)}}} \right. \kern-0em} {\xi (0)}} \gg 1$ ξ ~ t1/4.Заметим, что другие виды асимптотической зависимости ξ от времени подразумевают наличие иных механизмов аннигиляции. Если бы исчезновение дефектов происходило путем аннигиляции пар или четверок дисклинаций, процесс описывался бы уравнением $\frac{{d{{n}_{{dc}}}}}{{dt}} = - {{a}_{2}}n_{{dc}}^{2}$ или $\frac{{d{{n}_{{dc}}}}}{{dt}} = - {{a}_{4}}n_{{dc}}^{4}$ соответственно. Тогда зависимости размера “зерна” от времени асимптотически имели бы вид ξ ~ t1/2 или ξ ~ t1/6.
Из данных эксперимента [3] следует, что элементарные дислокации возникают вблизи дисклинаций в результате тепловых флуктуаций и впоследствии дрейфуют по пленке. Кроме того, появление и исчезновение дислокаций может быть связано со сближением или расхождением ближайших дисклинаций. Поскольку любые дефекты энергетически невыгодны, это затрудняет сближение дисклинаций в любой паре и, следовательно, их аннигиляцию. Вместе с тем присутствие в окрестности такой пары дефектов еще одной или двух дисклинаций облегчает процесс сближения, так как возникающая дислокация может быть поглощена этими дисклинациями.
Пусть имеются три или четыре дисклинации на характерном расстоянии r друг от друга. Авторы [3] полагают, что для сближения двух из них на толщину d одного слоя микроструктуры необходимо переместить возникающую при этом дислокацию на расстояние r, причем ее скорость υ пропорциональна эффективной движущей силе f. Эта сила в свою очередь определяется видом зависимости ориентационной свободной энергии деформации, связанной с наличием дефектов, от расстояния r между ними: E ~ ln(r/d). Изменение энергии при сближении дисклинаций на один слой ΔE ~ 1/r, сила f ~ ΔE/r ~ 1/r2, время сближения на один слой dt ~ r/υ ~ r3. Тогда закон движения dr/dt ~ –1/r3 соответствует зависимости r ~ ~ (tf – t)1/4, где tf задает момент времени, в который происходит аннигиляция.
Далее авторы [3] принимают, что временная зависимость расстояния между аннигилирующими дефектами описывает и эволюцию среднего расстояния между любыми дефектами (ξ ~ t1/4). Такое допущение сомнительно, поскольку среднее расстояние между дефектами определяется их общим количеством, а корреляции возникают лишь между дислокациями и дисклинациями, расположенными близко друг к другу.
Мы будем описывать кинетику процесса в терминах поверхностной плотности дислокаций и дисклинаций с помощью двух моделей. Упрощенная модель I описывает процесс аннигиляции дисклинаций при их тройных и четверных контактах:
(3)
$\frac{{d{{n}_{{dc}}}}}{{dt}} = - {{a}_{3}}n_{{dc}}^{3} - {{a}_{4}}n_{{dc}}^{4},\quad {{n}_{{dc}}}(0) = {{n}_{{dc0}}}$Для безразмерных величин ${{\tilde {n}}_{{dc}}} = {{n}_{{dc}}}{\text{/}}{{n}_{{dc0}}}$, τ = t/t0 имеем
(4)
$\frac{{d{{{\tilde {n}}}_{{dc}}}}}{{d\tau }} = - {{\alpha }_{3}}\tilde {n}_{{dc}}^{3} - {{\alpha }_{4}}\tilde {n}_{{dc}}^{4},\quad {{\tilde {n}}_{{dc}}}(0) = 1,$Введя обозначение $z = \frac{1}{{{{{\tilde {n}}}_{{dc}}}}}$, при a4 ≠ 0 нетрудно получить решение уравнения (4) z(τ) в неявном виде:
(5)
$\frac{{(z - 1)(z + 1 - 2\alpha )}}{2} + {{\alpha }^{2}}\ln \frac{{z + \alpha }}{{1 + \alpha }} = {{\alpha }_{3}}\tau ,\quad \alpha = \frac{{{{\alpha }_{3}}}}{{{{\alpha }_{4}}}}$Величина a3 имеет размерность отношения квадрата площади ко времени. Cвяжем единичное время t0 с характерным временем аннигиляции дисклинаций из сблизившейся тройки, оказавшейся на площади Sсr = 10d2 (d – период структуры): t0 = $S_{{{\text{сr}}}}^{2}{\text{/}}{{a}_{3}}$ = 100d4/a3. Cопоставляя экспериментальные значения корреляционной длины и времени c асимптотическим решением уравнения (1)
находим t0 ≈ 200 c по рис. 6 работы [3] при T = = 443 К, d ≈ 25 нм и t0 ≈ 1120 c по рис. 4 работы [4] при T = 438 К, d ≈ 40 нм.Рис. 1.
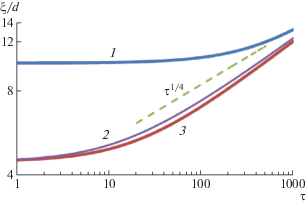
Зависимость характерного расстояния между дефектами $\xi = {1 \mathord{\left/ {\vphantom {1 {n_{{dc}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} \right. \kern-0em} {n_{{dc}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}$ от времени τ = t/t0 для модели I, рассчитанная по уравнению (4) при аннигиляции только троек дисклинаций (a3 = 100d4/t0, a4 = 0) для начальной поверхностной плотности ndс0 = 0.01/d2 (1) и 0.05/d2 (3), а также при аннигиляции троек и четверок дисклинаций (a3 = 100d4/t0, a4 = 1000d6/t0) для ndс0 = = 0.05/d2 (2). Штриховая линия – зависимость ξ ~ τ1/4.
Более подробное описание процесса исчезновения дефектов дается моделью II, основанной на анализе их поведения [3] и учитывающей взаимное влияние дислокаций и дисклинаций. Примем во внимание, что при сближении дисклинаций одновременно может произойти аннигиляция только двух или четырех дефектов, причем процесс аннигиляции пары затруднен, если в непосредственной близости находится дислокация. Будем считать, что величина s0 описывает площадь поверхности, на которую распространяется деформирующее влияние дислокации в пленке, и введем множитель f(s0ndl) для описания вероятности аннигиляции пары дисклинаций в присутствии дислокации. Величину f зададим двумя способами. Первый – линейно убывающая с ростом поверхностной плотности дислокаций функция: f = 1 – s0ndl. Аналогичный подход был использован нами ранее [29] при изучении роста частицы дисперсной фазы в расплаве гомополимеров А и В в присутствии диблок-сополимера АВ на поверхности частицы, контролирующего проникновение в нее макромолекул из непрерывной фазы. Второй способ – зависимость аррениусовского типа $f = {{e}^{{ - {{s}_{0}}{{n}_{{dl}}}}}}$, отвечающая энергетическому барьеру, пропорциональному поверхностной плотности дислокаций.
Изменение поверхностной плотности дислокаций ndl будем описывать уравнением, учитывающим несколько возможных путей их появления и исчезновения, зафиксированных при анализе изображений поверхности пленки [3]:
(6)
$\frac{{d{{n}_{{dc}}}}}{{dt}} = - {{a}_{2}}n_{{dc}}^{2}f({{s}_{0}}{{n}_{{dl}}}) - {{a}_{{4d}}}n_{{dc}}^{4},$(7)
$\frac{{d{{n}_{{dl}}}}}{{dt}} = {{b}_{0}}{{n}_{{dc}}} - {{b}_{1}}{{n}_{{dl}}}{{n}_{{dc}}} - {{b}_{2}}n_{{dl}}^{2} + (3{\text{/}}2){{a}_{2}}n_{{dc}}^{2}f({{s}_{0}}{{n}_{{dl}}}),$В правой части уравнения (7) первое слагаемое описывает спонтанное появление дислокаций вблизи одиночных дисклинаций, второе и третье слагаемые – возможность поглощения дислокации при сближении с дисклинацией и аннигиляцию пары подошедших друг к другу дислокаций, а четвертое – возникновение дислокаций при аннигиляции пары дисклинаций.
Заметим, что значения коэффициентов ai, bj (i = 2, 3, 4; j = 0, 1, 2) в уравнениях (3)–(7), задающих вероятности различных типов структурных перестроек, должны увеличиваться с ростом температуры. В частности, они определяют скорость сближения дефектов, попавших в поле деформации друг друга. Это делает нашу модель более гибкой, чем модель работы [3], в которой постулировался вязкий характер движения, что сразу влияло на вид уравнений движения, а не только на числовые коэффициенты в них.
Для безразмерных величин поверхностной плотности дефектов ${{\tilde {n}}_{{dc}}} = {{{{n}_{{dc}}}} \mathord{\left/ {\vphantom {{{{n}_{{dc}}}} {{{n}_{{dc0}}}}}} \right. \kern-0em} {{{n}_{{dc0}}}}}$, ${{\tilde {n}}_{{dl}}} = {{{{n}_{{dl}}}} \mathord{\left/ {\vphantom {{{{n}_{{dl}}}} {{{n}_{{dl0}}}}}} \right. \kern-0em} {{{n}_{{dl0}}}}}$ и времени τ = t/t0 уравнения (6) и (7) принимают вид
(8)
$\frac{{d{{{\tilde {n}}}_{{dc}}}}}{{d\tau }} = - {{\alpha }_{2}}\tilde {n}_{{dc}}^{2}f({{\tilde {s}}_{0}}{{\tilde {n}}_{{dl}}}) - {{\alpha }_{{4d}}}\tilde {n}_{{dc}}^{4},$(9)
$\frac{{d{{{\tilde {n}}}_{{dl}}}}}{{d\tau }} = {{\beta }_{0}}{{\tilde {n}}_{{dc}}} - {{\beta }_{1}}{{\tilde {n}}_{{dl}}}{{\tilde {n}}_{{dc}}} - {{\beta }_{2}}\tilde {n}_{{dl}}^{2} + (3{\text{/}}2){{\tilde {\alpha }}_{2}}\tilde {n}_{{dc}}^{2}f({{\tilde {s}}_{0}}{{\tilde {n}}_{{dl}}})$Здесь ${{\alpha }_{2}} = {{a}_{2}}{{t}_{0}}{{n}_{{dc0}}}$, ${{\tilde {s}}_{0}} = {{s}_{0}}{{n}_{{dl0}}}$, ${{\alpha }_{{4d}}} = {{a}_{{4d}}}{{t}_{0}}n_{{dc0}}^{3}$, β0 = = ${{{{b}_{0}}{{t}_{0}}{{n}_{{dc0}}}} \mathord{\left/ {\vphantom {{{{b}_{0}}{{t}_{0}}{{n}_{{dc0}}}} {{{n}_{{dl0}}}}}} \right. \kern-0em} {{{n}_{{dl0}}}}}$, ${{\beta }_{1}} = {{b}_{1}}{{t}_{0}}{{n}_{{dc0}}}$, ${{\beta }_{2}} = {{b}_{2}}{{t}_{0}}{{n}_{{dl0}}}$, ${{\tilde {\alpha }}_{2}}$ = = ${{a}_{2}}{{t}_{0}}n_{{dc0}}^{2}{\text{/}}{{n}_{{dl0}}}$ = α2t0ndc0/ndl0.
Таким образом, в модели II поверхностные плотности дисклинаций и дислокаций изменяются согласованно друг с другом.
Анализ процесса релаксации структуры пленки в эксперименте свидетельствует о том, что для дислокаций дрейф и аннигиляция происходят более интенсивно, чем для дисклинаций, а поверхностная плотность дислокаций в течение всего процесса созревания фаз в 10–15 раз превышает поверхностную плотность дисклинаций одного из типов (+1/2 или –1/2) [3]. При этом поверхностная плотность дисклинаций разного типа примерно одинакова, а отношение поверхностных плотностей дислокаций и дисклинаций постепенно растет со временем.
Если предположить, что последнее отношение при отжиге постоянно и равно с = ndl0/ndс0, то при a4d = 0 уравнение (6) c множителем f в виде экспоненты принимает вид
а его решение можно записать в квадратурах:(11)
$\int\limits_k^{{{k}_{0}}} {dx\frac{1}{{{{x}^{2}}}}{{e}^{x}}} = \frac{{{{a}_{2}}}}{{c{{s}_{0}}}}t,$Проанализируем теперь решения уравнений упрощенной модели I, которая при a4 = 0 предсказывает строго линейную зависимость ξ4 от t, и детальной модели II и сравним полученные зависимости.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Уменьшение количества дисклинаций при их тройных контактах описывается уравнением (3) упрощенной модели I при a3 ≠ 0, a4 = 0. Решение этого уравнения дается соотношением (2), которое представляет собой линейную зависимость величины (1/ndс)2 от времени. Асимптотическая зависимость размера бездефектной области ξ = $1{\text{/}}n_{{dc}}^{{1/2}}$ от времени вида ξ ~ t1/4, которая соответствует экспериментальным данным при достаточно высокой температуре отжига, должна выполняться при ${{n}_{{dс}}}(t){\text{/}}{{n}_{{dс}}}_{0} \ll 1$ или $t \gg 1{\text{/}}({{a}_{3}}{{n}_{{dc0}}})$, что при ${{t}_{0}}\, = \,S_{{{\text{cr}}}}^{2}{\text{/}}{{a}_{3}}$ = = 100d4/a3 соответствует $t{\text{/}}{{t}_{0}} \gg 0.01{\text{/}}{{({{n}_{d}}{{_{с}}_{0}})}^{2}}$. На рис. 1 в двойном логарифмическом масштабе построена зависимость ξ от безразмерного времени τ = = t/t0, рассчитанная из выражений (2) при a4 = 0 и (5) при a4 ≠ 0.
При созревании структуры путем аннигиляции дисклинаций только в тройках (a4 = 0) зависимость ξ от времени раньше выходит на асимптотику τ1/4 при большем начальном значении поверхностной плотности дефектов ndс0, поскольку кривая 3 соответствует впятеро большему значению ndс0 по сравнению с кривой 1. Для учета вклада аннигиляции квадруполей значение коэффициента а4 выбрано так, чтобы дисклинации, оказавшиеся на площади Sсr, исчезали за то же характерное время t0, что и при тройном контакте: ${{a}_{4}} = S_{{{\text{cr}}}}^{3}{\text{/}}{{t}_{0}}$ (Sсr = 10d2). Сравнивая кривые 2 и 3, видим, что учет аннигиляции квадруполей уменьшает наклон кривой ξ(t), причем эффект ослабевает со временем из-за снижения поверхностной плотности дефектов.
Рассмотрим теперь детальную модель II созревания структуры, учитывающую наличие дислокаций и взаимное влияние дисклинаций и дислокаций на ход процесса с помощью уравнений (6) и (7). Так как принимается, что дисклинации аннигилируют в парах и четверках, при стремлении поверхностной плотности дефектов к нулю основной вклад в убыль дисклинаций будет вносить первое слагаемое в уравнении (6), a f → 1 при ndl → 0. Следовательно, асимптотически процесс увеличения размера ξ в модели II описывается зависимостью ~t1/2. Такой режим может, однако, лежать вне экспериментально наблюдаемого диапазона значений поверхностной плотности дефектов.
Для численного решения кинетических уравнений сначала найдем поверхностную плотность дефектов ndl и ndс при a4d = 0, выбирая коэффициенты в уравнениях (6) и (7) таким образом, чтобы процесс роста бездефектных областей описывался кривой ξ(t), похожей на результат расчета для упрощенной модели I при a3 = 100d4/t0, a4 = 0. Кроме того, будем стремиться обеспечить согласованное уменьшение поверхностных плотностей дислокаций и дисклинаций, при котором их отношение постепенно увеличивается, как наблюдали экспериментально в работе [3]. Эти условия позволяют подобрать оптимальные значения коэффициентов a2, b0, b1, b2, s0 и построить на рис. 2 графики изменения ξ и ndl, ndс со временем для модели II с функциями f(s0ndl) вида 1 – s0ndl и ${{e}^{{ - \,{{s}_{0}}{{n}_{{dl}}}}}}$ при ndl0 = 0.1/d2, ndс0 = 0.01/d2. Для сравнения показана кривая 4, построенная по формуле (10), которая задает решение уравнения (7) при ndl/ndс = const. На рис. 2 и последующих рисунках зависимости ξ от τ представлены в двойном логарифмическом масштабе.
Рис. 2.
Зависимость размера ξ (а) и поверхностной плотности дислокаций ndl и дисклинаций nds (б) от времени τ = t/t0 для детальной модели II при a4d = 0 с коэффициентом f = 1 – s0ndl при a2 = 5d2/t0 (кривые 1 и 1') и f = ${{e}^{{ - \,{{s}_{0}}{{n}_{{dl}}}}}}$ при a2 = = 2d2/t0 (кривые 2 и 2'), а также в модели I при a3 = 100d4/t0 (кривые 3). Кривая 4 построена по уравнению (10) при c = 10 и a2 = 5d2/t0. Штриховой линией показан наклон зависимости ξ ~ τ1/4. Параметры модели: ndl0 = 0.1/d2, ndс0 = 0.01/d2, b0 = 30/t0, b1 = 10d2/t0, b2 = 30d2/t0, s0 = 9d2.
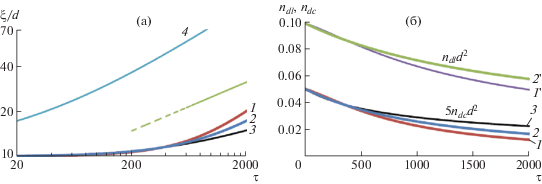
Сравнивая кривые 1, 2 (модель II) и 3 (модель I), приходим к выводу, что модель II, описывающая аннигиляцию при парных контактах дисклинаций, до времени ∼1000t0 дает результат, близкий к модели I, учитывающей аннигиляцию при контакте трех дисклинаций. Затем наклон кривых 1 и 2 в двойном логарифмическом масштабе начинает превышать 1/4. Кривая 2, рассчитанная с коэффициентом f вида ${{e}^{{ - \,{{s}_{0}}{{n}_{{dl}}}}}}$, демонстрирует более плавное изменение ξ, чем кривая 1, для которой f = 1 − s0ndl.
Кривая 4, описывающая приближенное решение системы уравнений (6) и (7) при ndl/ndс = = ndl0/ndс0 = const по формуле (10), идет гораздо выше кривой 1, отвечающая точному решению уравнений (6) и (7) с таким же значением коэффициента a2. Таким образом, даже медленное увеличение отношения ndl/ndс со временем существенно замедляет аннигиляцию дефектов.
Коэффициенты b0, b1 и b2 задают интенсивность процессов генерации дислокаций одиночными дисклинациями, парной аннигиляции дислокаций и поглощения дислокаций дисклинациями соответственно. Значения b1 и b2 описывают парные процессы и по порядку величины выбраны равными Sсr/t0. При этом значение b0 необходимо сделать достаточно большим, чтобы обеспечить согласованное изменение ndl и ndс и постепенный рост их отношения. В численных расчетах принимали, что b0 соответствует появлению нескольких десятков дислокаций за время t0.
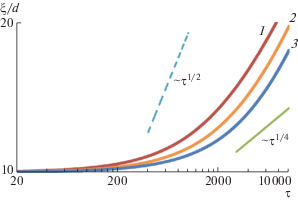
Решение системы уравнений модели II с учетом аннигиляции квадруполей будем искать при значении ${{a}_{{4d}}} = S_{{{\text{cr}}}}^{3}{\text{/}}{{t}_{0}}$ (Sсr = 10d2), таком же, как в модели I при расчете кривой 2 на рис. 1. С учетом возможности аннигиляции дисклинаций в парах и в четверках в детальной модели II удалось подобрать значения коэффициентов так, чтобы рост ξ описывался подобно упрощенной модели I при учете аннигиляции только в тройках (a3 ≠ 0, a4 = = 0) – кривые 1–3 на рис. 3. Значение коэффициента a2 выбрано несколько меньшим, чем для случая с а4d = 0 (рис. 2): а2 = 0.5d2/t0.
Рис. 3.
Зависимость размера ξ (а) и поверхностной плотности дислокаций ndl и дисклинаций ndс (б) от времени τ = t/t0 для модели II при a4d ≠ 0 с линейным коэффициентом f = 1 – s0ndl (1, 1') и exp(–s0ndl) (2, 2') при a2 = 0.5d2/t0, a4d = 1000d6/t0, а также для модели I при a3 = 100d4/t0 (3). Штриховой линией показана зависимость ξ ~ τ1/4. Параметры модели: ndl0 = 0.1/d2, ndс0 = 0.01/d2, b0 = 30/t0, b1 = 10d2/t0, b2 = 30d2/t0, s0 = 9d2.
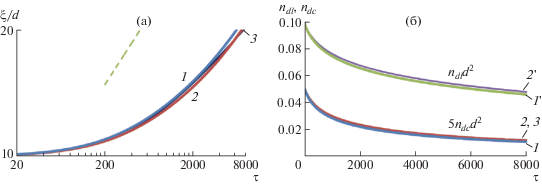
Таким образом, при определенном соотношении интенсивностей элементарных процессов одна и та же зависимость ξ(t) в некотором диапазоне времени может быть выведена как из упрощенной модели I, так и из детальной модели II. Далее мы исследуем влияние изменения значений отдельных коэффициентов на рост размера бездефектной области.
На рис. 4 представлены зависимости ξ от времени при трех различных значениях коэффициента b0, описывающего генерацию дислокаций одиночными дисклинациями за счет тепловых флуктуаций. Остальные параметры модели II постоянны, аннигиляция четверок дисклинаций не принимается во внимание (а4 = 0). Увеличение b0 соответствует росту отношения ndl/ndс при одинаковых значениях ndс и ξ, что приводит к более сильному подавлению парной аннигиляции и, как следствие, к замедлению роста ξ.
Изменение значения коэффициента b1 в несколько раз практически не влияет на вид зависимости ξ(t). Напротив, увеличение коэффициента b2, отвечающего за парную аннигиляцию дислокаций, снижает их поверхностную плотность, что ускоряет рост ξ (рис. 5). Бόльшая роль аннигиляции дислокаций по сравнению с их поглощением дисклинациями связана с тем, что для дислокаций поверхностная плотность и вероятность их парного контакта на заданной площади на порядок выше, чем поверхностная плотность дисклинаций и вероятность контакта дислокации с дисклинацией.
Рис. 4.
Зависимость размера ξ от времени τ = t/t0 для модели II при f = exp(–s0ndl) и b0 = 20/t0 (1), 30/t0 (2) и 40/t0 (3). Параметры модели: a2 = 5d2/t0, a4d = 0, b1 = = 10d2/t0, b2 = 30d2/t0, s0 = 9d2. Другие обозначения – как на рис. 3.
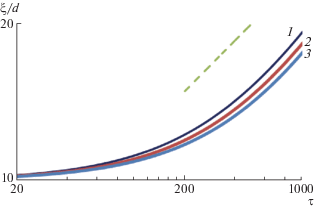
Рис. 5.
Зависимость размера ξ от времени τ = t/t0 для модели II при f = exp(–s0ndl) и b2 = 20d2/t0 (1), 30d2/t0 (2), 40d2/t0 (3). Параметры модели: a2 = 5d2/t0, a4d = 0, b0 = 30/t0, b1 = 10d2/t0, s0 = 9d2. Другие обозначения – как на рис. 3.
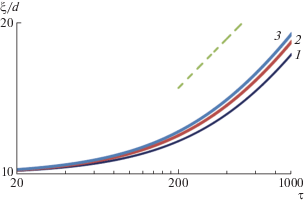
На рис. 6 представлены графики изменения ξ для различных значений коэффициента α4d: когда аннигиляции четверок вообще не происходит (кривая 3) и когда значения контролирующего этот процесс коэффициента a4d заметно отличаются друг от друга (кривые 1 и 2). Видно, что повышение интенсивности аннигиляции квадруполей ускоряет рост ξ, при этом ход процесса заметно меняется только при увеличении a4d на порядок, что связано с очень малой вероятностью контакта одновременно четырех дефектов.
Рис. 6.
Зависимость размера ξ от времени τ = t/t0 для модели II при f = exp(–s0ndl) и a4d = 200000d6/t0 (1), 20000d6/t0 (2) и 0 (3). Параметры модели: a2 = 5d2/t0, b0 = 30/t0, b1 = 10d2/t0, b2 = 30d2/t0, s0 = 9d2. Другие обозначения – как на рис. 3.
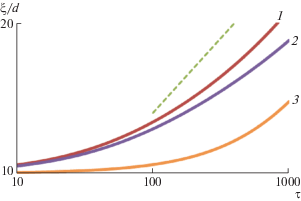
Зависимости ξ(t) при различных значениях площади поверхности s0, на которую распространяется деформирующее влияние дислокации в пленке и которая определяет значение коэффициента f в уравнении (6), представлены на рис. 7. Кривая 1, рассчитанная для s0 = 0, f = 1 и a4d = 0, демонстрирует, как происходила бы парная аннигиляция дисклинаций без влияния дислокаций. Асимптотикой такого процесса является зависимость ξ ~ t1/2. C увеличением s0 усиливается эффект подавления парной аннигиляции дисклинаций дислокациями, что замедляет рост ξ. Кроме того, чем больше значение s0, тем шире диапазон значений ndс, при котором существенна взаимозависимость ndс и ndl и возможна аппроксимация зависимости ξ(t), полученной для упрощенной модели I, зависимостью для детальной модели II.
Рис. 7.
Зависимость размера ξ от времени τ = t/t0 для модели II при f = exp(–s0ndl) и s0 = 0 (1), 5d2 (2) и 9d2 (3). Параметры модели: a2 = 5d2/t0, a4d = 0, b0 = = 30/t0, b1 = 10d2/t0, b2 = $30{{d}^{2}}{\text{/}}t_{0}^{2}$. Другие обозначения – как на рис. 3.
ЗАКЛЮЧЕНИЕ
В настоящей работе предложены кинетические модели, описывающие отжиг пленок диблок-сополимера со структурой горизонтально ориентированных цилиндров в терминах поверхностной плотности дефектов – дислокаций и дисклинаций. В экспериментах такие системы в большинстве случаев демонстрируют универсальное поведение с показателем степени α ≈ 1/4 в зависимости размера бездефектной области от времени вида ξ ~ tα.
Сопоставлены упрощенная модель аннигиляции дисклинаций при их тройных и четверных контактах и более детальная модель, в которой рассчитывается поверхностная плотность дисклинаций и дислокаций, аннигиляция дисклинаций происходит при их парных и четверных контактах, причем парная аннигиляция контролируется значением поверхностной плотности дислокаций.
В упрощенной модели с учетом аннигиляции дисклинаций только при их тройном контакте скорость роста размера бездефектной области асимптотически описывается зависимоcтью ~t1/4, а учет аннигиляции также в четверках дефектов в среднем уменьшает наблюдаемый показатель степени.
Детальная модель принимает во внимание, что сближение дисклинаций в паре затруднено присутствием дислокаций, тем не менее, аннигиляция происходит именно для пар дисклинаций (даже при сближении их троек). Уравнение для изменения количества дислокаций, учитывает несколько механизмов их появления и исчезновения, перечисленных в работе [3].
Aсимптотически размер бездефектной области будет зависеть от времени по закону ~t1/2 из-за учета парной аннигиляции дисклинаций. Однако численные расчеты показывают, что такая зависимость проявляется при очень малых, практически ненаблюдаемых, величинах поверхностной плотности дефектов. При определенном соотношении значений коэффициентов детальной модели она предсказывает такую же зависимость размера ξ от времени, как и упрощенная модель с аннигиляцией только в тройках дисклинаций. Поверхностная плотность дислокаций при этом контролируется в первую очередь их генерацией дисклинациями и парной аннигиляцией дислокаций.
В настоящее время активно изучаются различные способы ускорить процесс релаксации полимерной пленки при отжиге, в частности, лазерная и “холодная” зонная плавка [1, 2, 8, 10]. При этом разные типы воздействия соответствуют различным значениям показателя α. Кроме того, релаксацию структуры облегчает присутствие паров растворителя, пластифицирующих полимерную пленку, и приближение к температуре перехода от микрофазно расслоенного к неупорядоченному состоянию блок-сополимера [16, 17].
Интересным развитием подходов данной работы представляется исследование кинетики созревания структуры в случае, когда значения коэффициентов в модельных уравнениях зависят от температуры, изменяющейся при отжиге в соответствии со способом воздействия на пленку, или от концентрации сорбированного пленкой низкомолекулярного пластификатора.
Е.Н. Говорун и Я.В. Кудрявцев выражают благодарность Российскому фонду фундаментальных исследований (код проекта 16-03-00531) за финансовую поддержку. Численные расчеты выполнены Д.А. Филатовым при финансовой поддержке Министерства науки и высшего образования Российской Федерации.
Список литературы
Majewski P.W., Yager K.G. // J. Phys., Condens. Matter 2016 . V. 28. № 40. Art. 403002.
Majewski P.W., Yager K.G. // ACS Nano. 2015. V. 9. № 4. P. 3896.
Harrison C., Cheng Z., Sethuraman S., Huse D.A., Chaikin P.M., Vega D.A., Sebastian J.M., Register R.A., Adamson D.H. // Phys. Rev. E. 2002. V. 66. № 1. Art. 011706.
Black C.T., Guarini K.W. // J. Polym. Sci., Polym. Chem. 2004. V. 42. № 8. P. 1970.
Ruiz R., Bosworth J.K., Black C.T. // Phys. Rev. B 2008. V. 77. P. 054204.
Harrison C., Angelescu D.E., Trawick M., Cheng Z., Huse D.A., Chaikin P.M., Vega D.A., Sebastian J.M., Register R.A., Adamson D.H. // Europhys. Lett. 2004. V. 67. № 5. P. 800.
Ji S., Liu C.-C., Liao W., Fenske A.L., Craig G.S.W., Nealey P.F. // Macromolecules 2011. V. 44. № 11. P. 4291.
Merekalov A.S., Derikov Y.I., Ezhov A.A., Govorun E.N., Kudryavtsev Ya.V. // Polymer Science A. 2018. V. 60. № 6. P. 723.
Rudov A.A., Patyukova E.S., Neratova I.V., Khalatur P.G., Posselt D., Papadakis C.M., Potemkin I.I. // Macromolecules. 2013. V. 46. № 14. P. 5786.
Berry B.C., Bosse A.W., Douglas J.F., Jones R.L., Karim A. // Nano Lett. 2007. V. 7. № 9. P. 2789.
Samant S., Strzalka J., Yager K.G., Kisslinger K., Grolman D., Basutkar M., Salunke N., Singh G., Berry B., Karim A. // Macromolecules. 2016. V. 49. № 22. P. 8633.
Hill J.D., Millett P.C. // Sci. Rep. 2017. V. 7. Art. 5250.
Wan X., Gao T., Zhang L., Lin J. // Phys. Chem. Chem. Phys. 2017. V. 19. № 9. P. 6707.
Dixit N., Pape A., Rong L., Joseph E., Martin S.M. // Macromolecules. 2015. V. 48. № 4. P. 1144.
Singh A., Krishnan R., Puri S. // Eur. Polym. Lett. 2015. V. 109. № 2. P. 26006.
Li W., Nealey P.F., Pablo J.J., Müller M. // Phys. Rev. Lett. 2014. V. 113. Art. no. 168301.
Berezkin A.V., Papadakis C.M., Potemkin I.I. // Macromolecules. 2016. V. 49. № 1. P. 415.
Checco A., Ocko B.M., Rahman A., Black C.T., Tasin-kevych M., Giacomello A., Dietrich S. // Phys. Rev. Lett. 2014. V. 112. Art. 216101.
Jeong C.K., Jin H.M., Ahn J.-H., Park T.J., Yoo H.G., Koo M., Choi Y.-K., Kim S.O., Lee K.J. // Small. 2014. V. 10. № 2. P. 337.
Majewski P.W., Rahman A., Black C.T., Yager K.G. // Nat. Commun. 2015. V. 6. P. 7448.
Allen S.M., Cahn J.W. // Acta Metallurgica. 1979. V. 27. № 6. P. 1085.
Gonnella G., Orlandini E. Yeomans J.M. // Phys. Rev. Lett. 1997. V. 78. P. 1695.
Xu A.G., Gonnella G., Lamura A., Amati G., Massaioli F. // Europhys. Lett. 2005. V. 71. P. 651.
Mazenko G.F. // Phys. Rev. Lett. 1997. V. 78. № 3. P. 401.
Qian H., Mazenko G.F. // Phys. Rev. E 2003. V. 68. Art. 021109.
Yurke B., Pargellis A.N., Kovacs T., Huse D.A. // Phys. Rev. E. 1993. V. 47. P. 1525.
Kim B., Laachi N., Delaney K.T., Carilli M., Kramer E.J., Fredrickson G.H. // J. Appl. Polym. Sci. 2014. V. 131. № 24. P. 40790.
Shackelford J. Introduction to Materials Science for Engineers. Upper Saddle River: Pearson Prentice Hall, 2009.
Kudryavtsev Y.V., Govorun E.N., Litmanovich A.D. // Polymer Science A. 2000. V. 42. № 4. P. 412.
Дополнительные материалы отсутствуют.
Инструменты
Высокомолекулярные соединения (серия А)


