1. На главную
  2. Электронные версии
  3. Высокомолекулярные соединения (серия А)
  4. T. 62, № 2, 2020

Высокомолекулярные соединения (серия А), 2020, T. 62, № 2, стр. 138-145

ВЛИЯНИЕ КОНЦЕВЫХ СЕГМЕНТОВ НА ДИНАМИКУ

И. К. Островская a, Н. Ф. Фаткуллин a, *

a Казанский (Приволжский) федеральный университет. Институт физики
420008 Казань, Кремлевская ул., 18, Россия

* E-mail: nail.fatkullin@kpfu.ru

Поступила в редакцию 26.04.2019
После доработки 28.06.2019
Принята к публикации 20.08.2019

Полный текст (PDF)

Аннотация

Показано, что в расплавах линейных макромолекул эффекты динамической неоднородности, связанные с наличием концевых сегментов, не являются исчезающе малыми в пределе $N \to \infty $, где $N$ – число сегментов Куна в макромолекуле. Эффект носит частотную природу, т.е. разделение сегментов на “краевые”, более подвижные по сравнению со “срединными”, зависит во многом от времени наблюдения. С увеличением времени наблюдения происходит симметричный рост “краевых” участков полимерной цепи с обоих концов макромолекулы, охватывающий всю макромолекулу при временах порядка терминального времени релаксации. Эффект порождает нетривиальные экспериментально наблюдаемые следствия. Например, спад сигнала свободной индукции ядер дейтерия в монодисперсных полимерных расплавах макромолекул должен иметь протяженный участок со степенным законом затухания $g(t) \propto {{t}^{{ - \beta }}}$, где $\beta = 1$ для модели рептаций и $\beta = {{(\alpha - 2)}^{{ - 1}}}$ для изотропных ренормированных моделей Рауза: $\alpha > 2$ – экспонента молекулярно-массовой зависимости терминального времени релаксации макромолекул. При $\alpha \leqslant 2$ влияние эффектов динамической неоднородности на форму спада свободной индукции более слабое, хотя и наблюдаемое при достаточной точности измерений.

ВВЕДЕНИЕ

Большинство аналитических результатов, связанных с динамическими свойствами макромолекул, формулируется в асимптотическом пределе $N \to \infty $, где N – число сегментов Куна в макромолекуле [1–4]. При этом, как правило, пренебрегают динамической неоднородностью сегментов макромолекул, т.е. зависимостью динамических свойств сегментов от их удаленности от концов макромолекул, полагая очевидным, что соответствующие поправки должны быть исчезающе малы в указанном пределе (${{N}^{{ - 1}}} \to 0$). Хотя в общей формулировке подобный подход, на первый взгляд, казалось бы и не должен вызывать существенных возражений, при его приложении к конкретным экспериментальным ситуациям всегда остаются вопросы. Когда мы имеем дело с полимерными системами с ограниченными молекулярными массами, какие $N$ можно считать малыми, а какие большими? Является ли заданное значение $N$ одновременно большим или малым для различных экспериментов? Не может ли быть так, что ответ на первый вопрос зависит от типа эксперимента?

Родственные по сути вопросы, связанные с динамической неоднородностью полимерных систем, неоднократно поднимались в научной литературе [5–12]. Однако, насколько нам известно, ответы на них в отношении систем линейных гибкоцепных макромолекул в отличие от дендримеров [13, 14]) и линейных полужестких цепочек [16–21], не обсуждались с достаточной полнотой и ясностью в научной литературе.

В настоящей работе на ряде простых примеров показано, что эффекты динамической неоднородности сегментов макромолекул, порожденные наличием концевых сегментов, имеют частотную природу, т.е. зависят от соотношения между характерным временем наблюдения и терминальным временем релаксации макромолекул и могут быть экспериментально наблюдаемы.

ДИНАМИЧЕСКАЯ НЕОДНОРОДНОСТЬ ЗАТУХАНИЯ АВТОКОРРЕЛЯЦИОННОЙ ФУНКЦИИ ТАНГЕНЦИАЛЬНОГО ВЕКТОРA ЛИНЕЙНОЙ МАКРОМОЛЕКУЛЫ

Рассмотрим динамические свойства тангенциального вектора $n$-го сегмента макромолекулы, определяемого соотношением

(1)
${{{\mathbf{b}}}_{n}}\left( t \right) = \frac{\partial }{{\partial n}}{{{\mathbf{R}}}_{n}}\left( t \right),$
где ${{{\mathbf{R}}}_{n}}\left( t \right)$ обозначает радиус-вектор рассматриваемого сегмента в момент времени t, а номер сегмента n рассматривается как непрерывная переменная $0 \leqslant n \leqslant N$, общее число сегментов $N \gg 1$. Временная зависимость тангенциального вектора связана с пространственными поворотами обсуждаемого сегмента макромолекулы, обусловленными вращательными движениями. Простейшей количественной характеристикой подобных движений является динамическая бинарная автокорреляционная функция $\left\langle {{{{\mathbf{b}}}_{n}}\left( t \right) \cdot {{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle $. Эта функция в терминах существующих аналитических динамических моделей представима, в наиболее существенных чертах, следующей суммой динамических автокорреляционных функций нормальных мод Рауза (см, например, [1–3, 22–24]):
(2)
$\left\langle {{{{\mathbf{b}}}_{n}}\left( t \right){{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle = \frac{{2{{b}^{2}}}}{N}\sum\limits_{p = 1}^N {\exp \left\{ { - \frac{t}{{{{\tau }_{p}}}}} \right\}} {{\sin }^{2}}\left( {\frac{{\pi pn}}{N}} \right),$
где b – длина сегмента, ${{\tau }_{p}} = {{\bar {\tau }}_{s}}{{(N{\text{/}}p)}^{\alpha }}$ – время релаксации нормальной моды с номером p, ${{\bar {\tau }}_{s}}$ и $\alpha = 2{\kern 1pt} - {\kern 1pt} 3.5$ – параметры, зависящие от деталей динамической модели. Так, в модели Рауза α = 2, ${{\bar {\tau }}_{s}} = {{\tau }_{s}} = \zeta {{b}^{2}}{\text{/}}(3{{\pi }^{2}}{{k}_{{\text{B}}}}T)$ – время сегментальной релаксации.

В классической модели рептаций Дои–Эдварса макромолекула совершает когерентные рептации при временах ${{\tau }_{R}} = {{\tau }_{s}}{{N}^{2}} \ll t \ll {{\tau }_{d}} = 3{{\tau }_{s}}{{N}^{3}}{\text{/}}{{N}_{e}}$, где ${{N}_{e}}$ – число сегментов Куна между соседними зацеплениями, α = 2, ${{\bar {\tau }}_{s}} = 3{{\tau }_{e}}N{\text{/}}{{N}_{e}} = 3{{\tau }_{s}}N{{N}_{e}}$, τe = = ${{\tau }_{s}}N_{e}^{2}$ – характерное время зацеплений. В качестве сегмента в этом случае необходимо рассматривать сегмент примитивной цепи, а под числом сегментов N в соотношении (2) – число примитивных сегментов примитивной цепи, иными словами, число зацеплений, приходящихся на одну макромолекулу, т.е. $\tilde {N} = N{\text{/}}{{N}_{e}}$.

В $n$-ренормированных моделях Рауза в марковском пределе $\alpha = 2 + n{\text{/}}2$, ${{\bar {\tau }}_{s}} = {{\tau }_{e}}$ для временного интервала ${{\tau }_{e}} \ll t \ll {{\tau }_{1}}$, соответствующего зацепленным движениям, $n = 1,2,3$ – число ренормировок [23–26]).

Отметим, что в модели рептаций на временном интервале ${{\tau }_{e}} \ll t \ll {{\tau }_{R}}$, соответствующем некогерентным рептациям макромолекул, когда доминирующими оказываются процессы флуктуации контурной длины цепи, затухания нормальных мод Рауза примитивной цепи оказываются не экспоненциальными, а описываются так называемыми растянутыми экспонентами (см., например, работу [3]). Подобное поведение имеет место и в ренормированных моделях Рауза. Эти детали, однако, выходят за рамки обсуждения данной статьи. Источником динамической неоднородности сегментов линейных макромолекул в соотношении (2) является ${{\sin }^{2}}\left( {\pi pn{\text{/}}N} \right)$, где $n$ – номер сегмента. Традиционный подход, заключающийся в пренебрежении динамической неоднородностью сегментов, состоит в том, что в соотношении (2) осуществляется предусреднение по номерам сегментов, т.е. полагается, что

(3)
${{\sin }^{2}}\left( {\frac{{\pi pn}}{N}} \right) = \frac{1}{2}$

После этого для $N \gg 1$ на временном интервале ${{\bar {\tau }}_{s}} \ll t \ll {{\tau }_{1}}$ можно получить, заменяя суммирование по p в правой части уравнения (2) на интегрирование, следующее асимптотически точное соотношение [3, 22]:

(4)
$\left\langle {{{{\mathbf{b}}}_{n}}\left( t \right){{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle = \frac{{{{b}^{2}}}}{\alpha }\Gamma \left( {\frac{1}{\alpha }} \right){{\left( {\frac{{{{{\bar {\tau }}}_{s}}}}{t}} \right)}^{{\frac{1}{\alpha }}}},$
($\Gamma \left( {1{\text{/}}\alpha } \right)$ – гамма функция Эйлера). Зависимость обсуждаемой динамической функции от номера сегмента n, т.е. динамическая неоднородность, оказывается полностью потерянной.

Для количественного учета данной зависимости воспользуемся тождеством

(5)
$\sin \left( {\frac{{\pi pn}}{N}} \right) = \frac{{\exp \left\{ {i\frac{{\pi pn}}{N}} \right\} - \exp \left\{ { - i\frac{{\pi pn}}{N}} \right\}}}{{2i}}$

Подставим его в правую часть соотношения (2) и после ряда элементарных преобразований, получим формулу

(6)
$\begin{gathered} \left\langle {{{{\mathbf{b}}}_{n}}\left( t \right){{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle = \\ \, = \frac{{{{b}^{2}}}}{N}\sum\limits_{p = 1}^N {\exp \left\{ { - \frac{t}{{{{{\bar {\tau }}}_{s}}}}{{{\left( {\frac{p}{N}} \right)}}^{\alpha }}} \right\}} \left[ {1 - \cos \left( {2\frac{{\pi pn}}{N}} \right)} \right] \\ \end{gathered} $

При $N \gg 1$ суммирование по нормальным модам заменим на интегрирование и представим (6) в виде

(7)
$\begin{gathered} \left\langle {{{{\mathbf{b}}}_{n}}\left( t \right){{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle = \\ \, = \frac{{{{b}^{2}}}}{N}\int\limits_1^N {\exp \left\{ { - \frac{t}{{{{{\bar {\tau }}}_{s}}}}{{{\left( {\frac{p}{N}} \right)}}^{\alpha }}} \right\}} \left[ {1 - \cos \left( {2\frac{{\pi pn}}{N}} \right)} \right]dp \\ \end{gathered} $

Далее в правой части формулы (7) совершим замену переменных $x = t\bar {\tau }_{s}^{{ - 1}}{{\left( {p{\text{/}}N} \right)}^{\alpha }}$, позволяющую переписать ее следующим образом:

(8)
$\begin{gathered} \left\langle {{{{\mathbf{b}}}_{n}}\left( t \right){{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle = \frac{{{{b}^{2}}}}{\alpha }{{\left( {\frac{{{{{\bar {\tau }}}_{s}}}}{t}} \right)}^{{\frac{1}{\alpha }}}} \times \\ \, \times \int\limits_{t/{{\tau }_{1}}}^{t/{{{\bar {\tau }}}_{s}}} {\exp \left\{ { - x} \right\}{{x}^{{\frac{1}{\alpha } - 1}}}} \left[ {1 - \cos \left( {2\pi n{{{\left( {\frac{{x{{{\bar {\tau }}}_{s}}}}{t}} \right)}}^{{1/\alpha }}}} \right)} \right]dx, \\ \end{gathered} $
где ${{\tau }_{1}} = {{\bar {\tau }}_{s}}{{N}^{\alpha }}$ – терминальное время релаксации полимерной цепи.

Рассмотрим временной интервал ${{\bar {\tau }}_{s}} < t < {{\tau }_{1}}$ = = ${{\bar {\tau }}_{s}}{{N}^{\alpha }}$, в котором можно использовать асимптотически точную аппроксимацию

(9)
$\begin{gathered} \left\langle {{{{\mathbf{b}}}_{n}}\left( t \right){{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle = \frac{{{{b}^{2}}}}{\alpha }{{\left( {\frac{{{{{\bar {\tau }}}_{s}}}}{t}} \right)}^{{\frac{1}{\alpha }}}} \times \\ \, \times \int\limits_0^\infty {\exp \left\{ { - x} \right\}{{x}^{{\frac{1}{\alpha } - 1}}}} \left[ {1 - \cos \left( {2\pi n{{{\left( {\frac{{x{{{\bar {\tau }}}_{s}}}}{t}} \right)}}^{{1/\alpha }}}} \right)} \right]dx \\ \end{gathered} $

Для каждого сегмента с номером $n \leqslant N{\text{/}}2$ внутри обсуждаемого временного интервала можно выделить две части: начальные/малые времена $t < {{\bar {\tau }}_{s}}{{\left( {2\pi n} \right)}^{\alpha }} \equiv \tau \left( n \right)$ и поздние/большие времена $t > \tau \left( n \right)$. Вследствие симметрии концов макромолекул результаты для $n \geqslant N{\text{/}}2$ могут быть в дальнейшем легко получены путем подстановки $n \to N - n$.

Подынтегральная функция в правой части соотношения (9) содержит $\cos (2\pi n{{(x{{\bar {\tau }}_{s}}{\text{/}}t)}^{{1/\alpha }}})$ = = cos((xτ(n)/t)1/α), вклад которого в интеграл существенно различен на указанных временных интервалах.

Прежде всего отметим, что наличие в подынтегральном выражении правой части формулы (9) $\exp \{ - x\} $ и дополнительного ограничения α $ \approx 2{\kern 1pt} - {\kern 1pt} 3.5$ приводит к тому, что главный вклад в интеграл дает интегрирование при $x \propto 1$. При малых временах $t < \tau \left( n \right)$ аргумент косинуса при интегрировании правой части выражения (9) сильно меняется при $x \propto 1$. В связи с этим вклад соответствующего слагаемого мал из-за сильных осцилляций $\cos ({{(x\tau (n){\text{/}}t)}^{{1/\alpha }}})$. Обсуждаемая бинарная динамическая корреляционная функция может быть асимптотически точно оценена как

(10)
$\begin{gathered} \left\langle {{{{\mathbf{b}}}_{n}}\left( t \right){{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle = \frac{{{{b}^{2}}}}{\alpha }{{\left( {\frac{{{{{\bar {\tau }}}_{s}}}}{t}} \right)}^{{\frac{1}{\alpha }}}} \times \\ \, \times \int\limits_0^\infty {\exp \left\{ { - x} \right\}{{x}^{{\frac{1}{\alpha } - 1}}}} \left[ {1 - \cos \left( {2\pi n{{{\left( {\frac{{x{{{\bar {\tau }}}_{s}}}}{t}} \right)}}^{{1/\alpha }}}} \right)} \right]dx \cong \\ \, \cong \frac{{{{b}^{2}}}}{\alpha }{{\left( {\frac{{{{{\bar {\tau }}}_{s}}}}{t}} \right)}^{{\frac{1}{\alpha }}}}\int\limits_0^\infty {\exp \left\{ { - x} \right\}{{x}^{{\frac{1}{\alpha } - 1}}}} dx = \frac{{{{b}^{2}}}}{\alpha }{{\left( {\frac{{{{{\bar {\tau }}}_{s}}}}{t}} \right)}^{{\frac{1}{\alpha }}}}\Gamma \left( {\frac{1}{\alpha }} \right) \\ \end{gathered} $

Данный результат в точности совпадает с соотношением (4), т.е. с традиционной аппроксимацией (3). Полностью отсутствуют эффекты динамической неоднородности: зависимость обсуждаемой корреляционной функции от номера сегмента $n$. Он имеет простую интерпретацию: речь идет о начальном этапе эволюции, когда $t < \tau (n)$, динамика сегмента с номером $n$ еще не коррелирует с динамикой ближайшего концевого сегмента, и его динамика не отличается от динамики “срединных” сегментов.

При больших временах $t\, > \,\tau (n)$ аргумент $\cos ({{(x\tau (n){\text{/}}t)}^{{1/\alpha }}})$ мал при $x \propto 1$, и мы можем использовать аппроксимацию

(11)
$\begin{gathered} \cos \left( {2\pi n{{{\left( {\frac{{x{{{\bar {\tau }}}_{s}}}}{t}} \right)}}^{{1/\alpha }}}} \right) = \\ \, = \cos \left( {{{{\left( {\frac{{x\tau \left( n \right)}}{t}} \right)}}^{{1/\alpha }}}} \right) = 1 - \frac{1}{2}{{\left( {{{{\left( {\frac{{x\tau \left( n \right)}}{t}} \right)}}^{{1/\alpha }}}} \right)}^{2}} + ... \\ \end{gathered} $

Подставляя ее в формулу (9), получим соотношение

(12)
$\begin{gathered} \left\langle {{{{\mathbf{b}}}_{n}}\left( t \right){{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle = \frac{{{{b}^{2}}}}{\alpha }{{\left( {\frac{{{{{\bar {\tau }}}_{s}}}}{t}} \right)}^{{\frac{1}{\alpha }}}} \times \\ \, \times \int\limits_0^\infty {\exp \left\{ { - x} \right\}{{x}^{{\frac{1}{\alpha } - 1}}}} \left[ {1 - \cos \left( {2\pi n{{{\left( {\frac{{x{{{\bar {\tau }}}_{s}}}}{t}} \right)}}^{{1/\alpha }}}} \right)} \right]dx \cong \\ \, \cong \frac{{2{{\pi }^{2}}{{n}^{2}}{{b}^{2}}}}{\alpha }\Gamma \left( {\frac{3}{\alpha }} \right){{\left( {\frac{{{{{\bar {\tau }}}_{s}}}}{t}} \right)}^{{\frac{3}{\alpha }}}} \\ \end{gathered} $

Видно увеличение экспоненты временного спада бинарной корреляционной функции тангенциального вектора полимерной цепи с ${{\alpha }^{{ - 1}}}$ в выражении (10) до $3{{\alpha }^{{ - 1}}}$ в выражении (12). Кроме того, появилась динамическая неоднородность, зависимость обсуждаемой корреляционной функции от номера сегмента ${{n}^{2}}$ в правой части выражения (12), отсчитанного от ближайшего концевого сегмента макромолекулы. На начальном этапе динамики при $t < \tau \left( n \right)$ сегменты ведут себя как срединные, затем при $t > \tau \left( n \right)$ оказываются существенными концевые эффекты. Иными словами, для всех полимерных сегментов, эффекты динамической неоднородности, связанные с наличием концевых сегментов у линейных макромолекул, зависят от времени наблюдения, т.е. имеют частотный характер. Время $\tau \left( n \right) \equiv {{\bar {\tau }}_{s}}{{\left( {2\pi n} \right)}^{\alpha }}$, определяющее переход от динамики срединного поведения к динамики краевого/концевого поведения, зависит как ${{n}^{\alpha }}$ от номера сегмента, отсчитанного от ближайшего концевого сегмента. С увеличением времени наблюдения возрастает число сегментов, динамически коррелирующих с концевыми сегментами. Происходит увеличение длины динамически коррелированных участков макромолекулы с обоих концов в направлении к центральному сегменту. При временах порядка и бóльших терминального времени релаксации ($t > {{\tau }_{1}}$) рост прекращается, поскольку оба конца поглощают всю макромолекулу, становящуюся как бы одним большим краем. Последнее обстоятельство можно непосредственно увидеть из соотношения (2), в этом пределе доминирующим является вклад от наиболее длинноволновой нормальной моды:

(13)
$\left\langle {{{{\mathbf{b}}}_{n}}\left( t \right){{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle \cong \frac{{2{{b}^{2}}}}{N}\exp \left\{ { - \frac{t}{{{{\tau }_{1}}}}} \right\}{{\sin }^{2}}\left( {\frac{{\pi n}}{N}} \right)$

ДИНАМИЧЕСКАЯ НЕОДНОРОДНОСТЬ СРЕДНЕКВАДРАТИЧНЫХ СМЕЩЕНИЙ СЕГМЕНТОВ В СИСТЕМЕ ЦЕНТРА МАСС

Среднеквадратичное смещение сегмента с номером $n$ в лабораторной системе координат представляется в виде суммы вкладов от нормальных раузовских мод [1–3, 22]:

(14)
$\begin{gathered} \left\langle {{{{\left( {{{{\mathbf{R}}}_{n}}\left( t \right) - {{{\mathbf{R}}}_{n}}\left( 0 \right)} \right)}}^{2}}} \right\rangle = \left\langle {{{{\left( {{{{\mathbf{X}}}_{0}}(t) - {{{\mathbf{X}}}_{0}}(0)} \right)}}^{2}}} \right\rangle + \\ \, + 8\sum\limits_{p = 1}^N {\frac{{N{{b}^{2}}}}{{2{{\pi }^{2}}{{p}^{2}}}}\left( {1 - \exp \left\{ { - \frac{t}{{{{{\bar {\tau }}}_{s}}}}{{{\left( {\frac{p}{N}} \right)}}^{\alpha }}} \right\}} \right){{{\cos }}^{2}}\left( {\frac{{\pi pn}}{N}} \right)} \\ \end{gathered} $

Первое слагаемое в правой части соотношения (14) соответствует диффузионным смещениям центра масс полимерной цепи и определяется коэффициентом самодиффузии макромолекулы; оно доминирует при временах, больших терминального времени релаксации ($t > {{\tau }_{1}}$). Второе слагаемое обусловлено так называемым микроброуновским движением, оно связано с движениями полимерных сегментов в системе отсчета, связанной с центром масс макромолекулы. При временах $t < {{\tau }_{1}}$ именно оно дает главный вклад в соотношение (14). Рассмотрим его отдельно.

(15)
$\begin{gathered} \langle {{(\delta {{{{\mathbf{\tilde {R}}}}}_{n}}(t))}^{2}}\rangle \equiv \\ \, \equiv 8\sum\limits_{p = 1}^N {\frac{{N{{b}^{2}}}}{{2{{\pi }^{2}}{{p}^{2}}}}\left( {1 - \exp \left\{ { - \frac{t}{{{{{\bar {\tau }}}_{s}}}}{{{\left( {\frac{p}{N}} \right)}}^{\alpha }}} \right\}} \right){{{\cos }}^{2}}\left( {\frac{{\pi pn}}{N}} \right)} \\ \end{gathered} $

Как и в предыдущем разделе, заменим суммирование на интегрирование и совершим замену переменных $x = t{{\bar {\tau }}_{s}}^{{ - 1}}{{\left( {p{\text{/}}N} \right)}^{\alpha }}$. Тогда

(16)
$\begin{gathered} \langle {{(\delta {{{{\mathbf{\tilde {R}}}}}_{n}}(t))}^{2}}\rangle \equiv \\ \, \equiv \frac{4}{{{{\pi }^{2}}}}\frac{{{{b}^{2}}}}{\alpha }{{\left( {\frac{t}{{{{{\bar {\tau }}}_{s}}}}} \right)}^{{1/\alpha }}}\int\limits_{t/{{\tau }_{1}}}^{t/{{{\bar {\tau }}}_{s}}} {\frac{{1 - {{e}^{{ - x}}}}}{{{{x}^{{\frac{{1 + \alpha }}{\alpha }}}}}}} {{\cos }^{2}}\left( {\frac{1}{2}{{{\left( {\frac{{x\tau \left( n \right)}}{t}} \right)}}^{{1/\alpha }}}} \right)dx \\ \end{gathered} $

Для временного интервала ${{\bar {\tau }}_{s}} < t < {{\tau }_{1}} = {{\bar {\tau }}_{s}}{{N}^{\alpha }}$ по аналогии с соотношением (9) получим формулу

(17)
$\begin{gathered} \langle {{(\delta {{{{\mathbf{\tilde {R}}}}}_{n}}(t))}^{2}}\rangle \cong \\ \, \cong \frac{4}{{{{\pi }^{2}}}}\frac{{{{b}^{2}}}}{\alpha }{{\left( {\frac{t}{{{{{\bar {\tau }}}_{s}}}}} \right)}^{{1/\alpha }}}\int\limits_0^\infty {\frac{{1 - {{e}^{{ - x}}}}}{{{{x}^{{\frac{{1 + \alpha }}{\alpha }}}}}}} {{\cos }^{2}}\left( {\frac{1}{2}{{{\left( {\frac{{x\tau \left( n \right)}}{t}} \right)}}^{{1/\alpha }}}} \right)dx \\ \end{gathered} $

Мы вновь можем выделить для каждого сегмента начальные времена, когда $t < \tau \left( n \right)$, и большие времена, когда $\tau \left( n \right) < t < {{\tau }_{1}}$. Вклад ${{\cos }^{2}}({{(x\tau (n){\text{/}}t)}^{{1/\alpha }}}{\text{/}}2)$, зависящий от номера сегмента, различается на этих участках:

(18)
${{\cos }^{2}}\left( {\frac{1}{2}{{{\left( {\frac{{x\tau \left( n \right)}}{t}} \right)}}^{{1/\alpha }}}} \right) \cong \left\{ \begin{gathered} \frac{1}{2},\quad {{\tau }_{s}} < t < \tau \left( n \right) \hfill \\ 1,\quad \tau \left( n \right) < t < {{\tau }_{1}} \hfill \\ \end{gathered} \right.$

Подставив соотношение (18) в выражение (17) и выполнив элементарное интегрирование, получим

(19)
$\langle {{(\delta {{{\mathbf{\tilde {R}}}}_{n}}(t))}^{2}}\rangle \cong \left\{ \begin{gathered} \frac{{2{{b}^{2}}}}{{{{\pi }^{2}}}}\Gamma \left( {\frac{{\alpha - 1}}{\alpha }} \right){{\left( {\frac{t}{{{{{\bar {\tau }}}_{s}}}}} \right)}^{{1/\alpha }}},{{\tau }_{s}} < t < \tau \left( n \right) \hfill \\ \frac{{4{{b}^{2}}}}{{{{\pi }^{2}}}}\Gamma \left( {\frac{{\alpha - 1}}{\alpha }} \right){{\left( {\frac{t}{{{{{\bar {\tau }}}_{s}}}}} \right)}^{{1/\alpha }}},\tau \left( n \right) < t < {{\tau }_{1}} \hfill \\ \end{gathered} \right.$

Отметим, что аппроксимация ${{\cos }^{2}}({{(x\tau (n){\text{/}}t)}^{{1/\alpha }}}{\text{/}}2)$ = = 1/2 является стандартной и используется во всех известных нам работах, она соответствует полному пренебрежению динамической неоднородностью сегментов макромолекулы.

При временах $t > {{\tau }_{1}}$ среднеквадратичное смещение сегментов в системе отсчета, связанной с центром масс макромолекулы, стремится к не зависящему от времени значению

(20)
$\begin{gathered} \langle {{(\delta {{{{\mathbf{\tilde {R}}}}}_{n}}(t \to \infty ))}^{2}}\rangle \cong 8\sum\limits_{p = 1}^N {\frac{{N{{b}^{2}}}}{{2{{\pi }^{2}}{{p}^{2}}}}{{{\cos }}^{2}}\left( {\frac{{\pi pn}}{N}} \right)} \cong \\ \, \cong \frac{2}{3}N{{b}^{2}}\left( {{{{\left( {\frac{n}{N}} \right)}}^{3}} + {{{\left( {\frac{{N - n}}{N}} \right)}}^{3}}} \right) \\ \end{gathered} $

Как видно, оно сильно зависит от номера сегмента. Усреднение выражения (20) по номеру сегмента $n$ приводит к известному результату.

(21)
$\frac{1}{N}\sum\limits_n {\langle {{{(\delta {{{{\mathbf{\tilde {R}}}}}_{n}}(t \to \infty ))}}^{2}}\rangle } \cong 2R_{g}^{2} = \frac{{N{{b}^{2}}}}{3},$
где $R_{g}^{2} = N{{b}^{2}}{\text{/}}6$ – квадрат радиуса инерции макромолекулы.

ЭФФЕКТЫ ДИНАМИЧЕСКОЙ НЕОДНОРОДНОСТИ В СПАДЕ СВОБОДНОЙ ИНДУКЦИИ ЯДЕР ДЕЙТЕРИЯ

Ядра дейтерия имеют спин I = 1 и обладают электрическим квадрупольным моментом. Доминирующим механизмом спиновой релаксации ядер дейтерия, как правило, является флуктуация электрических квадрупольных взаимодействий, которые на порядки сильнее магнитных диполь-дипольных взаимодействий ядер дейтерия. Магнитные диполь-дипольные взаимодействия имеют как внутримолекулярные, так и межмолекулярные вклады. Причем, как показали исследования последних лет (см., например, работы [22, 26–28]), оба упомянутых типа вкладов в спиновую релаксацию важны для протонов, имеющих спин $I = 1{\text{/}}2$ и не обладающих поэтому квадрупольным электрическим моментом. В случае электрических квадрупольных взаимодействий вклад от внутримолекулярных компонент градиента локального электрического поля на дейтроне оказывается доминирующим. По этой причине спиновая релаксация дейтронов имеет преимущественно внутримолекулярную природу и содержит информацию о динамике пространственных поворотов полимерных сегментов, на которых расположены ядра дейтерия.

Один из простейших экспериментов, характеризующих динамику полимерных сегментов, – измерение методом ЯМР спада свободной индукции, представляющего собой отклик спиновой системы образца на $90^\circ $ радиочастотный импульс. Этот импульс выводит спиновую систему из начального состояния термодинамического равновесия, когда спины в среднем ориентированы в направлении приложенного постоянного магнитного поля вдоль оси Z (детали см. в работах [22, 26]). В дальнейшем эволюция системы осуществляется под действием внутренних локальных электромагнитных полей, создаваемых частицами системы и внешнего магнитного поля, индуцирующего ларморовскую прецессию с частотой ${{\omega }_{0}} = - \gamma {{Н}_{0}}$, где $\gamma $ – гиромагнитное отношение, H0 – напряженность внешнего магнитного поля. Тепловые флуктуации внутренних полей являются источником спиновой релаксации, приводящей к затуханию ларморовской прецессии в лабораторной системе координат. В рассматриваемом нами случае речь идет о спин-спиновой релаксации, причина которой – флуктуация градиентов электрических полей на ядрах дейтерия, вызванная ориентационными флуктуациями сегментов макромолекул.

При временах $t \gg {{\bar {\tau }}_{s}}$ нормированный спад свободной индукции ядер дейтерия во вращающейся системе координат имеет следующую структуру [22, 29]):

(22)
$g(t)\, = \,\frac{1}{N}\sum\limits_n {\left\langle {\exp \left\{ {i\frac{{{{{\tilde {\omega }}}_{D}}}}{{{{b}^{2}}}}\int\limits_0^t {(3{{b}_{{n,z}}}({{t}_{1}}){{b}_{{n,z}}}({{t}_{1}}) - {{b}^{2}})d{{t}_{1}}} } \right\}} \right\rangle } $

Здесь ${{\tilde {\omega }}_{D}}$ – остаточная часть секулярной части квадрупольных взаимодействий в частотных единицах, $b_{n}^{z}\left( {{{t}_{1}}} \right)$ – z-компонента тангенциального вектора полимерного сегмента с номером n в момент времени ${{t}_{1}}$, ${{b}^{2}} \equiv \langle b_{{n,x}}^{2}({{t}_{1}})\rangle + \langle b_{{n,y}}^{2}({{t}_{1}})\rangle + \langle b_{{n,z}}^{2}({{t}_{1}})\rangle $ – среднеквадратичная длина сегмента, угловые скобки обозначают усреднение по всем начальным равновесным конформациям и совместимым с ними динамическим траекториям макромолекул.

Расчет входящих в соотношение (22) динамических корреляционных функций, описывающих вращательные флуктуации полимерных сегментов, в общем случае является нерешенной проблемой неравновесной статистической физики. Следующее стандартное приближение – это приближение Андерсона–Вейсса или, в более общих терминах, приближение второго кумулянта, в котором спад свободной индукции имеет вид

(23)
$\begin{gathered} g\left( t \right) = \frac{1}{N}\sum\limits_n {\exp \left\{ { - {{{\left( {\frac{{{{{\tilde {\omega }}}_{D}}}}{{{{b}^{2}}}}} \right)}}^{2}}\int\limits_0^t {d\tau \left( {t - \tau } \right)} \times } \right.} \\ \left. {\mathop {\, \times }\limits_{_{{_{{}}}}}^{^{{^{{}}}}} \left\langle {(3{{b}_{{n,z}}}\left( \tau \right){{b}_{{n,z}}}\left( \tau \right) - {{b}^{2}})(3{{b}_{{n,z}}}\left( 0 \right){{b}_{{n,z}}}\left( 0 \right) - {{b}^{2}})} \right\rangle } \right\} \\ \end{gathered} $

В изотропных системах соотношение (23) для $t \gg {{\bar {\tau }}_{s}}$ эквивалентно формуле

(24)
$\begin{gathered} g\left( t \right) = \frac{1}{N}\sum\limits_n {\exp \left\{ { - 8{{{\left( {\frac{{{{{\tilde {\omega }}}_{D}}}}{{{{b}^{2}}}}} \right)}}^{2}}\int\limits_0^t {d\tau \left( {t - \tau } \right)} \times } \right.} \\ \,\left. {\mathop \times \limits_{_{{_{{}}}}}^{^{{^{{}}}}} \left\langle {\left( {{{b}_{{n,z}}}\left( \tau \right){{b}_{{n,x}}}\left( \tau \right)} \right)\left( {{{b}_{{n,z}}}\left( 0 \right){{b}_{{n,x}}}\left( 0 \right)} \right)} \right\rangle } \right\} \\ \end{gathered} $

В пределе слабой константы взаимодействия ${{\tilde {\omega }}_{D}} \to 0$, называемом в магнитном резонансе приближением коротких времен корреляций или пределом Редфилда, соотношение (24) допускает еще одно упрощение:

(25)
$g\left( t \right) = \frac{1}{N}\sum\limits_n {\exp \left\{ { - \frac{t}{{{{T}_{{2n}}}}}} \right\}} ,$
где вклад $n$-го сегмента в скорость спин-спиновой релаксации

(26)
$\frac{1}{{{{T}_{{2n}}}}} = 8{{\left( {\frac{{{{{\tilde {\omega }}}_{D}}}}{{{{b}^{2}}}}} \right)}^{2}}\int\limits_0^\infty {d\tau \left\langle {{{b}_{{n,z}}}\left( \tau \right){{b}_{{n,z}}}\left( 0 \right){{b}_{{n,x}}}\left( \tau \right){{b}_{{n,x}}}\left( 0 \right)} \right\rangle } $

Дальнейшая эволюция выражения (25) требует расчета динамической корреляционной функции

(27)
$B_{n}^{{xz}}\left( t \right) \equiv \left\langle {{{b}_{{n,z}}}\left( t \right){{b}_{{n,z}}}\left( 0 \right){{b}_{{n,x}}}\left( t \right){{b}_{{n,x}}}\left( 0 \right)} \right\rangle ,$
определяющей скорость спин-спиновой релаксации спина дейтрона, расположенного на сегменте с номером n. Связь корреляционной функции $B_{n}^{{xz}}\left( t \right)$ с бинарной корреляционной функцией $\left\langle {{{{\mathbf{b}}}_{n}}\left( t \right) \cdot {{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle $, обсуждавшейся выше, существенно отличается для разных динамических моделей расплавов линейных макромолекул.

Модель рептаций Дои–Эдвардса

В этой модели связь между $B_{n}^{{xz}}\left( t \right)$ и $\left\langle {{{{\mathbf{b}}}_{n}}\left( t \right) \cdot {{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle $ наиболее проста. Напомним, что в модели рептаций Дои–Эдвардса под полимерным сегментом в соотношении (2) подразумевается сегмент примитивной цепи, а N – число примитивных сегментов в примитивной цепи, т.е. число зацеплений, приходящихся на одну цепь. Примитивная цепь, как известно [1–3], имеет конформацию идеальной цепи, сегментами Куна которой являются примитивные сегменты. Ориентация различных примитивных сегментов не коррелирована, поэтому обе обсуждаемые корреляционные функции $B_{n}^{{xz}}\left( t \right)$ и $\left\langle {{{{\mathbf{b}}}_{n}}\left( t \right) \cdot {{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle $ при временах ${{\bar {\tau }}_{s}} = {{\tau }_{е}} \ll t$ пропорциональны вероятности того, что сегмент с номером n в момент времени $t$ располагается на исходном участке примитивной цепи

(28)
$\psi \left( {n,t} \right) = \frac{2}{{\tilde {N}}}\sum\limits_{p = 1}^{\tilde {N}} {\exp \left\{ { - \frac{t}{{{{\tau }_{p}}}}} \right\}} {{\sin }^{2}}\left( {\frac{{\pi pn}}{{\tilde {N}}}} \right)$

Здесь ${{\tau }_{p}} = {{\bar {\tau }}_{s}}{{(\tilde {N}{\text{/}}p)}^{2}} = 3{{\tau }_{s}}{{N}^{3}}{\text{/}}({{N}_{e}}{{p}^{2}})$, $\tilde {N} = N{\text{/}}{{N}_{e}}$ – число зацеплений, приходящихся на одну полимерную цепь, равное в модели Дои–Эдвардса числу примитивных сегментов. Отсюда следует

(29)
$B_{n}^{{xz}}\left( t \right) = \frac{2}{9}\frac{{{{b}^{4}}}}{{\tilde {N}}}\sum\limits_{p = 1}^{\tilde {N}} {\exp \left\{ { - \frac{t}{{{{\tau }_{p}}}}} \right\}} {{\sin }^{2}}\left( {\frac{{\pi pn}}{{\tilde {N}}}} \right)$

Подставляя соотношения (27) и (29) в формулу (26), находим следующее выражение для скорости спин-спиновой релаксации спина, расположенного на примитивном сегменте с номером $n$:

(30)
$\frac{1}{{{{T}_{{2n}}}}} = \frac{{16}}{9}\tilde {\omega }_{D}^{2}{{\bar {\tau }}_{s}}\tilde {N}\sum\limits_{p = 1}^N {\frac{{{{{\sin }}^{2}}\left( {\frac{{\pi pn}}{{\tilde {N}}}} \right)}}{{{{p}^{2}}}}} $

При $\tilde {N} \gg 1$ верхний предел суммирования можно положить равным бесконечности и воспользоваться известным соотношением [30]

(31)
$\sum\limits_{p = 1}^\infty {\frac{{{{{\sin }}^{2}}\left( {\frac{{\pi pn}}{{\tilde {N}}}} \right)}}{{{{p}^{2}}}}} = \frac{{{{\pi }^{2}}}}{2}\frac{n}{{\tilde {N}}}\left( {1 - \frac{n}{{\tilde {N}}}} \right)$

Далее с помощью формул (31) и (30) преобразуем соотношение (25) к виду

(32)
$\begin{gathered} {{g}^{{rep}}}\left( t \right) = \frac{1}{{\tilde {N}}}\sum\limits_n {\exp \left\{ { - \frac{8}{9}{{\pi }^{2}}{{{\tilde {\omega }}}_{D}}{{{\bar {\tau }}}_{s}}\tilde {N}\frac{n}{{\tilde {N}}}\left( {1 - \frac{n}{{\tilde {N}}}} \right)t} \right\}} = \\ \, = \frac{1}{{\tilde {N}}}\sum\limits_n {\exp \left\{ { - 6\frac{n}{{\tilde {N}}}\left( {1 - \frac{n}{{\tilde {N}}}} \right)\frac{t}{{\bar {T}_{2}^{{rep}}}}} \right\}} , \\ \end{gathered} $
где $1{\text{/}}\bar {T}_{2}^{{rep}} = 4{{\pi }^{2}}\tilde {\omega }_{D}^{2}{{\bar {\tau }}_{s}}\tilde {N}{\text{/}}27 = 4{{\pi }^{2}}\tilde {\omega }_{D}^{2}{{\tau }_{s}}{{N}_{e}}{{N}^{2}}{\text{/}}9$ – начальная скорость спин-спиновой релаксации. Отметим, что начальная скорость спин-спиновой релаксации может быть найдена из соотношений (30) и (31) усреднением по номеру сегмента $n$. На временном интервале ${{\bar {\tau }}_{s}} \ll t \ll {{\tau }_{1}} = {{\bar {\tau }}_{s}}{{N}^{2}}$, заменяя суммирование в соотношении (32) на интегрирование, получим следующее выражение для спада свободной индукции:

(33)
$\begin{gathered} {{g}^{{rep}}}\left( t \right) \cong \frac{2}{N}\int\limits_1^{N/2} {dn} \exp \left\{ { - 6\frac{n}{N}\left( {1 - \frac{n}{N}} \right)\frac{t}{{\bar {T}_{2}^{{rep}}}}} \right\} \cong \\ \, \cong \left\{ \begin{gathered} 1 - \frac{t}{{\bar {T}_{2}^{{rep}}}} + ...,\quad t \ll \bar {T}_{2}^{{rep}} \hfill \\ \frac{{\bar {T}_{2}^{{rep}}}}{{3t}},\quad \bar {T}_{2}^{{rep}} \ll t \ll N\bar {T}_{2}^{{rep}} \hfill \\ \end{gathered} \right. \\ \end{gathered} $

Мы видим протяженный временной участок со степенным законом затухания с показателем экспоненты равным единице, являющийся отражением динамической неоднородности сегментов полимерной цепочки. Отметим, что пренебрежение динамической неоднородностью полимерных сегментов приведет к более сильному, экспоненциальному закону затухания g(t) = $\exp \{ - t{\text{/}}\bar {T}_{2}^{{rep}}\} $. При временах $t \gg N\bar {T}_{2}^{{rep}}$ в выражении (32) доминируют два крайних слагаемых, и спад становится экспоненциальным:

(34)
$g\left( t \right) \cong \frac{2}{{\tilde {N}}}\exp \left\{ { - \frac{8}{9}{{\pi }^{2}}{{{\tilde {\omega }}}_{D}}{{{\bar {\tau }}}_{s}}\tilde {N}t} \right\} = \frac{2}{{\tilde {N}}}\exp \left\{ { - \frac{6}{{\tilde {N}}}\frac{t}{{\bar {T}_{2}^{{rep}}}}} \right\}$

Ренормированные модели Рауза

В этих моделях корреляционная функция $B_{n}^{{xz}}(t)$, определяемая соотношением (28), выражается через бинарную корреляционную функцию (2) существенно иным образом [23–26]:

(35)
$\begin{gathered} B_{n}^{{xz}}\left( t \right) \equiv \left\langle {{{b}_{{n,z}}}\left( t \right){{b}_{{n,z}}}\left( 0 \right){{b}_{{n,x}}}\left( t \right){{b}_{{n,x}}}\left( 0 \right)} \right\rangle = \\ \, = \left\langle {{{b}_{{n,z}}}\left( t \right){{b}_{{n,z}}}\left( 0 \right)} \right\rangle \left\langle {{{b}_{{n,x}}}\left( t \right){{b}_{{n,x}}}\left( 0 \right)} \right\rangle = \frac{1}{9}{{\left\langle {{{{\mathbf{b}}}_{n}}\left( t \right){{{\mathbf{b}}}_{n}}\left( 0 \right)} \right\rangle }^{2}} \\ \end{gathered} $

Пользуясь соотношениями (2) и (26), получим выражение для скорости спин-спиновой релаксации спина, расположенного на $n$-м сегменте,

(36)
$\frac{1}{{T_{{2,n}}^{{RR}}}} = \frac{{32}}{9}\tilde {\omega }_{D}^{2}{{\bar {\tau }}_{s}}{{N}^{{\alpha - 2}}}\sum\limits_{p,q = 1}^N {\frac{{{{{\sin }}^{2}}\left( {\frac{{\pi pn}}{N}} \right){{{\sin }}^{2}}\left( {\frac{{\pi qn}}{N}} \right)}}{{{{p}^{\alpha }} + {{q}^{\alpha }}}}} $

Подстановка соотношений (35), (36), (10), (12) в формулу (25) приводит к следующей формуле для спада свободной индукции, когда α > 2:

(37)
$\begin{gathered} {{g}^{{RR}}}(t) = \\ \, = \left\{ \begin{gathered} 1 - \frac{t}{{\bar {T}_{2}^{{RR}}}} + ...,\quad t < \bar {T}_{2}^{{RR}}, \hfill \\ \frac{{\Gamma \left( {\frac{1}{{\alpha - 2}}} \right)}}{{\alpha - 2}}{{\left( {\frac{t}{{\left( {\alpha - 1} \right)\bar {T}_{2}^{{RR}}}}} \right)}^{{\frac{1}{{2 - \alpha }}}}},\;\;{{N}^{2}}\bar {T}_{2}^{{RR}}\, > \,t\, > \,\bar {T}_{2}^{{RR}}, \hfill \\ \frac{1}{N}\exp \left( { - \frac{1}{{T_{{2,1}}^{{RR}}}}} \right),\quad t > {{T}_{{2,1}}} \propto N\bar {T}_{2}^{{RR}}. \hfill \\ \end{gathered} \right. \\ \end{gathered} $

Здесь $1{\text{/}}\bar {T}_{2}^{{RR}} \approx 8\pi \tilde {\omega }_{D}^{2}{{\bar {\tau }}_{s}}{{N}^{{\alpha - 2}}}{\text{/}}(9(\alpha - 2))$ – начальная скорость спада свободной индукции. Отметим, что численные коэффициенты в соотношении (37) могут быть оценены путем усреднения выражения (36) по номерам сегментов и заменой суммирования по номерам нормальных мод на интегрирование.

Случай α = 2 соответствует классической модели Рауза, которая формально может рассматриваться как 0-ренормированая модель Рауза. Среднюю начальную скорость спин-спиновой релаксации можно найти, усредняя выражение (36) по номерам сегментов, что позволяет сделать при $N \gg 1$ оценку, совпадающую с точностью до численных коэффициентов с известным результатом [31]

(38)
$\frac{1}{{{{{\bar {T}}}_{2}}^{R}}} \approx \frac{{4\pi }}{9}\tilde {\omega }_{D}^{2}{{\bar {\tau }}_{s}}\ln \left( {\frac{{\pi N}}{e}} \right)$

В обсуждаемом случае мы имеем слабую логарифмическую молекулярно-массовую зависимость. Дисперсия времен релаксаций в соотношениях (25) и (26) тоже оказывается логарифмической:

(39)
$\frac{1}{{{{{\bar {T}}}^{R}}_{{2,n}}}} \approx \frac{{4\pi }}{9}\tilde {\omega }_{D}^{2}{{\bar {\tau }}_{s}}\ln \left( {2\pi n} \right)$

Неэкспоненциальность спада свободной индукции в этом случае оказывается принципиально наблюдаемой, хотя и существенно более слабой (рис. 1) по сравнению с обсуждавшимися выше случаями:

(40)
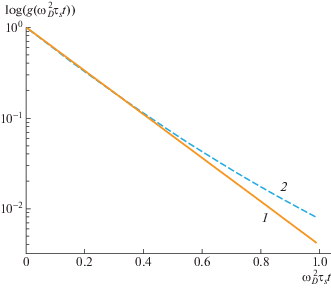
$g\left( t \right) = \frac{2}{N}\sum\limits_{n \leqslant N/2} {\exp \left\{ { - \frac{t}{{{{T}_{{2n}}}}}} \right\}} $
Рис. 1.

Спад свободной индукции ядер дейтерия для цепочки Рауза с числом сегментов N = 50 : 1 – без учета краевых эффектов, 2 – с учетом динамической неоднородности сегментов макромолекулы по формуле (40).

Отметим также, что, как хорошо известно, классическая модель Рауза из-за эффектов зацеплений применима лишь для сравнительно малых молекулярных масс $N < {{N}_{e}} = 30{\kern 1pt} - {\kern 1pt} 60$, так что разброс времен релаксаций, даваемый соотношением (39), не превышает в реальности одного порядка.

В случаях с α < 2, характерных для растворов макромолекул, где важны гидродинамические взаимодействия сегментов макромолекул, влияние эффектов динамической неоднородности сегментов макромолекул на форму спада свободной индукции оказывается еще более слабым.

ЗАКЛЮЧЕНИЕ

Динамическая неоднородность сегментов макромолекул в расплавах полимеров, связанная с наличием краевых сегментов, обладает нетривиальными свойствами: она имеет частотную природу. Последнее означает, что разделение сегментов на “краевые” и “срединные” зависит от времени наблюдения. Для каждого сегмента с номером $n$, отсчитанным от ближайшего конца макромолекулы, существует пороговое время, зависящее от номера сегмента $\tau \left( n \right) = {{\bar {\tau }}_{s}}{{\left( {2\pi n} \right)}^{\alpha }}$, которое является границей упомянутого разделения. При начальных временах (${{\bar {\tau }}_{s}} < t < \tau \left( n \right)$) отсутствует зависимость динамических корреляционных функций полимерных сегментов (см. соотношения (10), (19)) от номера сегмента, т.е. от их конкретного расположения в полимерной цепочке. Можно сказать, что при таких временах они динамически однородны и ведут себя аналогично срединным. При больших временах ($\tau \left( n \right) < t < {{\tau }_{1}}$) качественно меняется характер спада (см. соотношение (12)) бинарной корреляционной функции тангенциального вектора полимерной цепочки и появляется ее зависимость от номера сегмента. С ростом времени происходит увеличение с обоих концов цепи числа сегментов, проявляющих краевое поведение. При временах соизмеримых и больших терминального времени релаксации макромолекулы ${{\tau }_{1}}$, вообще говоря, вся цепочка оказывается одним большим краем, что видно из соотношения (20).

Частотная природа концевых эффектов порождает экспериментально наблюдаемые эффекты. Например, спад свободной индукции ядер дейтерия в полимерных расплавах должен содержать протяженный участок медленного степенного убывания со временем (см. соотношения (33) и (37)). Отметим, что соотношения (33) и (37) асимптотически точные в пределе слабой связи, когда оказывается корректным приближение коротких времен корреляций. В более общем случае, например в модели рептаций, возможны дополнительные эффекты, порождающие участки спада свободной индукции, убывающие с так называемой растянутой экспонентой [32]. Детальное рассмотрение этой более сложной ситуации, выходящей за пределы приближения коротких времен корреляций, является предметом дальнейших исследований авторов.

Список литературы

  1. Гросберг А.Ю., Хохлов А.Р. Статистическая физика макромолекул. М.: Наука, 1989. С. 344.

  2. Готлиб Ю.Я., Даринский А.А., Светлов Ю.Е. Физическая кинетика макромолекул. Л.: Химия, 1986. С. 271.

  3. Doi M., Edwards S.F. The Theory of Polymer Dynamics. Oxford: Clarendon Press, 1989.

  4. De Gennes P.G. Scaling Concepts in Polymer Physics. Ithaca: Cornell Univ. Press, 1979.

  5. Kimmich R., Bachus R. // Colloid. Polym. Sci. 1982. V. 260. № 10. P. 911.

  6. Huirua T.W.M., Wang R., Callaghan P.T. // Macromolecules. 1990. V. 23. № 6. P. 1658.

  7. Doi M. // J. Polym. Sci., Polym. Lett. Ed. 1981. V. 19. № 5. P. 265.

  8. Kimmich R., Köpf M. // Relaxation in Polymers. Progress in Colloid & Polymer Science. Steinkopff. 1989. V. 80. P. 8.

  9. Folland R., Charlesby A. // J. Polym. Sci., Polym. Lett. Ed. 1978. V. 16. № 7. P. 339.

  10. Gölz W.L.F., Zachmann H.G. // Macromol. Chem. Phys. 1975. V. 176. № 9. P. 2721.

  11. Berry G.C., Fox T.G. // Adv. Polym. Sci. 1968. V. 5. P. 261.

  12. Trutschel M.L., Mordvinkin A., Furtado F., Willner L., Saalwächter K. // Macromolecules. 2018. V. 51. № 11. P. 4108.

  13. Markelov D.A., Dolgushev M., Lahderanta E. // Ann. Reports NMR Spectroscopy. 2017. V. 91. P. 1.

  14. Dolgushev M., Markelov D.A., Fürstenberg F., Guérin T. // Phys. Rev. E. 2016. V. 94. № 1. P. 012502.

  15. Markelov D.A., Fürstenberg F., Dolgushev M. // Polymer. 2018. V. 144. P. 65.

  16. Bixon M., Zwanzig R. // J. Chem. Phys. 1978. V. 68. № 4. P. 1896.

  17. Готлиб Ю.Я., Светлов Ю.Е. // Высокомолек. соед. A. 1979. V. 21. № 7. P. 1531.

  18. Bawendi M.G., Freed K.F. // J. Chem. Phys. 1985. V. 83. № 5. P. 2491.

  19. Lagowski J.B., Noolandi J., Nickel B. // J. Chem. Phys. 1991. V. 95. № 2. P. 1266.

  20. Winkler R.G., Reineker P., Harnau L. // J. Chem. Phys. 1994. V. 101. № 9. P. 8119.

  21. Ha B.Y., Thirumalai D. // J. Chem. Phys. 1995. V. 103. № 21. P. 9408.

  22. Kimmich R., Fatkullin N. // Adv. Polym. Sci. 2004. V. 170. P. 1.

  23. Krutyeva M.A., Fatkullin N.F., Kimmich R. // Polymer Science A. 2005. V. 47. № 9. P. 1022.

  24. Fatkullin N.F., Shakirov T.M., Balakirev N.A. // Polymer Science A. 2010. V. 52. № 1. P. 72.

  25. Schweizer K.S. // J. Chem. Phys. 1989. V. 91. № 9. P. 5802.

  26. Fatkullin N., Gubaidullin A., Mattea C., Stapf S. // J. Chem. Phys. 2012. V. 137. № 22. P. 224907.

  27. Kimmich R., Fatkullin N. // Prog. Nucl. Magn. Reson. Spectrosc. 2017. V. 101. P. 18.

  28. Fatkullin N., Stapf S., Hofmann M., Meier R., Rössler E.A.// J. Non-Cryst. Solids. 2015. V. 407. P. 309.

  29. Kimmich R. NMR: Tomography, Diffusometry, Relaxometry. Berlin; Heidelberg: Springer Science & Business Media, 2012.

  30. Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. М.: Физматлит, 2003. Т. 1.

  31. Хазанович Т.Н. // Высокомолек. соед. 1963. Т. 5. № 1. С. 112.

  32. Fatkullin N.F., Körber T., Rössler E.A. // Polymer. 2018. V. 142. P. 310.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Высокомолекулярные соединения (серия А)

Архивы выпусков Информация о журнале Отправить рукопись в журнал