Высокомолекулярные соединения (серия А), 2020, T. 62, № 3, стр. 170-180
УПРУГИЕ МОДУЛИ И КОЭФФИЦИЕНТ ПУАССОНА АМОРФНЫХ ОРГАНИЧЕСКИХ ПОЛИМЕРОВ
С. Ш. Сангадиев a, М. В. Дармаев a, **, Д. С. Сандитов a, b, *
a Бурятский государственный университет имени Доржи Банзарова
670000 Улан-Удэ, ул. Смолина, 24а, Республики Бурятия, Россия
b Институт физического материаловедения Сибирского отделения Российской академии наук
670047 Улан-Удэ, ул. Сахьяновой, 6, Республики Бурятия, Россия
** E-mail: darmaev@bsu.ru
* E-mail: sanditov@bsu.ru
Поступила в редакцию 11.07.2019
После доработки 03.12.2019
Принята к публикации 17.12.2019
Аннотация
Импульсным методом молекулярной акустики измерена скорость продольных и поперечных звуковых волн в аморфных органических полимерах. Определены упругие модули и коэффициент Пуассона, а также введенный ранее эффективный модуль упругости. Показано, что у аморфных полимеров отношение модуля объемного сжатия к эффективному модулю упругости является однозначной функцией коэффициента Пуассона. Эффективный модуль упругости тесно связан с параметром Грюнайзена – мерой ангармонизма. Рассмотрена природа коэффициента Пуассона аморфных полимеров.
ВВЕДЕНИЕ
Упругое состояние изотропного твердого тела считается заданным (достаточно полно охарактеризованным), если известны два каких-либо модуля упругости или один модуль упругости и коэффициент Пуассона μ [1]:
где E – модуль упругости при одноосной деформации, G – модуль сдвига, B – модуль объемного сжатия. На основе измеренных значений продольной ${{{v}}_{l}}$ и поперечной ${{{v}}_{t}}$ скорости ультразвука и плотности ρ можно вычислить модуль сдвига и коэффициент Пуассона по формулам молекулярной акустики [1]:(2)
${\mu } = \frac{1}{2}\frac{{{{{({{{v}}_{l}}{\text{/}}{{{v}}_{t}})}}^{2}} - 2}}{{{{{({{{v}}_{l}}{\text{/}}{{{v}}_{t}})}}^{2}} - 1}}$Для кубических кристаллов квадрат среднеквадратичной скорости волн деформации ${v}_{k}^{2}$ является инвариантом суммы квадратов значений скорости распространения продольных и поперечных акустических волн [2, 3]:
Соотношение (3) оказывается справедливым и для кристаллов с другими решетками, а также для стекол [4–8].
Представляет определенный интерес произведение плотности на квадрат данной среднеквадратичной скорости [6, 7]:
Первоначально величина K была названа усредненным модулем упругости [6]. Такое название не совсем удачно, поскольку известные упругие модули E, G и B также относятся к усредненным величинам. Поэтому было предложено назвать величину K эффективным модулем упругости [7]. Тем более, что K зависит от ангармонизма [7, 8].
Настоящая работа посвящена измерению акустических и упругих свойств полимеров методом молекулярной акустики, а также установлению связи эффективного модуля упругости с упругими модулями и коэффициентом Пуассона применительно к аморфным органическим полимерам. Рассмотрена природа коэффициента Пуассона и его связь со структурно-чувствительными свойствами полимерных стекол.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Скорость ультразвука определяли импульсным методом [9–12]: исследуемый образец помещали между двумя буферными (металлическими или кварцевыми) стержнями, к внешним торцевым поверхностям которых крепили пьезокварцевые преобразователи [11, 12]. Измерение скорости ультразвука сводится к измерениям времени пробега акустического импульса в исследуемом образце и длины акустического пути.
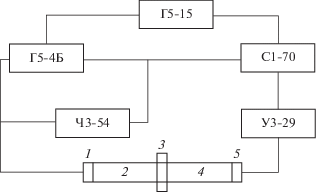
Блок-схема собранной установки приведена на рис. 1. Генератор Г5-15 осуществляет одновременный запуск двухканального генератора прямоугольных импульсов Г5-4Б и ждущей развертки осциллографа С1-70. Импульс первого канала генератора Г5-4Б подается на излучающий пьезоэлемент и возбуждает его на собственной частоте. Ультразвуковой импульс, возбужденный излучателем, проходит через буферные стержни и исследуемый образец. Далее он поступает на приемный пьезопреобразователь, где вследствие прямого пьезоэффекта возникает электрический сигнал. Затем электрический сигнал усиливается широкополосным усилителем У3-29 и подается на Y-вход электронного осциллографа. Генератор Г5-4Б позволяет задерживать импульс второго канала относительно первого, причем время задержки может быть измерено с высокой точностью (0.01 мкс) цифровым кварцевым частотомером Ч3-54. Задержанный импульс второго канала в отрицательной полярности подается на Z-вход осциллографа и служит в качестве подвижной метки времени. При отсчете метка времени совмещается с одним из максимумов высокочастотной составляющей импульса, наблюдаемого на экране осциллографа.
Рис. 1.
Блок-схема ультразвуковой установки: Г5-15, Г5-4Б – двухканальные генераторы прямоугольных импульсов; С1-70 – осциллограф с Z-входом; У3-29 – широкополосный усилитель; Ч3-54 – кварцевый частотомер; 1, 5 – кварцевые пластины; 2, 4 – буферные стержни; 3 – исследуемый образец.
Пьезопреобразователями электрических импульсов в продольные и поперечные акустические импульсы служили кварцевые пластины 1 и 5 соответствующих срезов с частотой колебаний 1 МГц (рис. 1). Буферные стержни 2 и 4, выполненные из кварцевых стержней, использовали для того, чтобы избежать наложения наведенного зондирующего импульса и ультразвукового импульса, прошедшего через исследуемый образец. Торцы образцов и буферных стержней обрабатывали с высокой точностью. Особые требования предъявляли к их параллельности (не более 1.5 мкм на диаметр). Длину образцов измеряли оптическим катетометром В630 с точностью до 2 мкм. Проведенные контрольные измерения показали удовлетворительное согласие с данными работ [13, 14]. Относительная погрешность величин ${{{v}}_{l}}$ и ${{{v}}_{t}}$ составляет 0.3–0.4%. Плотность находили методом гидростатического взвешивания в дистиллированной воде с точностью ±0.001 г/см3. Исследования осуществляли при комнатной температуре.
Для аморфных полимеров характерно сильное поглощение ультразвука. Поэтому измерения скорости звука выполняли на коротких, но толстых стержнях (модель “монеты”). Диаметр стержня составлял 20–30 мм, а его длина равнялась 5–8 мм. Для увеличения акустического пути использовали буферные кварцевые стержни. Установив время пробега импульса в буферных стержнях без образца и в стержнях с образцом, заключенным между ними, можно рассчитать скорость ультразвука по формуле [12]
Здесь l – длина образца, t0 – время пробега ультразвукового импульса в буферных стержнях.
Экспериментальные данные о продольной и поперечной скорости ультразвука исследованных аморфных полимеров сведены в табл. 1, где также приведены значения скорости звука в силикатных стеклах. Небольшое поглощение акустических колебаний в силикатных стеклах позволяет удлинить образец, вследствие чего можно не применять буферные стержни.
Таблица 1.
Скорость ультразвука ${{{v}}_{l}}$, ${{{v}}_{t}}$, плотность и упругие свойства аморфных полимеров
| №, п/п | Вещество | ${{{v}}_{l}}$, м/с | ${{{v}}_{t}}$, м/с | ρ, кг/м3 | E, МПа | B, МПа | G, МПа | μ |
|---|---|---|---|---|---|---|---|---|
| 1 | ПС | 2280 | 1155 | 1052 | 3691 | 2412 | 925 | 0.33 |
| 2 | Полиарилат | 2365 | 1000 | 1221 | 3424 | 3459 | 821 | 0.39 |
| 3 | МСП | 2570 | 1040 | 1138 | 3508 | 3898 | 835 | 0.40 |
| 4 | ПК | 2290 | 800 | 1197 | 2205 | 3500 | 514 | 0.43 |
| 5 | ПЭТФ | 2485 | 1100 | 1352 | 4460 | 4130 | 1077 | 0.38 |
| 6 | АБС | 2240 | 820 | 1053 | 2070 | 2875 | 486 | 0.42 |
| 7 | ПЭНП | 2100 | 1125 | − | − | − | − | 0.30 |
| 8 | ПЭВП | 2485 | 900 | − | − | − | − | 0.42 |
| 9 | Листовое силикатное стекло | 5610 | 3360 | 2470 | 68 000 | 26 984 | 18 579 | 0.22 |
| 10 | Кварцевое стекло ГСМ-700 | 5847 | 3607 | − | − | − | − | 0.19 |
Примечание. Здесь и в табл. 2 МСП – сополимер стирола, метилметакрилата и полибутадиенового каучука.
КОЭФФИЦИЕНТ ПУАССОНА КАК СТРУКТУРНО-ЧУВСТВИТЕЛЬНОЕ СВОЙСТВО АМОРФНЫХ ПОЛИМЕРОВ
Коэффициент Пуссона μ, который иногда называют коэффициентом поперечной деформации, равен отношению поперечной деформации тела к его продольному удлинению при одноосном растяжении [1]:
В отличие от упругих модулей величина μ выражает особенности не только прямой деформации в направлении действия внешней силы, но и поперечной деформации, происходящей в направлении, не совпадающем с направлением действия силы. Прямая деформация характеризует непосредственное сопротивление тела в направлении действия деформирующей силы, а поперечная деформация зависит от того, как это тело передает внешнее воздействие в других направлениях. Последнее определяется особенностями атомно-молекулярного строения тела и динамикой решетки. По этим и другим причинам коэффициент Пуассона оказывается более выраженным структурно-чувствительным свойством, чем упругие модули, хотя и меняется в небольших пределах.
Разберем связь коэффициента поперечной деформации μ с предельной упругой деформацией межатомной связи.
В модели ангармонического одномерного твердого тела – линейной цепочке связанных осцилляторов с кубическим потенциалом – сила, возвращающая атом в локальное равновесное положение (F = –(dU/dx)), выражается приближенным соотношением [15–18]
где гармонический a и ангармонический b коэффициенты определяются соответственно второй и третьей производными потенциальной энергии межатомного взаимодействия U(r) в точке равновесия r = r0 (в разложении функции U(r) в ряд Тейлора), $x = \Delta r = \left( {r - {{r}_{0}}} \right)$ – смещение атома. В области перегиба кривой U(x) величина силы F(x) при r = rm проходит через максимум. Отсюда предельное удлинение межатомной связи xm = $({{r}_{m}} - {{r}_{0}})$, соответствующее максимуму силы Fm, вычисляется отношением гармонического a и ангармонического b коэффициентов: xm = Δrm = $a{\text{/}}b$. Отнесем его к равновесному межатомному расстоянию r0:Относительная предельная деформация межатомной связи Δrm/r0 оказывается тесно связанной с параметром Грюнайзена γD, характеризующим нелинейность силы межатомного взаимодействия и ангармонизм колебаний решетки:
Формула (7) выводится достаточно строго [15–17]; известен вариант с привлечением квантовой механики, включая область низких значений температуры (T < θD) [15]. Она остается справедливой при переходе к трехмерному твердому телу [18–20]. В статье в Приложении дается ее приближенный вывод [21].
Из выражений (6) и (7) следует, что предельная деформация межатомной связи обратно пропорциональна параметру Грюнайзена
Для расчета γD наряду с известным уравнением Грюнайзена (см. Приложение) задействованы другие соотношения, например формула Беломестных–Теслевой [4]:
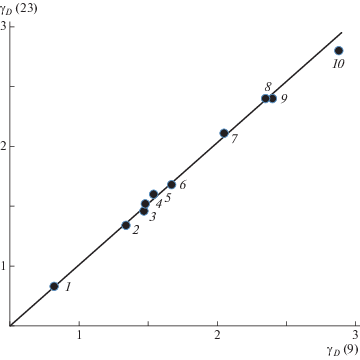
установленная с привлечением молекулярной акустики, термодинамики и теории упругости. Примечательно, что сравнительно простое соотношение (9) находится в удовлетворительном согласии с уравнением Грюнайзена для различных твердых тел (рис. 2) [4–6].Рис. 2.
Линейная корреляция между значениями параметра Грюнайзена γD, полученными по уравнению (23) и по формуле (9), для кристаллов Be (1), LiF (2), NaCl (3), LiCl (4), KCl (5), KBr (6), Al (7), Ag (8), Pd (9) и Au (10), использованы данные работ [6, 7].
Подстановка γD из формулы (9) в равенство (8) приводит к заключению, что относительная деформация связи Δrm/r0 является однозначной функцией коэффициента Пуассона:
(10)
$\frac{{{\Delta }{{r}_{m}}}}{{{{r}_{0}}}} = \frac{{2 - 3{\mu }}}{{9\left( {1 + {\mu }} \right)}}$По формуле (10) была рассчитана величина Δrm/r0 для исследованных полимеров. Она колеблется в небольших пределах от 0.05 до 0.08 (табл. 2) и согласуется с имеющимися данными работ [16, 20, 22]. Величина Δrm/r0 представляет собой деформацию, при которой достигается максимум силы межатомного (межмолекулярного) притяжения и происходит переход от упругой к неупругой деформации.
Таблица 2.
Коэффициент Пуассона μ и рассчитанные на его основе предельная деформация межатомной связи Δrm/r0, критическая деформация сдвига εc и объемная плотность энергии межмолекулярного взаимодействия аморфных органических полимеров
| Полимеры | μ | $\left( {\frac{{\Delta {{r}_{m}}}}{{{{r}_{0}}}}} \right)$ | ${{{\varepsilon }}_{{\text{c}}}}$ | $\frac{U}{V},{\text{МПа}}$ |
|---|---|---|---|---|
| ПС | 0.33 | 0.08 | 0.08 | 1845 |
| ПЭТФ | 0.38 | 0.07 | 0.06 | 2081 |
| Полиарилат | 0.39 | 0.07 | 0.05 | 1650 |
| МСП | 0.40 | 0.06 | 0.05 | 1684 |
| АБС | 0.42 | 0.06 | 0.04 | 957 |
| ПК | 0.43 | 0.05 | 0.03 | 1039 |
Остановимся на связи коэффициента поперечной деформации с потенциалом межатомного взаимодействия Ми:
где r – расстояние между атомами; m, n – показатели, характеризующие силы притяжения и отталкивания атомов соответственно; A, B – постоянные. Данный потенциал справедлив для центральносимметричного потенциального поля, например, для ионных кубических кристаллов. Тем не менее он вполне успешно используется для стеклообразных систем.В своих работах С.В. Немилов [23, 24] для неорганических стекол различного состава установил эмпирическое соотношение, однозначно связывающее коэффициент Пуассона μ с произведением параметров потенциала Ми mn:
В.Б. Лазаревым с соавторами [25] показано, что обратная величина произведения mn имеет смысл критической деформации εc, при которой твердое тело теряет устойчивость при сдвиге:
При выводе этого равенства было использовано приближение упругоизотропного поликристаллического тела с модифицированным потенциалом Ми, который не связан с представлениями о парности и центральности межатомного взаимодействия [25].
Полагая применимыми соотношения (11) и (12) к исследуемым полимерным стеклам, можно из них найти произведение mn как функцию μ и критическую деформацию εc = 1/mn:
(13)
${{{\varepsilon }}_{{\text{c}}}} = \frac{{\left( {1 - 2{\mu }} \right)}}{{3\left( {1 + {\mu }} \right)}}$Результаты расчета приведены в табл. 2. Критическая деформация εc ∼ 0.03–0.08 по порядку величины близка к относительной предельной деформации межатомных (межмолекулярных) связей Δrm/r0.
Для объемного упругого модуля B стекол, согласно работам [23, 24], справедливо соотношение Грюнайзена
Из данных о величинах B и mn была рассчитана объемная плотность энергии межмолекулярного взаимодействия U/V для полимеров (табл. 2).
Обращает на себя внимание то обстоятельство, что в определении коэффициента Пуассона речь идет об обычных “тихих” статических упругих деформациях, однако величина μ оказывается однозначной функцией параметров, характеризующих динамические и критические процессы.
Среди работ, посвященных природе коэффициента Пуассона особого внимания заслуживает подход Берлина, Ротенбурга и Басерста [26, 27]. Авторами представлена модель (модель БРБ) случайно упакованных атомов в виде сфер, взаимодействующих друг с другом в месте контакта двумя видами сил: нормальных к плоскости контакта (центральных сил) и тангенциальных (сил трения), действующих по касательной к данной плоскости. Предполагается, что нормальные fn и тангенциальные ft силы пропорциональны соответствующим смещениям атома xn и xt из равновесного положения:
где аn и аt – нормальная и тангенциальная жесткости. Из модели БРБ следует, что коэффициент Пуассона можно определить отношением сдвиговой и изгибной жесткостей λ = аt /аn [26]:Важно то, что в формулу (14) входит микроскопический параметр λ, анализ содержания которого может дать некоторую полезную информацию о природе коэффициента поперечной деформации. При λ = 0 имеем µ = 0.25, что соответствует ансамблю частиц с центральными силами (an $ \gg $ at). С ростом λ величина µ уменьшается и при λ = 1, µ = 0, а в пределе при λ → ∞ (at $ \gg $ an) µ = –1. Видно, что модель БРБ предсказывает возможность существования тел с отрицательным коэффициентом Пуассона µ < 0 и приводит к нижнему теоретическому пределу µ = –1 [1]. Примечательно, что в последнее время получены изотропные твердые тела с отрицательным коэффициентом поперечной деформации (μ < 0) [26–29]. В 1987 году впервые был синтезирован полимерный изотропный пеноматериал с коэффициентом Пуассона μ = –0.7 (см. работы [26, 27]).
Поскольку сдвиговая жесткость at связана с силой трения, можно ожидать зависимость λ = = at/an от нелинейных эффектов, в частности от ангармонизма, мерой которого служит параметр Грюнайзена γD. В самом деле, из соотношения (14) и (9) вытекает однозначная связь λ с параметром Грюнайзена:
Следовательно, в уравнении БРБ (14) в неявном виде заложена зависимость коэффициента Пуассона от ангармонизма.
В аморфных органических полимерах на коэффициент Пуассона µ заметное влияние оказывают боковые разветвления основной цепи макромолекулы (“боковые привески” главной цепи) [30]. Минимальными значениями µ и γD обладает полиэтилен, у которого роль “боковой привески” выполняет легкий атом водорода. Замещение атомов водорода более крупными и тяжелыми атомами фтора при переходе от полиэтилена к политетрафторэтилену приводит к росту γD и соответственно увеличению μ. Далее, при замене фтора в повторяющемся звене политетрафторэтилена атомом хлора и при переходе к политетрафторхлорэтилену наблюдается еще бόльший рост µ [30].
Если происходит замещение легких атомов более крупными и тяжелыми, то на боковых (а также концевых) участках цепей усиливается нелинейность силы межмолекулярного взаимодействия и ангармонизм колебаний решетки γD, что снижает относительную сдвиговую жесткость связей λ. В свою очередь, снижение λ приводит к возрастанию коэффициента Пуассона μ (выражения (14) и (15)).
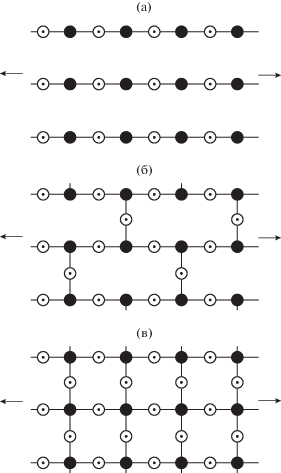
Очевидна зависимость относительной тангенциальной жесткости λ от плотности поперечных связей n, определяемой как число валентных связей на один катион n у ряда полимеров и стекол (рис. 3) [31]. Так, у линейных аморфных полимеров (резина, полистирол), имеющих связанность 2 (рис. 3а), n = 0 и µ ∼ 0.40–0.45; для линейно-разветвленных структур со связанностью 3 (B2O3, P2O5, As2O3) n = 1 и µ ∼ 0.3 (рис. 3б); для структурных сеток со связностью 4 (SiO2, GeO2) n = 2 и µ ∼ 0.15, т.е. соотношение ∼0.3 : 2.0 (рис. 3в). Видно, что с ростом плотности поперечных валентных связей ослабляется нелинейность силы взаимодействия атомов, убывает ангармонизм γD и в соответствии с зависимостью (15) растет относительная сдвиговая жесткость связей λ, а это, согласно формуле БРБ (14), влечет снижение коэффициента поперечной деформации μ.
Рис. 3.
Схемы линейной (а), линейно-разветвленной (б) и сетчатой (в) структур аморфных веществ [31] при n = 0, 1, 2 и μ ∼ 0.4, 0.3, 0.15 соответственно. Светлые кружки – анионы, темные – катионы; стрелки указывают напряжение растяжения.
Согласно подходу Кузьменко [32], коэффициент Пуассона твердых тел характеризует их способность противодействовать изменению объема. Чем больше μ, тем меньше изменение объема тела при деформации. Верхний предел μ = 0.5 следует из условия, что изменение объема при деформировании полностью компенсируется противодействием вещества (ΔV = 0). Данное условие относится к жидкостям; у твердых тел полной компенсации изменения объема не бывает, и для них μ < 0.5. В теории Пинеды [33] рассмотрено согласованное изменение коэффициента Пуассона и параметра Грюнайзена применительно к металлическим стеклам. В рамках этой теории можно на качественном уровне обосновать взаимосвязь величин μ и γD. В своих работах Т.А. Конторова [34, 35] объясняет это явление существованием вполне определенной связи между гармоническим и ангармоническим коэффициентами и полученной ею функциональной зависимости от них линейных и нелинейных свойств твердых тел.
ЭФФЕКТИВНЫЙ МОДУЛЬ УПРУГОСТИ, УПРУГИЕ МОДУЛИ И КОЭФФИЦИЕНТ ПУАССОНА
Из формулы модуля объемного сжатия B кубических кристаллов:
а также из соотношения для произведения плотности и квадрата среднеквадратичной скорости звука ${v}_{k}^{2}$ [2, 3]: видно, что при выполнении условия Коши C12 = = C44, когда между однородно деформированными областями кубической решетки действуют центральные силы, величина $K = {\rho }{v}_{k}^{2}$ совпадает с модулем объемного сжатия, т.е. K = B. Во всех других случаях произведение ${\rho }{v}_{k}^{2}$ отлично от B. Здесь C11, C12 и C44 – упругие постоянные второго порядка.Так же, как и отношение модуля сдвига G к модулю объемного сжатия B [1], т.е.
величины G/K и B/K являются однозначными функциями коэффициента Пуассона μ.Разделив $G = {\rho }{v}_{s}^{2}$ на $K = {\rho }{v}_{k}^{2}$, получаем соотношение
С помощью формулы (3) правую часть этого равенства выразим через квадраты продольной и поперечной скорости звука как
(18)
$\frac{{{v}_{t}^{2}}}{{{v}_{k}^{2}}} = 3{{\left( {\frac{{{v}_{l}^{2}}}{{{v}_{t}^{2}}} + 2} \right)}^{{ - 1}}}$В теории упругости отношение ${v}_{l}^{2}{\text{/}}{v}_{t}^{2}$ у изотропных тел является функцией коэффициента Пуассона [1]
Подставив (19) в выражение (18), а затем (18) в соотношение (17), приходим к формуле, где отношение G/K является функцией только коэффициента Пуассона:
Из комбинации данной формулы с равенством (16) следует, что отношение B/K также есть однозначная функция μ:
Таким образом, во-первых, как и модуль сдвига, величина $K = {\rho }{v}_{k}^{2}$ выражается через произведение плотности на квадрат скорости звука и, во-вторых, при выполнении условия Коши она совпадает с модулем объемного сжатия. В-третьих, как и отношения упругих модулей, величины G/K и B/K считаются однозначными функциями коэффициента Пуассона. Поэтому произведение ${\rho }{v}_{k}^{2}$, обладающее характерными признаками упругих модулей, вполне может быть названо эффективным (или характерным) модулем упругости.
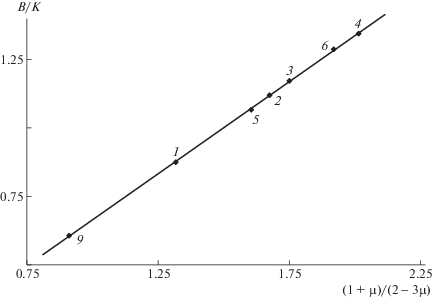
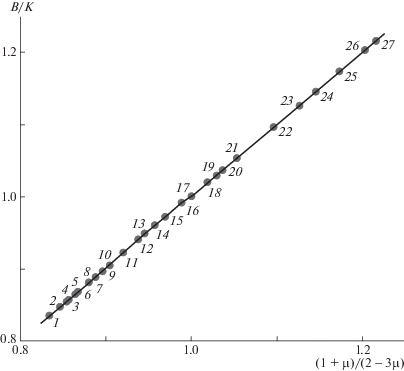
При установлении зависимостей G/K и B/K от коэффициента Пуассона в виде соотношений (20) и (21) были использованы формулы для кристаллов с кубическими решетками. Тем не менее, например, зависимость (21) оказалась оправданной не только для кристаллических твердых тел с другими решетками, но и для неорганических стекол [6, 7]. В качестве еще одного примера проверки выражения (21) мы применили его к многокомпонентным промышленным оптическим стеклам. (Необходимые экспериментальные данные взяты из справочника [36].) Как видно на рис. 4, зависимость отношения B/K от функции коэффициента Пуассона (1 + μ)/(2 – 3μ) линейна, причем прямая проходит через начало координат с наклоном, равным единице, что подтверждает справедливость формулы (21).
Рис. 4.
Зависимость отношения модуля объемного сжатия к эффективному модулю упругости B/K от функции коэффициента Пуассона (1 + µ)/(2 – 3µ) для многокомпонентных оптических стекол [36]: 1 – ЛК-7, 2 – КФ-6, 3 – Ф-6, 4 – КФ-7, 5 – К-14, 6 – ЛФ-5, 7 – К-8, 8 – КФ-4, 9 – Ф-13, 10 – К-19, 11 – Ф-4, 12 – ТФ-1, 13 – БК-6, 14 – БФ-21, 15 – БФ-8, 16 – БК-10, 17 – ТФ-7, 18 – ФК-14, 19 – ТК-13, 20 – ТК-23, 21 – БФ-11, 22 – ТК-17, 23 – ОФ-2, 24 – СТК-7, 25 – СТК-9, 26 – ЛК-4, 27 – ТБФ-4.
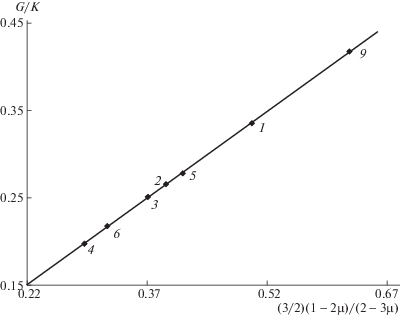
Как и следовало ожидать, для исследованных нами аморфных полимеров (табл. 1) отношения B/K и G/K линейно зависят от функций коэффициента Пуассона (1 + μ)/(2 – 3μ) и (3/2)(1 – 2μ)/(2 – 3μ) соответственно и описываются уравнениями прямых, проходящих через начало координат (рис. 5 и 6). Тангенс угла наклона прямых близок к единице. Таким образом, зависимости (20) и (21) удовлетворительно выполняются для рассмотренных полимеров.
Рис. 6.
Зависимость отношения модуля сдвига к эффективному модулю упругости G/K от функции коэффициента Пуассона $\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right){{\left( {1 - 2{\mu }} \right)} \mathord{\left/ {\vphantom {{\left( {1 - 2{\mu }} \right)} {\left( {2 - 3{\mu }} \right)}}} \right. \kern-0em} {\left( {2 - 3{\mu }} \right)}}$ для аморфных полимеров.
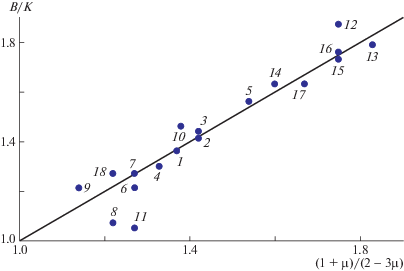
На рис. 7 представлен аналогичный график для других аморфных органических полимеров, построенный на основе данных работы [37]. Несмотря на значительный разброс экспериментальных точек, все они (за исключением двух–трех полимеров) удовлетворительно согласуются с зависимостью (21): прямая проходит через начало координат и ее наклон равен единице. Разброс точек здесь обусловлен, по-видимому, разной тепловой предысторией образцов. У образцов исследованных аморфных полимеров тепловая предыстория была одинаковая. Поэтому на рис. 5 и 6 практически нет разброса точек.
Рис. 7.
Зависимость отношения модуля объемного сжатия к эффективному модулю упругости B/K от функции коэффициента Пуассона (1 + μ)/(2 – 3μ) для аморфных органических полимеров при T = 240 K [37]: 1 – ПС, 2 – ПВХ, 3 – ПВФ, 4 – ПММА, 5 – ПК, 6 – полифенилизобутилсилсесквиоксан, 7 – эпоксидная смола ЭД-5, 8 – ПОМ, 9 – ПЭВД, 10 – ПП, 11 – ПТФЭ, 12 – политрифторэтилен, 13 – найлон-6, 14 – найлон-7, 15 – найлон-11, 16 – найлон-12, 17 – поли-4-метилпентен-1, 18 – ПВДФ.
Одной из особенностей величины $K = {\rho }{v}_{k}^{2}$ является ее связь с параметром Грюнайзена γD – мерой ангармонизма. В самом деле, из сравнения равенства (21) с формулой (9) следует взаимосвязь эффективного модуля упругости K и параметра Грюнайзена γD:
В заключение обратим внимание на то обстоятельство, что по рассмотренным выше материалам возникают вопросы, которые остаются без ответа. Во-первых, почему линейная (гармоническая) величина μ оказывается однозначной функцией сугубо нелинейной (ангармонической) величины γD (см. аналогичный пример в работе [38])? Во-вторых, почему у ряда изотропных твердых тел коэффициент Пуассона оказывается отрицательным? Это означает поперечное расширение тела при его одноосном растяжении, что противоречит здравому смыслу. В-третьих, почему формулы, относящиеся к анизотропным кубическим кристаллам, оказываются оправданными для изотропных стеклообразных материалов? Эти вопросы требуют в дальнейшем детального изучения.
ЗАКЛЮЧЕНИЕ
Методом молекулярной акустики определены модули упругости и коэффициент Пуассона для ряда органических аморфных полимеров. Применительно к этим материалам рассмотрен эффективный упругий модуль K = ρ${v}_{k}^{2}$. У исследованных аморфных полимеров отношение модуля объемного сжатия к эффективному модулю упругости является однозначной функцией коэффициента Пуассона. Особенностью величины K можно назвать ее связь с параметром Грюнайзена – мерой ангармонизма. На данном этапе приходится допускать однозначную зависимость коэффициента Пуассона от параметра Грюнайзена (от ангармонизма), что требует дальнейшего рассмотрения. По данным о коэффициенте Пуассона для исследованных аморфных полимеров рассчитаны критическая деформация, при которой твердое тело теряет устойчивость при сдвиге, а также предельная упругая деформация межмолекулярной (межатомной) связи. Результаты расчетов согласуются с имеющимися в литературе данными.
Авторы выражают благодарность Г.В. Козлову за предоставленные образцы аморфных полимеров.
Работа выполнена при финансовой поддержке Министерства науки и высшего образования (грант № 3.5406.2017/8.9).
Список литературы
Ландау Л.Д., Лифшиц Е.М. Теория упругости. М.: Наука, 1965.
Киттель Ч. Введение в физику твердого тела. М.: Физматгиз, 1962.
Леонтьев К.Л. // Акуст. журн. 1981. Т. 47. № 4. С. 554.
Беломестных В.Н., Теслева Е.П. // Журн. техн. физики. 2004. Т. 74. № 8. С. 140.
Беломестных В.Н. // Письма в ЖТФ. 2001. Т. 30. № 3. С. 15.
Сандитов Д.С., Беломестных В.Н. // Журн. техн. физики. 2011. Т. 81. № 11. С. 77.
Сандитов Д.С., Дармаев М.В. // Неорганические материалы. 2019. Т. 55. № 6. С. 94.
Сандитов Д.С., Дармаев М.В. // Изв. вузов. Сер. Физика. 2015. Т. 58. № 5. С. 89.
Сангадиев С.Ш., Цыдыпов Ш.Б. // Научн. тр. молодых ученых. Улан-Удэ: БГУ, 1996. С. 15. Ч. 1.
Сангадиев С.Ш. // Сб. научн. тр. Сер. Физ.-мат. науки. Физика. Улан-Удэ: ВСГТУ, 1998. С. 82. Ч. 2.
Мак-Скимин Г. // Физическая акустика / Под. ред. У. Мэзона. М.: Мир, 1966. Т. 1. Ч. А.
Перепечко И.И. Акустические методы исследования полимеров. М.: Химия, 1973.
Заварыкина Л.Н., Зотова В.В., Неручев Ю.А. // Ультразвук и физико-химические свойства вещества. Курск: Курский гос. педагогический ун-т, 1978. С. 7.
Маринин В.А. // Журн. физ. химии. 1951. Т. 25. С. 641.
Бурштейн А.И. Молекулярная физика. Новосибирск: Наука, 1986.
Петров В.А., Башкарев А.Я., Веттегрень В.И. Физические основы прогнозирования долговечности конструкционных материалов. СПб.: Политехника, 1993.
Лейбфрид Г. // Микроскопические теории механических и тепловых свойств кристаллов. М.; Л.: Физматгиз, 1963.
Френкель Я.И. Введение в теорию металлов. Л.; М.: ОГИЗ, 1948.
Сандитов Д.С., Козлов Г.В. // Физ. хим. стекла. 1995. Т. 21. № 6. С. 549.
Козлов Г.В., Сандитов Д.С. Ангармонические эффекты и физико-механические свойства полимеров. Новосибирск: Наука, 1994.
Сандитов Д.С., Мантатов В.В. // Физ. хим. стекла. 1983. Т. 3. № 3. С. 287.
Бартенев Г.М. Прочность и механизм разрушения полимеров. М.: Химия, 1984.
Немилов С.В. // Тр. 5-го Всесоюз. совещания “Стеклообразное состояние”. Л.: Наука, 1971. С. 10.
Немилов С.В. // Докл. АН СССР. 1968. Т. 181. № 6. С. 1427.
Лазарев В.Б., Баланкин А.С., Изотов А.Д., Кожушко А.А. Структурная устойчивость и динамическая прочность неорганических материалов. М.: Наука, 1993.
Берлин А.А., Ротенбург Л., Басэрст Р. // Высокомолек. соед. Серия Б. 1991. Т. 33 № 8. С. 619.
Берлин А.А., Ротенбург Л., Басэрст Р. // Высокомолек. соед. А. 1992. Т. 34. № 7. С. 6.
Сандитов Д.С., Мельниченко Т.Д., Мантатов В.В., Петрушова О.В., Мельниченко Т.Н. // Деформация и разрушение материалов. 2009. № 4. С. 11.
Конёк Д.А., Войцеховски К.В., Плескачевский Ю.М., Шилько С.В. // Механика композит. матер. конструкций. 2004. Т. 10. № 1. С. 35.
Перепечко И.И. Свойства полимеров при низких температурах. М.: Химия, 1977.
Bridge B., Patel N.D., Waters D.N. // Phys. Status Solidi. A. 1983. V. 77. № 2. P. 655.
Кузьменко В.А. Новые схемы деформирования твердых тел. Киев: Наукова думка, 1973.
Pineda E. // Phys. Rev. B. 2006. V. 73. P. 104109-1–104109-6.
Конторова Т.А. // Некоторые проблемы прочности твердых тел. М.; Л.: Изд-во АН СССР, 1959. С. 99.
Жузе В.П., Конторова Т.А. // Журн. техн. физики. 1958. Т. 28. № 8. С. 727.
Оптические стекла. Справочник. Под ред. Г.Т. Петровского. Л.: ГОИ им. С.И. Вавилова, 1975.
Голубь П.Д. // Вестн. Барнаульского гос. пед. ун-та. Сер. Естеств. и точн. науки. 2008. № 8. С. 101.
Barker R. // J. Appl. Phys. 1963. V. 34. № 1. P. 107.
Sanditov D.S. // Polymer Science A. 2016. V. 58. № 5. P. 710.
Дополнительные материалы отсутствуют.
Инструменты
Высокомолекулярные соединения (серия А)