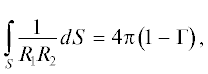Высокомолекулярные соединения (серия С), 2022, T. 64, № 2, стр. 121-134

ИЗГИБНАЯ ЖЕСТКОСТЬ РАЗВЕТВЛЕННЫХ ПОЛИМЕРНЫХ ЩЕТОК НА МЕМБРАНЕ КОНЕЧНОЙ ТОЛЩИНЫ

И. В. Михайлов^a, *, А. А. Даринский^a, Т. М. Бирштейн^a

^a Институт высокомолекулярных соединений Российской академии наук
199004 Санкт-Петербург, Большой пр., 31, Россия

^* E-mail: I.V.Mikhailov-IMC.RAS@yandex.ru

Поступила в редакцию 05.04.2022
После доработки 30.07.2022
Принята к публикации 01.08.2022

EDN: BGJPZX
DOI: 10.31857/S2308114722700194

Аннотация

Развита теория наведенной изгибной жесткости плоских полимерных щеток, симметрично привитых к обеим поверхностям мембраны конечной толщины и погруженных в низкомолекулярный растворитель. Для построения теории использованы как аналитический, так и численный варианты метода самосогласованного поля. Определены зависимости среднего и гауссового модулей Хельфриха щеток от степени полимеризации, параметра разветвленности и плотности прививки цепей к поверхностям мембраны. Показано, что с ростом толщины мембраны абсолютные значения обоих модулей увеличиваются. При этом меняется соотношение между модулями для линейных и разветвленных цепей при одинаковых степенях полимеризации и плотностях прививки. Для тонких мембран модули изгибной жесткости для щеток из линейных цепей больше, чем для щеток из разветвленных цепей. Однако с увеличением собственной толщины мембраны модули щеток из разветвленных макромолекул могут сравняться по величине и даже превысить модули щеток, образованных их линейными аналогами.

ВВЕДЕНИЕ

Различные мембранные системы, в частности липосомы (липидные бислойные везикулы), используются как контейнеры для направленной доставки лекарств или генов в клетки живых организмов. Однако фосфолипидные контейнеры могут быть быстро обнаружены системой мононуклеарных фагоцитов и поглощены печенью и селезенкой [1, 2]. Времена их циркуляции в крови малы, поскольку процессы распознавания, связывания и поглощения происходят в течение нескольких минут [3]. Распознавание липосом может быть предотвращено путем ковалентного связывания цепей полиэтиленгликоля с фосфолипидами, что приводит к более длительному удержанию везикул в крови [4, 5]. В то же время ПЭГ как средство для создания “липосом-невидимок” имеет существенный недостаток из-за своего линейного строения: количество концевых групп для дальнейшей функционализации в нем крайне мало [4, 5]. Хорошей альтернативой ПЭГ для направленной доставки лекарств является разветвленный полиглицерин, который обладает высокой биосовместимостью и растворимостью в воде и имеет большую долю гидроксильных групп, способных к функционализации [6–9]. Кроме того, разветвленный полиглицерин проявляет повышенное отталкивание белков по сравнению с ПЭГ [10, 11].

Альтернативой модифицированным липосомам для инкапсуляции различных веществ могут служить полимеросомы. Как правило, полимеросомы собираются из линейных трехблочных сополимеров (например, из полипропиленоксида в качестве среднего блока и сополимера метилметакрилата и глицерина в качестве внешних блоков [12]). Также гигантские везикулы могут быть образованы путем объединения линейных и сверхразветвленных полимеров (например, бислоев, состоящих из диблоков полистирола и гиперразветвленного полиглицерина [13]).

Липосомы, декорированные гидрофильными полимерами, и полимерсомы могут рассматриваться как гидрофобные мембраны, покрытые гидрофильными цепями. Степень покрытия может быть охарактеризована плотностью прививки, которая равна количеству полимерных цепей на единицу площади поверхности мембраны. Со структурной точки зрения полимерсомы имеют более высокую толщину гидрофобного слоя, чем липосомы. Толщина данного слоя может варьироваться в довольно широком диапазоне и может быть такой же и даже большей, чем толщина гидрофильного полимерного покрытия. Увеличение толщины вызывает повышение жесткости мембраны при изгибе и, как следствие, приводит к росту размера везикулы. Вот почему полимерсомы обычно имеют больший диаметр и объем инкапсуляции, чем липосомы (см., например, обзор [14]).

Если плотность прививки достаточно высока, так что привитые макромолекулы образуют полимерную щетку, ее влияние на изгибную жесткость мембраны становится значительным. Из-за взаимодействия между привитыми макромолекулами в щетке возникает дополнительный вклад в изгибную жесткость мембраны (так называемая наведенная изгибная жесткость). Наведенная изгибная жесткость может быть сравнима с собственной жесткостью “голой” мембраны или даже значительно превышать ее и, как следствие, определять размер, форму и стабильность модифицированных наномембран.

Изгибная жесткость липидных мембран, полимерных щеток или других тонких нанослоев характеризуется средним ${{\kappa }_{C}}$ и гауссовым ${{\kappa }_{G}}$ модулями. Энергия деформации ${{\mathcal{F}}_{{def}}}$ тонкой мембраны, согласно теории Хельфриха [15], может быть представлена в следующей форме:

(1)

Здесь $\Delta F\left( {{{R}_{1}},{{R}_{2}}} \right)$ изменение свободной энергии (на единицу площади) в каждой точке поверхности мембраны, равномерно изогнутой с локальными радиусами кривизны ${{R}_{1}}$ и ${{R}_{2}}$, $1{\text{/}}{{R}_{0}}$ – спонтанная кривизна, интеграл берется по площади срединной поверхности мембраны. При симметричном строении мембраны $1{\text{/}}{{R}_{0}} = 0,$ и исходным состоянием с нулевой энергией является плоская конфигурация ($1{\text{/}}{{R}_{1}} = 1{\text{/}}{{R}_{2}} = 0$).

Если мембрана образует везикулу, средний модуль ${{\kappa }_{C}}$ определяет ее равновесный размер и амплитуду отклонения от равновесной сферической формы. Гауссов модуль ${{\kappa }_{G}}$ характеризует топологическую стабильность мембранных систем. Когда он принимает отрицательные значения, стабильной является односвязная поверхность типа везикулы. Если ${{\kappa }_{G}}$ положителен, липидная система формирует сложные сетчатые структуры, подобные пористой губке. Однако в случае замкнутой поверхности интегральный вклад гауссова члена в упругую энергию, согласно теореме Гаусса–Бонне, остается постоянным [16]:

(2)

где ${{\Gamma }}$ – целочисленная константа, определяемая типом поверхности (родом поверхности). ${{\Gamma }}$ = 0 для квазисферической замкнутой поверхности, ${{\Gamma }}$ = 1 для тороидальной поверхности, ${{\Gamma }}$ = 2 для двойного тороида и т.д. В результате правая часть уравнения (1) всегда остается постоянной, и равновесный размер липосом определяется только средним модулем.

Значения κ_C и κ_G можно найти из анализа инкрементного увеличения свободной энергии плоской мембраны при ее изгибе в сферическую, $\Delta F({{R}_{1}} = {{R}_{2}} = R)$ и в цилиндрическую, ΔF $({{R}_{1}} = R,~1{\text{/}}{{R}_{2}} = 0)$ поверхности. Обычно предполагается, что наведенная изгибная жесткость привитых щеток аддитивно складывается с собственной жесткостью “голой” мембраны.

Существует ряд теоретических работ, в которых исследована зависимость наведенной изгибной жесткости полимерных щеток, состоящих из линейных цепей, от плотности прививки и молекулярной массы привитых цепей, а также качества растворителя [17, 18]. В нашей предыдущей работе [19] теория была обобщена для случая щеток, образованных разветвленными макромолекулами. При этом рассматривались два предельных случая: непроницаемая и проницаемая для цепей мембрана. В первом случае количество цепей с обеих сторон мембраны оставалось неизменным при ее изгибе. Во втором случае цепи могли свободно перераспределяться при изгибе с вогнутой на выпуклую сторону мембраны, чтобы компенсировать увеличение энергии межмолекулярного взаимодействия. В случае непроницаемой мембраны модули наведенной изгибной жесткости в хорошем растворителе зависят от структурных параметров привитых цепей следующим образом:

(3)

$\frac{{{{\kappa }_{C}}}}{{{{k}_{{\text{B}}}}T}} = \frac{{9{{{(2{{{v}}^{4}})}}^{{1/3}}}}}{{16}}{{\left( {\frac{{{{\pi \eta }}}}{2}} \right)}^{{ - 2/3}}}{{N}^{3}}{{{{\sigma }}}^{{7/3}}},$

(4)

$\frac{{{{\kappa }_{G}}}}{{{{k}_{{\text{B}}}}T}} = \frac{{12{{{(2{{{v}}^{4}})}}^{{1/3}}}}}{{35}}{{\left( {\frac{{{{\pi \eta }}}}{2}} \right)}^{{ - 2/3}}}{{N}^{3}}{{{{\sigma }}}^{{7/3}}}$

Здесь N – степень полимеризации, σ – плотность прививки, ${v}$ – второй вириальный коэффициент, η – коэффициент, характеризующий топологию привитых цепей. Для линейных цепей η = 1, а для любых разветвленных полимеров η ≥ 1. Способы вычисления топологических коэффициентов η для различных макромолекулярных архитектур, включая звезды, дендроны, гребнеобразные, а также циклические полимеры, обобщены в работах [20–22].

Интересно, что соотношение

(5)

$\frac{{{{\kappa }_{G}}}}{{{{\kappa }_{C}}}} = - \frac{{64}}{{105}}$

не зависит от η, т.е. от архитектуры цепей в щетке.

Когда цепи могут проходить сквозь мембрану (такое возможно, например, для жидкой липидной мембраны), модули намного меньше и существенно слабее зависят от степени полимеризации:

(6)

$\frac{{\kappa _{C}^{*}}}{{{{k}_{{\text{B}}}}T}} = \frac{{9{{{(2{{{v}}^{4}})}}^{{1/3}}}}}{{16}}{{\left( {\frac{{{{\pi \eta }}}}{2}} \right)}^{{ - 4/3}}}{{N}^{2}}{{{{\sigma }}}^{{5/3}}},$

(7)

$\frac{{\kappa _{G}^{*}}}{{{{k}_{{\text{B}}}}T}} = \frac{{12{{{(2{{{v}}^{4}})}}^{{1/3}}}}}{{35}}{{\left( {\frac{{{{\pi \eta }}}}{2}} \right)}^{{ - 2/3}}}{{N}^{3}}{{{{\sigma }}}^{{7/3}}}$

Главный вывод, следующий из формул (3)–(7) состоит в том, что при одинаковых степенях полимеризации N и плотностях прививки σ абсолютные значения модулей уменьшаются с ростом разветвленности привитых цепей.

Однако приведенные выше теоретические зависимости получены при предположении, что собственная толщина мембраны мала по сравнению с толщиной щетки, и ее влиянием на наведенную жесткость можно пренебречь. В то же время, как уже говорилось выше, для ряда систем, в частности полимерсом, собственная толщина мембраны может быть того же порядка, что и толщина щетки. В настоящей работе показано, что при реалистических значениях толщины мембраны ее влияние на наведенную изгибную жесткость может быть очень существенным. Как и в работе [19], мы применяем два взаимодополняющих варианта метода самосогласованного поля (ССП): аналитический метод, использующий приближение сильного растяжения цепей, и численный решеточный метод Схойтенса–Флира.

Статья структурирована следующим образом. Сначала приведено описание применяемой модели мембраны с конечной толщиной и моделей привитых цепей. Далее рассмотрены аналитический и численный варианты метода самосогласованного поля, используемые для расчета наведенной изгибной жесткости мембраны. Затем представлены результаты аналитического подхода, учитывающего эффект собственной толщины мембраны. Изложенная в настоящей работе теория является обобщением теории, развитой ранее для расчета наведенной изгибной жесткости щеток, состоящих из цепей, плотно привитых к обеим сторонам очень тонкой мембраны, когда влиянием собственной толщины мембраны можно пренебречь. Кроме случая хорошего растворителя, который рассматривался в работе [19], в настоящей работе проанализирован случай тета-растворителя. Результаты аналитической теории сопоставлены с результатами, полученными с помощью численного варианта метода самосогласованного поля. В разделе, посвященном обсуждению результатов, изложены некоторые рекомендации по применению развитой теории к реальным мембранным системам.

МОДЕЛЬ

Объектом исследования в настоящей работе является мембрана конечной толщины D, декорированная с обеих сторон полимерными цепями различного строения (рис. 1).

Рис. 1.

Поперечное сечение полимерной щетки в плоской (верхний рисунок) и изогнутой (нижний рисунок) конфигурациях. Разветвленные полимерные цепи привиты с двух сторон к мембране с толщиной D. Пунктирные линии показывают срединные линии мембран.

Модель мембраны

Для общности мы предполагаем, что мембрана состоит из жидкого несжимаемого материала, и количество материала на единичную площадь s₀ срединной поверхности мембраны при изгибе остается постоянным. Объемная доля частиц, из которых состоит мембрана, определяется выражением

(8)

${{\varphi }_{m}} = \frac{{{{{v}}_{0}}}}{{2{{d}_{0}}{{s}_{0}}}},$

где ${{{v}}_{0}}$ – объем одной частицы в мембране (мономерного звена полимерной цепи в полимеросоме или липида в липосоме), ${{d}_{0}} = D{\text{/}}2$ – половина толщины мембраны.

При цилиндрическом изгибе объем мембраны V(R) и площадь ее срединной поверхности S(R) зависят от радиуса кривизны R как

(9)

$V(R) = \pi l[{{(R{\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} d(R))}^{2}}{\kern 1pt} {\kern 1pt} - {\kern 1pt} {\kern 1pt} {\kern 1pt} {{(R{\kern 1pt} {\kern 1pt} - {\kern 1pt} {\kern 1pt} d(R))}^{2}}] = 4\pi lRd(R),$

(10)

$S\left( R \right) = 4\pi lR$

(l – длина мембраны как цилиндра).

При условии несжимаемости мембраны объемная доля φ = const, таким образом, можно составить равенство

(11)

${{\varphi }_{m}} = \frac{{{{{v}}_{0}}}}{{2{{d}_{0}}{{s}_{0}}}} = \frac{{S\left( R \right)}}{{{{s}_{0}}}}{{{v}}_{0}}\frac{1}{{V\left( R \right)}} = \frac{{{{{v}}_{0}}}}{{2d\left( R \right){{s}_{0}}}},$

из которого следует, что толщина мембраны сохраняется при любом радиусе кривизны цилиндрического изгиба:

(12)

$d\left( R \right) = {{d}_{0}}$

При сферическом изгибе величины V(R) и S(R) меняются по другим законам:

(13)

$\begin{gathered} V\left( R \right) = \frac{4}{3}\pi [{{\left( {R + d\left( R \right)} \right)}^{3}} - {{\left( {R - d\left( R \right)} \right)}^{3}}] = \\ = 8\pi {{R}^{2}}d\left( R \right)\left[ {1 + \frac{1}{3}{{{\left( {\frac{{d\left( R \right)}}{R}} \right)}}^{2}}} \right], \\ \end{gathered} $

(14)

$S\left( R \right) = 4\pi {{R}^{2}}$

Следовательно, при сохранении количества материала мембраны на единицу площади срединной поверхности и соблюдении условия несжимаемости

(15)

$\begin{gathered} {{\varphi }_{m}} = \frac{{{{{v}}_{0}}}}{{2{{d}_{0}}{{s}_{0}}}} = \frac{{S\left( R \right)}}{{{{s}_{0}}}}{{{v}}_{0}}\frac{1}{{V\left( {R,d} \right)}} = \\ = \frac{{{{{v}}_{0}}}}{{2{{s}_{0}}d\left( R \right)}}{{\left[ {1 + \frac{1}{3}{{{\left( {\frac{{d\left( R \right)}}{R}} \right)}}^{2}}} \right]}^{{ - 1}}}, \\ \end{gathered} $

толщина мембраны немного уменьшается с ростом кривизны 1/R:

(16)

$\frac{{{{d}_{0}}}}{{d\left( R \right)}} = 1 + \frac{1}{3}{{\left( {\frac{{d\left( R \right)}}{R}} \right)}^{2}}.$

Точное аналитическое решение данного уравнения выглядит так

(17)

$\frac{{d\left( R \right)}}{{{{d}_{0}}}} = 2\frac{R}{{{{d}_{0}}}}\sinh \left\{ {\frac{1}{3}{\text{Arsinh}}~\left( {\frac{1}{3}\frac{{{{d}_{0}}}}{R}} \right)} \right\}$

Зависимость d(R) можно представить в виде разложения по малому параметру d₀/R:

(18)

$d\left( R \right) = {{d}_{0}}\left[ {1 - \frac{1}{3}{{{\left( {\frac{{{{d}_{0}}}}{R}} \right)}}^{2}} + \ldots } \right]$

Как будет показано далее, при расчете модулей наведенной изгибной жесткости квадратичным членом и членами более высокого порядка в разложении (18) можно пренебречь. Значит, толщину мембраны при сферическом изгибе можно также в хорошем приближении считать неизменной для слабо изогнутых мембран.

Модель полимерной щетки

Предполагается что привитые цепи состоят из одинаковых мономерных звеньев и различаются только степенью полимеризации, т.е. числом N звеньев, а также параметром η, характеризующим топологию цепей. Все спейсеры в разветвленных цепях описываются моделью свободносочлененной цепи с длиной статистического сегмента a. В дальнейшем все пространственные характеристики будут выражаться в единицах длины a. Плотность прививки цепей характеризуется безразмерным отношением $\sigma = {{a}^{2}}{\text{/}}s$, где s – площадь, приходящаяся на одну привитую цепь на одной из сторон мембраны. Значения σ соответствуют так называемому “режиму щетки”, при котором межмолекулярные взаимодействия привитых цепей доминируют над внутримолекулярными. Мы также предполагаем, что число привитых цепей на каждой стороне мембраны не меняется при ее изгибе.

МЕТОД

Изменение свободной энергии при изгибной деформации привитых полимерных бислоев мы рассчитываем методом самосогласованного поля. Метод основан на предположении о равномерном распределении плотности полимера вдоль каждого единичного слоя, параллельного плоскости прививки. Другими словами, объемная доля полимера φ(r) в точке, находящейся на расстоянии r от плоскости прививки, зависит только от координаты r. Такое приближение справедливо, если поперечные размеры привитых цепей заметно превышают расстояния между соседними точками прививки. В этом случае соседние цепи существенно перекрываются, что сглаживает неоднородность распределения объемной доли полимера вдоль поверхности. Тот факт, что распределение плотности φ(r) (как и другие характеристики щетки) предполагаются зависимыми только от координаты r, направленной нормально к поверхности прививки, позволяет свести задачу к рассмотрению одномерного случайного блуждания мономерных звеньев цепи вдоль данной координаты. Рассмотрение ансамбля привитых цепей заменяется рассмотрением отдельной цепи со средним распределением плотности мономерных звеньев φ(r). Взаимодействие такой цепи с окружающими цепями учитывается не явным образом, а с помощью эффективного поля u(r) (эффективного химического потенциала), созданного самой цепью и ее окружением.

Свободная энергия (в единицах k_BT), приходящаяся на единицу площади срединной поверхности, состоит из двух вкладов:

(19)

$F = {{F}_{{int}}} + {{F}_{{conf}}}.$

Первый вклад ${{F}_{{int}}}~$отвечает за объемные взаимодействия привитых цепей. Он может быть найден путем интегрирования плотности объемных взаимодействий ${{f}_{{int}}}$ по всему объему щетки:

(20)

где S – площадь срединной поверхности, L(z)dz – объем слоя толщины dz, который находится на расстоянии z от начала радиус-вектора R кривизны изгиба (или от поверхности прививки в плоской конфигурации).

$\begin{gathered} S = {{l}^{2}}, \\ L\left( z \right) = l~--\,{\text{плоская\;конфигурация}}~\,\,(m = 1) \\ \end{gathered} $

$\begin{gathered} S = 2\pi lR,~\quad L(z)\, = \,2\pi lz \\ ~--\,{\text{цилиндрическая\;конфигурация}}\,{\text{\;}}(m = 2) \\ \end{gathered} $

(21)

$\begin{gathered} S = 4\pi {{R}^{2}},~\quad L(z) = 4\pi {{z}^{2}}~~ \\ --\,{\text{сферическая\;конфигурация\;}}\,(m = 3) \\ \end{gathered} $

Здесь и далее индексами m = 1, 2, 3 обозначены плоская, цилиндрическая и сферические геометрии поверхности прививки соответственно.

Плотность свободной энергии объемных взаимодействий ${{f}_{{int}}}$ может быть получена из энергии смешения Флори ${{f}_{{{\text{FH}}}}}$ как функции объемной доли полимера φ после вычитания энергии при бесконечном разбавлении ${{f}_{{{\text{FH}}}}}$(φ → 0):

(22)

$\begin{gathered} {{f}_{{int}}}{\text{\;}} = {{f}_{{{\text{FH}}}}}\left( {{\varphi }} \right) - {{f}_{{{\text{FH}}}}}\left( {{{\varphi }} \to 0} \right) = \\ = \left( {1 - \varphi } \right)\ln \left( {1 - \varphi } \right) + \chi \varphi \left( {1 - \varphi } \right) - \varphi \left( {\chi - 1} \right). \\ \end{gathered} $

Параметр Флори–Хаггинса χ определяет качество растворителя: χ = 0 соответствует атермическому растворителю, χ < 0.5 – хорошему растворителю, χ = 0.5 – тета-растворителю и χ > 0.5 – плохому растворителю. Конформационный вклад ${{F}_{{conf}}}$ в свободную энергию отражает изменение конформационной энтропии привитых цепей при изгибе и может быть определен различными способами в зависимости от выбранного подхода.

В настоящей работе использованы два взаимодополняющих подхода: аналитический метод ССП и численный метод ССП Схойтенса–Флира, успешно примененные ранее [18, 19] для оценки изгибной жесткости полимерных щеток на тонкой мембране в хорошем растворителе. Аналитический подход основан на приближении сильного гауссового растяжения цепей [23]. Его преимуществом является возможность получения функциональных зависимостей модулей Хельфриха от структурных характеристик щетки. Численный подход свободен от ограничений, налагаемых приближением сильного растяжения цепей, но требует отдельных расчетов для каждого набора параметров. Его результаты могут служить тестом для проверки справедливости аналитических формул, а также для оценки модулей за пределами области применимости аналитического подхода.

Аналитический подход

Аналитический подход предполагает, что для каждого малого участка цепи конформационная энергия рассчитывается как энергия упругого растяжения гауссовой цепи:

(23)

$\delta {{F}_{{conf}}} = \frac{3}{{2{{a}^{2}}}}\frac{{\delta {{z}^{2}}}}{{\delta n}}$

Другими словами, каждый сегмент цепи, содержащий δn мономерных звеньев, считается растянутым на величину δz перпендикулярно к поверхности прививки. Кроме гауссовой (линейной) упругости макромолекул, предполагается также возможность распределения концевых мономерных звеньев цепей по всей щетке без ограничений на нахождение вблизи поверхности прививки (отсутствие так называемой “мертвой зоны”). Как было показано в работе [24], это условие выполняется для слабо изогнутых щеток.

Эффективный химический потенциал u(r) определяется из соотношения

(24)

$u\left( r \right) = {{a}^{3}}\frac{{\delta {{f}_{{int}}}\left\{ {\varphi \left( r \right)} \right\}}}{{\delta \varphi \left( r \right)}}$

В работах [25, 26] показано, что потенциал u(r) для щетки в режиме линейной упругости имеет параболическую форму:

(25)

$u(r) = \frac{3}{{2{{a}^{2}}}}{{k}^{2}}({{H}^{2}} - {{r}^{2}}),$

где H – толщина щетки, k – преобразованный топологический параметр

(26)

$k = \frac{{\pi \eta }}{{2N}},$

пропорциональный топологическому параметру η, который повышается с увеличением разветвленности цепей в щетке.

Для достаточно малых значений локальной плотности мономерных звеньев (φ ≪ 1) плотность осмотической части ${{f}_{{int}}}$ свободной энергии (см. уравнение (22)) можно представить в виде степенного ряда по малому параметру φ:

(27)

${{a}^{3}}{{f}_{{int}}}\left( \varphi \right) = {v}{{\varphi }^{2}} + w{{\varphi }^{3}} + \ldots ,$

где $v$ = (1 − 2χ)/2 и w = 1/6 – второй и третий вириальный коэффициенты соответственно.

С помощью уравнений (27) и (25), можно получить распределение объемной доли полимера в условиях хорошего (0 < χ < 0.5) и тета-растворителей:

$\varphi \left( r \right) = \frac{3}{{4{v}}}{{k}^{2}}({{H}^{2}} - {{r}^{2}}),\quad {\text{хороший\;растворитель}}$

(28)

$\varphi \left( r \right) = \frac{{\sqrt 3 }}{k}\sqrt {{{H}^{2}} - {{r}^{2}}} ,~~{\text{тета - растворитель}}$

Распределение объемной доли полимера должно удовлетворять условию нормировки

(29)

$\mathop \smallint \limits_{r = 0}^{r = {{H}_{{\left( m \right) \pm }}}} \varphi \left( r \right){{\left( {1 \pm \frac{d}{R} \pm \frac{r}{R}} \right)}^{{m - 1}}}dr = N\sigma $

Из этого условия можно получить выражение для толщины щетки H₁ в плоской конфигурации:

$\begin{gathered} \frac{{{{H}_{1}}}}{a} = {{\left( {\frac{{2{v}N\sigma }}{{{{k}^{2}}}}} \right)}^{{1/3}}} = {{\left( {\frac{{8{v}}}{{{{\pi }^{2}}{{\eta }^{2}}}}} \right)}^{{1/3}}}N{{\sigma }^{{1/3}}},{\text{\;\;\;\;}} \\ {\text{хороший\;растворитель}} \\ \end{gathered} $

(30)

$\begin{gathered} \frac{{{{H}_{1}}}}{a} = {{\left( {\frac{{4N\sigma }}{{\sqrt 3 \pi k}}} \right)}^{{1/2}}} = {{\left( {\frac{8}{{\sqrt 3 {{\pi }^{2}}\eta }}} \right)}^{{1/2}}}N{{\sigma }^{{1/2}}},~~~~ \\ {\text{тета - растворитель}} \\ \end{gathered} $

Выражения для толщины H_(m)+ и H_(m)− щеток на вогнутой и выпуклой поверхностях мембраны с радиусами кривизны R − d и R + d могут быть представлены в виде разложения в ряд по малому параметру H₁/R:

(31)

${{H}_{{\left( m \right) \pm }}} = {{H}_{1}}\left( {1 + {{a}_{{\left( m \right) \pm }}}\frac{{{{H}_{1}}}}{R} + {{b}_{{\left( m \right) \pm }}}\frac{{H_{1}^{2}}}{{{{R}^{2}}}} + \ldots } \right).$

Коэффициенты a_(m)± и b_(m)± могут быть получены из условия (29).

Свободная энергия объемных взаимодействий на единицу площади срединной поверхности может быть рассчитана с помощью формул

$\begin{gathered} {{F}_{{int\left( m \right) \pm }}} = {v}\frac{{{{k}_{B}}T}}{{{{a}^{2}}}}\mathop \smallint \limits_{r = 0}^{r = {{H}_{{\left( m \right) \pm }}}} {{\varphi }^{2}}\left( r \right){{\left( {1 \pm \frac{d}{R} \pm \frac{r}{R}} \right)}^{{m - 1}}}dr, \hfill \\ ~{\text{хороший\;растворитель}} \hfill \\ \end{gathered} $

(32)

$\begin{gathered} {{F}_{{int\left( m \right) \pm }}} = w\frac{{{{k}_{B}}T}}{{{{a}^{2}}}}\mathop \smallint \limits_{r = 0}^{r = {{H}_{{\left( m \right) \pm }}}} {{\varphi }^{3}}\left( r \right){{\left( {1 \pm \frac{d}{R} \pm \frac{r}{R}} \right)}^{{m - 1}}}dr, \\ ~{\text{тета - растворитель}} \\ \end{gathered} $

Исходя из условия минимизации свободной энергии $\frac{{\delta F\left\{ \varphi \right\}}}{{\delta \varphi }} = 0,$ легко показать, что конформационный вклад в свободную энергию может быть представлен в виде

(33)

${{F}_{{conf\left( m \right) \pm }}} = \mathop \smallint \limits_{r = 0}^{r = {{H}_{{\left( m \right) \pm }}}} \frac{{3{{k}^{2}}}}{2}\varphi \left( r \right){{r}^{2}}{{\left( {1 \pm \frac{d}{R} \pm \frac{r}{R}} \right)}^{{m - 1}}}dr,$

как для хорошего, так и для тета-растворителя.

Согласно приведенным выше уравнениям для монослоя привитого полимера, объемный и конформационный вклады в свободную энергию пропорциональны друг другу и имеют вид

$\begin{gathered} {{F}_{{int\left( 1 \right)}}} = 2{{F}_{{conf\left( 1 \right)}}} = \frac{3}{{10{v}}}{{k}^{4}}{{\left( {\frac{{{{H}_{1}}}}{a}} \right)}^{5}} = \frac{3}{5}{{\left( {\pi {v}\eta } \right)}^{{2/3}}}N{{\sigma }^{{5/3}}}, \\ {\text{хороший\;растворитель}} \\ \end{gathered} $

(34)

$\begin{gathered} {{F}_{{int\left( 1 \right)}}} = {{F}_{{conf\left( 1 \right)}}} = \frac{{3\sqrt 3 \pi }}{{32}}{{k}^{3}}{{\left( {\frac{{{{H}_{1}}}}{a}} \right)}^{4}} = \frac{{\sqrt 3 {{\pi }^{2}}}}{4}\eta N{{\sigma }^{2}},~ \\ {\text{тета - растворитель}} \\ \end{gathered} $

Изменение объемного и конформационного вкладов при изгибе щетки может быть также представлено в виде ряда Маклорена:

(35)

$\begin{gathered} \Delta {{F}_{{int\left( m \right) \pm }}}\left( R \right) = \\ = {{F}_{{\left( 1 \right)int}}}\left( {1 + {{a}_{{int\left( m \right) \pm }}}\frac{{{{H}_{1}}}}{R} + {{b}_{{int\left( m \right) \pm }}}\frac{{H_{1}^{2}}}{{{{R}^{2}}}} + \ldots } \right), \\ \end{gathered} $

(36)

$\begin{gathered} \Delta {{F}_{{conf\left( m \right) \pm }}}\left( R \right) = \\ = {{F}_{{\left( 1 \right)conf}}}\left( {1 + {{a}_{{conf\left( m \right) \pm }}}\frac{{{{H}_{1}}}}{R} + {{b}_{{conf\left( m \right) \pm }}}\frac{{H_{1}^{2}}}{{{{R}^{2}}}} + \ldots } \right) \\ \end{gathered} $

Коэффициенты ${{a}_{{int\left( m \right) \pm }}},~{{b}_{{int\left( m \right) \pm }}}$, ${{a}_{{conf\left( m \right) \pm }}},~{{b}_{{conf\left( m \right) \pm }}}$ могут быть получены с помощью уравнений (28)–(33). Далее будут представлены результаты расчета этих коэффициентов и получены выражения для модулей изгибной жесткости, которые затем будут сопоставлены с результатами численного метода ССП.

Численный подход

Численный вариант метода ССП Схойтенса–Флира основан на среднеполевом и решеточном приближениях. Пространство представляется как решетка с характерным размером узлов a и фиксированным объемом на один узел a³ (далее параметр a будет использоваться как единица длины). Узлы решетки расположены в слоях с номерами z = 1, z_max. Число узлов решетки в z-м слое L(z) зависит от геометрии системы (см. уравнение (21)).

Для концевых слоев решетки применялись периодические зеркальные условия. Первые сегменты каждой привитой цепи были прикреплены к поверхности прививки, т.е. были зафиксированы в слое, прилегающем к мембране. Для щеток, привитых к обеим сторонам изогнутой мембраны, первые сегменты были закреплены в слоях решетки z = R – d − 1 и z = R + d, где R – радиус кривизны, d – половина толщины мембраны.

Привитые цепи моделировались как свободносочлененные. В данной модели два связанных сегмента всегда занимают соседние узлы решетки, а дальними корреляциями пренебрегается. Следовательно, перекрывание сегментов в одном узле решетки, в принципе, разрешено, но в среднем по слою решетки практически предотвращается за счет соблюдения условия несжимаемости.

В основе численного метода ССП лежит оптимизация функционала свободной энергии $\mathcal{F}$ для каждой стороны двуслойной щетки

(37)

$\begin{gathered} \mathcal{F}\left\{ {u,\varphi } \right\} = {{F}_{{conf}}}\left\{ {\varphi \left[ u \right]} \right\} + \\ + \;{{F}_{{int}}}\left\{ \varphi \right\} + \mathop \sum \limits_z {{\Lambda }}\left( z \right)\left( {\varphi \left( z \right) + {{\varphi }_{s}}\left( z \right) - 1} \right) \\ \end{gathered} $

путем оптимизации функции объемной доли полимерных цепей φ(z) в соответствии с функцией сопряженного химического потенциала u(z). Значения вектора Λ(z), задающие поле Лагранжа, вычисляются в ходе итеративной процедуры так, чтобы функционал принимал минимальное значение. В отличие от аналитического подхода в численном методе конформационная энергия вычисляется как отрицательный логарифм статистической суммы всех возможных конформаций привитых цепей на решетке в эффективном внешнем поле u(z) за вычетом работы этого поля. Детали численного метода подробно описаны в наших предыдущих работах [18, 19].

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Результаты аналитического подхода

Коэффициенты из уравнений (31), (35), (36) представлены в табл. 1–3 . Во всех таблицах приведенная толщина мембраны d/H₁ обозначается как ω. Коэффициенты ${{a}_{{int + }}}$ и ${{a}_{{int - }}}$, а так же ${{a}_{{conf + }}}$ и ${{a}_{{conf - }}}$ (табл. 2 и 3 ) одинаковы по величине, но отличаются по знаку (вследствие специфической симметрии рассмотренных систем), поэтому полное изменение ∆F(R) свободной энергии, равное сумме изменений свободной энергии привитых полимерных слоев на вогнутой (−) (35) и на выпуклой (+) (36) сторонах изогнутой мембраны, не содержит линейного члена H₁/R. В конечном итоге ∆F(R) может быть представлено в виде функции квадрата кривизны 1/R² срединной поверхности изогнутой мембраны как

(38)

$\begin{gathered} \Delta {{F}_{{\left( m \right)}}}\left( R \right) = \frac{{H_{1}^{2}}}{{{{R}^{2}}}}[({{b}_{{int\left( m \right) - }}} + {{b}_{{int\left( m \right) + }}}){{F}_{{int\left( 1 \right)}}} + \\ + \,({{b}_{{conf\left( m \right) - }}} + {{b}_{{conf\left( m \right) + }}}){{F}_{{conf\left( 1 \right)}}} + \sigma \alpha _{{\left( m \right)}}^{2}]. \\ \end{gathered} $

Таблица 1.

Коэффициенты, характеризующие изменение толщины щеток на вогнутой (−) и выпуклой (+) сторонах мембраны при цилиндрической (m = 2) и сферической (m = 3) изгибных деформациях

Растворитель	m	${{a}_{ - }} = - {{a}_{ + }}$	${{b}_{ \pm }}$
Хороший	2	$\frac{1}{8} + \frac{\omega }{3}$	$\left( {\frac{1}{8} + \frac{\omega }{3}} \right)\left( {\frac{3}{8} + \frac{{2\omega }}{3}} \right) \pm \frac{\beta }{3}$
Хороший	3	$\frac{1}{4} + \frac{{2\omega }}{3}$	$\left( {\frac{1}{4} + \frac{{2\omega }}{3}} \right)\left( {\frac{3}{4} + \frac{{4\omega }}{3}} \right) - \left( {\frac{{{{\omega }^{2}}}}{3} + \frac{\omega }{4} + \frac{1}{{15}}} \right) \pm \frac{\beta }{3}$
Тета	2	$\frac{2}{{3\pi }} + \frac{\omega }{2}$	$\left( {\frac{2}{{3\pi }} + \frac{\omega }{2}} \right)\left( {\frac{5}{{3\pi }} + \frac{{3\omega }}{4}} \right) \pm \frac{\beta }{2}$
Тета	3	$\frac{4}{{3\pi }} + \frac{{2\omega }}{2}$	$\left( {\frac{4}{{3\pi }} + \frac{{2\omega }}{2}} \right)\left( {\frac{{10}}{{3\pi }} + \frac{{6\omega }}{4}} \right) - \left( {\frac{{{{\omega }^{2}}}}{2} + \frac{{4\omega }}{{3\pi }} + \frac{1}{8}} \right) \pm \frac{\beta }{3}$

Таблица 2.

Коэффициенты, характеризующие изменение энергии объемных взаимодействий в щетке на вогнутой (−) и выпуклой (+) сторонах мембраны при цилиндрической (m = 2) и сферической (m = 3) изгибных деформациях

Растворитель	m	${{a}_{{int \pm }}}$	${{b}_{{int \pm }}}$
Хороший	2	$5{{a}_{ \pm }} \pm \frac{5}{{16}} \pm \omega $	$10a_{ \pm }^{2} \pm 5{{a}_{ \pm }}\left( {\omega + \frac{3}{8}} \right) + 5{{b}_{ \pm }}$
Хороший	3	$5{{a}_{ \pm }} \pm \frac{5}{8} \pm 2\omega $	$10a_{ \pm }^{2} \pm 10{{a}_{ \pm }}\left( {\omega + \frac{3}{8}} \right) + 5{{b}_{ \pm }} + {{\omega }^{2}} + \frac{5}{8}\omega + \frac{1}{7}$
Тета	2	$4{{a}_{ \pm }} \pm \frac{{16}}{{15\pi }} \pm \omega $	$6a_{ \pm }^{2} \pm 4{{a}_{ \pm }}\left( {\omega + \frac{4}{{3\pi }}} \right) + 4{{b}_{ \pm }}$
Тета	3	$4{{a}_{ \pm }} \pm \frac{{32}}{{15\pi }} \pm 2\omega $	$6a_{ \pm }^{2} \pm 8{{a}_{ \pm }}\left( {\omega + \frac{4}{{3\pi }}} \right) + 4{{b}_{ \pm }} + {{\omega }^{2}} + \frac{{32}}{{15\pi }}\omega + \frac{1}{6}$

Таблица 3.

Коэффициенты, характеризующие изменение конформационной свободной энергии щеток на вогнутой (−) и выпуклой (+) сторонах мембраны при цилиндрическом (m = 2) и сферическом (m = 3) изгибах

Растворитель	m	${{a}_{{conf \pm }}}$	${{b}_{{conf \pm }}}$
Хороший	2	$5{{a}_{ \pm }} \pm \frac{5}{8} \pm \omega $	$10a_{ \pm }^{2} \pm 5{{a}_{ \pm }}\left( {\omega + \frac{3}{4}} \right) + 5{{b}_{ \pm }}$
Хороший	3	$5{{a}_{ \pm }} \pm \frac{5}{4} \pm 2\omega $	$10a_{ \pm }^{2} \pm 10{{a}_{ \pm }}\left( {\omega + \frac{3}{4}} \right) + 5{{b}_{ \pm }} + {{\omega }^{2}} + \frac{5}{4}\omega + \frac{3}{7}$
Тета	2	$4{{a}_{ \pm }} \pm \frac{{32}}{{15\pi }} \pm \omega $	$6a_{ \pm }^{2} \pm 4{{a}_{ \pm }}\left( {\omega + \frac{8}{{3\pi }}} \right) + 4{{b}_{ \pm }}$
Тета	3	$4{{a}_{ \pm }} \pm \frac{{64}}{{15\pi }} \pm 2\omega $	$6a_{ \pm }^{2} \pm 8{{a}_{ \pm }}\left( {\omega + \frac{8}{{3\pi }}} \right) + 4{{b}_{ \pm }} + {{\omega }^{2}} + \frac{{64}}{{15\pi }}\omega + \frac{1}{2}$

После подстановки всех необходимых коэффициентов из табл. 1–3 в формулу (38) изменение свободной энергии записывается при цилиндрическом изгибе в виде

$\begin{gathered} \Delta {{F}_{{\left( 2 \right)}}}\left( R \right) = \frac{{H_{1}^{2}}}{{{{R}^{2}}}} \cdot \left[ {\frac{9}{{128{v}}}{{k}^{4}}{{{\left( {\frac{{{{H}_{1}}}}{a}} \right)}}^{5}}{{{\left( {1 + \frac{8}{3}\omega } \right)}}^{2}}} \right], \\ {\text{\;хороший\;растворитель}} \\ \end{gathered} $

(39)

$\begin{gathered} \Delta {{F}_{{\left( 2 \right)}}}(R) = \frac{{H_{1}^{2}}}{{{{R}^{2}}}} \cdot \left[ {\frac{2}{{\sqrt 3 \pi }}{{k}^{3}}{{{\left( {\frac{{{{H}_{1}}}}{a}} \right)}}^{5}}{{{\left( {1 + \frac{{3\pi }}{4}\omega } \right)}}^{2}}} \right]~,~ \\ {\text{тета - растворитель}} \\ \end{gathered} $

а при сферическом изгибе как

$\begin{gathered} \Delta {{F}_{{\left( 3 \right)}}}\left( R \right) = \frac{{H_{1}^{2}}}{{{{R}^{2}}}} \cdot \left[ {\frac{{{{k}^{4}}}}{{v}}{{{\left( {\frac{{{{H}_{1}}}}{a}} \right)}}^{5}}\left( {\frac{{219}}{{1120}} + \frac{9}{8}\omega + \frac{7}{5}{{\omega }^{2}}} \right)} \right], \\ {\text{\;хороший\;растворитель}} \\ \end{gathered} $

(40)

$\begin{gathered} \Delta {{F}_{{\left( 3 \right)}}}\left( R \right) = \frac{{H_{1}^{2}}}{{{{R}^{2}}}} \cdot \left[ {\frac{2}{{\sqrt 3 \pi }}{{k}^{3}}{{{\left( {\frac{{{{H}_{1}}}}{a}} \right)}}^{4}}{{{\left( {1 + \frac{{3\pi }}{4}\omega } \right)}}^{2}}} \right],~ \\ {\text{тета - растворитель}} \\ \end{gathered} $

Средний модуль изгибной жесткости κ_C = $2{{\Delta }}{{F}_{{(2)}}}(R){{R}^{2}}$ (удвоенный коэффициент пропорциональности между изменением свободной энергии ∆F₍₂₎ при цилиндрическом изгибе и квадратом кривизны 1/R²) может быть записан в виде

$\begin{gathered} \frac{{{{\kappa }_{C}}}}{{{{k}_{{\text{B}}}}T}} = \frac{9}{{64{v}}}{{k}^{4}}{{\left( {\frac{{{{H}_{1}}}}{a}} \right)}^{7}}{{\left( {1 + \frac{8}{3}\omega } \right)}^{2}},~ \\ {\text{хороший\;растворитель}} \\ \end{gathered} $

(41)

$\begin{gathered} \frac{{{{\kappa }_{C}}}}{{{{k}_{{\text{B}}}}T}} = \frac{4}{{\sqrt 3 \pi }}{{k}^{3}}{{\left( {\frac{{{{H}_{1}}}}{a}} \right)}^{6}}{{\left( {1 + \frac{{3\pi }}{4}\omega } \right)}^{2}}, \\ {\text{\;тета - растворитель}} \\ \end{gathered} $

а гауссов модуль как

$\begin{gathered} {{\kappa }_{С}} = - \frac{6}{{35}}{{k}^{4}}H_{1}^{7}\left( {1 + \frac{{35}}{4}\omega + \frac{{35}}{2}{{\omega }^{2}}} \right), \\ {\text{\;хороший\;растворитель}} \\ \end{gathered} $

(42)

$\begin{gathered} {{\kappa }_{G}} = \frac{{\sqrt 3 \pi }}{{16}}{{k}^{3}}H_{1}^{6}\left( {1 + \frac{{32}}{\pi }\omega + 18{{\omega }^{2}}} \right), \\ {\text{\;тета - растворитель}} \\ \end{gathered} $

Из приведенных формул видно, что рост толщины мембраны приводит к увеличению абсолютных значений обоих модулей.

Выражения для модулей изгибной жесткости также можно представить в виде зависимостей от средней толщины (первого момента функции распределения объемной доли полимера ⟨H⟩) щетки в плоской конфигурации.

Средний модуль имеет вид

(43)

${{\kappa }_{C}}\left( D \right) = {{\kappa }_{C}}\left( 0 \right){{\left( {1 + \frac{1}{2}\frac{D}{{\left\langle H \right\rangle }}} \right)}^{2}}$

Гауссов модуль равен

$\begin{gathered} {{\kappa }_{C}}\left( D \right) = {{\kappa }_{C}}\left( 0 \right)\left( {1 + \frac{{27}}{{32}}\frac{D}{{\left\langle H \right\rangle }} + \frac{{63}}{{256}}\frac{{{{D}^{2}}}}{{{{{\left\langle H \right\rangle }}^{2}}}}} \right),~ \\ {\text{хороший\;растворитель}} \\ \end{gathered} $

(44)

$\begin{gathered} {{\kappa }_{G}}\left( D \right) = {{\kappa }_{G}}\left( 0 \right)\left( {1 + \frac{{128}}{{15{{\pi }^{2}}}}\frac{D}{{\left\langle H \right\rangle }} + \frac{8}{{3{{\pi }^{2}}}}\frac{{{{D}^{2}}}}{{{{{\left\langle H \right\rangle }}^{2}}}}} \right), \\ {\text{\;тета - растворитель}} \\ \end{gathered} $

Именно в такой форме далее приведено сравнение зависимостей модулей от толщины щетки, полученных аналитическим и численным методами ССП.

Результаты численного подхода

Как и в аналитическом варианте, в численном варианте метода ССП для получения модулей изгибной жесткости рассчитываются изменения свободной энергии (на единицу площади срединной поверхности) для цилиндрического (∆F₂) и сферического (∆F₃) изгибов мембраны. Модули находятся из наклонов зависимостей (∆F₂(1/R) и ∆F₃(1/R)) от квадрата кривизны изгиба 1/R² в пределе 1/R → 0.

При сравнении аналитических и численных результатов следует иметь в виду, что аналитические результаты корректны только в ограниченной области значений N и σ, когда растяжение привитых цепей остается гауссовым. Каждой степени полимеризации N и параметру разветвленности η соответствует критическая величина плотности прививки σ, выше которой данное условие не выполняется. Нижний предел – значение σ с которого начинается режим щетки, т.е. привитые цепи начинают перекрываться. Области применимости аналитического метода более подробно описаны в приложении к работе [19]. В этой работе, где рассматривались тонкие мембраны, было получено хорошее согласие между результатами обоих подходов на допустимом интервале σ. В случае толстой мембраны результаты численного и аналитического методов также хорошо соответствуют друг другу. В качестве примера на рис. 2 и 3 сопоставлены аналитические и численные результаты для зависимостей модулей изгибной жесткости от толщины мембраны и качества растворителя.

Рис. 2.

Зависимости среднего κ_C и гауссового κ_G модулей изгибной жесткости от толщины мембраны в атермическом и тета-растворителях для линейных цепей и дендронов четвертого поколения. Степень полимеризации N = 310, плотность прививки σ = 0.01. Точки – данные, полученные численным методом, пунктирные линии – аналитические зависимости (см. уравнения (43) и (44)).

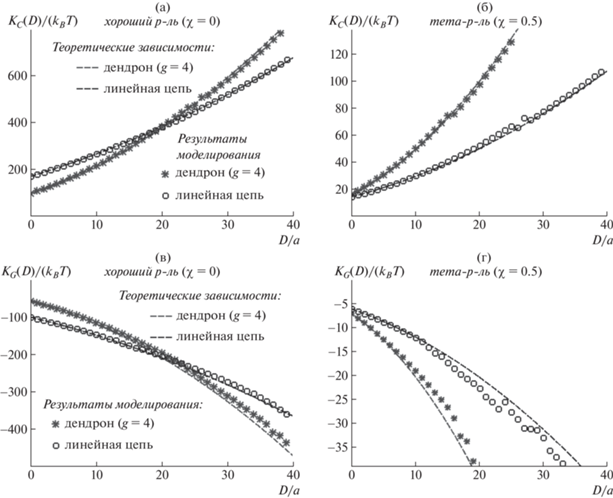
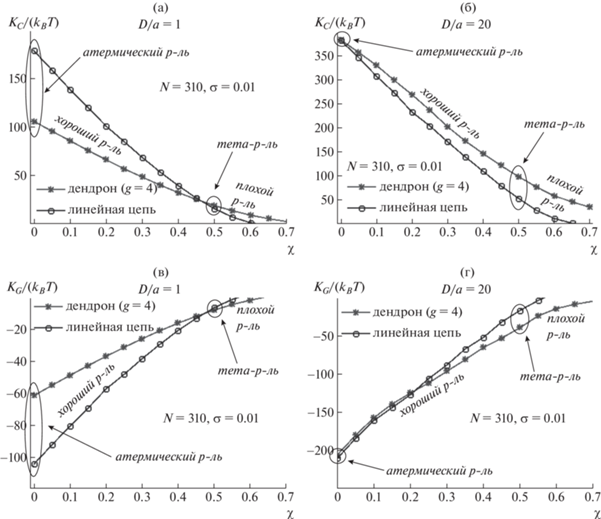
Рис. 3.

Изменение модулей изгибной жесткости при ухудшении качества растворителя (увеличении параметра Флори–Хаггинса χ) при разных значениях толщины мембраны D. Данные получены с помощью численного метода ССП.

Как было показано ранее, для тонких мембран замена линейных цепей разветвленными с теми же параметрами N и σ способствует уменьшению абсолютных значений обоих модулей. Для толстых мембран появляется дополнительный эффект, действующий в противоположном направлении. Для щеток из разветвленных цепей увеличение толщины мембраны приводит к более сильному росту модулей по сравнению с таковым в щетках из линейных цепей. В результате модули при больших толщинах мембраны D для щеток из разветвленных цепей становятся больше, чем для щеток из линейных цепей. Значение D в точке перехода увеличивается с ростом разветвленности.

В тета-растворителе величины ${{\kappa }_{C}}$ и абсолютные значения ${{\kappa }_{G}}$ для мембран с привитыми разветвленными цепями всегда больше, чем для мембран с линейными цепями, так как для тонких мембран модули не зависят от разветвленности цепей.

В отличие от аналитического подхода численный подход позволяет рассматривать не только крайние случаи атермического (χ = 0) и тета- (χ = = 0.5) растворителей, но и щетки при других значениях параметра Флори–Хаггинса χ. На рис. 3 видно, что для тонкой мембраны разница между модулями щеток из линейных и разветвленных цепей монотонно уменьшается с ухудшением качества растворителя. Для “толстой” мембраны наблюдается противоположное поведение: разница модулей увеличивается с ростом χ.

Приложение теории к липидным мембранам, декорированным линейными или разветвленными цепями

Во многих биомедицинских приложениях липидные мембраны для защиты от агрессивных сред декорируют полимерными цепями. Как правило, используются линейный полиэтиленгликоль или разветвленный полиглицерин в силу их хорошей биосовместимости. Мономерные звенья этих полимеров имеют сходную химическую структуру с размером a порядка 0.39 нм. В данном разделе мы применим развитую выше теорию для оценки влияния прививки на средний модуль изгибной жесткости липидной мембраны. В качестве липидной мембраны выбран бислой, состоящий из диолеоилфосфатидилхолина в водном растворе. Толщина каждого липидного монослоя составляет d₀ = 3.846a, а каждый липид занимает площадь A₀ = 4.27a² на поверхности мембраны. Предполагается, что доля X_p липидов декорирована линейными полимерами или дендронами полиглицерина. Отталкивание между привитыми макромолекулами приводит к тому, что поверхность мембраны растягивается и площадь A, приходящаяся на один липид, становится больше, чем A₀ для непривитой мембраны. Равновесная площадь A может быть найдена из условия баланса между латеральным давлением ${{{{\Pi }}}_{p}}\left( A \right)$, создаваемым привитыми цепями, и изменением ${{\Delta }}{{{{\Pi }}}_{{mem}}}\left( A \right)$ латерального давления в самой мембране:

(45)

${{{{\Pi }}}_{p}}\left( A \right) = {{\Delta }}{{{{\Pi }}}_{{mem}}}\left( A \right)$

Значение ${{{{\Pi }}}_{p}}\left( A \right)~$может быть определено из уравнения

(46)

${{{{\Pi }}}_{p}} = - \frac{{\partial {{F}_{p}}}}{{\partial A}},$

где ${{F}_{p}}$ – свободная энергия привитого полимерного слоя, приходящаяся на один липид:

$\begin{gathered} {{F}_{p}} = \frac{9}{{10}}{{\left( {2{v}\lambda } \right)}^{{2/3}}}N{{a}^{{4/3}}}{{X}_{p}}{{\left( {\frac{{{{X}_{p}}}}{A}} \right)}^{{2/3}}},~ \\ {\text{хороший\;растворитель}} \\ \end{gathered} $

(47)

$\begin{gathered} {{F}_{p}} = \frac{{\sqrt 3 }}{{{{\pi }^{2}}}}\lambda N{{a}^{2}}{{X}_{p}}\frac{{{{X}_{p}}}}{A},~ \\ {\text{тета - растворитель}} \\ \end{gathered} $

Подставляя выражения (47) в уравнение (46), получаем

$\begin{gathered} {{{{\Pi }}}_{p}} = - \frac{3}{{5{{a}^{2}}}}{{\left( {2{v}\lambda } \right)}^{{2/3}}}N{{\left( {\frac{{{{a}^{2}}{{X}_{p}}}}{A}} \right)}^{{4/3}}}, \\ {\text{\;хороший\;растворитель}} \\ \end{gathered} $

(48)

$\begin{gathered} {{{{\Pi }}}_{p}} = - \frac{{\sqrt 3 }}{{{{a}^{2}}{{\pi }^{2}}}}\lambda N{{\left( {\frac{{{{a}^{2}}{{X}_{p}}}}{A}} \right)}^{2}},~ \\ {\text{тета - растворитель}} \\ \end{gathered} $

Величину ${{\Delta }}{{{{\Pi }}}_{{mem}}}\left( A \right)$ можно найти с помощью вириального разложения

(49)

$\begin{gathered} \frac{{{{\Delta }}{{{{\Pi }}}_{{mem}}}\left( A \right)}}{{{{k}_{{\text{B}}}}T}}{\text{\;}} = \left( {\frac{1}{A} - \frac{1}{{{{A}_{0}}}}} \right) + \\ + {{B}_{2}}\left( {\frac{1}{{{{A}^{2}}}} - \frac{1}{{A_{0}^{2}}}} \right) + {{B}_{3}}\left( {\frac{1}{{{{A}^{3}}}} - \frac{1}{{A_{0}^{3}}}} \right) + \ldots \\ \end{gathered} $

Значения параметров B₂ = 16.5a², B₃ = 33.67a⁴ для липидных мембран на основе диолеоилфосфатидилхолина были получены из экспериментальных данных в работе [27].

Используя уравнения (45), (48) и (49) можно найти равновесную площадь на один липид A как функцию доли привитых липидов ${{X}_{p}}$. Из-за латерального растяжения мембраны, индуцированного прививкой цепей, ее толщина d также будет отличаться от исходного значения d₀; она может быть определена из условия сохранения объема

(50)

$d = \frac{{{{A}_{0}}}}{A}{{d}_{0}}.$

Зависимости приведенной толщины d/d₀ мембраны и эффективной плотности прививки ${{X}_{p}}{\text{/}}A~$ от степени покрытия липидов ${{X}_{p}}$ представлены на рис. 4. Следует иметь в виду, что эти данные корректны только в области значений ${{X}_{p}}$, ограниченной вертикальными штриховыми линиями. “Режим щетки” начинается с определенного значения плотности прививки. В то же время рост ${{X}_{p}}$ приводит к уменьшению толщины мембраны. При толщине, примерно в два раза меньшей собственной толщины мембраны d₀, мембрана разрушается.

Рис. 4.

Приведенная толщина мембраны d/d₀ и эффективная плотность прививки X_p/A как функции доли X_p липидов, декорированных полимерными цепями (линейными цепями и симметричными дендронами с разным числом поколений g) в условиях хорошего растворителя. Степень полимеризации N = 105.

Из полученных данных можно рассчитать зависимости наведенного среднего модуля изгиба k_C от ${{X}_{p}}$ (рис. 5).

Рис. 5.

Средние модули изгибной жесткости двусторонних полимерных щеток, состоящих из полиэтиленгликоля (линейных цепей) и разветвленных полиглицерин-дендронов разных поколений (g = 1, 2, 3), привитых к диолеоилфосфатидилхолиновой мембране. Степень полимеризации привитых цепей N = 105.

Полный средний модуль изгибной жесткости ${{\kappa }_{{total}}}$ мембраны, покрытой полимерной щеткой, состоит из полимерного вклада ${{\kappa }_{С}}$ и собственного модуля ${{\kappa }_{{mem}}}$ липидной мембраны

(51)

${{\kappa }_{{total}}} = {{\kappa }_{С}} + {{\kappa }_{{mem}}}$

Собственный модуль мембраны может быть получен с помощью соотношения

(52)

${{\kappa }_{{mem}}} = {{d}^{2}}\left( {\frac{1}{A} + \frac{{2{{B}_{2}}}}{{{{A}^{2}}}} + \frac{{3{{B}_{3}}}}{{{{A}^{3}}}} + \ldots } \right),$

где учитываются только члены разложения не выше третьего порядка.

Рисунок 6 демонстрирует зависимости полного модуля мембраны от X_p для привитых линейных цепей и дендронов в хорошем растворителе. Видно, что прививка линейных цепей способна увеличить средний модуль изгибной жесткости мембраны почти в два с половиной раза. В то же время влияние прививки дендронов существенно слабее и практически исчезает для дендронов третьего поколения.

Рис. 6.

Средние модули изгибной жесткости липидных мембран, декорированных полиэтиленгликолем (линейными цепями) или разветвленными полиглицерин-дендронами разных поколений (g = 1, 2, 3), привитыми к диолеоилфосфатидилхолиновой мембране. Степень полимеризации привитых цепей N = 105.

Предсказания для изгибной жесткости полимеросом, покрытых разветвленными полимерами

Построенная теория предсказывает, что декорирование липосом линейными цепями приводит к более сильному увеличению изгибной жесткости, чем декорирование дендронами при той же степени полимеризации N и плотности прививки σ. Этот эффект обусловлен двумя факторами. Во-первых, толщина самой липосомы мала по сравнению с толщиной привитой щетки. Следовательно, даже если не учитывать растяжение мембраны из-за прививки цепей, увеличение ее среднего модуля изгибной жесткости в случае линейных цепей будет больше, чем для их разветвленных аналогов. Во-вторых, прививка разветвленных цепей приводит к более сильному растяжению поверхности липосомы и соответственно к более значительному уменьшению толшины липидной мембраны. Уменьшение толшины мембраны также ослабляет влияние привитых дендронов на изгибную жесткость мембраны по сравнению с линейными цепями. Разветвленная щетка может быть более эффективна, чем щетка из линейных цепей, если толщина самой мембраны сопоставима с толщиной щетки и ее упругие свойства сильнее, чем в случае липосом. Такая ситуация наблюдается в полимерсомах, где внутренний гидрофобный слой может рассматриваться как мембрана, а гидрофильные блоки – как привитые цепи. Основываясь на результатах развитой нами теории, можно предположить, что для полимерсом в хорошем растворителе замена линейных внешних блоков на разветвленные с теми же параметрами N и σ может увеличить их изгибную жесткость (при сохранении длины гидрофобного блока). Для полимеросом в тета-растворителе покрытие из разветвленных цепей всегда будет приводить к большему увеличению изгибной жесткости по сравнению с покрытием из линейных цепей.

ЗАКЛЮЧЕНИЕ

В настоящей работе развита теория наведенной изгибной жесткости полимерных щеток, симметрично привитых к обеим поверхностям плоской мембраны и погруженных в низкомолекулярный растворитель. В отличие от предыдущих работ в данной работе учитывается собственная толщина мембраны. Кроме того, рассмотрен эффект изменения качества растворителя. Использованы два варианта подхода, основанного на методе самосогласованного поля – аналитический и численный. С помощью аналитического подхода получены выражения для среднего и гауссового модулей Хельфриха как функций степени полимеризации, параметра разветвленности и плотности прививки макромолекул для случаев хорошего и тета-растворителей. Результаты аналитического подхода находятся в хорошем согласии с результатами, полученными с помощью более строгого численного варианта метода ССП. Основные результаты заключаются в следующем: абсолютные значения модулей наведенной изгибной жесткости растут с увеличением толщины мембраны; эффект замены в привитой щетке линейных цепей на их разветвленные аналоги зависит от качества растворителя, в который погружена щетка. В хорошем растворителе для тонких мембран прививка линейных щеток приводит к большему росту модулей, чем прививка разветвленных щеток с той же степенью полимеризации и плотностью прививки. Для толстых мембран наблюдается противоположный эффект: прививка разветвленных цепей сильнее влияет на увеличение модулей изгибной жесткости, чем прививка линейных цепей. В тета-растворителе при любой толщине мембраны наведенная жесткость, вызванная прививкой щеток из разветвленных цепей, больше, чем для щеток из соответствующих линейных цепей. Разница между модулями изгибной жесткости монотонно возрастает с увеличением собственной толщины мембраны.

В качестве примера применения теории рассмотрена бислойная мембрана на основе диолеоилфосфатидилхолина с привитыми цепями полиэтиленгликоля или разветвленного полиглицерина. Показано, что при реальных значениях структурных молекулярных параметров прививка разветвленного полимера практически не влияет на модуль изгибной жесткости мембраны. Заметный эффект дает только декорирование мембраны полиэтиленгликолем. На основе полученных данных также выдвинута гипотеза о том, что для более толстых и жестких мембран полимеросом прививка разветвленных цепей может давать больший вклад в изменение изгибного модуля гидрофобной мембраны, сопоставимый с вкладом от прививки аналогичных линейных цепей.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 16-13-10485).

Список литературы

Juliano R., Stamp D. // Biochem. Biophys. Res. Commun. 1975. V. 63. P. 651.
Allen T., Cullis P. // Adv. Drug Deliv. Rev. 2013. V. 65. P. 36.
Allen T., Hansen C. // Biochim. Biophys. Acta, Biomembr. 1991. V. 1068. P. 133.
Lasic D., Needham D. // Chem. Rev. 1995. V. 95. P. 2601.
van Vlerken L., Vyas T., Amiji M. // Pharm. Res. 2007. V. 24. P. 1405.
Wilms D., Stiriba S., Frey H. // Acc. Chem. Res. 2010. V. 43. P. 129.
Hofmann A.M., Wurm F., Huhn E., Nawroth T., Langguth P., Frey H. // Biomacromolecules. 2010. V. 11. P. 568.
Kasza G., Kali G., Domjan A., Petho L., Szarka G., Ivan B. // Macromolecules. 2017. V. 50. P. 3078.
Wagener K., Worm M., Pektor S., Schinnerer M., Thiermann R., Miederer M., Frey H., Rösch F. // Biomacromolecules. 2018. V. 19. P. 2506.
Siegers C., Biesalski M., Haag R. // Chem. – A Eur. J. 2004. V. 10. P. 2831.
Yeh P., Kainthan R., Zou Y., Chiao M., Kizhakkedathu J.N. // Langmuir. 2008. V. 24. P. 4907.
Schöps R., Amado E., Müller S., Frey H., Kressler J. // Faraday Disc. 2013. V. 166. P. 303.
Ernenwein D., Vartanian A., Zimmerman S. // Macromol. Chem. Phys. 2015. V. 216. P. 1729.
Rideau E., Dimova R., Schwille P., Wurm F., Landfester K. // Chem. Soc. Rev. 2018. V. 47. P. 8572.
Helfrich W., Naturforsch Z.// J. Biosci. C. 1973. V. 28. P. 693.
Carmo M. Differential Geometry of Curves and Surfaces. New Jersey: Englewood Cliffs, 1993.
Milner S., Witten T. // J. Phys. (Paris) 1988. V. 49. P. 1951.
Birshtein T., Iakovlev P., Amoskov V., Leermakers F., Zhulina E., Borisov O. // Macromolecules. 2008. V. 41. P. 478.
Mikhailov I., Leermakers F., Borisov O., Zhulina E., Darinskii A., Birshtein T. // Macromolecules. 2018. V. 51. P. 3315.
Pickett G. // Macromolecules. 2001. V. 34. P. 8784.
Zhulina E., Leermakers F., Borisov O. // Macromolecules. 2015. V. 48. P. 8025.
Zhulina E., Leermakers F., Borisov O. // Macromolecules. 2016. V. 49. P. 8758.
Semenov A.N. // Sov. Phys. JETP. 1985. V. 61. P. 733.
Wijmans A., Zhulina E. // Macromolecules. 1993. V. 26. P. 7214.
Milner S., Witten T., Cates M. // Macromolecules. 1988. V. 21. P. 2610.
Жулина Е.Б., Прямицын В.А., Борисов О.В. // Высокомолек. соед. А. 1989. Т. 31. № 1. С. 185.
Marsh D. // Biophys. J. 2001. V. 81. P. 2154.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Высокомолекулярные соединения (серия С)

Архивы выпусков Информация о журнале Отправить рукопись в журнал