Водные ресурсы, 2020, T. 47, № 1, стр. 33-45
Морфология грядового рельефа речных русел
А. Ю. Сидорчук *
Московский государственный университет им. М.В. Ломоносова
119899
, Москва,, Россия
* E-mail: fluvial05@gmail.com
Поступила в редакцию 27.11.2018
После доработки 27.11.2018
Принята к публикации 11.04.2019
Аннотация
Проведено исследование линеаризованных уравнений двухмерной гидравлики методом малых возмущений в широком диапазоне размеров гряд при больших значениях числа Фруда и гидравлических сопротивлений. Сохранение трехмерных эффектов в осредненных по глубине уравнениях движения, неразрывности и деформации дало возможность выделить области сочетания гидравлических характеристик потока, которым соответствуют русловые гряды разных размеров и морфологии. Исследования подтвердили результаты ранее проведенного анализа для спокойных потоков с малыми гидравлическими сопротивлениями и показали новые виды связей морфологии грядового рельефа с гидравлическими характеристиками потока для потоков с большими числами Фруда и большими гидравлическими сопротивлениями. Дополнительно, для двухмерных ультрамикроформ установлена связь их длины с гидравлическими сопротивлениями. Выявлен новый класс макроформ – двухмерные макроформы. Верификация результатов теоретического анализа по данным измерений морфологии русловых образований и гидравлических характеристик потока показала, что анализ линеаризованных уравнений двухмерной гидродинамики методом малых возмущений позволяет определить морфологию и размеры русловых форм как в спокойных, так и в бурных потоках. Системы порог – плес в бурных потоках горных рек представляют собой ультрамикроформы (двухмерные и трехмерные), которые являются аналогом антидюн (в бурных потоках) и рифелей (в спокойных потоках), полученных в больших лотках с песчаным аллювием. Наиболее распространены в реках трехмерные макроформы. Если эти макроформы хорошо развиты в широких руслах (при ширине потока больше полуширины макроформы), их длина определяется глубиной русла. Макроформы в более узком русле не получают полного развития, их длины ограничены шириной русла и могут быть вычислены только через эту ширину.
Попытки теоретического описания грядового рельефа речного русла предпринимались неоднократно. Так, уже в середине XX в. насчитывалось более 50 гипотез причин формирования речных излучин [6]. Примерно в это же время в теории руслового процесса начал применяться метод малых возмущений [10, 21]. Большое количество работ показало эффективность этого метода при решении самых разных задач. К.В. Гришанин [2] так характеризовал сложившуюся ситуацию: “В своей совокупности исследования… позволяют высоко оценить вклад, внесенный методом малых возмущений в решение проблемы о происхождении волнообразного рельефа подвижного дна. Будучи применен после многих лет исканий и догадок, метод малых возмущений поставил, наконец, решение этой проблемы на научную основу”. Наиболее важны работы Р. Калландера [11], Г. Паркера [25], И. Фредсо [16] и А.Е. Михинова [7], в которых проведен специальный анализ решений двухмерных уравнений движения потока и деформации дна русла. Главная сложность этого подхода заключается в невозможности современными математическими методами аналитически решить полные нелинейные уравнения для возмущений потока и дна русла. Эти уравнения необходимо упростить (линеаризовать) таким образом, чтобы их можно было решить, но при этом не потерять существенные элементы решения. Найдено такое упрощение уравнений гидродинамики, при котором результаты теоретических расчетов неплохо соответствуют данным измерений в русловых лотках и в натурных реках [9, 26]. Исследование этих уравнений методом малых возмущений было проведено для довольно узкого диапазона определяющих переменных. В численных расчетах число Фруда Fr изменялось в пределах 0.1–0.5, а гидравлическое сопротивление назначалось <0.02. Эти значения характерны для больших равнинных рек. В то же время метод малых возмущений с успехом применялся и в области больших чисел Фруда, однако для решения узких вопросов, например при исследовании формирования антидюн [21]. Поэтому предлагается рассмотреть теорию формирования грядового рельефа речного русла в широком диапазоне размеров гряд при больших значениях числа Fr и гидравлических сопротивлений и сравнить результаты теоретических расчетов с данными измерений на натурных реках и в экспериментальных лотках.
ГИДРОДИНАМИЧЕСКИЕ ПРИЧИНЫ ОБРАЗОВАНИЯ ГРЯДОВОГО РЕЛЬЕФА РЕЧНОГО РУСЛА
М.А. Великанов [1] сформулировал главный постулат теории руслового процесса – принцип взаимодействия потока и русла, который лежит в основе гидродинамического подхода к решению проблемы морфодинамики речных русел. Н.И. Маккавеев [6] так формулирует этот принцип: “… процесс руслообразования можно определить как процесс “отображения” поверхностью твердой среды (т.е. грунтами, слагающими ложе) особенностей движения воды и перемещаемых ею наносов…”.
Как указано в [2, 21], количественное описание этого “отображения” возможно с помощью метода малых возмущений. Будем использовать уравнения движения потока в криволинейных ортогональных координатах [3]. В наиболее общей форме их интегрирование по глубине провел Н.А. Картвелишвили [4]. Автором проведено исследование этих уравнений методом малых возмущений с учетом кривизны потока и русла, неустойчивости свободной поверхности потока и, дополнительно, неустойчивости размываемого дна [9, 26]. Важно, что в двухмерных уравнениях движения сохранены эффекты, связанные с негидростатическим распределением давления по глубине потока и циркуляцией потока на повороте. Анализ малых возмущений потока и русла в рамках этих уравнений проводится в стандартной форме [5]. В подинтегральных выражениях компоненты скорости, глубина и отметки свободной поверхности потока, кривизна ортогональных координат записываются в виде суммы двух составляющих – для основного осредненного потока и для возмущения. Рассмотрена наиболее простая конфигурация основного потока – прямолинейное прямоугольное в поперечном сечении русло с одинаковыми глубинами и скоростями. Возмущенный поток предполагается установившимся, неравномерным, отметки свободной поверхности и дна изменяются в пространстве и во времени. Гидравлические сопротивления записываются через формулу Шези. Уравнения линеаризуются – члены, содержащие произведения и степени компонент возмущений, отбрасываются. В результате получена следующая система уравнений для возмущений потока и дна русла в безразмерной форме:
(1)
$\begin{gathered} {{\alpha }_{{uU}}}\frac{{\partial u}}{{\partial {{s}_{1}}}} + {{\alpha }_{{U{v}}}}\frac{{\partial {v}}}{{\partial {{s}_{2}}}} + \frac{1}{{{\text{F}}{{{\text{r}}}^{2}}}}\frac{{\partial h}}{{\partial {{s}_{1}}}} + \\ + \,\,\beta \frac{{{{\partial }^{3}}h}}{{\partial s_{1}^{3}}} + {{\alpha }_{{uU}}}\lambda u - {{\alpha }_{{uU}}}\frac{\lambda }{2}d = 0, \\ {{\alpha }_{{U{v}}}}\frac{{\partial {v}}}{{\partial {{s}_{1}}}} - {{\alpha }_{{U2}}}\gamma {v} + \frac{{\text{1}}}{{{\text{F}}{{{\text{r}}}^{{\text{2}}}}}}\frac{{\partial h}}{{\partial {{s}_{2}}}} + \beta \frac{{{{\partial }^{3}}h}}{{\partial s_{1}^{2}\partial {{s}_{2}}}} + {{\alpha }_{{{v}U}}}\frac{\lambda }{2}{v} = 0, \\ {{\alpha }_{u}}\frac{{\partial u}}{{\partial {{s}_{1}}}} + {{\alpha }_{{v}}}\frac{{\partial {v}}}{{\partial {{s}_{2}}}} + {{\alpha }_{U}}\frac{{\partial d}}{{\partial {{s}_{1}}}} + \frac{{\partial d}}{{\partial t}} = 0, \\ M\frac{{\partial u}}{{\partial {{s}_{1}}}} + \frac{M}{4}\frac{{\partial {v}}}{{\partial {{s}_{2}}}} + \left( {1 - \varepsilon } \right)\frac{{\partial \left( {h - d} \right)}}{{\partial t}} = 0. \\ \end{gathered} $$\lambda = \frac{{{\text{2g}}}}{{{{C}^{2}}}},\,\,{\text{Fr}} = \frac{U}{{\sqrt {{\text{g}}D} }},\,\,u = \frac{{u{\text{*}}}}{U},\,\,~{v} = \frac{{{v}{\text{*}}}}{U},\,\,h = \frac{{h{\text{*}}}}{D},$ $d = \frac{{d{\text{*}}}}{D},$ $~{{s}_{1}} = \frac{{s_{1}^{*}}}{D},\,\,~{{s}_{2}} = \frac{{s_{2}^{*}}}{D},\,\,~t = \frac{U}{D}t{\text{*}}$ и M – безразмерный расход наносов: $0.015{\kern 1pt} {{\alpha }_{{uU2}}}\frac{{{{U}^{2}}}}{{U_{{CR}}^{3}}}\left( {U - {{U}_{{CR}}}} \right)\frac{{{{D}_{s}}}}{D}$; ε – пористость донных грунтов; размерные переменные: C – коэффициент в формуле Шези; U и D – скорость и глубина основного потока; u*, v*, h* и d* – продольная и поперечная скорость, отметка свободной поверхности и глубина возмущений потока; $s_{1}^{*}$, $s_{2}^{*}$ и t* – продольная и поперечная координаты, время; критическая скорость начала движения наносов ${{U}_{{CR}}} = 4.6D_{s}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}{{D}^{{{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}}}}$, Ds – диаметр частиц влекомых наносов.
Кинематические коэффициенты αi и β определяются видом распределения скоростей основного и возмущенного потокoв по вертикали. На основании некоторых гипотез о виде этих эпюр приняты значения: αU2 = 0.75; αvU = 0.86; αv = 1; αu = 1; αU = 0.86; β = 0.86; αuU2 = 0.75. Коэффициент $\gamma = \frac{{1 - 7.2{{\sqrt D } \mathord{\left/ {\vphantom {{\sqrt D } C}} \right. \kern-0em} C}}}{{7.4 - 13.0{{\sqrt {\text{g}} } \mathord{\left/ {\vphantom {{\sqrt {\text{g}} } C}} \right. \kern-0em} C}}}$ появляется при замене кривизны продольных линий возмущенного потока K1 придонной поперечной скоростью по формуле И.Л. Розовского [8]:
Он изменяется обычно в пределах 0.08–0.1.Возмущения скоростей потока, его свободной поверхности и глубины записываются в виде движущихся продольных синусоидальных волн с изменяющейся во времени амплитудой. Амплитуда в первом приближении увеличивается во времени по экспоненте. Тогда после введения безразмерной комплексной скорости $c = \frac{{{{c}_{R}} + i{{c}_{i}}}}{U}$ волны возмущений записываются в виде:
(3)
$\begin{gathered} u = A\left( {{{s}_{2}}} \right)\exp \left[ {i{{k}_{1}}\left( {{{s}_{1}} - ct} \right)} \right], \\ {v} = B\left( {{{s}_{2}}} \right)\exp \left[ {i{{k}_{1}}\left( {{{s}_{1}} - ct} \right)} \right], \\ h = P\left( {{{s}_{2}}} \right)\exp \left[ {i{{k}_{1}}\left( {{{s}_{1}} - ct} \right)} \right], \\ d = T\left( {{{s}_{2}}} \right)\exp \left[ {i{{k}_{1}}\left( {{{s}_{1}} - ct} \right)} \right]. \\ \end{gathered} $Здесь cR – скорость продольного перемещения волны, ci – скорость увеличения амплитуды, k1 – продольное волновое число = 2πD/LX (LX – длина волны). Физический смысл имеют только действительные части в выражениях (3).
Комплексные функции A, B, P и T описывают форму возмущений в поперечном направлении. В результате подстановки (3) в (1) и исключения из полученной системы функций A, B и T получается обыкновенное дифференциальное уравнение второго порядка, аналогичное хорошо изученному дифференциальному уравнению, которое описывает свободные колебания:
здесь(5)
$k_{2}^{2} = \frac{{{{b}_{2}}\left( { - {{a}_{3}}{{c}_{1}}{{d}_{4}} - {{a}_{4}}{{c}_{3}}{{d}_{1}} + {{a}_{1}}{{c}_{3}}{{d}_{4}} + {{a}_{4}}{{c}_{1}}{{d}_{3}}} \right)}}{{{{c}_{2}}\left( {{{a}_{4}}{{b}_{3}}{{d}_{1}} - {{a}_{1}}{{b}_{3}}{{d}_{4}} - {{a}_{3}}{{b}_{4}}{{d}_{1}} + {{a}_{1}}{{b}_{4}}{{d}_{3}}} \right)}},$Уравнение (4) описывает изменение возмущений отметок свободной поверхности P поперек потока. Для функции P граничные условия у берегов потока могут быть не равными нулю. В таком случае уравнение (4) имеет нетривиальные решения при всех действительных собственных значениях. Это приводит к непрерывности спектра волн возмущений как в продольном, так и поперечном направлениях, что является важным отличием предлагаемого решения от решений в предыдущих работax [7, 11, 16, 25], в которых спектр волн возмущений в поперечном направлении был дискретным.
Таким образом, возмущения отметок свободной поверхности (и возмущения всех других гидравлических характеристик потока, в том числе безразмерных отметок дна Z0) приобретают вид смещающейся вдоль потока би-синусоиды с экспоненциально меняющейся во времени амплитудой:
(6)
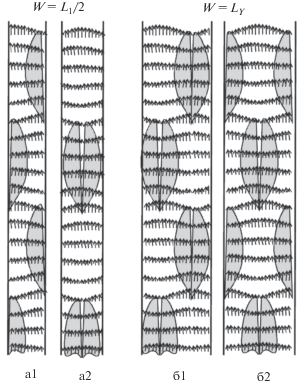
${{Z}_{0}} = \exp \left( {\frac{{2\pi D}}{{{{L}_{X}}}}{{c}_{i}}t} \right)\sin \left[ {\frac{{2\pi D}}{{{{L}_{X}}}}\left( {{{s}_{1}} - {{c}_{R}}t} \right)} \right]\sin \frac{{\mu \pi {{s}_{2}}}}{W}D,$Рис. 1.
Вид возмущений отметок дна русла при показателях формы волны μ = 2W/LY, равных 1 (индекс а1, а2) и 2 (индекс б1, б2). Если поперечная форма волны возмущения записывается через синус, то система волн асимметричная (индекс а1, б1), если через косинус – симметричная (индекс а2, б2). Здесь LY – длина волны в поперечном направлении (ширина волны), W – ширина русла.
ТЕОРЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГРЯДОВОГО РЕЛЬЕФА РЕЧНОГО РУСЛА
Уравнение (5) представляет собой дисперсионное соотношение в виде алгебраического уравнения второго порядка относительно комплексной скорости c:
Коэффициенты в уравнении (7) являются сложными функциями безразмерных волновых чисел, гидравлического сопротивления, числа Fr и безразмерного расхода наносов, а также коэффициентов αi, β, γ. Их запись громоздка (приложение в [9]). В этой связи знак и величина скорости изменения амплитуды волны возмущения дна русла определялись численно. Расчеты проведены в широком диапазоне безразмерных длин LX/D и ширин LY/D волн с различными гидравлическими характеристиками основного потока. Волны возмущений с отрицательной скоростью изменения амплитуды в дальнейшем не рассматривались, а для волн с растущей амплитудой, которым соответствуют грядовые формы руслового рельефа, строились поля скорости роста амплитуды в координатах безразмерных длины и ширины волн (т.е. русловых гряд) для различных комбинаций гидравлических характеристик основного потока (рис. 2).
Рис. 2.
Поле скорости роста амплитуды возмущений отметок дна русла (т.е. русловых гряд) в координатах логарифмов безразмерных длины LX/D и ширины LY/D гряд для Fr = 0.6 и λ = 0.1. Гребень A соответствует максимуму скорости роста амплитуд трехмерных гряд, гребень B – двухмерных ультрамикроформ. Точка N_1 соответствует локальному максимуму скорости роста амплитуд трехмерных ультрамикроформ, N_2 – макроформ.
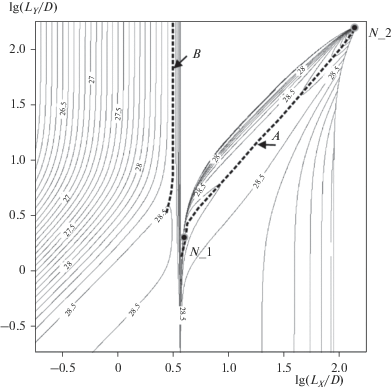
У этого поля скорости роста амплитуд волн возмущений (спектра) два важных свойства. Во-первых, оно непрерывно, континуально. Во-вторых, оно имеет сложный рельеф. Видны гребни A и B максимумов скорости роста амплитуд волн возмущений с характерными перегибами, а также локальные максимумы скорости роста амплитуд. По совокупности этих линий и точек можно выделить группы волн возмущений, обладающих близкими свойствами. Таких главных групп выделено четыре [9, 26]: ультрамикроформы, микроформы, мезоформы и макроформы. Для некоторых характерных точек на рис. 2 спектра волн возмущений (точек N_1 и N_2, а также для точек на линии В) можно получить связи безразмерной длины и ширины волн (грядовых форм) с гидравлическими характеристиками основного потока.
В большинстве работ по применению метода малых возмущений для решения проблемы происхождения грядового рельефа речного русла, как в пионерных [11, 16, 25], так и в современных [12, 13], анализируются такие двухмерные уравнения движения, где распределение давления по глубине принимается по статическому закону. В этом случае на двухмерном спектре, показанном на рис. 2, не выявляются ни гребень B, ни локальные максимумы на линии А, которые можно было бы интерпретировать как грядовые формы разных типов. Гребень B на спектре, который отображает самые малые двухмерные гряды – ультрамикроформы, впервые получен А.Е. Михиновым [7] в результате использования уравнений движения в приближении Буссинеска с учетом влияния динамического давления. Это показало необходимость сохранения трехмерных эффектов в двухмерных уравнениях.
Ультрамикроформы
А.Е. Михиновым предложена и формула для расчета длин двухмерных ультрамикроформ [7]:
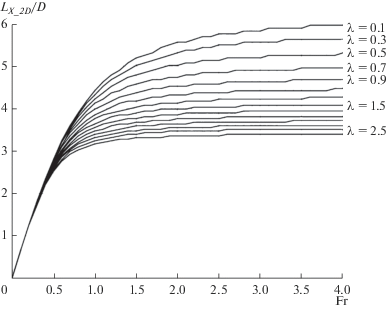
Детальные расчеты для точек на гребне B при LY_2D/LX_2D >10 показали, что безразмерный шаг двухмерных ультрамикроформ LX_2D/D зависит как от числа Fr, так и от гидравлических сопротивлений (рис. 3). Аппроксимация этой зависимости (коэффициент корреляции >0.98) выглядит так:
(9)
$\frac{{{{L}_{{X{\kern 1pt} \_{\kern 1pt} 2D}}}}}{D} = a\left[ {1 - \exp \left( { - b{\text{Fr}}} \right)} \right].$Рис. 3.
Зависимость безразмерных длин двухмерных ультрамикроформ от числа Fr при разных гидравлических сопротивлениях.
Точка N_2 – это локальный максимум скорости увеличения амплитуды самых малых трехмерных гряд – трехмерных ультрамикроформ. Этот максимум получен в [9]. Безразмерные длины трехмерных ультрамикроформ зависят только от числа Fr, и эта зависимость может быть выражена простым уравнением
Двухмерные и трехмерные ультрамикроформы выражены на грядовом дне речного русла в широком диапазоне значений числа Fr и гидравлических сопротивлений (численные расчеты проведены для 0.01 < Fr < 4 и 0.02 < λ < 4). Однако степень их выраженности разная в пределах диаграммы Fr–λ. Скорость роста амплитуд ультрамикроформ 2πc/LX при разных сочетаниях Fr и λ может быть больше то у трехмерных, то у двухмерных ультрамикроформ, границы раздела показаны на рис. 4.
Рис. 4.
Области сочетания гидравлических характеристик потока, которым соответствуют различные типы ультрамикроформ. Номера соответствуют пунктам списка литературы, из которых взяты данные об условиях формирования ультрамикроформ.
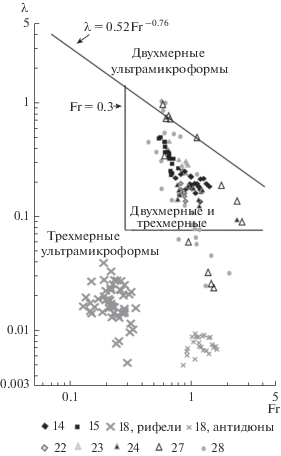
Двухмерные ультрамикроформы перегораживают русло по всей ширине, так как их ширина существенно больше их длины и ширины русла W. Трехмерные ультрамикроформы изометричны, их ширина LY_3D рассчитывается по формуле (12). Если
(13)
$\frac{W}{{{{L}_{{Y{\kern 1pt} \_{\kern 1pt} 3D}}}}} \leqslant 2\,\,\,{\text{или}}\,\,\,\frac{W}{D} \leqslant 12.56{\text{Fr,}}$Морфологические характеристики таких русел довольно хорошо исследованы [14, 15, 17–20, 22–24, 27, 28]. Для измерений в лотках [15, 18, 20, 22, 27] гидравлические характеристики потока достаточно достоверны, для натурных объектов [17, 23, 24, 28] они иногда не измерены, а вычислены, как в [14].
Несколько точек на рис. 4 попадают в область существования теоретических двухмерных ультрамикроформ. Это верховья рек Коваи и Тарамакау (Кемр Крик), Новая Зеландия [28]. Аллювий в этих руслах представлен крупными валунами и глыбами (рис. 2 в [28]), поэтому достоверно идентифицировать тип гряд не представляется возможным. Во всяком случае гидравлические условия формирования двухмерных ультрамикроформ – физический предел образования аллювиальных форм.
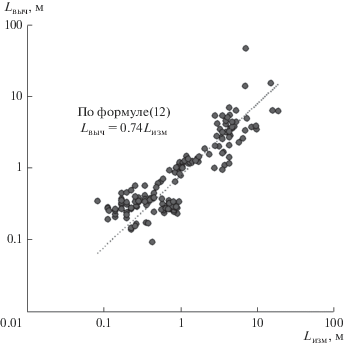
Основная часть исследованных русел в горных реках и в лотках с большими уклонами характеризуется ультрамикроформами смешанного типа, когда двухмерные гряды сочетаются с трехмерными (рис. 4). Длины этих ультрамикроформ, рассчитанные по формулам (9) и (12), в целом укладываются на линейные связи с измеренными длинами гряд. Разброс измеренных и вычисленных длин гряд велик. Это связано не только с неточностью измерений, так как разброс примерно одинаков для связей, полученных как при экспериментах в лотках, так на натурных объектах. В первую очередь, здесь сказываются стохастические свойства грядового рельефа русла.
Расчеты по формуле (9) существенно занижают длины двухмерных гряд, в ~2 раза по сравнению с измеренными значениями.
В область существования русел с трехмерными ультрамикроформами попадают некоторые горные реки Новой Зеландии и русла в экспериментальных лотках, где гидравлические сопротивления λ < 0.075. Сюда же попадают результаты измерений в больших лотках с песчаными и гравийными наносами, где формируются рифели и антидюны [18]. Значения длин трехмерных ультрамикроформ, рассчитанные по формуле (12), вполне удовлетворительно ложатся на линейные связи с измеренными длинами гряд (рис. 6). Формула (12) занижает длины гряд на 25%, так что эмпирический коэффициент равен 8.4.
Макроформы
Точка N_3 – это локальный максимум скорости увеличения амплитуды больших трехмерных гряд – макроформ. Этот максимум появляется на теоретическом спектре (рис. 2) в результате учета в двухмерных уравнениях движения поперечной циркуляции потока [9]. Придонная поперечная скорость в этой циркуляции выражена формулой (2) на основании разработок И.Л. Розовского [8]. Как результат, в структуре коэффициентов дисперсионного соотношения (5) и (7) появляется выражение (–γ + λ/2). Если знак этого выражения положительный, т.е. λ > 1.6–0.2, то макроформы на теоретическом спектре на рис. 2 не выражены. При Fr > 1 и $\lambda < 0.09{\text{ln}}\left( {{\text{Fr}}} \right) + 0.02$ макроформы на теоретическом спектре сливаются с ультрамикроформами (рис. 7) и иерархическая структура грядового рельефа речного русла упрощается.
Рис. 7.
Скорости роста амплитуд трехмерных гряд вдоль гребня А в зависимости от значений Fr при λ = 0.1.
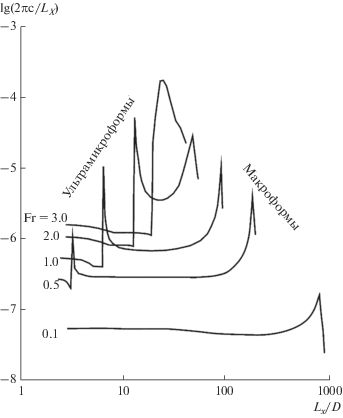
Ранее предполагалось, что зависимость безразмерных длин макроформ от основных факторов [9] может быть выражена относительно простым уравнением:
(14)
$\frac{{{{L}_{{X{\kern 1pt} \_{\kern 1pt} {\text{mak}}}}}}}{D} = \frac{{6.28}}{{\lambda {\text{Fr}}}}.$Численные решения дисперсионного соотношения в широком диапазоне значений числа Fr и λ показали, что формула (14) удовлетворительно аппроксимирует искомую связь при Fr < 0.6 и λ < 0.016. При больших значениях Fr и λ безразмерные длины макроформ LX_mak/D изменяются сложным образом с изменением гидравлических характеристик основного потока (рис. 8). В целом выдерживается обратная связь с числом Fr, но коэффициенты в формуле этой связи по-разному аппроксимируются в разных областях. Так, можно предложить следующие аппроксимации (они не единственные):
(15)
$\begin{gathered} \frac{{{{L}_{{X{\kern 1pt} \_{\kern 1pt} {\text{mak}}}}}}}{D} = \frac{{9.35}}{{\lambda {\text{Fr}}}}{{\left( {\frac{{2\gamma - \lambda }}{\lambda }} \right)}^{{\left( { - 0.27{\text{F}}{{{\text{r}}}^{2}} + 0.13{\text{Fr}} - 0.34} \right)}}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{Fr}} \leqslant 0.8, \hfill \\ \frac{{{{L}_{{X{\kern 1pt} \_{\kern 1pt} {\text{mak}}}}}}}{D} = \frac{{2.45}}{\lambda }\exp \left( {\frac{{1.25}}{{{\text{Fr}}}}} \right){{\left( {\frac{{2\gamma - \lambda }}{\lambda }} \right)}^{{\left( {0.55{\text{F}}{{{\text{r}}}^{2}} - 1.62{\text{Fr}}0.56} \right)}}},\,\,\,\,0.8 < {\text{Fr}} \leqslant 1.3, \hfill \\ \frac{{{{L}_{{X{\kern 1pt} \_{\kern 1pt} {\text{mak}}}}}}}{D} = \frac{{2.45}}{\lambda }\exp \left( {\frac{{1.25}}{{{\text{Fr}}}}} \right){{\left( {\frac{{2\gamma - \lambda }}{\lambda }} \right)}^{{\left( {0.04{\text{F}}{{{\text{r}}}^{2}} - 0.2{\text{Fr}}0.43} \right)}}},\,\,\,\,\,1.3 < {\text{Fr}} \leqslant 2.6, \hfill \\ \frac{{{{L}_{{X{\kern 1pt} \_{\kern 1pt} {\text{mak}}}}}}}{D} = \lambda {{\left( {\frac{{2\gamma - \lambda }}{\lambda }} \right)}^{{\left( {0.04{\text{F}}{{{\text{r}}}^{2}} - 0.2{\text{Fr}}0.43} \right)}}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{Fr}} > 2.6. \hfill \\ \end{gathered} $Рис. 8.
Зависимость безразмерных длин макроформ от числа Fr при разных гидравлических сопротивлениях.
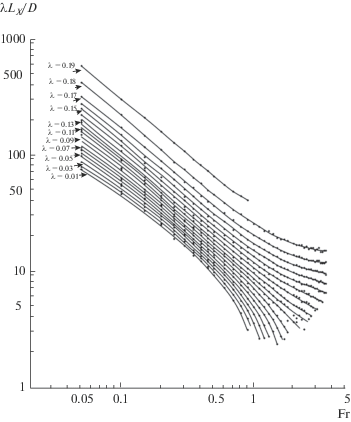
Еще более сложно меняется степень удлиненности макроформ. Она в основном определяется величиной числа Fr, однако вид и знак этой связи зависит от гидравлического сопротивления: при λ < 0.07 удлиненность макроформ уменьшается с увеличением числа Fr, в противном случае – увеличивается (рис. 9). Отношение длины и ширины макроформ аппроксимируется следующими формулами:
(16)
$\begin{gathered} \frac{{{{L}_{{X{\kern 1pt} \_{\kern 1pt} {\text{mak}}}}}}}{{{{L}_{{Y{\kern 1pt} \_{\kern 1pt} {\text{mak}}}}}}} = a{\text{F}}{{{\text{r}}}^{2}} + b{\text{Fr}} + c, \\ a = - \frac{{0.02}}{\lambda },\,\,\,\,b = \frac{{0.0073}}{\lambda },\,\,\,\,c = \frac{{0.27}}{{\sqrt \lambda }},\,\,\,\,\lambda \leqslant 0.07, \\ a = 0.24{{\left( {\frac{{2\gamma - \lambda }}{\lambda }} \right)}^{{0.8}}},\,\,\,\,b = - 0.79\left( {\frac{{2\gamma - \lambda }}{\lambda }} \right) + 1.15, \\ c = 0.66{{\left( {\frac{{2\gamma - \lambda }}{\lambda }} \right)}^{{0.8}}},\,\,\,\,\lambda > 0.07. \\ \end{gathered} $Рис. 9.
Зависимость степени удлиненности макроформ от числа Fr при разных гидравлических сопротивлениях.
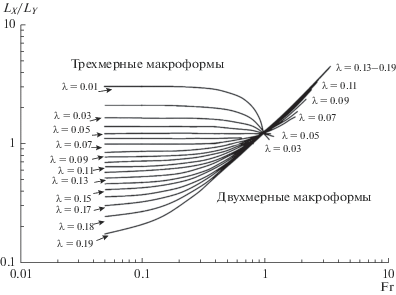
При этом макроформы могут быть двухмерными: LX_mak/LY_mak < 1 и трехмерными: LX/LY > 1 (рис. 9). Двухмерные макроформы расположены в области
(17)
$0.2 > \lambda \geqslant \frac{{0.0875}}{{1.25 - {\text{F}}{{{\text{r}}}^{{1.8}}}}},\,\,\,\,{\text{Fr}} \leqslant 0.9.$При числах Fr > 0.9 макроформы трехмерны.
Для трехмерных макроформ показатель формы волны μ = 2W/LY является также и показателем формы русла: при μ ≤ 1 русло однорукавное, при 1 < μ ≤ 2 − русло двухрукавное и т.д. В таком случае формулу (16) можно записать через ширину русла
(18)
${{L}_{{X{\kern 1pt} \_{\kern 1pt} {\text{mak}}}}} = \frac{{2W}}{\mu }\left( {a{\text{F}}{{{\text{r}}}^{2}} + b{\text{Fr}} + c} \right).$Эта зависимость – важное дополнение к формулам (14)–(15) для расчета длин макроформ.
Теория показывает, что макроформы появляются в рельефе речного русла при наличии поперечной циркуляции потока. Использование формулы И.Л. Розовского [8] для оценки придонной поперечной скорости приводит к появлению в дисперсионном соотношении выражения (–γ + + λ/2). Если знак этого выражения положительный, т.е. λ > 0.16–0.2, то макроформы на теоретическом спектре не выражены. Большие значения гидравлических сопротивлений характерны для горных рек. Тем не менее значений λ > 0.2 для описанных в литературе русел с макроформами не встречено. Эти эмпирические данные подтверждают результаты теоретических расчетов (рис. 10).
Рис. 10.
Области сочетания гидравлических характеристик потока, которым соответствуют различные типы макроформ. Цифрой 19 отмечены данные из работы [19].
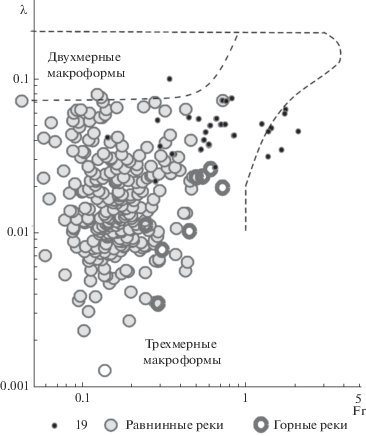
На равнинных реках и в предгорьях макроформы определяют морфологический тип русла. В большинстве случаев это трехмерные макроформы, которые развиты или в однорукавных (открытые кружки на рис. 10), или в многорукавных (закрытые кружки) руслах. Для горных рек также характерны трехмерные макроформы.
Теоретические расчеты выявили область двухмерных макроформ. В эту область попадают некоторые реки Карелии и Кольского полуострова с малыми уклонами и значительными гидравлическими сопротивлениями. Эти реки обычно текут по скальному ложу, характеризуются дефицитом наносов и практически лишены аллювиального рельефа русла. Тип макроформ для этих рек сложно определить. Немногие реки с аллювиальным руслом, попадающие в эту область, характеризуются прямолинейным слабоизвилистым руслом или очень крутыми излучинами. Оба варианта могут свидетельствовать в пользу предположения о двухмерности развитых в этих руслах макроформ. Тем не менее этот вопрос требует дальнейшего изучения.
Зависимости безразмерных длин трехмерных макроформ от основных факторов выражены уравнениями (15) и (19).
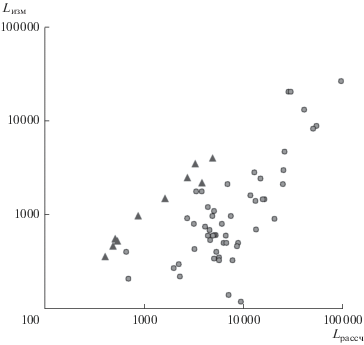
Наблюдения показывают, что формула (15) хорошо описывает шаг побочней и осередков в достаточно широком русле (рис. 11, треугольники), где выполняется условие $\frac{{2W}}{{{{L}_{Y}}}} = \mu \gg 1$. В таком русле имеются условия для полного развития макроформ. При μ ⪡ 1 в относительно узком русле размеры макроформ обычно меньше теоретических (рис. 11, кружки), рассчитанных по формуле (15). Размеры таких трехмерных макроформ хорошо описываются формулой (19) при правильном выборе значения μ. В узких руслах реализуются более короткие и менее развитые макроформы или даже мезоформы. Такие макроформы, и тем более мезоформы, менее вытянуты, чем наиболее развитые макроформы.
Рис. 11.
Соответствие длин макроформ, рассчитанных по формуле (15), измеренным длинам макроформ в полугорных многорукавных реках с широким руслом (треугольники) и в меандрирующих однорукавных руслах равнинных рек (кружки).
ЗАКЛЮЧЕНИЕ
Наличие трехмерных эффектов в осредненных по глубине уравнениях движения, неразрывности и деформации существенно увеличивает возможности линеаризованного анализа этих уравнений. На двухмерном спектре скорости роста амплитуд возмущений дна русла появляется сложный рельеф, который позволяет выделить отдельные области русловых гряд разных размеров и морфологии: ультрамикроформы, микроформы, мезоформы и макроформы. В отдельных случаях (ультрамикроформы и макроформы) возможно построить теоретические связи морфологических характеристик русловых гряд с гидравлическими характеристиками потока.
Расширение анализа на высококинетичные потоки с большими числами Fr и большими гидравлическими сопротивлениями позволило выявить новые особенности таких связей. Получен вид этих связей, который оказался гораздо более сложным, чем это следовало из ранее проведенного анализа для спокойных потоков с малыми гидравлическими сопротивлениями. Так, для двухмерных ультрамикроформ установлена связь их длины с гидравлическими сопротивлениями. Выявлен новый класс макроформ – двухмерные макроформы.
Верификация результатов теоретического анализа по данным измерений морфологии русловых образований и гидравлических характеристик потока показала, что анализ линеаризованных уравнений двухмерной гидродинамики методом малых возмущений позволяет определить морфологию и размеры русловых форм как в спокойных, так и в бурных потоках. Системы порог– плес в бурных потоках горных рек представляют собой ультрамикроформы (двухмерные и трехмерные), которые являются аналогом антидюн (в бурных потоках) и рифелей (в спокойных потоках), полученных в больших лотках с песчаным аллювием. Связь их размеров с гидравлическими характеристиками потока – глубиной русла, числом Fr и величинами гидравлических сопротивлений – в целом вполне удовлетворительно описывается теоретическими формулами. Однако коэффициенты в этих формулах требуют калибровки по натурным данным – длины теоретических трехмерных ультрамикроформ на 15–20% меньше натурных при тех же гидравлических характеристиках потока, а двухмерных с элементами трехмерности – вдвое меньше. Выяснение причин таких расхождений требует дополнительных исследований.
Макроформы в натурных потоках не формируются при гидравлическом сопротивлении λ > 0.2, что подтверждает теоретические результаты. В область существования двухмерных макроформ, полученную в теории, попадает весьма небольшое число (3–4) из исследованных в 230 участков рек. Морфология таких русловых образований требует дальнейшего изучения. Наиболее распространены в реках трехмерные макроформы. Если эти макроформы хорошо развиты в широких руслах (при ширине потока большей, чем полуширина макроформы), то их длину можно рассчитать как по глубине русла, числу Fr и величинам гидравлических сопротивлений по (15), так и по ширине русла, числу Fr и величинам λ по (19). Макроформы в более узком русле не получают полного развития, их длины могут быть вычислены только по (19), так как они ограничены шириной русла.
Список литературы
Великанов М.А. Гидрология суши. Л.: Гидрометеоиздат, 1948. 530 с.
Гришанин К.В. Устойчивость русел рек и каналов. Л.: Гидрометеоиздат, 1974. 143 с.
Картвелишвили Н.А. Потоки в недеформируемых руслах. Л.: Гидрометеоиздат, 1973. 279 с.
Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. Ч. 2. М.; Л.: Гостехиздат, 1948. 560 с.
Линь Ц.Ц. Теория гидродинамической устойчивости. М.: Изд-во иностр. лит., 1958. с. 194.
Маккавеев Н.И. Русло реки и эрозия в ее бассейне. М.: Изд-во АН СССР, 1955. 346 с.
Михинов А.Е. Неустойчивость донных волн в деформируемом русле // Метеорология и гидрология. 1983. № 11. С. 84–91.
Розовский И.Л. Движение воды на повороте открытого русла. Киев: Изд. АН УССР, 1957. 188 с.
Сидорчук А.Ю. Структура рельефа речного русла. СПб.: Гидрометеоиздат, 1992. 126 с.
Anderson A.G. On the development of stream meanders // Proc. 12th Congress IAHR/ Fort Collins, 1967. V. 1. P. 370–378.
Callander R.A. Instability and river channels // J. Fluid Mechanics. 1969. V. 36. № 3. P. 465–480.
Colombini M. A decade’s investigation of the stability of erodible stream beds // J. Fluid Mechanics. 2014. V. 756. P. 1–4.
Colombini M. Revisiting the linear theory of sand dune formation // J. Fluid Mechanics. 2004. V. 502. P. 1–16.
Curran J.H., Wilcock P.R. Characteristic dimensions of the step-pool bed configuration: An experimental study // Water Res. Research. 2005. V. 41. № 2. P. 1–11.
Curran J.H., Wohl E.E. Large woody debris and flow resistance in step-pool channels, Cascade Range, Washington // Geomorphol. 2003. V. 51. P. 141–157.
Fredsoe J. Meandering and braiding of rivers // J. Fluid Mechanics. 1978. V. 84. № 4. P. 609–624.
Grant G.E., Swanson F.J., Wolman M.G. Pattern and origin of stepped-bed morphology in high-gradient streams, Western Cascades, Oregon // Geol. Soci. Am. Bull. 1990. V. 102. P. 340–352.
Guy H.P., Simons D.B., Richardson E.V. Summary of alluvial channel data from flume experiments 1956–61 // U.S. Geol. Survey Prof. Paper. 1966. 462-I. P. 1–47.
Harnischmacher S. Thresholds in small rivers? Hypotheses developed from fluvial morphological research in western Germany // Geomorphol. 2007. V. 92. P. 119–133.
Harrison L.R., Keller E.A. Modeling forced pool–riffle hydraulics in a boulder-bed stream, southern California // Geomorphol. 2007. V. 83 № 3, 4. P. 232–248.
Kennedy J.F. The mechanics of dunes and antidunes in erodible-bed channels // J. Fluid Mechanics. 1963. V. 16. № 4. P. 521–544.
Lee A.J. The hydraulics of steep streams. Thesis submitted for the degree of Doctor of Philosophy. Sheffield: Univ. Sheffield, 1998.
Lenzi M.A. Step-pool evolution in the Rio Cordon, Northeastern Italy // Earth Surf. Process. Landforms. 2001. V. 26. P. 991–1008.
Nickolotsky A., Pavlowsky R.T. Morphology of step-pools in a wilderness headwater stream: The importance of standardizing geomorphic measurements // Geomorphol. 2007. V. 83. P. 294–306.
Parker G. On the cause and characteristic scales of meandering and braiding in rivers // J. Fluid Mechanics. 1976. V. 76. № 3. P. 457–480.
Sidorchuk A. The structure of river bed relief // Coherent flow structures in open channels. Chichester: Wiley, 1996. P. 397–421.
Whittaker J.G. Flow and sediment movement in stepped channels. Thesis submitted for the degree of Doctor of Philosophy. Canterbury: Univ. Canterbury, 1982.
Wohl E.E., Wilcox A. Channel geometry of mountain streams in New Zealand // J. Hydrol. 2005. V. 300. P. 252–266.
Дополнительные материалы отсутствуют.