Водные ресурсы, 2021, T. 48, № 2, стр. 155-163

ВВЕДЕНИЕ

Внутренние водоемы (озера и водохранилища) занимают 1.3–1.8% общей площади материков [16, 21], имеют большое значение в социально-экономическом развитии соответствующих регионов и являются объектом исследования во многих задачах гидрологии, экологии, метеорологии и климатологии. Термогидродинамические характеристики озер и водохранилищ оказывают существенное влияние на ряд процессов региональной циркуляции атмосферы. Помимо этого, изменения температуры в озерах и водохранилищах могут способствовать процессам эвтрофикации [3, 6, 7], т.е. повышению биологической продуктивности водных объектов, в частности в результате роста биомассы диатомовых и вредоносных сине-зеленых водорослей, что может приводить к массовому замору рыбы и ухудшению качества воды.

Также нельзя не отметить роль внутренних водоемов в изменении климата и реакцию водных объектов на эти изменения [1, 13, 28]. В регионах с большим количеством озер и водохранилищ наблюдается выраженное потепление климата [12], в связи с этим отмечается более ранний период вскрытия льда и более короткая продолжительность ледостава. Для учета взаимодействия внутренних водоемов и атмосферы необходимо включать в климатические модели расчет термогидродинамических и биологических характеристик вод суши. Важно корректное воспроизведение термогидродинамики озер в мезомасштабных моделях атмосферы, где пространственное разрешение достигает нескольких километров, что меньше по сравнению с характерными горизонтальными размерами крупных внутренних водоемов.

Важный аспект при моделировании термогидродинамики внутренних водоемов – правильное описание процессов перемешивания, в том числе связанных с гравитационными (сейшевыми) колебаниями. Сейши возникают вследствие горизонтального перераспределения массы и действия градиента гидростатического давления и не принимаются во внимание в большинстве существующих одномерных (по вертикали) моделей. Однако при моделировании озер и водохранилищ с горизонтальными размерами, существенно меньшими, чем внутренний радиус деформации Россби ${{L}_{R}}$, сила Кориолиса становится пренебрежимо малой в сравнении с силой горизонтального градиента давления [10], а модели, не учитывающие сейши, не позволяют получить корректное описание поля скорости в подобных водоемах, что может приводить к заметной ошибке толщины перемешанного слоя (речь идет о завышении данного значения, особенно в период летней стратификации озер и водохранилищ [27]). Для умеренных широт ${{L}_{R}}~$ составляет 2–3 км, и следует ожидать, что сейши будут значимым образом влиять на процессы перемешивания в относительно небольших озерах, которые составляют большую часть внутренних водоемов суши [5].

Задача настоящего исследования – оценка влияния горизонтальных размеров водоема на процессы перемешивания в озерах и водохранилищах, в частности на толщину перемешанного слоя. Для упрощения анализа рассмотрены водоемы идеализированной формы и с постоянным по времени атмосферным воздействием.

МЕТОДЫ ОПИСАНИЯ ПРОЦЕССОВ ТЕРМОГИДРОДИНАМИКИ ВНУТРЕННИХ ВОДОЕМОВ

К настоящему времени созданы математические модели различной пространственной размерности, позволяющие рассчитать распределение термогидродинамических величин во внутренних водоемах. Наиболее детальное описание дают трехмерные модели [4, 13, 18], основа которых – осредненная по Рейнольдсу система уравнений термогидродинамики в приближении Буссинеска и гидростатики [2]. Именно такая система рассматривается в настоящей работе для описания циркуляции термически стратифицированного внутреннего водоема. Пренебрежение эффектами коротковолновой радиации справедливо для небольших временны́х масштабов в теплое время года ночью и в холодное время, когда воздействие ветра на гидродинамику водоема практически отсутствует. Таким образом, постановка задачи в настоящей работе – относительно грубое приближение к условиям в природе, однако она позволяет в чистом виде выделить влияние горизонтальных размеров водного объекта на вертикальное распределение температуры, которое, очевидно, имеет место и в реальных объектах. В указанных условиях система уравнений принимает следующий вид:

Здесь ${\mathbf{u}} = \left( {u,{v},w} \right)$ – вектор скорости; $\eta $ – отклонение свободной поверхности от равновесного состояния; T – температура; ρ – плотность; ${{K}_{m}}$(λ_m) и ${{K}_{h}}$(λ_h) – коэффициенты вертикальной (горизонтальной) турбулентной вязкости и температуропроводности соответственно; ν, χ' – коэффициенты молекулярной вязкости и температуропроводности; f – параметр Кориолиса (принимается постоянным); g – ускорение свободного падения; z – вертикальная координата, проходящая от дна водоема z = –H(x, y) до поверхности; t – время.

В системе уравнений (1)–(6) $A\left( q \right)$ – оператор адвекции:

а ${{D}_{H}}\left( {q,~\lambda } \right)$ и ${{D}_{z}}\left( {q,~K} \right)$ – операторы горизонтальной и вертикальной диффузии с коэффициентами $\lambda $ и К соответственно:

Для изучения гидрологических и термодинамических характеристик внутренних водоемов сезонных, годовых и климатических масштабов на сегодняшний день наиболее подходят одномерные модели, отличающиеся вычислительной простотой. Одномерную систему уравнений, описывающую вертикальное распределение импульса и тепла, можно получить осреднением приведенных выше трехмерных уравнений (1)–(6) по горизонтальному сечению водоема [11, 26]:

Здесь А(z) – площадь горизонтального сечения водоема, p – гидростатическое давление, горизонтальная черта означает осреднение по A(z). Здесь в соответствии со сказанным выше поток тепла на нижней границе положен равным 0, а поток импульса считается постоянным на границе каждого горизонтального сечения (величины, обозначенные индексом “bot”).

При записи систем уравнений (1)–(6) и (7)–(9) предположена также справедливость градиентного приближения для описания турбулентных потоков. Для задач настоящей работы представляется важным, чтобы вертикальное перемешивание в трехмерной и одномерной моделях представлялось схожим образом. Поэтому для расчета коэффициентов ${{K}_{m}}$ и ${{K}_{h}}$ в обеих моделях далее используется двухпараметрическое k–ε-замыкание в стандартной формулировке [8, 20]. Оно основано на прогностических уравнениях для кинетической энергии турбулентности (ТКЭ, k) и скорости ее диссипации ε:

Здесь слагаемое $P$ соответствует генерации энергии турбулентности за счет сдвига скорости; B описывает генерацию или потребление энергии за счет действия сил плавучести; ${{\delta }_{k}},{{\delta }_{\varepsilon }}$ – турбулентные числа Шмидта для ТКЭ и скорости диссипации соответственно; ${{C}_{{1\varepsilon }}}$, ${{C}_{{2\varepsilon }}}$, ${{C}_{{3\varepsilon }}}$ – эмпирические константы; ${{C}_{\varepsilon }}$ и ${{C}_{{\varepsilon ~T}}}$ – функции устойчивости для импульса и скалярных величин, полагаемые постоянными.

Система уравнений одномерной модели (7)–(13) не замкнутая, параметризации требуют первое, третье и четвертое слагаемые в правой части (8)–(9). Трехмерная и одномерная системы уравнений дополняются необходимыми граничными условиями.

ПАРАМЕТРИЗАЦИЯ ГРАДИЕНТА ДАВЛЕНИЯ И ГОРИЗОНТАЛЬНОЙ ВЯЗКОСТИ ДЛЯ ОДНОМЕРНОЙ МОДЕЛИ

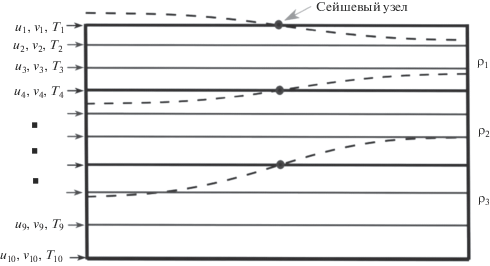
Представлен вывод параметризации горизонтального градиента давления и силы горизонтальной вязкости для двухмерного водоема без учета силы Кориолиса. Случай трехмерного водоема с учетом вращения Земли и без горизонтальной вязкости рассмотрен в [10]. Для учета сейш используется метод, основанный на явном воспроизведении первой горизонтальной моды. Пусть жидкость состоит из N слоев (рис. 1) постоянной плотности ${{\rho }_{i}}$ (${{\rho }_{{i + 1}}} > {{\rho }_{i}})$. Толщину каждого слоя ${{h}_{i}}$ запишем в виде: ${{h}_{i}} = {{H}_{i}} + h_{i}^{{\text{'}}}$ (${{H}_{i}}$ – толщина i-го слоя в состоянии покоя жидкости, $h_{i}^{{\text{'}}}$ – отклонение толщины, причем $\left| {{{h_{i}^{{\text{'}}}} \mathord{\left/ {\vphantom {{h_{i}^{{\text{'}}}} {{{H}_{i}}}}} \right. \kern-0em} {{{H}_{i}}}}} \right| \ll 1,$ H – глубина водоема). Задача рассматривается для прямоугольника $[{{ - {{L}_{x}}} \mathord{\left/ {\vphantom {{ - {{L}_{x}}} 2}} \right. \kern-0em} 2},~{{{{L}_{x}}} \mathord{\left/ {\vphantom {{{{L}_{x}}} 2}} \right. \kern-0em} 2}]~ \times \left[ {0,~H} \right]$. Решение этой задачи эквивалентно решению трехмерной задачи в области $[{{ - {{L}_{x}}} \mathord{\left/ {\vphantom {{ - {{L}_{x}}} 2}} \right. \kern-0em} 2},~{{{{L}_{x}}} \mathord{\left/ {\vphantom {{{{L}_{x}}} 2}} \right. \kern-0em} 2}]$ × $[{{ - {{L}_{y}}} \mathord{\left/ {\vphantom {{ - {{L}_{y}}} 2}} \right. \kern-0em} 2},~{{{{L}_{y}}} \mathord{\left/ {\vphantom {{{{L}_{y}}} 2}} \right. \kern-0em} 2}] \times \left[ {0,~H} \right]$, в которой поток импульса на поверхности направлен вдоль оси x, а компонента скорости по оси y равна 0.

Для каждого слоя можно записать следующие линеаризованные уравнения движения, неразрывности и гидростатики:

Воспользовавшись тем обстоятельством, что во внутренних водоемах энергия мод с первым горизонтальным волновым числом, как правило, преобладает в спектре внутренних колебаний [19, 25], представим решение системы (14)–(16) в виде ряда Фурье до первой гармоники и осредним результат по горизонтальному сечению, которое в данном случае есть $[{{ - {{L}_{x}}} \mathord{\left/ {\vphantom {{ - {{L}_{x}}} 2}} \right. \kern-0em} 2},~{{{{L}_{x}}} \mathord{\left/ {\vphantom {{{{L}_{x}}} 2}} \right. \kern-0em} 2}]$. В результате получим: где введено обозначение ${{\Delta }_{x}}\overline {h_{i}^{{\text{'}}}} $ – разность величин $h_{i}^{{\text{'}}}$, осредненным по правой ($[0,{{{{L}_{x}}} \mathord{\left/ {\vphantom {{{{L}_{x}}} 2}} \right. \kern-0em} 2}]$) и по левой ($\left[ {{{ - {{L}_{x}}} \mathord{\left/ {\vphantom {{ - {{L}_{x}}} 2}} \right. \kern-0em} 2},~0} \right]$) половинам сечения [17]. Данная система связывает осредненную по горизонтали компоненту скорости со средним градиентом давления. В системе (17)–(18) вертикальное распределение переменных является кусочно-постоянным, в отличие от системы (7)–(9), которая сформулирована относительно дифференцируемых по z функций. Используем уравнения (17)–(18) для замыкания системы (7)–(9); для этого в непрерывном по вертикали профиле плотности воды $\rho = \rho \left[ {\bar {T}\left( {z,t} \right)} \right]$ выделим N слоев с толщинами ${{H}_{i}} = {{z}_{{i + 1}}} - {{z}_{i}},~$ в каждом из которых плотность меняется по глубине незначительно. В каждом таком слое горизонтальный градиент давления можно рассчитать с помощью (17)–(18) c использованием в качестве $\overline {{{u}_{i}}} $ осредненной по вертикали в пределах слоя горизонтальной скорости из одномерной модели $\bar {u}\left( {z,t} \right)$; при этом этот градиент будет иметь постоянное значение внутри каждого полуинтервала $\left[ {{{z}_{i}},~{{z}_{{i + 1}}}} \right).$ Дополненная таким образом система уравнений одномерной модели записывается в следующем виде:

Полученную модель можно классифицировать как 1.5-мерную, так как в ней частично учитываются эффекты горизонтальной неоднородности заданной формы; с математической точки зрения здесь присутствуют элементы уравнений в частных производных, обыкновенных дифференциальных и интегральных уравнений. В дальнейшем изложенное замыкание одномерной системы будет называться также параметризацией сейш, так как оно позволяет явно воспроизводить сейши с горизонтальным волновым номером 1.

ПОСТАНОВКА ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

В численных экспериментах использовалась одномерная модель LAKE (подробное описание – в [9]), дополненная параметризацией сейш. Модель развивается в МГУ им. М.В. Ломоносова и включена в последнюю версию модели деятельного слоя суши, развиваемой Институтом вычислительной математики (ИВМ) им. Г.И. Марчука РАН [2] и МГУ. Для верификации одномерной модели использовалась трехмерная гидростатическая модель, разрабатываемая в НИВЦ МГУ и ИВМ РАН на основе единого гидродинамического кода, объединяющего подходы DNS (Direct Numerical Simulation), LES (Large-Eddy Simulation) и RANS (Reynolds-Averaged Navier-Stokes) для расчета геофизических турбулентных течений [22, 23]. Численный метод решения системы уравнений (1)–(6) основан на консервативных конечно-разностных методах дискретизации на прямоугольных сетках и использовании полунеявного метода для аппроксимации по времени, в котором адвективный перенос и горизонтальная диффузия описываются явными схемами.

Значения эмпирических констант в k–ε замыкании одномерной и трехмерной моделей согласованы с приведенными в статье [27], их выбор обосновывается, например, в работах [14, 15]. Отметим, что турбулентное число Прандтля принято константой ${\text{P}}{{{\text{r}}}_{t}} = {{{{K}_{m}}} \mathord{\left/ {\vphantom {{{{K}_{m}}} {{{K}_{h}}}}} \right. \kern-0em} {{{K}_{h}}}} = 1.25$, а константа ${{C}_{{3\varepsilon }}}$, определяющая изменение скорости диссипации под действием сил плавучести, полагалась равной $1.14{\text{\;}}$ при B > 0 и $ - 0.4$ при B < 0.

С применением одномерной и трехмерной моделей проведены следующие эксперименты: верификация на основе численной реализации классического лабораторного эксперимента Като–Филлипса [17], результаты которого служат основным материалом для калибровки турбулентных замыканий для сдвиговых течений в стратифицированной жидкости, и расчеты с идеализированными водоемами прямоугольного вертикального сечения при различных горизонтальных размерах (10 и 1000 м).

В эксперименте Като–Филлипса рассматривается однородная по горизонтали стратифицированная жидкость, а вертикальные границы отсутствуют. Начальный профиль температуры линейный, а единственным источником турбулентности считается ветер, обеспечивающий постоянный поток импульса на поверхности. В классической постановке, описанной в [17], рассматривался кольцевой резервуар, на поверхности которого создавалось напряжение трения в направлении по окружности. Внутренний и внешний диаметры составляли 152.4 и 106.7 см соответственно; таким образом, ширина канала была равна 22.8 см. Глубина резервуара составляла 28 cм.

Результаты данного эксперимента хорошо описывает теоретическая формула изменения толщины перемешанного слоя во времени [24]:

где ${{h}_{{ML~}}}$ – толщина перемешанного слоя, $u{\kern 1pt} *$ – скорость трения на поверхности ($u* = \sqrt {{\tau \mathord{\left/ {\vphantom {\tau {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}}} $).

Для численной реализации эксперимента Като–Филлипса приведенные выше уравнения одномерной и трехмерной моделей дополнены следующими граничными условиями на дне:

на поверхности: В трехмерной модели задавались условия периодичности по горизонтальным координатам.

Для серии экспериментов с наличием вертикальных стенок трехмерная модель была дополнена боковыми граничными условиями:

Примечательно, что в одномерной модели боковые граничные условия не задаются, но первая горизонтальная мода полей скорости и давления, для которой получена параметризация сейш, удовлетворяет условиям выше.

Во всех экспериментах заданы следующие параметры:

глубина водоема – 10 м;

время расчета – 7 либо 30 дней;

начальный градиент температуры – ${{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial z}}} \right. \kern-0em} {\partial z}} = $ = 1.5°C/м, что соответствует частоте Брента–Вяйсяля (частоте плавучести) – $N = 4 \times {{10}^{{ - 2}}}$ c^–1;

поток импульса на поверхности – $\tau = {{10}^{{ - 2}}}$ Н/м²,

сила Кориолиса не учитывается.

При изложенных выше граничных условиях, параметрах эксперимента и выборе однородных по y начальных условий трехмерная задача становится двухмерной, что соответствует предположениям, используемым выше в одномерной модели.

ДИНАМИКА ТОЛЩИНЫ ПЕРЕМЕШАННОГО СЛОЯ

Обе модели в рамках численной реализации классического эксперимента Като–Филлипса продемонстрировали хорошее согласие с аналитическим решением. Что касается экспериментов с водоемами конечного размера, то продемонстрировано, что с увеличением продольного размера водоема толщина перемешанного слоя также возрастает (рис. 2).

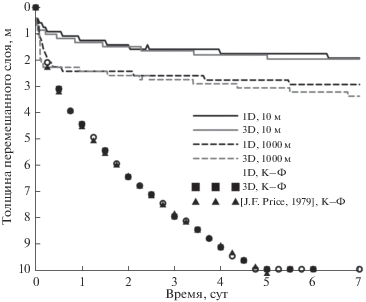
Важно отметить, что, насколько известно авторам, лабораторного эксперимента для подобных условий не проводилось, и эмпирическая оценка, аналогичная (19), отсутствует; поэтому в качестве “эталонного” результата в данном случае авторы полагают возможным считать результат, полученный трехмерной гидростатической моделью. Одномерная модель демонстрирует хорошее согласие с трехмерной: параметризация горизонтального градиента давления и вязкости позволяет реалистично воспроизвести толщину перемешанного слоя. Глубина перемешанного слоя ${{h}_{{ML}}}$ существенно зависит от горизонтальных размеров водоема, и чем больше водоем, тем ближе она становится к результату классического эксперимента Като–Филлипса, где вертикальные стенки отсутствуют. Ограничение ${{h}_{{ML}}}$ при наличии вертикальных стенок объясняется тем, что в водоеме в этом случае возникает градиент гидростатического давления, действующий противоположно потоку импульса из атмосферы. Это приводит к установлению квазистационарной циркуляции в перемешанном слое. В бесконечном по горизонтали слое воды (эксперимент Като–Филлипса) горизонтальный градиент давления не возникает, поток импульса из атмосферы приводит к монотонному и неограниченному увеличению максимальной скорости в перемешанном слое, что, в свою очередь, способствует быстрому росту ${{h}_{{ML}}}$.

ВЕРТИКАЛЬНАЯ СТРУКТУРА ТЕЧЕНИЯ

В численных экспериментах для прямоугольных водоемов с различными горизонтальными размерами проведен также анализ вертикального распределения температуры, скорости течения и коэффициента турбулентной вязкости. Продолжительность численных экспериментов составила 30 дней, остальные параметры расчетов описаны выше. Сравнения между одномерной и трехмерной моделями проводились на 7-й и 30-й дни расчетов.

Сопоставлены профили вертикального распределения температуры (рис. 3).

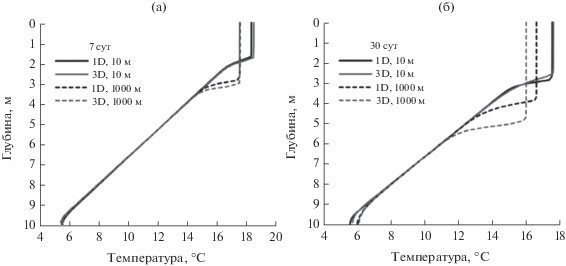
Продемонстрировано хорошее согласие между моделями на временны́х масштабax в несколько дней. Различия между результатами, полученными с помощью рассмотренных в работе моделей, для больших временны́х интервалов (≥30 дней) для водоема длиной 1000 м могут быть связаны с особенностями моделей: напомним, что одномерная модель построена на осреднении трехмерных уравнений, а параметризация градиента давления учитывает сейши только первой горизонтальной моды. Примечательно при этом, что для водоема длиной 10 м на 30-й день две модели дают практически идентичныe профили температуры.

Это позволяет предположить, что в трехмерной модели доля кинетической энергии гармоник с волновым номером >1 в общей кинетической энергии больше для водоема длиной 1000 м, чем для водоема длиной 10 м.

Таким образом, первая горизонтальная мода, параметризованная в одномерной модели, хуже описывает поле скорости для водоема длиной 1000 м, чем для водоема длиной 10 м, что приводит к менее точному воспроизведению вертикального турбулентного обмена и скорости заглубления перемешанного слоя.

Отметим, что результаты обсуждаемых численных экспериментов для временнóго масштаба за пределами 7–10 дней представляют сугубо теоретический интерес. Дело в том, что в постановке эксперимента поток импульса из атмосферы, определяемый ветром, имеет постоянные скорость и направление в течение всего времени расчета. В природе подобной ситуации не бывает. Во-первых, статистически значим суточный ход ветра: как правило, ветер сильнее днем и слабее ночью. Во-вторых, изменения ветра синоптического временнóго масштаба связаны с прохождением циклонов и антициклонов, время жизни которых составляет, как правило, 7–10 дней; так что для небольших временны́х масштабов (не более нескольких дней) в крайне редких случаях возможна ветровая обстановка, подобная заданной в эксперименте.

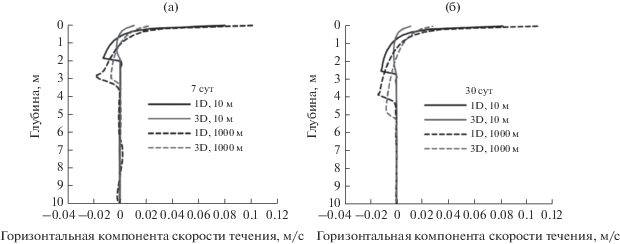
Помимо распределения температуры воды, проанализировано также вертикальное распределение скорости течения (рис. 4).

В профилях скорости течений в нижней части перемешанного слоя наблюдаются противоположные направления градиента давления и скорости ветра, а сама структура течения квазистационарная. В термоклине наблюдаются гравитационные колебания, амплитуда которых подавляется горизонтальной вязкостью.

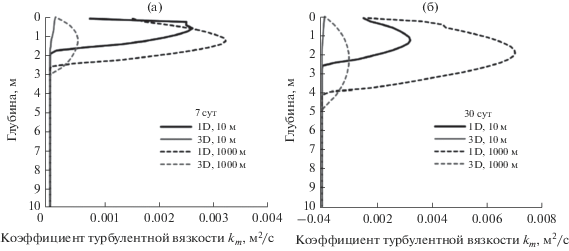
Профили коэффициента турбулентной вязкости (рис. 5) показывают, что ее значения в перемешанном слое в одномерной модели намного больше, чем в трехмерной. Это можно объяснить следующим механизмом: в обеих моделях трение между противоположно направленными верхним и нижним течениями существует вследствие вертикальной турбулентной вязкости, но в трехмерной модели воспроизводятся также вертикальные “ветви” циркуляционной ячейки, роль которых заключается в переносе импульса между верхней и нижней границами перемешанного слоя. Это способствует уменьшению разности скорости течений в трехмерной модели, так что в одномерной модели сдвиг скорости оказывается сильнее. В соответствии с формулой (10) в одномерной модели больше оказывается и генерация турбулентной кинетической энергии, что и приводит к завышению коэффициента турбулентной вязкости. В связи с этим при описании, например, турбулентного переноса фитопланктона и парниковых газов по вертикали в перемешанном слое результаты одномерной модели могут содержать заметные ошибки, и этот аспект требует дальнейших исследований.

ЗАКЛЮЧЕНИЕ

По результатам настоящего исследования можно заключить, что горизонтальные размеры водоемов оказывают существенное влияние на глубину верхнего перемешанного слоя и с увеличением размера водоема увеличивается скорость заглубления термоклина. Подтверждена необходимость учета сейшевых колебаний для корректного описания динамики перемешивания в водоемах с горизонтальными размерами намного меньшими, чем радиус деформации Россби. Предложенная В.М. Степаненко параметризация градиента давления и горизонтальной вязкости для одномерной модели LAKE позволяет с достаточной точностью воспроизводить толщину перемешанного слоя. При этом важно отметить, что одномерная модель завышает значения скорости течений, а в связи с этим – и значения коэффициента турбулентной вязкости. Авторы планируют исследовать, насколько данный факт будет влиять на корректность расчетов при моделировании, в частности, процессов переноса фитопланктона и парниковых газов в реальных водных объектах.