Водные ресурсы, 2022, T. 49, № 2, стр. 172-183

ВВЕДЕНИЕ

Водоносный слой прибрежной части суши, состоящий из пористого материала, фильтруя через себя воду, может участвовать в обмене между морскими и подземными водами. При постоянстве уровня моря и без капиллярных эффектов уровень подземных вод будет таким же, как и в море. Если по какой-то причине, например во время прилива или отлива, уровень воды в море изменится, то это приведет к дополнительному притоку воды из моря в пористую береговую среду или к оттоку в обратном направлении. При этом уровни подземных и морских вод станут выравниваться. При достаточно медленном изменении уровня воды в море естественно ожидать, что уровень подземных вод на линии их соприкосновения (урез воды) будет тоже одинаков, т. е. подземная вода успевает реагировать на медленные изменения уровня моря на месте соприкосновения вод. Следует отметить, что процесс фильтрации морской воды в прибрежной зоне без условий промерзания уже рассматривался в ряде работ, например в [1, 2, 9].

В данной работе будут рассматриваться именно медленные вариации уровня морской воды с периодом колебаний, намного превышающим 10 мин. Если же морской берег в зоне уреза воды частично покрыть непроницаемым для воды материалом (лед, промерзший грунт, искусственное покрытие плитами, как на набережных), то это затруднит водообмен между морем и берегом даже при медленных вариациях уровня моря. В этом случае уровень подземной воды на урезе может не совпадать с уровнем моря. Такая ситуация может наблюдаться в зимнее время, когда пористая среда берега отделена от морской воды слоем промерзшего грунта или намерзшего на берег льда, в том числе и на его подводной части. Этот намерзший лед или промерзший грунт могут уходить под воду и заканчиваться на некоторой глубине. Будем считать, что лед не полностью перекрывает возможность для морской воды проникать в береговой грунт, но затрудняет водообмен между морем и водоносным слоем береговой зоны.

Тем не менее в стационарном случае в силу справедливости закона гидростатики уровни морской воды и подземной воды должны совпадать. В нестационарном случае, когда уровень морской воды меняется со временем, например в приливном море, возможно несовпадение уровней воды в море и подземной воды в районе уреза.

Возникает целый ряд вопросов о поведении подземных вод в подобных ситуациях; прежде всего следующие: как меняется уровень подземных вод в водоносном слое в зимнее время, каков перепад уровней воды в море и водоносном слое в районе уреза воды, – и все другие связанные такой задачей вопросы.

ФИЗИЧЕСКАЯ МОДЕЛЬ

Рассмотрим плоскую модель, изображенную на (рис. 1). Направим горизонтальную ось $x$ от моря в сторону берега, вертикальную ось $y$ – вверх. Средний уровень морской воды соответствует значению $y = 0$. Береговой материал – двух сортов. Ниже уровня $y = - H$ – водонепроницаемое основание (например, каменный щит скальные породы). Выше уровня $y = - H$ – пористый грунт, который служит водоносным слоем для подземных вод. Подземная вода занимает нижнюю часть водоносного слоя и нигде не выходит на поверхность пористого грунта.

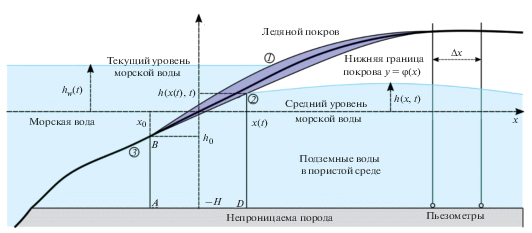
Пусть между морской водой и пористым береговым материалом находится водонепроницаемая прослойка, имитирующего лед и промерзший грунт. Верхняя граница этой прослойки может быть произвольной формы. Нижняя граница прослойки примыкает к пористому береговому материалу и подземной воде. Уравнение нижней границы обозначим как $y = \varphi \left( x \right)$. Положим, что водонепроницаемая прослойка уходит под морскую воду и оканчивается в точке $\left( {{{x}_{0}},{{h}_{0}}} \right)$ – на рисунке это самая левая точка водонепроницаемой прослойки.

Обозначим $y = h\left( {x,t} \right)$ – искомый уровень подземных вод – как функцию от координаты $x$ и времени t. В некоторой точке с переменной координатой $x$ ($x = x\left( t \right))$ уровень $y = h\left( {x\left( t \right),t} \right)$ примыкает к нижней границе водонепроницаемой прослойки. Координаты точки пересечения $\left( {x\left( t \right),h\left( {x\left( t \right),t} \right)} \right)$ определяют положение внутреннего уреза подземных вод. Сразу оговорим важное ограничение предлагаемой модели – как урез морской воды, так и урез подземной воды скользят по разным сторонам водонепроницаемой прослойки, нигде не опускаясь ниже самой глубокой точки этой прослойки с координатами $\left( {{{x}_{0}},{{h}_{0}}} \right)$. В обозначениях на рис. 1 указанные ограничения выражаются неравенствами ${{h}_{w}}\left( t \right) > {{h}_{0}},~$ $h\left( {x\left( t \right),t} \right) > {{h}_{0}}$. В свою очередь, в этих же условиях ${{h}_{0}} < 0$.

Обозначим переменный уровень моря как $y = {{h}_{w}}\left( t \right)$. В нестационарном случае уровень морской воды $y = {{h}_{w}}\left( t \right)$ может не совпадать с уровнем уреза подземной воды $y = h\left( {x\left( t \right),t} \right)$. Положение обоих урезов для морских вод и подземных вод, вообще говоря, различное (рис. 1). Так как под свободной поверхностью будем понимать неограниченную поверхность жидкости, то в диапазоне значений ${{x}_{0}} < x < x\left( t \right)$ у подземных вод нет свободной поверхности, а для значений $x > x\left( t \right)$ свободная поверхность определена.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

В случае, когда горизонтальный размер рассматриваемого явления $L$ значительно превосходит его вертикальный размер H ($H \ll L$), а в толще подземных вод справедливо приближение гидростатики, горизонтальная компонента скорости $u\left( {x,t} \right)$, подчиняющаяся закону Дарси, не зависит от вертикальной координаты $y$ и выражается через свободную поверхность $h\left( {x,t} \right)$ соотношением [7, 10]

$C$ – коэффициент фильтрации, имеющий размерность скорости, $\left( {\frac{M}{C}} \right).$

Закон сохранения массы воды в пористой среде, примененный к исследуемому случаю, выглядит следующим образом [7, 10]:

здесь $m$ – пористость среды – безразмерная величина.

Вместе с законом Дарси закон сохранения массы (2) образует уравнение Буссинеска, описывающее поведение свободной поверхности подземной воды $h\left( {x,t} \right){\kern 1pt} {\kern 1pt} :$

В коэффициенте фильтрации $C$ содержатся свойства как самой пористой среды, так и фильтрующейся жидкости: $\rho $ – плотность воды, ${\text{g}}$ – ускорение свободного падения, µ – коэффициент динамической вязкости воды, $k$ – коэффициент проницаемости, характеристика исключительно пористой среды. Все перечисленные характеристики принимаем за постоянные величины. Способ оценки указанных фильтрационных характеристик через натурный эксперимент будет описан позже.

Для упрощения дальнейших рассуждений введем еще одну константу:

В результате получим нелинейное уравнение теплопроводности, описывающее поведение поверхности подземных вод:

которое следует решать в диапазоне $x\left( t \right) \leqslant x < \infty $, т. е. там, где определена свободная поверхность подземной воды. На участке $ - {{x}_{0}} \leqslant x < x\left( t \right)$ подземная вода есть, но свободная поверхность отсутствует, поэтому здесь подход с уравнением Буссинеска неприменим.

Рассмотрим эту область в виде криволинейной трапеции $~ABCD$ отдельно (рис. 1). Здесь вертикальный отрезок $AB$ имеет координату $x = {{x}_{0}}$, а его длина $H + {{h}_{0}}$ равна высоте потока подземной воды на входе в область $ABCD$. Поясним, что точка $B$ находится под водой, поэтому ${{h}_{0}} < 0$. Точка $C~$ совпадает с урезом подземной воды – местом, где подземная вода соприкасается с нижней границей водонепроницаемой прослойки (лед и промерзший грунт). Вертикальный отрезок $CD$ имеет переменную координату $x~$ $\left( {x = x\left( t \right)} \right)$, а его длина равна высоте потока подземной воды на выходе из области $ABCD$. В любом вертикальном сечении области $ABCD$ с координатой $x$ из диапазона $ - {{x}_{0}} \leqslant x < x\left( t \right)$ высота потока – $~H + \varphi \left( x \right)$, а сам поток $Q\left( t \right)$ одинаков для любых сечений, но в общем случае может зависеть от времени как от параметра

(время $t$ – параметр). В соотношении (7) $u\left( {x,t} \right)$ – средняя горизонтальная компонента скорости в сечении $ - H < y < \varphi \left( x \right)$ при выбранном значении $x$ из диапазона $ - {{x}_{0}} \leqslant x < x\left( t \right).$

Далее для краткости $t$ опустим. Отсюда находим среднюю по толщине скорость потока $u\left( x \right)$ для данного сечения:

С другой стороны, из закона Дарси локальная компонента горизонтальной скорости связана с давлением $p$ соотношением Вообще говоря, скорости $u\left( {x,y} \right)$ и $\bar {u}\left( x \right)$ различны. Первая – локальная, вторая – средняя в данном вертикальном сечении. Обе скорости связаны соотношением Далее будет интересовать случай, когда скорости $u\left( {x,y} \right)$ и $\bar {u}\left( x \right)$ слабо отличаются друг от друга. Это выполняется, например, в приближении мелкой воды в области $ABCD$. Принимая это допущение, получаем связь Детальное обсуждение слабого различия скоростей $u\left( {x,y} \right)$ и $\bar {u}\left( x \right)$ и возможности замены $u\left( {x,y} \right)$ на $\bar {u}\left( x \right)$ дано в Приложении 1.

Интегрируя соотношение (11) по $x$ в диапазоне $ - {{x}_{0}} \leqslant x < x\left( t \right),$ найдем выражение, связывающее поток $Q\left( t \right)$ с перепадом уровней подземной воды и вод моря:

здесь $h = h\left( {x\left( t \right),t} \right)~--~$ вертикальная координата уреза подземной воды. При выводе этого соотношения предположили справедливость приближения гидростатики на вертикальных отрезках $AB$ и $CD$. Закон Дарси должен выполняться везде.

Согласно (12), выразим поток подземной воды $Q~$ через перепад уровней $\left( {h - {{h}_{w}}} \right){\kern 1pt} {\kern 1pt} :$

Отметим особенность соотношения (13). Если глубина погружения кромки водонепроницаемой прослойки равна $ - H$, то $H + \varphi \left( {~{{x}_{0}}} \right) = 0$. Это означает, что проход в подземный водоносный слой для морской воды полностью перекрыт водонеприницаемой прослойкой и взаимный переток морской воды в подземный водоносный слой и обратно отсутствует. Формально в соотношении (13) интеграл в знаменателе расходится ($\int_{{{x}_{0}}}^{x~\left( t \right)} {\frac{{dx}}{{H + \varphi \left( x \right)}} = \infty )} $ и поток обращается в ноль $\left( {Q = 0} \right)$, что естественно.

Заменим переменную интегрирования с $x$ на $y$ с помощью связи $x = F\left( y \right)$, где $x = F\left( y \right)$ – обратная функция к $y = \varphi \left( x \right)$. Окончательно получим выражение

Пусть функция $F{\kern 1pt} '\left( y \right)$ раскладывается в ряд Тейлора по $y$: тогда написанный выше интеграл аналитически вычисляется, при этом угол α $F{\kern 1pt} '\left( y \right)$ – угол наклона касательной к линии $y = \varphi \left( x \right)$ при $y = 0$.

Соотношения (13), (14) справедливы для любого $x$ из диапазона $ - {{x}_{0}} \leqslant x < x\left( t \right)$, в том числе и на урезе подземной воды при $x = x\left( t \right)$. На этой же границе можно вычислить поток $Q$, используя параметры уравнения Буссинеска:

Приравняв выражения (14) и (15), выведенные двумя разными способами, получим соотношение

которое при $x = x\left( t \right)$ естественно трактовать как граничное условие для уравнения Буссинеска на подвижной границе.

Если ограничиться плоским профилем нижней границы водонепроницаемой пластины, то интеграл в (16) вычисляется так:

и граничное условие на подвижной границе $x = x\left( t \right)$ примет следующий вид:

ПОСТАНОВКА ЗАДАЧИ

Окончательно сформулируем математическую часть задачи. Требуется решить уравнение Буссинеска:

– в области $x\left( t \right) \leqslant x < \infty $ с граничным условием при $x = x\left( t \right){\kern 1pt} {\kern 1pt} :$и условием отсутствия течений $\frac{{\partial h}}{{\partial x}} \to 0$ на бесконечности $x \to \infty $.

Поскольку в соотношении (20) принято обозначение $h = h\left( {x\left( t \right),t} \right) = \varphi \left( {x(t} \right))$, то граничное условие (20) можно представить в следующем виде:

и трактовать как ограничение на производную $\frac{{\partial h}}{{\partial x}}$ в подвижной точке $x = x\left( t \right)$. Задача (19)–(20), или в другой трактовке (19)–(20а), представляет собой нелинейную задачу с нелинейным граничным условием на подвижной границе $x = x\left( t \right)$, положение которой заранее неизвестно, и поведение $x\left( t \right)$ придется определять в процессе самого решения.

В указанной постановке следует задать начальное распределение уровня грунтовых вод ${{\Phi }}\left( x \right) = h\left( {x,0} \right)$, что автоматически определит начальную $x$ – координату уреза подземных вод $x\left( 0 \right)$. Конечно, следует также задать временной ход уровня морской воды ${{h}_{w}}\left( t \right)$.

Подобная математическая ситуация известна в гидродинамике в теории гравитационных поверхностных волн, когда на поверхности жидкости ставятся два нелинейных граничных условия, но положение самой границы переменно и неизвестно. Ее положение и эволюция определяют в процессе решения. Один из подходов, позволяющий продвинуться в решении волновых задач и значительно упрощающий само решение, – линеаризация уравнений. В данной ситуации поступим похожим образом. Полная математическая постановка задачи (19)–(20), или (19)–(20а), и ее полноценное исследование и решение в настоящей работе не рассматриваются.

Важный параметр, благодаря которому происходит обмен водой между морем и прибрежным водоносным слоем, – перепад уровня морской воды и уреза подземной воды $\left( {h - {{h}_{w}}} \right)$, который входит в граничное условие.

Неизвестная подвижная граница $x = x\left( t \right)$, на которой следует ставить граничное условие (20), сильно усложняет задачу. Возможный вариант, позволяющий продвинуться в решении проблемы, – использование подвижной системы координат $X = x - x\left( t \right)$, в которой уравнение Буссинеска видоизменится, данный способ решения поставленной задачи используется в [12]:

Диапазон значений $X$, в котором следует решать уравнение (21), станет неподвижным и с известными границами $0 < X < \infty $, а само граничное условие

останется прежним и будет ставиться при неподвижном значении $X = 0$.

ЛИНЕЙНАЯ ЗАДАЧА

Обращаем внимание на то, что появившееся в уравнении (21) новое слагаемое $\dot {x}\left( t \right)\frac{{\partial h}}{{\partial X}}$ фактически нелинейное, поскольку переменная координата $x\left( t \right)$ связана с высотой уреза подземной воды через соотношение $h\left( {x\left( t \right),t} \right)~$ – искомую неизвестную функцию $h\left( {x,t} \right)$ при $x = x\left( t \right)$. При линеаризации задачи это слагаемое исчезнет, а само уравнение преобразуется в линейное уравнение теплопроводности:

с линейным граничным условием при $X = 0$В граничное условие входит постоянная величина, имеющая размерность обратной длины, которую обозначим как $S$

В результате граничное условие запишется так:

Вся информация о форме дна и глубине расположения кромки водонепроницаемой прослойки содержится в параметре $S$. Если форма дна плоская, то параметр $S$ упростится и примет следующий вид: Напомним, что ${{h}_{0}}$ – глубина погружения кромки водонепроницаемой прослойки и в принятой системе координат ${{h}_{0}} < 0$, при этом $S > 0.$ Если безразмерный параметр $\left| {\frac{{{{h}_{0}}}}{H}} \right| \ll 1$ мал, то соотношение (27) дополнительно упростится:

РЕШЕНИЕ ЛИНЕАРИЗОВАННОЙ ЗАДАЧИ БЕЗ НАЧАЛЬНЫХ УСЛОВИЙ

Зададим колебание уровня моря соотношением

Решая уравнение (23) с граничным условием (26), получим решение в виде

Здесь волновое число задачи $k$ и одновременно параметр пространственного затухания волн определяются частотой колебаний уровня моря ${{\omega }}$ и фильтрационными характеристиками среды прибрежной зоны – глубиной залегания водонепроницаемого щита $H$, коэффициентом фильтрации $C$ и пористостью среды $m$. Согласно (30), при гармоническом характере колебаний уровня моря в глубь водоносного слоя проникает бегущая от берега и пространственно затухающая волна.

Для сравнения приведем выражение для колебаний уровня подземных вод при тех же условиях, но в отсутствие водонепроницаемой прослойки (береговой наледи и промерзшего берегового грунта), с непрерывным уровнем поземных и морских вод на урезе, полученное в [2, 4, 6 ]:

Детальнее обсудим выражения (30) и (30а). В соотношении (30) $A{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \frac{{\left( {1 + G} \right){\kern 1pt} G}}{{1 + {{{\left( {1{\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} G} \right)}}^{2}}}}a,B{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \frac{G}{{1{\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} {{{\left( {1 + G} \right)}}^{2}}}}a,$ $~G = \frac{S}{k}$. Безразмерный параметр $G~$ из диапазона $0 < G < \infty $ определяет амплитуду колебаний уровня подземных вод и задержку сигнала на урезе при $X = 0$: Здесь ${{\varphi }_{0}}$ – скачок начальной фазы, ${{t}_{{0~}}}$ – время запаздывания отклика колебаний подземной воды на колебания уровня моря.

Коэффициент ослабления

монотонно растет от 0 до 1 в диапазоне значений $0 < ~\,\,G < \infty .$ Проникающая волна колебаний уровня подземных вод сильно ослабевает $\left( {\mathbb{K} \ll 1} \right)$ при малых значениях параметра $G$ и практически не ослабевает $\left( {\sim 1} \right)$ при больших значениях $G$. Сильное ослабление соответствует глубокому залеганию кромки водонепроницаемой прослойки: ${{h}_{0}}\sim - H$; хорошее проникновение волны колебания уровня соответствует малым значениям: ${{h}_{0}}\sim 0$. Приливное колебание уровня подземных вод на урезе запаздывает по сравнению с приливными колебаниями уровня моря. Возникающая разность фаз ${{\varphi }_{0}}$ и время запаздывания ${{t}_{0}}$ также зависят от безразмерного параметра $G$: Сильно ослабленная проникающая волна имеет на урезе максимальный сдвиг фаз: $~{{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}$ – и максимально возможное время задержки – одну восьмую периода колебаний уровня моря: ${{\left( {{{t}_{0}}} \right)}_{{{\text{max}}}}} = {{~T} \mathord{\left/ {\vphantom {{~T} 8}} \right. \kern-0em} 8}$. Значительная по амплитуде проникающая в водоносный слой волна на урезе практически не запаздывает.

Сравнивая соотношения (30) и (30а), делаем вывод, что гармонические колебания уровня моря вызывают появление в водоносном слое прогрессивной волны той же частоты, что и у колебаний уровня моря. Прогрессивная волна убегает от уреза по водоносному слою с экспоненциально затухающей амплитудой по мере удаления от моря. Степень пространственного угасания амплитуды такая же, как и в отсутствие водонепроницаемой прослойки (т. е. наледи на береговом склоне или промерзшего грунта в прибрежной зоне).

Наличие водонепроницаемой прослойки привело к следующим новым свойствам:

1. амплитуда колебаний уреза подземной воды уменьшилась по сравнению с аналогичной амплитудой в отсутствие водонепроницаемой прослойки;

2. образовался разрыв между уровнем моря и уровнем подземной воды на урезе;

3. если в отсутствие водонепроницаемой прослойки следует ожидать синфазного колебания уровня моря и уреза подземной воды, то при наличии такой прослойки происходит запаздывание отклика колебаний уреза подземной воды по сравнению с колебаниями уровня моря, или возникнет скачок начальной фазы в колебаниях уреза подземной воды.

ПЕРЕПАД УРОВНЕЙ МОРСКОЙ ВОДЫ И УРЕЗА ПОДЗЕМНОЙ ВОДЫ

В представленной модели допускается разрыв между уровнем моря и урезом подземной воды. Выпишем уровень подземной воды на урезе $X = 0{\kern 1pt} {\kern 1pt} :$

При этом уровень морской воды может отличаться от уровня подземной воды:

Разность уровней во времени можно представить в следующем виде:

где $\mathbb{M}$ – безразмерный параметр, который обозначает перепад колебаний уровней морской воды и уреза подземных вод

Как следует из (36), уровень моря и уровень подземных вод на урезе не совпадают. Их разность гармонически меняется со временем с тем же периодом, что и колебание уровня моря. Половину времени уровень моря выше уровня подземных вод, половину времени наоборот.

Коэффициент ослабления амплитуды перепада уровней $\mathbb{M}$ зависит от безразмерного параметра $G$ и монотонно убывает от 1 до 0 в диапазоне значений 0 < $G~$ < $\infty $. Колебание перепада уровней происходит со сдвигом фаз ψ, который также зависит от параметра $G$:

Соответствующий временной сдвиг ${{\tilde {t}}_{0}}$ в соотношении (36) зависит как от сдвига фаз ψ, так и от частоты колебаний уровня моря: Большой перепад уровней соответствует запаздыванию проникновения волны в водоносный слой, что должно наблюдаться при малых $G$. При этом сдвиг фаз мал. Это понятно – уровень морской воды колеблется, а в водоносный слой колебания передаются слабо. Поэтому разность уровней практически совпадает с колебаниями уровня моря, разность фаз ψ отсутствует.

Малый перепад уровней соответствует большим значениям $G$, что равносильно хорошему проникновению колебаний уровня в водоносный слой или отсутствию препятствий в виде водонепроницаемой прослойки.

Для численной оценки описанных эффектов приведем расчетные значения всех параметров задачи для различных $G$. В табл. 1 представлены следующие параметры:

1) $\mathbb{K} = \frac{G}{{\sqrt {1 + {{{\left( {1 + G} \right)}}^{2}}} }}$ – коэффициент ослабления амплитуды колебаний уровня подземных вод по сравнению с амплитудой колебания уровня моря;

2) ${{\varphi }_{0}}$ – сдвиг фаз между колебанием уровня моря и колебанием уреза подземных вод;

3) ${{t}_{0}}~--{\text{\;}}$ временнáя задержка вертикальных колебаний уреза подземных вод относительно колебаний уровня моря для полусуточного лунного прилива;

4) $\mathbb{M} = \frac{{\sqrt {{{{\left( {2 + G} \right)}}^{2}} + {{G}^{2}}} }}{{1 + {{{\left( {1 + G} \right)}}^{2}}}}$ – отношение разницы уровней морской воды и уреза подземных вод к амплитуде колебаний уровня моря;

5) ψ – сдвиг фаз между перепадом уровней морской и подземных вод и колебанием морской поверхности, соответствующее время задержки: ${{\tilde {t}}_{0}} = \frac{\psi }{{2\pi }}T$.

НАТУРНЫЙ ЭКСПЕРИМЕНТ НА оз. ШПИЦБЕРГЕН

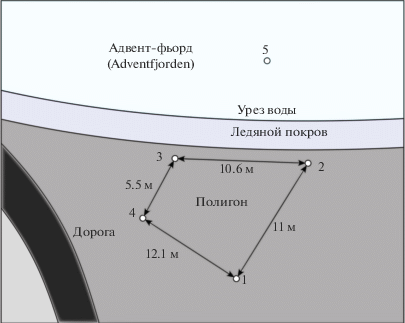
В январе 2013 г. авторами данной работы проводилось полевое исследование на экспериментальном полигоне в г. Лонгиербьюен (оз. Шпицберген, Норвегия). Суть работы заключалась в фиксации колебаний уровней воды в Адвент-фьорде (Adventfjorden) и уровня грунтовой воды в прибрежной зоне фьорда.

Для проведения измерений на берегу фьорда был оборудован специальный полигон, на котором установили четыре датчика измерения порового давления (пьезометры) в грунте прибрежной зоны и один датчик давления, который находился на дне фьорда. Принципиальная схема устройства полигона представлена на рис. 1, 2.

На береговой части полигона находились четыре точки измерения, в которых располагались датчики давления на глубинах 5.5 и 4 м от уровня земли и датчики температуры (рис. 1, 2). В точке 5 измерялось придонное давление морской воды. Точность глубины положения датчиков с учетом локальных неровностей поверхности земли оценивается в 5 см. Из-за уклонов, перекосов, неровностей поверхности Земли на полигоне датчики оказались на разных горизонтах, при этом точность их положения относительно друг друга оценивается в 10–15 см. Далее было оценено, что примерно на такую же величину отклоняется свободная поверхность подземной воды, соответствующая эффекту накачки, дополнительному подъему уровня подземных вод, связанному с нелинейными эффектами подземной гидродинамики.

Поэтому показания датчиков абсолютных значений давления не использовались для восстановления положения свободной поверхности подземных вод. Горизонты положения всех датчиков давления гарантировали, что все они расположены заметно ниже уровня морской воды на любой стадии прилива и ниже уровня промерзания почвы, что в свою очередь фиксировалось датчиками температуры, которые были помещены в те же каналы, что и пьезометры. Измерения температуры в грунте проводились в точках 1–4 на глубинах 0.5, 2, 4, 6 м ниже уровня грунта и в атмосфере на высоте 1 м. Измерение давления в море проводилось на дне в ~5 м от берега в непосредственной близости от прибрежного полигона.

Ввиду того, что прямые измерения параметров математической модели были затруднены, было принято решение оценить фильтрационные свойства грунта прибрежной зоны фьорда на основе косвенных вычислений и при задержке фиксации одного и того же колебания уровня подземной воды на разных датчиках, которые располагались на одной линии (датчики 2–1, 3–4).

Исходя из полученных данных проводилась оценка фильтрационных свойств грунта, что подробно изложено в работе [4]. Так, например, для полигона на оз. Шпицберген оценка волнового числа $k$, которое использовалось в (30), составила $0.018\frac{1}{{\text{м}}}$, а коэффициента ${\rm K}$ из (23) – $34 \times {{10}^{{ - 3}}}\frac{{\text{м}}}{{\text{с}}}$.

Из полученных оценок фильтрационных свойств грунта на оз. Шпицберген можно получить оценки для описываемых в данной работе эффектов (табл. 2).

К сожалению, неизвестна глубина залегания кромки водонепроницаемой прослойки ${{h}_{0}}$, поэтому в качестве возможных значений ${{h}_{0}}$ выбраны три варианта – 1, 2 и 3 м. Как показали расчеты, проникающая в прибрежный водоносный слой волна имеет амплитуду колебаний на урезе 0.4–0.8 амплитуды колебаний уровня моря. Для полусуточного лунного прилива задержка сигнала на урезе – в пределах от 20 мин до 1 ч. Между морем и подземной водой на урезе существует заметный перепад уровней, который колеблется с частотой прилива и амплитудой 0.2–0.7 амплитуды прилива. Данные расчета по вполне конкретному полигону показали, что предлагаемый эффект заметен.

В работе [1] изучался нелинейный отклик уровня подземных вод на приливные колебания уровня моря без наличия льда и промерзшего грунта на границе море – береговой грунт. В качестве граничных условий применялось условие непрерывности уровня воды при переходе из моря в береговой водоносный горизонт. Другими словами, на всех стадиях эволюции уровня подземной воды внешний урез морской воды совпадал с внутренним урезом поземных вод. Отметим, что в данных работах и работах многих других авторов, например [5], рассматривались исключительно медленные вариации уровня моря – приливы. Именно для медленных движений можно надеяться на то, что уровень подземных вод успеет среагировать на подъем или снижение уровня моря, что и приведет к выравниванию обоих уровней на месте их соприкосновения – урезе морской воды.

В результате этих исследований был теоретически объяснен и экспериментально подтвержден эффект поднятия среднего уровня подземных вод над средним уровнем моря – так называемый пампинг-эффект, или эффект накачки. В формальные математические соотношения, описывающие это явление, входит частота колебаний уровня моря, так что расчетный подъем среднего уровня подземных вод увеличивается с ростом частоты колебаний. В результате для высокочастотной части спектра колебаний моря отклик в подъеме среднего уровня подземных вод становится нереально большим. По этой причине вся изложенная теория применялась исключительно для низких частот, и для полусуточных приливов она давала вполне реальные результаты.

Одно из возможных объяснений несостоятельности теории пампинг-эффекта на высоких частотах может быть связано с тем, что идея непрерывного сращивания уровней морской и подземной вод на урезе оказывается неверной. Подземная вода в силу значительной инерционности процессов фильтрации не успевает подстроить свой уровень под уровень уреза морской воды. В результате урез морской воды может не совпадать с урезом подземной вод.

В данной работе рассматривается ситуация, когда наличие льда и промерзшего прибрежного грунта препятствует прямому обмену морских и подземных вод, поскольку воды разделены водонепроницаемой прослойкой, и только ниже кромки указанной прослойки водообмен возможен. При таком подходе, как показано выше, допускается перепад уровней подземных вод и уровней морской воды. Амплитуда колебаний уровня подземных вод $a{\kern 1pt} *$ уменьшается с коэффициентом ослабления $\mathbb{K}$ по сравнению с амплитудой колебаний уровня моря (см. (36), (37)): $a{\kern 1pt} * = \mathbb{K}a$.

ВЫВОДЫ

При гармоническом колебании уровня моря в водоносном слое прибрежной зоны формируется прогрессивная волна, убегающая от моря в сторону берега и имеющая ту же частоту колебаний, что и уровень моря. Амплитуда колебаний подземной воды экспоненциально затухает при удалении от моря. На длину и фазовые скорости волн, проникающих в водоносный слой, водонепроницаемая прослойка влияния не оказывает. Наличие льда и мерзлого грунта в прибрежной зоне моря как препятствия для фильтрации морской воды в береговой грунт приводит к уменьшению водообмена между морем и прибрежным подземным водоносным слоем, вследствие этого уменьшается амплитуда колебаний уровня подземной воды в сравнении с амплитудой колебаний поверхности грунтовых вод при отсутствии водонепроницаемой прослойки. Вычислен соответствующий коэффициент ослабления амплитуды. В предложенной модели допускается разрыв между уровнями моря и грунтовой воды и выведены соответствующие соотношения, описывающие эволюцию этого разрыва. Новым свойством представленной модели оказалась временнáя задержка сигнала в подземном водоносном слое в виде скачка начальной фазы колебаний уровня грунтовых вод на урезе.

Статья посвящена коллеге и большому другу ее авторов, эксперту в области пампинг-эффекта, доктору физ.-мат. наук, профессору, заведующему лабораторией гидродинамики Института водных проблем РАН – Валерию Николаевичу Зырянову, которого не стало в феврале 2021 г.