Водные ресурсы, 2022, T. 49, № 2, стр. 184-195

ВВЕДЕНИЕ

Классическая физическая кинетика изучает “термодинамические” стохастические ансамбли частиц, расположенных в термостате. Ансамбль броуновских частиц – наиболее известный стохастический ансамбль физической кинетики. Подробное описание ансамбля медленных броуновских частиц приведено, например, в монографиях [5, 27].

В гидродинамике хорошо известны также не “термодинамические” стохастические системы. Возможность распространения методов физической кинетики на турбулентные гидродинамические течения однородной жидкости обсуждается в монографии [20]. Попытка построения стохастических уравнений Ланжевена для элементарных вихрей турбулентного конвективного пограничного слоя рассмотрена, например, в работах [10, 18].

Специальный подход к построению уравнений Ланжевена для задач турбулентной конвекции над горизонтальной нагретой поверхностью рассмотрен в работах [2−4, 28, 29]. Известно, что в условиях турбулентной конвекции над нагретой поверхностью возникает система изолированных плавучих вихрей (термиков), всплывающих в практически неподвижном окружении. Конвективные термики зарождаются в сравнительно тонком поверхностном слое вблизи нагретой поверхности. Существенно, что процесс возникновения термиков связан с неустойчивостью поверхностного слоя и является случайным, поэтому система термиков является стохастическим ансамблем.

В работах [2−4, 28, 29] рассмотрены различные модели систем конвективных термиков, построенные по аналогии с ансамблем броуновских частиц в термостате. Использование такой аналогии позволяет найти для системы конвективных термиков обобщенные распределения Максвелла и Больцмана, существование которых подтверждено данными измерений.

Уровнем конвекции в геофизической гидродинамике называют уровень, на котором средняя архимедова сила в термиках равна нулю. В настоящей работе предложена кинетическая модель системы медленных сферических конвективных термиков фиксированного радиуса, использующая аналогию с классическим ансамблем броуновских частиц. Показано, что для описания системы термиков в тонком слое, включающем в себя уровень конвекции, можно использовать кинетические уравнения, практически идентичные уравнениям классического броуновского движения. В рамках предложенного подхода установлено, что средняя скорость системы термиков на уровне конвекции равна нулю. Предложенная аналогия обеспечивает строгое математическое обоснование модели системы термиков в тонком слое, включающем уровень конвекции. Более того, аналогия с броуновскими частицами позволяет строго определить “кинетическую” температуру системы термиков, а также установить существование распределения Максвелла по вертикальным скоростям. Приведено также сопоставление полученных результатов как с натурными, так и с численными экспериментами.

Настоящее исследование – продолжение и обоснование положений, изложенных в работах [2−4, 28, 29].

ВТОРОЙ МОМЕНТ ВЕРТИКАЛЬНОЙ СКОРОСТИ ТУРБУЛЕНТНОГО КОНВЕКТИВНОГО СЛОЯ

Пусть $t$ – время; $x$, $y$, $z$ – декартова система координат, в которой оси $x$, $y$ лежат на плоской нагретой подстилающей поверхности, а направление вертикальной оси $z$ противоположно направлению ускорения силы тяжести ${\text{g}}$; $w~$ – компонента вектора скорости вдоль оси $z$.

Рассмотрим неподвижный слой атмосферы, расположенный в поле силы тяжести и ограниченный снизу плоской горизонтальной подстилающей поверхностью $z = 0$. Допустим, что в начальный момент времени $t = 0$ на нижнюю границу неподвижной среды начинает поступать положительный поток тепла. В случае интенсивного прогревания среды над горизонтальной границей области формируется турбулентный конвективный слой высотой $h$.

Допустим, что $w = w\left( {x,y,z,t} \right)$, ${{\Theta }} = {{\Theta }}\left( {x,y,z,t} \right)$ – локальные значения вертикальной скорости и потенциальной температуры в турбулентном конвективном слое; ${{{{\Theta }}}_{0}} = {\text{const}}$ – средняя фоновая потенциальная температура неподвижного статического слоя перемешивания; $\theta = {{\left( {{{\Theta }} - {{{{\Theta }}}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\Theta }} - {{{{\Theta }}}_{0}}} \right)} {{{{{\Theta }}}_{0}}}}} \right. \kern-0em} {{{{{\Theta }}}_{0}}}} = \theta \left( {x,y,z,t} \right)$ – безразмерная пульсация потенциальной температуры [1, 19]. Величину ${\text{g}}\theta \left( {x,y,z,t} \right)$ будем называть локальной “адиабатической” плавучестью [26].

Усредняя по площади различные произведения плавучести ${\text{g}}\theta $ и вертикальной скорости $w$ на произвольном уровне $z$, получим общий турбулентный момент Рейнольдса $\overline {{{{\left( {{\text{g}}\theta } \right)}}^{m}}{{w}^{n}}} $. Здесь и далее знак черты “–” обозначает операцию усреднения по площади; $m \geqslant 0$,$~n \geqslant 0$ – целые числа.

В частности, при $m = 1$, $n = 1$ получим выражение для потока плавучести ${\text{g}}{{S}_{\theta }} = \overline {{\text{g}}\theta w} $. Величину потока плавучести на подстилающей поверхности $z = 0$ будем обозначать символом ${\text{g}}{{S}_{\theta }} = {{\left. {{\text{g}}\overline {\theta w} } \right|}_{{z{\kern 1pt} = {\kern 1pt} 0}}}$, где $\left[ {{\text{g}}{{S}_{\theta }}} \right] = {{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {{{{\text{с}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{с}}}^{{\text{3}}}}}}$ – размерность потока плавучести.

Существование параметров ${\text{g}}{{S}_{\theta }}$ и $h$ позволяет определить параметры Дирдорффа ${{w}_{D}}$ и ${\text{g}}{{\theta }_{D}}$ в следующей форме [8]:

С учетом параметров Дирдорффа (1) получим безразмерные выражения для потока плавучести и второго момента вертикальной скорости где ${{F}_{{\theta w}}}\left( {{z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h}} \right)$, ${{F}_{{ww}}}\left( {{z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h}} \right)$ – положительные безразмерные функции.

При описании кинетических свойств ансамбля конвективных термиков особую роль играет второй момент вертикальной скорости $\overline {{{w}^{2}}} $.

Безразмерные вертикальные профили ${{\overline {{{w}^{2}}} } \mathord{\left/ {\vphantom {{\overline {{{w}^{2}}} } {w_{D}^{2}}}} \right. \kern-0em} {w_{D}^{2}}}$ получены:

а) в лабораторных экспериментах [9, 12, 30];

б) в численных экспериментах [22, 24];

в) в экспериментах в ветровом канале [11];

г) в натурных атмосферных экспериментах Minnesota 1973 и AMTEX-1975 [7, 15].

Результаты измерений безразмерного второго момента вертикальной скорости, полученные в лабораторных экспериментах [9, 12, 30], а также в численных экспериментах [22], представлены на рис. 1a.

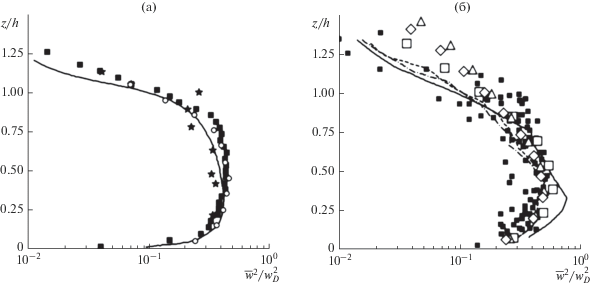
Значения безразмерного второго момента вертикальной скорости, полученные при измерениях в ветровом канале и в численных экспериментах [11], а также в натурных экспериментах [7, 15], представлены на рис. 1б.

Результаты экспериментов, представленные на рис. 1a, 1б, показывают, что умеренный ветер практически не оказывает влияния на вертикальный профиль второго момента вертикальной скорости ${{\overline {{{w}^{2}}} } \mathord{\left/ {\vphantom {{\overline {{{w}^{2}}} } {w_{D}^{2}}}} \right. \kern-0em} {w_{D}^{2}}}$. В частности, согласно измерениям,

Соотношение (3) впервые установлено в [7].

КОНВЕКТИВНЫЕ ТЕРМИКИ И ТОНКАЯ СТРУКТУРА ПОГРАНИЧНОГО СЛОЯ

Конвективными термиками называют изолированные плавучие вихри, движение которых происходит в практически неподвижном окружении. Атмосферные термики зарождаются в сравнительно тонком поверхностном слое вблизи нагретой поверхности, а затем поднимаются наверх под действием архимедовой силы [23]. Существенно, что процесс возникновения термиков связан с неустойчивостью поверхностного слоя и является случайным. Взаимодействие конвективных вихрей друг с другом и своим окружением также является случайным процессом, поэтому система термиков является стохастическим ансамблем.

Наглядно получить представления о системе восходящих термиков можно на основе лабораторного моделирования, выполненного при высоких числах Рэлея [13, 25]. Возникновение атмосферных термиков при нагревании подстилающей поверхности наблюдается в многочисленных натурных экспериментах [15]. Системы термиков возникают также и в пограничном слое океана при резком охлаждении его поверхности. Однако при этом хаотическое движение термиков имеет нисходящий характер [3, 4]. Результаты экспериментов [13], представленные на рис. 2, отчетливо демонстрируют хаотический характер нисходящего движения термиков.

Изолинии нулевой плавучести ${\text{g}}\theta = 0$ достаточно четко отделяют более теплый, восходящий термик от окружающей среды. Это обстоятельство позволяет рассматривать систему термиков как ансамбль частиц. Определим $k$-й конвективный термик как плавучий объем ${{V}_{{\theta k}}}$, ограниченный поверхностью ${{\Sigma }_{{\theta k}}}$ с нулевой плавучестью ${\text{g}}\theta = 0$. Тогда среднюю скорость ${{\hat {w}}_{k}}$ и плавучесть ${\text{g}}{{\hat {\theta }}_{k}}$ для $k$-го термика можно представить в следующей форме:

Будем далее обозначать угловыми скобками $\left\langle {} \right\rangle $ усреднение по всем термикам ансамбля. С учетом соотношений (4) и принятого обозначения построим средние по ансамблю от вертикальной скорости $\left\langle {\hat {w}} \right\rangle $ и плавучести и $\left\langle {{\text{g}}\hat {\theta }} \right\rangle $. Для ансамбля атмосферных термиков средние $\left\langle {\hat {w}} \right\rangle $ и $\left\langle {{\text{g}}\hat {\theta }} \right\rangle $ определены в натурном эксперименте [15]. Измерения безразмерной средней плавучести ансамбля термиков ${{\left\langle {{\text{g}}\hat {\theta }} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {{\text{g}}\hat {\theta }} \right\rangle } {{\text{g}}{{\theta }_{D}}}}} \right. \kern-0em} {{\text{g}}{{\theta }_{D}}}}$, полученные в [15], представлены на рис. 3.

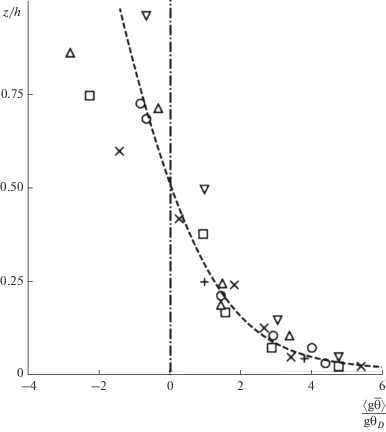
Уровнем конвекции в геофизической гидродинамике называют уровень, на котором средняя плавучесть системы термиков равна нулю: $\left\langle {{\text{g}}\hat {\theta }} \right\rangle = 0$. Согласно экспериментальным результатам [15], представленным на рис. 3, уровень конвекции системы атмосферных конвективных термиков находится на уровне ${z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h} \approx {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$.

ДИНАМИЧЕСКОЕ УРАВНЕНИЕ ДВИЖЕНИЯ ТЕРМИКА В ОКРЕСТНОСТИ УРОВНЯ КОНВЕКЦИИ

Характерные размеры атмосферных термиков изменяются от нескольких десятых долей до сотни метров. Пусть $R$ – средний радиус ансамбля термиков. Согласно измерениям [15], для величины среднего радиуса системы термиков справедлива аппроксимация ${R \mathord{\left/ {\vphantom {R h}} \right. \kern-0em} h} = 0.08{{({z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h})}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}$ (рис. 4).

Для описания движения системы термиков в тонком слое, включающем в себя уровень конвекции, используем простейшую модель, в рамках которой все термики представляют собой идентичные жесткие сферы фиксированного радиуса $R$. Средний радиус системы термиков $R$ в окрестности уровня конвекции ${z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h} \approx {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ можно определить, опираясь на данные измерений, представленные на рис. 4. При высоте атмосферного конвективного слоя $h \approx 1000~$ м средний радиус атмосферных термиков $R \approx 60$ м. Кроме того, будем предполагать, что в окрестности уровня конвекции воздух сильно завихренный и обладает коэффициентом турбулентности $\nu \approx 10~$ м²/с. Характерные значения скорости и положительные пульсации температуры атмосферных термиков имеют порядок $0.2\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ и $0.3^\circ {\text{C}}$ соответственно. Очевидно, что в окрестности уровня конвекции плавучесть термиков ${\text{g}}{{\hat {\theta }}_{k}}$ становится малой. Поэтому при построении гидродинамической модели будем считать, что движение термиков происходит достаточно медленно. В этих условиях при ${{\hat {w}}_{k}} \approx 0.2\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$, $R \approx 60$ м и $\nu \approx 10~$ м²/с соответствующая оценка числа Рейнольдса примет вид: $\operatorname{Re} = {{{{{\hat {w}}}_{k}}R} \mathord{\left/ {\vphantom {{{{{\hat {w}}}_{k}}R} \nu }} \right. \kern-0em} \nu } \approx 0.12$.

В случае ${\text{Re}} \ll 1$ в уравнении движения термика можно использовать приближение Стокса, линейно зависящее от скорости. Тогда

${{\gamma }_{0}} = \left( {{9 \mathord{\left/ {\vphantom {9 2}} \right. \kern-0em} 2}} \right)\nu {{R}^{{ - 2}}}$ – коэффициент подвижности, его размерность $\left[ {{{\gamma }_{0}}} \right] = {{{\text{с}}}^{{ - 1}}}$.

Первое слагаемое в правой части динамического уравнения движения (5) соответствует силе плавучести Архимеда; второе слагаемое соответствует силе трения Стокса. Второе уравнение в системе (5) представляет начальное условие $\hat {w}_{k}^{0}$. Модель сферического термика фиксированного радиуса $R$ рассматривалась в работах [2, 15].

Пусть $\left\langle {{\text{g}}{{{\hat {\theta }}}_{k}}~} \right\rangle $ – усредненная по ансамблю средняя плавучесть термиков; ${\text{g}}\hat {\theta }_{k}^{{\text{'}}} = {\text{g}}{{\hat {\theta }}_{k}} - \left\langle {{\text{g}}{{{\hat {\theta }}}_{k}}} \right\rangle $ – флуктуация плавучести. С учетом принятого обозначения представим уравнение (5) в форме

Согласно [16], на уровне конвекции ${z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h} \approx {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ средняя плавучесть термиков равна нулю, т. е. $\left\langle {{\text{g}}{{{\hat {\theta }}}_{k}}} \right\rangle = 0$. Поэтому в окрестности уровня конвекции динамическое уравнение (6) можно упростить: Будем рассматривать далее флуктуацию плавучести ${\text{g}}\hat {\theta }_{k}^{{\text{'}}}$ в уравнении (7) как случайную силу. Опуская индекс $k$ и символ крышки в уравнении движения (7), получим стохастическое уравнение движения системы термиков Существенно, что статистическое среднее случайной силы $\left\langle {{\text{g}}\theta {\kern 1pt} {\text{'}}} \right\rangle $ равно нулю, так как Для сопоставления с классической теорией броуновского движения используем специальное обозначение для случайной силы, полагая, что где ${{q\left( t \right)} \mathord{\left/ {\vphantom {{q\left( t \right)} m}} \right. \kern-0em} m}$ – обозначение случайной силы.

Подстановка (10) в (8) приводит к уравнению

Динамическое уравнение в форме (11) впервые использовалось для описания классического ансамбля идентичных броуновских частиц. При этом считалось, что $m$ – масса частицы, $q\left( t \right)$ – случайная сила взаимодействия частицы со средой, такая что $\left\langle {q\left( t \right)} \right\rangle = 0$. Последнее условие означает, что среднее значение случайной силы $\left\langle {q\left( t \right)} \right\rangle $ не оказывает влияния на динамику системы частиц.

Для построения абстрактного стохастического уравнения Ланжевена ансамбля “медленных” конвективных термиков на основе (11) необходимо задать случайную силу ${{q\left( t \right)} \mathord{\left/ {\vphantom {{q\left( t \right)} m}} \right. \kern-0em} m}$.

УРАВНЕНИЕ ЛАНЖЕВЕНА ДЛЯ АНСАМБЛЯ “МЕДЛЕННЫХ” КОНВЕКТИВНЫХ ТЕРМИКОВ В ОКРЕСТНОСТИ УРОВНЯ КОНВЕКЦИИ И ЕГО СЛЕДСТВИЯ

Пусть ${{W}^{2}} > 0$ – некоторая постоянная, размерность которой соответствует квадрату скорости: $\left[ {{{W}^{2}}} \right] = {{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {{{{\text{с}}}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{с}}}^{{\text{2}}}}}}$. Физический смысл постоянной ${{W}^{2}}$ будет установлен далее. Без ограничения общности можно считать, что

Здесь параметр ${{D}_{E}}$ – коэффициент диффузии Эйнштейна, размерность $\left[ {{{D}_{E}}} \right] = {{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {{{{\text{с}}}^{{\text{2}}}}}}} \right. \kern-0em} {{{{\text{с}}}^{{\text{2}}}}}}$; $\xi \left( t \right)$ – произвольная функция времени, размерность $\left[ \xi \right] = {{{\text{с}}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}$.

С обозначениями (12) стохастическое уравнение (11) примет следующий вид:

Заметим, что значение вертикальной скорости $w\left( t \right)$ в уравнении (13) может быть как положительным, так и отрицательным.

Интегрирование (13) приводит к уравнению Орнштейна:

Будем предполагать далее, что случайная функция $\xi \left( t \right)$ в уравнениях (13), (14) удовлетворяет соотношениям Здесь угловые скобки $\left\langle {} \right\rangle $ обозначают усреднение по ансамблю; $\delta \left( t \right)$ – дельта-функция Дирака.

Первое соотношение (15) показывает, что средняя случайная сила не оказывает влияния на динамику ансамбля. Это соотношение уже обсуждалось ранее (уравнение (9)). Второе соотношение (15) означает отсутствие корреляции между случайной силой и случайным начальным условием. Третье соотношение (15) соответствует белому шуму Гаусса. Это уравнение указывает, что $\delta $ – коррелированность случайной силы $\xi \left( t \right)$ во времени.

Рассмотрим первое следствие динамического уравнения Орнштейна. Усреднение уравнения (14) по ансамблю приводит к равенству

Выполним в уравнении (16) предельный переход при $t \to \infty $. Тогда с учетом (15) найдем, что Здесь ${{\left\langle w \right\rangle }_{{{\text{eq}}}}}$ соответствует равновесному значению средней по ансамблю скорости частиц. Равенство (17) показывает, что на уровне конвекции $\left\langle {{\text{g}}\hat {\theta }} \right\rangle = 0$, средняя скорость системы термиков, совершающих как восходящее, так и нисходящее движение, равна нулю. В рамках принятой динамической модели (13), (15) этот результат – крайне правдоподобный.

Рассмотрим второе следствие динамического уравнения Орнштейна. Умножим уравнение (14) на $2D_{E}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}\xi \left( t \right)$, тогда

Усреднение равенства (18) по ансамблю с учетом (15) и свойства дельта-функции Дирака приводит к равенству Из соотношения (19) следует, что Уравнение (20) устанавливает связь коэффициента диффузии Эйнштейна ${{D}_{E}}$ и усредненных по ансамблю случайных функций $\left\langle {\xi \left( t \right)w\left( t \right)} \right\rangle $. В известном смысле уравнение (20) – аналог выражения для коэффициента турбулентности в полуэмпирической теории Прандтля.

Рассмотрим третье следствие динамического уравнения Орнштейна. Умножим уравнение (13) на $2w\left( t \right){{{\text{e}}}^{{2{{\gamma }_{0}}t}}}$, тогда

Усреднение (21) по ансамблю с учетом (19) приводит к равенству Проинтегрируем (22) по времени и тождественно преобразуем полученное соотношение, так что Выполним в уравнении (23) предельный переход при $t \to \infty $. Тогда с учетом (12) найдем, что Здесь ${{\left\langle {{{w}^{2}}} \right\rangle }_{{{\text{eq}}}}}$ соответствует равновесному значению среднего по ансамблю от квадрата скорости частиц. Таким образом, согласно (24), в стохастической системе (13), (15) параметр ${{W}^{2}}$ формирует равновесное значение среднего ${{\left\langle {{{w}^{2}}} \right\rangle }_{{{\text{eq}}}}}$ от квадрата вертикальной скорости элементов ансамбля.

Априорное задание величины ${{W}^{2}}$ следует выполнять так, чтобы равенство (24) могло обеспечить выполнение общих принципов неравновесной статистической механики для стохастического ансамбля.

Рассмотрим ансамбль сферических броуновских частиц, расположенных в термостате $T$. В этом случае следует считать, что ${{W}^{2}} = {{{{k}_{{\text{B}}}}T} \mathord{\left/ {\vphantom {{{{k}_{{\text{B}}}}T} m}} \right. \kern-0em} m}$ (${{k}_{{\text{B}}}}~$ – постоянная Больцмана). При этом соотношение (24) реализует закон равномерного распределения энергии по степеням свободы. Этот способ задания величины ${{W}^{2}}$ использован для описания классического ансамбля броуновских частиц [5, 27].

Рассмотрим теперь не “термодинамические” ансамбли сферических элементов, для которых известны либо временные, либо пространственные средние. Для таких систем определены выражения $\overline {{{w}^{2}}} $, в которых знак черты сверху соответствует усреднению по времени или пространственному усреднению Рейнольдса. Положим ${{W}^{2}} = \overline {{{w}^{2}}} $ в соотношении (24), тогда

Равенство (25) следует интерпретировать как реализацию временнóй или пространственной формы гипотезы эргодичности. Этот подход использован для описания обобщенного ансамбля “медленных” конвективных термиков [4].

Преобразуем уравнения (13), (15) с учетом гипотезы эргодичности (25) и будем рассматривать полученное уравнение только в области $w > 0$, тогда

Полученное уравнение (26) будем называть далее уравнением Ланжевена для системы “медленных” конвективных термиков.

УРАВНЕНИЕ ФОККЕРА–ПЛАНКА И ФУНКЦИЯ ГРИНА АНСАМБЛЯ “МЕДЛЕННЫХ” КОНВЕКТИВНЫХ ТЕРМИКОВ В ОКРЕСТНОСТИ УРОВНЯ КОНВЕКЦИИ

Так как (26) включает в себя случайную силу $D_{E}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}\xi \left( t \right)$, то величина вертикальной скорости $w$ в уравнении Ланжевена – также случайная величина. Это обстоятельство приводит к необходимости вероятностного описания. Пусть ${{f}_{w}} = {{f}_{w}}\left( {w,t} \right)$ – функция плотности вероятности распределения конвективных термиков по скоростям, заданная на фазовом пространстве ${{\Omega }}_{w}^{ + } = \left\{ {w{\kern 1pt} :0 \leqslant w < \infty } \right\}$. Тогда

Второе уравнение (27) будем называть далее условием нормировки.

В монографиях [5, 27] показано, что для ансамблей частиц, удовлетворяющих уравнениям Ланжевена, плотности вероятности ${{f}_{w}}\left( {w,t} \right)$ удовлетворяет ассоциированным уравнениям Фоккера–Планка. В случае уравнения Ланжевена (26) ассоциированное уравнение Фоккера–Планка имеет следующий вид:

Решение кинетического уравнения Фоккера–Планка (28) предполагает задание начальных и краевых условий. В качестве начального условия можно использовать произвольную положительную функцию $f_{w}^{0} = f_{w}^{0}\left( w \right)$ такую, что В качестве краевых условий уравнения (28) примем следующие соотношения: Первая строка системы (30) означает, что функция ${{f}_{w}}\left( {w,t} \right)$ достаточно быстро убывает при $w \to \infty $. Вторая строка (30) соответствует предположению о существовании локального максимума функции ${{f}_{w}}\left( {w,t} \right)$ на границе фазового пространства скоростей при $w \to 0$. Краевые условия в формуле (30) могут рассматриваться как условие отсутствия полного диффузионного потока на границах фазового пространства.

Интегрирование уравнения Фоккера–Планка (28) по пространству скоростей $\Omega _{w}^{ + }$ с учетом краевых условий (30) приводит к равенству

Следовательно, краевые условия (30) согласованы с условием нормировки (27).

Решение задачи (28), (30) можно выполнить с помощью метода Грина. Пусть ${{w}_{0}}$ – произвольная точка пространства Максвелла: $0 \leqslant w < \infty $. Функцией Грина задачи (28), (30) будем называть фундаментальное решение $G\left( {w,{{w}_{0}},t} \right)$, соответствующее начальному условию в форме дельта-функции Дирака: $f_{w}^{0}\left( w \right) = \delta \left( {w - {{w}_{0}}} \right)$. Следуя [27], можно показать, что функция Грина задачи (28), (30) имеет следующий вид:

Поэтому в соответствии с методом Грина справедливо равенство Соотношение (33) представляет собой общую аналитическую форму нестационарного решения (28), (30), соответствующую произвольному начальному условию $f_{w}^{0}$.

ОБОБЩЕННОЕ РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА ДЛЯ АНСАМБЛЯ КОНВЕКТИВНЫХ ТЕРМИКОВ. СОПОСТАВЛЕНИЕ С ЭКСПЕРИМЕНТАЛЬНЫМИ ДАННЫМИ

Кинетическая форма уравнения Фоккера–Планка (28), (30) допускает стационарное решение в форме обобщенного одномерного распределения Максвелла

Классическое одномерное распределения Максвелла по скоростям для броуновских частиц или молекул идеального газа следует из распределения (34), если считать, что средний параметр $\overline {{{w}^{2}}} $ пропорционален температуре среды.

Заметим, что из соотношения (32) следует, что

Таким образом, согласно (35), распределение Максвелла (34) также является пределом функции Грина (32) при $t \to \infty $. Справедливо и более общее утверждение. Можно показать, что стационарное решение Максвелла (34) является пределом при $t \to \infty $ нестационарного решения (28), (30) при любых начальных условиях [4].

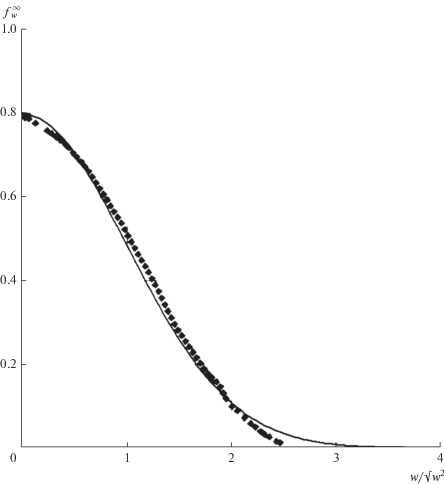
Сопоставим обобщенное распределение Максвелла (34) с известными данными численных и натурных экспериментов. Численное моделирование турбулентной конвекции на основе уравнений Буссинеска выполнено в работе [14]. В этом исследовании, в частности, представлены численные эксперименты, позволяющие построить функцию плотности вероятности по нормированным скоростям ${w \mathord{\left/ {\vphantom {w {{{w}_{D}}}}} \right. \kern-0em} {{{w}_{D}}}}$ для ансамбля конвективных термиков на уровне ${z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h} = 0.5$. Результаты этих экспериментов удобно представить в зависимости от нормированной переменной ${w \mathord{\left/ {\vphantom {w {\sqrt {\overline {{{w}^{2}}} } }}} \right. \kern-0em} {\sqrt {\overline {{{w}^{2}}} } }}$ $\overline {({{w}^{2}}} = 0.45w_{D}^{2}$ в соответствии с (3)). Сопоставление обобщенного распределения Максвелла (34) с результатами [14] представлено на рис. 5.

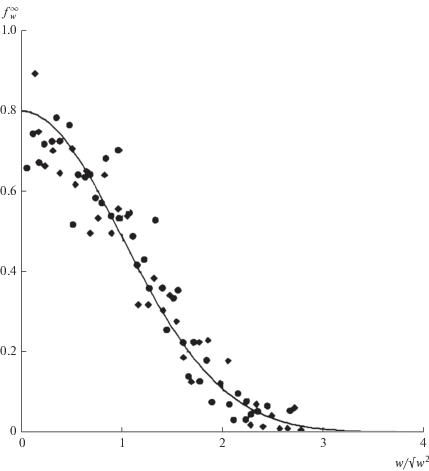
Функции плотности вероятности по нормированным вертикальным скоростям ${w \mathord{\left/ {\vphantom {w {{{w}_{D}}}}} \right. \kern-0em} {{{w}_{D}}}}$ в системе термиков на уровнях ${z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h} = 0.42$ и ${z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h} = 0.55$ построены в [6]. Результаты этих экспериментов удобно представить в зависимости от нормированной переменной ${w \mathord{\left/ {\vphantom {w {\sqrt {\overline {{{w}^{2}}} } }}} \right. \kern-0em} {\sqrt {\overline {{{w}^{2}}} } }}$ ($\overline {{{w}^{2}}} = 0.45w_{D}^{2}$ в соответствии с (3)). Сопоставление обобщенного распределения Максвелла (34) с результатами баллонных измерений в [6] представлено на рис. 6.

Результаты численных и натурных экспериментов, представленные на рис. 5 и 6, убедительно демонстрируют существование обобщенного распределения Максвелла в стохастической модели системы “медленных” конвективных термиков.

ЗАКЛЮЧЕНИЕ

Рассмотрена математическая модель стохастической системы “медленных” сферических конвективных термиков фиксированного радиуса в тонком слое, включающем в себя уровень конвекции. Показано, что предложенная модель системы “медленных” конвективных термиков подобна классической модели ансамбля броуновских частиц, расположенных в термостате. Такая аналогия позволяет использовать для системы “медленных” конвективных термиков уравнение Ланжевена и сопутствующее уравнение Фоккера–Планка в формах, известных в физической кинетике для ансамбля броуновских частиц.

В рамках предложенной модели установлено, что на уровне конвекции средняя скорость системы “медленных” конвективных термиков равна нулю. Показано, что для системы термиков уровня конвекции существует кинетический аналог температуры, соответствующий второму моменту вертикальной скорости. Установлено, что сопутствующее уравнение Фоккера–Планка имеет стационарное решение, которое следует интерпретировать как обобщенное распределение Максвелла. Численные и натурные эксперименты на уровне конвекции убедительно демонстрируют соответствие обобщенного распределения Максвелла результатам вычислений и данным атмосферных измерений.

Это соответствие не только обеспечивает корректность модели системы “медленных” конвективных термиков, но и открывает возможность широкого использования методов физической кинетики для описания турбулентной конвекции.