Журнал вычислительной математики и математической физики, 2019, T. 59, № 3, стр. 429-440
Об одном методе вероятностно-статистического анализа плотности низкочастотной турбулентной плазмы
1 Новосибирский гос. технический университет
1630073 Новосибирск, пр-т Карла Маркса, Россия
2 Новосибирский гос. университет
630090 Новосибирск, ул. Пирогова, 2, Россия
* E-mail: nicky1978@mail.ru
Поступила в редакцию 16.10.2017
Аннотация
В рамках феноменологии потока памяти построена модель нестационарного шума, которая применена для стохастического моделирования временного ряда значений плотности плазмы термоядерной установки. Приведен статистический тест, который на определенном уровне значимости позволяет проверять адекватность предложенной модели по ее соответствию экспериментальным данным. Библ. 13. Фиг. 6. Табл. 1.
1. ВВЕДЕНИЕ
В настоящей работе оценивается адекватность модели нестационарного шума, полученной в работе [1]. Оценка адекватности выполняется на выборке значений плотности низкочастотной турбулентной плазмы, измеренной в периферийной области удержания плазмы термоядерной установки Токамак Т-10 (выборка предоставлена В.П. Будаевым), при этом мера адекватности модели определяется реально достигнутым уровнем значимости полученного в данной работе статистического критерия. Дадим краткое описание используемой модели из [1]. Нестационарный шум реализуется случайной последовательностью с конечными вторыми моментами и является скачками случайного блуждания с сильно зависимыми приращениями. Дисперсия этого случайного блуждания имеет степенное поведение по времени, при этом показатель степенного изменения может находиться в диапазоне (0, 4), т.е. модель реализует суб- и супердиффузионный режим переноса.
Отметим, что в работе [2] к аналогичным выборочным данным применяется мультифрактальный подход, при этом в рамках логпуассоновской модели получен закон изменения дисперсии для процесса блуждания частиц, причем этот закон имеет степенной характер с параметром степенного изменения в диапазоне (1.2, 1.8), что говорит о супердиффузионном режиме переноса. В настоящей работе получен супердиффузионный режим переноса для модели блуждания, построенной по временному ряду значений плотности плазмы, при этом параметр степенного изменения дисперсии также находится в диапазоне (1.2, 1.8).
Заметим, что аномальное поведение дисперсии процесса блуждания частиц, полученное в [2], послужило мотивацией к попытке установить соответствие между временным рядом плотности плазмы и моделью нестационарного шума из [1], которая также порождает аномальные режимы переноса. Кроме того, параметры нелокальности, возникающие в модели нестационарного шума, имеют вполне конкретную физическую интерпретацию (см. разд. 2). После оценки адекватности модель нестационарного шума можно использовать для стохастического моделирования временного ряда значений плотности плазмы.
Отметим книгу [3] (см. также [4]), в которой эмпирическая функция распределения стационарного отрезка временного ряда флуктуаций плотности плазмы и его первой разности аппроксимируются сдвиг-масштабной смесью нормальных распределений. В настоящей работе замечено существенное отличие эмпирической функции распределения стационарной составляющей временного ряда значений плотности плазмы от нормального распределения (см. замечание 2), но вопрос аппроксимации этой функции распределения смесью нормальных распределений не рассматривается.
2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И СТРУКТУРА РАБОТЫ
Пусть (${{X}_{i}}$; $i = 1,2,\; \ldots $) – последовательность стационарных (в широком смысле) случайных величин с конечным вторым моментом. В дальнейшем всюду будем предполагать степенной характер закона изменения дисперсии суммы ${{S}_{n}} = \sum\nolimits_{k = 1}^n \,{{X}_{k}}$ с показателем ${\text{H}} \in (0,1)$, а именно:
(1)
$\left\langle {S_{n}^{2}} \right\rangle - {{\left\langle {{{S}_{n}}} \right\rangle }^{2}} \sim {{\sigma }^{2}}{{n}^{{2{\text{H}}}}},\quad n \to \infty ,$Отметим, что последовательность (${{X}_{i}}$; $i = 1,2,\; \ldots $) может, в частности, являться суммой стационарных шумов, из которых выделяется шум с наибольшим параметром Хёрста (см. замечание 1).
Замечание 1. Пусть (${{X}_{i}}$; $i = 1,2,\; \ldots $) и (${{Y}_{i}}$; $i = 1,2, \ldots $) – две заданные на одном вероятностном пространстве последовательности с нулевым средним, каждая из которых является стационарным шумом. Обозначим
${{S}_{n}} = \sum\nolimits_{i = 1}^n \,{{X}_{i}}$, ${{Z}_{n}} = \sum\nolimits_{i = 1}^n \,{{Y}_{i}}$ и ${{W}_{n}} = \sum\nolimits_{i = 1}^n \,({{X}_{i}} + {{Y}_{i}})$, $n \geqslant 1$.
Пусть $\left\langle {S_{n}^{2}} \right\rangle \sim \sigma _{1}^{2}{{n}^{{2{{{\text{H}}}_{1}}}}}$ и $\left\langle {Z_{n}^{2}} \right\rangle \sim \sigma _{2}^{2}{{n}^{{2{{{\text{H}}}_{2}}}}}$, $n \to \infty $, при этом ${{{\text{H}}}_{1}} > {{{\text{H}}}_{2}}$. Тогда для последовательности (${{\xi }_{i}}$; $i = 1,2,\; \ldots $), где ${{\xi }_{i}} = {{X}_{i}} + {{Y}_{i}}$ имеет место соотношение $\left\langle {W_{n}^{2}} \right\rangle \sim \sigma _{1}^{2}{{n}^{{2{{{\text{H}}}_{1}}}}}$. Действительно, выполняется равенство $\left\langle {W_{n}^{2}} \right\rangle = \left\langle {S_{n}^{2}} \right\rangle + \left\langle {Z_{n}^{2}} \right\rangle + 2\left\langle {{{S}_{n}},{{Z}_{n}}} \right\rangle $, кроме того, в силу неравенства Коши–Буняковского имеем $\left| {\left\langle {{{S}_{n}},{{Z}_{n}}} \right\rangle } \right| \leqslant \sqrt {\left\langle {S_{n}^{2}} \right\rangle \left\langle {Z_{n}^{2}} \right\rangle } $, стало быть, $\left\langle {{{S}_{n}},{{Z}_{n}}} \right\rangle {\text{/}}{{n}^{{2{{{\text{H}}}_{1}}}}} \to 0$. Откуда выводим справедливость соотношения $\left\langle {W_{n}^{2}} \right\rangle \sim \sigma _{1}^{2}{{n}^{{2{{{\text{H}}}_{1}}}}}$ при $n \to \infty $.
Используя последовательность (${{X}_{i}}$; $i = 1,2,\; \ldots $), определим нестационарный шум в виде
(2)
${{\rho }_{k}} = \sum\limits_{i = 0}^{k - 1} \,{{X}_{{k - i}}}\Delta {{p}_{\nu }}(i),\quad k = 1,2,\; \ldots ,$Пусть $a = \left\langle {{{X}_{1}}} \right\rangle $. Заметим, что выполняется равенство
(3)
${{\rho }_{k}} = a{{k}^{\nu }} + \sum\limits_{i = 0}^{k - 1} \,({{X}_{{k - i}}} - a)\Delta {{p}_{\nu }}(i),\quad k = 1,2,\; \ldots .$Отметим, что стационарная структура $({{X}_{k}})$ ассоциируется нами (см. [1]) с нелокальностью воздействия внешних факторов, имеющих в определенном смысле неизменный по времени характер. Параметр ${\text{H}}$ в этом случае отражает персистентность или антиперсистентность этих внешних факторов. Правая часть (2) представляет собой поток памяти, порождаемый случайной последовательностью $({{X}_{k}})$ и управляемый степенной функцией ${{p}_{\nu }}$ (см. [6], [7]).
2.1. Структура работы
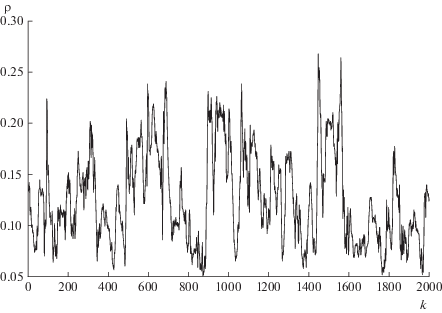
Итак, будем рассматривать экспериментально полученную выборку временного ряда значений плотности низкочастотной турбулентной плазмы (единица измерения времени 1 мкс): $\rho = ({{\rho }_{k}};\;k = 1,\; \ldots ,\;n)$. Сигнал плотности нормирован на величину средней плотности плазмы на краю центральной зоны в Токамаке Т-10, которая составляет величину $1 \times {{10}^{{13}}}$ частиц/см3 (это типичное значение в токамаках) (см. [2, с. 907]). Исследованный сигнал измерен в зоне, где наблюдается явление перемежаемости с признаками дальних корреляций. На фиг. 1 приведен график упомянутого временного ряда.
Фиг. 1.
График временного ряда значений плотности плазмы, $\rho = {{({{\rho }_{k}})}_{{k = 1,\; \ldots ,\;5 \times {{{10}}^{5}}}}}$.
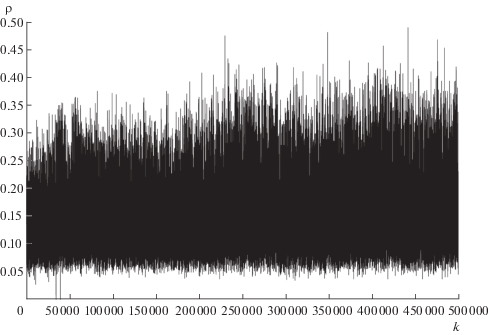
Заметим, что при визуальном анализе этого графика наблюдается слабо возрастающая тенденция представленного временного ряда, это позволяет заранее предположить наличие степенного тренда с параметром степенного изменения $0 \leqslant \nu \leqslant 0.5$ (см. соотношение (3)).
Проверим адекватность модели нестационарного шума (2) на соответствие этим выборочным данным. Для этого мы реализуем следующую схему.
Схема оценки адекватности модели. 1. Для каждого $\nu \in [0,1]$ решаем систему (2) (в данной работе значение $\nu $ выбирается из множества {$k{\text{/}}{{10}^{3}}$: $k = 0, \ldots ,\;5 \times {{10}^{2}}$}). В итоге получаем последовательность ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$ (зависящую от $\nu $).
2. Используя метод 1 (см. п. 3.1), с помощью последовательности ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$ находим оценки параметров степенного изменения дисперсии ${{S}_{n}} = \sum\nolimits_{k = 1}^n \,{{X}_{k}}$, а именно: оценку $H{\text{*}}(\nu )$ параметра Хёрста и оценку $\sigma {\text{*}}(\nu )$ коэффициента степенного изменения.
3. На выборке ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$ определяем меру соответствия ${{{\text{M}}}_{e}}(\nu )$ (где $e$ – наперед заданный уровень значимости) основной гипотезе о степенном поведении дисперсии ${{S}_{n}}$ и стационарности этой последовательности (см. п. 3.2, метод 2).
4. Выбираем $\nu {\text{*}}$, для которого ${{{\text{M}}}_{e}}(\nu )$ принимает максимальное значение.
5. Получаем пару значений $(\nu *,{\text{H*}})$ и значение меры соответствия ${{{\text{M}}}_{e}}(\nu {\kern 1pt} {\text{*}})$, при котором можно говорить об адекватности модели (2) по ее соответствию выборочным данным.
Далее, используя выборку (${{X}_{k}}$), соответствующую оценке $\nu {\text{*}}$, реализуем схему стохастического моделирования временного ряда $({{\rho }_{k}})$ (см. п. 3.3, метод 3 и п. 3.4).
В п. 3.5 приводятся численные результаты оценки адекватности модели нестационарного шума на выборке значений плотности плазмы, а также результаты стохастического моделирования.
В разд. 4 представлена модель блуждания, построенная по временному ряду значений плотности плазмы, для которой установлен супердиффузионный режим переноса.
Разд. 5 представляет собой заключение, в котором собраны основные результаты настоящей работы.
3. МЕТОДОЛОГИЯ
В дальнейшем будем обозначать через $a{\text{*}} = \tfrac{1}{n}\sum\nolimits_{i = 1}^n \,{{X}_{i}}$ оценку математического ожидания $a = \left\langle {{{X}_{1}}} \right\rangle $.
3.1. Вычисление параметра Хёрста
Приведем метод дисперсий (см., например, [8], [9]), который будет использоваться для поиска параметра Хёрста и коэффициента степенного изменения (см. соотношение (1)). Отметим, что для вычисления этих параметров в этом методе используются условия стационарности последовательности (${{X}_{k}}$) и степенного поведения дисперсии суммы ${{S}_{n}} = \sum\nolimits_{k = 1}^n \,{{X}_{k}}$.
Метод 1. 1. Центрируем выборку ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$, т.е. найдем $X_{k}^{ * } = {{X}_{k}} - a{\kern 1pt} *$, $k = 1,\; \ldots ,\;n$. В итоге получаем выборку ${{(X_{k}^{ * })}_{{k = 1,\; \ldots ,\;n}}}$.
2. Для $L = 0,\; \ldots ,\;m - 2$ ($m = [lo{{g}_{2}}(n)]$, где $[ \cdot ]$ – целая часть числа) масштабируем данные:
$X_{j}^{{(L)}} = \sum\nolimits_{i = (j - 1){{2}^{L}} + 1}^{j{{2}^{L}}} \,X_{i}^{ * }$, $j = 1,\; \ldots ,\;{{2}^{{m - L}}}$.
3. Находим стандартное отклонение ${{\bar {V}}_{L}}$ масштабированных данных:
4. Составляем модель линейной регрессии $ln{{\bar {V}}_{L}} = HLln2 + b + {{\varepsilon }_{L}}$, $L = 0,\; \ldots ,\;m - 2$, где ${{\varepsilon }_{L}}$ – ошибки модели.
5. Методом наименьших квадратов находим оценку ${\text{H*}}$ параметра Хёрста ${\text{H}}$ и свободный коэффициент $b$. Используя $b$, определяем оценку $\sigma * = expb$ параметра $\sigma $.
3.2. Проверка стационарности
Центрированную гауссовскую последовательность $f = ({{f}_{k}};\;k = 1,\; \ldots ,\;n)$ будем называть фрактальным шумом с параметром ${\text{H}} \in (0,1)$ (см., например, [8]), если ее ковариационная матрица $R = {{({{r}_{{ij}}})}_{{i,j = 1,\; \ldots ,\;n}}}$ имеет вид
(4)
${{r}_{{ij}}} = \frac{{{{\delta }^{2}}}}{2}\left( {{{{\left| {i - j + 1} \right|}}^{{2{\text{H}}}}} + {{{\left| {i - j - 1} \right|}}^{{2{\text{H}}}}} - 2{{{\left| {i - j} \right|}}^{{2{\text{H}}}}}} \right),$Непосредственно из определения следует стационарность последовательности $({{f}_{k}})$ и закон изменения дисперсии суммы $\left\langle {{{{\left( {\sum\nolimits_{k = 1}^n \,{{f}_{k}}} \right)}}^{2}}} \right\rangle = {{\delta }^{2}}{{n}^{{2{\text{H}}}}}$ (в случае ${\text{H}} = 1{\text{/}}2$ получаем белый шум).
Для любой невырожденной ковариационной матрицы $R$ гауссовской последовательности найдется ортогональная матрица $C$ и диагональная $D$ такие, что ${{C}^{{\text{т }}}}RC = D$ (для поиска матриц $C$ и $D$ автор использовал функцию eig математического пакета Matlab). Пусть $B = \sqrt D $. Отметим, что произведение $({{B}^{{ - 1}}}{{C}^{{\text{т }}}}){{f}^{{\text{т }}}}$ дает вектор ${{\eta }^{{\text{т }}}}$ с независимыми стандартными нормальными компонентами (см., например, [10]).
В следующем методе 2 мы приведем критерий проверки того, что выборка ($X_{j}^{{(\tau )}}$, $j = 1,\; \ldots ,\;[n{\text{/}}\tau ]$), где $X_{j}^{{(\tau )}} = \sum\nolimits_{i = (j - 1)\tau + 1}^{j\tau } \,({{X}_{i}} - a*)$ и $1 \leqslant \tau < n$ (напомним, что $a* = \tfrac{1}{n}\sum\nolimits_{i = 1}^n \,{{X}_{i}}$) является фрактальным шумом. Отметим, что масштабный параметр $\tau $ необходимо выбирать так, чтобы $\tau \gg 1$ и $n{\text{/}}\tau \gg 1$. Условие $n{\text{/}}\tau \gg 1$ обеспечивает корректное применение критерия Пирсона для проверки нормальности (см. ниже п. 6). Условие $\tau \gg 1$ должно обеспечить близость распределения случайной величины $\sum\nolimits_{i = 1}^\tau \,{{X}_{i}} - \tau a$ к нормальному закону, а также близость $\left\langle {{{{\left( {\sum\nolimits_{i = 1}^\tau \,{{X}_{i}} - \tau a} \right)}}^{2}}} \right\rangle $ к ${{\sigma }^{2}}{{\tau }^{{2{\text{H}}}}}$ (см. соотношение (1)).
Метод 2. 1. Методом дисперсий (см. метод 1) находим оценки $\sigma {\text{*}}$ и ${\text{H*}}$ параметров $\sigma $ и ${\text{H}}$ соответственно.
2. Центрируем с помощью $a{\text{*}}$ выборку (${{X}_{k}}$; $k = 1,\; \ldots ,\;n$). Получаем $X_{k}^{ * } = {{X}_{k}} - a{\text{*}}$, $k = 1,\; \ldots ,\;n$.
3. Формируем выборку
4. Определяем ковариационную матрицу $R$ (см. соотношение 4), где $\delta = \sigma {\text{*}}{{\tau }^{{{\text{H*}}}}}$ (учитываем степенное поведение дисперсии блока длины $\tau $).
5. Используя матрицу $R$, находим матрицы $B$ и $C$. Умножив ${{B}^{{ - 1}}}{{C}^{{\text{т }}}}$ на вектор ${{(X_{j}^{{(\tau )}};\;j = 1, \ldots ,\;\left[ {n{\text{/}}\tau } \right])}^{{\text{т }}}}$, получаем выборку (${{\eta }_{i}}$; $i = 1,\; \ldots ,\;[n{\text{/}}\tau ]$).
6. На реализации выборки (${{\eta }_{i}}$; $i = 1,\; \ldots ,\;[n{\text{/}}\tau ]$) найдем реально достигнутый уровень значимости критерия Пирсона при основной гипотезе о стандартной нормальности выборки.
6.1. Пусть $m = [n{\text{/}}\tau ]$ (здесь $[ \cdot ]$ – целая часть числа). Разобьем числовую ось на $k = [lo{{g}_{2}}m] + 1$ непересекающихся интервалов ${{\Delta }_{1}},{{\Delta }_{2}},\; \ldots ,{{\Delta }_{k}}$ так, чтобы $m{{\Phi }_{{0,1}}}({{\Delta }_{1}}) = m{{\Phi }_{{0,1}}}({{\Delta }_{2}}) = \ldots = m{{\Phi }_{{0,1}}}({{\Delta }_{k}}) = m{\text{/}}k$, где ${{\Phi }_{{0,1}}}$ – функция распределения стандартного нормального закона. Определяем на выборке (${{\eta }_{i}}$; $i = 1,\; \ldots ,\;[n{\text{/}}\tau ]$) значение статистики Пирсона $\Pi = \sum\nolimits_{i = 1}^k {{\left( {\tfrac{{{{\nu }_{i}} - m{\text{/}}k}}{{m{\text{/}}k}}} \right)}^{2}}$, где ${{\nu }_{i}}$ – число попаданий элементов выборки (${{\eta }_{i}}$) в ${{\Delta }_{i}}$, $i = 1,\; \ldots ,\;k$.
6.2. Имея в виду три оцениваемых параметра $a$, $\sigma $ и ${\text{H}}$, находим реально достигнутый уровень значимости критерия Пирсона, а именно: $\varepsilon (\tau ) = 1 - \chi _{{k - 4}}^{2}(\Pi )$, где $\chi _{{k - 4}}^{2}( \cdot )$ – известное распределение ${{\chi }^{2}}$ с $k - 4$ степенями свободы.
Заметим, что при дополнительных ограничениях на последовательность (${{X}_{k}}$), включая условие ${\text{H}} > 1{\text{/}}2$ и $\left\langle {X_{1}^{\alpha }} \right\rangle < + \infty $ при некотором $\alpha > 2$, из [11, теорема 3] следует “весьма грубая” оценка ${{\varepsilon }_{\tau }} = O\left( {{{\tau }^{{ - \frac{{\alpha - 2}}{{2(\alpha + 1)}}}}}} \right)$ нормальной аппроксимации распределения $\sum\nolimits_{i = 1}^\tau {{X}_{i}} - \tau a$.
При гипотезе о стационарности выборки ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$ и степенном поведении дисперсии (см. соотношение (1)) (в дальнейшем эту гипотезу будем называть основной) приведем метод вычисления меры соответствия этой гипотезе. Выберем целочисленный интервал $T = \left\{ {\tau \in {{\mathbb{Z}}_{ + }}{\text{:}}\;{{\tau }_{1}} \leqslant \tau \leqslant {{\tau }_{2}}} \right\}$ такой, что ${{\tau }_{1}} \gg 1$ и $n{\text{/}}{{\tau }_{2}} \gg 1$.
Если для значительного числа точек $\tau $ интервала $T$ (далее, мы формализуем, что это значит) удастся установить на некотором уровне значимости $e$, что выборка ($X_{j}^{{(\tau )}}$, $j = 1,\; \ldots ,\;[n{\text{/}}\tau ]$) является фрактальным шумом, то это и будет подтверждать основную гипотезу для выборки ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$.
Пусть $X$ – произвольное подмножество множества ${{\mathbb{Z}}_{ + }}$, через $l(X)$ будем обозначать число целых точек множества $X$. Для каждого значения $\tau $ из интервала $T$ найдем реально достигнутый уровень значимости: $\varepsilon (\tau )$ (см. п. 6.2). Заранее выберем некоторый уровень значимости $e$. Из интервала $T$ выделим подмножество $S = \left\{ {\tau \in T{\text{:}}\;\varepsilon (\tau ) > e} \right\}$. Определим отношение ${{{\text{M}}}_{e}} = l(S){\text{/}}l(T)$. В дальнейшем значение ${{{\text{M}}}_{e}}$ будем называть мерой соответствия основной гипотезе (о стационарности выборки ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$ и степенном поведении дисперсии). Отметим, что при уровне значимости $e$ принимается ${{{\text{M}}}_{e}} \times 100$% (от общего числа $l(T)$) гипотез о том, что последовательность ($X_{j}^{{(\tau )}}$, $j = 1,\; \ldots ,\;[n{\text{/}}\tau ]$) для каждого $\tau \in S$ является фрактальным шумом. Следовательно, достаточно большое значение ${{{\text{M}}}_{e}}$ (скажем, более 0.05) свидетельствует в пользу принятия основной гипотезы для исследуемого ряда наблюдений ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$.
В настоящей работе исследуется выборка объемом $n = 500{\kern 1pt} {\kern 1pt} 001$, при этом $\tau $ выбирается из промежутка $T = [100,\;1000]$. В этом случае $m = [n{\text{/}}\tau ] \geqslant 500$ и $m{{\Phi }_{{0,1}}}({{\Delta }_{1}}) \geqslant 51$ (см. п. 6.1). Значение $e$ будем выбирать равным 0.05. Отметим, во-первых, что увеличение ${{\tau }_{2}}$ (правой границы интервала $T$) может привести к значительной погрешности при вычислении $\varepsilon ({{\tau }_{2}})$, возникающей при замене распределения статистики Пирсона на распределение ${{\chi }^{2}}$, и, во-вторых, уменьшение ${{\tau }_{1}}$ (левой границы интервала $T$) может привести к значительному отклонению распределения $\sum\nolimits_{i = 1}^{{{\tau }_{1}}} \,{{X}_{i}} - {{\tau }_{1}}a$ от нормального закона, а также отклонению $\left\langle {{{{\left( {\sum\nolimits_{i = 1}^{{{\tau }_{1}}} \,{{X}_{i}} - {{\tau }_{1}}a} \right)}}^{2}}} \right\rangle $ от ${{\sigma }^{2}}\tau _{1}^{{2{\text{H}}}}$.
Заметим, что из-за отсутствия точных оценок нормальной аппроксимации распределения $\sum\nolimits_{i = 1}^\tau \,{{X}_{i}}$ и оценок скорости сходимости в теореме Пирсона не представляется возможным выбрать интервал ${{T}_{0}}$, для которого $mi{{n}_{{\tau \in {{T}_{0}}}}}\varepsilon (\tau )$ определит реально достигнутый уровень значимости при проверке вышеприведенной основной гипотезы. Поэтому рассматривается достаточно широкий интервал $T$, границы которого определяются априорными соображениями о “накоплении нормальности” и “корректности применения критерия Пирсона”. На этом интервале ${{{\text{M}}}_{e}}$ показывает относительное число всех превышений заранее заданного уровня значимости $e$ в множестве $\left\{ {\varepsilon (\tau ){\text{:}}\;\tau \in T} \right\}$, при этом величина ${{{\text{M}}}_{e}}$ (как это отмечено выше) определяет уровень соответствия основной гипотезе.
3.3. Моделирование стационарного шума
Пусть (${{Y}_{k}}$; $k = 1,\; \ldots ,\;n$) – некоторая центрированная стационарная последовательность случайных величин с ковариационной функцией $\gamma (l)$, $l = 0,\; \ldots ,\;n - 1$. Обозначим через $F$ распределение случайной величины ${{Y}_{1}}$. Будем моделировать стационарную последовательность с маргинальным распределением $F$ и ковариационной функцией $\gamma (l)$, $l = 0,\; \ldots ,\;n - 1$, методом обратной функции (см., например, [12], [13]).
Положим $Y_{k}^{ * } = {{F}^{{ - 1}}}({{\Phi }_{{0,1}}}(g(k)))$, $k = 1,\; \ldots ,\;n$, где ${{\Phi }_{{0,1}}}$ – функция распределения стандартного нормального закона, ($g(k)$; $k = 1,\; \ldots ,\;n$) – некоторая стационарная гауссовская последовательность с нулевым средним, единичной дисперсией и ковариационной функцией $\theta (l)$, $l = 0,\; \ldots ,\;n - 1$, ${{F}^{{ - 1}}}(t) = inf\left\{ {x{\text{:}}\;F(x) \geqslant t} \right\}$ – квантильное преобразование функции $F$. Отметим, что распределения случайных величин $Y_{1}^{ * }$ и ${{Y}_{1}}$ совпадают. Очевидно, что для ковариационной функции $\gamma {\text{*}}(l) = \left\langle {Y_{1}^{ * }Y_{{l + 1}}^{ * }} \right\rangle $, $l = 0,\; \ldots ,\;n - 1$, последовательности $(Y_{k}^{ * })$ выполняется соотношение
(5)
$\gamma {\text{*}}(l) = \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{F}^{{ - 1}}}} } ({{\Phi }_{{0,1}}}(u)){{F}^{{ - 1}}}({{\Phi }_{{0,1}}}(\text{v})){{f}_{\theta }}(u,\text{v})dud\text{v},$Если удается подобрать гауссовскую последовательность ($g(k)$; $k = 1,\; \ldots ,\;n$) такую, что $\gamma {\text{*}}(l) = \gamma (l)$ для всех $l = 0,\; \ldots ,\;n - 1$, то можно говорить о том, что $(Y_{k}^{ * })$ моделирует последовательность $({{Y}_{k}})$ (совпадают маргинальные распределения и ковариационные функции).
Отметим, что в данной работе нам неизвестно маргинальное распределение $F$ и ковариационная функция $\gamma $. Поэтому $F$ мы заменим на эмпирическую функцию распределения ${{F}_{n}}$, построенную по выборке (${{Y}_{k}}$; $k = 1,\; \ldots ,\;n$), а функцию $\gamma (l)$ заменим на ее оценку ${{\gamma }_{n}}(l) = \tfrac{1}{{n - l}}\sum\nolimits_{k = 1}^{n - l} \,{{Y}_{k}}{{Y}_{{k + l}}}$, где $l = 0,\; \ldots ,\;m$. Далее, рассмотрим соотношение (5) как уравнение относительно $\theta $, в котором в качестве левой части возьмем ${{\gamma }_{n}}(l)$. Решение этого уравнения обозначим через ${{\theta }_{n}}(l)$, $l = 0,\; \ldots ,\;m$. Отметим, что положительная определенность матрицы ${{({{a}_{{ij}}})}_{{i,j = 1,\; \ldots ,\;m + 1}}}$, где ${{a}_{{ij}}} = {{\theta }_{n}}\left( {\left| {i - j} \right|} \right)$, обеспечивает существование гауссовской последовательности $({{g}_{n}}(k))$ и, стало быть, возможность моделирования методом обратной функции.
Значение $m$ подбирается так, что выполняются следующие два условия: во-первых, $n - m \gg 1$ и, во-вторых, $m \gg 1$. Первое условие должно обеспечить близость оценки ${{\gamma }_{n}}(l)$ к истинному значению $\gamma (l)$. В итоге получаем последовательность $Y_{k}^{ * } = F_{n}^{{ - 1}}\left( {{{\Phi }_{{0,1}}}({{g}_{n}}(k))} \right)$, $k = 1,\; \ldots ,\;m + 1$. Второе условие обеспечивает достаточно большой объем выборки $(Y_{k}^{ * })$. Объединим вышесказанное в методе 3.
Пусть имеется стационарный ряд наблюдений ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$. Через $\beta * = \sqrt {\tfrac{1}{n}\sum\nolimits_{i = 1}^n \,{{{({{X}_{i}} - a*)}}^{2}}} $ обозначим оценку стандартного отклонения $\beta = \sqrt {\left\langle {X_{1}^{2}} \right\rangle - {{{\left\langle {{{X}_{1}}} \right\rangle }}^{2}}} $.
Метод 3. 1. Находим оценки $a{\text{*}}$ и $\beta {\text{*}}$ параметров $a$ и $\beta $ соответственно.
2. Центрируем и нормируем последовательность ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$ с помощью $a{\text{*}}$ и $\beta {\text{*}}$ соответственно, получаем последовательность ${{({{Y}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$.
3. Выбираем $m$, так что $n - m \gg 1$ и $m \gg 1$.
4. Находим ${{\gamma }_{n}}(l) = \tfrac{1}{{n - l}}\sum\nolimits_{k = 1}^{n - l} \,{{Y}_{k}}{{Y}_{{k + l}}}$, где $l = 0,\; \ldots ,\;m$.
5. Решаем уравнение (5) относительно $\theta $, получаем последовательность ${{\theta }_{n}}(l)$, $l = 0,\; \ldots ,\;m$.
6. Для матрицы $A = {{({{a}_{{ij}}})}_{{i,j = 1,\; \ldots ,\;m + 1}}}$, где ${{a}_{{ij}}} = {{\theta }_{n}}\left( {\left| {i - j} \right|} \right)$, находим ортогональную матрицу $C$ и диагональную $D$, такие что ${{C}^{{\text{т }}}}AC = D$. Вычисляем $B = \sqrt D $.
7. Моделируем гауссовский вектор $\eta = ({{\eta }_{1}},\; \ldots ,\;{{\eta }_{{m + 1}}})$ с независимыми стандартными нормальными компонентами.
8. Находим вектор ${{g}_{n}} = {{({{g}_{n}}(k))}_{{k = 1,\; \ldots ,\;m + 1}}}$ в виде $g_{n}^{{\text{т }}} = (CB){{\eta }^{T}}$.
9. По выборке ${{({{Y}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$ определяем квантильное преобразование $F_{n}^{{ - 1}}$ функции распределения ${{F}_{n}}$.
10. Находим последовательность $Y_{k}^{ * } = F_{n}^{{ - 1}}({{\Phi }_{{0,1}}}({{g}_{n}}(k)))$, $k = 1,\; \ldots ,\;m + 1$.
11. Моделируем последовательность ${{X}_{k}}$ в виде ${{X}_{k}} = \beta {\text{*}}Y_{k}^{ * } + a{\text{*}}$, $k = 1,\; \ldots ,\;m + 1$.
3.4. Моделирование нестационарного шума
Напомним, что мы имеем выборку ${{({{\rho }_{k}})}_{{k = 1,\; \ldots ,\;n}}}$. Формируем выборку ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$, зависящую от $\nu $ (см. п. 2.1). Используя схему проверки адекватности модели (см. п. 2.1), применяя методы 1, 2, находим оценку $\nu {\text{*}}$ параметра $\nu $. В итоге получаем выборку ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$, определяемую значением $\nu {\text{*}}$. Применяя метод 3, моделируем стационарную последовательность ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;m + 1}}}$, где $m$ такое, что $n - m \gg 1$ и $m \gg 1$. Далее, моделируем нестационарный шум $({{\rho }_{k}})$:
3.5. Численные результаты
Рассматривается выборка ${{({{\rho }_{k}})}_{{k = 1,\; \ldots ,\;n}}}$ объемом $n = 500{\kern 1pt} {\kern 1pt} 001$, состоящая из значений плотности плазмы, измеренных в последовательные моменты времени с шагом $1$ мкс.
В табл. 1 для части значений параметра $\nu $ приведены реально достигнутые уровни значимости $\varepsilon (\tau ,\nu )$ критерия Пирсона при $490 \leqslant \tau \leqslant 510$ (напомним, что весь исследуемый диапазон $T = [100,\;1000]$). Кроме того, в последних двух строках для каждого $\nu $ приведено значение меры соответствия ${{{\text{M}}}_{e}}$ (см. п. 3.2), обозначим его через ${{{\text{M}}}_{e}}(\nu )$, где $e = 0.05$ (реализована схема оценки адекватности модели (см. п. 2.1) с применением методов 1 и 2). Отметим, что, например, в случае $\nu = 0.058$ получены достаточно высокие реально достигнутые уровни значимости, минимальный из которых равен 0.005.
Таблица 1.
Реально достигнутый уровень значимости $\varepsilon (\tau ,\nu )$ критерия Пирсона
| $\tau $ | $\nu $ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.02 | 0.057 | 0.058 | 0.059 | 0.06 | 0.061 | 0.062 | 0.09 | 0.1 | |
| 490 | 0.000 | 0.000 | 0.129 | 0.118 | 0.306 | 0.233 | 0.110 | 0.043 | 0.014 | 0.005 |
| 491 | 0.000 | 0.000 | 0.025 | 0.026 | 0.040 | 0.001 | 0.021 | 0.150 | 0.001 | 0.000 |
| 492 | 0.000 | 0.000 | 0.254 | 0.138 | 0.048 | 0.270 | 0.227 | 0.036 | 0.003 | 0.000 |
| 493 | 0.000 | 0.000 | 0.042 | 0.035 | 0.011 | 0.034 | 0.053 | 0.023 | 0.000 | 0.000 |
| 494 | 0.000 | 0.010 | 0.182 | 0.298 | 0.262 | 0.200 | 0.196 | 0.196 | 0.134 | 0.004 |
| 495 | 0.000 | 0.063 | 0.035 | 0.037 | 0.042 | 0.027 | 0.034 | 0.042 | 0.110 | 0.031 |
| 496 | 0.000 | 0.000 | 0.124 | 0.213 | 0.167 | 0.034 | 0.123 | 0.335 | 0.017 | 0.000 |
| 497 | 0.000 | 0.000 | 0.295 | 0.293 | 0.210 | 0.300 | 0.341 | 0.200 | 0.022 | 0.003 |
| 498 | 0.000 | 0.000 | 0.059 | 0.045 | 0.045 | 0.054 | 0.060 | 0.209 | 0.017 | 0.002 |
| 499 | 0.000 | 0.000 | 0.103 | 0.103 | 0.117 | 0.069 | 0.046 | 0.063 | 0.000 | 0.000 |
| 500 | 0.000 | 0.000 | 0.076 | 0.107 | 0.108 | 0.111 | 0.008 | 0.072 | 0.000 | 0.000 |
| 501 | 0.000 | 0.000 | 0.200 | 0.360 | 0.492 | 0.271 | 0.449 | 0.336 | 0.002 | 0.000 |
| 502 | 0.000 | 0.000 | 0.413 | 0.533 | 0.778 | 0.336 | 0.449 | 0.590 | 0.030 | 0.001 |
| 503 | 0.000 | 0.000 | 0.047 | 0.092 | 0.051 | 0.019 | 0.008 | 0.021 | 0.000 | 0.000 |
| 504 | 0.000 | 0.000 | 0.014 | 0.013 | 0.002 | 0.005 | 0.005 | 0.011 | 0.001 | 0.000 |
| 505 | 0.000 | 0.000 | 0.003 | 0.005 | 0.007 | 0.029 | 0.012 | 0.029 | 0.000 | 0.000 |
| 506 | 0.000 | 0.000 | 0.090 | 0.047 | 0.105 | 0.059 | 0.005 | 0.040 | 0.003 | 0.000 |
| 507 | 0.000 | 0.000 | 0.408 | 0.521 | 0.461 | 0.277 | 0.228 | 0.491 | 0.003 | 0.000 |
| 508 | 0.000 | 0.000 | 0.002 | 0.007 | 0.014 | 0.011 | 0.018 | 0.038 | 0.000 | 0.000 |
| 509 | 0.000 | 0.000 | 0.032 | 0.006 | 0.023 | 0.048 | 0.023 | 0.049 | 0.000 | 0.000 |
| 510 | 0.000 | 0.000 | 0.279 | 0.101 | 0.035 | 0.008 | 0.092 | 0.004 | 0.038 | 0.000 |
| ${{M}_{{0.05}}}$ | 0.029 | 0.081 | 0.292 | 0.274 | 0.271 | 0.269 | 0.274 | 0.271 | 0.139 | 0.119 |
Обозначим точку максимума функции $y = {{{\text{M}}}_{e}}(\nu )$ через $\nu {\text{*}}(e)$. Фиг. 2 иллюстрирует тот факт, что функция $y = {{{\text{M}}}_{e}}(\nu )$, для уровня $e$, равного 0.05, достигает максимального значения 0.292 при $\nu = 0.057$. Поэтому получаем, что $\nu {\text{*}}(0.05) = 0.057$, при этом ${\text{H*}} = 0.727$, $a* = 0.084$, $\beta * = 0.050$ и $\sigma * = 0.068$. Заметим, что усредненный уровень значимости $\bar {\varepsilon }(\nu {\text{*}}(0.05)) = \tfrac{1}{{901}}\sum\nolimits_{\tau = 100}^{1000} \,\varepsilon (\tau ,\nu {\text{*}}(0.05))$ равен 0.072.
Отметим, что при $0.01 \leqslant e \leqslant 0.1$ значение точки максимума $\nu {\text{*}}(e)$ находится в интервале $[0.057,\;0.066]$, т.е. получаем диапазон возможных значений параметра $\nu $.
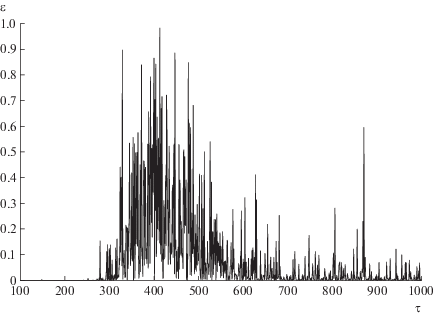
Приведем график $\varepsilon = \varepsilon (\tau ,\nu {\text{*}}(0.05))$, $\tau \in T$, где $T = [100,\;1000]$ (см. фиг. 3). Этот график иллюстрирует, что на интервале $279 \leqslant \tau \leqslant 1000$ наблюдаются достаточно большие реально достигнутые уровни значимости.
Фиг. 3.
График реально достигнутых уровней значимости, $\varepsilon = \varepsilon (\tau ,0.057)$, $\tau \in [100,\;1000]$.
Замечание 2. Пусть $X = {{({{X}_{k}})}_{{k = 1,\; \ldots ,\;n}}}$ – выборка, определяемая значением $\nu = \nu {\text{*}}(0.05)$. Обозначим через ${{F}_{n}}$ эмпирическую функцию распределения этой выборки, кроме того, пусть ${{\Phi }_{{a*,\beta *}}}$ – функция распределения нормального закона с параметрами
Применим полученные методы к моделированию временного ряда значений плотности плазмы. Выбрав $m = 2000$, будем моделировать, используя метод 3, последовательность ${{({{X}_{k}})}_{{k = 1,\; \ldots ,\;m + 1}}}$. Далее, получаем последовательность ${{({{\rho }_{k}})}_{{k = 1,\; \ldots ,\;m + 1}}}$ (см. соотношение (6)). Приведем графики реализации такой последовательности (см. фиг. 4 и 5).
Фиг. 4.
График смоделированного временного ряда, $\rho = {{({{\rho }_{k}})}_{{k = 1,\; \ldots ,\;2001}}}$.
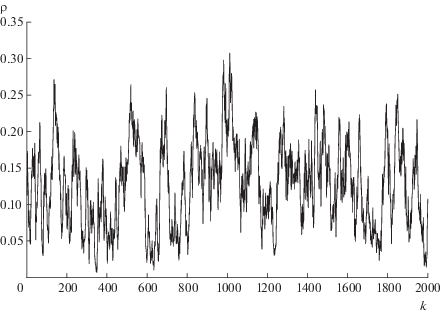
Фиг. 5.
График смоделированного временного ряда, $\rho = {{({{\rho }_{k}})}_{{k = 1,\; \ldots ,\;2001}}}$.
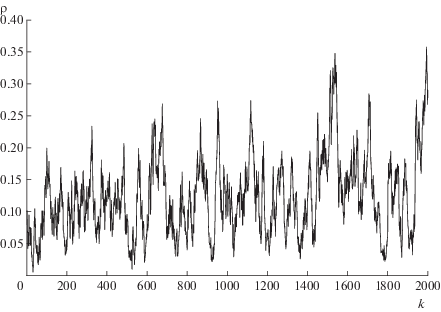
Приведем визуальный анализ графиков, представленных на фиг. 4 и 5 (напомним, что соответствующие временные ряды смоделированы, используя весь временной ряд плотности плазмы). График на фиг. 5 (в отличие от графика на фиг. 4) иллюстрирует слабую нестационарность, характерную для графика всего реального временного ряда (см. фиг. 1) (здесь также наблюдается слабо возрастающая тенденция). График на фиг. 4 подобен графику реального временного ряда плотности плазмы, состоящего из первых $2000$ наблюдений (см. фиг. 6). Подводя итог, c учетом меры соответствия ${{M}_{{0.05}}}(0.057) = 0.292$ можно говорить о нестационарном режиме поведения реального временного ряда плотности плазмы (при этом не всегда возможно выделить возрастающую тенденцию в течение первых 2 мс).
Заметим, что ключевым моментом в методе 3 является, во-первых, численное решение уравнения (5) относительно $\theta $ и получение последовательности ${{(\theta (k))}_{{k = 0,\; \ldots ,\;m}}}$, а во-вторых, проверка положительной определенности матрицы $A = {{({{a}_{{ij}}})}_{{i,j = 1,\; \ldots ,\;m + 1}}}$, где ${{a}_{{ij}}} = \theta \left( {\left| {i - j} \right|} \right)$. Отметим, что собственные значения матрицы $A$ изменяются в диапазоне (0.01, 28.92).
4. МОДЕЛЬ БЛУЖДАНИЯ
Построим блуждание ${{Z}_{n}} = \sum\nolimits_{k = 1}^n \,{{\rho }_{k}}$, $n \geqslant 0$, где ${{\rho }_{k}}$ определено в (2). При дополнительных ограничениях на $({{X}_{i}})$ (см. [1, условие (H)]) выполняется соотношение
(7)
$\left\langle {Z_{n}^{2}} \right\rangle - {{\left\langle {{{Z}_{n}}} \right\rangle }^{2}} \sim {{\sigma }^{2}}s_{{\nu ,{\text{H}}}}^{2}{{n}^{\alpha }},\quad n \to \infty ,$Выше получено, что $\nu * = 0.057$ и ${\text{H*}} = 0.727$, следовательно, оценка $\alpha {\text{*}}$ показателя $\alpha $ для выборки значений плотности плазмы равна 1.569, что означает супердиффузионный режим переноса.
5. ЗАКЛЮЧЕНИЕ
В работе представлена модель нестационарного шума и проверена адекватность этой модели на ее соответствие экспериментальным данным, являющимся временным рядом значений плотности плазмы термоядерной установки. Получены достаточно высокие реально достигнутые уровни значимости (см. табл. 1), по совокупности которых можно говорить об адекватности предложенной модели. Приведен метод моделирования временного ряда значений плотности плазмы, основанный на известном методе обратной функции моделирования негауссовских процессов.
Отметим также, что получен степенной закон изменения по времени дисперсии процесса частичных сумм временного ряда значений плотности плазмы с показателем $\alpha * = 1.569$.
Автор благодарен В.А. Селезневу и А.П. Ковалевскому за плодотворное обсуждение тематики работы.
Автор крайне признателен В.П. Будаеву за предоставленную выборку.
Список литературы
Аркашов Н.С., Селезнев В.А. О формировании соотношения нелокальностей в модели аномальной диффузии // Теор. и матем. физ. 2017. Т. 193. № 1. С. 115–132.
Будаев В.П., Савин С.П., Зеленый Л.М. Наблюдения перемежаемости и обобщенного самоподобия в турбулентных пограничных слоях лабораторной магнитосферной плазмы: на пути к определению количественных характеристик переноса // Успехи физ. наук. 2011. Т. 189. № 9. С. 905–952.
Королев В.Ю. Вероятностно-статистический анализ хаотических процессов с помощью смешанных гауссовских моделей. Декомпозиция волатильности финансовых индексов и турбулентной плазмы. М.: ИПИ РАН, 2007.
Батанов Г.М., Горшенин А.К., Королев В.Ю., Малахов Д.В., Скворцова Н.Н. Эволюция вероятностных характеристик низкочастотной турбулентной плазмы // Матем. моделирование. 2011. Т. 23. № 5. С. 35–55.
Mandelbrot B., Van Ness J. Fractional Brownian motions, fractional noise and applications // SIAM Review. 1968. V. 10. P. 422–437.
Олемской А.И., Флат А.Я. Использование концепции фрактала в физике конденсированной среды // Успехи физ. наук. 1993. Т. 163. 12. С. 1–50.
Нигматуллин Р.Р. Дробный интеграл и его физическая интерпретация // Теор. и матем. физ. 1992. Т. 90. № 3. С. 354–368.
Cannon M.J., Percival D.B., Caccia D.C., Raymond G.M., Bassingthwaighte J.B. Evaluating scaled window variance methods for estimating the Hurst coefficient of time series // Physica A. 1997. V. 241. P. 606–626.
Кроновер Р. M. Фракталы и хаос в динамических системах. М.: Постмаркет, 2000.
Ширяев А.Н. Вероятность. М.: Наука, 1980.
Аркашов Н.С., Борисов И.С. Гауссовская аппроксимация процессов частных сумм скользящих средних // Сиб. матем. журнал. 2004. Т. 45. № 6. С. 1221–1255.
Пиранашвили З.А. Некоторые вопросы статистико-вероятностного моделирования случайных процессов // Вопросы исследования операций. Тбилиси: Мецниереба, 1966.
Пригарин С.М. Модели случайных процессов и полей в методах Монте-Карло. Palmarium Academic Publishing, 2014.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики