Журнал вычислительной математики и математической физики, 2019, T. 59, № 3, стр. 441-464
KP1-Схема ускорения внутренних итераций для уравнения переноса в трехмерной геометрии, согласованная с нодальными схемами. Основные уравнения и численные результаты
А. М. Волощенко *
ИПматем.
125047 Москва, Миусская пл., 4, Россия
* E-mail: volosch@kiam.ru
Поступила в редакцию 17.01.2018
После доработки 10.05.2018
Аннотация
Для уравнения переноса в трехмерной $r,\vartheta ,z$ геометрии построена $K{{P}_{1}}$-схема ускорения сходимости внутренних итераций, согласованная с нодальными Linear Discontinues (LD) и Linear Best (LB)-схемами 3-го и 4-го порядка точности по пространственным переменным. Для решения ${{P}_{1}}$ системы для ускоряющих поправок предложен алгоритм, основанный на использовании циклического метода расщепления (МР) в сочетании с методом прогонки для решения вспомогательных систем двухточечных уравнений. Рассмотрена модификация алгоритма на случай трехмерной $x,y,z$ геометрии. Приведены численные примеры использования $K{{P}_{1}}$-схемы для решения характерных задач переноса излучения в трехмерной геометрии, в том числе задач с существенной ролью анизотропии рассеяния и при решении сильно-гетерогенных задач с преобладающей ролью рассеяния. Библ. 26. Фиг. 7. Табл. 8.
ВВЕДЕНИЕ
Алгоритм ускорения итераций по интегралу рассеяния является существенным элементом численной методики решения уравнения переноса, основанной на использовании метода дискретных ординат. Расчеты полей излучения в активной зоне и радиационной защите ядерно-технических установок в неодномерных геометриях требуют значительных затрат процессорного времени. Поэтому, с практической точки зрения, разработка эффективного алгоритма ускорения для 3D геометрий является актуальной задачей, позволяя сократить время расчета типичного варианта в 3–10 и более раз. В данной работе нами будет построена $K{{P}_{1}}$-схема ускорения внутренних итераций для уравнения переноса в 3D геометрии, согласованная с нодальными LD и LB-схемами 3 -го и 4-го порядка точности по пространственным переменным.
Предлагаемый алгоритм представляет собой реализацию $K{{P}_{1}}$-схемы (см. [1]) (известной также как DSA [2], [3] или ${{P}_{1}}SA$-схема [4]–[7]) ускорения внутренних итераций для практически важного случая LD и LB-схем в 3D $r,\vartheta ,z$ и $x,y,z$ геометриях, позволяющего обеспечить быструю сходимость разностного решения при сгущении пространственной сетки задачи. Согласованность построенной $K{{P}_{1}}$-схемы ускорения с разностной аппроксимацией уравнения переноса, как и в случае взвешенной алмазной (WDD)-схемы [2], обеспечивает ее устойчивость и слабую зависимость эффекта ускорения от выбора пространственной сетки. Более подробно необходимость использования согласованных схем ускорения для обеспечения устойчивости алгоритма ускорения рассмотрена в [2], [3]. Предложенный алгоритм реализован в 3D ${{S}_{n}}$ программе КАТРИН-2.5 из пакета программ CNCSN [8]. Он представляет собой развитие $K{{P}_{1}}$-схемы ускорения, согласованной со взвешенной алмазной (WDD)-схемой, предложенной ранее в работах [9], [10] и реализованной в 1D, 2D и 3D ${{S}_{n}}$ программах из пакета CNCSN, а также $K{{P}_{1}}$-схемы ускорения, согласованной со взвешенной WLD–WLB-схемой в 1D геометриях (см. [11], [12]).
Обзор предшествующих работ по $K{{P}_{1}}$-схеме ускорения и другим вариантам схем ускорения внутренних итераций имеется в [1], [3], [9]. $K{{P}_{1}}$-схема ускорения, согласованная с нодальной схемой на неструктурированной сетке в 3D $x,y,z$ геометрии, в которой линейные поправки используются для коррекции нулевого пространственного момента решения в ячейке, предложена в работе [13]. Построение $K{{P}_{1}}$-схемы ускорения мы проведем на примере уравнения переноса в $r,\vartheta ,z$ геометрии. Изменения в алгоритме для случая $x,y,z$ геометрии будут также указаны.
Последовательность изложения в данной работе следующая. В разделах 1 и 2 рассмотрено построение WLD–WLB-схемы и согласованной $K{{P}_{1}}$-схемы ускорения на примере уравнения переноса в $r,\vartheta ,z$ геометрии. Для решения ${{P}_{1}}$ системы для ускоряющих поправок предлагается использовать метод расщепления (МР) [1], [22]. Реализация МР применительно к случаю $K{{P}_{1}}$-схемы ускорения, согласованной с WLD–WLB-схемой в $r,\vartheta ,z$ геометрии, рассмотрена в отдельной статье [14], представляющей вторую часть данной работы. В разделе 3 указаны изменения, которые нужно внести в алгоритм ускорения для случая $x,y,z$ геометрии. В разделе 4 представлены численные результаты использования $K{{P}_{1}}$-схемы ускорения при решении типичных задач переноса излучения в трехмерной геометрии. В разделе 5 приведены численные результаты, позволяющие оценить скорость сходимости DD, адаптивной WDD (AWDD), LD и LB-схем в $x,y,z$ и $r,\vartheta ,z$ геометриях при сгущении пространственной сетки задачи.
Для нумерации формул используются 2 цифры: первая обозначает номер раздела, вторая – номер формулы в разделе.
1. WLB-WLD-СХЕМА 2-4-ГО ПОРЯДКА ТОЧНОСТИ ДЛЯ УРАВНЕНИЯ ПЕРЕНОСА В ТРЕХМЕРНОЙ $r,\vartheta ,z$ ГЕОМЕТРИИ
В $r,\vartheta ,z$ геометрии уравнение переноса нейтрального излучения (нейтроны, фотоны) имеет вид
(1.1)
$\eta \frac{{\partial \psi }}{{\partial \vartheta }} + \mu r\frac{{\partial \psi }}{{\partial z}} + \xi \frac{\partial }{{\partial r}}\left( {r\psi } \right) - \frac{\partial }{{\partial \varphi }}(\eta \psi ) + \sigma r\psi (r,\vartheta ,z;\mu ,\varphi ) = rS(r,\vartheta ,z;\mu ,\varphi ),$(1.2)
$\xi = ({\mathbf{\Omega }}{{{\mathbf{n}}}_{r}}) = \sqrt {1 - {{\mu }^{2}}} \cos \varphi ,\quad \eta = ({\mathbf{\Omega }}{{{\mathbf{n}}}_{\vartheta }}) = \sqrt {1 - {{\mu }^{2}}} \sin \varphi ,\quad \mu = ({\mathbf{\Omega }}{{{\mathbf{n}}}_{z}}) = \cos \theta ,$Для граничных направлений $\varphi = \pi $ и $\varphi = 2\pi $, используемых для организации расчета ячеек в $r,\vartheta ,z$ геометрии, уравнение (1.1) имеет вид
(1.3)
$\mu r\frac{{\partial \psi }}{{\partial z}} + \xi \left[ {\frac{\partial }{{\partial r}}\left( {r\psi } \right) - \psi } \right] + \sigma r\psi (r,z,\mu ,\varphi ) = rS(r,z,\mu ,\varphi ).$(1.4)
$\begin{gathered} \psi (r,\vartheta = {{\vartheta }_{0}},z,{\mathbf{\Omega }}) = {{F}_{0}}(r,z,{\mathbf{\Omega }}) + \int\limits_{({\mathbf{\Omega }}'{{{\mathbf{n}}}_{\vartheta }}) < 0} {{{R}_{0}}({\mathbf{\Omega }},{\mathbf{\Omega }}{\kern 1pt} ')\psi (r,\vartheta = {{\vartheta }_{0}},z,{\mathbf{\Omega }}{\kern 1pt} ')d{\mathbf{\Omega }}{\kern 1pt} '} ,\quad ({\mathbf{\Omega }}{{{\mathbf{n}}}_{\vartheta }}) > 0, \\ \psi (r,\vartheta = {{\vartheta }_{{{\text{end}}}}},z,{\mathbf{\Omega }}) = {{F}_{{{\text{end}}}}}(r,z,{\mathbf{\Omega }}) + \int\limits_{({\mathbf{\Omega }}'{{{\mathbf{n}}}_{\vartheta }}) > 0} {{{R}_{{{\text{end}}}}}({\mathbf{\Omega }},{\mathbf{\Omega }}{\kern 1pt} ')\psi (r,\vartheta = {{\vartheta }_{{{\text{end}}}}},z,{\mathbf{\Omega }}{\kern 1pt} ')d{\mathbf{\Omega }}{\kern 1pt} '} ,\quad ({\mathbf{\Omega }}{{{\mathbf{n}}}_{\vartheta }}) < 0, \\ \end{gathered} $Построение семейства WLD-WLB-схем мы проведем на примере уравнения переноса в $r,\vartheta ,z$ геометрии. Для аппроксимации интеграла рассеяния введем квадратуру на единичной сфере угловых направлений (8 октантов): $ - 1 \leqslant \xi ,\eta ,\mu \leqslant 1$, $0 \leqslant \theta \leqslant \pi $, $0 \leqslant \varphi \leqslant 2\pi $ следующего вида:
(1.5)
$\begin{gathered} \int\limits_{ - 1}^1 {d\mu \int\limits_0^{2\pi } {d\varphi f(\mu ,\varphi ) = } } \int\limits_{ - 1}^1 {d\mu \int\limits_0^\pi {d\varphi f(\mu ,\varphi ) + \int\limits_{ - 1}^1 {d\mu \int\limits_\pi ^{2\pi } {d\varphi f(\mu ,\varphi )} } = } } \\ = \;\sum\limits_{l = 1}^{{{L}_{1}}} {\sum\limits_{m = 1}^{M_{l}^{{(1)}}} {w_{{l,m}}^{{(1)}}f\left( {\mu _{l}^{{(1)}},\varphi _{{l.m}}^{{(1)}}} \right)} } + \sum\limits_{l = 1}^{{{L}_{2}}} {\sum\limits_{m = 1}^{M_{l}^{{(2)}}} {w_{{l,m}}^{{(2)}}f\left( {\mu _{l}^{{(2)}},\varphi _{{l.m}}^{{(2)}}} \right).} } \\ \end{gathered} $Уравнение баланса нулевого порядка получается путем интегрирования уравнения (1.1) по разностной ячейке $({{r}_{{i - 1/2}}},{{r}_{{i + 1/2}}}) \times ({{\vartheta }_{{j - 1/2}}},{{\vartheta }_{{j + 1/2}}}) \times ({{z}_{{k - 1/2}}},{{z}_{{k + 1/2}}}) \times ({{\varphi }_{{l,m + 1/2}}},{{\varphi }_{{l,m - 1/2}}}) \times ({{\mu }_{{l - 1/2}}},{{\mu }_{{l + 1/2}}})$, $i = 1,\;...,\;I$, $j = 1,\;...,\;J$, $k = 1,\;...,\;K$ (ниже мы опускаем целые индексы в тех случаях, когда это не вызывает недоразумений)
(1.6)
$\begin{gathered} \left| \eta \right|\Delta r{{v}_{z}}({{\psi }_{P}} - {{\psi }_{F}}) + \left| \mu \right|{{v}_{r}}{{v}_{\vartheta }}({{\psi }_{T}} - {{\psi }_{B}}) + {{v}_{z}}{{v}_{\vartheta }} \times \\ \times \;\left[ {\left| \xi \right|({{A}^{ + }}{{\psi }_{R}} - {{A}^{ - }}{{\psi }_{L}}) + \frac{C}{w}({{\alpha }_{{m + 1/2}}}{{\psi }_{{m + 1/2}}} - {{\alpha }_{{m - 1/2}}}{{\psi }_{{m - 1/2}}})} \right] + \sigma V\psi = VS, \\ \end{gathered} $(1.7)
$\Delta {{\vartheta }_{j}} = {{v}_{{\vartheta ,j}}} = {{\vartheta }_{{j + 1/2}}} - {{\vartheta }_{{j - 1/2}}},\quad {{V}_{{i,j,k}}} = \Delta {{z}_{k}}{{v}_{{r,i}}}{{v}_{{\vartheta ,j}}},$Для построения нодальной WLB-WLD-схемы 2–4-го порядка точности, кроме уравнения баланса нулевого порядка (1.6), нам потребуются также уравнения баланса первого порядка по ячейке, получаемые интегрированием уравнения (1.1) по разностной ячейке с весами $2\left( {r - {{r}_{i}} - \delta _{i}^{c}} \right){\text{/}}\Delta r$, $2(\vartheta - {{\vartheta }_{j}}){\text{/}}\Delta \vartheta $ и $2(z - {{z}_{k}}){\text{/}}\Delta z$, где $\delta _{i}^{c}$ – малое отклонение от центра ячейки, выбираемое из условия $\int_{{{r}_{{i - 1/2}}}}^{{{r}_{{i + 1/2}}}} {\left( {r - {{r}_{i}} - \delta _{i}^{c}} \right)rd} r = 0$:
(1.8)
$\begin{gathered} \left| \eta \right|v_{{r0}}^{1}{{v}_{z}}\left( {\psi _{P}^{r} - \psi _{F}^{r}} \right) - \left| \eta \right|\Delta r{{v}_{z}}{{\delta }^{c}}({{\psi }_{P}} - {{\psi }_{F}}) + {{v}_{z}}{{v}_{\vartheta }} \times \\ \times \;\left\{ {\xi \left[ {{{A}^{ + }}\left( {\frac{{\Delta r}}{2} - {{s}_{r}}{{\delta }^{c}}} \right){{\psi }_{R}} + {{A}^{ - }}\left( {\frac{{\Delta r}}{2} + {{s}_{r}}{{\delta }^{c}}} \right){{\psi }_{L}} - {{v}_{r}}\psi } \right] + \frac{{{{C}^{r}}}}{w}} \right.\left( {{{\alpha }_{{m + 1/2}}}\psi _{{m + 1/2}}^{r} - {{\alpha }_{{m - 1/2}}}\psi _{{m - 1/2}}^{r}} \right) - \\ - \;\left. {{{\delta }^{c}}\frac{C}{w}({{\alpha }_{{m + 1/2}}}{{\psi }_{{m + 1/2}}} - {{\alpha }_{{m - 1/2}}}{{\psi }_{{m - 1/2}}})} \right\} + \left| \mu \right|v_{r}^{1}{{v}_{\vartheta }}(\psi _{T}^{r} - \psi _{B}^{r}) + \sigma {{V}^{r}}{{\psi }^{r}} = {{V}^{r}}{{S}^{r}}, \\ \end{gathered} $(1.9)
$\begin{gathered} \eta \Delta r{{v}_{\vartheta }}{{v}_{z}}\left[ {\frac{1}{2}\left( {{{\psi }_{P}} + {{\psi }_{F}}} \right) - \psi } \right] + v_{\vartheta }^{1}{{v}_{z}}\left[ {\left| \xi \right|\left( {{{A}^{ + }}\psi _{R}^{\vartheta } - {{A}^{ - }}\psi _{L}^{\vartheta }} \right) + \frac{C}{w}\left( {{{\alpha }_{{m + 1/2}}}\psi _{{m + 1/2}}^{\vartheta } - {{\alpha }_{{m - 1/2}}}\psi _{{m - 1/2}}^{\vartheta }} \right)} \right] + \\ + \;\sigma {{V}^{\vartheta }}{{\psi }^{\vartheta }} + \left| \mu \right|{{v}_{r}}v_{\vartheta }^{1}(\psi _{T}^{\vartheta } - \psi _{B}^{\vartheta }) = {{V}^{\vartheta }}{{S}^{\vartheta }}, \\ \end{gathered} $(1.10)
$\begin{gathered} \left| \eta \right|\Delta rv_{z}^{1}(\psi _{P}^{z} - \psi _{F}^{z}) + \mu V\left[ {\frac{1}{2}\left( {{{\psi }_{T}} + {{\psi }_{B}}} \right) - \psi } \right] + v_{z}^{1}{{v}_{\vartheta }} \times \\ \times \;\left[ {\left| \xi \right|\left( {{{A}^{ + }}\psi _{R}^{z} - {{A}^{ - }}\psi _{L}^{z}} \right) + \frac{C}{w}\left( {{{\alpha }_{{m + 1/2}}}\psi _{{m + 1/2}}^{z} - {{\alpha }_{{m - 1/2}}}\psi _{{m - 1/2}}^{z}} \right)} \right] + \sigma {{V}^{z}}{{\psi }^{z}} = {{V}^{z}}{{S}^{z}}, \\ \end{gathered} $(1.11)
$\begin{gathered} \psi _{{i,j,k,l,m}}^{r} = \frac{1}{{V_{{i,j,k}}^{r}}}\int\limits_{{{r}_{{i - 1/2}}}}^{{{r}_{{i + 1/2}}}} {\int\limits_{{{\vartheta }_{{j - 1/2}}}}^{{{\vartheta }_{{j + 1/2}}}} {\int\limits_{{{z}_{{k - 1/2}}}}^{{{z}_{{k + 1/2}}}} {{{\psi }_{{l,m}}}(r,\vartheta ,z)(r - {{r}_{i}} - \delta _{i}^{c})rdrd\vartheta dz} } } , \\ \psi _{{i,j,k,l,m}}^{\vartheta } = \frac{1}{{V_{{i,j,k}}^{\vartheta }}}\int\limits_{{{r}_{{i - 1/2}}}}^{{{r}_{{i + 1/2}}}} {\int\limits_{{{\vartheta }_{{j - 1/2}}}}^{{{\vartheta }_{{j + 1/2}}}} {\int\limits_{{{z}_{{k - 1/2}}}}^{{{z}_{{k + 1/2}}}} {{{\psi }_{{l,m}}}(r,\vartheta ,z)(\vartheta - {{\vartheta }_{j}})rdrd\vartheta dz} } } , \\ \end{gathered} $(1.12)
$V = {{v}_{r}}{{v}_{\vartheta }}{{v}_{z}},\quad V_{{i,j,k}}^{r} = \frac{2}{{\Delta r}}\int\limits_{{{r}_{{i - 1/2}}}}^{{{r}_{{i + 1/2}}}} {\int\limits_{{{\vartheta }_{{j - 1/2}}}}^{{{\vartheta }_{{j + 1/2}}}} {\int\limits_{{{z}_{{k - 1/2}}}}^{{{z}_{{k + 1/2}}}} {{{{\left( {r - {{r}_{i}} - \delta _{i}^{c}} \right)}}^{2}}rdrd\vartheta dz = v_{r}^{1}{{v}_{\vartheta }}{{v}_{z}}} } } ,$Отметим, что выбор (1.12) нормировочного коэффициента $V_{{i,k}}^{r}$ в определении первого радиального пространственного момента ${{\psi }^{r}}$ (1.11) гарантирует выполнение условия: дополнительное уравнение LB-схемы ${{\psi }_{{i + 1/2}}} = 2{{\psi }^{r}} + {{\psi }_{{i - 1/2}}}$ по $r$ удовлетворяется точно на линейных по $r$ решениях вида: $\psi (r) = a + br$.
Для получения разностной схемы к четырем точным балансным уравнениям (1.6)–(1.12) следует добавить 16 дополнительных уравнений, которые соответствуют WLB-WLD-схеме
(1.13)
$\psi _{R}^{z} = {{\psi }^{z}} + T_{{R,r}}^{z}{{s}_{r}}{{s}_{z}}{{\psi }^{r}} + T_{{R,\vartheta }}^{z}{{s}_{\vartheta }}{{s}_{z}}{{\psi }^{\vartheta }},\quad \psi _{P}^{r} = {{\psi }^{r}} + T_{{P,\vartheta }}^{r}{{s}_{r}}{{s}_{\vartheta }}{{\psi }^{\vartheta }} + T_{{P,z}}^{r}{{s}_{r}}{{s}_{z}}{{\psi }^{z}},$(1.14)
$\begin{gathered} {{\psi }_{{m + 1/2}}} = (1 + {{P}_{\xi }})\left( {\psi - \frac{2}{{\Delta r}}{{\delta }^{c}}{{\psi }^{r}}} \right) - {{P}_{\xi }}{{\psi }_{{m - 1/2}}},\quad \psi _{{m + 1/2}}^{r} = \left( {1 + P_{\xi }^{r}} \right){{\psi }^{r}} - P_{\xi }^{r}\psi _{{m - 1/2}}^{r}, \\ \psi _{{m + 1/2}}^{\vartheta } = \left( {1 + P_{\xi }^{\vartheta }} \right){{\psi }^{\vartheta }} - P_{\xi }^{\vartheta }\psi _{{m - 1/2}}^{\vartheta },\quad \psi _{{m + 1/2}}^{z} = {{\left( {1 + P_{\xi }^{z}} \right)}^{z}} - P_{\xi }^{z}\psi _{{m - 1/2}}^{z},\quad 0 \leqslant {{P}_{\xi }},P_{\xi }^{r},P_{\xi }^{\vartheta },P_{\xi }^{z} \leqslant 1. \\ \end{gathered} $(1.15)
$0 \leqslant {{P}_{t}} \leqslant 1,\quad {{Q}_{t}} = 1\;\;{\text{и л и }}\;\;{{P}_{t}} = 0,\quad {1 \mathord{\left/ {\vphantom {1 {{{E}^{ - }}}}} \right. \kern-0em} {{{E}^{ - }}}} \leqslant {{Q}_{r}} < 1,\quad {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3} \leqslant {{Q}_{z}} < 1\;\;{\text{и л и }}\;\;{{P}_{t}} = 0,\quad {{Q}_{t}} > 1,$Веса $T_{{R,r}}^{\vartheta }$, $T_{{R,z}}^{\vartheta }$, $T_{{R,r}}^{z}$, $T_{{R,\vartheta }}^{z}$, $T_{{P,\vartheta }}^{r}$, $T_{{P,z}}^{r}$, $T_{{P,r}}^{z}$, $T_{{P,\vartheta }}^{z}$, $T_{{T,\vartheta }}^{r}$, $T_{{T,z}}^{r}$, $T_{{T,r}}^{\vartheta }$ и $T_{{T,z}}^{\vartheta }$, аналогично случаю 2D геометрии [16], могут быть использованы в алгоритме коррекции отрицательных потоков по пространственным переменным. Однако, если пространственная сетка задачи не слишком грубая (2–3 интервала на пробег для верхних ведущих групп энергетической сетки, определяющих перенос нейтронов на больших расстояниях от источника), такая коррекция, как показал численный эксперимент, вообще говоря, не требуется. В данной работе вышеуказанные весовые коэффициенты полагаются равными нулю.
Случай ${{P}_{t}} = {{Q}_{t}} = 1$, ${{T}_{t}} = 0$ соответствует LB-схеме 4-го порядка точности, случай ${{P}_{t}} = 0$, ${{Q}_{t}} = 1$, ${{T}_{t}} = 0$ соответствует LD-схеме 3-го порядка точности. Как и в случае 1D криволинейных геометрий, дополнительное уравнение WDD-схемы по угловой переменной, связывающее входящие и выходящие радиальные пространственные моменты нулевого порядка ${{\psi }_{{m \pm 1/2}}}$ на гранях ${{\xi }_{{l,m \pm 1/2}}}$ разностной ячейки, включает член ~${{\psi }^{r}}$, позволяющий учесть различие в пространственном весовом множителе в определении $\psi $ и ${{\psi }_{{m \pm 1/2}}}$. Отметим, что дополнительные уравнения (1.14) выполняются точно на постоянных по углу $\varphi $ и линейных по пространственным переменным $r$, $\vartheta $ и $z$ решениях
(1.16)
$\psi (r,\vartheta ,z,\mu ,\varphi ) = \psi + \frac{2}{{\Delta r}}\left( {r - {{r}_{i}} - \delta _{i}^{c}} \right){{\psi }^{r}} + \frac{2}{{\Delta \vartheta }}\left( {\vartheta - {{\vartheta }_{j}}} \right){{\psi }^{\vartheta }} + \frac{2}{{\Delta z}}\left( {z - {{z}_{k}}} \right){{\psi }^{z}}.$В дальнейшем ограничим выбор весов $P_{\xi }^{r}$, $P_{\xi }^{\vartheta }$и $P_{\xi }^{z}$ в экстраполяционных соотношениях для $\psi _{{m + 1/2}}^{r}$, $\psi _{{m + 1/2}}^{\vartheta }$ и $\psi _{{m + 1/2}}^{z}$ (1.14) условием
Система дополнительных уравнений WLB–WLD-схемы является итогом серии работ автора в этом направлении, обзор которых содержится в [14]. Она соответствует аппроксимации решения в пределах разностной ячейки кусочно-линейными элементами с возможными разрывами на гранях ячейки, а также изломами внутри ячейки. Геометрическая интерпретация WLB-WLD-схемы для плоской геометрии приведена в [14] на фиг. 1.2.2 и 1.2.3 , а для WLD-схемы в $x,z$ геометрии на фиг. 1.10.2 , а также в [16] (фиг. 8.1 ). В случае плоской геометрии WLB-схема может быть также получена из M2-схемы Вадьянатана [15] 4-го порядка точности путем использования для экспоненты рациональной аппроксимации 3–4-го порядка точности (уравнение (1.2.46) из [14]).
Подстановка дополнительных уравнений (1.13), (1.14) в балансные соотношения (1.6), (2.2), (2.3) и (2.4) приводит к следующей системе уравнений относительно пространственных моментов решения в ячейке $\psi $, ${{\psi }^{r}}$, ${{\psi }^{\vartheta }}$ и ${{\psi }^{z}}$:
(1.18)
$\begin{gathered} {{a}_{{11}}}\psi + {{a}_{{12}}}{{\psi }^{r}} + {{a}_{{13}}}{{\psi }^{\vartheta }} + {{a}_{{14}}}{{\psi }^{z}} = {{b}_{1}},\quad {{a}_{{21}}}\psi + {{a}_{{22}}}{{\psi }^{r}} + {{a}_{{23}}}{{\psi }^{\vartheta }} + {{a}_{{24}}}{{\psi }^{z}} = {{b}_{2}}, \\ {{a}_{{31}}}\psi + {{a}_{{32}}}{{\psi }^{r}} + {{a}_{{33}}}{{\psi }^{\vartheta }} + {{a}_{{34}}}{{\psi }^{z}} = {{b}_{3}},\quad {{a}_{{41}}}\psi + {{a}_{{42}}}{{\psi }^{r}} + {{a}_{{43}}}{{\psi }^{\vartheta }} + {{a}_{{44}}}{{\psi }^{z}} = {{b}_{4}}, \\ \end{gathered} $(1.19)
$\begin{gathered} {{a}_{{33}}} = \left| \eta \right|\Delta r{{v}_{\vartheta }}{{v}_{z}}\frac{1}{2}\left( {{{Q}_{\vartheta }} + {{P}_{\vartheta }}} \right) + v_{\vartheta }^{1}{{v}_{z}}\left[ {\left| \xi \right|{{A}^{ + }} + \frac{C}{w}{{\alpha }_{{m + 1/2}}}} \right] + \left| \mu \right|{{v}_{r}}v_{\vartheta }^{1} + \sigma {{V}^{\vartheta }},\quad {{a}_{{34}}} = 0, \\ {{a}_{{41}}} = - \mu V\frac{1}{2}\left( {1 + {{P}_{z}}} \right),\quad {{a}_{{42}}} = 0,\quad {{a}_{{43}}} = 0, \\ \end{gathered} $Система балансных уравнений для граничных ячеек с $m = 1{\text{/}}2$ (${{\xi }_{{l,1/2}}} = - \sqrt {1 - \mu _{l}^{2}} $), используемых для нахождения граничных значений потока ${{\psi }_{{i,j,k,l,1/2}}}$, $\psi _{{i,j,k,l,1/2}}^{r}$, $\psi _{{i,j,k,l,1/2}}^{\vartheta }$ и $\psi _{{i,j,k,l,1/2}}^{z}$ по угловой переменной $\xi $, состоит из уравнения баланса нулевого порядка (1.21), в котором используется более точное, чем в случае WDD-схемы соотношение:
(1.20)
${{\psi }_{{i,j,k,l,1/2}}} \simeq \psi _{{i,j,k,l}}^{{(0)}} - \frac{2}{{\Delta r}}{{\delta }^{c}}\psi _{{i,j,k,l}}^{r},$(1.21)
$\left| \mu \right|{{v}_{r}}{{v}_{\vartheta }}({{\psi }_{T}} - {{\psi }_{B}}) + {{v}_{\vartheta }}{{v}_{z}}\left| \xi \right|\left[ {({{A}^{ + }}{{\psi }_{R}} - {{A}^{ - }}{{\psi }_{L}}) + ({{A}^{ - }} - {{A}^{ + }})\left( {\psi - \frac{2}{{\Delta r}}{{\delta }^{c}}{{\psi }^{r}}} \right)} \right] + \sigma V\psi = VS,$(1.22)
$\begin{gathered} \left| \mu \right|v_{r}^{1}{{v}_{\vartheta }}\left( {\psi _{T}^{r} - \psi _{B}^{r}} \right) + {{v}_{\vartheta }}{{v}_{z}}\xi \left[ {{{A}^{ + }}\left( {\frac{{\Delta r}}{2} - {{s}_{r}}{{\delta }^{c}}} \right){{\psi }_{R}} + {{A}^{ - }}\left( {\frac{{\Delta r}}{2} + {{s}_{r}}{{\delta }^{c}}} \right){{\psi }_{L}} - \left( {{{v}_{r}} - {{\delta }^{c}}C} \right)\psi - {{C}^{r}}{{\psi }^{r}}} \right] + \\ + \;\sigma {{V}^{r}}{{\psi }^{r}} = {{V}^{r}}{{S}^{r}}, \\ \end{gathered} $(1.23)
$v_{\vartheta }^{1}{{v}_{z}}\left| \xi \right|\left[ {\left( {{{A}^{ + }}\psi _{R}^{\vartheta } - {{A}^{ - }}\psi _{L}^{\vartheta }} \right) + \left( {{{A}^{ - }} - {{A}^{ + }}} \right){{\psi }^{\vartheta }}} \right] + \left| \mu \right|{{v}_{r}}v_{\vartheta }^{1}\left( {\psi _{T}^{\vartheta } - \psi _{B}^{\vartheta }} \right) + \sigma {{V}^{\vartheta }}{{\psi }^{\vartheta }} = {{V}^{\vartheta }}{{S}^{\vartheta }},$(1.24)
$\mu V\left[ {\frac{1}{2}\left( {{{\psi }_{T}} + {{\psi }_{B}}} \right) - \psi } \right] + v_{z}^{1}{{v}_{\vartheta }}\left| \xi \right|\left[ {\left( {{{A}^{ + }}\psi _{R}^{z} - {{A}^{ - }}\psi _{L}^{z}} \right) + \left( {{{A}^{ - }} - {{A}^{ + }}} \right){{\psi }^{z}}} \right] + \sigma {{V}^{z}}{{\psi }^{z}} = {{V}^{z}}{{S}^{z}}.$(1.25)
${{a}_{{11}}}\psi + {{a}_{{12}}}{{\psi }^{r}} + {{a}_{{13}}}{{\psi }^{z}} = {{b}_{1}},\quad {{a}_{{21}}}\psi + {{a}_{{22}}}{{\psi }^{r}} + {{a}_{{23}}}{{\psi }^{z}} = {{b}_{2}},\quad {{a}_{{31}}}\psi + {{a}_{{32}}}{{\psi }^{r}} + {{a}_{{33}}}{{\psi }^{z}} = {{b}_{3}},$(1.26)
${{a}_{{31}}} = - \frac{1}{2}\mu V\left( {1 + {{P}_{z}}} \right),\quad {{a}_{{32}}} = 0,\quad {{a}_{{33}}} = \left| \mu \right|V\frac{1}{2}\left( {{{Q}_{z}} + {{P}_{z}}} \right) + {{v}_{\vartheta }}v_{z}^{1}\left| \xi \right|{{A}^{ - }} + \sigma {{V}^{z}},$(1.27)
${{\psi }^{\vartheta }} = \frac{{{{V}^{\vartheta }}{{S}^{\vartheta }} + v_{\vartheta }^{1}{{v}_{z}}\left| \xi \right|{{A}^{ - }}\psi _{L}^{\vartheta } + \left| \mu \right|{{v}_{r}}v_{\vartheta }^{1}\psi _{B}^{\vartheta }}}{{v_{\vartheta }^{1}{{v}_{z}}\left| \xi \right|{{A}^{ - }} + \left| \mu \right|{{v}_{r}}v_{\vartheta }^{1} + \sigma {{V}^{\vartheta }}}}.$2. ПОСТРОЕНИЕ $K{{P}_{1}}$-СХЕМЫ УСКОРЕНИЯ ВНУТРЕННИХ ИТЕРАЦИЙ В $r,\vartheta ,z$ ГЕОМЕТРИИ
Перепишем уравнение баланса и систему дополнительных уравнений WLD-WLB-схемы в $r,\vartheta ,z$ геометрии на $(n + 1)$-й внутренней итерации в более удобном для последующего изложения виде
(2.1)
$\begin{gathered} \eta \Delta r{{v}_{z}}\left( {\psi _{{j + 1/2}}^{{n + 1/2}} - \psi _{{j - 1/2}}^{{n + 1/2}}} \right) + \mu {{v}_{r}}{{v}_{\vartheta }}\left( {\psi _{{k + 1/2}}^{{n + 1/2}} - \psi _{{k - 1/2}}^{{n + 1/2}}} \right) + \\ + \;{{v}_{z}}{{v}_{\vartheta }}\left[ {\xi \left( {{{A}_{{i + 1/2}}}\psi _{{i + 1/2}}^{{n + 1/2}} - {{A}_{{i - 1/2}}}\psi _{{i - 1/2}}^{{n + 1/2}}} \right) + \frac{C}{w}\left( {{{\alpha }_{{m + 1/2}}}\psi _{{m + 1/2}}^{{n + 1/2}} - {{\alpha }_{{l,m - 1/2}}}\psi _{{m - 1/2}}^{{n + 1/2}}} \right)} \right] + \\ + \;{{\sigma }_{t}}V{{\psi }^{{n + 1/2}}} = V\sum\limits_{\kappa = 0}^{\rm K} {\frac{{2\kappa + 1}}{{4\pi }}} {\kern 1pt} {{\sigma }_{{s,\kappa }}}\sum\limits_{\nu = - \kappa }^\kappa {Y_{\kappa }^{\nu }(\mu ,\varphi )} \Phi _{\kappa }^{{\nu ,n}} + VF, \\ \end{gathered} $(2.2)
$\begin{gathered} \eta v_{{r0}}^{1}{{v}_{z}}\left( {\psi _{{j + 1/2}}^{r} - \psi _{{j - 1/2}}^{r}} \right) - \eta \Delta r{{v}_{z}}{{\delta }^{c}}\left( {{{\psi }_{{j + 1/2}}} - {{\psi }_{{j - 1/2}}}} \right) + {{v}_{z}}{{v}_{\vartheta }} \times \\ \times \left\{ {\xi \left[ {{{A}_{{i + 1/2}}}\left( {\frac{{\Delta r}}{2} - {{\delta }^{c}}} \right){{\psi }_{{i + 1/2}}} + {{A}_{{i - 1/2}}}\left( {\frac{{\Delta r}}{2} + {{\delta }^{c}}} \right){{\psi }_{{i - 1/2}}} - {{v}_{r}}\psi } \right] + } \right.\frac{{{{C}^{r}}}}{w}\left( {{{\alpha }_{{m + 1/2}}}\psi _{{m + 1/2}}^{r} - {{\alpha }_{{m - 1/2}}}\psi _{{m - 1/2}}^{r}} \right) - \\ - \;\left. {{{\delta }^{c}}\frac{C}{w}\left( {{{\alpha }_{{m + 1/2}}}{{\psi }_{{m + 1/2}}} - {{\alpha }_{{m - 1/2}}}{{\psi }_{{m - 1/2}}}} \right)} \right\} + \mu v_{r}^{1}{{v}_{\vartheta }}\left( {\psi _{{k + 1/2}}^{r} - \psi _{{k - 1/2}}^{r}} \right) + \sigma {{V}^{r}}{{\psi }^{r}} = {{V}^{r}}{{S}^{r}}, \\ \end{gathered} $(2.3)
$\begin{gathered} \eta \Delta r{{v}_{\vartheta }}{{v}_{z}}\left[ {\frac{1}{2}\left( {{{\psi }_{{j + 1/2}}} + {{\psi }_{{j - 1/2}}}} \right) - \psi } \right] + v_{\vartheta }^{1}{{v}_{z}} \times \\ \times \;\left[ {\xi \left( {{{A}_{{i + 1/2}}}\psi _{{i + 1/2}}^{\vartheta } - {{A}_{{i - 1/2}}}\psi _{{i - 1/2}}^{\vartheta }} \right) + \frac{C}{w}\left( {{{\alpha }_{{m + 1/2}}}\psi _{{m + 1/2}}^{\vartheta } - {{\alpha }_{{m - 1/2}}}\psi _{{m - 1/2}}^{\vartheta }} \right)} \right] + \\ + \;\mu {{v}_{r}}v_{\vartheta }^{1}\left( {\psi _{{k + 1/2}}^{\vartheta } - \psi _{{k - 1/2}}^{\vartheta }} \right) + \sigma {{V}^{\vartheta }}{{\psi }^{\vartheta }} = {{V}^{\vartheta }}{{S}^{\vartheta }}, \\ \end{gathered} $(2.4)
$\begin{gathered} \eta \Delta rv_{z}^{1}\left( {\psi _{{j + 1/2}}^{z} - \psi _{{j - 1/2}}^{z}} \right) + \mu V\left[ {\frac{1}{2}\left( {{{\psi }_{{k + 1/2}}} + {{\psi }_{{k - 1/2}}}} \right) - \psi } \right] + v_{z}^{1}{{v}_{\vartheta }} \times \\ \times \;\left[ {\xi \left( {{{A}_{{i + 1/2}}}\psi _{{i + 1/2}}^{z} - {{A}_{{i - 1/2}}}\psi _{{i - 1/2}}^{z}} \right) + \frac{C}{w}\left( {{{\alpha }_{{m + 1/2}}}\psi _{{m + 1/2}}^{z} - {{\alpha }_{{m - 1/2}}}\psi _{{m - 1/2}}^{z}} \right)} \right] + \sigma {{V}^{z}}{{\psi }^{z}} = {{V}^{z}}{{S}^{z}}. \\ \end{gathered} $(2.5)
${{a}_{r}} = \left\{ \begin{gathered} {1 \mathord{\left/ {\vphantom {1 {\left( {{{Q}_{r}} + {{P}_{r}}} \right)}}} \right. \kern-0em} {\left( {{{Q}_{r}} + {{P}_{r}}} \right)}},\quad \xi > 0, \hfill \\ {{{{P}_{r}}} \mathord{\left/ {\vphantom {{{{P}_{r}}} {\left( {{{Q}_{r}} + {{P}_{r}}} \right)}}} \right. \kern-0em} {\left( {{{Q}_{r}} + {{P}_{r}}} \right)}},\quad \xi < 0, \hfill \\ \end{gathered} \right.\quad {{b}_{r}} = - \left\{ \begin{gathered} {{{{P}_{r}}} \mathord{\left/ {\vphantom {{{{P}_{r}}} {\left( {{{Q}_{r}} + {{P}_{r}}} \right)}}} \right. \kern-0em} {\left( {{{Q}_{r}} + {{P}_{r}}} \right)}},\quad \xi > 0, \hfill \\ {1 \mathord{\left/ {\vphantom {1 {\left( {{{Q}_{r}} + {{P}_{r}}} \right)}}} \right. \kern-0em} {\left( {{{Q}_{r}} + {{P}_{r}}} \right)}},\quad \xi < 0, \hfill \\ \end{gathered} \right.$(2.6)
${{a}_{\vartheta }} = \left\{ \begin{gathered} {1 \mathord{\left/ {\vphantom {1 {\left( {{{Q}_{\vartheta }} + {{P}_{\vartheta }}} \right)}}} \right. \kern-0em} {\left( {{{Q}_{\vartheta }} + {{P}_{\vartheta }}} \right)}},\quad \eta > 0, \hfill \\ {{{{P}_{\vartheta }}} \mathord{\left/ {\vphantom {{{{P}_{\vartheta }}} {\left( {{{Q}_{\vartheta }} + {{P}_{\vartheta }}} \right)}}} \right. \kern-0em} {\left( {{{Q}_{\vartheta }} + {{P}_{\vartheta }}} \right)}},\quad \eta < 0, \hfill \\ \end{gathered} \right.\quad {{b}_{\vartheta }} = - \left\{ \begin{gathered} {{{{P}_{\vartheta }}} \mathord{\left/ {\vphantom {{{{P}_{\vartheta }}} {\left( {{{Q}_{\vartheta }} + {{P}_{\vartheta }}} \right)}}} \right. \kern-0em} {\left( {{{Q}_{\vartheta }} + {{P}_{\vartheta }}} \right)}},\quad \eta > 0, \hfill \\ {1 \mathord{\left/ {\vphantom {1 {\left( {{{Q}_{\vartheta }} + {{P}_{\vartheta }}} \right)}}} \right. \kern-0em} {\left( {{{Q}_{\vartheta }} + {{P}_{\vartheta }}} \right)}},\quad \eta < 0, \hfill \\ \end{gathered} \right.$(2.7)
${{a}_{z}} = \left\{ \begin{gathered} {1 \mathord{\left/ {\vphantom {1 {\left( {{{Q}_{z}} + {{P}_{z}}} \right)}}} \right. \kern-0em} {\left( {{{Q}_{z}} + {{P}_{z}}} \right)}},\quad \mu > 0, \hfill \\ {{{{P}_{z}}} \mathord{\left/ {\vphantom {{{{P}_{z}}} {\left( {{{Q}_{z}} + {{P}_{z}}} \right)}}} \right. \kern-0em} {\left( {{{Q}_{z}} + {{P}_{z}}} \right)}},\quad \mu < 0, \hfill \\ \end{gathered} \right.\quad {{b}_{z}} = - \left\{ \begin{gathered} {{{{P}_{z}}} \mathord{\left/ {\vphantom {{{{P}_{z}}} {\left( {{{Q}_{z}} + {{P}_{z}}} \right)}}} \right. \kern-0em} {\left( {{{Q}_{z}} + {{P}_{z}}} \right)}},\quad \mu > 0, \hfill \\ {1 \mathord{\left/ {\vphantom {1 {\left( {{{Q}_{z}} + {{P}_{z}}} \right)}}} \right. \kern-0em} {\left( {{{Q}_{z}} + {{P}_{z}}} \right)}},\quad \mu < 0, \hfill \\ \end{gathered} \right.$(2.8)
${{\psi }^{{\vartheta ,n + 1/2}}} = a\psi _{{i + 1/2}}^{{\vartheta ,n + 1/2}} + \left( {1 - a} \right)\psi _{{i - 1/2}}^{{\vartheta ,n + 1/2}},\quad {{\psi }^{{z,n + 1/2}}} = a\psi _{{i + 1/2}}^{{z,n + 1/2}} + \left( {1 - a} \right)\psi _{{i - 1/2}}^{{z,n + 1/2}},\quad a = \left\{ \begin{gathered} 1,\quad \xi > 0, \hfill \\ 0,\quad \xi < 0, \hfill \\ \end{gathered} \right.$(2.9)
${{\psi }^{{r,n + 1/2}}} = b\psi _{{j + 1/2}}^{{r,n + 1/2}} + \left( {1 - b} \right)\psi _{{j - 1/2}}^{{r,n + 1/2}},\quad {{\psi }^{{z,n + 1/2}}} = b\psi _{{j + 1/2}}^{{z,n + 1/2}} + \left( {1 - b} \right)\psi _{{j - 1/2}}^{{z,n + 1/2}},\quad b = \left\{ \begin{gathered} 1,\quad \eta > 0, \hfill \\ 0,\quad \eta < 0, \hfill \\ \end{gathered} \right.$(2.10)
${{\psi }^{{r,n + 1/2}}} = c\psi _{{k + 1/2}}^{{r,n + 1/2}} + \left( {1 - c} \right)\psi _{{k - 1/2}}^{{r,n + 1/2}},\quad {{\psi }^{{\vartheta ,n + 1/2}}} = c\psi _{{k + 1/2}}^{{\vartheta ,n + 1/2}} + \left( {1 - c} \right)\psi _{{k - 1/2}}^{{\vartheta ,n + 1/2}},\quad c = \left\{ \begin{gathered} 1,\quad \mu > 0, \hfill \\ 0,\quad \mu < 0. \hfill \\ \end{gathered} \right.$(2.11)
$\psi _{{m + 1/2}}^{{n + 1/2}} = (1 + {{P}_{\xi }}){{\psi }^{{n + 1/2}}} - {{P}_{\xi }}\psi _{{m - 1/2}}^{{n + 1/2}} = \sum\limits_{m' = 1/2,1,..,m} {d_{{m'}}^{m}\psi _{{m'}}^{{n + 1/2}}} ,\quad 0 \leqslant {{P}_{\xi }} \leqslant 1.$(2.12)
$\begin{gathered} \psi _{{1/2,j,k,l,m}}^{{n + 1/2}} = F_{{j,k,l,m}}^{{\operatorname{int} }} + \sum\limits_{{{\xi }_{{l',m'}}} < 0} {{{w}_{{l',m'}}}R_{{lm,l'm'}}^{{\operatorname{int} }}\psi _{{1/2,j,k,l',m'}}^{{n + 1/2}}} ,\quad {{\xi }_{{l,m}}} > 0, \\ \psi _{{I + 1/2,j,k,l,m}}^{{n + 1/2}} = F_{{j,k,l,m}}^{{{\text{ext}}}} + \sum\limits_{{{\xi }_{{l',m'}}} > 0} {{{w}_{{l',m'}}}R_{{lm,l'm'}}^{{{\text{ext}}}}\psi _{{I + 1/2,j,k,l',m'}}^{n}} ,\quad {{\xi }_{{l,m}}} < 0, \\ \end{gathered} $(2.13)
$\begin{gathered} \psi _{{i,1/2,k,l,m}}^{{n + 1/2}} = F_{{i,k,l,m}}^{0} + \sum\limits_{{{\eta }_{{l',m'}}} < 0} {{{w}_{{l',m'}}}R_{{lm,l'm'}}^{0}\psi _{{i,1/2,k,l',m'}}^{{n + 1/2}}} ,\quad {{\eta }_{{l,m}}} > 0, \\ \psi _{{i,J + 1/2,k,l,m}}^{{n + 1/2}} = F_{{i,k,l,m}}^{{{\text{end}}}} + \sum\limits_{{{\eta }_{{l',m'}}} > 0} {{{w}_{{l',m'}}}R_{{lm,l'm'}}^{{{\text{end}}}}\psi _{{i,J + 1/2,k,l',m'}}^{n}} ,\quad {{\eta }_{{l,m}}} < 0, \\ \end{gathered} $(2.14)
$\begin{gathered} \psi _{{i,j,1/2,l,m}}^{{n + 1/2}} = F_{{i,j,l,m}}^{{{\text{bot}}}} + \sum\limits_{{{\mu }_{{l'}}} < 0} {{{w}_{{l',m'}}}R_{{lm,l'm'}}^{{{\text{bot}}}}\psi _{{i,j,1/2,l',m'}}^{{n + 1/2}}} ,\quad {{\mu }_{l}} > 0, \\ \psi _{{i,j,K + 1/2,l,m}}^{{n + 1/2}} = F_{{i,j,l,m}}^{{{\text{top}}}} + \sum\limits_{{{\mu }_{{l'}}} > 0} {{{w}_{{l',m'}}}R_{{lm,l'm'}}^{{{\text{top}}}}\psi _{{i,j,K + 1/2,l',m'}}^{n}} ,\quad {{\mu }_{l}} < 0. \\ \end{gathered} $При использовании периодических граничных условий, например, по переменной $\vartheta $, что имеет место при наличии поворотной симметрии для сектора симметрии $\left( {{{\vartheta }_{0}},{{\vartheta }_{{{\text{end}}}}}} \right)$, граничные условия (2.13) заменяются следующими:
(2.15)
$\begin{gathered} \psi _{{i,1/2,k,l,m}}^{{n + 1/2}} = \psi _{{i,J + 1/2,k,l,m}}^{n},\quad {{\eta }_{{l,m}}} > 0, \\ \psi _{{i,J + 1/2,k,l,m}}^{{n + 1/2}} = \psi _{{i,1/2,k,l,m}}^{n},\quad {{\eta }_{{l,m}}} < 0. \\ \end{gathered} $Для ускорения сходимости внутренних итераций в $K{{P}_{1}}$-схеме используются линейные поправки к нулевому и первым угловым моментам решения следующего вида:
(2.16)
$\begin{gathered} {{\psi }^{{\alpha ,n + 1}}} = {{\psi }^{{\alpha ,n + 1/2}}} + \frac{1}{{4\pi }}\left( {{{f}^{{\alpha ,0}}} + 3\xi {{f}^{{\alpha ,r}}} + 3\eta {{f}^{{\alpha ,\vartheta }}} + 3\mu {{f}^{{\alpha ,z}}}} \right),\quad \alpha = 0,r,\vartheta ,z, \\ \psi _{{i \pm 1/2}}^{{\beta ,n + 1}} = \psi _{{i \pm 1/2}}^{{\beta ,n + 1/2}} + \frac{1}{{4\pi }}\left( {f_{{i \pm 1/2}}^{{\beta ,0}} + 3\xi f_{{i \pm 1/2}}^{{\beta ,r}}} \right),\quad \beta = 0,\vartheta ,z, \\ \end{gathered} $(2.17)
$\begin{gathered} \psi _{{j \pm 1/2}}^{{\beta ,n + 1}} = \psi _{{j \pm 1/2}}^{{\beta ,n + 1/2}} + \frac{1}{{4\pi }}\left( {f_{{j \pm 1/2}}^{{\beta ,0}} + 3\eta f_{{j \pm 1/2}}^{{\beta ,\vartheta }}} \right),\quad \beta = 0,r,z, \\ \psi _{{k \pm 1/2}}^{{\beta ,n + 1}} = \psi _{{k \pm 1/2}}^{{\beta ,n + 1/2}} + \frac{1}{{4\pi }}\left( {f_{{k \pm 1/2}}^{{\beta ,0}} + 3\mu f_{{k \pm 1/2}}^{{\beta ,z}}} \right),\quad \beta = 0,r,\vartheta . \\ \end{gathered} $Для получения системы уравнений для определения ускоряющих поправок ${{f}^{{\alpha ,0}}}$, ${{f}^{{\alpha ,r}}}$, ${{f}^{{\alpha ,\vartheta }}}$ и ${{f}^{{\alpha ,z}}}$, воспользуемся следующей процедурой, близкой к “4-step” процедуре Ларсена [3], которая обеспечивает построение согласованной схемы ускорения. Прежде всего подействуем на уравнения баланса (2.1)–(2.4) операторами проектирования ${{\hat {L}}_{0}}$, ${{\hat {L}}_{r}}$, ${{\hat {L}}_{\vartheta }}$ и ${{\hat {L}}_{z}}$:
(2.18)
$\begin{gathered} {{{\hat {L}}}_{0}}\psi = \sum\limits_{l,m} {{{w}_{{l,m}}}{{\psi }_{{i,j,k,l,m}}}} ,\quad {{{\hat {L}}}_{r}}\psi = \sum\limits_{l,m} {{{w}_{{l,m}}}{{\xi }_{{l,m}}}{{\psi }_{{i,j,k,l,m}}}} , \\ {{{\hat {L}}}_{\vartheta }}\psi = \sum\limits_{l,m} {{{w}_{{l,m}}}{{\eta }_{{l,m}}}{{\psi }_{{i,j,k,l,m}}}} ,\quad {{{\hat {L}}}_{z}}\psi = \sum\limits_{l,m} {{{w}_{{l,m}}}{{\mu }_{l}}{{\psi }_{{i,j,k,l,m}}}} , \\ \end{gathered} $(2.19)
$\begin{gathered} \Delta r{{v}_{z}}\left( {f_{{j + 1/2}}^{{0,\vartheta }} - f_{{j - 1/2}}^{{0,\vartheta }}} \right) + {{v}_{r}}{{v}_{\vartheta }}\left( {f_{{k + 1/2}}^{{0,z}} - f_{{k - 1/2}}^{{0,z}}} \right) + {{v}_{\vartheta }}{{v}_{z}}\left( {{{A}_{{i + 1/2}}}f_{{i + 1/2}}^{{0,r}} - {{A}_{{i - 1/2}}}f_{{i - 1/2}}^{{0,r}}} \right) + {{\sigma }^{{00}}}V{{f}^{{0,0}}} = V{{Q}^{{0,0}}}, \\ \frac{1}{3}{{v}_{\vartheta }}{{v}_{z}}\left[ {\left( {{{A}_{{i + 1/2}}}f_{{i + 1/2}}^{{0,0}} - {{A}_{{i - 1/2}}}f_{{i - 1/2}}^{{0,0}}} \right) - C{{f}^{{0,0}}}} \right] + \left( {{{\sigma }^{{11}}}V + {{M}_{r}}C{{v}_{\vartheta }}{{v}_{z}}} \right){{f}^{{0,r}}} = V{{Q}^{{0,r}}}, \\ \frac{1}{3}\Delta r{{v}_{z}}\left( {f_{{j + 1/2}}^{{0,0}} - f_{{j - 1/2}}^{{0,0}}} \right) + \left( {{{\sigma }^{{11}}}V + {{M}_{\vartheta }}C{{v}_{\vartheta }}{{v}_{z}}} \right){{f}^{{0,\vartheta }}} = V{{Q}^{{0,\vartheta }}}, \\ \frac{1}{3}{{v}_{r}}{{v}_{\vartheta }}\left( {f_{{k + 1/2}}^{{0,0}} - f_{{k - 1/2}}^{{0,0}}} \right) + {{\sigma }^{{11}}}V{{f}^{{0,z}}} = V{{Q}^{{0,z}}}, \\ \end{gathered} $(2.20)
$\begin{gathered} {{v}_{\vartheta }}{{v}_{z}}\frac{1}{3}\left[ {{{A}_{{i + 1/2}}}\left( {\frac{{\Delta r}}{2} - {{\delta }^{c}}} \right)f_{{i + 1/2}}^{{0,0}} + {{A}_{{i - 1/2}}}\left( {\frac{{\Delta r}}{2} + {{\delta }^{c}}} \right)f_{{i - 1/2}}^{{0,0}} - {{v}_{r}}{{f}^{{0,0}}} - {{C}^{r}}{{f}^{{r,0}}} + C{{\delta }^{c}}{{f}^{{0,0}}}} \right] - \\ - \;{{v}_{\vartheta }}{{v}_{z}}{{\delta }^{c}}{{M}_{r}}C{{f}^{{0,r}}} + \left( {{{\sigma }^{{11}}}{{V}^{r}} + M_{r}^{r}{{C}^{r}}{{v}_{\vartheta }}{{v}_{z}}} \right){{f}^{{r,r}}} = {{V}^{r}}{{Q}^{{r,r}}}, \\ \end{gathered} $(2.21)
$v_{\vartheta }^{1}{{v}_{z}}\frac{1}{3}\left[ {\left( {{{A}_{{i + 1/2}}}f_{{i + 1/2}}^{{\vartheta ,0}} - {{A}_{{i - 1/2}}}f_{{i - 1/2}}^{{\vartheta ,0}}} \right) - C{{f}^{{\vartheta ,0}}}} \right] + \left( {{{\sigma }^{{11}}}{{V}^{\vartheta }} + M_{r}^{\vartheta }Cv_{\vartheta }^{1}{{v}_{z}}} \right){{f}^{{\vartheta ,r}}} = {{V}^{\vartheta }}{{Q}^{{\vartheta ,r}}},$(2.22)
$v_{z}^{1}{{v}_{\vartheta }}\frac{1}{3}\left[ {\left( {{{A}_{{i + 1/2}}}f_{{i + 1/2}}^{{z,0}} - {{A}_{{i - 1/2}}}f_{{i - 1/2}}^{{z,0}}} \right) - C{{f}^{{z,0}}}} \right] + \left( {{{\sigma }^{{11}}}{{V}^{z}} + M_{r}^{z}Cv_{z}^{1}{{v}_{\vartheta }}} \right){{f}^{{z,r}}} = {{V}^{z}}{{Q}^{{z,r}}},$(2.23)
$\begin{gathered} {{Q}^{{\alpha ,\vartheta }}} = {{\sigma }_{{s,1}}}\left( {{{\Phi }^{{\alpha ,\vartheta ,n + 1/2}}} - {{\Phi }^{{\alpha ,\vartheta ,n}}}} \right),\quad {{Q}^{{\alpha ,z}}} = {{\sigma }_{{s,1}}}\left( {{{\Phi }^{{\alpha ,z,n + 1/2}}} - {{\Phi }^{{\alpha ,z,n}}}} \right), \\ \alpha = 0,r,\vartheta ,z,\quad {{\sigma }^{{00}}} = \sigma - {{\sigma }_{{s,0}}},\quad {{\sigma }^{{11}}} = \sigma - {{\sigma }_{{s,1}}}, \\ \end{gathered} $(2.24)
$\begin{gathered} {{M}_{\vartheta }} = \frac{3}{{4\pi }}\sum\limits_{l,m} {{{\eta }_{{l,m}}}\left( {{{\alpha }_{{l,m + 1/2}}}\pi _{{l,m + 1/2}}^{\vartheta } - {{\alpha }_{{l,m - 1/2}}}\pi _{{l,m - 1/2}}^{\vartheta }} \right)} , \\ M_{r}^{r} = M_{r}^{\vartheta } = M_{r}^{z} \equiv {{{\bar {M}}}_{r}} = \frac{3}{{4\pi }}\sum\limits_{l,m} {{{\xi }_{{l,m}}}\left( {{{\alpha }_{{l,m + 1/2}}}\bar {\pi }_{{l,m + 1/2}}^{r} - {{\alpha }_{{l,m - 1/2}}}\bar {\pi }_{{l,m - 1/2}}^{r}} \right)} , \\ \end{gathered} $Величины $\pi _{{l,m \pm 1/2}}^{r}$, $\pi _{{l,m \pm 1/2}}^{\vartheta }$, $\bar {\pi }_{{l,m \pm 1/2}}^{r}$, $\bar {\pi }_{{l,m \pm 1/2}}^{\vartheta }$ в (2.24) могут быть вычислены с помощью следующих рекуррентных соотношений:
(2.25)
$\begin{gathered} \pi _{{l,m + 1/2}}^{r} = \left( {1 + P_{{l,m}}^{\xi }} \right){{\xi }_{{l,m}}} - P_{{l,m}}^{\xi }\pi _{{l,m - 1/2}}^{r},\quad \pi _{{l,1/2}}^{r} = {{\xi }_{{l,1/2}}}, \\ \pi _{{l,m + 1/2}}^{\vartheta } = \left( {1 + P_{{l,m}}^{\xi }} \right){{\eta }_{{l,m}}} - P_{{l,m}}^{\xi }\pi _{{l,m - 1/2}}^{\vartheta },\quad \pi _{{l,1/2}}^{\vartheta } = {{\eta }_{{l,1/2}}} = 0, \\ \bar {\pi }_{{l,m + 1/2}}^{r} = {{\xi }_{{l,m}}},\quad \bar {\pi }_{{l,1/2}}^{r} = {{\xi }_{{l,1/2}}},\quad \bar {\pi }_{{l,m + 1/2}}^{\vartheta } = {{\eta }_{{l,m}}},\quad \bar {\pi }_{{l,1/2}}^{\vartheta } = {{\eta }_{{l,1/2}}} = 0. \\ \end{gathered} $ к уравнениям (2.6), (2.9) и операторов ${{\hat {L}}_{0}}$ и ${{\hat {L}}_{z}}$ к уравнениям (2.7), (2.10)
к уравнениям (2.6), (2.9) и операторов ${{\hat {L}}_{0}}$ и ${{\hat {L}}_{z}}$ к уравнениям (2.7), (2.10)(2.26)
$\begin{gathered} {{f}^{{r,0}}} = {{A}^{{r,0}}}f_{{i + 1/2}}^{{0,0}} + {{A}^{{r,1}}}f_{{i + 1/2}}^{{0,r}} + {{B}^{{r,0}}}f_{{i - 1/2}}^{{0,0}} + {{B}^{{r,1}}}f_{{i - 1/2}}^{{0,r}} - \left( {{{A}^{{r,0}}} + {{B}^{{r,0}}}} \right){{f}^{{0,0}}} - \left( {{{A}^{{r,1}}} + {{B}^{{r,1}}}} \right){{f}^{{0,r}}}, \\ {{f}^{{r,r}}} = \frac{1}{3}{{A}^{{r,1}}}f_{{i + 1/2}}^{{0,0}} + {{A}^{{r,2}}}f_{{i + 1/2}}^{{0,r}} + \frac{1}{3}{{B}^{{r,1}}}f_{{i - 1/2}}^{{0,0}} + {{B}^{{r,2}}}f_{{i - 1/2}}^{{0,r}} - \frac{1}{3}\left( {{{A}^{{r,1}}} + {{B}^{{r,1}}}} \right){{f}^{{0,0}}} - \left( {{{A}^{{r,2}}} + {{B}^{{r,2}}}} \right){{f}^{{0,r}}}, \\ \end{gathered} $(2.27)
$\begin{gathered} {{f}^{{\vartheta ,0}}} = {{A}^{{\vartheta ,0}}}f_{{j + 1/2}}^{{0,0}} + {{A}^{{\vartheta ,1}}}f_{{j + 1/2}}^{{0,\vartheta }} + {{B}^{{\vartheta ,0}}}f_{{j - 1/2}}^{{0,0}} + {{B}^{{\vartheta ,1}}}f_{{j - 1/2}}^{{0,\vartheta }} - \left( {{{A}^{{\vartheta ,0}}} + {{B}^{{\vartheta ,0}}}} \right){{f}^{{0,0}}} - \left( {{{A}^{{\vartheta ,1}}} + {{B}^{{\vartheta ,1}}}} \right){{f}^{{0,\vartheta }}}, \\ {{f}^{{\vartheta ,\vartheta }}}\, = \,\frac{1}{3}{{A}^{{\vartheta ,1}}}f_{{j + 1/2}}^{{0,0}}\, + \,{{A}^{{\vartheta ,2}}}f_{{j + 1/2}}^{{0,\vartheta }}\, + \,\frac{1}{3}{{B}^{{\vartheta ,1}}}f_{{j - 1/2}}^{{0,0}}\, + \,{{B}^{{\vartheta ,2}}}f_{{j - 1/2}}^{{0,\vartheta }}\, - \,\frac{1}{3}\left( {{{A}^{{\vartheta ,1}}}\, + \,{{B}^{{\vartheta ,1}}}} \right){{f}^{{0,0}}}\, - \,\left( {{{A}^{{\vartheta ,2}}} + {{B}^{{\vartheta ,2}}}} \right){{f}^{{0,\vartheta }}}, \\ \end{gathered} $(2.28)
$\begin{gathered} {{f}^{{z,0}}} = {{A}^{{z,0}}}f_{{k + 1/2}}^{{0,0}} + {{A}^{{z,1}}}f_{{k + 1/2}}^{{0,z}} + {{B}^{{z,0}}}f_{{k - 1/2}}^{{0,0}} + {{B}^{{z,1}}}f_{{k - 1/2}}^{{0,z}} - \left( {{{A}^{{z,0}}} + {{B}^{{z,0}}}} \right){{f}^{{0,0}}} - \left( {{{A}^{{z,1}}} + {{B}^{{z,1}}}} \right){{f}^{{0,z}}}, \\ {{f}^{{z,z}}} = \frac{1}{3}{{A}^{{z,1}}}f_{{k + 1/2}}^{{0,0}} + {{A}^{{z,2}}}f_{{k + 1/2}}^{{0,z}} + \frac{1}{3}{{B}^{{z,1}}}f_{{k - 1/2}}^{{0,0}} + {{B}^{{z,2}}}f_{{k - 1/2}}^{{0,z}} - \frac{1}{3}\left( {{{A}^{{z,1}}} + {{B}^{{z,1}}}} \right){{f}^{{0,0}}} - \left( {{{A}^{{z,2}}} + {{B}^{{z,2}}}} \right){{f}^{{0,z}}}, \\ \end{gathered} $(2.29)
$\begin{gathered} {{A}^{{\vartheta ,0}}} = \frac{1}{{4\pi }}\sum\limits_{l,m} {{{w}_{{l,m}}}{{a}_{\vartheta }}} ,\quad {{A}^{{\vartheta ,1}}} = \frac{3}{{4\pi }}\sum\limits_{l,m} {{{w}_{{l,m}}}{{\eta }_{{l,m}}}{{a}_{\vartheta }}} ,\quad {{A}^{{\vartheta ,2}}} = \frac{3}{{4\pi }}\sum\limits_{l,m} {{{w}_{{l,m}}}\eta _{{l,m}}^{2}{{a}_{\vartheta }}} , \\ {{B}^{{\vartheta ,0}}} = \frac{1}{{4\pi }}\sum\limits_{l,m} {{{w}_{{l,m}}}{{b}_{\vartheta }}} ,\quad {{B}^{{\vartheta ,1}}} = \frac{3}{{4\pi }}\sum\limits_{l,m} {{{w}_{{l,m}}}{{\eta }_{{l,m}}}{{b}_{\vartheta }}} ,\quad {{B}^{{\vartheta ,2}}} = \frac{3}{{4\pi }}\sum\limits_{l,m} {{{w}_{{l,m}}}\eta _{{l,m}}^{2}{{b}_{\vartheta }}} , \\ \end{gathered} $(2.30)
${{f}^{{\vartheta ,0}}} = \frac{1}{2}\left( {f_{{i + 1/2}}^{{\vartheta ,0}} + f_{{i - 1/2}}^{{\vartheta ,0}}} \right) + \frac{3}{4}\left( {f_{{i + 1/2}}^{{\vartheta ,r}} - f_{{i - 1/2}}^{{\vartheta ,r}}} \right),\quad {{f}^{{\vartheta ,r}}} = \frac{1}{4}\left( {f_{{i + 1/2}}^{{\vartheta ,0}} - f_{{i - 1/2}}^{{\vartheta ,0}}} \right) + \frac{1}{2}\left( {f_{{i + 1/2}}^{{\vartheta ,r}} + f_{{i - 1/2}}^{{\vartheta ,r}}} \right),$(2.31)
${{f}^{{z,0}}} = \frac{1}{2}\left( {f_{{i + 1/2}}^{{z,0}} + f_{{i - 1/2}}^{{z,0}}} \right) + \frac{3}{4}\left( {f_{{i + 1/2}}^{{z,r}} - f_{{i - 1/2}}^{{z,r}}} \right),\quad {{f}^{{z,r}}} = \frac{1}{4}\left( {f_{{i + 1/2}}^{{z,0}} - f_{{i - 1/2}}^{{z,0}}} \right) + \frac{1}{2}\left( {f_{{i + 1/2}}^{{z,r}} + f_{{i - 1/2}}^{{z,r}}} \right),$(2.32)
${{f}^{{r,0}}} = \frac{1}{2}\left( {f_{{j + 1/2}}^{{r,0}} + f_{{j - 1/2}}^{{r,0}}} \right) + \frac{3}{4}\left( {f_{{j + 1/2}}^{{r,\vartheta }} - f_{{j - 1/2}}^{{r,\vartheta }}} \right),\quad {{f}^{{r,\vartheta }}} = \frac{1}{4}\left( {f_{{j + 1/2}}^{{r,0}} - f_{{j - 1/2}}^{{r,0}}} \right) + \frac{1}{2}\left( {f_{{j + 1/2}}^{{r,\vartheta }} + f_{{j - 1/2}}^{{r,\vartheta }}} \right),$(2.33)
${{f}^{{z,0}}} = \frac{1}{2}\left( {f_{{j + 1/2}}^{{z,0}} + f_{{j - 1/2}}^{{z,0}}} \right) + \frac{3}{4}\left( {f_{{j + 1/2}}^{{z,\vartheta }} - f_{{j - 1/2}}^{{z,\vartheta }}} \right),\quad {{f}^{{z,\vartheta }}} = \frac{1}{4}\left( {f_{{j + 1/2}}^{{z,0}} - f_{{j - 1/2}}^{{z,0}}} \right) + \frac{1}{2}\left( {f_{{j + 1/2}}^{{z,\vartheta }} + f_{{j - 1/2}}^{{z,\vartheta }}} \right),$(2.34)
${{f}^{{r,0}}} = \frac{1}{2}\left( {f_{{k + 1/2}}^{{r,0}} + f_{{k - 1/2}}^{{r,0}}} \right) + \frac{3}{4}\left( {f_{{k + 1/2}}^{{r,z}} - f_{{k - 1/2}}^{{r,z}}} \right),\quad {{f}^{{r,z}}} = \frac{1}{4}\left( {f_{{k + 1/2}}^{{r,0}} - f_{{k - 1/2}}^{{r,0}}} \right) + \frac{1}{2}\left( {f_{{k + 1/2}}^{{r,z}} + f_{{k - 1/2}}^{{r,z}}} \right),$(2.35)
${{f}^{{\vartheta ,0}}} = \frac{1}{2}\left( {f_{{k + 1/2}}^{{\vartheta ,0}} + f_{{k - 1/2}}^{{\vartheta ,0}}} \right) + \frac{3}{4}\left( {f_{{k + 1/2}}^{{\vartheta ,z}} - f_{{k - 1/2}}^{{\vartheta ,z}}} \right),\quad {{f}^{{\vartheta ,z}}} = \frac{1}{4}\left( {f_{{k + 1/2}}^{{\vartheta ,0}} - f_{{k - 1/2}}^{{\vartheta ,0}}} \right) + \frac{1}{2}\left( {f_{{k + 1/2}}^{{\vartheta ,z}} + f_{{k - 1/2}}^{{\vartheta ,z}}} \right).$(2.36)
$l_{0}^{r}f_{{1/2,j,k}}^{{\beta ,0}} + 3l_{1}^{r}f_{{1/2,j,k}}^{{\beta ,r}} = 0,\quad m_{0}^{r}f_{{I + 1/2,j,k}}^{{\beta ,0}} + 3m_{1}^{r}f_{{I + 1/2,j,k}}^{{\beta ,r}} = \lambda _{{j,k}}^{{\beta ,r}},\quad \beta = 0,\vartheta ,z,$(2.37)
$\begin{gathered} l_{p}^{r} = \sum\limits_{{{\xi }_{{l,m}}} > 0} {{{w}_{{l,m}}}{{\xi }_{{l,m}}}\left( {\xi _{{l,m}}^{p} - \sum\limits_{{{\xi }_{{l',m'}}} < 0} {{{w}_{{l'm'}}}\xi _{{l'm'}}^{p}R_{{lm,l'm'}}^{{\operatorname{int} }}} } \right)} ,\quad m_{p}^{r} = \sum\limits_{{{\xi }_{{l,m}}} < 0} {{{w}_{{l,m}}}{{\xi }_{{l,m}}}\left( {\xi _{{l,m}}^{p} - \sum\limits_{{{\xi }_{{l'm'}}} > 0} {{{w}_{{l',m'}}}\xi _{{l',m'}}^{p}R_{{lm,l'm'}}^{{{\text{ext}}}}} } \right)} , \\ p = 0,1,\quad \lambda _{{j,k}}^{{\beta ,r}} = 4\pi \sum\limits_{{{\xi }_{{l,m}}} < 0} {{{w}_{{l,m}}}{{\xi }_{{l,m}}}\sum\limits_{{{\xi }_{{l'm'}}} > 0} {{{w}_{{l'm'}}}R_{{lm,l'm'}}^{{ext}}\left( {\psi _{{I + 1/2,j,k,l'm'}}^{{\beta ,n + 1/2}} - \psi _{{I + 1/2,j,k,l'm'}}^{{\beta ,n}}} \right)} } . \\ \end{gathered} $(2.38)
$l_{0}^{\vartheta }f_{{i,1/2,k}}^{{\beta ,0}} + 3l_{1}^{\vartheta }f_{{i,1/2,k}}^{{\beta ,\vartheta }} = 0,\quad m_{0}^{\vartheta }f_{{i,J + 1/2,k}}^{{\beta ,0}} + 3m_{1}^{\vartheta }f_{{i,J + 1/2,k}}^{{\beta ,\vartheta }} = \lambda _{{i,k}}^{{\beta ,\vartheta }},\quad \beta = 0,r,z,$(2.39)
$\begin{gathered} l_{p}^{\vartheta }\, = \,\sum\limits_{{{\eta }_{{l,m}}} > 0} {{{w}_{{l,m}}}{{\eta }_{{l,m}}}\left( {\eta _{{l,m}}^{p}\, - \,\sum\limits_{{{\eta }_{{l',m'}}} < 0} {{{w}_{{l',m'}}}\eta _{{l',m'}}^{p}R_{{lm,l',m'}}^{0}} } \right)} ,\quad m_{p}^{\vartheta }\, = \,\sum\limits_{{{\eta }_{{l,m}}} < 0} {{{w}_{{l,m}}}{{\eta }_{{l,m}}}\left( {\eta _{{l,m}}^{p}\, - \,\sum\limits_{{{\eta }_{{l',m'}}} > 0} {{{w}_{{l',m'}}}\eta _{{l',m'}}^{p}R_{{lm,l',m'}}^{{{\text{end}}}}} } \right)} , \\ p = 0,1,\quad \lambda _{{i,k}}^{{\beta ,\vartheta }} = 4\pi \sum\limits_{{{\eta }_{{l,m}}} < 0} {{{w}_{{l,m}}}{{\eta }_{{l,m}}}\sum\limits_{{{\eta }_{{l',m'}}} > 0} {{{w}_{{l',m'}}}R_{{lm,l',m'}}^{{{\text{end}}}}\left( {\psi _{{i,J + 1/2,k,l',m'}}^{{\beta ,n + 1/2}} - \psi _{{i,J + 1/2,k,l',m'}}^{{\beta ,n}}} \right)} } . \\ \end{gathered} $(2.40)
$\begin{gathered} l_{0}^{\vartheta }\left( {f_{{i,1/2,k}}^{{\beta ,0}} - f_{{i,J + 1/2,k}}^{{\beta ,0}}} \right) + 3l_{1}^{\vartheta }\left( {f_{{i,1/2,k}}^{{\beta ,\vartheta }} - f_{{i,J + 1/2,k}}^{{\beta ,\vartheta }}} \right) = \lambda _{{i,k}}^{{\beta ,\vartheta ,{\text{end}}}}, \\ m_{0}^{\vartheta }\left( {f_{{i,J + 1/2,k}}^{{\beta ,0}} - f_{{i,1/2,k}}^{{\beta ,0}}} \right) + 3m_{1}^{\vartheta }\left( {f_{{i,J + 1/2,k}}^{{\beta ,\vartheta }} - f_{{i,1/2,k}}^{{\beta ,\vartheta }}} \right) = \lambda _{{i,k}}^{{\beta ,\vartheta ,0}},\quad \beta = 0,r,z, \\ \end{gathered} $(2.41)
$\begin{gathered} l_{p}^{\vartheta } = \sum\limits_{{{\eta }_{{l,m}}} > 0} {{{w}_{{l,m}}}{{\eta }_{{l,m}}}\eta _{{l,m}}^{p}} ,\quad m_{p}^{\vartheta } = \sum\limits_{{{\eta }_{{l,m}}} < 0} {{{w}_{{l,m}}}{{\eta }_{{l,m}}}\eta _{{l,m}}^{p}} ,\quad p = 0,1, \\ \lambda _{{i,k}}^{{\beta ,\vartheta ,0}} = 4\pi \sum\limits_{{{\eta }_{{l,m}}} < 0} {{{w}_{{l,m}}}{{\eta }_{{l,m}}}\left( {\psi _{{i,1/2,k,l',m'}}^{{\beta ,n + 1/2}} - \psi _{{i,1/2,k,l',m'}}^{{\beta ,n}}} \right)} , \\ \lambda _{{i,k}}^{{\beta ,\vartheta ,{\text{end}}}} = 4\pi \sum\limits_{{{\eta }_{{l,m}}} > 0} {{{w}_{{l,m}}}{{\eta }_{{l,m}}}\left( {\psi _{{i,J + 1/2,k,l',m'}}^{{\beta ,n + 1/2}} - \psi _{{i,J + 1/2,k,l',m'}}^{{\beta ,n}}} \right)} . \\ \end{gathered} $(2.42)
$l_{0}^{z}f_{{i,j,1/2}}^{{\beta ,0}} + 3l_{1}^{z}f_{{i,j,1/2}}^{{\beta ,z}} = 0,\quad m_{0}^{z}f_{{i,j,K + 1/2}}^{{\beta ,0}} + 3m_{1}^{z}f_{{i,j,K + 1/2}}^{{\beta ,z}} = \lambda _{{i,j}}^{{\beta ,z}},\quad \beta = 0,r,\vartheta ,$(2.43)
$\begin{gathered} l_{p}^{z} = \sum\limits_{{{\mu }_{l}} > 0} {{{w}_{{l,m}}}{{\mu }_{l}}\left( {\mu _{l}^{p} - \sum\limits_{{{\mu }_{{l',m'}}} < 0} {{{w}_{{l',m'}}}\mu _{{l'}}^{p}R_{{lm,l',m'}}^{{{\text{bot}}}}} } \right)} ,\quad m_{p}^{z} = \sum\limits_{{{\mu }_{l}} < 0} {{{w}_{{l,m}}}{{\mu }_{l}}\left( {\mu _{l}^{p} - \sum\limits_{{{\mu }_{{l'}}} > 0} {{{w}_{{l',m'}}}\mu _{{l'}}^{p}R_{{lm,l',m'}}^{{{\text{top}}}}} } \right)} , \\ p = 0,1,\quad \lambda _{{i,k}}^{{\beta ,z}} = 4\pi \sum\limits_{{{\mu }_{l}} < 0} {{{w}_{{l,m}}}{{\mu }_{l}}\sum\limits_{{{\mu }_{{l'}}} > 0} {{{w}_{{l',m'}}}R_{{lm,l',m'}}^{{{\text{top}}}}\left( {\psi _{{i,j,K + 1/2,l',m'}}^{{\beta ,n + 1/2}} - \psi _{{i,j,K + 1/2,l',m'}}^{{\beta ,n}}} \right).} } \\ \end{gathered} $(2.44)
$\lambda _{{j,k}}^{{\beta ,r}} = \lambda _{{i,k}}^{{\beta ,\vartheta }} = \lambda _{{i,j}}^{{\beta ,z}} = 0,\quad \lambda _{{i,k}}^{{\beta ,\vartheta ,0}} = \lambda _{{i,k}}^{{\beta ,\vartheta ,{\text{end}}}} = 0.$(2.45)
$f_{{i,1/2,k}}^{{\beta ,0}} = f_{{i,J + 1/2,k}}^{{\beta ,0}},\quad f_{{i,1/2,k}}^{{\beta ,\vartheta }} = f_{{i,J + 1/2,k}}^{{\beta ,\vartheta }}.$Полученная сеточная аппроксимация ${{P}_{1}}$ системы для ускоряющих поправок является следствием используемой разностной аппроксимации уравнения переноса, что является необходимым условием для построения согласованной схемы ускорения.
Учитывая, что в 2D и 3D геометриях в задачах с существенной ролью анизотропии рассеяния, когда выполняется неравенство
(2.46)
$\lambda = {{\mu }_{0}}c{\text{/}}(1 - {{\mu }_{0}}c) > 1,\quad {\text{г д е }}\quad {{\mu }_{0}} = {{\sigma }_{{s1}}}{\text{/}}{{\sigma }_{{s0}}},\quad c = {{\sigma }_{{s0}}}{\text{/}}{{\sigma }_{t}},$3. $K{{P}_{1}}$-СХЕМА УСКОРЕНИЯ ВНУТРЕННИХ ИТЕРАЦИЙ В $x,y,z$ ГЕОМЕТРИИ
Односкоростное уравнение переноса в $x,y,z$ геометрии имеет вид (1.15). Все расчетные формулы $K{{P}_{1}}$-схемы для $x,y,z$ геометрии получаются из соответствующих формул для $r,\vartheta ,z$ геометрии путем замены:
(3.1)
$\begin{gathered} r \to x,\quad \vartheta \to y,\quad {{A}_{{i \pm 1/2}}} \to 1,\quad C \to 0,\quad {{C}^{r}} \to 0,\quad {{\delta }^{c}} \to 0,\quad {{v}_{i}} \to \Delta {{x}_{i}}, \\ {{M}_{r}} \to 0,\quad {{M}_{\vartheta }} \to 0,\quad {{{\bar {M}}}_{r}} \to 0,\quad {{{\bar {M}}}_{\vartheta }} \to 0. \\ \end{gathered} $4. ЧИСЛЕННЫЕ ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ $K{{P}_{1}}$-СХЕМЫ УСКОРЕНИЯ ВНУТРЕННИХ ИТЕРАЦИЙ В 3D ГЕОМЕТРИИ
В данном разделе мы приведем некоторые численные результаты, позволяющие оценить эффективность вышеописанного варианта согласованной $K{{P}_{1}}$-схемы. Использовался поточечный критерий сходимости внутренних итераций по скалярному потоку $\varepsilon = {{10}^{{ - 4}}}$. Для решения ${{P}_{1}}$ системы использовался циклический МР с длиной цикла $J = 16$.
При расчете тестовых задач 1–4 использовались LD и LB-схемы с весом ${{P}_{\xi }} = 1$ в дополнительном уравнении (1.14) по угловой переменной, WLD и WLB-схемы с весом ${{P}_{\xi }}$, выбираемым посредством AWDD-схемы (см. [19], [10]), обеспечивающей положительность экстраполяции по угловой переменной. Использовался следующий вариант алгоритма выбора веса ${{P}_{\xi }}$:
(4.1)
${{P}_{\xi }} = \left\{ \begin{gathered} 1,\quad {{U}_{\xi }} \leqslant U_{\xi }^{0}, \hfill \\ P\left( {{{U}_{\xi }},{{\delta }_{\xi }}} \right),\quad {{U}_{\xi }} > U_{\xi }^{0}, \hfill \\ \end{gathered} \right.\quad {{\delta }_{\xi }} = \frac{{{{\alpha }_{{l,m + 1/2}}}}}{{{{\alpha }_{{l,m - 1/2}}} + {{\alpha }_{{l,m + 1/2}}}}},\quad {{U}_{\xi }} = b_{\xi }^{'}\left| {{{u}_{\xi }}} \right|,\quad {{u}_{\xi }} = \frac{{{{\psi }_{{m - 1/2}}} - \psi }}{\psi },$В качестве критерия сходимости итераций МР использовался поблочный критерий (уравнение (4.4) из [10]) с размером ребра блока $N = 3$ и ${{\varepsilon }_{{P1}}} = 0.4$. Расчетные времена приведены для ПК Intel Core i7 4770K.
Прежде всего представим результаты использования $K{{P}_{1}}$-схемы для расчета двух тестовых задач из работы [5], обобщенных на случай $x,y,z$ геометрии. Геометрия и состав зон для этих задач для случая $x,y$ геометрии определены на фиг. 1 (задача 1, EIR-2) и фиг. 2 (задача 2, железо-водная композиция). Эти стандартные задачи обычно используются, чтобы продемонстрировать, как работает алгоритм ускорения при решении сложных задач. Успешное решение этих задач, как правило, невозможно без использования согласованных схем ускорения.
Фиг. 1.
Сечение 3D расчетной области тестовой задачи EIR2 [5] в $x,y,z$ геометрии при $18 < z < 78$. Области $0 < z < 18$ и $78 < z < 96$ заполнены материалом 5 в пределах $0 < x < 96$, $0 < y < 86$.
Фиг. 2.
Сечение 3D железо-водной композиции [5] в $x,y,z$ геометрии при $0 < z < 12$. Расположение зон и источника по оси $z$ повторяет их расположение по осям $x$ и $y$ (композиция полностью симметрична по переменным $x$, $y$ и $z$).

При переходе к $x,y,z$ геометрии в задаче 1 полагалось, что поперечное сечение 3D расчетной области при $18 < z < 78$ совпадает с приведенным на фиг. 1, а области $0 < z < 18$ и $78 < z < 96$ заполнены материалом 5 (т.е. материалом отражателя) в пределах $0 < x < 96$, $0 < y < 86$. При переходе к $x,y,z$ геометрии в задаче 2 полагалось, что поперечное сечение 3D расчетной области при $0 < z < 12$ совпадает с приведенным на фиг. 2, на нижней границе области используется условие зеркального отражения, а расположение зон и источника по оси $z$ повторяет их расположение по осям $x$ и $y$ (композиция полностью симметрична по переменным $x$, $y$ и $z$).
В табл. 1 приведено число внутренних итераций, требуемое для решения задач 1 и 2 без ускорения и при использовании $K{{P}_{1}}$-схемы в сочетании с циклическим МР для решения ${{P}_{1}}$ системы. В квадратных и круглых скобках приведены соответственно среднее (по внутренним итерациям) число итераций МР и процессорное время (мин); значение параметра $n \geqslant 1$ показывает, что задача считалась с увеличенной в $10 \times {{2}^{n}}$ начальной верхней границей спектра $\Lambda $ для достижения устойчивости (или повышения эффективности) МР.
Таблица 1
| Задача | Метод | |||||||
|---|---|---|---|---|---|---|---|---|
| Без ускорения | $K{{P}_{1}}$ + МР | |||||||
| Step | AWDD | LD | LB | Step | AWDD | LD | LB | |
| Задача 1. Композиция EIR-2 в $x,y,z$ геометрии, сетка 112 × 100 × 112, ${{S}_{8}}{{P}_{0}}$ | 148 (2.58) | 170 (4.47) | 172 (14.8) | 172 (14.8) | 5 [10.4] (0.25) | 16 [15.1] (1.08) n = 2 |
9 [8.9] (1.8) | 13 [13.3] (3.1) n = 4 |
| Задача 2. Железо-водная композиция в $x,y,z$ геометрии, сетка 40 × 40 ×40, ${{S}_{8}}{{P}_{1}}$ | 938 (0.85) | 1282 (2.04) | 1328 (6.26) | 1329 (6.55) | 7 [15.4] (0.019) | 16 [13.9] (0.049) n = 2 |
13 [10] (0.143) | 11 [14.4] (0.135) n = 2 |
В табл. 2 приведено суммарное (по 26 группам) число внутренних итераций при расчете модели быстрого реактора (задача 3, фиг. 3) в $r,\vartheta ,z$ геометрии на пространственной сетке (82 × 3 × 35) для сектора зеркальной симметрии 60° в ${{S}_{8}}{{P}_{1}}$ приближении при точности сходимости внутренних итераций $\varepsilon = {{10}^{{ - 3}}}$. В активной зоне был задан пространственно постоянный источник со спектром деления ${}^{{235}}U$. В данной задаче отсутствует зависимость источника и решения от азимутального угла $\vartheta $. Таким образом, расчет в $r,\vartheta ,z$ геометрии приводит к результатам, идентичным расчету в $r,z$ геометрии. В круглых скобках приведено процессорное время (мин). Данная задача позволяет продемонстрировать эффект ускорения для типичной задачи радиационной защиты.
Таблица 2
| Метод | |||||
|---|---|---|---|---|---|
| Без ускорения | $K{{P}_{1}}$ + МР | ||||
| AWDD | WLD | WLB | AWDD | WLD | WLB |
| 961 (0.8) | 961 (2.14) | 960 (2.13) | 163 (0.2) | 164 (0.57) | 153 (0.63) |
Фиг. 3.
Сечение 3D модели быстрого реактора в $r,\vartheta ,z$ геометрии при $0 < \vartheta < {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}$.
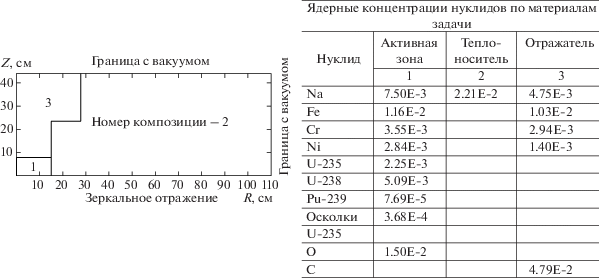
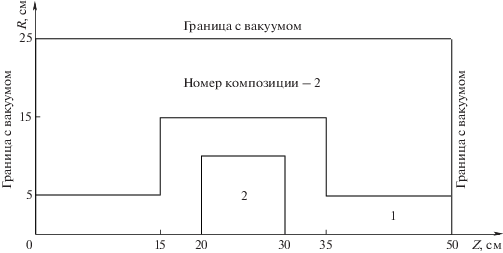
Применим далее рассматриваемый алгоритм к решению сильно-гетерогенной задачи с малым поглощением из [23] в $r,\vartheta ,z$ геометрии (задача 4). Данная задача позволяет продемонстрировать, как работает схема ускорения в экстремальных условиях. Расчетная область этой задачи представляет собой гетерогенный цилиндр радиусом 25 см и высотой 50 см. Аксиальное сечение задачи изображено на фиг. 4. Зависимость геометрии и источников от переменной $\vartheta $ отсутствует. Внутренний цилиндрический канал заполнен материалом 1. Окружающая канал среда, а также центральный диск внутри канала заполнены материалом 2. Плотность материала 1 существенно меньше плотности материала 2. На нижний торец канала ($z = 0$, $0 \leqslant r \leqslant 5$ см) падает единичный изотропный источник. Имеется также внутренний изотропный источник с интенсивностью ${{10}^{{ - 6}}}$ частиц/см$^{3}$, распределенный равномерно по всей расчетной области. В $r,\vartheta ,z$ геометрии расчет проводился для сектора симметрии $0 < \vartheta < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. Для случая $x,y,z$ геометрии может быть определена аналогичная задача, расчетная область которой представляет собой гетерогенный параллелепипед с каналом, имеющим квадратное сечение. Аксиальное сечение этого параллелепипеда в плоскости $OXZ$совпадает с аксиальным сечением гетерогенного цилиндра (фиг. 4). В $x,y,z$ геометрии расчет этой задачи может быть выполнен для 1/4 расчетной области с условиями зеркального отражения на границах $x = 0$ и $y = 0$.
В табл. 3 и 4 для некоторого набора значений полных сечений материалов 1 (${{\sigma }_{{t,1}}}$) и 2 (${{\sigma }_{{t,2}}}$), а также величин отношения сечения рассеяния к полному сечению $c = {{{{\sigma }_{s}}} \mathord{\left/ {\vphantom {{{{\sigma }_{s}}} {{{\sigma }_{t}}}}} \right. \kern-0em} {{{\sigma }_{t}}}}$, приведено число внутренних итераций при решении задачи 4 в $r,\vartheta ,z$ и $x,y,z$ геометриях на пространственной сетке 50 × 3 × 100 и 50 × 50 × 100 шагов соответственно с использованием шаговой (Step), AWDD, LD и LB-схем в ${{S}_{6}}$ приближении с точностью сходимости итераций ${{10}^{{ - 5}}}$ при точности решения $P1$ системы для ускоряющих поправок ${{\varepsilon }_{{P1}}}$ = 0.5 для Step и AWDD-схем и ${{\varepsilon }_{{P1}}}$ = 0.4 для LD и LB-схем.
Таблица 3
| $r,\vartheta ,z$ Геометрия | ${{\sigma }_{{t,2}}}$ | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 102 | 101 | ||||||||
| ${{\sigma }_{{t,1}}}$ | $c$ | Step | AWDD | LD | LB | Step | AWDD | LD | LB |
| 10–3 | 0.999 | 37 | 74 | 63 | 105 | 45 | 76 | 97 | 101 (n = 4) |
| 0.99 | 21 | 37 | 48 | 74 | 35 | 50 | 41 | 55 | |
| 10–3 | 0.999 | 30 | 61 | 61 | 65 | 32 | 61 | 61 | 65 (n = 2) |
| 0.99 | 20 | 47 | 35 | 49 | 29 | 47 | 35 | 49 | |
| 100 | 0.999 | 8 | 24 | 23 | 22 | 12 | 17 | 17 | 17 (n = 2) |
| 0.99 | 7 | 22 | 14 | 31 | 8 | 15 | 15 | 15 | |
Таблица 4
| $x,y,z$ Геометрия | ${{\sigma }_{{t,2}}}$ | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 102 | 101 | ||||||||
| ${{\sigma }_{{t,1}}}$ | $c$ | Step | AWDD | LD | LB | Step | AWDD | LD | LB |
| 10–3 | 0.999 | 37 | a* | a | a | 46 | a | a | a |
| 0.99 | 15 | 82 | 37 | 68 (n = 2) | 33 | 48 | 42 | 49 (n = 2) | |
| 10–3 | 0.999 | 30 | a | a | a | 32 | a | a | a |
| 0.99 | 14 | 62 | 34 | 64 (n = 2) | 28 | 41 | 35 | 47 (n = 2) | |
| 100 | 0.999 | 8 | a | 26 (n = 2) | a | 11 | a | 18 (n = 2) | a |
| 0.99 | 9 | 22 | 14 | 36 (n = 2) | 9 | 20 | 13 | 21 (n = 2) | |
Как следует из результатов, приведенных в табл. 3, в $r,\vartheta ,z$ геометрии эффективность согласованной $K{{P}_{1}}$-схемы ускорения падает по мере увеличения отношения ${{{{\sigma }_{{t2}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{t2}}}} {{{\sigma }_{{t1}}}}}} \right. \kern-0em} {{{\sigma }_{{t1}}}}}$ и увеличения доли рассеяния, хотя и остается на приемлемом уровне. При решении задачи 4 в $x,y,z$ геометрии (табл. 4) тенденция аналогична, но при ${{\sigma }_{{t,1}}} \leqslant {{10}^{{ - 2}}}$ и $c = 0.999$ $K{{P}_{1}}$-схема ускорения остается работоспособной только в сочетании со Step-схемой.
5. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ ИСПОЛЬЗОВАНИЯ AWDD, LD И LB-СХЕМ В ТРЕХМЕРНЫХ ГЕОМЕТРИЯХ
В данном разделе мы приведем численные результаты для трехмерных $x,y,z$ и $r,\vartheta ,z$ геометрий, демонстрирующие сравнительную точность DD, AWDD, LD и LB-схем. Использовалось два варианта AWDD-схемы, отличающихся выбором корректирующих функций (П.12) и (П.13) и параметров монотонизации ${{b}_{r}} = {{b}_{\vartheta }} = {{b}_{z}} = 2$, ${{b}_{\xi }} = 1$ и ${{b}_{r}} = {{b}_{\vartheta }} = {{b}_{z}} = 1.6$, ${{b}_{\xi }} = 1$ [10], обозначенные как AWDD1 и AWDD2 соответственно.
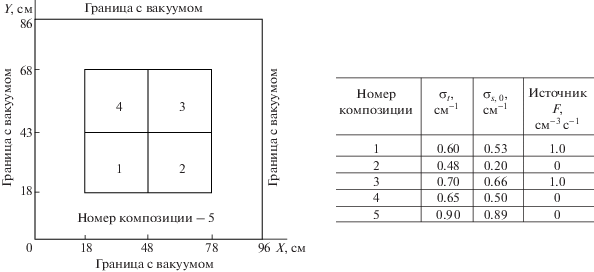
В качестве тестовой задачи 5 рассмотрим обобщение одногрупповой 4-х зонной задачи с изотропным рассеянием в плоской геометрии (см. [24]) на случай 3D $x,y,z$ геометрии (см. фиг. 5). Вариант этой же задачи, но для $r,\vartheta ,z$ геометрии, представляет собой сектор симметрии $60^\circ $ с продольным сечением, получаемым путем замены на фиг. 5 $x \to r$.
Фиг. 5.
Задача 5 в $x,y,z$ геометрии [24]. Указаны полное сечение $\sigma $, сечение рассеяния ${{\sigma }_{s}}$, внутренний изотропный источник $F$ и число шагов пространственной сетки по зонам по переменным $x$, $y$ и $z$.
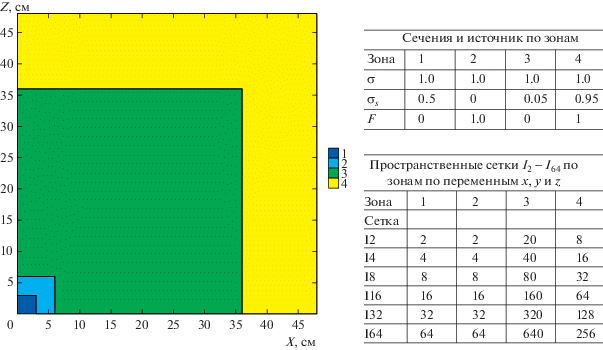
В качестве точного решения задачи 5 в $x,y,z$ геометрии использовалось ее решение, полученное с использованием LD-схемы 3-го порядка точности на равномерной пространственной сетке с шагом $\Delta x = \Delta r = \Delta z = {3 \mathord{\left/ {\vphantom {3 {16}}} \right. \kern-0em} {16}}$ (число пространственных интервалов по зонам по каждой из пространственных переменных составило: 16 + 16 + 160 + 64) с квадратурой Лебедева на сфере ${{L}_{{16,2}}}$ [25]. Квадратура Лебедева ${{L}_{{N,M}}}$ задается посредством двух параметров: N – порядок квадратуры (число параллелей на полусфере), N = 2, 4, 6, 8, …; M – порядок аксиальной симметрии квадратуры: M = = 1, 2, … . В качестве точного решения задачи в $r,\vartheta ,z$ геометриях использовалось ее решение, полученное с использованием LD-схемы 3-го порядка точности на равномерной пространственной сетке с шагом $\Delta x = \Delta r = \Delta z = {3 \mathord{\left/ {\vphantom {3 {64}}} \right. \kern-0em} {64}}$ (число пространственных интервалов по радиальным и аксиальным зонам составило: 64 + 64 + 640 + 256, по азимутальной зоне, состоящей из сектора симметрии $60^\circ $, – 3 интервала) с квадратурой ${{L}_{{16,2}}}$. Точность сходимости итераций составляла ${{10}^{{ - 9}}}$. Для ускорения внутренних итераций использовалась согласованная $K{{P}_{1}}$-схема ускорения итераций, что позволило уменьшить число внутренних итераций в рассматриваемой задаче с примерно 300 до 13–22.
В табл. 5 и 6 (для $x,y,z$ геометрии), 7 и 8 (для $r,\vartheta ,z$ геометрии) показаны относительные ошибки ${{\delta }_{{{\text{average}}}}}$ и ${{\delta }_{{{\text{sum}}}}}$ (5.1) в расчете нулевого пространственного момента скалярного потока $\Phi _{{i,j,k}}^{{(0)}}$ и полного числа частиц $\sum\nolimits_{i,j,k} {\Phi _{{i,j,k}}^{{(0)}}{{V}_{{i,j,k}}}} $.В скобках указано количество пространственных ячеек с отрицательным значением скалярного потока
(5.1)
${{\delta }_{{{\text{average}}}}} = \mathop {\max }\limits_{i,j,k \in {{K}_{l}}} \frac{{\Phi _{{i,j,k}}^{{(0)}} - \Phi _{{i,j,k}}^{{(0)ex}}}}{{\Phi _{{i,j,k}}^{{(0)ex}}}},\quad {{\delta }_{{{\text{sum}}}}} = \frac{{\sum\limits_{i,j,k}^{} {\Phi _{{i,j,k}}^{{(0)}}{{V}_{{i,j,k}}}} - \int\limits_0^X {\int\limits_0^Y {\int\limits_0^Z {{{\Phi }^{{ex}}}(x,y,z)dV} } } }}{{\int\limits_0^X {\int\limits_0^Y {\int\limits_0^Z {{{\Phi }^{{ex}}}(x,y,z)dV} } } }}.$Из табл. 5–8 можно сделать следующие выводы. Использование DD-схемы для решения задачи 5 в $x,y,z$ и $r,\vartheta ,z$ геометриях для каждой из использованных пространственных сеток приводит к появлению отрицательных скалярных потоков. Для LD или LB-схем уменьшение шага пространственной сетки приводит к исчезновению отрицательных потоков. При этом не наблюдается проблем со сходимостью итерационного процесса. При использовании же редких пространственных сеток LD и, в особенности, LB-схема нуждаются в коррекции отрицательных потоков.
Таблица 5
| $x,y,z$ Геометрия, ${{\delta }_{{{\text{average}}}}}$, % | ||||||
|---|---|---|---|---|---|---|
| Шаг $\Delta x$, $\Delta z$ | Зона | Схема | ||||
| DD | AWDD1 | AWDD2 | LD | LB | ||
| 3/2 | 1 | –7.1E+1 | 4.1E+1 | 4.3E+1 | –1.1E+1 | 1.3E+1 |
| 2 | 1.2E+1 | –3.7E+0 | –3.7E+0 | –2.5E+0 | 2.0E+0 | |
| 3 | 6.0E+8 (6388) | 7.9E+3 | 8.5E+3 | –5.8E+2 (645) | 1.5E+6 (278) | |
| 4 | –1.4E+1 | –1.9E+1 | –1.8E+1 | –5.0E+0 | –1.2E+0 | |
| 3/4 | 1 | –1.6E+1 | 6.0E+0 | 9.5E+0 | –1.8E+0 | 2.2E+0 |
| 2 | –1.0E+1 | 6.6E+0 | 6.8E+0 | –2.5E+0 | –1.1E+0 | |
| 3 | –1.3E+7 (34 477) | 2.0E+2 | 2.7E+2 | –5.5E+1 | 1.7+3 (10) | |
| 4 | –1.0E+1 | –1.3E+1 | 1.3E+1 | –3.0E+0 | 6.3E–1 | |
| 3/8 | 1 | –4.9E+0 | –3.2E+0 | –3.3E+0 | 6.9E–1 | 6.4E–1 |
| 2 | –8.6E+0 | 1.0E+1 | 7.6E+0 | –2.0E+0 | –7.7E–1 | |
| 3 | –5.8E+6 (148 033) | 6.7E+1 | 3.2E+1 | 1.4E+1 | –2.9E+1 | |
| 4 | –6.8E+0 | 1.4E+1 | 1.1E+1 | –1.8E+0 | –4.2E–1 | |
| 3/16 | 1 | –1.5E+0 | 1.3E+0 | 1.2E+0 | ||
| 2 | –4.8E+0 | 1.4E+1 | 1.4E+1 | |||
| 3 | –4.7E+6 (1 045 539) | 5.1E+1 | 3.5E+1 | |||
| 4 | –3.2E+0 | 1.5E+1 | 1.5E+1 | |||
Таблица 6
| $x,y,z$ Геометрия, ${{\delta }_{{{\text{sum}}}}}$, % | |||||
|---|---|---|---|---|---|
| Шаг $\Delta x$, $\Delta z$ | Схема | ||||
| DD | AWDD1 | AWDD2 | LD | LB | |
| 3/2 | –6.5E–2 | –3.8E+0 | –4.2E+0 | –2.6E–1 | –3.2E–2 |
| 3/4 | –1.9E–2 | –1.5E+0 | –1.6E+0 | –4.8E–2 | –9.3E–4 |
| 3/8 | –3.9E–3 | –4.9E–1 | –5.3E–1 | –7.3E–3 | 5.9E–4 |
| 3/16 | 1.1E–4 | –1.5E–1 | –1.6E–1 | –1.8E–3 | –5.0E–4 |
Таблица 7.
Относительная ошибка аппроксимации ${{\delta }_{{{\text{average}}}}}$ (5) при решении задачи 5 (фиг. 5) в $r,\vartheta ,z$ геометрии с квадратурой ${{L}_{{16,2}}}$, %. В скобках указано количество пространственных ячеек с отрицательным значением скалярного потока
| $r,\vartheta ,z$ Геометрия, ${{\delta }_{{{\text{average}}}}}$, % | ||||||
|---|---|---|---|---|---|---|
| Шаг $\Delta r$, $\Delta z$ | Зона | Схема | ||||
| DD | AWDD1 | AWDD2 | LD | LB | ||
| 3/2 | –4.8E+1 | 3.6E+1 | 3.8E+1 | –7.5E+0 | 1.1E+1 | |
| 7.4E+0 | –3.0E+0 | –3.0E+0 | –1.6E+0 | 1.6E+0 | ||
| 8.7E+7 (810) | 5.5E+3 | 5.9E+3 | –3.0E+2 (45) | 2.9E+5 (39) | ||
| –8.6E+0 | –1.4E+1 | –1.4E+1 | –3.1E+0 | 9.6E–1 | ||
| 3/4 | 1 | –1.2E+1 | 5.1E+0 | 7.5E+0 | 1.5E+0 | 2.0E+0 |
| 2 | –6.6E+0 | 5.1E+0 | 5.2E+0 | –1.5E+0 | 1.6E+0 | |
| 3 | –1.6E+6 (51 380) | 1.6E+2 | 2.2E+2 | –3.0E+1 | 4.4E+2 | |
| 4 | –5.8E+0 | –9.3E+0 | 9.7E+0 | –1.7E+0 | 5.7E–1 | |
| 3/8 | 1 | –3.6E+0 | –3.8E+0 | –3.3E+0 | 8.3E–1 | 5.6E–1 |
| 2 | –5.3E+0 | 7.5E+0 | 7.6E+0 | –1.2E+0 | 1.1E+0 | |
| 3 | –3.8E+5 (4811) | 4.3E+1 | 3.2E+1 | –1.0E+1 | –1.2E+1 | |
| 4 | –3.8E+0 | 1.0E+1 | 1.1E+1 | –9.9E–1 | 3.0E–1 | |
| 3/16 | 1 | 1.4E+0 | –1.9E+0 | –1.9E+0 | 3.4E–1 | 1.4E–1 |
| 2 | –3.7E+0 | 8.3E+0 | 8.4E+0 | –9.1E–1 | 5.8E–1 | |
| 3 | 2.5E+5 (16 144) | 3.0E+1 | –1.6E+1 | –5.3E+0 | –4.3E+0 | |
| 4 | –2.2E+0 | 8.8E+0 | 9.0E+0 | –5.6E–1 | –1.6E–1 | |
| 3/32 | 1 | 5.6E–1 | –1.0E+0 | –9.9E–1 | 1.6E–1 | 5.9E–2 |
| 2 | –2.1E+0 | 7.5E+0 | 7.6E+0 | –5.2E–1 | 2.7E–1 | |
| 3 | 7.5E+4 (51 380) | 2.4E+1 | –1.5E+1 | 2.7E+0 | –1.4E+0 | |
| 4 | –1.1E+0 | 6.6E+0 | 6.8E+0 | –2.5E–1 | –1.1E–1 | |
Таблица 8
| $r,\vartheta ,z$ Геометрия, ${{\delta }_{{{\text{sum}}}}}$, % | |||||
|---|---|---|---|---|---|
| Шаг Δr, Δz | Схема | ||||
| DD | AWDD1 | AWDD2 | LD | LB | |
| 3/2 | –6.1E–2 | –3.7E+0 | –4.0E+0 | –2.2E–1 | –1.0E–2 |
| 3/4 | –1.9E–2 | –1.4E+0 | –1.5E+0 | –4.2E–2 | –9.3E–4 |
| 3/8 | –4.8E–3 | –4.8E–1 | –5.3E–1 | –8.4E–3 | –4.4E–4 |
| 3/16 | –1.1E–3 | –1.5E–1 | –1.6E–1 | –1.8E–3 | –5.0E–4 |
| 3/32 | –2.1E–4 | –4.1E–2 | –4.6E–2 | –3.4E–4 | –1.6E–4 |
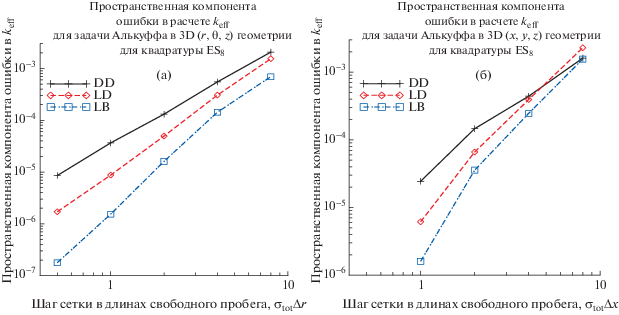
Приведем далее результаты (см. фиг. 7), показывающие скорость сходимости ${{k}_{{{\text{eff}}}}}$ в зависимости от выбора пространственной сетки и разностной схемы при фиксированной квадратуре $E{{S}_{8}}$ для 2-х зонной задачи из [26] в $r,\vartheta ,z$ геометрии, изображенной на фиг. 6 и ее аналога в $x,y,z$ геометрии. В случае $x,y,z$ геометрии на левой, передней и нижней границах расчетной области использовалось условие зеркального отражения. В $r,\vartheta ,z$ геометрии расчет проводился для сектора симметрии $60^\circ $; на нижней границе расчетной области использовалось условие зеркального отражения. В $r,\vartheta ,z$ геометрии задача решалась с квадратурой $E{{S}_{8}}$ с равномерной пространственной сеткой из 10, 20, 40, 80 и 160 интервалов по радиальной и аксиальной переменным; по азимутальной переменной использовалась равномерная сетка из 3-х интервалов. В качестве точного использовалось значение ${{k}_{{{\text{eff}}}}}$, рассчитанное по LD-схеме на сетке из 320 × 3 × 320 интервалов с точностью сходимости итераций ${{10}^{{ - 9}}}$. В $x,y,z$ геометрии использовалась квадратура $E{{S}_{8}}$ и равномерная пространственная сетка из 10, 20, 40 и 80 интервалов по пространственным переменным. В качестве точного использовалось значение ${{k}_{{{\text{eff}}}}}$, рассчитанное по LD-схеме на сетке из 80 × 80 × 80 интервалов с точностью сходимости итераций ${{10}^{{ - 9}}}$.
Фиг. 6.
Задача 6 в $r,\vartheta ,z$ геометрии [26]. Указаны сечение поглощения ${{\sigma }_{a}}$, полное сечение ${{\sigma }_{t}}$, сечение рассеяния ${{\sigma }_{s}}$, $\nu {{\sigma }_{f}}$ по зонам.

6. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Представленные результаты численного эксперимента показывают, что LD и LB-схемы имеют высокую скорость сходимости расчетных результатов в $r,\vartheta ,z$ и $x,y,z$ геометриях при сгущении пространственной сетки задачи, а разработанный вариант алгоритма ускорения внутренних итераций обеспечивает значительный выигрыш во времени расчета варианта. Вместе с тем, как показывают результаты решения задачи 4 в $x,y,z$ геометрии, существует класс задач, для которых эффективность алгоритма ускорения падает.
Опыт решения практических задач радиационной защиты с использованием $K{{P}_{1}}$-схемы, согласованной с LD-схемой, показал, что данный алгоритм за счет использования более редкой пространственной сетки и стабильно работающего алгоритма ускорения позволяет значительно уменьшить расчетное время варианта при сохранении необходимой точности расчета пространственных распределений потоков излучения. Кроме того, он хорошо сходится и при решении задач, в которых $K{{P}_{1}}$-схема, согласованная с AWDD-схемой, оказывается малоэффективной или неустойчивой (что обычно является следствием использования неудачной аппроксимации геометрии задачи).
Список литературы
Марчук Г.И., Лебедев В.И. Численные методы в теории переноса нейтронов. М.: Атомиздат, 1981.
Alcouffe R.E. Diffusion synthetic acceleration methods for the diamond-differenced discrete-ordinates equations // Nucl. Sci. and Eng. 1977. V. 64. № 2. P. 344.
Adams M.L., Larsen E.W. Fast iterative methods for discrete-ordinates particle transport calculations // Progress in Nuclear Energy. 2002. V. 40. Iss. 1. P. 3.
Lorence L.J., Morel J.E., Larsen E.W. An ${{S}_{2}}$ synthetic acceleration method for the one-dimensional ${{S}_{N}}$ equations with linear discontinuous spatial differencing // Nucl. Sci. Eng. 1989. V. 101. № 2. P. 341.
Khalil H. A nodal diffusion technique for synthetic acceleration of nodal Sn calculations // Nucl. Sci. and Eng. 1985. V. 90. № 3. P. 263.
Voloschenko A.M. Consistent P1 synthetic acceleration scheme for transport equation in 3D geometries. // Proc. of Intern. Conf. on Mathematics and Computation, Supercomputing, Reactor Physics and Nuclear and Biological Applications. Avignon, France, September 12–15, 2005, paper 070.
Волощенко А.М., Воронков А.В., Сычугова Е.П. Согласованная ${{P}_{1}}SA$-схема ускорения внутренних и внешних итераций для уравнения переноса нейтронов и фотонов в одномерных геометриях в пакете РЕАКТОР // Препринт ИПМ им. М.В. Келдыша РАН. 1996. № 2.
CNCSN 2009: One, Two- and Three-Dimensional Coupled Neutral and Charged Particle Discrete Ordinates Parallel Multi-Threaded Code System // RSICC code package CCC-726. 2009.
Волощенко А.М. $K{{P}_{1}}$-схема ускорения внутренних итераций для уравнения переноса в двумерной геометрии, согласованная со взвешенной алмазной схемой // Ж. вычисл. матем. и матем. физ. 2001. Т. 41. № 9. С. 1379.
Волощенко А.М. KP1-схема ускорения внутренних итераций для уравнения переноса в трехмерной геометрии, согласованная со взвешенной алмазной схемой // Ж. вычисл. матем. и матем. физ. 2009. Т. 49. № 2. С. 1.
Волощенко А.М., Кондратенко Е.П. $K{{P}_{1}}$-схема ускорения внутренних итераций, согласованная с семейством WLM–WLD-схем для уравнения переноса в одномерных геометриях // Препринт ИПМ им. М.В. Келдыша АН СССР, 1986. № 197.
Voloschenko A.M. ${{P}_{1}}SA$ Scheme for Acceleration of Inner Iterations Convergence Consistent with the Weighted Nodal Scheme for Transport Equation in 1D Geometries // Proc. of International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering (M&C 2011), Rio de Janeiro, RJ, Brazil, May 8–12, 2011.
Коконков Н.И., Николаева О.В. $K{{P}_{1}}$ итерационный метод решения уравнения переноса в трехмерных областях на неструктурированных сетках // Ж. вычисл. матем. и матем. физ. 2015. Т. 55. № 10. С. 95.
Волощенко А.М. Адаптивные положительные аппроксимации и согласованная KP1-схема ускорения итераций для уравнения переноса в задачах радиационной защиты. Докторская диссертация. М.: ИПМ им. М.В. Келдыша РАН, 2015, http://www.keldysh.ru/council/3/D00202403/voloshchenko_diss.pdf.
Vaidyanathan R.A. Finite Moments Algorithm for Particle Transport Problems // Nucl. Sci. Eng. 1979. V. 71. P. 46.
Voloschenko A.M. Some Improvements in Solving of the Transport Equation by the Use of the Family of Weighted Nodal Schemes // Proc. of International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering (M&C 2011), Rio de Janeiro, RJ, Brazil, May 8–12, 2011.
Carlson B.G. A method of characteristics and other improvements in solution methods for the transport equation // Nucl. Sci. Eng. 1976. V. 61. P. 408.
Басс Л.П., Волощенко А.М., Гермогенова Т.А. // Методы дискретных ординат в задачах о переносе излучения. М. ИПМ им. М. В. Келдыша АН СССР, 1986.
Voloschenko A.M., Germogenova T.A. Numerical Solution of the Time-Dependent Transport Equation with Pulsed Sources // Transp. Theory and Stat. Phys. 1994. V. 23. № 6. P. 845.
Alcouffe R.E. An Adaptive Weigthed Diamond-Differencing Method for Three-Dimensional XYZ Geometry // Trans. Am. Nucl. Soc. 1993. V. 68A. P. 206.
Adams M.L., Wareing T.A. Diffusion-synthetic acceleration given anisotropic scattering, general quadratures, and multidimensions // Trans. Am. Nucl. Soc. 1993. V. 68A. P. 203.
Марчук Г.И. Методы расщепления. М.: Наука, 1988.
Warsa J.S., Wareing T.A., Morel J.A. Krylov iterative methods applied to multidimensional ${{S}_{n}}$ calculations in the presence of material discontinuities // Proceedings of M&C 2003 – Nuclear Mathematical and Computational Sciences: A Century in Review – A Century Anew, paper No. 134, April 6–10, Gatlinburg, USA, 2003.
Alcouffe R.E., Larsen E.W., Miller W.F., Wienke B.R. Computational Efficiency of Numerical Methods for the Multigroup Discrete Ordinates Neutron Transport Equations in Slab Geometry Case // Nucl. Sci. Eng. 1979. V. 71. P. 111.
Казаков А.Н., Лебедев В.И. Квадратурные формулы типа Гаусса для сферы, инвариантные относительно группы диэдра // Труды Математического института РАН. 1994. Т. 203. С. 100.
Alcouffe R.E. A Robust Linear Discontinuous Method for the RZ SN Transport Equation // Trans. Am. Nucl. Soc. 2003. V. 89. P. 363.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики