Журнал вычислительной математики и математической физики, 2019, T. 59, № 3, стр. 409-428
Математическое моделирование течений вязкого газа в пространстве между двумя коаксиально вращающимися концентрическими цилиндрами и сферами
М. В. Абакумов *
МГУ
119991 Москва, Ленинские горы, Россия
* E-mail: vmabk@cs.msu.ru
Поступила в редакцию 04.06.2018
Аннотация
Описывается методика построения консервативных разностных схем годуновского типа для расчета течений вязкого газа в цилиндрических и сферических координатах. Проводятся двумерные и трехмерные расчеты течений в пространстве между двумя коаксиально вращающимися концентрическими цилиндрами и сферами. Моделируются различные типы вихревых течений, характерные и для несжимаемой жидкости. Также отмечаются отличия от несжимаемого случая. Результаты демонстрируют возможность исследования цилиндрических и сферических течений Куэтта в рамках математической модели вязкого газа путем прямого численного моделирования с использованием явных разностных схем. Библ. 24. Фиг. 16.
ВВЕДЕНИЕ
Исследованию течений вязкой жидкости между вращающимися цилиндрами и сферами уделяли существенное внимание многие, в том числе всемирно известные ученые (см., например, обзоры [1]–[4]). Такой интерес неслучаен, поскольку изучение механизмов возникновения вихревых структур, характерных для таких течений, является важным элементом для понимания более сложных природных процессов. Здесь можно отметить атмосферные явления, течения в жидком ядре Земли и других планет, влияние крупномасштабных вихревых структур на эволюцию аккреционных дисков звездных систем.
В случае бесконечных коаксиально вращающихся цилиндров уравнения Навье–Стокса допускают стационарное решение, в котором скорость и давление зависят только от расстояния до оси вращения [5], [6]. Такое решение описывает так называемое основное течение (течение Куэтта). В ходе экспериментальных и теоретических исследований Тейлор впервые исследовал устойчивость основных течений и показал возможность возникновения вихревых вторичных течений (см. [7]). В предположении малости зазора между цилиндрами им было получено условие возникновения неустойчивости при сонаправленном вращении цилиндров. Позднее было показано (см. [8]), что условие справедливо и в более общем случае.
Течения между коаксиально вращающимися концентрическими сферами являются существенно более сложными для аналитического и численного исследования (см. [2]). Связано это в том числе и с тем, что не удается получить аналитические решения, описывающие основные течения. Более того, вид основных течений между вращающимися сферами существенно зависит от определяющих параметров. Так, например, при достаточно малых числах Рейнольдса характерными являются симметричные относительно оси вращения и экваториальной плоскости течения, в которых на дифференциальное вращение накладываются меридиональные циркуляции. В зависимости от соотношения скоростей вращения сфер возможны различные типы циркуляции в меридиональной плоскости (см. [9]). Не менее существенно развитие и устойчивость основных течений зависят и от относительной толщины зазора между сферами (см. [10]).
В настоящей работе моделируются течения вязкого газа между коаксиально вращающимися концентрическими цилиндрами и сферами. Газ описывается системой уравнений Навье–Стокса, в которой тензор вязких напряжений учитывается как в уравнении движения, так и в уравнении энергии. Помимо сжимаемости, специфичным здесь является также и то, что даже в случае цилиндров отсутствуют стационарные решения, описывающие основные течения, отличные от твердотельного вращения. Это связано с наличием вязких слагаемых в уравнении энергии, которые описывают переход кинетической энергии в тепловую за счет трения слоев газа.
В работе проведены двумерные и трехмерные расчеты по явным консервативным разностным схемам годуновского типа повышенного порядка точности, адаптированным по авторской методике (см. [11], [12]) для расчетов течений вязкого газа в цилиндрических и сферических координатах. В двумерных вариантах расчеты проводились в одном слое разностных ячеек при фиксированном значении полярного угла в предположении цилиндрической симметрии течения (2.5D-приближение).
Поскольку, как уже отмечалось, в рассматриваемом случае вязкого газа неизвестны аналитические решения, описывающие основные течения, в качестве начальных данных во всех проводимых расчетах задавались постоянные параметры покоящегося газа. Газ приводился в движение исключительно за счет вязкого трения о вращающиеся поверхности цилиндров или сфер. Таким образом, моделируемые течения не определялись каким-либо специфическим выбором начального состояния.
В ходе моделирования исследовалось влияние на характер течений соотношения угловых скоростей цилиндров и сфер, толщины зазора между ними, числа Рейнольдса и числа Маха. В случае вращающихся цилиндров показано, что при различных соотношениях этих параметров возможно возникновение квазистационарных периодических вихревых структур, содержащих один, два или более ряда разнонаправленных вихрей. Моделировались различные типы основных течений между вращающимися сферами, в том числе течение Стюартсона–Праудмэна [13], [14], которое возникает при достаточно больших значениях числа Рейнольдса и малых отклонениях в угловых скоростях сонаправленного вращения сфер. Проведено сравнение полученных результатов с данными экспериментальных и теоретических исследований для несжимаемой жидкости, а также расчетами других авторов.
1. ПОСТАНОВКА ЗАДАЧИ
Рассматривается система уравнений вязкого идеального газа (см. [5], [6]):
(1)
$\begin{gathered} {\frac{{\partial (\rho {\mathbf{v}})}}{{\partial t}} + \operatorname{div} (\rho {\mathbf{v}} \otimes {\mathbf{v}}) = \operatorname{div} {\mathbf{\Pi }}}, \\ {\frac{{\partial (\rho E)}}{{\partial t}} + {\text{div}}(\rho E{\mathbf{v}}) = {\text{div}}({\mathbf{\Pi v}})},\quad {E = \varepsilon + {{{\mathbf{v}}}^{2}}{\text{/}}2},\quad {{\mathbf{\Pi }} = - p{\mathbf{I}} + {\mathbf{\sigma }}}, \\ \end{gathered} $В цилиндрической системе координат ($r$, $\varphi $, $z$) переход к прямоугольным декартовым координатам ($x$, $y$, $z$) определяется равенствами: $x = r\cos \varphi $, $y = r\sin \varphi $, где $r \geqslant 0$, $\varphi \in [0;2\pi )$. Система (1) может быть записана [15] в следующей векторной форме:
(2)
${{\mathbf{G}} = (\rho \text{v},\rho \text{v}u,\rho {{\text{v}}^{2}} + p,\rho \text{v}w,\rho \text{v}H{{)}^{{\text{т }}}},}\quad {{\mathbf{H}} = (\rho w,\rho wu,\rho w\text{v},\rho {{w}^{2}} + p,\rho wH{{)}^{{\text{т }}}}},$Компоненты тензора вязких напряжений ${\mathbf{\sigma }}$ примут вид
В сферической системе координат ($r$, $\varphi $, $\psi $) переход к прямоугольным декартовым координатам ($x$, $y$, $z$) определяется равенствами $x = r\cos \varphi \cos \psi $, $y = r\sin \varphi \cos \psi $, $z = r\sin \psi $, где $r\; \geqslant \;0$, $\varphi \in [0;2\pi )$, $\psi \in [ - \pi {\text{/}}2;\pi {\text{/}}2]$. В сферических координатах система (1) также может быть записана в векторной форме:
(3)
${{\mathbf{G}} = (\rho \text{v},\rho \text{v}u,\rho {{\text{v}}^{2}} + p,\rho \text{v}w,\rho \text{v}H{{)}^{{\text{т }}}}},\quad {{\mathbf{H}} = (\rho w,\rho wu,\rho w\text{v},\rho {{w}^{2}} + p,\rho wH{{)}^{{\text{т }}}},}$Компоненты тензора вязких напряжений ${\mathbf{\sigma }}$ примут вид
В классическом варианте задача о течении вещества в пространстве между двумя коаксиально вращающимися бесконечными цилиндрами (течение Тейлора–Куэтта) рассматривается применительно к вязкой несжимаемой жидкости (см. [5], [6]), движение которой описывается уравнениями Навье–Стокса. Соответствующие уравнения получаются из системы (2), если считать плотность постоянной по пространству и во времени ($\rho = {\text{const}}$), а также исключить из рассмотрения уравнение энергии.
Рассматривается течение жидкости между двумя бесконечными цилиндрами с радиусами ${{R}_{1}}$ и ${{R}_{2}}$ (${{R}_{1}} < {{R}_{2}}$), которые вращаются вокруг своей оси, совпадающей с осью $z$ цилиндрических координат, с угловыми скоростями ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$ соответственно. Ищется стационарное цилиндрически симметричное решение, удовлетворяющее условиям
(4)
$\frac{{\partial {\kern 1pt} \cdot }}{{\partial t}} = 0,\quad u = w = 0,\quad \text{v} = \text{v}(r),\quad p = p(r).$(5)
$p{\kern 1pt} {\text{'}} = \rho {{\text{v}}^{2}}{\text{/}}r,\quad \text{v}{\kern 1pt} {\text{''}} + \text{v}{\kern 1pt} {\text{'/}}r - \text{v}{\text{/}}{{r}^{2}} = 0.$С учетом граничных условий прилипания $\text{v}({{R}_{1}}) = {{R}_{1}}{{\Omega }_{1}}$, $\text{v}({{R}_{2}}) = {{R}_{2}}{{\Omega }_{2}}$ получается известное (см. [5], [6]) решение
(6)
$\begin{gathered} {\text{v}(r) = ar + b{\text{/}}r,}\quad {p(r) = \rho \left( {{{{(ar)}}^{2}} - {{{\left( {b{\text{/}}r} \right)}}^{2}} + 4ab\ln r} \right){\text{/}}2 + {{p}_{0}},} \\ {a = \frac{{{{\Omega }_{2}}R_{2}^{2} - {{\Omega }_{1}}R_{1}^{2}}}{{R_{2}^{2} - R_{1}^{2}}}},\quad {b = \frac{{({{\Omega }_{1}} - {{\Omega }_{2}})R_{1}^{2}R_{2}^{2}}}{{R_{2}^{2} - R_{1}^{2}}}},\quad \left( {{u = w = 0},\;{\rho = {\text{const}}}} \right), \\ \end{gathered} $Если при тех же предположениях (4) в совокупности с условием $\rho = {\text{const}}$ искать стационарное решение полной системы (2), то наряду с равенствами (5) из уравнения энергии получим
Аналогичное исследование наличия стационарных решений может быть проведено и для случая течения между двумя коаксиально вращающимися с угловыми скоростями ${{\Omega }_{1}}$ и ${{\Omega }_{2}}$ концентрическими сферами с радиусами ${{R}_{1}}$ и ${{R}_{2}}$. Введем сферическую систему координат с центром, совпадающим с центрами обеих сфер, и осью вращения сфер $\psi = \pm \pi {\text{/}}2$. Будем искать стационарные цилиндрически симметричные решения системы уравнений (3), удовлетворяющие условиям
(7)
$\frac{{\partial {\kern 1pt} \cdot }}{{\partial t}} = 0,\quad u = w = 0,\quad \text{v} = \text{v}(r,\psi ),\quad p = p(r,\psi ),\quad (\rho = {\text{const}}).$(8)
$\begin{gathered} \frac{{\partial p}}{{\partial r}} = \frac{{\rho {{\text{v}}^{2}}}}{r} \\ \end{gathered} ,\quad \begin{gathered} \frac{{\partial p}}{{\partial \psi }} = - \rho {{\text{v}}^{2}}\operatorname{tg} \psi \\ \end{gathered} .$Пусть $V(\xi )$ – произвольная первообразная функции ${{\text{v}}^{2}}(\xi ){\text{/}}\xi $, тогда общее решение первого уравнения (8) может быть записано в виде $p = \rho V(r\cos \psi ) + C(\psi )$, где $C(\psi )$ – произвольная дифференцируемая функция. Подставляя это решение во второе уравнение (8), получаем
Таким образом, получается, что функции $p = p({{r}_{c}})$ и $\text{v} = \text{v}({{r}_{c}})$ зависят лишь от расстояния до оси вращения сфер – цилиндрического радиуса ${{r}_{c}} = r\cos \psi $. С учетом этого обстоятельства оба уравнения (8) сводятся к одному и тому же обыкновенному дифференциальному уравнению $p{\text{'}} = \rho {{\text{v}}^{2}}{\text{/}}{{r}_{c}}$. Равенство
Общее решение $\text{v}({{r}_{c}}) = ar\cos \psi + b{\text{/}}(r\cos \psi )$ дифференциальных уравнений (5) должно удовлетворять условиям прилипания $\text{v}({{R}_{1}},\psi ) = {{\Omega }_{1}}{{R}_{1}}\cos \psi $, $\text{v}({{R}_{2}},\psi ) = {{\Omega }_{2}}{{R}_{2}}\cos \psi $ при всех $\psi \in [ - \pi {\text{/}}2;\pi {\text{/}}2]$. Отсюда получим, что $b = 0$, ${{\Omega }_{1}} = {{\Omega }_{2}} = \Omega $, $a = \Omega $. То есть, даже без учета уравнения энергии отсутствуют решения без меридиональных циркуляций (где $u = w = 0$) при различных скоростях вращения сфер.
Отметим, что в предположениях (7) из уравнения энергии системы (3) получим
Поскольку для системы (1) отсутствуют стационарные решения, описывающие безвихревые течения с осевой симметрией в пространстве между вращающимися цилиндрами и сферами, отличные от твердотельного вращения, в ходе дальнейшего моделирования задавались постоянные параметры неподвижного газа. Газ приходил в движение исключительно за счет вязкого трения вследствие условий прилипания на вращающихся границах. Исследовались возникающие в результате установившиеся течения.
Задачи ставились следующим образом. Для случая вращающихся цилиндров численно решалась система (2) в ограниченной области цилиндрических координат ${{R}_{1}}\;\leqslant \;r\;\leqslant \;{{R}_{2}}$, $0\;\leqslant \;\varphi \;\leqslant \;2\pi $, $0\;\leqslant \;z\;\leqslant \;H$. На поверхностях цилиндров задавались условия прилипания ${\mathbf{v}}({{R}_{1}},\varphi ,z) = (0,{{\Omega }_{1}}{{R}_{1}},0)$, ${\mathbf{v}}({{R}_{2}},\varphi ,z) = (0,{{\Omega }_{2}}{{R}_{2}},0)$, на верхней и нижней границе области – условия непротекания $w(r,\varphi ,0) = 0$, $w(r,\varphi ,H) = 0$. Условия на верхней и нижней границе фактически определяют отсутствие осевой компоненты скорости и проскальзывание (отсутствие трения), что характерно для границы между вихревыми ячейками. Такие условия позволяют моделировать периодические вихревые течения в ограниченной области (см. п. 4). Для случая вращающихся сфер численно решалась система (3) в области сферических координат ${{R}_{1}}\;\leqslant \;r\;\leqslant \;{{R}_{2}}$, $0\;\leqslant \;\varphi \;\leqslant \;2\pi $, $ - \pi {\text{/}}2\;\leqslant \;\psi \;\leqslant \;\pi {\text{/}}2$. На поверхностях сфер задавались условия прилипания ${\mathbf{v}}({{R}_{1}},\varphi ,\psi ) = (0,{{\Omega }_{1}}{{R}_{1}}\cos \psi ,0)$, ${\mathbf{v}}({{R}_{2}},\varphi ,\psi ) = (0,{{\Omega }_{2}}{{R}_{2}}\cos \psi ,0)$. Как уже отмечалось во введении, в 2.5D-приближении численное решение обеих систем осуществлялось в одном слое разностных ячеек при фиксированном значении полярного угла $\varphi $ в предположении цилиндрической симметрии течения.
В начальный момент времени задавались постоянные параметры покоящегося газа
2. РАЗНОСТНЫЕ СХЕМЫ
В работах [11], [12] описана методика построения разностных схем для криволинейных координат на базе произвольной декартовой схемы годуновского типа (см. [17], [18]). Предложенный способ позволяет оставить без изменения алгоритмы вычисления разностных потоков взятой за основу декартовой схемы. Далее опишем лишь основную идею этого подхода и приведем построенные разностные схемы для цилиндрических и сферических координат.
Для определенности рассмотрим случай цилиндрических координат. Наряду с уравнениями (2) рассматривается вспомогательная система
Учтем криволинейность разностной ячейки. Для этого аппроксимируем интегральные соотношения баланса массы, импульса и энергии:
(9)
${\int\limits_V \left[ {\rho (t + \tau ){\mathbf{v}}(t + \tau ) - \rho (t){\mathbf{v}}(t)} \right]dV + \int\limits_t^{t + \tau } \int\limits_\Sigma [\rho ({\mathbf{v}},{\mathbf{n}}){\mathbf{v}} + p{\mathbf{n}}]d\Sigma dt = 0},$Введем произвольную декартову прямоугольную систему координат (${{y}_{1}}$, ${{y}_{2}}$, ${{y}_{3}}$). Орты (${{{\mathbf{i}}}_{1}}$, ${{{\mathbf{i}}}_{2}}$, ${{{\mathbf{i}}}_{3}}$) выбранной декартовой системы образуют базис, который далее будем называть опорным. Предположим, что участок границы $\tilde {\Sigma }$ разностной ячейки задан параметрически:
Приходим к следующим равенствам, аппроксимирующим уравнения (9):
В результате применения описанного подхода для цилиндрической разностной ячейки с центром в точке ($r$, $\varphi $, $z$) и постоянных шагов сетки ${{h}_{r}}$, ${{h}_{\varphi }}$, ${{h}_{z}}$ получаются следующие разностные уравнения [11]:
Для аппроксимации вязких слагаемых уравнений (2) и (3) декартовы сеточные потоки модифицируются следующим образом:
В цилиндрических координатах компоненты ${\mathbf{\sigma }}$ аппроксимировались следующим образом:
Приведем также выражения для разностных добавок в сферической схеме
В уравнениях энергии обеих схем добавки к разностным потокам вводятся следующим образом:
В работах [11], [12] показано, что приведенные разностные схемы с указанной модификацией потоков аппроксимируют системы уравнений (2) и (3) со вторым порядком, если разностные потоки в базовой декартовой схеме вычисляются с тем же или более высоким порядком точности по шагам сетки. В расчетах, описываемых далее, декартовы сеточные потоки первого порядка аппроксимации рассчитывались методом Роу [19] с модификациями Эйнфельдта [20], позволяющими избежать появления нефизических разрывов в численных решениях. Использовалась коррекция сеточных потоков методом Ошера [21], в результате которой порядок аппроксимации потоков повышался до третьего.
Остановимся на аппроксимации условий прилипания на вращающихся поверхностях цилиндров и сфер. Для определенности рассмотрим границу внутреннего цилиндра радиуса ${{R}_{1}}$. Условия на этой границе имеют вид $u = 0$, $\text{v} = {{\Omega }_{1}}{{R}_{1}}$, $w = 0$. Исходя из первого равенства, получаем ${\mathbf{F}}_{{1/2jk}}^{{(l)}} = 0$, $l = 1,3,4,5$; ${\mathbf{F}}_{{1/2jk}}^{{(2)}} = {{p}_{{1/2jk}}}$. Граничное давление ${{p}_{{1/2jk}}}$ определялось из уравнения равновесия $p_{r}^{'} = \rho \Omega _{1}^{2}{{R}_{1}}$, которое аппроксимировалось со вторым порядком в узлах при $i = 1{\text{/}}2$ с использованием значений сеточных функций при $i = 1$ и $i = 2$. Условия прилипания учитывались и при аппроксимации компонент тензора вязких напряжений ${\mathbf{\sigma }}$. С учетом этих условий компоненты на поверхности цилиндра примут вид
3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
Параметрами, определяющими течения между вращающимися цилиндрами и сферами, являются: число Рейнольдса, которое в данной работе рассчитывается по формуле ${\text{Re}} = {{\Omega }_{1}}{{R}_{1}}({{R}_{2}} - {{R}_{1}}){{\nu }^{{ - 1}}}$, отношение угловых скоростей $\omega = {{\Omega }_{2}}{\text{/}}{{\Omega }_{1}}$ и относительная величина зазора $d = ({{R}_{2}} - {{R}_{1}}){\text{/}}{{R}_{1}}$. В рассматриваемом сжимаемом случае добавляется зависимость от числа Маха, которое с учетом начальных условий (см. разд. 1) рассчитывалось в соответствии со скоростями вращения цилиндров или сфер ${\text{M}} = \max ({{R}_{1}}\left| {{{\Omega }_{1}}} \right|,{{R}_{2}}\left| {{{\Omega }_{2}}} \right|)$. Целью проводимых в работе расчетов являлось исследование влияния этих параметров на характерные особенности моделируемых течений.
Основная сложность моделирования течений между бесконечными цилиндрами состоит в том, что расчеты приходится проводить в ограниченной по высоте $z$ расчетной области. Неизбежно проявляется влияние геометрии области и условий на ее верхней и нижней границах. Поэтому для получения в расчетах характерных для рассматриваемой задачи периодических по высоте $z$ решений необходимы дополнительные усилия.
В настоящей работе расчеты течений между цилиндрами проводились следующим образом. На верхней и нижней границах расчетной области задавались условия непротекания $w(r,\varphi ,0) = 0$, $w(r,\varphi ,H) = 0$ и свободные граничные условия (равенство нулю производной по $z$) для прочих компонент скорости, плотности и давления. Фиксировались радиусы цилиндров ${{R}_{1}} = 0.5$ и ${{R}_{2}} = 1.0$, скорости их вращения (параметры $\omega $ и ${\text{M}}$ при заданных начальных условиях), а также коэффициент вязкости $\nu $, исходя из требуемого значения числа Рейнольдса. Для выбора высоты расчетной области $H$ в основном расчете проводился предварительный расчет на достаточно грубой сетке при больших по сравнению с ${{R}_{2}} - {{R}_{1}}$ значениях $H$. Малые вычислительные погрешности постепенно развивались в регулярные возмущения, которые на ранних стадиях наиболее заметны по значениям изначально нулевой осевой компоненты скорости $w$ (см. фиг. 1). По характеру этих возмущений можно с достаточной точностью определить период развивающегося вихревого течения по направлению оси цилиндров. В основном расчете высота $H$ выбиралась равной трем найденным периодам, а в начальные данные вносились периодические возмущения осевой компоненты скорости
(10)
$w(1,1,k) = \varepsilon \sin \left( {6\pi (k - 0.5){{h}_{z}}{\text{/}}H} \right),\quad k = 1,2,\; \ldots ,{{N}_{z}},\quad {{N}_{z}}{{h}_{z}} = H.$Фиг. 1.
Формирование регулярной структуры возмущений при $\omega = 0$, ${\text{Re}} = 300$, ${\text{M}} = 0.1$.

Перейдем к описанию результатов расчетов. Начнем с варианта, в котором внутренний цилиндр вращался, а внешний покоился, т.е. $\omega = 0$. На данном примере опишем особенности, характерные и для прочих вариантов моделируемых течений между цилиндрами. Здесь и в большинстве описываемых далее расчетов выбирались значения ${\text{Re}} = 300$ и ${\text{M}} = 0.1$. Развивающиеся малые начальные возмущения (10) приводят к возникновению регулярного вихревого течения. На развитых стадиях характерными являются грибовидные возмущения прежде однородного по высоте цилиндров распределения плотности, представленные на фиг. 2. Как легко видеть на фигуре, при указанном выше способе выбора параметра $H$ течение периодично по высоте, а три вихревые ячейки (пары соседних разнонаправленных вихрей) не отличаются друг от друга. Периодичность течения не нарушается в ходе длительного расчетного времени, соответствующего сотням оборотов вращающегося цилиндра. Устанавливается регулярная квазистационарная вихревая структура, содержащая один ряд разнонаправленных вихрей (см. фиг. 3), характерная (см. [6]) для сонаправленного вращения цилиндров. Такие течения обычно называют вторичными, имея в виду наличие в несжимаемом случае стационарных, зависящих только от $r$, основных течений (возможно неустойчивых). Еще раз отметим, что в рассматриваемом случае вихревое течение не является стационарным, поскольку переход кинетической энергии в тепловую вследствие трения приводит к монотонному росту температуры и (при неизменной плотности) давления. Однако расположение вихрей и распределение плотности в установившемся режиме практически не меняется во времени.
Фиг. 3.
Установившаяся вихревая структура при $\omega = 0$, ${\text{Re}} = 300$, ${\text{M}} = 0.1$.

При рассматриваемых значениях ${{R}_{1}}$ и ${{R}_{2}}$ условие устойчивости ${{\Omega }_{1}}R_{1}^{2} < {{\Omega }_{2}}R_{2}^{2}$ первичного течения для сонаправленно вращающихся цилиндров (и несжимаемой жидкости) (см. [7]) примет вид $\omega > 0.25$. Продемонстрируем определяющее влияние этого условия на характер моделируемых течений. На фиг. 4а приведены результаты расчета при $\omega = 0.23$. Здесь и далее в силу периодичности течений приводятся фрагменты их изображений в части расчетной области. Как легко видеть, по-прежнему устанавливается вихревая структура, похожая на описанную ранее, правда с несколько иным распределением плотности. При $\omega = 0.26$ ситуация меняется. Малые возмущения развиваются в вихревую структуру и начинают проявляться похожие на описанные выше изменения распределения плотности (см. фиг. 4б), однако, далее эта неоднородность по высоте практически исчезает (см. фиг. 4в). При этом значения радиальной и осевой компонент скорости $u$ и $w$ на три порядка меньше характерных значений вращательной компоненты $\text{v}$.
Фиг. 4.
Течения при ${\text{Re}} = 300$, ${\text{M}} = 0.1$: (а) $\omega = 0.23$, (б), (в) $\omega = 0.26$.
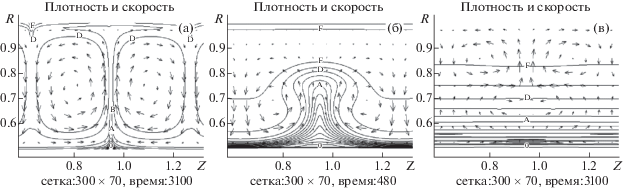
Таким образом, в диапазоне $0\;\leqslant \;\omega < 0.25$ реализуются вихревые течения, характерные для сонаправленного движения цилиндров (см. [6]) и содержащие один ряд разнонаправленных вихрей. С дальнейшим увеличением $\omega $ картина моделируемых течений качественно меняется. На развитых стадиях практически отсутствует неоднородность распределения плотности по высоте цилиндров, а интенсивность вихрей ослабевает. В ходе расчетов стационарного течения ($\omega = 1$) каких-либо неоднородностей и вовсе не возникает. Точное решение хорошо воспроизводится и практически не изменяется в течение длительного расчетного времени порядка сотен оборотов цилиндров. Отклонения плотности от изначально постоянного значения, неизбежно возникающие из-за погрешностей схемы, составляют не более 0.1%.
Далее опишем результаты моделирования течений при разнонаправленном вращении цилиндров ($\omega \;\leqslant \;0$). Как видно на фиг. 5, при уменьшении $\omega $ (и неизменных ${\text{Re}}$ и ${\text{M}}$) картина вихревого течения усложняется. Наблюдается постепенный переход к течениям, отличительной особенностью которых является наличие двух рядов вихрей. Характерными являются различия в абсолютных значениях скоростей вихрей. Так, при $\omega = - 0.5$ (фиг. 5в) в ряде вихрей, расположенном ближе к внешнему цилиндру, значения скорости более чем на порядок меньше. Подобные различия интенсивности вихрей отмечаются, в частности, в [6].
Фиг. 5.
Течения при ${\text{Re}} = 300$, ${\text{M}} = 0.1$: (а) $\omega = - 0.2$, (б) $\omega = - 0.35$, (в) $\omega = - 0.5$.

При дальнейшем уменьшении параметра $\omega $ картина течения еще более усложняется. На фиг. 6 приведены результаты расчета при $\omega = - 1$ на различные последовательные моменты времени. Как видно на фигурах, сначала также развивается регулярная периодическая структура, содержащая два ряда вихрей. Однако здесь она отделена от границы внешнего цилиндра зоной, в которой на начальном этапе неоднородность плотности по высоте цилиндров и движение в меридиональной плоскости практически отсутствуют (фиг. 6а). Далее уже в этой зоне возникают грибовидные возмущения плотности (фиг. 6б) и вихри слабой интенсивности. На развитой стадии (сто оборотов цилиндров) деление на зоны становится еще более ярко выраженным (фиг. 6в). Также отмечается возникновение высокочастотных вихревых возмущений малой интенсивности около границы внешнего цилиндра.
Описанная выше тенденция разделения течения на зоны сохраняется и при меньших значениях $\omega $. На фиг. 7 приведены результаты расчета при $\omega = - 1.5$. Здесь также образуется внутренняя зона течения, где устанавливается регулярная периодическая структура, содержащая два ряда вихрей, аналогичная той, что устанавливалась во всем пространстве между цилиндрами при $\omega = - 0.5$ (фиг. 5в). Далее во внешней зоне развиваются еще более ярко выраженные, чем при $\omega = - 1$, грибовидные возмущения плотности (фиг. 7б), связанные с возникновением вихревых ячеек с меньшими периодом и интенсивностью по сравнению с установившимися ранее во внутренней зоне. Вследствие малой интенсивности вихрей процесс установления течения во внешней зоне происходит существенно медленнее, чем ранее во внутренней. Однако к моменту времени, соответствующему ста оборотам внутреннего цилиндра, течение во внешней зоне в свою очередь разделяется на два слоя. В слое, примыкающем к внутренней зоне, устанавливается ряд разнонаправленных вихрей слабой интенсивности с тем же периодом, что и у вихрей внутренней зоны. В слое, примыкающем к внешнему цилиндру, проявляются вихревые возмущения большей частоты. Отметим также, что плотность в обоих слоях меняется незначительно, а ее максимальные по всей расчетной области значения достигаются около границы внешнего цилиндра.
Далее исследуем влияние на моделируемые течения значений числа Рейнольдса ${\text{Re}}$ и числа Маха ${\text{M}}$. Для этого в качестве базового выберем описанный ранее вариант течения при $\omega = - 0.5$, ${\text{Re}} = 300$ и ${\text{M}} = 0.1$ (фиг. 5в). На фиг. 8 демонстрируются результаты расчетов при ${\text{Re}} = 150$, ${\text{Re}} = 600$ и неизменных прочих параметрах за исключением значения $H$, которое, как и ранее, подбиралось индивидуально для каждого расчета описанным выше способом с целью обеспечения периодичности возникающих течений по высоте расчетной области. Сравнение с фиг. 5в позволяет сделать вывод, что с увеличением числа Рейнольдса увеличивается период вихревых течений. Кроме того, при достаточно больших значениях ${\text{Re}}$ регулярное вихревое течение становится неустойчивым. Так, при ${\text{Re}} = 600$ устанавливается вихревая структура (фиг. 8б), аналогичная наблюдаемой при ${\text{Re}} = 300$. Однако в ходе дальнейших расчетов структура разрушается. Осуществляется переход к турбулентному течению, которое сопровождается хаотичным образованием грибовидных возмущений плотности у границы внутреннего цилиндра (фиг. 8в).
Фиг. 8.
Течения при $\omega = - 0.5$, ${\text{M}} = 0.1$: (а) ${\text{Re}} = 150$, (б), (в) ${\text{Re}} = 600$.

Существенно влияет на характер моделируемых течений и число Маха. С его увеличением возрастают отклонения от изначально постоянного распределения плотности, т.е. сильнее проявляется фактор сжимаемости газа. Так, если при ${\text{M}} = 0.1$ (фиг. 5в) это отклонение не превышает $8\% $, то при ${\text{M}} = 0.25$ (фиг. 9а) оно достигает 45%, а при ${\text{M}} = 0.4$ (фиг. 9б) – 70%. Характерным является возникновение зоны уплотнения около внешнего цилиндра (фиг. 9б). Кроме того, с ростом числа Маха активнее проявляется нестабильность регулярной структуры вихрей около внешнего цилиндра. При достаточно больших значениях числа Маха указанная нестабильность приводит к развалу установившейся регулярной вихревой структуры (фиг. 9в).
Фиг. 9.
Течения при $\omega = - 0.5$, ${\text{Re}} = 300$: (а) ${\text{M}} = 0.25$, (б), (в) ${\text{M}} = 0.4$.
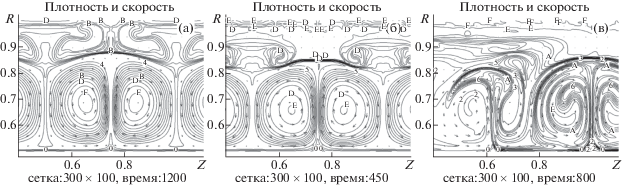
Как уже отмечалось, описанные выше расчеты проводились в одном слое разностных ячеек при фиксированном значении полярного угла в предположении цилиндрической симметрии течения (2.5D-приближение). Для проверки адекватности такого приближения для некоторых вариантов 2.5D-расчетов были проведены их трехмерные аналоги. В частности, проведены трехмерные расчеты базового варианта при $\omega = - 0.5$, ${\text{Re}} = 300$ и ${\text{M}} = 0.1$. Возмущения осевой компоненты скорости здесь по-прежнему задавались в виде (10), что определяло изначальную неоднородность малых возмущений по полярному углу. Несмотря на это, на развитых стадиях устанавливалось однородное по полярному углу течение, совпадающее в любой меридиональной плоскости с описанным ранее 2.5D-течением.
Перейдем к описанию результатов моделирования течений между сферами. При малых значениях величины зазора $d$ течения в окрестности экваториальной плоскости близки к описанным ранее для случая вращающихся цилиндров. Для иллюстрации этого факта приведем результаты двух расчетов при $d = 0.05$, проведенных в близких по размерам областях в цилиндрической и сферической геометрии (см. фиг. 10). Выбирались следующие параметры расчетных областей: ${{R}_{1}} = 10$, ${{R}_{2}} = 10.5$, $z \in [0;1.5]$ в цилиндрических координатах и $\psi \in [ - 0.075;0.075]$ в сферических. Для обоих расчетов ${\text{Re}} = 550$, $\omega = - 1$, ${\text{M}} = 0.5$, на верхних и нижних границах областей (на фигурах справа и слева), как и ранее, задавались условия непротекания. Как легко видеть, результаты расчетов по двум различным схемам (цилиндрической и сферической) чрезвычайно близки.
Фиг. 10.
Течения в тонком зазоре при $\omega = - 1$, ${\text{Re}} = 550$, ${\text{M}} = 0.5$: (а) между цилиндрами, (б) между сферами.

Как уже отмечалось, при достаточно малых значениях числа Рейнольдса аналитические исследования и результаты экспериментов (см. [9], [10]) свидетельствуют о возможности возникновения трех различных типов течений несжимаемой жидкости между сферами в зависимости от соотношения угловых скоростей их вращения. Далее приведем результаты моделирования подобных течений для характерных значений параметра $\omega $ и $d = 1$.
При $\omega = - 0.1$ доминирует вращение внутренней сферы и реализуется течение первого типа. При ${\text{Re}} = 125$ и ${\text{M}} = 0.05$ возникает устойчивая картина, содержащая два симметричных вихря, в которых движение вдоль границы внутренней сферы направлено от полюсов к экватору (см. фиг. 11а). Здесь и далее, поскольку имеет место симметрия течения относительно экваториальной плоскости, приводится картина течения в верхней половине расчетной области. При увеличении числа Маха (${\text{M}} = 0.5$) картина течения качественно меняется. Возникает еще одна пара симметричных вихрей меньшей интенсивности (см. фиг. 11б). При этом вихри, расположенные ближе к экватору, не являются устойчивыми. Наблюдаются их колебательные возмущения, которые носят квазипериодический характер. При других соотношениях параметров, например, при ${\text{M}} = 0.25$ и ${\text{Re}} = 625$ можно получить более ярко выраженную картину подобного течения (см. фиг. 11в).
Фиг. 11.
Течения первого типа при $\omega = - 0.1$: (а) ${\text{Re}} = 125$, ${\text{M}} = 0.05$; (б) ${\text{Re}} = 125$, ${\text{M}} = 0.5$; (в) ${\text{Re}} = 625$, ${\text{M}} = 0.25$.
При $\omega = - 0.5$ реализуется течение второго типа, содержащее две пары разнонаправленных вихрей. На фиг. 12а представлены результаты расчета при ${\text{Re}} = 125$ и ${\text{M}} = 0.05$. При увеличении числа Маха (см. фиг. 12б, ${\text{M}} = 0.25$) картина течения существенно меняется. Внутренние вихри смещаются к полюсам, возникает застойная зона (справа), внешние вихри приобретают более сложную форму. При этом картина в целом не является устойчивой. Наблюдаются пространственные флуктуации, которые также носят периодический характер. При других соотношениях параметров Re и M можно получить и другие варианты течений (см. фиг. 12в, ${\text{Re}} = 250$, ${\text{M}} = 0.1$). Отметим, что чрезвычайно похожие картины течений получены в ходе моделирования течений несжимаемой жидкости между вращающимися сферами при близких параметрах в работе [22].
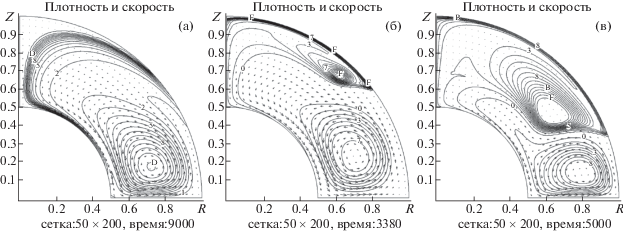
Фиг. 12.
Течения второго типа при $\omega = - 0.5$: (а) ${\text{Re}} = 125$, ${\text{M}} = 0.05$; (б) ${\text{Re}} = 125$, ${\text{M}} = 0.25$; (в) ${\text{Re}} = 250$, ${\text{M}} = 0.1$.

При преобладающем вращении внешней сферы возникают течения третьего типа. На фиг. 13а приведены результаты расчета при $\omega = - 1.5$, ${\text{Re}} = 75$, ${\text{M}} = 0.03$. Течение содержит пару симметричных вихрей, вращающихся таким образом, что движение вдоль границы внутренней сферы направлено от экватора к полюсам. При большем числе Маха ${\text{M}} = 0.3$ (см. фиг. 13б) такая картина становится неустойчивой, возникает пространственная флуктуация вихрей. При ${\text{Re}} = 190$ и ${\text{M}} = 0.15$ получается устойчивая картина, содержащая застойную зону (справа), с более сложной формой вихрей (см. фиг. 13в).
Фиг. 13.
Течения третьего типа при $\omega = - 1.5$: (а) ${\text{Re}} = 75$, ${\text{M}} = 0.03$; (б) ${\text{Re}} = 75$, ${\text{M}} = 0.3$; (в) ${\text{Re}} = 190$, ${\text{M}} = 0.15$.
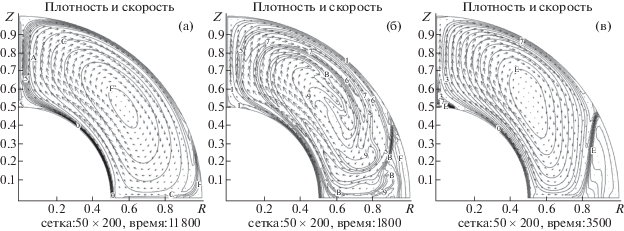
Течения первого типа также характерны для сонаправленного движения сфер при $0\;\leqslant \;\omega \;\leqslant \;1$ [9], [10]. На фиг. 14а приведены результаты расчета при $\omega = 0$, ${\text{Re}} = 200$, ${\text{M}} = 0.25$, где $d = 1{\text{/}}3$. При уменьшении относительной величины зазора между сферами при неизменных прочих параметрах характер течения меняется. Так, при $d = 1{\text{/}}4$ сначала также развивается течение первого типа. Однако оно оказывается неустойчивым и далее перестраивается во вторичное течение, содержащее две пары симметричных относительно экватора вихрей (см. фиг. 14б). При $d \approx 1{\text{/}}6$ стадия возникновения течения первого типа и вовсе отсутствует. Сразу развивается течение, содержащее три пары симметричных вихрей (см. фиг. 14в). Эти результаты демонстрируют определяющее влияние величины зазора между сферами на характер моделируемых течений.
Фиг. 14.
Течения при $\omega = 0$, ${\text{Re}} = 200$, ${\text{M}} = 0.25$: (а) $d = 1{\text{/}}3$, (б) $d = 1{\text{/}}4$, (в) $d \approx 1{\text{/}}6$.
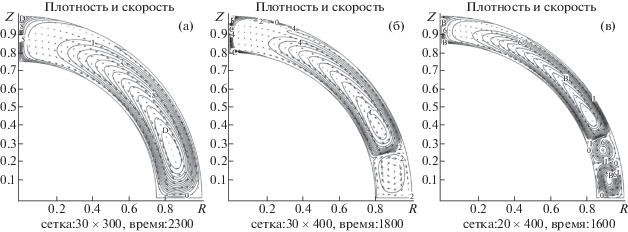
Для несжимаемой жидкости аналитически достаточно детально исследован случай почти твердотельного вращения сфер при ${\text{Re}} \gg 1$ и ${{\Omega }_{1}} = (1 - \varepsilon ){{\Omega }_{2}}$, где $0 < \varepsilon \ll 1$. В этом случае возникает течение, которое имеет достаточно сложную структуру, впервые исследованную Праудмэном [14] и впоследствии более детально описанную Стюартсоном [13]. Течение разделяется на две зоны вертикальным цилиндрическим сдвиговым слоем. Снаружи этого слоя жидкость вращается твердотельно с угловой скоростью внешней сферы во внешней зоне, и с некоторой промежуточной между скоростями вращения двух сфер угловой скоростью во внутренней зоне. Внутри сдвигового слоя угловая скорость зависит лишь от расстояния до оси вращения и возрастает по мере удаления от нее на отрезке между указанными значениями. Во внутренней зоне и внутри сдвигового слоя вблизи границ сфер возникают слои Экмана (см. [23]), которые характеризуются большими градиентами меридиональной скорости. Перетекание жидкости во внутренней зоне между слоями Экмана осуществляется от медленнее вращающейся внутренней сферы к внешней в вертикальном направлении. Сдвиговый слой в свою очередь состоит из трех (согласно [13]) участков различной толщины. В среднем возникает возвратное течение от внешней сферы к внутренней также в направлении, параллельном вертикальной образующей слоя.
На фиг. 15 представлены результаты расчета при ${{\Omega }_{1}} = 0.135$, ${{\Omega }_{2}} = 0.15$ (${{\Omega }_{1}} = 0.9{{\Omega }_{2}}$), ${\text{Re}} = 3400$, ${\text{M}} = 0.1$ и $d = 1$. Как видно на фигуре, в рассматриваемом сжимаемом случае также возникает течение, обладающее всеми описанными выше характеристиками. В [13] получены оценки характерных размеров слоев в зависимости от числа Рейнольдса. Для приведенного расчета характерные толщины слоев с достаточной точностью совпадают с оценочными. Важно также отметить, что с указанными параметрами проводились и трехмерные расчеты. Полученные результаты не имеют отличий от полученных в 2.5D-приближении, поскольку в ходе моделирования не возникает неоднородностей течения по полярному углу.
Фиг. 15.
Течение Стюартсона–Праудмэна при ${{\Omega }_{1}} = 0.9{{\Omega }_{2}}$, ${\text{Re}} = 3400$, ${\text{M}} = 0.1$.

Характерные элементы течения Стюартсона–Праудмэна могут проявляться и в случаях, когда вращение сфер не определяет движение вещества, близкое к твердотельному. В качестве примера приведем результаты расчета с параметрами, совпадающими с выбираемыми в ходе моделирования течения несжимаемой жидкости в работе [24]: $\omega = 1{\text{/}}8$, ${\text{Re}} = 1100$ (${\text{Re}} = 2000$ по способу расчета в [24]), ${{R}_{1}} = 0.35$ и ${{R}_{2}} = 1$. При таких значениях возникает ярко выраженный джет, направленный от внутренней сферы к внешней вблизи экваториальной плоскости, “размазанный” по пространству слой Стюартсона, слои Экмана и почти вертикальные потоки жидкости между ними. На фиг. 16 приведены линии уровня угловой скорости, плотности и векторы скорости в меридиональной плоскости установившегося на момент времени $T = 2800$ течения в ходе расчета при ${\text{M}} = 0.1$. Приведенные на фиг. 16 результаты чрезвычайно близки к полученным в работе [24].
Фиг. 16.
Течение при ${\text{Re}} = 1100$, ${{R}_{1}} = 0.35$, ${{R}_{2}} = 1$, $\omega = 1{\text{/}}8$.

В качестве заключения отметим, что при небольших значениях числа Маха (0.1 и менее) результаты моделирования, описанные выше, хорошо соотносятся с экспериментальными данными и теоретическими исследованиями течений несжимаемой жидкости между цилиндрами и сферами. Таким образом, продемонстрирована возможность исследования таких течений в рамках модели вязкого газа путем прямого численного моделирования с использованием явных консервативных разностных схем годуновского типа.
Автор выражает безмерную благодарность своему учителю, Юрию Петровичу Попову, недавно ушедшему из жизни, который положил начало этой работе.
Список литературы
Линь Ц.-Ц. Теория гидродинамической устойчивости. М.: Изд-во иностр. лит., 1958.
Joseph D.D. Stability of fluid motions I. New York: Springer-Verlag, 1976.
DiPrima R.C., Stuart J.T. Hydrodynamic stability // J. Appl. Mech. 1983. V. 50. № 4b. P. 983–991.
Дразин Ф. Введение в теорию гидродинамической устойчивости. М.: Физматлит, 2005.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. T. VI. Гидродинамика. М.: Наука, 1986.
Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидродинамика. Ч. 2. М.: Физматлит, 1963.
Taylor G.I. Stability of a viscous liquid contained between two rotating cylinders // Phil. Trans. Roy. Soc. 1923. V. A223. P. 289–343.
Synge J.L. On stability of viscous liquid between two rotating coaxial cylinders // Proc. Roy. Soc. 1938. V. A167. P. 250–256.
Яворская И.М., Астафьева К.М. Течения вязкой жидкости в сферических слоях. Обзор. Препринт ИКИ АН СССР: Пр-06-10. М., 1974.
Монахов А.А. Граница устойчивости основного течения в сферических слоях // Изв. РАН. МЖГ. 1996. № 4. P. 66–70.
Abakumov M.V. Method for the construction of Godunov-type difference schemes in curvilinear coordinates and its application to cylindrical coordinates // Comput. Math. and Modeling. 2014. V. 25. № 3. P. 315–333.
Abakumov M.V. Construction of Godunov-type difference schemes in curvilinear coordinates and an application to spherical coordinates // Comput. Math. and Modeling. 2015. V. 26. № 2. P. 184–203.
Stewartson K. On almost rigid rotations // J. Fluid Mech. 1966. V. 26. № 01. P. 131–144.
Proudman I. The almost-rigid rotation of viscous fluid between concentric spheres // J. Fluid Mech. 1956. V. 1. № 05. P. 505–516.
Кочин Н.Е. Векторное исчисление и начала тензорного исчисления. М.: Наука, 1965.
Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. М.: Наука, 1992.
Годунов С.К. Разностный метод численного расчета разрывных решений гидродинамики // Матем. сборник. 1959. Т. 47(89). № 3. С. 271–306.
Годунов С.К., Забродин А.В., Прокопов Г.П. Разностная схема для двумерных нестационарных задач газовой динамики и расчет обтекания с отошедшей ударной волной // Ж. вычисл. матем. и матем. физ. 1961. Т. 1. № 6. С. 1020–1050.
Roe P.L. Characteristic-based schemes for the Euler equations // Ann. Rev. Fluid Mech. 1986. V. 18. № 1. P. 337–365.
Einfeldt B. On Godunov-type methods for gas dynamics // SIAM J. Numer. Anal. 1988. V. 25. № 2. P. 294–318.
Chakravarthy S.R., Osher S. A new class of high accuracy TVD schemes for hyperbolic conservationlaws // 23rd Aerospace Sciences Meeting. American Institute of Aeronautics and Astronautics, 1985. P. 1–11.
Жиленко Д.Ю., Кривоносова О.Э., Никитин Н.В. Развитие пространственных структур течения при ламинарно-турбулентном переходе в широком сферическом слое // Докл. АН. 2007. Т. 414. № 1. С. 39–43.
Eкman V.W. On the influence of the Earth’s rotation on ocean currents // Ark. Mat. Astron. Fys. 1905. V. 2. № 11. P. 1–52.
Gissinger C., Ji H., Goodman J. Instabilities in magnetized spherical couette flow // Physical Review. 2011. V. 84. № 2. P. 1–10.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики





