1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 59, № 3, 2019

Журнал вычислительной математики и математической физики, 2019, T. 59, № 3, стр. 494-504

Сравнение алгоритмов решения задачи определения толщин слоев оптических покрытий в режиме “on-line”

Т. Ф. Исаев 1, *, И. В. Кочиков 2, **, Д. В. Лукьяненко 1, ***, А. В. Тихонравов 2, ****, А. Г. Ягола 1, *****

1 МГУ, Физ. фак-т
119992 Москва, Ленинские горы, Россия

2 МГУ, НИВЦ
119992 Москва, Ленинские горы, Россия

* E-mail: temurisaev@gmail.com
** E-mail: igor@kochikov.ru
*** E-mail: lukyanenko@physics.msu.ru
**** E-mail: tikh@srcc.msu.ru
***** E-mail: yagola@physics.msu.ru

Поступила в редакцию 18.07.2018

Полный текст (PDF)

Аннотация

Рассмотрены основные алгоритмы определения толщин слоев напыляемых многослойных оптических покрытий. Проведено сравнение этих алгоритмов. На серии модельных численных экспериментов показано преимущество одного из этих алгоритмов, а именно модифицированного T-алгоритма, позволяющего уменьшить влияние кумулятивного эффекта накопления ошибок в определяемых толщинах слоев. Библ. 23. Фиг. 5.

Ключевые слова: функционал невязки,  напыляемый слой, математическое ожидание, “on-line” мониторинг.

1. ВВЕДЕНИЕ

Управление процессом напыления оптических покрытий на основе широкополосного оптического контроля (мониторинга) приобретает в настоящее время все большее значение. Первые широкополосные системы были использованы для этих целей еще в конце 70-х годов прошлого века (см. [1], [2]). Уже в этих ранних работах были продемонстрированы возможности таких систем. Бурное развитие вычислительной техники и появление фотодиодных решеток для одновременной регистрации спектральных данных на большом числе точек спектра открыли новые горизонты для развития широкополосных оптических систем мониторинга. Большая часть используемых и разрабатываемых ныне систем ориентируется на так называемый прямой мониторинг покрытий, при котором измерения коэффициентов пропускания/отражения производятся непосредственно на одном из производимых образцов покрытий (см. [3]–[5]).

Огромным преимуществом систем прямого широкополосного мониторинга является присущий им механизм самокомпенсации ошибок напыления. Возможность наличия такого механизма отмечалась рядом авторов уже давно [1], [6], но фактическое его существование было доказано лишь недавно [7]. Однако, наряду с указанным положительным свойством прямого широкополосного оптического мониторинга, существует и связанная с ним серьезная проблема. Это – существование кумулятивного эффекта накопления ошибок контроля толщин слоев при большом числе слоев покрытия [8]. Преодоление негативных последствий данного эффекта возможно за счет использования более современных алгоритмов предсказания времени прерывания напыления слоя и определения фактических значений толщин уже напыленных слоев в режиме “on-line”. Теоретические исследования данного рода связаны в первую очередь с определением путей построения таких алгоритмов.

В силу того, что уже существует ряд алгоритмов определения толщин напыляемых слоев в режиме “on-line” (например, рассмотренные в [9] $S$-алгоритм, T-алгоритм, ленточные алгоритмы), необходимо найти объективный критерий сравнения надежности различных алгоритмов. Такой критерий естественно строить на основе оценки чувствительности используемого алгоритмом функционала по отношению к ошибкам в толщинах слоев покрытия. В процессе исследования необходимо также выяснить, из какого набора данных “on-line” измерений толщина текущего напыляемого слоя определяется наиболее надежно. Тесно связанным с этой задачей является вопрос о том, увеличивается ли точность определения толщины текущего слоя, если в процессе работы алгоритма искать не только толщину текущего слоя, но и одновременно переопределять заново толщины уже напыленных слоев. В силу того, что различные факторы, приводящие к ошибкам в толщинах слоев, являются случайными, решение поставленных задач следует искать на основе статистического анализа, вводя некоторые разумные предположения о характере случайных ошибок.

Структура данной работы такова. В разд. 2 описана общая структура $S$- и T-алгоритмов (и их модификаций) определения оптических параметров напыленного многослойного покрытия. В разд. 3 проведено подробное сравнение этих алгоритмов на основе результатов численных расчетов, выполненных с использованием исследуемых алгоритмов. Основные выводы приведены в заключении.

2. ОПИСАНИЕ АЛГОРИТМОВ

2.1. Основные предположения и вывод основных уравнений

Пусть $d_{1}^{t},\; \ldots ,\;d_{m}^{t}$ – теоретические значения толщин слоев напыляемого покрытия (т.е. те значения, которые получены в результате решения задачи синтеза покрытия и которые мы пытаемся воспроизвести при напылении покрытия). Вследствие производственных ошибок, включающих в себя также и ошибки, связанные с контролем напыления, истинные значения толщин напыленных слоев отличаются от теоретических значений. Обозначим истинные значения толщины как $d_{1}^{a},\; \ldots ,\;d_{j}^{a},\; \ldots $, где $j$ – номер напыляемого в текущий момент слоя. В дальнейшем будем считать, что $d_{j}^{a}$ мало отличаются от $d_{j}^{t}$, и будем это использовать в ходе различных оценок, производя разложение по соответствующим порядкам малости.

Пусть ${{T}^{j}}\left( {d_{1}^{a},\; \ldots ,\;d_{j}^{a},\lambda } \right)$ и ${{R}^{j}}\left( {d_{1}^{a},\; \ldots ,\;d_{j}^{a},\lambda } \right)$ – коэффициенты пропускания и отражения покрытия в конце напыления $j$-го слоя. Здесь $\lambda $ – длина волны излучения, которая соответствует некоторой точке из набора длин волн $\{ \lambda \} $, на котором производятся измерения коэффициентов $T$ и $R$. В дальнейшем для сокращения выкладок будем рассматривать только коэффициент пропускания $T$. Все выкладки для $R$ аналогичны приводимым ниже.

Пусть $T_{{{\text{meas}}}}^{j}(\lambda )$ – измеренный коэффициент пропускания в конце напыления $j$-го слоя. Тогда величина

(1)
$\delta T_{{{\text{meas}}}}^{j}(\lambda ) = T_{{{\text{meas}}}}^{j}(\lambda ) - {{T}^{j}}\left( {d_{1}^{a},\; \ldots ,\;d_{j}^{a},\lambda } \right)$
есть ошибка измерений в момент окончания напыления $j$-го слоя.

Введем функционал, который будем называть парциальным оценочным функционалом:

(2)
${{F}^{j}} \equiv {{F}^{j}}({{d}_{1}},\; \ldots ,\;{{d}_{j}}) = \frac{1}{L}\sum\limits_{\{ \lambda \} } \,{{[{{T}^{j}}({{d}_{1}},\; \ldots ,\;{{d}_{j}},\lambda ) - T_{{{\text{meas}}}}^{j}(\lambda )]}^{2}}.$
Здесь $L$ – общее число точек множества точек измерений $\{ \lambda \} $, ${{d}_{1}},\; \ldots ,\;{{d}_{j}}$ – переменные значения толщин слоев (аргументы функционала ${{F}^{j}}$).

Предположим, что

${{d}_{i}} = d_{i}^{a} + {{h}_{i}},$
где ${{h}_{i}}$ – малые отклонения переменных ${{d}_{i}}$ от истинных значений толщин напыленных слоев $d_{i}^{a}$.

Тогда ${{T}^{j}}({{d}_{1}},\; \ldots ,\;{{d}_{j}},\lambda )$ можно представить в виде

(3)
${{T}^{j}}({{d}_{1}},\; \ldots ,\;{{d}_{j}},\lambda ) = {{T}^{j}}(d_{1}^{a},\; \ldots ,\;d_{j}^{a},\lambda ) + \sum\limits_{i = 1}^j \frac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}{{h}_{i}}.$
В этом выражении производные $\tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}$ должны быть взяты при значениях ${{d}_{i}} = d_{i}^{a}$. Однако, поскольку истинные значения толщин $d_{i}^{a}$ неизвестны и поскольку выше было введено предположение о том, что $d_{i}^{a}$ близки к теоретическим значениям толщин слоев $d_{i}^{t}$, в дальнейшем все производные будем вычислять при значениях толщин слоев, равных теоретическим значениям.

Пользуясь (1) и (3), запишем парциальный функционал ${{F}^{j}}$ в виде:

(4)
${{F}^{j}} = \frac{1}{L}\sum\limits_{\{ \lambda \} } {{\left[ {\sum\limits_{i = 1}^j \frac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}{{h}_{i}} - \delta T_{{{\text{meas}}}}^{j}(\lambda )} \right]}^{2}}.$

Выделим в выражении для функционала (4) ошибку в толщине одного из слоев с номером $i$, $1 \leqslant i \leqslant j$, и перепишем (4) в виде

(5)
${{F}^{j}} = \frac{1}{L}\sum\limits_{\{ \lambda \} } {{\left[ {\frac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}{{h}_{i}} + \sum\limits_{l \ne i} \frac{{\partial {{T}^{j}}}}{{\partial {{d}_{l}}}}{{h}_{l}} - \delta T_{{{\text{meas}}}}^{j}(\lambda )} \right]}^{2}}.$

Функционал (5) является квадратичным функционалом относительно ${{h}_{i}}$. Из условия минимума этого функционала по ${{h}_{i}}$ получаем

(6)
${{h}_{i}} = \frac{{\left[ {\tfrac{1}{L}\sum\limits_{\{ \lambda \} } \tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}\delta T_{{{\text{meas}}}}^{j}(\lambda ) - \sum\limits_{l \ne i} \left( {\tfrac{1}{L}\sum\limits_{\{ \lambda \} } \tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}\tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{l}}}}} \right){{h}_{l}}} \right]}}{{\left[ {\tfrac{1}{L}\sum\limits_{\{ \lambda \} } {{{\left( {\tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}} \right)}}^{2}}} \right]}}.$
Полученное выражение (6) будет основным при дальнейших рассмотрениях. Введем следующие обозначения:
$\beta _{i}^{j} = \frac{1}{L}\sum\limits_{\{ \lambda \} } \frac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}\delta T_{{{\text{meas}}}}^{j}(\lambda ),\quad \alpha _{{il}}^{j} = \frac{1}{L}\sum\limits_{\{ \lambda \} } \frac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}\frac{{\partial {{T}^{j}}}}{{\partial {{d}_{l}}}},\quad \mu _{i}^{j} = \frac{1}{L}\sum\limits_{\{ \lambda \} } {{\left( {\frac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}} \right)}^{2}}$
и перепишем (6) в виде

(7)
${{h}_{i}} = \frac{{\left[ {\beta _{i}^{j} - \sum\limits_{l \ne i} \,\alpha _{{il}}^{j}{{h}_{l}}} \right]}}{{\left[ {\mu _{i}^{j}} \right]}}.$

Важной чертой данного выражения является то, что оно не зависит от того, каким образом найдены значения ${{h}_{l}}$. В частности, оно может быть использовано для оценок, связанных с работой различных алгоритмов определения ошибок в толщинах слоев в режиме “on-line”. В этом случае ${{h}_{l}}$ – это те значения, которые найдены из соответствующего условия минимума функционала, например, из условия минимума функционала по всем ${{h}_{i}}$.

Если для определения ${{h}_{i}}$ используется не один, а сумма нескольких парциальных функционалов, то выражение (7) естественным образом обобщается на этот случай.

Пусть для определения ${{h}_{i}}$ используется некоторый набор парциальных функционалов ${{F}^{j}}$ с индексами $j$ из некоторого множества $J$, и ${{h}_{i}}$ определяются из условия минимума функционала

(8)
$F = \sum\limits_{j \in J} \,{{F}^{j}}$
по ${{h}_{i}}$. Тогда по аналогии с (7) для ${{h}_{i}}$ получаем выражение
(9)
${{h}_{i}} = \frac{{\left[ {\sum\limits_{j \in J,j \geqslant i} \beta _{i}^{j} - \sum\limits_{j \in J,j \geqslant i} \,\sum\limits_{l = 1,l \ne i}^j \alpha _{{il}}^{j}{{h}_{l}}} \right]}}{{\left[ {\sum\limits_{j \in J,j \geqslant i} \mu _{i}^{j}} \right]}}.$
Здесь суммирование ведется по всем $j$, соответствующим выбранной совокупности парциальных функционалов. При этом в выражении (9) суммирование ведется только по тем $j$, которые больше или равны $i$. Это связано с тем, что переменная толщина ${{d}_{i}}$ и соответствующая ей ошибка ${{h}_{i}}$ не входят в парциальные функционалы с номерами, меньшими $i$.

Различные алгоритмы определения толщин слоев в режиме “on-line” определяются выбором функционалов невязки, из условия минимума которых и находятся значения толщин слоев ${{d}_{i}}$ или же соответствующие им ошибки ${{h}_{i}} = {{d}_{i}} - d_{i}^{a}$. Наиболее широко используемыми алгоритмами являются так называемые $S$-алгоритм (“sequential algorithm”) и T-алгоритм (“triangular algorithm”) [9].

В случае $S$-алгоритма для определения толщины $i$-го слоя используется только парциальный функционал с номером $i$. Все найденные ранее толщины слоев и соответствующие им ошибки ${{h}_{1}},\; \ldots ,\;{{h}_{{i - 1}}}$ фиксируются и принимаются равными ранее найденным значениям. При этом ошибка ${{h}_{i}}$ оказывается связанной с предыдущими ошибками в толщинах слоев выражением, непосредственно следующим из (9):

${{h}_{i}} = \frac{{\beta _{i}^{i}}}{{\mu _{i}^{i}}} - \sum\limits_{l = 1}^{i - 1} \left( {\frac{{\alpha _{{il}}^{i}}}{{\mu _{i}^{i}}}} \right){{h}_{l}}.$
В данном выражении первый член в правой части учитывает ошибку в толщине $i$-го слоя, связанную непосредственно с ошибкой измеренных данных для этого слоя, а второй член описывает влияние ошибок в толщинах предыдущих слоев на точность контроля текущего слоя. Известно (см. [10]), что с ростом числа слоев покрытия влияние ошибок в предыдущих слоях на точность контроля текущего слоя может очень сильно увеличиваться – это так называемый кумулятивный эффект в ошибках контроля толщин слоев.

Одной из важнейших целей при выборе алгоритма определения толщин слоев является уменьшение влияния кумулятивного эффекта на точность определения толщины текущего слоя. Такое уменьшение может быть достигнуто за счет более точного определения толщин уже напыленных слоев. Именно в связи с этим и был предложен T-алгоритм, основанный на использовании суммы парциальных функционалов для всех слоев с номерами от $1$ до $i$. При его использовании определяется не только толщина $i$-го слоя ${{d}_{i}}$, но и переопределяются все ранее найденные толщины ${{d}_{1}},\; \ldots ,\;{{d}_{{i - 1}}}$. В [11] было показано, что в ряде случаев T-алгоритм оказывается более надежным, чем $S$-алгоритм.

В определенном смысле $S$- и T-алгоритмы являются крайними вариантами всего множества возможных алгоритмов определения толщин слоев. Другие алгоритмы решения данной задачи могут быть получены за счет выбора других комбинаций парциальных функционалов, а также за счет выбора других совокупностей определяемых и фиксируемых толщин слоев.

2.2. Оценка точности определения толщины слоя

В общем случае, не делая упрощающих предположений о характере ошибок в толщинах слоев, невозможно получить аналитические оценки точности определения толщин слоев. Однако такие оценки необходимы для получения качественных выводов о свойствах алгоритмов, для сравнения различных алгоритмов и для выбора наиболее рационального из них. Поэтому необходимо ввести соответствующие практике предположения о характере ошибок в толщинах слоев, которые позволили бы провести необходимые аналитические выкладки.

В данном разделе рассмотрим вопрос об оценке точности нахождения толщин уже напыленных слоев. Существующую задачу будем называть задачей восстановления параметров слоев (т.е. истинных толщин слоев). Вопрос о выборе алгоритма, позволяющего минимизировать ошибку в толщине последнего слоя в процессе его напыления, рассмотрим позже. При этом задачу определения толщины напыляемого слоя будем называть задачей мониторинга, а алгоритм ее решения – алгоритмом мониторинга.

При исследовании задачи восстановления сделаем следующие упрощающие предположения. Пусть все ошибки в толщинах слоев – независимые случайные величины, распределенные по нормальному закону с нулевым математическим ожиданием. Это предположение оправдано, когда продолжительность напыления слоев (а тем самым и ошибка в толщине слоя) определяется большим числом случайных факторов (см., например, [12]). В то же время при использовании других методов (например, на основе широкополосного мониторинга) ошибки в толщинах слоев могут быть коррелированы [13]. Предположим далее, что среднеквадратичные отклонения для ошибок в толщинах слоев одинаковы и равны $\sigma $.

Ошибки в измерительных данных $\delta T_{{{\text{meas}}}}^{j}(\lambda )$ также будем считать распределенными по нормальному закону с нулевым математическим ожиданием и среднеквадратичным отклонением

$\left\langle {\delta T_{{{\text{meas}}}}^{j}(\lambda )} \right\rangle = {{\sigma }_{{{\text{meas}}}}}.$

При этом предположим, что ${{\sigma }_{{{\text{meas}}}}}$ не зависит как от номера слоя $j$, так и от длины волны $\lambda $.

Перепишем выражение (9) в виде

(10)
${{h}_{i}} = \sum\limits_{j \in J,j \geqslant i} \,\sum\limits_{\{ \lambda \} } \,\beta _{i}^{j}(\lambda )\delta T_{{{\text{meas}}}}^{j}(\lambda ) + \sum\limits_{j \in J,j \geqslant i} \,\sum\limits_{l = 1,l \ne i}^j \,c_{{il}}^{j}{{h}_{l}},$
где
$\beta _{i}^{j}(\lambda ) = \frac{{\tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}}}{{\sum\limits_{j \in J,ji} \,\sum\limits_{\{ \lambda \} } {{{\left( {\tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}} \right)}}^{2}}}},\quad c_{{il}}^{j} = \frac{{\sum\limits_{\{ \lambda \} } \tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}\tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{l}}}}}}{{\sum\limits_{j \in J,ji} \,\sum\limits_{\{ \lambda \} } {{{\left( {\tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}} \right)}}^{2}}}}.$
Поменяем во втором члене в правой части (10) порядки суммирования по $j$ и $l$. Получим

(11)
${{h}_{i}} = \sum\limits_{\{ \lambda \} } \,\sum\limits_{j \in J,j \geqslant i} \beta _{i}^{j}(\lambda )\delta T_{{{\text{meas}}}}^{j}(\lambda ) + \sum\limits_{l = 1,l \ne i}^{{{j}_{{{\text{max}}}}}} \left( {\sum\limits_{j \in J,j \geqslant \max \{ i,l\} } c_{{il}}^{j}} \right){{h}_{l}}.$

В этом выражении ${{j}_{{{\text{max}}}}}$ обозначает максимальный номер парциального функционала из набора парциальных функционалов $J$, используемых для определения ошибок в толщинах слоев ${{h}_{i}}$.

При сделанных выше предположениях о характере ошибок $\delta T_{{{\text{meas}}}}^{j}(\lambda )$ и ${{h}_{l}}$ математическое ожидание ${{h}_{i}}$, вычисленное на основании соотношения (11), будет равно нулю. Вычислим с помощью этого соотношения среднеквадратичное отклонение ${{h}_{i}}$, которое обозначим через ${{\sigma }^{J}}({{h}_{i}})$, и получим

(12)
${{\sigma }^{J}}({{h}_{i}}) = {{\left[ {{{{\left( {B_{i}^{J}} \right)}}^{2}}\sigma _{{{\text{meas}}}}^{2} + {{{\left( {C_{i}^{J}} \right)}}^{2}}{{\sigma }^{2}}} \right]}^{{\tfrac{1}{2}}}}.$
Введенный в выражении (12) верхний индекс $J$ призван указать, что все соответствующие величины зависят от выбора набора парциальных функционалов $J$. При этом для $B_{i}^{J}$ и $C_{i}^{J}$ получаем следующие значения:

(13)
$B_{i}^{J} = \frac{{{{{\left[ {\sum\limits_{j \in J,j \geqslant i} \,\sum\limits_{\{ \lambda \} } {{{\left( {\beta _{i}^{j}(\lambda )} \right)}}^{2}}} \right]}}^{{\tfrac{1}{2}}}}}}{{\left[ {\sum\limits_{j \in J,j \geqslant i} \,\sum\limits_{\{ \lambda \} } {{{\left( {\tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}} \right)}}^{2}}} \right]}},\quad C_{i}^{J} = \frac{{{{{\left[ {\sum\limits_{l = 1,l \ne i}^{{{j}_{{{\text{max}}}}}} {{{\left( {\sum\limits_{j \in J,j \geqslant \max \{ i,l\} } \,\sum\limits_{\{ \lambda \} } \tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}\tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{l}}}}} \right)}}^{2}}} \right]}}^{{\tfrac{1}{2}}}}}}{{\left[ {\sum\limits_{j \in J,j \geqslant i} {\,\sum\limits_{\{ \lambda \} } {{{\left( {\tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}} \right)}}^{2}}} } \right]}}.$

Зададим соотношение между ${{\sigma }_{{{\text{meas}}}}}$ и $\sigma $. Пусть

(14)
${{\sigma }_{{{\text{meas}}}}} = \alpha \sigma .$
Тогда из (12) получаем выражение
(15)
${{\sigma }^{J}}({{h}_{i}}) = A_{i}^{J}\sigma ,$
(16)
$A_{i}^{J} = {{\left[ {{{\alpha }^{2}}{{{\left( {B_{i}^{J}} \right)}}^{2}} + {{{\left( {C_{i}^{J}} \right)}}^{2}}} \right]}^{{\tfrac{1}{2}}}}.$
Таким образом, каждому слою покрытия можно сопоставить оценку точности определения его толщины, выражаемую коэффициентом $A_{i}^{J}$ в формуле (15). Естественно, что эта оценка зависит от выбора набора парциальных функционалов, используемых для решения задачи восстановления параметров слоев. Полученная оценка может быть использована и для поиска более эффективных алгоритмов решения задачи восстановления.

2.3. Модифицированные $S$- и T-алгоритмы

В случае $S$-алгоритма для определения толщин слоев используется только один парциальный функционал, соответствующий последнему напыленному слою $j$. При этом определяется толщина только последнего слоя ${{d}_{j}}$, а толщины всех предыдущих слоев ${{d}_{1}},\; \ldots ,\;{{d}_{{j - 1}}}$ принимаются равными ранее найденным значениям. Как уже отмечалось ранее, при использовании данного алгоритма может наблюдаться сильный кумулятивный эффект накопления ошибок.

Для построения модифицированного $S$-алгоритма применим полученную в предыдущем пункте оценку (данная оценка для $S$-алгоритма впервые была сделана в [16], здесь же мы ее повторяем для целостности изложения материала). В принципе один парциальный функционал может использоваться для нахождения всех толщин напыленных слоев. При определении этих толщин из условия минимума функционала для $i$-го слоя с $ij$ получим оценку

(17)
${{\sigma }^{j}}({{h}_{i}}) = A_{i}^{j}\sigma ,$
(18)
$A_{i}^{j} = {{\left[ {{{\alpha }^{2}}{{{\left( {B_{i}^{j}} \right)}}^{2}} + {{{\left( {C_{i}^{j}} \right)}}^{2}}} \right]}^{{\tfrac{1}{2}}}},$
а $B_{i}^{j}$ и $C_{i}^{j}$ в свою очередь определяются выражениями

(19)
$B_{i}^{j} = \frac{1}{{{{{\left[ {\sum\limits_{\{ \lambda \} } {{{\left( {\tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}} \right)}}^{2}}} \right]}}^{{\tfrac{1}{2}}}}}},\quad C_{i}^{j} = \frac{{{{{\left[ {\sum\limits_{l = 1,l \ne i}^j {{{\left( {\sum\limits_{\{ \lambda \} } \tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}\tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{l}}}}} \right)}}^{2}}} \right]}}^{{\tfrac{1}{2}}}}}}{{\left[ {\sum\limits_{\{ \lambda \} } {{{\left( {\tfrac{{\partial {{T}^{j}}}}{{\partial {{d}_{i}}}}} \right)}}^{2}}} \right]}}.$

В предлагаемом модифицированном $S$-алгоритме $j$-й парциальный функционал может использоваться для определения не только толщины $j$-го слоя ${{d}_{j}}$, но и для переопределения толщин ряда напыленных ранее слоев. Номера тех слоев, толщины которых будут переопределяться, найдем следующим образом. Пусть

(20)
$A_{i}^{j} < \mathop {min}\limits_{1 \leqslant k \leqslant j - 1} A_{i}^{k}.$
Тогда для данного номера слоя $i$ его толщина переопределяется на $j$-м шаге решения задачи восстановления, т.е. при решении задачи восстановления после напыления $j$-го слоя. В противном случае толщина $i$-го слоя останется равной ранее найденному значению.

В результате применения такого алгоритма на последнем шаге напыления будут найдены толщины слоев, которым можно сопоставить коэффициенты

(21)
${{A}_{i}} = \mathop {min}\limits_{1 \leqslant j \leqslant m} A_{i}^{j}.$
Набор коэффициентов $\{ {{A}_{1}},\; \ldots ,\;{{A}_{m}}\} $ можно рассматривать как оценку точности работы модифицированного $S$-алгоритма.

В случае T-алгоритма на $j$-м шаге решения задачи восстановления для определения толщин слоев используется сумма всех парциальных функционалов с номерами от $1$ до $j$. В модифицированном T-алгоритме предлагается использовать ту же сумму парциальных функционалов, но определять не все толщины, как в T-алгоритме, а только те, для которых выполняется аналогичное (20) неравенство, в котором, однако, используются коэффициенты $A_{i}^{j}$, вычисляемые по отличным от (16)–(19) формулам.

В случае T-алгоритма в формулах (13) и (16) на $j$-м шаге множество индексов $J$ – это все индексы $k$ от $1$ до $j$, и для выражения $A_{i}^{j}$ получаем соотношения

(22)
$A_{i}^{j} = {{\left[ {{{\alpha }^{2}}{{{\left( {B_{i}^{j}} \right)}}^{2}} + {{{\left( {C_{i}^{j}} \right)}}^{2}}} \right]}^{{\tfrac{1}{2}}}},$
где
(23)
$B_{i}^{j} = \frac{1}{{{{{\left[ {\sum\limits_{k = i}^j \,\sum\limits_{\{ \lambda \} } {{{\left( {\tfrac{{\partial {{T}^{k}}}}{{\partial {{d}_{i}}}}} \right)}}^{2}}} \right]}}^{{\tfrac{1}{2}}}}}},\quad C_{i}^{j} = \frac{{{{{\left[ {\sum\limits_{l = 1,l \ne i}^j {{{\left( {\sum\limits_{k = \max \{ i,l\} }^j \,\sum\limits_{\{ \lambda \} } \tfrac{{\partial {{T}^{k}}}}{{\partial {{d}_{i}}}}\tfrac{{\partial {{T}^{k}}}}{{\partial {{d}_{l}}}}} \right)}}^{2}}} \right]}}^{{\tfrac{1}{2}}}}}}{{\left[ {\sum\limits_{k = i}^j \,\sum\limits_{\{ \lambda \} } {{{\left( {\tfrac{{\partial {{T}^{k}}}}{{\partial {{d}_{i}}}}} \right)}}^{2}}} \right]}}.$

Как и в случае модифицированного $S$-алгоритма, модифицированному T-алгоритму можно сопоставить набор коэффициентов $\{ {{A}_{1}},\; \ldots ,\;{{A}_{m}}\} $, в котором теперь ${{A}_{i}}$ вычисляются по формулам (21)–(23). Этот набор можно рассматривать как оценку точности работы модифицированного T-алгоритма.

3. СРАВНЕНИЕ АГОРИТМОВ

Для сравнения различных алгоритмов решения задачи определения толщин слоев многослойного оптического покрытия были выбраны три различных покрытия, которые состоят из поочередно напыляемых слоев с высоким показателем преломления ($H$) из материала ${\text{Zr}}{{{\text{O}}}_{2}}$ (нечетные слои) и слоев с низким показателем преломления ($L$) из материала ${\text{Si}}{{{\text{O}}}_{2}}$ (четные слои).

Алгоритмы сравнивались при решении задач с симулированными экспериментальными данными. В качестве модельных задач были рассмотрены три покрытия – поляризатор (28 слоев), горячее зеркало (40 слоев) и трехполосный фильтр (51 слой) с заданными псевдослучайными ошибками в толщинах слоев (${{\sigma }_{d}} \sim 6\% $ от толщины слоя). Для данных покрытий были вычислены спектральные зависимости коэффициента пропускания, на которые наложены случайные (${{\sigma }_{{{\text{rand}}}}} \sim 1\% $) и флуктационные (${{\sigma }_{{{\text{fluc}}}}} \sim 0.5\% $) ошибки. Коэффициенты преломления для напыляемых слоев и подложки ($S$) считались постоянными (${{n}_{H}} = 2.05$, ${{n}_{L}} = 1.45$, ${{n}_{S}} = 1.5$), поглощение отсутствовало. Моделирование измерений выполнялось в диапазоне длин волн 450–1000 нм. Процедура симуляции спектральных характеристик подробно описана в [15].

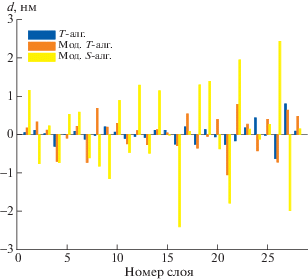
На фиг. 1 показаны толщины слоев 40-слойного горячего зеркала, заданные при моделировании и восстановленные с помощью различных алгоритмов. Как видно, все три алгоритма способны качественно восстановить толщины слоев достаточно хорошо. Фиг. 2 содержит диаграммы ошибок определенных толщин слоев.

Фиг. 1.

Модельная задача для 40-слойного горячего зеркала. Толщины слоев, заданные при моделировании, в сравнении с толщинами, определенными различными алгоритмами.

Фиг. 2.

Модельная задача для 40-слойного горячего зеркала. Ошибки толщин слоев, определенных различными алгоритмами.

Как и следовало ожидать, наибольшие ошибки наблюдаются при использовании модифицированного $S$-алгоритма, в то время как полный и модифицированный T-алгоритмы характеризуются меньшими значениями ошибок. При заданных уровнях случайных шумов определяемые толщины содержат ошибки, как правило, не превосходящие 1%.

Для восстановления толщин слоев во всех случаях оптимизировался функционал (8) с различным выбором подмножеств определяемых толщин и входных данных. На фиг. 3 показаны значения этих функционалов в точке минимума; эти значения примерно соответствуют заданному уровню шумов $1{\text{--}}2\% $.

Фиг. 3.

Модельная задача для 40-слойного горячего зеркала. Значения функционала (8) после напыления каждого слоя для различных алгоритмов.

Поведение алгоритмов для случая трехполосного фильтра аналогично уже рассмотренному случаю. Фиг. 4 иллюстрирует ошибки восстановления толщин слоев.

Фиг. 4.

Модельная задача для трехполосного фильтра. Ошибки толщин слоев, определенных различными алгоритмами.

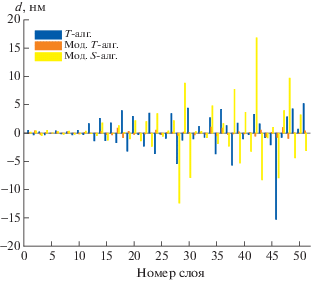
Заметим, что в обоих рассмотренных случаях наиболее затратный по времени (и, как правило, наиболее надежный) T-алгоритм приводит к заметным ошибкам в толщинах последних напыляемых слоев, в то время как его модифицированный аналог обеспечивает высокую точность восстановления. Это подтверждает предположение, лежащее в основе построения модифицированных алгоритмов – а именно то, что дополнительные данные, отягощенные ошибками, могут приводить к существенному (и неверному) переопределению толщин слоев, которые уже были более надежно определены по предыдущим наборам данных; по этой причине в модифицированных алгоритмах предлагается варьировать только те слои, для которых предполагается восстановление толщин с более высокой точностью.

Результаты моделирования 28-слойного поляризатора (фиг. 5) в целом воспроизводят характерные черты уже рассмотренных дизайнов. Отметим эффект накопления ошибок, присущий $S$-алгоритму, приводящий к тому, что ошибки в последующих слоях прогрессивно нарастают.

Фиг. 5.

Модельная задача для 28-слойного поляризатора. Ошибки толщин слоев, определенных различными алгоритмами.

4. ЗАКЛЮЧЕНИЕ

В статье рассмотрены разновидности алгоритмов определения толщин слоев напыляемых многослойных оптических покрытий, необходимые для организации оптического мониторинга процесса напыления. Дано описание модифицированных $S$- и T-алгоритмов, в которых уточнению подвергается некоторое специально определяемое подмножество толщин слоев. Сравнительная эффективность алгоритмов оценивается на примере модельных задач для различных типов многослойных оптических покрытий.

Показано, что модифицированный T-алгоритм, как правило, не уступает в точности восстановления полному T-алгоритму, а в ряде случаев и превосходит его, особенно при определении толщин последних слоев многослойного покрытия. Это подтверждает обоснованность подхода к оптимизации, в котором варьируются толщины только того подмножества слоев, для которых дополнительные данные обеспечивают их уточнение. Кроме того, модифицированный алгоритм обеспечивает более высокое быстродействие, что имеет большое практическое значение при их применении в процедурах “on-line” мониторинга.

Список литературы

  1. Vidal B., Fornier A., Pelletier E. Optical monitoring of nonquarterwave multilayer filters // Appl. Opt. 1978. V. 17. P. 1038–1047.

  2. Vidal B., Fornier A., Pelletier E. Wideband optical monitoring of nonquarterwave multilayer filters // Appl. Opt. 1979. V. 18. P. 3851–3856.

  3. Ristau D. Characterization and monitoring // In: Optical Interference Coatings, edited by N. Kaiser and H.K. Pulker, Berlin: Springer-Verlag, 2003. P. 181–205.

  4. Ristau D., Ehlers H., Gross T., Lappschies M. Optical broadband monitoring of conventional and ion processes // Appl. Opt. 2006. V. 45. P. 1495–1501.

  5. Wilbrandt S., Stenzel O., Kaiser N., Trubetskov M.K., Tikhonravov A.V. In situ optical characterization and reengineering of interference coatings // Appl. Optics. 2008. V. 47. P. 49–54.

  6. Macleod H. Monitoring of optical coatings // Appl. Optics. 1981. V. 20. P. 82–89.

  7. Tikhonravov A.V., Trubetskov M.K., Amotchkina T.V. Investigation of the error self-compensation effect associated with broadband optical monitoring // Appl. Optics. 2011. V. 50. № 9. P. 111–116.

  8. Macleod H. Thin film optical filters. McGraw-Hill, 1986.

  9. Tikhonravov A.V., Trubetskov M.K. Stabilization of computational algorithms for the characterization of thin film coatings // Numerical Meth. and Program. 2005. V. 6. P. 96–104.

  10. Tikhonravov A.V., Trubetskov M.K., Amotchkina T.V. Investigation of the effect of accumulation of thikhness errors in optical coating production using broadband optical monitoring // Appl. Optics. 2006. V. 45. P. 7026–7034.

  11. Tikhonravov A.V., Trubetskov M.K. On-line characterization and re-optimization of optical coatings // Proc. of SPIE. 2003. V. 5250. P. 406–413.

  12. Tikhonravov A.V., Trubetskov M.K. Computational manufacturing as a bridge between design and production // Appl. Optics. 2005. V. 44. P. 6877–6884.

  13. Tikhonravov A., Kochikov I., Yagola A. Error self-compensation mechanism in the optical coating production with direct broad band monitoring // Optics Express. 2017. V. 25. № 22. P. 27225–27233.

  14. Isaev T.F., Lukyanenko D.V., Tikhonravov A.V., Yagola A.G. Algorithms for solving inverse problems in the optics of layered media based on comparing the extrema of spectral characteristics // Comp. Math. and Math. Phys. 2017. V. 57. № 5. P. 867–875.

  15. Исаев Т.Ф., Кочиков И.В., Лукьяненко Д.В., Тихонравов А.В., Ягола А.Г. Повышение точности широкополосного контроля процесса напыления оптических покрытий // Вестн. МГУ. Серия 3: Физика, астрономия. 2018. Volume. № number. С. 1–15.

  16. Tikhonravov A.V., Gorokh A. Modified sequential algorithm for the on-line characterization of optical coatings // Optics Express. 2015. V. 23. № 18. P. 23561–23569.

  17. Furman Sh.A., Tikhonravov A.V. Basics of optics of multilayer systems // Edit. Frontieres, Gif-sur-Yvette, 1992.

  18. Tikhonravov A.V., Zhupanov V.G., Fedoseev V.N., Trubetskov M.K. Design and production of antireflection coating for the 8–10 $\mu $m spectral region // Optics Express. 2014. V. 22. № 26. P. 32174–32179.

  19. Tikhonravov A.V., Trubetskov M.K. Modern design tools and a new paradigm in optical coating design // Appl. Optics. 2012. V. 51. P. 7319–7332.

  20. Amotchkina T.V., Trubetskov M.K., Pervak V., Schlichting S., Ehlers H., Ristau D., Tikhonravov A.V. Comparison of algorithms used for optical characterization of multilayer optical coatings // Appl. Optics. 2011. V. 50. P. 3389–3395.

  21. Тихонравов А.В. О методе синтеза оптических покрытий, использующим необходимые условия оптимальности // Вестн. МГУ. Сер. физ.-астрономия. 1982. Т. 23. № 6. С. 91–93.

  22. Tikhonravov A.V., Trubetskov M.K., Kokarev M.A., Amotchkina T.V., Duparre A., Quesnel E., Ristau D., Gunster S. Effect of systematic errors in spectral photometric data on the accuracy of determination of optical parameters of dielectric thin films // Appl. Optics. 2002. V. 41. № 13. P. 2555–2560.

  23. Tikhonravov A., Trubetskov M., DeBell G. On the accuracy of optical thin film parameter determination based on spectrophotometric data // Proc. of SPIE. 2003. V. 5188. P. 190–199.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал