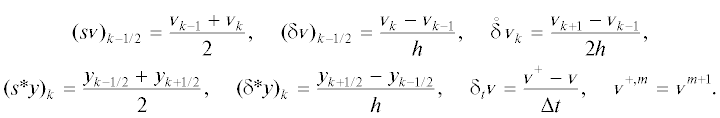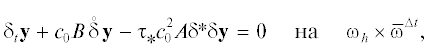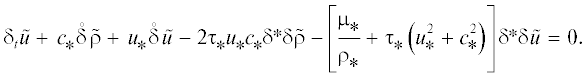Журнал вычислительной математики и математической физики, 2019, T. 59, № 3, стр. 481-493
Условия L2-диссипативности линеаризованных явных разностных схем с регуляризацией для уравнений 1D баротропной газовой динамики
А. А. Злотник 1, *, Т. А. Ломоносов 1, **
1 НИУ Высшая школа экономики
101000 Москва, ул. Мясницкая, 20, Россия
* E-mail: azlotnik@hse.ru
** E-mail: tlomonosov@hse.ru
Поступила в редакцию 12.06.2018
Аннотация
Изучаются явные двухслойные по времени и симметричные по пространству разностные схемы, построенные посредством аппроксимации 1D баротропных квазигазо/квазигидродинамических систем уравнений. Они линеаризуются на постоянном решении с ненулевой скоростью, и для них выводятся как необходимые, так и достаточные условияL2-диссипативности решений задачи Коши в зависимости от числа Маха. Эти условия различаются между собой не более чем в 2 раза. Результаты существенно развивают известные для линеаризованной схемы Лакса–Вендроффа. Выполняются также численные эксперименты по анализу применимости найденных условий в нелинейной постановке для нескольких схем при различных числах Маха. Библ. 18. Фиг. 6. Табл. 2.
ВВЕДЕНИЕ
Квазигазо/квазигидродинамические (КГД/КГДД) системы уравнений можно рассматривать как регуляризованные системы уравнений газовой динамики. С ними связан класс явных двухслойных по времени и симметричных по пространству разностных схем, достаточно активно используемых при численном решении многих задач [1]–[3]. Баротропные КГД/КГДД системы были введены и изучены в [4]–[7]. Соответствующие разностные схемы применялись при расчете задач мелкой воды, двухкомпонентных течений с поверхностными эффектами, астрофизических задач и др. [8]–[11].
Вопросы теории указанных разностных схем, включая практически важный анализ условий их устойчивости в зависимости от параметров схем, пока разработаны недостаточно. Для 1D разностных схем, линеаризованных на постоянном решении с нулевой скоростью ${{u}_{ * }} = 0$, достаточные условия ${{L}^{2}}$-диссипативности масштабированных решений были получены в [3], [12] энергетическим методом. Более точные критерии (необходимые и достаточные условия) в баротропном случае при ${{u}_{ * }} = 0$ выведены недавно в [13] спектральным методом.
В настоящей работе в баротропной постановке впервые анализируется случай ${{u}_{ * }} \ne 0$ и выводятся как необходимые, так и достаточные условия ${{L}^{2}}$-диссипативности решений задачи Коши в зависимости от числа Маха M. Эти условия различаются между собой не более чем в 2 раза и содержат существенную для практики информацию. В том числе выяснено, что при использовании КГД системы можно обеспечить независимость условия на число Куранта от ${\text{M}}$. Вывод условий базируется на новых результатах для абстрактных разностных схем с регуляризацией и спектральном подходе (см. [14]). Эти результаты существенно развивают известные для линеаризованной схемы Лакса–Вендроффа в [15]. Они применимы также для анализа схем изучаемого типа для полной 1D системы уравнений газовой динамики [16].
Приводятся также результаты численных экспериментов с использованием КГД системы в связи с анализом применимости найденных условий в нелинейной постановке при решении задачи Римана в изэнтропическом случае при ${\text{M}}$ = 2,4,6,8. Расчеты выполнены для трех схем – схемы стандартного типа и двух схем с энергетически диссипативными дискретизациями по пространству из [17]. Подчеркнем, что линеаризация всех трех схем на постоянном решении одинаковая. Однако в нелинейной постановке свойства устойчивости последних двух схем оказываются существенно лучше, чем у схемы стандартного типа, тем более с ростом ${\text{M}}$, и эти свойства в определенной степени соответствуют найденным условиям.
1. УСЛОВИЯ ${{L}^{2}}$-ДИССИПАТИВНОСТИ АБСТРАКТНОЙ ЯВНОЙ ДВУХСЛОЙНОЙ СХЕМЫ С РЕГУЛЯРИЗАЦИЕЙ
Пусть ${{\omega }_{h}}$ – равномерная сетка на $\mathbb{R}$ с узлами ${{x}_{k}} = kh$, $k \in \mathbb{Z}$ и шагом $h = X{\text{/}}N$, а $\omega _{h}^{ * }$ – вспомогательная сетка с узлами ${{x}_{{k - 1/2}}} = (k - 0.5)h$, $k \in \mathbb{Z}$. Пусть $\mathop {\bar {\omega }}\nolimits^{\Delta t} $ – равномерная сетка по $t$ на $[0,\infty )$ с узлами ${{t}_{m}} = m\Delta t$, $m \geqslant 0$, и шагом $\Delta t > 0$. Введем сеточные операторы
Пусть $H$ – гильбертово пространство вектор-функций со значениями из ${{\mathbb{C}}^{n}}$, заданных и суммируемых в квадрате на ${{\omega }_{h}}$, со скалярным произведением ${{({\mathbf{v}},{\mathbf{y}})}_{H}} = h\sum\nolimits_{k = - \infty }^{ + \infty } {{{{({{{\mathbf{v}}}_{k}},{{{\mathbf{y}}}_{k}})}}_{{{{\mathbb{C}}^{n}}}}}} $.
Рассмотрим сначала абстрактную явную двухслойную по времени и симметричную трехточечную по пространству линейную разностную схему
где ${{{\mathbf{y}}}^{m}} \in H$ при $m \geqslant 0$, $A = A{\text{*}}$ и $B = B{\text{*}}$ – матрицы (вязких и конвективных слагаемых) порядка $n$, ${{c}_{0}} > 0$ – характерная скорость, ${{\tau }_{ * }} > 0$ – параметр регуляризации. При $A = {{B}^{2}}$, ${{\tau }_{ * }} = \Delta t{\text{/}}2$ устойчивость подобной линеаризованной схемы Лакса–Вендроффа изучена в [15].Поставим вопрос об условиях справедливости оценки
(2)
$\mathop {sup}\limits_{m \geqslant 0} {{\left\| {{{{\mathbf{y}}}^{m}}} \right\|}_{H}} \leqslant {{\left\| {{{{\mathbf{y}}}^{0}}} \right\|}_{H}}\quad \forall {{{\mathbf{y}}}^{0}} \in H.$(4)
$\Delta t = \tilde {\beta }\frac{h}{{{{c}_{0}}}},\quad {{\tau }_{ * }} = \alpha \frac{h}{{{{c}_{0}}}}$Для этого в соответствии с [14] рассмотрим частные решения вида ${\mathbf{y}}_{k}^{m} = {{e}^{{{\mathbf{i}}k\xi }}}{{{\mathbf{v}}}^{m}}(\xi )$, $k \in \mathbb{Z}$, $m \geqslant 0$, где ${\mathbf{i}}$ – мнимая единица и $0 \leqslant \xi \leqslant 2\pi $ – параметр. Их подстановка в (3) с учетом (4) дает
(5)
${{{\mathbf{v}}}^{ + }} = G{\mathbf{v}}\quad {\text{н а }}\mathop {\quad \bar {\omega }}\nolimits^{\Delta t} ,\quad G = I - \tilde {\beta }F,\quad F = F(\sigma ) = 4\sigma \alpha A \pm {\mathbf{i}}2\sqrt {\sigma (1 - \sigma )} B.$Следующая теорема вытекает из [16]. Для полноты дадим ее с доказательством.
Теорема 1. 1. Выполнение матричного неравенства
(6)
$\tilde {\beta }\left( {2\sigma \alpha {{A}^{2}} + \frac{{1 - \sigma }}{{2\alpha }}{{B}^{2}} \pm {\mathbf{i}}\sqrt {\sigma (1 - \sigma )} [A,B]} \right) \leqslant A\quad \forall 0 < \sigma \leqslant 1,$2. Выполнение матричных неравенств
(7)
$2\alpha \tilde {\beta }A \leqslant I,\quad \frac{{\tilde {\beta }}}{{2\alpha }}{{B}^{2}} \leqslant A$Доказательство. 1. По аналогии с леммой 1 из [13] доказывается, что выполнение спектрального неравенства
необходимо и достаточно для справедливости оценки (2); здесь и ниже ${{\lambda }_{{max}}}(C)$ – максимальное из собственных значений матрицы $C$ (когда они вещественные).Это неравенство эквивалентно матричному неравенству $G{\text{*}}G \leqslant I$, т.е. неравенству
2. По непрерывности неравенство (6) выполняется и при $\sigma = 0$. При $\sigma = 1,0$ оно дает
Далее, для любого ${\mathbf{z}} \in H$ справедливы соотношения
Замечание 1. 1. Для $A \geqslant 0$ первое неравенство (7) эквивалентно неравенству $\tilde {\beta } \leqslant 1{\text{/}}[2\alpha {{\lambda }_{{max}}}(A)].$ Второе неравенство (7) влечет свойство $A \geqslant 0$.
2. Если $A = {{B}^{2}} + D$, где $D$ – диагональная матрица с элементами ${{d}_{{ii}}} \geqslant 0,\;1 \leqslant i \leqslant N$, причем ${{d}_{{{{i}_{0}}{{i}_{0}}}}} = 0$, а ${{a}_{{{{i}_{0}}{{i}_{0}}}}} \ne 0$ для некоторого ${{i}_{0}}$, то второе неравенство (7) сводится просто к числовому неравенству $\tilde {\beta } \leqslant 2\alpha $.
3. Если ${{B}^{2}} \leqslant A$, то неравенство (8) выполнено при $\tilde {\beta } \leqslant 1{\text{/}}\left[ {2\alpha {{\lambda }_{{max}}}(A) + {{{(2\alpha )}}^{{ - 1}}}} \right].$
Замечание 2. Неравенства (7) с удвоенными левыми частями
влекут неравенство (8) и поэтому служат более простым достаточным условием.2. РАЗНОСТНЫЕ СХЕМЫ С РЕГУЛЯРИЗАЦИЕЙ ДЛЯ 1D УРАВНЕНИЙ БАРОТРОПНОЙ ГАЗОВОЙ ДИНАМИКИ, ИХ ЛИНЕАРИЗАЦИЯ И L2–ДИССИПАТИВНОСТЬ
1D баротропная КГД система уравнений состоит из регуляризованных уравнений баланса массы и импульса
(11)
${{\partial }_{t}}\rho + {{\partial }_{x}}j = 0,\quad {{\partial }_{t}}(\rho u) + {{\partial }_{x}}[ju + p(\rho ) - \Pi ] = 0,$(12)
$j = \rho u - \rho w,\quad \rho w = \tau u{{\partial }_{x}}(\rho u) + \rho \hat {w},\quad \rho \hat {w} = \tau [\rho u{{\partial }_{x}}u + p{\kern 1pt} '(\rho )],$(13)
$\Pi = \mu {{\partial }_{x}}u + u\rho \hat {w} + \tau p{\kern 1pt} '(\rho ){{\partial }_{x}}(\rho u).$КГДД система проще и отличается тем, что в ней $\rho w = \rho \hat {w} = \tau [\rho u{{\partial }_{x}}u + p{\kern 1pt} '(\rho )]$, $\Pi = \mu {{\partial }_{x}}u + u\rho \hat {w}$.
Обе системы переходят в баротропные системы уравнений газовой динамики при $\tau = \mu = 0$ и Навье–Стокса вязкого сжимаемого газа при $\tau = 0$, $\mu > 0$.
Сначала рассмотрим явную двухслойную по времени и симметричную по пространству стандартного типа аппроксимацию КГД уравнений (11)–(13):
(14)
${{\delta }_{t}}\rho + \delta {\text{*}}j = 0,\quad {{\delta }_{t}}(\rho u) + \delta {\text{*}}(jsu + p(s\rho ) - \Pi ) = 0\quad {\text{н а }}\quad {{\omega }_{h}},$(15)
$j = (s\rho )su - (s\rho )w,\quad (s\rho )w = (s\tau )[\delta (\rho u)]su + (s\rho )\hat {w},\quad (s\rho )\hat {w} = (s\tau )[(s\rho )(su)\delta u + \delta p(\rho )],$В [17] были построены две нестандартные пространственные аппроксимации КГД уравнений (11)–(13), диссипативные по энергии (их обобщения на многомерный случай даны в [18]). В сочетании с явным методом Эйлера по времени первая из них (схема А) имеет вид
(17)
${{\delta }_{t}}\rho + \delta {\text{*}}j = 0,\quad {{\delta }_{t}}(\rho u) + \delta {\text{*}}(jsu - \Pi ) + s{\text{*}}[(s\rho )\delta {\text{h}}(\rho )] = 0,$(18)
$j = (s\rho )su - (s\rho )w,\quad (s\rho )w = [{{(\tau {{\partial }_{x}})}_{h}}(\rho u)]su + (s\rho )\hat {w},\quad \hat {w} = (s\tau )[(su)\delta u + \delta {\text{h}}(\rho )],$(19)
$\Pi = \mu \delta u + (su)(s\rho )\hat {w} + p{\kern 1pt} '(s\rho ){{(\tau {{\partial }_{x}})}_{h}}(\rho u),$(20)
${{(\tau {{\partial }_{x}})}_{h}}(\rho u) = \left( {s\frac{\tau }{{{\text{h'}}(\rho )}}} \right)\{ [\delta h(\rho )]su + p{\kern 1pt} '(s\rho )\delta u\} .$Обратим внимание на нестандартные зависящие от ${\text{h}}(\rho )$ дискретизации ${{\partial }_{x}}p(\rho )$ в (17), (19) и $\tau {{\partial }_{x}}(\rho u)$ в (18), (19) согласно (20).
Схема Б со второй из аппроксимаций имеет вид
В схеме Б наряду с обычными усреднениями $s\rho $, $su$ применяются нестандартные усреднения $\rho $ и $p{\kern 1pt} '(\rho )$, зависящие от ${\text{h}}$:
В изэнтропическом случае введенные усреднения принимают вид
(21)
${{s}_{p}}\rho = \frac{{\gamma - 1}}{\gamma }\frac{{\rho _{ + }^{\gamma } - \rho _{ - }^{\gamma }}}{{\rho _{ + }^{{\gamma - 1}} - \rho _{ - }^{{\gamma - 1}}}},\quad \widetilde {p{\kern 1pt} '(\rho )} = \frac{{\gamma {{p}_{1}}}}{{\gamma - 1}}\frac{{{{\rho }_{ - }} + {{\rho }_{ + }}}}{2}\frac{{\rho _{ + }^{{\gamma - 1}} - \rho _{ - }^{{\gamma - 1}}}}{{{{\rho }_{ + }} - {{\rho }_{ - }}}}\quad {\text{п р и }}\quad {{\rho }_{ - }} \ne {{\rho }_{ + }}.$Схему (14)–(16) линеаризуем на постоянном решении ${{\rho }_{ * }} \equiv {\text{const}} > 0$, ${{u}_{ * }} \equiv {\text{const}}$. Пусть ${{c}_{ * }} = \sqrt {p{\kern 1pt} '({{\rho }_{ * }})} $ – фоновая скорость звука, а ${{\tau }_{ * }} = \tau ({{\rho }_{ * }},{{u}_{ * }})$, ${{\mu }_{ * }} = \mu ({{\rho }_{ * }},{{u}_{ * }})$. Запишем решение схемы в виде $\rho = {{\rho }_{ * }}(1 + \tilde {\rho })$, $u = {{u}_{ * }} + {{c}_{ * }}\tilde {u}$, отбросим члены второго порядка малости по отношению к масштабированным (безразмерным) возмущениям $\tilde {\rho }$, $\tilde {u}$ и получим линеаризованную схему
Пусть коэффициент вязкости задается обычной КГД-формулой $\mu = {{\alpha }_{S}}\tau (\rho ,u)\rho p{\kern 1pt} '(\rho )$, где ${{\alpha }_{S}} \geqslant 0$ – параметр. Тогда ${{\mu }_{ * }} = {{\alpha }_{S}}{{\tau }_{ * }}{{\rho }_{ * }}c_{ * }^{2}$. Положив ${{c}_{0}} = {{c}_{ * }}$, можно схему (22), (23) переписать в векторном виде (1) с(24)
${\mathbf{y}} = \left( {\begin{array}{*{20}{c}} {\tilde {\rho }} \\ {\tilde {u}} \end{array}} \right),\quad B = \left( {\begin{array}{*{20}{c}} {\text{M}}&1 \\ 1&{\text{M}} \end{array}} \right),\quad A = \left( {\begin{array}{*{20}{c}} {{{{\text{M}}}^{2}} + 1}&{2{\text{M}}} \\ {2{\text{M}}}&{{{\alpha }_{S}} + {{{\text{M}}}^{2}} + 1} \end{array}} \right),$Линеаризации на постоянном решении схем А и Б имеют такой же вид.
Отметим, что первая формула (4) на практике обычно берется в виде
Теорема 2. Рассмотрим схему (22), (23) , т.е. (1), (4), (24).
1. Для нее необходимое условие ${{L}^{2}}$-диссипативности (7) принимает вид
(25)
$\beta \leqslant 2min\left\{ {\widehat \alpha ,\frac{{\mathop {\widehat \alpha }\nolimits_{{\text{opt}}}^2 }}{{\widehat \alpha }}} \right\},$В случае ${{\alpha }_{S}} = 0$ правая часть этого условия максимальна, а само условие становится не только необходимым, но и достаточным, и упрощается до
2. Достаточное условие ${{L}^{2}}$-диссипативности (8) выполнено при
(27)
$\beta \leqslant 2{{\left( {\frac{1}{{\widehat \alpha }} + \frac{{\widehat \alpha }}{{\widehat \alpha _{{{\text{opt}}}}^{2}}}} \right)}^{{ - 1}}}.$Доказательство. Матрицы $A$, $B$ в (24) вещественны и симметричны. При этом
Кроме того, при ${{\alpha }_{S}} = 0$ имеем ${{B}^{2}} = A$, $[A,B] = 0$ и, значит, неравенство (6) сводится к
Обратим внимание на то, что при ${{\alpha }_{S}} > 0$ величина ${{\widehat \alpha }_{{{\text{opt}}}}}$ возрастает по ${\text{|M|}}$ (как нетрудно проверить) и стремится к $1{\text{/}}2$ при $\left| {\text{M}} \right| \to \infty $. Поэтому член $\widehat \alpha _{{{\text{opt}}}}^{2}{\text{/}}\widehat \alpha $ в условии (25) и правая часть условия (27) возрастают по $\left| {\text{M}} \right|$ и стремятся к $1{\text{/}}(4\widehat \alpha )$ и $1{\text{/}}[2\widehat \alpha + {{(2\widehat \alpha )}^{{ - 1}}}]$ соответственно при $\left| {\text{M}} \right| \to \infty $, и в пределе при $\left| {\text{M}} \right| \to \infty $ условие (25) снова переходит в (26).
Очевидно, что правые части условий (25) и (27) максимальны при $\widehat \alpha = {{\widehat \alpha }_{{{\text{opt}}}}}$ и равны соответственно $2{{\widehat \alpha }_{{{\text{opt}}}}}$ и ${{\widehat \alpha }_{{{\text{opt}}}}}$; при этом
Если вместо указанной выше формулы ${{\tau }_{ * }} = \widehat \alpha h{\text{/}}({{c}_{ * }} + \left| {{{u}_{ * }}} \right|)$ использовать стандартную ${{\tau }_{ * }} = \alpha h{\text{/}}{{c}_{ * }}$, то в условиях (25) и (27) следует заменить $\widehat \alpha $ на $\alpha ({\text{|M|}} + 1)$. При этом при ${{\alpha }_{S}} > 0$ значение ${{\alpha }_{{{\text{opt}}}}} = {{\widehat \alpha }_{{{\text{opt}}}}}{\text{/}}(\left| {\text{M}} \right| + 1)$ станет убывать по ${\text{|M|}}$ и стремиться к $0$ при $\left| {\text{M}} \right| \to \infty $, что неудобно на практике.
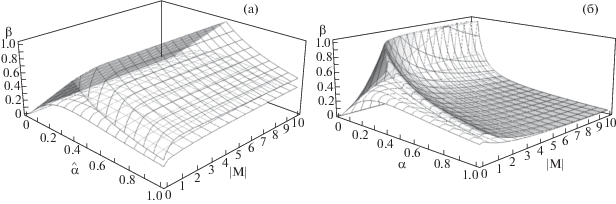
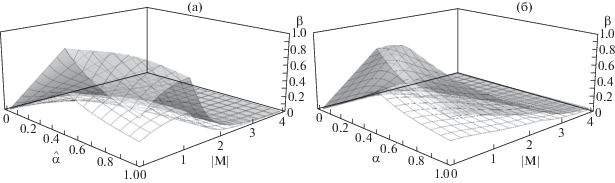
В типичном случае ${{\alpha }_{S}} = 1$ правые части условий (25) и (27) (верхняя и нижняя поверхности) представлены на фиг. 1а. Результаты замены в них $\widehat \alpha $ на $\alpha (\left| {\text{M}} \right| + 1)$ представлены на фиг. 1б; наблюдаются негативные изменения в графиках.
Фиг. 1.
Правые части условий (25) и (27) (верхняя и нижняя поверхности) при ${{\alpha }_{S}} = 1$ (а). Они же после замены $\widehat \alpha $ на $\alpha (\left| {\text{M}} \right| + 1)$ (б).
При ${\text{M}} = 0$, т.е. ${{u}_{ * }} = 0$, условие (25) переходит в
полученное в [13] с помощью прямого анализа условия (9) и являющееся критерием (и необходимым, и достаточным условием).Обратимся к КГДД системе. С учетом указанных выше упрощений ей отвечает упрощенная линеаризованная схема (22), (23) , а именно, схема (1) с теми же ${\mathbf{y}}$, $B$ и иной $A$:
(28)
${\mathbf{y}} = \left( {\begin{array}{*{20}{c}} {\tilde {\rho }} \\ {\tilde {u}} \end{array}} \right),\quad B = \left( {\begin{array}{*{20}{c}} {\text{M}}&1 \\ 1&{\text{M}} \end{array}} \right),\quad A = \left( {\begin{array}{*{20}{c}} 1&{\text{M}} \\ {\text{M}}&{{{\alpha }_{S}} + {{{\text{M}}}^{2}}} \end{array}} \right).$Теорема 3. Рассмотрим схему (1), (4), (28) .
1. Для нее необходимое условие ${{L}^{2}}$-диссипативности (7) принимает вид
(29)
$\beta \leqslant min\left\{ {\frac{{2\widehat \alpha {{\alpha }_{S}}}}{{q({{\alpha }_{S}},{\text{M}}) + \sqrt {{{q}^{2}}({{\alpha }_{S}},{\text{M}}) - {{\alpha }_{S}}{{{({{{\text{M}}}^{2}} - 1)}}^{2}}} }},\frac{{{{{(\left| {\text{M}} \right| + 1)}}^{2}}}}{{2\widehat \alpha {{\lambda }_{{\max }}}(A)}}} \right\},$(30)
${{\lambda }_{{{\text{max}}}}}(A) = \frac{{{{\alpha }_{S}} + {{{\text{M}}}^{2}} + 1}}{2} + \sqrt {{{{\left( {\frac{{{{\alpha }_{S}} + {{{\text{M}}}^{2}} + 1}}{2}} \right)}}^{2}} - {{\alpha }_{S}}} .$2. Достаточное условие ${{L}^{2}}$-диссипативности (10) получается из (29) в результате замены $\beta $ на $2\beta $.
Доказательство. Матрицы $A$, $B$ в (28) вещественны и симметричны. Легко проверяются свойство $A \geqslant 0$ и формула (30). С помощью замечания 1.1 первое неравенство (7) принимает вид $\tilde {\beta } \leqslant 1{\text{/}}[2\alpha {{\lambda }_{{{\text{max}}}}}(A)]$.
Анализ второго неравенства (7) сложнее. Положив $\zeta = \tilde {\beta }{\text{/}}(2\alpha )$, перепишем его в виде
(31)
$\zeta \leqslant \frac{1}{{{{{\text{M}}}^{2}} + 1}},\quad \zeta \leqslant \frac{{{{\alpha }_{S}} + {{{\text{M}}}^{2}}}}{{{{{\text{M}}}^{2}} + 1}},$(32)
$det(A - \zeta {{B}^{2}}) = {{p}_{2}}(\zeta ) \equiv {{({{{\text{M}}}^{2}} - 1)}^{2}}{{\zeta }^{2}} - [{{({{{\text{M}}}^{2}} - 1)}^{2}} + {{\alpha }_{S}}({{{\text{M}}}^{2}} + 1)]\zeta + {{\alpha }_{S}} \geqslant 0.$Пусть ${\text{|M|}} \ne 1$. Заметим, что
Если вместо указанной выше формулы ${{\tau }_{ * }} = \widehat \alpha h{\text{/}}({{c}_{ * }} + {\text{|}}{{u}_{ * }}{\text{|}})$ использовать стандартную ${{\tau }_{ * }} = \alpha h{\text{/}}{{c}_{ * }}$, то опять в условии (29) следует заменить $\widehat \alpha $ на $\alpha ({\text{|M|}} + 1)$.
В типичном случае ${{\alpha }_{S}} = 1$ правая часть условия (29) (верхняя поверхность) и его половина – в соответствии с теоремой 3, п. 2 (нижняя поверхность) представлены на фиг. 2а. Результаты замены в них $\widehat \alpha $ на $\alpha (\left| {\text{M}} \right| + 1)$ представлены на фиг. 2б; возникающие различия опять существенны. Графики достаточно быстро стремятся к 0 с ростом ${\text{|M|}}$; это вполне соответствует тому, что КГДД система изначально не предназначена для расчета течений с большими числами Маха. Сами же полученные выше результаты представляют интерес и при умеренных числах Маха.
Фиг. 2.
Правая часть условия (29) и его половина (верхняя и нижняя поверхности) при ${{\alpha }_{S}} = 1$ (а). Они же после замены $\widehat \alpha $ на $\alpha ({\text{|M|}} + 1)$ (б).
При ${\text{M}} = 0$, т.е. ${{u}_{ * }} = 0$, условие (29) переходит в условие
Отметим, что при ${{\alpha }_{S}} = 0$ схема (1), (4), (28) неустойчива (правая часть (29) равна 0) в отличие от схемы (1), (24) .
3. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ И АНАЛИЗ УСТОЙЧИВОСТИ В НЕЛИНЕЙНОЙ ПОСТАНОВКЕ
Численные эксперименты выполнены для модельных уравнения состояния $p(\rho ) = {{\rho }^{\gamma }}$ с $\gamma = 5{\text{/}}3$ и задачи Римана с начальными данными
(33)
${{\rho }_{0}}(x) = \left\{ \begin{gathered} 1,\quad x < 0, \hfill \\ 0.5,\quad x > 0, \hfill \\ \end{gathered} \right.\quad {{u}_{0}}(x) = \left\{ \begin{gathered} U,\quad x < 0, \hfill \\ 0,\quad x > 0, \hfill \\ \end{gathered} \right.$Задача решалась с применением КГД-системы для ${{M}_{0}} = 2,4,6,8$ на отрезке $[ - X{\text{/}}2,X{\text{/}}2]$ с $X = 0.6$ и шагом $h = 0.002$ при $0 \leqslant t \leqslant {{t}_{{{\text{ф и н }}}}}$ с ${{t}_{{{\text{ф и н }}}}} = 0.05$. Брались модифицированная формула $\tau = \widehat \alpha h{\text{/}}({\text{|}}u{\text{|}} + {{c}_{s}}(\rho ))$, где ${{c}_{s}}(\rho ) = \sqrt {p{\kern 1pt} '(\rho )} $ – скорость звука, и ${{\alpha }_{S}} = 1$.
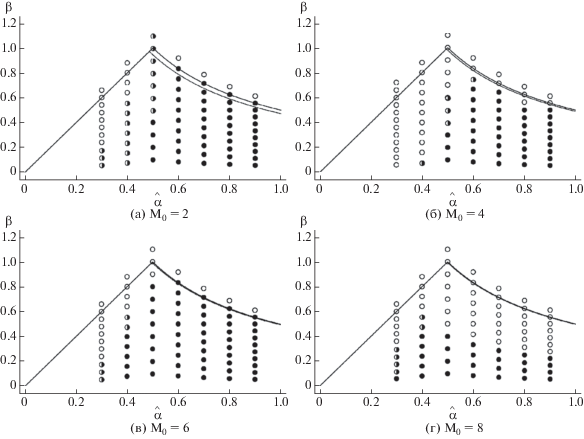
Результаты расчетов отражены на фиг. 3–5 для схемы стандартного типа и схем А и Б соответственно. На них пунктирной и сплошной линией изображены графики правых частей необходимых условий (25) при ${\text{M}} = {{{\text{M}}}_{0}}$ и (26) соответственно. Различие между ними невелико, уменьшается с ростом ${{{\text{M}}}_{0}}$ и визуально исчезает при ${{{\text{M}}}_{0}} = 8$.
Фиг. 3.
Практический анализ устойчивости для разных ${{{\text{M}}}_{0}}$ в зависимости от $\widehat \alpha $ при $\tau = \widehat \alpha h{\text{/}}({\text{|}}u{\text{|}} + {{c}_{s}})$ для схемы стандартного типа.

Фиг. 4.
Практический анализ устойчивости для разных ${{{\text{M}}}_{0}}$ в зависимости от $\widehat \alpha $ при $\tau = \widehat \alpha h{\text{/}}({\text{|}}u{\text{|}} + {{c}_{s}})$ для схемы А.
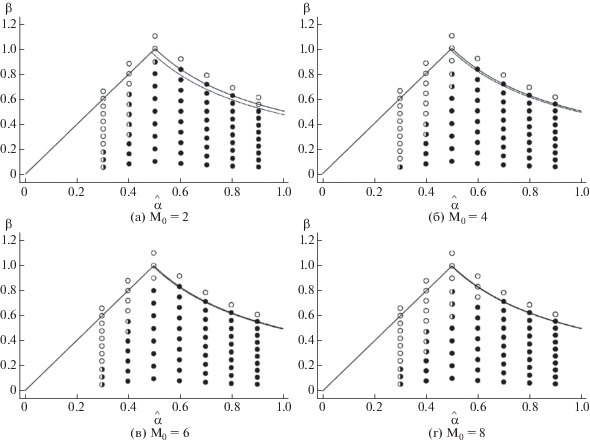
Фиг. 5.
Практический анализ устойчивости для разных ${{{\text{M}}}_{0}}$ в зависимости от $\widehat \alpha $ при $\tau = \widehat \alpha h{\text{/}}({\text{|}}u{\text{|}} + {{c}_{s}})$ для схемы Б.
Тестировались значения $\widehat \alpha = 0.3,0.4,\; \ldots ,0.9$ и $\beta = 0.1kmin\{ 2\widehat \alpha ,1{\text{/}}(2\widehat \alpha )\} $, $k = 1,2,\; \ldots ,\;10$ (и $k = 11$ для схем А и Б) в долях от его максимального значения в условии (26).
Для анализа качества численных решений было решено использовать величину ${{\varepsilon }_{V}}$ – отклонение их относительной вариации от 1 (на момент времени $t = {{t}_{{{\text{ф и н }}}}}$):
 вариации $\rho $ и $u$.
вариации $\rho $ и $u$.
На фигурах точки с ${{\varepsilon }_{V}} \in [0,0.1]$, $(0.1,0.2],(0.2,\infty ]$ помечены закрашенными, полузакрашенными, незакрашенными кружками (окружностями) соответственно; здесь ${{\varepsilon }_{V}} = \infty $ означает, что расчет не был завершен из-за переполнения или появления отрицательных значений $\rho $. Условно можно считать, что они отвечают устойчивым, промежуточным, неустойчивым решениям соответственно, поскольку графики первых содержат только незначительные одиночные впадинки/пички, к тому же (как было проверено) не растущие во времени и тем самым вполне приемлемые на практике (в сложных расчетах), а графики последних – наоборот, уже заметные осцилляции. Забегая вперед, отметим, что довольно типичная ситуация отражена на фиг. 6. Подчеркнем, что при подсчете вариации учитывается амплитуда каждой впадинки/пичка, причем дважды, так что значение ${{\varepsilon }_{V}} = 0.1$ не так уж велико.
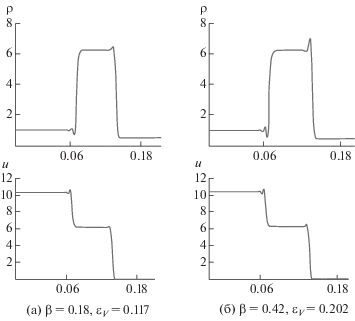
Фиг. 6.
Численные решения для ${{{\text{M}}}_{0}} = 8$, $\widehat \alpha = 0.3$, $\beta = 0.18$ и $0.42$ для $t = {{t}_{{{\text{ф и н }}}}}$ по схеме Б.
Для схемы стандартного типа (фиг. 3) устойчивые результаты намного (кратно) хуже отвечающих необходимому условию (26), причем соответствие ухудшается с ростом ${{{\text{M}}}_{0}}$ и для ${{{\text{M}}}_{0}} = 8$ становится минимальным (или вовсе исчезает) в зависимости от $\widehat \alpha $. При этом при $\widehat \alpha \geqslant 0.5$ соответствие лучше, чем при $\widehat \alpha = 0.4,0.3$.
Для схем А и особенно Б результаты существенно лучше. Для схемы А (фиг. 4) устойчивые результаты хорошо соответствуют необходимому условию (26) при $\widehat \alpha \geqslant 0.6$ для ${{{\text{M}}}_{0}} = 2,4,6$ (также при $\widehat \alpha = 0.5$ для ${{{\text{M}}}_{0}} = 6$). Для ${{{\text{M}}}_{0}} = 8$ соответствие хуже. Соответствие также намного хуже при $\widehat \alpha = 0.5,0.4$ и особенно 0.3.
Для схемы Б (фиг. 5) устойчивые результаты очень хорошо соответствуют необходимому условию (26) при $\widehat \alpha \geqslant 0.6$ для всех ${{{\text{M}}}_{0}} = 2,4,6,8$ (также при $\widehat \alpha = 0.5$ для ${{{\text{M}}}_{0}} = 2,6$). Но это соответствие резко падает с уменьшением $\widehat \alpha $ от 0.5 и становится плохим при $\widehat \alpha = 0.3$.
Довольно типичные численные решения с ${{\varepsilon }_{V}} \approx 0.1$ и ${{\varepsilon }_{V}} \approx 0.2$ для ${{{\text{M}}}_{0}} = 4$ при $\widehat \alpha = 0.4$ для $t = {{t}_{{{\text{ф и н }}}}}$ по схеме Б показаны на фиг. 6. В случае ${{\varepsilon }_{V}} \approx 0.1$ заметны незначительные одиночные впадинки/пички, а в случае ${{\varepsilon }_{V}} \approx 0.2$ наблюдаются уже заметные осцилляции.
Дополнительно для примера в табл. 1 и 2 приведены значения ${{\varepsilon }_{V}}$ для ${{{\text{M}}}_{0}} = 8$ при различных $\widehat \alpha $ и $\beta = 0.1kmin\{ 2\widehat \alpha ,1{\text{/}}(2\widehat \alpha )\} $ для схем А и Б соответственно. Прочеркам соответствует разрушение численных решений к моменту $t = {{t}_{{{\text{ф и н }}}}}$. Это более детальная информация, чем на фиг. 4г и 5г соответственно. Обратим внимание на то, что ${{\varepsilon }_{V}}$ не убывает по $\beta $ при каждом $\widehat \alpha $ – это естественно. При этом при $\widehat \alpha = 0.6,0.7,0.8,0.9$ происходит резкий финальный скачок от малых значений ${{\varepsilon }_{V}}$ к большим (для схемы Б) или к ситуации с разрушением решения (для схемы А и частично Б). Кроме того, ${{\varepsilon }_{V}}$ быстро убывает по $\widehat \alpha $ при каждом $k$ (с частичным исключением $k = 0.9$ в табл. 2), что довольно неожиданно. В том числе при каждом $k$ значения ${{\varepsilon }_{V}}$ при $\widehat \alpha = 0.7,0.8,0.9$ на несколько порядков меньше, чем при меньших $\widehat \alpha $. Поэтому такие значения $\widehat \alpha $ с успехом могут использоваться на практике.
Таблица 1.
Значения ${{\varepsilon }_{V}}$ для ${{{\text{M}}}_{0}} = 8$ при различных $\widehat \alpha $ и $\beta = 0.1kmin\{ 2\widehat \alpha ,1{\text{/}}(2\widehat \alpha )\} $ для схемы А
| $\widehat \alpha $ | $k = 1$ | $k = 2$ | $k = 3$ | $k = 4$ | $k = 5$ | $k = 6$ | $k = 7$ | $k = 8$ | $k = 9$ | $k = 10$ | $k = 11$ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | – | – | – | – | – | – | – | – | – | – | – |
| 0.3 | 9.6E–02 | 1.0E–01 | 1.1E–01 | 1.3E–01 | 1.4E–01 | 1.5E–01 | – | – | – | – | – |
| 0.4 | 2.7E–02 | 3.3E–02 | 4.9E–02 | 6.4E–02 | 8.5E–02 | 1.0E–01 | 1.2E–01 | – | – | – | – |
| 0.5 | 5.0E–03 | 7.6E–03 | 1.1E–02 | 2.1E–02 | – | – | – | – | – | – | – |
| 0.6 | 2.3E–05 | 1.1E–04 | 2.7E–04 | 7.8E–04 | – | – | – | – | – | – | – |
| 0.7 | 1.7E–10 | 7.7E–09 | 1.1E–07 | 7.4E–07 | – | – | – | – | – | – | – |
| 0.8 | 4.3E–15 | 4.1E–15 | 3.1E–14 | 5.7E–12 | – | – | – | – | – | – | – |
| 0.9 | 5.6E–15 | 4.1E–15 | 4.1E–15 | 4.7E–15 | – | – | – | – | – | – | – |
Таблица 2.
Значения ${{\varepsilon }_{V}}$ для ${{{\text{M}}}_{0}} = 8$ при различных $\widehat \alpha $ и $\beta = 0.1kmin\{ 2\widehat \alpha ,1{\text{/}}(2\widehat \alpha )\} $ для схемы Б
| $\widehat \alpha $ | $k = 1$ | $k = 2$ | $k = 3$ | $k = 4$ | $k = 5$ | $k = 6$ | $k = 7$ | $k = 8$ | $k = 9$ | $k = 10$ | $k = 11$ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 3.2E–01 | 3.4E–01 | 3.7E–01 | – | – | – | – | – | – | – | – |
| 0.3 | 9.7E–02 | 1.1E–01 | 1.2E–01 | 1.3E–01 | 1.6E–01 | 1.6E–01 | 2.0E–01 | 2.2E–01 | – | – | – |
| 0.4 | 2.3E–02 | 3.0E–02 | 3.5E–02 | 4.1E–02 | 6.2E–02 | 6.8E–02 | 9.6E–02 | 9.9E–02 | 1.0E–01 | – | – |
| 0.5 | 2.8E–03 | 6.1E–03 | 8.8E–03 | 1.1E–02 | 2.0E–02 | 3.0E–02 | 4.2E–02 | 5.5E–02 | – | – | – |
| 0.6 | 1.4E–05 | 6.4E–05 | 2.0E–04 | 4.4E–04 | 9.5E–04 | 1.4E–03 | 2.9E–03 | 3.9E–03 | – | – | – |
| 0.7 | 4.5E–11 | 3.1E–09 | 5.0E–08 | 3.6E–07 | 1.9E–06 | 5.9E–06 | 1.6E–05 | 4.1E–05 | 8.9E–05 | 1.7E–04 | 4.7E–01 |
| 0.8 | 4.4E–15 | 4.4E–15 | 1.1E–14 | 1.6E–12 | 7.8E–11 | 1.2E–09 | 9.7E–09 | 5.4E–08 | 2.1E–07 | 6.9E–07 | 7.9E–01 |
| 0.9 | 5.1E–15 | 4.4E–15 | 4.4E–15 | 4.4E–15 | 1.5E–14 | 7.3E–14 | 2.5E–14 | 1.2E–12 | 2.2E–11 | 2.3E–10 | 1.1 |
Полученные результаты служат в пользу применения схем А и особенно Б с энергетически диссипативными дискретизациями по пространству.
Список литературы
Четверушкин Б.Н. Кинетические схемы и квазигазодинамическая система уравнений. М.: МАКС Пресс, 2004.
Елизарова Т.Г. Квазигазодинамические уравнения и методы расчета вязких течений. М.: Научный мир, 2007.
Шеретов Ю.В. Динамика сплошных сред при пространственно-временном осреднении. Москва–Ижевск: Регулярная и хаотическая динамика, 2009.
Злотник А.А., Четверушкин Б.Н. О параболичности квазигазодинамической системы уравнений, ее гиперболической 2-го порядка модификации и устойчивости малых возмущений для них // Ж. вычисл. матем. и матем. физ. 2008. Т. 48. № 3. С. 445–472.
Злотник А.А. О параболичности квазигидродинамической системы уравнений и устойчивости малых возмущений для нее // Матем. заметки. 2008. Т. 83. № 5. С. 667–682.
Злотник А.А. Энергетические равенства и оценки для баротропных квазигазо- и квазигидродинамических систем уравнений // Ж. вычисл. матем. и матем. физ. 2010. Т. 50. № 2. С. 325–337.
Злотник А.А. О построении квазигазодинамических систем уравнений и баротропной системе с потенциальной массовой силой // Матем. моделирование. 2012. Т. 24. № 4. С. 65–79.
Булатов О.В., Елизарова Т.Г. Регуляризованные уравнения мелкой воды и эффективный метод численного моделирования течений в неглубоких водоемах // Ж. вычисл. матем. и матем. физ. 2011. Т. 51. № 1. С. 170–184.
Zlotnik A., Gavrilin V. On a conservative finite-difference method for 1D shallow water flows based on regularized equations // In: Math. problems in meteorological modeling. Math. in Industry. V. 24. A. Bátkai, P. Csomós, A. Horányi, etc., eds. Cham: Springer, 2016. P. 16–31.
Balashov V., Zlotnik A., Savenkov E. Analysis of a regularized model for the isothermal two-component mixture with the diffuse interfac // Russ. J. Numer. Anal. Math. Model. 2017. V. 32. № 6. P. 347–358.
Елизарова Т.Г., Злотник А.А., Истомина М.А. Гидродинамические аспекты формирования спирально-вихревых структур во вращающихся газовых дисках // Астрономический ж. 2018. Т. 95. № 1. С. 11–21.
Сухомозгий А.А., Шеретов Ю.В. Анализ устойчивости одной разностной схемы решения уравнений Сен–Венана в теории мелкой воды. В сб.: Примен. функц. анализа в теории приближений. Тверь: ТвГУ. 2013. С. 48–60.
Zlotnik A., Lomonosov T. On conditions for weak conservativeness of regularized explicit finite-difference schemes for 1D barotropic gas dynamics equations. In: Differential and difference equations with applications. Springer Proc. Math. & Statist. V. 230 Cham.: Springer, 2018. P. 635–647. Cм. тaкжe: https://arxiv.org/abs/1803.09899
Годунов С.К., Рябенький В.С. Разностные схемы. М.: Наука, 1977.
Рихтмайер Р., Мортон К. Разностные методы решения краевых задач. М.: Мир, 1972.
Злотник А.А., Ломоносов Т.А. Об условиях ${{L}^{2}}$-диссипативности линеаризованных явных КГД-разностных схем для уравнений одномерной газовой динамики // Докл. АН. 2018. Т. 482. № 4. С. 375–380.
Злотник А.А. Пространственная дискретизация одномерной баротропной квазигазодинамической системы уравнений и уравнение энергетического баланса // Матем. моделирование. 2012. Т. 24. № 10. С. 51–64.
Злотник А.А. О консервативных пространственных дискретизациях баротропной квазигазодинамической системы уравнений с потенциальной массовой силой // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 2. С. 301–317.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики