1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 59, № 3, 2019

Журнал вычислительной математики и математической физики, 2019, T. 59, № 3, стр. 505-515

О механизме перемещения агрегатов частиц в вязкой жидкости в переменном однородном внешнем поле

С. И. Мартынов 1, *, Л. Ю. Ткач 1, **

1 Югорский гос. ун-т
628012 Ханты-Мансийск, ул. Чехова, 16, Россия

* E-mail: martynvsi@mail.ru
** E-mail: leonilla7777@mail.ru

Поступила в редакцию 18.07.2018

Полный текст (PDF)

Аннотация

Предложен механизм перемещения агрегатов сферических частиц в вязкой жидкости и приведены результаты численного моделирования их динамики при воздействии внешнего однородного поля. Агрегаты рассматриваются как система частиц, имеющих заряд или дипольный момент, на которые действуют как силы гидродинамического взаимодействия, так и внутренние силы, удерживающие их в агрегате. При этом частицы в отсутствие внешнего воздействия находятся в положении минимума энергии взаимодействия, а суммарный заряд или дипольный момент системы равны нулю. В результате воздействия внешнего поля происходит деформация агрегата, а затем, после выключения поля, процесс восстановления агрегата из-за действия внутренних сил, стремящихся вернуть систему частиц в положение равновесия. Течение в окружающей агрегат вязкой жидкости, возникающее в результате относительного перемещения частиц, создает гидродинамическую силу, перемещающую центр тяжести агрегата в определенном направлении относительно приложенного поля. Проведены численные расчеты перемещения 6 модельных агрегатов, состоящих из заряженных или дипольных частиц. Предложенный механизм перемещения агрегатов может быть использован для управления массопереносом в системе жидкость–частицы. Библ. 15. Фиг. 4. Табл. 2.

Ключевые слова: численное моделирование, вязкая жидкость, частицы, гидродинамическое взаимодействие, энергия взаимодействия, внешнее однородное поле, самодвижущиеся агрегаты частиц.

Моделирование динамики большого числа частиц в вязкой жидкости приобретает в последние годы все больший интерес, что обусловлено практикой создания новых материалов на основе вязкой жидкости с определенной микроструктурой частиц в ней, а также с потребностью разработки новых подходов к моделированию поведения таких сред при воздействии на них различных внешних полей. С этой проблемой связано еще одно современное направление исследований жидких систем, которые получили название активные коллоиды (синтетические или живые), в которых можно управлять движением агрегатов частиц в заданном направлении воздействием различных внешних полей (см. [1]–[4]). Интерес к таким системам связан с растущим запросом на нанотехнологические приложения по разработке автономно двигающихся устройств с целью доставки с их помощью, например, лекарств к пораженной клетке или элементов микроскопических аппаратов с их последующей сборкой. В то же время имеются известные проблемы с моделированием динамики таких систем. Поскольку они находятся в неравновесном состоянии, то методы термодинамики или статистической физики в большинстве случаев к ним не применимы. Наиболее активно используются такие подходы, как метод прямого численного моделирования и феноменологический метод построения моделей. Однако во всех этих подходах гидродинамическое взаимодействие частиц учитывается в сильно упрощенном виде: в виде вязкого трения, действующего на частицу, или в приближении среднего поля (эффективная вязкость суспензий).

Между тем в системах жидкость–частицы имеется два механизма взаимодействия частиц, принципиально различающихся между собой по своей природе. Первый механизм обусловлен силами, действующими непосредственно между частицами, и связан с физическими свойствами вещества, из которого созданы частицы, а второй – гидродинамическими силами взаимодействия частиц в жидкости. Оба механизма всегда присутствуют в системе жидкость–частицы и в результате таких взаимодействий частицы в жидкости могут образовывать устойчивые структуры или агрегаты, в которых частицы удерживаются силами, действующими непосредственно между ними (см. [5]–[7]). Наиболее характерным примером сил, относящихся к первому механизму взаимодействия, являются силы кулоновского взаимодействия, если частицы заряжены, или силы диполь-дипольного взаимодействия, если частицы имеют дипольный момент. Классическая теория устойчивости коллоидов [8] исходит из наличия потенциального барьера вокруг частиц, который определяет их возможность сближаться на минимальное расстояние между собой. Этот барьер определяется суммарной энергией взаимодействия частиц, в которой учитывается как энергия отталкивания, так и энергия притяжения частиц. Поэтому положение и количество частиц в агрегате определяются условием минимума энергии взаимодействия всех частиц, формирующих агрегат. Соответственно этим же условием определяются размеры и форма агрегата. Наличие потенциальной энергии взаимодействия и условия минимума ее в точках, занимаемых частицами, приводят к тому, что при отклонении частицы из этого положения возникает сила, стремящаяся вернуть частицу в исходное состояние.

Сила гидродинамического взаимодействия определяет динамику агрегата в вязкой жидкости. Как известно из классической механики, действие внутренних сил не меняет положение центра тяжести системы. Между тем в природе существует множество живых организмов, перемещающихся в окружающей их жидкой или газообразной среде за счет действия внутренних сил. Это происходит благодаря наличию у таких организмов специального двигательного аппарата, периодические движения которого формирует в окружающей среде течение, создающее движущую силу со стороны этой среды на организм и перемещающую его. Причем движение двигательного аппарата в одну сторону создает течение, действующее на организм с большей силой, чем при движении того же двигательного аппарата в противоположную сторону. Это достигается за счет формы плавников у рыб и ластообразных, ориентация которых относительно тела организма при отталкивании создает большую гидродинамическую силу, чем при возвращении в исходное положение. Изменение формы поперечного сечения при отталкивании и возвращении в исходное положение используют водоплавающие птицы (перепончатое строение лапок), медузы, осьминоги и многие другие живые организмы. Этот же прием используют спортсмены-гребцы: ориентации лопасти весла в воде и при возвращении по воздуху в исходное состояние такие, чтобы создавать максимальную и минимальную силу сопротивления. Конечно же, для организмов большой массы существенное значение имеет возникающая инерция движения. Имеются и другие примеры из окружающей нас природы, демонстрирующие возможности живых организмов управлять своим движением за счет внутренних сил. Так кошки переворачиваются в воздухе за счет поочередного выбрасывания и поджимания передних и задних лап, тем самым меняя момент инерции вращения передней и задней части туловища. За счет этого скорость вращения и соответственно угол поворота части тела в одном направлении больше, чем при возвратном движении, что и позволяет этим животным совершить переворот. Все это происходит в соответствии с законом классической механики о моменте количества движения системы, который не меняется при действии внутренних сил.

Управление движением агрегатов частиц в вязкой жидкости должно основываться на использовании указанных выше двух механизмов взаимодействия. В сочетании с анализом движения живых организмов это позволяет проектировать микроаппараты для перемещения в вязкой жидкости и способы воздействия на их части, имитирующие двигательный аппарат, внешними полями или другими источниками энергии. В работах [9], [10] на основе анализа движения плавающих организмов в природе предложен способ перемещения агрегатов за счет моментов внутренних сил, действующих на пары частиц, которые своим вращением имитируют двигательный аппарат организма и формируют характерное вихревое течение в окружающей вязкой жидкости, создающее перемещающую агрегат гидродинамическую силу. В качестве источника энергии, приводящего в движение частицы, обладающие магнитным дипольным моментом, было предложено использование переменного внешнего магнитного поля. Как было показано, при этом вращение частиц не меняет своего направления. Ниже предлагаются модели агрегатов частиц, в которых под действием внешнего поля происходит относительное перемещение частиц, а после его выключения частицы меняют направления своего движения и стремятся вернуться в исходное состояние минимума энергии потенциального взаимодействия частиц в агрегате. При этом из-за изменения формы агрегата гидродинамическая сила от возникающего течения в окружающей вязкой жидкости перемещает центр тяжести системы частиц в определенном направлении относительно приложенного поля.

В настоящей работе на основе результатов, полученных в работах [11]–[13], предлагается механизм перемещения агрегатов частиц при учете как внутренних сил, удерживающих частицы в агрегате, так и сил гидродинамического взаимодействия между ними. Ниже представлены результаты динамики агрегатов частиц при воздействии внешнего поля. Рассмотрены случаи перемещения различных модельных агрегатов, в которых частицы обладают электрическим зарядом или дипольным моментом. При этом суммарный электрический заряд или дипольный момент агрегата равны нулю.

1. ПОСТАНОВКА ЗАДАЧИ И МЕТОД РЕШЕНИЯ

Рассматривается $N$ твердых сферических частиц, помещенных в несжимаемую жидкость плотности $\rho $ и вязкости $\eta $. Частицы могут быть произвольного радиуса и разной плотности. Предполагается, что между частицами действуют силы взаимодействия – притяжения и отталкивания, – удерживающие их в положении равновесия, в котором потенциальная энергия взаимодействия $U$ минимальная. Будем считать энергию взаимодействия частиц в агрегате $U$ как сумму энергий парных взаимодействий частиц с номерами $i$ и $j$

$U = \tfrac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{{U}_{{ij}}},} } \quad i \ne j.$
Здесь необходимо отметить следующее. Как указывалось в работе [13], при учете энергии взаимодействия большого числа частиц возникает проблема, аналогичная случаю гидродинамического взаимодействия [11]: при сложении сил парных взаимодействий, имеющих вид, пропорциональный ${{r}^{{ - n}}}$, где $n \leqslant 3$, получаем расходящиеся ряды для большого числа взаимодействующих частиц. И хотя для определения потенциала взаимодействующих частиц решается линейная задача (обычно это уравнения Пуассона или Лапласа с соответствующими граничными условиями), однако граничные условия для потенциала на поверхности каждой частицы являются интегральными в том смысле, что описывают суммарный вклад от взаимодействия выделенной частицы со всеми остальными. Вследствие чего в граничных условиях для потенциала нельзя отделить результат взаимодействия с выделенной частицей от результата взаимодействий со всеми остальными частицами. Поэтому решение задачи о потенциальном взаимодействии трех и более частиц нельзя представить в виде суммы решений задач о взаимодействии пар частиц, где суммирование берется по всем возможным комбинациям пар из заданной конфигурации частиц. Погрешность представления потенциального взаимодействия всех частиц в виде их парных взаимодействий тем больше, чем больше число частиц, участвующих в таком взаимодействии. Вообще говоря, для корректного учета такого рода сил взаимодействия для большого числа частиц необходимо найти решение уравнений в областях вне и внутри частиц с соответствующими граничными условиями. Решение этой нетривиальной задачи не является целью данной работы, поэтому используется метод парных взаимодействий, дающий достаточную точность для того числа частиц в агрегате, которые будут рассмотрены ниже.

Считая, что относительное положение частиц определяется радиус-векторами ${{{\mathbf{r}}}_{{ij}}}$, соединяющими центры $i$ и $j$ частиц, из условия минимальности энергии взаимодействия следует, что в положении равновесия каждой частицы с индексом $i$ должно выполняться равенство

$\mathop {\left( {\tfrac{{\partial {{U}_{i}}}}{{\partial {\mathbf{x}}}}} \right)}\nolimits_{{{{\mathbf{r}}}_{{ij}}} = {\mathbf{r}}_{{ij}}^{0}} = 0,\quad {{U}_{i}} = \sum\limits_{j = 1}^N {{{U}_{{ij}}}} ,$
здесь ${\mathbf{r}}_{{ij}}^{0}$ – радиус-векторы, соответствующие положению равновесия частиц в агрегате.

В настоящей работе используется метод, основанный на представлении динамики агрегата, как динамики системы частиц, образующих агрегат, при учете как внутренних сил или наложенных связей, которые удерживают частицы в агрегате, так и сил гидродинамического взаимодействия между ними. Этот подход предложен в работах [13], [10] и дает хорошее согласие с экспериментальными результатами. Суть метода в том, что записываются уравнения движения каждой частицы с учетом всех сил, действующих на нее со стороны всех других частиц, в том числе и силы гидродинамического взаимодействия, а также уравнения вращательного движения, с учетом моментов, действующих на частицы. Система уравнений записывается в виде

(1.1)
${\mathbf{F}}_{k}^{{(i)}} + {\mathbf{F}}_{k}^{{(e)}} + {\mathbf{F}}_{k}^{{(h)}} = 0,\quad {\mathbf{T}}_{k}^{{(i)}} + {\mathbf{T}}_{k}^{{(e)}} + {\mathbf{T}}_{k}^{{(h)}} = 0;$
здесь ${\mathbf{F}}_{k}^{{(h)}}$ – силы, ${\mathbf{T}}_{k}^{{(h)}}$ – моменты сил со стороны жидкости, ${\mathbf{F}}_{k}^{{(e)}}$, ${\mathbf{T}}_{k}^{{(e)}}$ – внешние силы и моменты сил, ${\mathbf{F}}_{k}^{{(i)}}$, ${\mathbf{T}}_{k}^{{(i)}}$ – внутренние, действующие на частицу с номером $k$. Причем, ${\mathbf{F}}_{k}^{{(i)}} = - \nabla {{U}_{k}}$. На поверхности частиц задаются граничные условия для скорости жидкости, аналогичные работе [9]. Считается, что внутренние силы не зависят от течения жидкости, а только от относительного положения частиц в агрегате. Система (1) содержит $6N$ алгебраических уравнений. Для численного решения системы уравнений использовалась специальная программа для персонального компьютера (см. [10], [13]), которая в качестве исходных данных получает только желаемую точность вычислений, координаты и радиусы частиц, скорость внешнего потока и приложенные внешние силы и моменты. Программа сама составляет и находит численное решение системы уравнений, а результат выводит в уже обработанном виде. Для учета гидродинамического взаимодействия частиц в жидкости при определении сил ${\mathbf{F}}_{k}^{h}$ и моментов ${\mathbf{T}}_{k}^{h}$ использовался метод, предложенный в [11], [12]. Метод основан на представлении решения уравнений Стокса в виде мультипольного разложения с тензорными коэффициентами и позволяет учитывать гидродинамическое взаимодействие большого числа частиц в вязкой жидкости. Для получения корректных вычислительных результатов учитывались слагаемые с тензорными коэффициентами шестого порядка, что дало погрешность вычислений в десятые доли процента. Такая погрешность получена при компьютерном моделировании, когда вместо реальных параметров задачи используются модельные. Это связано с тем, что для реальных течений Стокса размеры частиц должны быть достаточно малыми,что затрудняет нахождение численного решения системы уравнений и визуализацию результатов. Поэтому применялись метод подобия и модельные параметры. При компьютерном моделировании задаются размер частицы $\hat {a}$, вязкость несущей жидкости $\hat {\eta }$, величина внешней силы $\hat {F}$, действующей на каждую частицу, и ее направление, а также промежуток времени $\hat {t}$. Детально такой метод моделирования и связь между реальными и модельными параметрами представлены в работах [10], [13].

2. ДИНАМИКА МОДЕЛЬНЫХ АГРЕГАТОВ ЗАРЯЖЕННЫХ ЧАСТИЦ В ВЯЗКОЙ ЖИДКОСТИ В ПЕРМЕННОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ

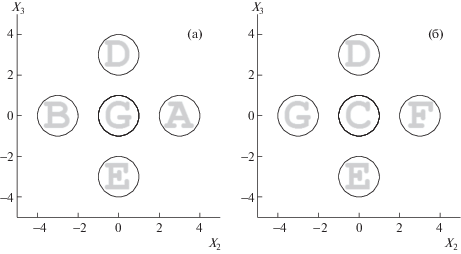
Рассмотрим агрегат, состоящий из семи частиц: центральная частица $C$ и шесть $A$, $B$, $C$, $D$, $E$, $F$, $G$, расположенных вокруг центральной на расстоянии $3a$, где $a$ – радиус центральной частицы (фиг. 1). Заряд частицы $C$ положительный и равный по величине $6q$, где $q$ – отрицательный заряд у каждой из шести других частиц, агрегат в целом заряжен нейтрально. Энергия взаимодействия частиц в агрегате складывается из энергии притяжения ${{U}_{1}}$ между центральной положительно заряженной частицей и каждой из шести отрицательно заряженных частиц, энергии отталкивания ${{U}_{2}}$ между отрицательно заряженными частицами и энергией отталкивания не электрической природы ${{U}_{3}}$ (см. [8]). Суммарная энергия, например в точке, занимаемой частицей $A$, имеет вид

(2.1)
$\begin{gathered} U = {{U}_{1}} + {{U}_{2}} + {{U}_{3}},\quad {{U}_{1}} = - k\frac{{6{{q}^{2}}}}{{{{r}_{{CA}}}}}, \\ {{U}_{2}} = k\frac{{{{q}^{2}}}}{{{{r}_{{DA}}}}} + k\frac{{{{q}^{2}}}}{{{{r}_{{EA}}}}} + k\frac{{{{q}^{2}}}}{{{{r}_{{GA}}}}} + k\frac{{{{q}^{2}}}}{{{{r}_{{FA}}}}} + k\frac{{{{q}^{2}}}}{{{{r}_{{BA}}}}},\quad {{U}_{3}} = \frac{\gamma }{{r_{{CA}}^{2}}}; \\ \end{gathered} $
здесь $k$ – коэффициент пропорциональности в законе Кулона, неизвестный коэффициент $\gamma $ определяется из условия равенства нулю сил в положении устойчивого равновесия. Для показанного на фиг. 1 положения частиц имеем следующие равенства: ${{r}_{{CA}}} = r$, ${{r}_{{DA}}} = {{r}_{{EA}}} = {{r}_{{GA}}} = {{r}_{{FA}}} = r\sqrt 2 $, ${{r}_{{BA}}} = 2r$. С учетом этих соотношений выражение (2) для потенциальной энергии частицы $A$ примет вид

(2.2)
$U = - k\frac{{(11 - 4\sqrt 2 ){{q}^{2}}}}{{2r}} + \frac{\gamma }{{{{r}^{2}}}}.$
Фиг. 1.

Структура первого агрегата. Единица измерения по осям – $1$ радиус.

Из условия равенства нулю силы, действующей на частицу $A$ в положении $r = 3a$, получим

$\gamma = k{{q}^{2}}a(8.25 - 3\sqrt 2 ).$

Агрегат находится в жидкости вязкости $\eta $. На систему накладывается однородное электрическое поле напряженности ${\mathbf{E}}$. Поле действует в течение промежутка времени $T$, после чего выключается. В результате действия поля происходит деформация агрегата, так как противоположно заряженные частицы перемещаются в электрическом поле в разных направлениях. Деформация приводит к появлению внутренних сил, стремящихся вернуть частицы в исходное состояние. В течение времени $\tau $, пока поле отключено, происходит восстановление агрегата к состоянию, близкому равновесному. Затем вновь включается электрическое поле на промежуток времени $T$ и вновь происходит деформация с последующим частичным восстановлением системы за промежуток времени $\tau $. Так как агрегат находится в вязкой жидкости, то в результате его деформации формируется течение и возникает гидродинамическая сила, действующая на частицы в агрегате. Цель работы – показать, что действие гидродинамических сил приводит к перемещению центра тяжести агрегата в направлении приложенного поля.

Как было указано выше, для получения корректных вычислительных результатов при компьютерном моделировании вместо реальных параметров задачи используются модельные. Поэтому рассмотрим модельную структуру, подобную реальной, помещенную в жидкость с модельной вязкостью $\hat {\eta } = 1$ г/(см ⋅ с), размерами частиц, пропорциональными $\hat {a} = 1$ см, потенциалом внутренних сил $\hat {U}$, равным:

(2.3)
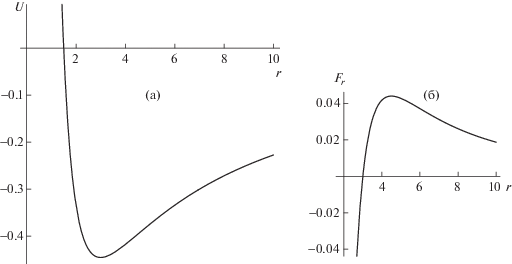
$\hat {U} = - k\frac{{(11 - 4\sqrt 2 ){{{\hat {q}}}^{2}}}}{{2\hat {r}}} + \frac{{\hat {\gamma }}}{{{{{\hat {r}}}^{2}}}}.$

Будем полагать модельный заряд частиц $\hat {q}$ таким, что $k{{\hat {q}}^{2}}{\text{/}}\hat {a} = 5 \times {{10}^{{ - 11}}}$ н$ \cdot $м. Тогда получаем выражение для коэффициента $\hat {\gamma } = {{\hat {a}}^{2}}(8.25 - 3\sqrt 2 )$. В этом случае зависимость энергии частицы $A$ в поле остальных частиц имеет вид (см. фиг. 2а). Соответственно сила, действующая на частицу $A$, представлена на фиг. 2б. Как видно из графиков, потенциальная энергия и соответствующая сила имеют типичный вид для классической теории устойчивости коллоидов. Модельное электрическое поле с напряжением ${\mathbf{\hat {E}}}$ создает силу, действующую на заряд $\hat {q}$ и равную $\hat {E}\hat {q} = 0.5$ г ⋅ см/с$^{2}$. Импульс силы создается за промежуток времени $\hat {T}$, модельное время релаксации системы $\hat {\tau }$. Было проведено численное моделирование динамики четырех модельных агрегатов рассмотренной выше структуры, но разными размерами частиц и временами $\hat {T}$, $\hat {\tau }$. Величина напряженности модельного электрического поля ${\mathbf{\hat {E}}}$ считалась одинаковой для всех трех агрегатов. Первый агрегат состоял из частиц одного размера $\hat {a} = 1$ см. Во втором агрегате центральная частица имела размер $\hat {a} = 1$ см, а остальные – $\hat {a} = 0.3$ см. Третий агрегат отличался от второго размером центральной частицы $\hat {a} = 0.5$ см. Четвертый агрегат отличался от третьего размером частицы $B$ – $\hat {a} = 1$ см. Результаты расчетов динамики агрегатов за промежуток времени $\Delta \hat {t} = 24$ с приведены в табл. 1. Параметром ε указана погрешность вычислений. Как видно из таблицы, имеется существенная зависимость результатов от относительных размеров частиц, а также от времени воздействия поля. Поскольку сумма внешних сил, действующих на частицы в агрегате со стороны электрического поля, равна нулю, а внутренние силы не могут изменить положение центра тяжести системы частиц, то перемещение агрегатов обусловлено действием гидродинамических сил. В результате взаимодействия частиц формируется течение в окружающей агрегат вязкой жидкости, создающей силу, перемещающую агрегат. Гидродинамическое воздействие жидкости, вызывающее перемещение агрегата, может быть более эффективным за счет изменения площади поперечного сечения частиц при их возвращении в положение равновесия, аналогично механике плавающих организмов. Это может быть достигнуто применением частиц несферической формы. На фиг. 3 представлена динамика первого агрегата последовательно за периоды времени $\hat {T}$ и $\hat {\tau }$. Динамика других моделей агрегатов аналогична представленной.

Фиг. 2.

(а) Потенциальная энергия взаимодействия. (б) Сила взаимодействия.

Таблица 1.  

Результаты моделирования динамики агрегатов заряженных частиц

  Агрегат 1 Агрегат 2 Агрегат 3 Агрегат 4
$\hat {T}$, с 4 4 2 4
$\hat {\tau }$, с 4 4 4 4
$\Delta \hat {l}$, см 0.10390386 0.74893905 0.375180 0.0298373
ε 0.00018365 0.00014164 4.6472 × 10–9 3.5897 × 10–9
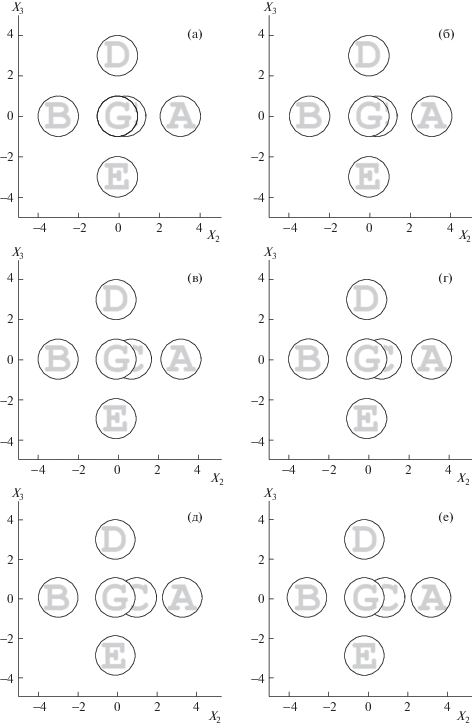
Фиг. 3.

Динамика первого агрегата. Единица измерения по осям – $1$ радиус. Последовательность кадров: (а), (в), (д) – после действия приложенного поля; (б), (г), (е) – после релаксации системы. Интервал модельного времени между соседними кадрами равен $4$ с.

Значения реальных параметров можно определить согласно формулам пересчета, приведенным в [10], [13]. Так, реальное время действия поля $T$ и время релаксации $\tau $ определяются согласно правилу

(2.4)
$t = \frac{{{{a}^{2}}\hat {\eta }\hat {t}}}{{{{{\hat {a}}}^{2}}\eta }}.$

Так, для агрегата из частиц размера $a = {{10}^{{ - 4}}}$ см и реальной вязкости жидкости $\eta = {{10}^{{ - 2}}}$ г/(см ⋅ с) получаем $T = 4 \times {{10}^{{ - 6}}}$ с. Величина заряда частиц определяется из соотношения для реальной и модельной величин сил

(2.5)
$F = \frac{{{{\eta }^{2}}}}{{\mathop {\hat {\eta }}\nolimits^2 }}\hat {F}.$

Для кулоновской силы взаимодействия зарядов получаем

(2.6)
$k\frac{{{{q}^{2}}}}{{{{a}^{2}}}} = k\frac{{\mathop {\hat {q}}\nolimits^2 }}{{\mathop {\hat {a}}\nolimits^2 }}.$

С учетом выбранного модельного заряда $\hat {q}$ и значения $k \approx 9 \times {{10}^{9}}$ н ⋅ м$^{2}/$Кл$^{2}$ получаем величину реального заряда частиц $q \approx 750 \times {{10}^{{ - 19}}}$ Кл. Аналогичные вычисления для напряженности электрического поля $E$ дают при учете реального заряда частиц величину $E = 670$ Кв/м. Это достаточно большое напряжение, но оно много меньше, чем величина пробивного напряжения для большинства углеводородных жидкостей. Полученный результат перемещения агрегата может быть получен и при меньших значениях напряжения за счет увеличения времени воздействия электрического поля. Например, увеличив время воздействия до 1 с, можно уменьшить напряженность поля до значения $E = 0.670$ Кв/м. Таким образом, предложенный механизм перемещения агрегатов в электрическом поле может быть реализован при реальных значениях параметров системы жидкость–частицы. Возможны и другие конструкции агрегатов из заряженных частиц, а также и варианты воздействия внешнего поля на частицы агрегата. Например, был рассмотрен вариант, когда переменное поле действует в одном направлении с модельным временем $\hat {T}$, а затем в противоположном направлении с модельным временем $\hat {T}{\text{/}}2$. На примере первого агрегата было проведено численное моделирование и показано, что перемещение центра тяжести составило $0.0677132$ при погрешности вычислений $2.3446 \times {{10}^{{ - 5}}}$. Это меньше, чем при первом варианте воздействия, однако вопрос о параметрах внешнего поля, действие которого приводит к более высокой скорости перемещения агрегата, требует дополнительного изучения и проведения новых численных расчетов.

Необходимо также отметить, что поскольку за период релаксации $\hat {\tau }$ система полностью не восстанавливает свое первоначальное состояние (выше указывалось, каким способом достигается полное восстановление агрегата), то через определенный промежуток времени агрегат может разрушиться на отдельные частицы под действием приложенного поля. Если в жидкости таких агрегатов много, то в силу того, что система из отдельных положительно и отрицательно заряженных частиц неустойчива, можно предполагать новую сборку агрегата из частиц, ранее принадлежащих разным агрегатам. Поскольку положительно и отрицательно заряженные частицы во внешнем поле двигаются в противоположных направлениях, то наиболее вероятное место новой сборки находится между двумя распавшимися агрегатами по направлению вектора приложенного поля. Распад и последующая сборка нового агрегата, но в новом месте, могут рассматриваться как “фазовое” перемещение агрегата.

3. ДИНАМИКА МОДЕЛЬНЫХ АГРЕГАТОВ ДИПОЛЬНЫХ ЧАСТИЦ В ВЯЗКОЙ ЖИДКОСТИ В ПЕРЕМЕННОМ МАГНИТНОМ ПОЛЕ

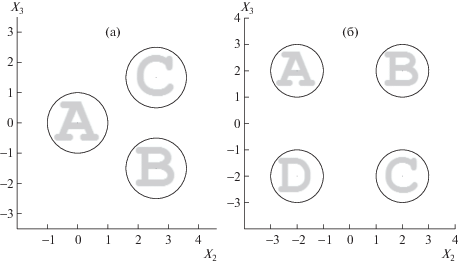
Другим примером частиц, взаимодействие которых может приводить к образованию агрегатов в жидкости, являются частицы с дипольным моментом $m$. Простейший агрегат состоит из двух дипольных частиц, суммарный момент которых может быть равен нулю. Такая ориентация соответствует минимуму энергии взаимодействия, однако не является устойчивой. Приложенное внешнее магнитное поле, лежащее в плоскости диполей и направленное под любым, не равным нулю, углом к ним, приводит их во вращательное движение. Причем вращение частиц происходит в противоположных направлениях. Как показано в [9], такое вращение создает гидродинамическую силу, перемещающую систему частиц в направлении, перпендикулярном плоскости, в которой лежат оси вращения частиц. Если выключить внешнее поле, то в результате действия диполь-дипольного взаимодействия частицы стремятся к новому положению равновесия с ориентацией диполей вдоль одной прямой. Как показали [14] результаты численного анализа равновесных значений и динамики суммарного магнитного момента системы, состоящей из N диполей, при больших N имеют место плоскостные кольцеобразные цепочки связанных диполей. В случае $2 < N < 8$ равновесным является только нулевое значение суммарного магнитного момента диполей, расположенных в вершинах правильного многоугольника. При N > 8 имеет место бистабильность и устанавливается не менее двух равновесных состояний: с нулевым значением суммарного магнитного момента и с максимальным значением ${{M}_{{{\text{max}}}}} = m(7N + 8){\text{/}}11$. Ниже на фиг. 4а приведена динамика агрегата, состоящего из трех дипольных частиц $A$, $B$, $C$ радиуса $\hat {a} = 1$ см, расположенных в углах правильного треугольника. Агрегат помещен в жидкость с модельной вязкостью $\hat {\eta } = 1$ г/(см ⋅ с). Диполи имеют следующую ориентацию: ${{{\mathbf{\hat {m}}}}_{A}} = (0,0,\hat {m})$, ${{{\mathbf{\hat {m}}}}_{B}} = (0, - \hat {m}\sqrt 3 {\text{/}}2, - \hat {m}{\text{/}}2)$, ${{{\mathbf{\hat {m}}}}_{C}} = (0,\hat {m}\sqrt 3 {\text{/}}2, - \hat {m}{\text{/}}2)$. Для простоты вычислений внешнее поле ${\mathbf{\hat {H}}}$ направлено вдоль диполя частцы $A$. Поскольку суммарный момент равен нулю, то внешнее однородное поле приводит в противоположное вращение с угловой скоростью $\hat {\omega }$ два других диполя, создавая вихревое течение в вязкой жидкости, благодаря которому они перемещаются вдоль оси $O{{X}_{2}}$. Внешнее поле действует промежуток времени $\hat {T}$. После выключения внешнего поля система стремится вернуться в исходное состояние, поскольку это состояние устойчивого равновесия. Через время $\hat {\tau }$ вновь включается внешнее магнитное поле, и агрегат вновь перемещается в направлении, перпендикулярном приложенному полю. Суммарное перемещение центра тяжести системы равно $\Delta \hat {l}$.

Фиг. 4.

Агрегаты с дипольными частицами. Единица измерения по осям – $1$ радиус.

Аналогично приводится в движение и перемещается агрегат из четырех дипольных частиц (фиг. 4б) с соответствующими ориентациями диполей ${{{\mathbf{\hat {m}}}}_{A}} = (0,\hat {m}\sqrt 2 {\text{/}}2),\hat {m}\sqrt 2 {\text{/}}2)$, ${{{\mathbf{\hat {m}}}}_{B}} = $ ${{{\mathbf{\hat {m}}}}_{B}} = (0,\hat {m}\sqrt 2 {\text{/}}2), - \hat {m}\sqrt 2 {\text{/}}2)$, ${{{\mathbf{\hat {m}}}}_{C}} = (0, - \hat {m}\sqrt 2 {\text{/}}2), - \hat {m}\sqrt 2 {\text{/}}2)$, ${{{\mathbf{\hat {m}}}}_{D}} = (0, - \hat {m}\sqrt 2 {\text{/}}2),\hat {m}\sqrt 2 {\text{/}}2)$. Магнитное поле ${\mathbf{\hat {H}}}$ прикладывается вдоль оси $O{{X}_{2}}$. Причем, так как величина диполей одинакова, а суммарный момент равен нулю, то со стороны внешнего магнитного поля на каждый диполь действует одинаковый по величине момент. Однако направление момента и соответственно вращение частиц попарно противоположное. Такое вращение приводит к перемещению агрегата в отрицательном направлении оси $O{{X}_{3}}$. В табл. 2 приведены результаты динамики агрегатов для модельных значений параметров. Поскольку за время действия приложенного поля угол поворота частиц небольшой, то для упрощения вычислений моменты, действущие на частицы, считались постоянными: $\hat {m} \cdot \hat {H} = 0.5$, ${{\hat {m}}^{2}}{\text{/}}{{\hat {a}}^{2}} = 0.1$ для агрегата из трех диполей и $\hat {m} \cdot \hat {H} = 1$, ${{\hat {m}}^{2}}{\text{/}}{{\hat {a}}^{2}} = 0.2$ для агрегата из четырех диполей. Модельное время для вычисления перемещения для обоих агрегатов равно $24$ с. По модельным значениям приложенного поля и дипольного момента так же, как и в случае агрегата из заряженных частиц, определяются значения реальных параметров системы жидкость–частицы.

Таблица 2.  

Результаты моделирования динамики агрегатов дипольных частиц

  3 диполя 4 диполя
$\hat {T}$, с 4 4
$\hat {\tau }$, с 4 2
$\Delta \hat {l}$, см 0.0183039 0.0454
$\hat {\omega }$, с–1 0.003986689 0.0397385
ε 1.5711 × 10–6 1.2634 × 10–6

Аналогичный подход может быть применен для расчета перемещения других структур агрегатов дипольных частиц с нулевым суммарным магнитным моментом в однородном внешнем магнитном поле. В случае, когда магнитный момент системы дипольных частиц не равен нулю, перемещение агрегата может быть осуществлено при наложении градиентного магнитного поля [15].

ЗАКЛЮЧЕНИЕ

Предложен механизм перемещения агрегата заряженных или дипольных частиц во внешнем переменном однородном поле. Причем суммарный заряд или дипольный момент агрегатов равен нулю. Механизм перемещения основан на использовании энергии взаимодействия частиц в агрегате в качестве одной из составляющих относительного перемещения частиц в агрегате. Вторая составляющая – переменное внешнее поле, действующее на заряженные или дипольные частицы в агрегате. Благодаря действию этих составляющих происходит формирование течения в окружающей агрегаты вязкой жидкости за счет относительных перемещений его частиц. Сформированное течение в окружающей жидкости создает гидродинамическую силу, действующую на агрегат и перемещающую его в определенном направлении относительно приложенного поля. Меняя направление поля, можно управлять движением агрегатов частиц. Учитывается гидродинамическое взаимодействие всех частиц, из которых состоит агрегат. Проведено компьютерное моделирование перемещений такого рода агрегатов в вязкой жидкости с помощью специального программного комплекса. Проведен численный расчет динамики 4 модельных структур, образованных из 7 заряженных частиц разного размера, определенным образом соединенных между собой, и двух модельных структур дипольных частиц при различных периодах времени воздействия внешнего поля. Результаты численного моделирования позволяют определить, какая из моделей агрегатов частиц перемещается с большей скоростью. На основе предложенного подхода можно изучать возможность перемещения агрегатов разной геометрической формы во внешнем переменном однородном поле.

Список литературы

  1. Арансон И.С. Активные коллоиды // Успехи физ. наук. 2013. Т. 183. № 1. С. 87–102.

  2. Ebbens S.J. Active colloids: Progress and challenges towards realising autonomous applications // Current Opinion in Colloid and Interface Sci. 2016. V. 21. P. 14–23.

  3. Patteson A.E., Gopinath A., Arratiaa P.E. Active colloids in complex fluids //Current Opinion in Colloid and Interface Sci. 2016. V. 21. P. 86–96.

  4. Zhang J., Luijten E., Grzybowskic B.A., Granick S. Active colloids with collective mobility status and research opportunities // Chem. Soc. Rev. 2017. V. 46. P. 5551–5569.

  5. Ефремов И.Ф. Периодические коллоидные структуры Л.: Химия, 1971. 192 с.

  6. Niu R., Palberg T. Seedless assembly of colloidal crystals by inverted micro-fluidic pumping // Soft Matter. 2018. V. 14. P. 3435–3442.

  7. Dickinson E. Structure and rheology of colloidal particle gels: insight from computer simulation // Adv. Colloid Interface Sci. 2013. Nov. 199–200. P. 114–127.

  8. Дерягин Б.В., Чураев Н.В., Муллер В.М. Поверхностные силы. М.: Наука, 1985. 398 с.

  9. Мартынов С.И., Ткач Л.Ю. Об одной модели динамики самодвижущихся агрегатов частиц в вязкой жидкости // Нелинейная динамика. 2016. Т. 12. № 4. С. 605–618.

  10. Мартынов С.И., Ткач Л.Ю. Динамика цепочечных агрегатов частиц в потоке вязкой жидкости // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 5. С. 133–148.

  11. Мартынов С.И. Гидродинамическое взаимодействие частиц // Изв. РАН. Механ. жидкости и газа. 1998. № 2. С. 112–119.

  12. Баранов В.Е., Мартынов С.И. Влияние гидродинамического взаимодействия на скорость осаждения большого числа частиц в вязкой жидкости // Изв. РАН. Механ. жидкости и газа. 2004. № 1. С. 152–164.

  13. Мартынов С.И., Ткач Л.Ю. Моделирование динамики агрегатов частиц в вязкой жидкости // Ж. вычисл. матем. и матем. физ. 2015. Т. 55. № 2. С. 109–118.

  14. Шутый А.М. Равновесные значения и динамика суммарного магнитного момента систем магнитных диполей // Ж. эксперим. и теор. физ. 2010. Т. 137. Вып. 2. С. 277–286.

  15. Ландау Л.Д. Электродинамика сплошных сред / Л.Д. Ландау, Е.М. Лифшиц. М. : Наука, 1982. 620 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал