Журнал вычислительной математики и математической физики, 2019, T. 59, № 3, стр. 516-525

Решение задач гидродинамики в усеченных расчетных областях

И. И. Потапов¹, К. С. Снигур^1, *

¹ ВЦ ДВО РАН
680000 Хабаровск, ул. Ким Ю Чена, 65, Россия

Поступила в редакцию 18.07.2018

DOI: 10.1134/S004446691903013X

Аннотация

Предложена математическая модель для решения задачи гидродинамики в усеченной расчетной области, которая включает систему квазигидродинамических уравнений и граничные условия Донга на границе вытекания. Разработан алгоритм решения задачи гидродинамики с применением метода конечных элементов и метода контрольных объемов. Выполнено численное моделирование движения потока Коважного и движения потока за обратным уступом в усеченных расчетных областях. Выполненный в работе сравнительный анализ показал, что предложенная математическая модель адекватно описывает движение гидродинамического потока в усеченной области. Библ. 17. Фиг. 9. Табл. 2.

Ключевые слова: гидродинамический поток, усеченная расчетная область, обратный уступ, квазигидродинамические уравнения, математическое моделирование.

ВВЕДЕНИЕ

При решении гидродинамических задач часто возникает проблема установки корректных граничных условий на выходной границе области. Для граничных условий Дирихле не всегда известен профиль скорости. Для граничных условий Неймана на установление потока при высоких числах Рейнольдса требуется значительное удлинение расчетной области, которое ведет к росту вычислительных затрат.

Для преодоления ограничений граничных условий Неймана на установление были предложены граничные условия, позволяющие выполнять расчет в усеченных расчетных областях. В работе [1] были предложены конвективные граничные условия для усеченной области. Данные граничные условия изначально были предложены для гиперболических уравнений и с уравнениями Навье–Стокса математически точным способом они не согласуются, поэтому их применение может приводить к значительным искажениям решения.

Граничные условия неотражения [2], [3] для усеченных областей основаны на волновом уравнении и сводят к минимуму ложные артефакты поля скорости на выходной границе. Такие граничные условия подходят только для струйных вихревых потоков с умеренными и высокими числами Рейнольдса, так как требуют некоторых знаний о структуре потока за выходной границей усеченной расчетной области.

Свободные граничные условия (“do-nothing” boundary condition) были предложены в [4], где интегральный член по поверхности вытекания в слабой формулировке уравнений Навье–Стокса переносится в левую часть и включается в матрицу масс. Такие условия подходят только для непериодических течений, так как они никак не ограничивают приток энергии через выходную границу области (см. [5]).

В 2014 г. Донг (см. [6]) предложил граничное условие, которое не вызывает неконтролируемого роста энергии при решении задач в усеченных расчетных областях. Граничное условие Донга успешно используется при решении уравнений Навье–Стокса (см. [7]–[12]).

В настоящей работе сформулирована математическая постановка, основанная на системе квазигидродинамических уравнений и позволяющая решать задачу гидродинамики в усеченной расчетной области. На границе усечения расчетной области используются граничные условия Донга [6]. Предложен алгоритм решения задачи. Выполнены численные эксперименты для задачи о движении потока Коважного и задачи о движении потока за обратным уступом.

1. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ

Для описания движения двумерного гидродинамического потока вязкой несжимаемой жидкости используются квазигидродинамические уравнения (см. [13])

(1.1)

$\frac{{\partial {{u}_{i}}}}{{\partial t}} + {{\nabla }_{j}}\left( {{{u}_{i}}{{u}_{j}}} \right) + \frac{1}{\rho }{{\nabla }_{i}}p = {{\nabla }_{j}}\left[ {\eta \left( {{{\nabla }_{j}}{{u}_{i}} + {{\nabla }_{i}}{{u}_{j}}} \right)} \right] - \frac{2}{3}{{\nabla }_{i}}\left( {\eta {{\nabla }_{k}}{{u}_{k}}} \right) + {{\nabla }_{j}}\left[ {\eta \left( {{{\omega }_{i}}{{u}_{j}} + {{\omega }_{j}}{{u}_{i}}} \right)} \right],$

(1.2)

$\nabla _{i}^{2}p = \frac{\rho }{\sigma }{{\nabla }_{i}}{{u}_{i}} - {{\alpha }_{r}}\rho {{\nabla }_{i}}\left( {u_{j}^{{}}{{\nabla }_{j}}u_{i}^{{}}} \right),$

где

(1.3)

${{\omega }_{i}} = \sigma \left( {{{u}_{j}}{{\nabla }_{j}}{{u}_{i}} + \frac{1}{\rho }{{\nabla }_{i}}p} \right),\quad i,j = 1,2.$

Уравнения (1.1)–(1.3) замыкаются начальными условиями

(1.4)

${{u}_{i}} = {{u}_{{i,0}}},\quad {{x}_{i}} \in \Omega $

и граничными условиями

(1.5)

${{u}_{i}} = {{u}_{{i,{\text{in}}}}}(y),\quad {{\nabla }_{j}}p{{n}_{j}} = {{c}_{{{\text{in}}}}}\left( y \right),\quad {{x}_{i}} \in {{\Omega }_{{{\text{in}}}}},$

(1.6)

${{\nabla }_{j}}{{u}_{i}}{{n}_{j}} = {{q}_{{i,{\text{out}}}}}\left( y \right),\quad p = \left( {\eta {{\nabla }_{j}}{{u}_{k}}} \right){{n}_{j}}{{n}_{k}} - S,\quad {{x}_{i}} \in {{\Omega }_{{{\text{out}}}}},$

(1.7)

${{u}_{i}} = {{u}_{{i,}}}_{{{\text{bed}}}}(x),\quad {{n}_{j}}{{\nabla }_{j}}p = 0,\quad {{x}_{i}} \in {{\Omega }_{{{\text{bed}}}}},$

(1.8)

${{u}_{i}} = {{u}_{{i,{\text{top}}}}}\left( x \right),\quad {{n}_{j}}{{\nabla }_{j}}p = 0,\quad {{x}_{i}} \in {{\Omega }_{{{\text{top}}}}},$

(1.9)

${{q}_{{i,{\text{out}}}}} = \frac{1}{{\eta \rho }}\left( {p + S - {{\nabla }_{j}}{{u}_{j}}} \right){{n}_{i}},\quad i,j,k = 1,2$.

В уравнениях (1.1)–(1.9) ${{u}_{i}}$ – вектор скорости потока, $t$ – время, $\rho $ – плотность воды, $p$ – давление жидкости, $\eta = {\text{const}}$ – кинематическая вязкость жидкости, $\sigma = \gamma \,\Delta t$ – параметр сглаживания по времени [14], $0 \leqslant \gamma \leqslant 1$ – численный коэффициент, ${{\alpha }_{r}}$ – штрафующий коэффициент для стабилизации счета, вводится для обеспечения условия $\left| {{{\nabla }_{j}}p{{n}_{j}}} \right| > {{\alpha }_{r}}\left| {\rho {{\nabla }_{i}}\left( {u_{j}^{{}}{{\nabla }_{j}}u_{i}^{{}}} \right)} \right|$ на границе ${{\Omega }_{{in}}}$.Величина $\Omega = {{\Omega }_{{{\text{in}}}}} \cup {{\Omega }_{{{\text{bed}}}}} \cup {{\Omega }_{{{\text{out}}}}} \cup {{\Omega }_{{{\text{top}}}}}$ – граница расчетной области $V$, включающая входную, нижнюю, выходную и верхнюю границы области соответственно, ${{f}_{0}}$ – начальное распределение функции в расчетной области, ${{u}_{{i,{\text{in}}}}}$, ${{u}_{{i,{\text{bed}}}}}$, ${{u}_{{i,{\text{top}}}}}$ – распределение значений вектора скорости на соответствующей границе, ${{c}_{{{\text{in}}}}}\left( y \right)$ – распределение потока давления на входной границе, ${{q}_{{i,{\text{out}}}}}\left( y \right)$ – распределение потоков вектора скорости на выходной границе, ${{n}_{i}}$ – вектор нормали к соответствующей границе расчетной области, ${{U}_{0}}$ – средняя горизонтальная скорость потока,

$S = \frac{\rho }{4}\left| {{{u}_{k}}} \right|\left( {1 - \tanh \frac{{{{u}_{k}}{{n}_{k}}}}{{{{U}_{0}}\delta }}} \right)$

есть предложенный Донгом (см. [6]) ограничитель поступления кинетической энергии в область через границу вытекания, имеющий вид сглаженной ступенчатой функции, где $\delta $ – коэффициент сглаживания ($\delta \to 0$).

Параметры $\sigma $ и $\,{{\alpha }_{r}}$ выбирались эмпирически для каждой задачи.

2. МЕТОД РЕШЕНИЯ ЗАДАЧИ

Решение задачи (1.1)–(1.9) выполнялось с применением метода контрольных объемов для определения поля горизонтальной и вертикальной скоростей и метода конечных элементов для определения поля давления. Расчеты производились на треугольной регулярной сетке. В расчетах использовались дискретные аналоги задачи (1.1)–(1.9), полученные в [15].

При изложении алгоритма и полученных результатов для удобства используются следующие соглашения по обозначениям $x \equiv {{x}_{1}},\;y \equiv {{x}_{2}},\;u \equiv {{u}_{1}},\;v \equiv {{u}_{2}}$ там, где это не приводит к противоречиям.

Алгоритм решения задачи (1.1)–(1.9) состоит из следующих шагов.

1. Разбиение расчетной области на регулярную сетку с узлами $({{x}_{l}};{{y}_{m}})$, ${{x}_{l}} = l\Delta x$, $l = 0...{{N}_{x}}$, ${{y}_{m}} = m\Delta y$, $m = 0...{{N}_{y}}$.

2. Установка начальных условий (1.4) во всей расчетной области.

3. Выполнение на каждой итерации по времени $n = \overline {0...{{N}_{t}}} $ с шагом по времени $\Delta t$ следующих действий.

a. Решение уравнения (1.2) с помощью метода конечных элементов с граничными условиями (1.5)–(1.8), где условие (1.6) для давления на выходной границе имеет следующую дискретную по времени форму:

(2.1)

${{p}^{{n + 1}}} = \left( {\eta {{\nabla }_{j}}u_{k}^{n}} \right){{n}_{j}}{{n}_{k}} - \frac{\rho }{4}\left| {u_{k}^{n}} \right|\left( {1 - \tanh \frac{{u_{k}^{n}{{n}_{k}}}}{{{{U}_{0}}\delta }}} \right),\quad {{x}_{i}} \in {{\Omega }_{{{\text{out}}}}}.$

б. Решение уравнений (1.1) с помощью метода контрольных объемов с граничными условиями (1.5)–(1.9), где условие (1.6) для скоростей на выходной границе имеет следующую дискретную по времени форму:

(2.2)

${{\nabla }_{j}}u_{i}^{{n + 1}}{{n}_{j}} = \frac{1}{{\eta \rho }}\left( {{{p}^{{n + 1}}} + \frac{\rho }{4}\left| {u_{k}^{n}} \right|\left( {1 - \tanh \frac{{u_{k}^{n}{{n}_{k}}}}{{{{U}_{0}}\delta }}} \right) - {{\nabla }_{j}}u_{j}^{n}} \right){{n}_{i}},\quad {{x}_{i}} \in {{\Omega }_{{{\text{out}}}}}.$

Остальные граничные условия будут определены ниже, исходя из специфики конкретной задачи.

В работе Донга (см. [6]) предлагается несколько алгоритмов расчета уравнений Навье–Стокса со свободными граничными условиями. Для контрольно-объемного метода предлагается трехшаговый алгоритм расчета с вычислением промежуточных скоростей потока. Для конечно-элементного метода предлагается двухшаговый алгоритм расчета, включающий модифицированные уравнения движения и модифицированное уравнение Пуассона, и не требующий вычисления промежуточной скорости потока и производных выше первого порядка.

В настоящей работе для решения задачи (1.1)–(1.9) авторами предложен двухшаговый алгоритм, который не требует вычисления промежуточной скорости потока и модификации основных уравнений, и адаптирует алгоритм постановки граничных условий Донга (см. [6]).

4. ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ

Для верификации предложенного алгоритма решения гидродинамической задачи выполнены следующие численные эксперименты:

– решение задачи о движении потока Коважного в усеченной области;

– решение задачи о движении потока за обратным уступом в усеченной области.

Задача о движении потока Коважного

Поток Коважного является стационарным потоком и имеет точное решение вида (см. [16], [6])

(3.1)

$u\left( {x,y} \right) = 1 - {{e}^{{\lambda x}}}\cos 2\pi y,\quad v\left( {x,y} \right) = \frac{\lambda }{{2\pi }}{{e}^{{\lambda x}}}\sin 2\pi y,$

(3.2)

$p\left( x \right) = \frac{1}{2}\left( {1 - {{e}^{{2\lambda x}}}} \right),\quad \lambda = \frac{1}{{2\eta }} - \sqrt {\frac{1}{{4{{\eta }^{2}}}} + 4{{\pi }^{2}}} .$

В данной задаче на верхней и нижней границах расчетной области следует устанавливать периодические граничные условия, но в настоящей работе для простоты счета задача решалась в рамках одного периода с граничными условиями отражения на верхней и нижней границах, поэтому переопределим граничные условия (1.6) и (1.7) следующим образом:

$\frac{{\partial u}}{{\partial y}} = 0,\quad v = 0,\quad \frac{{\partial p}}{{\partial y}} = 0,\quad (x,y) \in {{\Omega }_{{{\text{bed}}}}},$

$\frac{{\partial u}}{{\partial y}} = 0,\quad v = 0,\quad \frac{{\partial p}}{{\partial y}} = 0,\quad (x,y) \in {{\Omega }_{{{\text{top}}}}}.$

На боковых границах области выполняются граничные условия (1.5), (1.6), (2.1), (2.2), где значения ${{u}_{{{\text{in}}}}}$, ${{v}_{{{\text{in}}}}}$ и ${{с }_{{{\text{in}}}}}$ определяются в соответствии с точным решением (3.1), (3.2).

Задача решалась при следующих параметрах: $H = 1$ м, ${{U}_{0}} = 1$ м с^–1, $Q = 1$ м² с^–1, ${{\rho }_{w}} = 1000$ кг м^–3, $\operatorname{Re} = 40$, $\eta = 0.025$ м² с^–1, $T = 10$ с, $\Delta t = {{10}^{{ - 4}}}$ с, $\Delta x = \Delta y = 0.0126$ м, ${{\alpha }_{r}} = 5 \cdot {{10}^{{ - 2}}}$, $\sigma = {{10}^{{ - 4}}}$ с, $\delta = 0.05$, ${{u}_{0}} = 0$, ${{v}_{0}} = 0$. Исходя из аналитического решения (3.1), (3.2), длина расчетной области L, достаточная для установления потока (условие ${{\nabla }_{i}}{{u}_{i}} \approx {{10}^{{ - 5}}}$) при вышеуказанных параметрах, равна 6 м. Расчеты выполнялись в расчетных областях с различной длиной, равной 6, 3, 1 и 0.6 м. Для верификации предложенной модели выполнено сравнение расчетных данных с аналитическими данными в вертикальном сечении $x = 0.6$ м и горизонтальном сечении $y = 0.5$ м во всех расчетных областях.

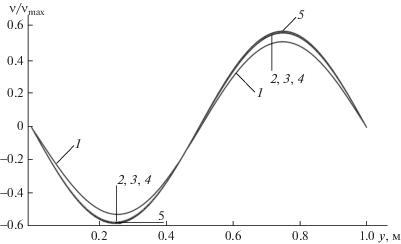
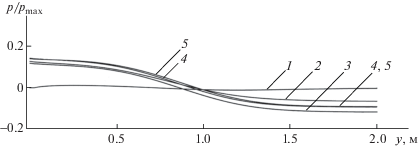
На фиг. 1–4 показаны профили изменения характеристик потока в безразмерном виде, для обезразмеривания использовались следующие величины: ${{u}_{{\max }}} = 2$ м с^–1, ${{v}_{{\max }}} = 0.15$ м с^–1, ${{p}_{{\max }}} = 500$ кг м^–1 с^–1. Номера профилей указывают, при какой длине расчетной области они были получены: 1 – для 0.6 м, 2 – для 1 м, 3 – для 3 м, 4 – для 6 м, 5 – аналитическое решение (3.1), (3.2).

Фиг. 1.

Графики горизонтальной скорости в вертикальном сечении $x = 0.6$ м.

Фиг. 2.

Графики вертикальной скорости в вертикальном сечении $x = 0.6$ м.

Фиг. 3.

Графики давления в вертикальном сечении $x = 0.6$ м.

Фиг. 4.

Графики давления в горизонтальном сечении $y = 0.5$ м.

Рассмотрим профили характеристик потока в сечении $x = 0.6$ м, которые показаны на фиг. 1–3 . На фиг. 1 и 2 видно, что профили скорости 1 имеют наибольшее отклонение от соответствующих аналитических профилей 5, максимальная относительная погрешность для горизонтальной скорости равна 0.49%, для вертикальной скорости равна 6.25%; максимальное отличие остальных профилей горизонтальной и вертикальной скоростей составляет менее 1.1%. На фиг. 3 профиль давления 1 имеет максимальное отклонение от аналитического профиля 5 в 3.7%, отклонение остальных профилей не превышает 1.5%. Более подробно значения максимальной относительной погрешности расчетных данных, полученных в сечении $x = 0.6$ м, представлены в табл. 1.

Таблица 1.

Максимальная относительная погрешность расчетов $\delta \left( f \right)$ в сечении $x = 0.6$ м в задаче о движении потока Коважного и время расчета задачи

	L, м
	0.6 (профиль 1)	1 (профиль 2)	3 (профиль 3)	6 (профиль 4)
$\delta \left( u \right)$	0.49%	0.24%	0.07%	0.02%
$\delta \left( \text{v} \right)$	6.25%	1.10%	0.09%	0.02%
$\delta \left( p \right)$	3.70%	1.38%	0.90%	0.81%
Время расчета, с	13 862	18 797	73 035	137 751

На фиг. 4 показаны профили давления в горизонтальном сечении $y = 0.5$ м. Следует отметить, что продольные профили давления 1 и 2 имеют более пологую форму по сравнению с профилями 3–5, что отражается на точности всего решения. Это связано с граничным условием (1.6), (2.1), которое устанавливает близкие к нулю значения давления на выходе, вне зависимости от длины области и структуры потока.

Из сравнительного анализа видно, что при расчете в области, полностью включающей зону перестроения потока, граничные условия (1.6), (2.1), (2.2) никак не влияют на точность расчетов (во всех графиках профили 3, 4 практически совпадают с аналитическими профилями 5). В чрезмерно усеченной расчетной области, включающей зону перестроения потока не полностью, граничные условия (1.6), (2.1), (2.2) негативно влияют на точность решения (профили 1, 2).

Выполненный сравнительный анализ численных расчетов с аналитическим решением подтверждает способность предложенной математической модели описывать движение гидродинамического потока в усеченной расчетной области.

Задача о движении потока за обратным уступом

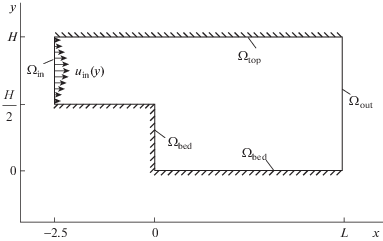
Для верификации предложенной математической модели на классе отрывных течений рассмотрим движение потока за обратным уступом. Расчетная область задачи приведена на фиг. 5. В область расширения поступает поток с профилем распределения скоростей ${{u}_{{{\text{in}}}}}$ и ${{v}_{{{\text{in}}}}}$ и градиентом давления ${{с }_{{{\text{in}}}}}$:

${{u}_{{{\text{in}}}}}(y) = \frac{1}{{2\eta \rho }}{{c}_{{{\text{in}}}}}y(y - H),\quad v_{{{\text{in}}}}^{{}} = 0,\quad {{с }_{{{\text{in}}}}} = - 12\frac{{\eta \rho Q}}{{{{H}^{3}}}},$

где $Q$ – расход жидкости, $H$ – глубина потока.

Фиг. 5.

Расчетная область задачи о течении за обратным уступом.

На верхней и нижней границах расчетной области устанавливаются условия прилипания

$u_{{{\text{bed}}}}^{{}} = u_{{{\text{top}}}}^{{}} = 0,\quad v_{{{\text{bed}}}}^{{}} = v_{{{\text{top}}}}^{{}} = 0.$

Для расчета использовались следующие параметры: $H = 2$ м, ${{U}_{0}} = 0.75$ м с^–1, $Q = 1$ м² с^–1, ${{\rho }_{w}} = 1000$ кг м^–3, $\operatorname{Re} = 100$, $\eta = 0.01$ м² с^–1, $T = 20$ с, $\Delta t = 2.5 \times {{10}^{{ - 3}}}$ с, $\Delta x = \Delta y = 0.025$ м, ${{\alpha }_{r}} = 5 \times {{10}^{{ - 3}}}$, $\sigma = 1.75 \times {{10}^{{ - 3}}}$ с, $\delta = 0.05$, ${{u}_{0}} = 0$, ${{v}_{0}} = 0$. Длина расчетной области L, достаточная для установления потока при вышеуказанных параметрах, равна 20 м (см. [13]). Численные эксперименты выполнялись в расчетных областях с различной длиной, равной 20, 10, 8, 6 и 5 м. Для оценки влияния граничных условий (1.6), (2.1), (2.2) на точность расчетов выполнено сравнение расчетных данных в вертикальном сечении $x = 5$ м и горизонтальном сечении $y = 1$ м во всех расчетных областях.

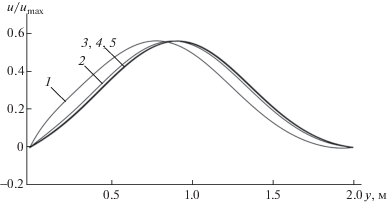
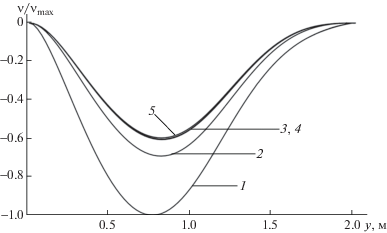
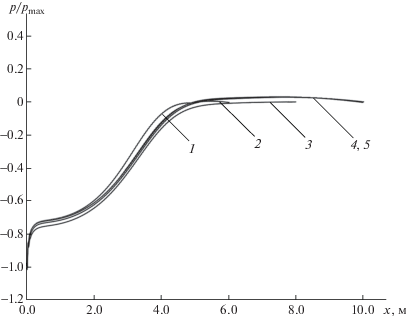
На фиг. 6–9 показаны профили изменения характеристик потока в безразмерном виде, для обезразмеривания использовались следующие величины: ${{u}_{{\max }}} = 1.75$м с^–1, ${{v}_{{\max }}} = 0.2$ м с^–1, ${{p}_{{\max }}} = 300$ кг м^–1 с^–1. Номера профилей указывают, при какой длине расчетной области они были получены: 1 – для 5 м, 2 – для 6 м, 3 – для 8 м, 4 – для 10 м, 5 – для 20 м. Профили 1–4, полученные в усеченных областях со граничными условиями (1.6), (2.1), (2.2) на выходной границе, сравнивались с профилем 5, полученным в 20-метровой области с граничными условиями установления на выходной границе

$\frac{{\partial u}}{{\partial x}} = 0,\quad \frac{{\partial v}}{{\partial x}} = 0,\quad p = 0,\quad \left( {x,y} \right) \in {{\Omega }_{{{\text{out}}}}}.$

Фиг. 6.

Графики горизонтальной скорости в вертикальном сечении $x = 5$ м.

Фиг. 7.

Графики вертикальной скорости в вертикальном сечении $x = 5$ м.

Фиг. 8.

Графики давления в вертикальном сечении $x = 5$ м.

Фиг. 9.

Графики давления в горизонтальном сечении $y = 1$ м.

Рассмотрим профили характеристик потока в вертикальном сечении $x = 5$ м, которые показаны на фиг. 6–8 . Профиль горизонтальной скорости 1, рассчитанный по граничным условиям (1.6), (2.2), имеет максимальное отклонение от профиля 5, достигающее 14.38%. Профили вертикальной скорости и давления 1, рассчитанные по граничным условиям (1.6), (2.1), (2.2), значительно отличаются от соответствующих расчетных профилей 5 на 40.01 и 18.57% соответственно. Профиль давления 1 на фиг. 8 практически является константой, близкой к нулю, что соответствует состоянию установления потока, однако поток в рассматриваемом сечении не является установившимся, и в более длинных областях в данном сечении профиль давления не является постоянной функцией. Более подробно значения максимальной относительной погрешности расчетных данных, полученных в сечении $x = 5$ м, представлены в табл. 2.

Таблица 2.

Максимальная относительная погрешность расчетов $\delta \left( f \right)$ в сечении $x = 5$ м в задаче о движении потока за обратным уступом и время расчета задачи

	L, м
	5 (профиль 1)	6 (профиль 2)	8 (профиль 3)	10 (профиль 4)
$\delta \left( u \right)$	14.38%	3.03%	0.10%	0.08%
$\delta \left( \text{v} \right)$	40.01%	8.45%	0.57%	0.37%
$\delta \left( p \right)$	18.57%	3.29%	0.07%	0.39%
Время расчета, с	6 889	7 870	10 599	12 354

На фиг. 9 показаны профили давления в горизонтальном сечении $y = 1$ м. На графике видно, что профили 3 и 4 совпадают с аналитическим профилем 5, следовательно, усечение области до 8 м не вызывает искажения поля давления. Усечение области до 5 м и 6 м приводит к искажению профилей 1 и 2 в зоне убывания давления. Из сравнения графиков можно сделать вывод, что чрезмерное усечение области до 5 м и 6 м сказывается падением точности расчета вертикальной скорости и давления, относительная погрешность достигает 40.01%. В области длиной 8 м и 10 м относительная погрешность скоростей и давления не превышает 0.57%.

Таким образом, предложенная математическая модель корректно описывает процесс движения потока Коважного и потока за обратным уступом в усеченной расчетной области при малых числах Рейнольдса $\operatorname{Re} \leqslant 100$.

Анализ полученных результатов показывает, что предложенная математическая постановка и алгоритм расчета позволяют с высокой степенью точности получать решение для задач гидродинамики при усечении расчетных областей. Как видно из табл. 1 и 2 , усечение расчетной области при сохранении требуемой расчетной точности позволяет существенно уменьшить вычислительные затраты.

Для выполнения расчетов были использованы вычислительные ресурсы ЦКП “Центр данных ДВО РАН” [17].

Список литературы

Orlanski I. A simple boundary condition for unbounded hyperbolic flows // J. Comput. Phys. 1976. V. 21. P. 251–269.
Hedstrom G.W. Nonreflecting boundary conditions for nonlinear hyperbolic systems // J. Comput. Phys. 1979. V. 30. P. 222–237.
Rudy D.H., Strikwerda J.C. A nonreflecting outflow boundary condition for subsonic Navier–Stokes calculations // J. Comput. Phys. 1980. V. 36. P. 55–70.
Papanastasiou T.C., Malamataris N., Ellwood K. A new outflow boundary condition // Int. J. Numer. Meth. Fl. 1992. V. 14. P. 587–608.
Braack M., Mucha P.B. Directional do-nothing condition for the Navier–Stokes equations // J. Comput. Math. 2014. V. 32. Is. 5. P. 507–521.
Dong S., Karniadakis E.G., Cryssostomidis C. A robust and accurate outflow boundary condition for incompressible flow simulations on severely-truncated unbounded domains // J. Comput. Phys. 2014. V. 261. P. 83–105. doi 10.1016/j.jcp.2013.12.042
Lombard J.-E.W., Moxey D., Hoessler J.F.A., Dhandapani S., Taylor M.J.T., Sherwin S.J. Implicit large-eddy simulation of a wingtip vortex // AIAA J. 2015. V. 54. Is. 2. P. 1–13.
Cantwella C.D., Moxeya D., Comerforda A., Bolisa A., Roccoa G., Mengaldoa G., de Graziaa D., Yakovlevb S., Lombarda J.-E., Ekelschota D., Jordia B., Xua H., Mohamieda Y., Eskilssonc C., Nelsonb B., Vosa P., Biottoa C., Kirbyb R.M., Sherwin S.J. Nektar++: An open-source spectral/element framework // CPC. 2015. 17 p.
Miron Ph., Vétel J. Towards the detection of moving separation in unsteady flows // J. Fluid Mech. 2015. V. 779. P. 819–841.
Fan P. The standard upwind compact difference schemes for incompressible flow simulations // J. Comput. Phys. 2016. V. 322. P. 74–112.
Garcia A.Q., Gomes A.A., Hecke M.B. On the performance of the DG method with a directional do-nothing boundary condition // J. Braz. Soc. Mech. Sci. & Eng. Technical paper. 2017. V. 39. Is. 10. P. 3919–3929.
Delorme Y.T., Puri K., Nordstrom J., Linders V., Dong S., Frankel S.H. A simple and efficient incompressible Navier–Stokes solver for unsteady complex geometry flows on truncated domains // Comput. Fluids. 2017. V. 150. P. 84–94.
Елизарова Т.Г. Квазигазодинамические уравнения и численные методы расчета вязких течений. М.: Научный мир, 2007, 352 с. URL: http://elizarova.imamod.ru/ (Английский перевод – Elizarova T.G. Quasi-Gas Dynamic equations. (Seria – Computational Fluid and Solid Mechanics) Ed. K. J. Bathe. Springer-Verlag Berlin Heidelberg, 2009, 286 p.)
Елизарова Т.Г. Осреднение по времени как приближенный способ построения квазигазодинамических и квазигидродинамических уравнений // Ж. вычисл. матем. и матем. физ. 2011. Т. 51. № 11. С. 2096–2105.
Снигур К.С. Математическое моделирование русловых процессов в каналах с песчано-гравийным основанием. Дис. канд. физ.-матем. наук. Хабаровск: ВЦ ДВО РАН, 2016.
Kovasznay L.I.G. Laminar flow behind a two-dimensional grid // Math. Proc. Cambridge. 1948. V. 44. Is. 1. P. 58–62.
Центр коллективного пользования “Центр данных ДВО РАН” [Электронный ресурс]: сайт. Хабаровск: ВЦ ДВО РАН. URL: http://lits.ccfebras.ru (дата обращения: 09.04.2018).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал