Журнал вычислительной математики и математической физики, 2019, T. 59, № 4, стр. 649-669

ВВЕДЕНИЕ

Условия реализации прямой звуковой линии (ПЗЛ) сначала в симметричных плоских соплах, а затем и в осесимметричных соплах кругового поперечного сечения были установлены Ф.И. Франклем [1] и Г. Гёртлером [2]. Эти условия сводятся к трем очевидным требованиям к набегающему потоку (однородность по энтропии и полной энтальпии, плоскопараллельность или отсутствие закрутки) и к равенству нулю первой производной по осевой координате x от продольной компоненты скорости на оси x в минимальном сечении сопла. Первыми серьезный вклад в исследование течений с обеих сторон от ПЗЛ внесли К. Гудерлей [3] и Л.В. Овсянников [4]–[6] и несколько позже – О.С. Рыжов [7]. В частности, согласно [3], [4] ПЗЛ ограничивают дозвуковые течения в критических струях. Прямолинейность звуковых линий в потенциальных плоскопараллельных и незакрученных осесимметричных течениях с числами Маха М ≤ 1 следует и из теоремы, доказанной в [8] (см. также [9]).

Важное свойство сопел с ПЗЛ – возможность раздельного рассмотрения и расчета течений в их сужающейся (дозвуковой) и расширяющейся (сверхзвуковой) частях. Это свойство широко используется при решении важных для приложений задач профилирования сверхзвуковых частей плоских и осесимметричных сопел, в первую очередь, – оптимальных контуров осесимметричных сопел ракетных двигателей, реализующих максимум тяги. Построение таких контуров осуществляется методом характеристик, современная реализация которого изложена в [10]. Однако отход от ПЗЛ в рамках метода характеристик невозможен. Поэтому в [11]–[16] Ю.Д. Шмыглевский с коллегами развили подходы, позволяющие рассчитывать сверхзвуковое течение вблизи звуковой линии и строить начальную характеристику требуемого семейства, а для кольцевых сопел – начальные характеристики обоих семейств. В [17] кроме течений, рассмотренных в [11]–[16], изучались сверхзвуковые течения, одна из границ которых – нормальная к ПЗЛ также звуковая линия тока, профилируемая в процессе расчета. Интерес к ограниченным звуковой линией тока сверхзвуковым течениям возник в связи с задачами оптимального профилирования [18]–[20], решения которых содержат отрезки звуковых линий тока. В [3]–[6] такое пересечение звуковых линий могло иметь место со стороны дозвукового потока, например, для истекающих в затопленное пространство критических струй. Подобные пересечения (на ПЗЛ – верхней и нижних границах дозвукового потока) возникают при натекании на клин звуковой струи конечной ширины [21], [22].

Ниже плоские и осесимметричные течения с обеих сторон от ПЗЛ изучаются в рамках единого подхода, который опирается на справедливые в рассматриваемой области универсальные уравнения околозвукового приближения, квадратичную для одной компоненты вектора скорости и кубичную для другой зависимость от продольной координаты и на интегрирование (в осесимметричном случае – численное) получающихся в результате обыкновенных дифференциальных уравнений. Околозвуковой расчет сверхзвукового потока завершается построением начальной характеристики (или характеристик разных семейств), пересчетом на газ с конкретными термодинамическими свойствами и началом расчета методом характеристик. Последний начинается с контрольного счета начальной характеристики. При в значительной степени систематизирующем и уточняющем характере данного исследования развитый подход содержит ряд новых моментов, прежде всего, связанных со сверхзвуковыми осесимметричными течениями, одна из границ которых – звуковая линия тока.

1. ИСХОДНЫЕ УРАВНЕНИЯ, УРАВНЕНИЯ ОКОЛОЗВУКОВОГО ПРИБЛИЖЕНИЯ И ИХ СЛЕДСТВИЯ

В рассматриваемых далее стационарных изоэнергетических и изэнтропических течениях идеального газа вектор его скорости V и скорость звука а отнесем к критической скорости. Поэтому для их критических значений (с индексом “звездочка”) имеем ${{V}_{*}} = \left| {{{{\mathbf{V}}}_{*}}} \right| = {{а }_{*}}$ = 1. Ось x декартовых координат xyz или цилиндрических xrφ направим по нормали к плоской звуковой поверхности в направлении потока. При этом параметры плоскопараллельного течения не будут зависеть от z, незакрученного осесимметричного – от φ, а плоские звуковые поверхности, представимые отрезками оси y или r, станут ПЗЛ. На них в силу выбора масштаба скорости х-компонента вектора V равна единице. Итак, если (1 + u) есть х-компонента V, а $\text{v}$ – его компонента, нормальная к оси х, то на ПЗЛ u = $\text{v}$ = 0. При принятых обозначениях установленное в [1], [2] условие реализации ПЗЛ в плоских симметричных и осесимметричных соплах состоит в выполнении на оси х в минимальном сечении таких сопел равенства

Неизвестные u и $\text{v}$ удовлетворяют двум уравнениям: равенству нулю нормальной к плоскости xy или xr компоненты rot V и следствию уравнения неразрывности, которое для плоскопараллельного  течения  в  принятых  обозначениях записывается в форме (а² – известная функция V, т.е. u и $\text{v}$) В силу изэнтропичности и изоэнергетичности течения коэффициент при дu/дх вблизи ПЗЛ равен σ²u. Множитель σ², вычисляемый при критических значениях давления р и плотности ρ, равен “фундаментальной производной”, определяемой равенством (ω = 1/ρ и s – удельные объем и энтропия газа) Последнее выражение справедливо для совершенного газа с постоянными теплоемкостями и их отношением (показателем адиабаты) – γ.

Уравнение (1.2) в околозвуковом приближении и условие безвихренности (в точной записи) принимают вид

Наконец, преобразование двух переменных приводит уравнения (1.3) к универсальной (одинаковой для газов с разными термодинамическими свойствами) околозвуковой форме

При ${{u}_{ \circ }} > 0$ течение сверхзвуковое, а описывающая его система уравнений (1.5) гиперболическая. Ее С^±-характеристики в плоскости $x{{y}_{ \circ }}$ определяются уравнениями

с верхним (нижним) знаком, отвечающим С⁺ (С^–)-характеристике.

Из решений с ПЗЛ, удовлетворяющих условию (1.1) и уравнениям (1.3) или (1.5) в [3]–[8], [11]–[17] основное внимание уделялось тем, для которых справедливы представления (символ V как модуль скорости далее оговаривается)

Подстановка (1.7) в (1.5) дает обыкновенные дифференциальные уравнения и их следствия

Проинтегрировав первое уравнение (1.9), придем к решениям (b – постоянная интегрирования)

Из изученных в [3]–[7] случаев для дальнейшего интересны решения с b ≠ 0, в которых после перехода к новым переменным различаются положительные и отрицательные b.

Положительные b отвечают сверхзвуковым течениям. При этом |b| = b и

Получающиеся отсюда для $U^\circ \gg 1$ асимптотические формулы справедливы со своими $y_{{\infty k}}^{ \circ }$ для всех рассмотренных ниже течений (для осесимметричных – с заменой y на r), а также без “градусов”. Они же при $U^\circ \to \infty $ описывают в околозвуковом приближении центрированные волны разрежения (или сжатия) в концевых точках отрезков плоских и осесимметричных ПЗЛ.

Если b < 0, то |b| = – b и

В этом решении в силу определения u и формул (1.4) и (1.10) отрицательным $ - 1 \leqslant U^\circ < 0$ отвечает дозвуковое течение, ограниченное сверху и снизу кривыми звуковыми линиями, которые подходят по нормали к ПЗЛ в точках х = 0, $y^\circ = \pm y_{0}^{ \circ }$. Такие пересечения имеют место в упоминавшихся выше критических струях. Первым значения $y_{{\infty 1}}^{ \circ }$, $y_{{\infty 2}}^{ \circ }$ и $y_{0}^{ \circ }$ и связи между ними установил Л.В. Овсянников [5] с привлечением двоякопериодической эллиптической функции Вейерштрасса. Здесь их значения определены численным интегрированием.

Форма звуковых линий тока (в частности, границ критических струй), на которых u = 0, определяется любым из двух эквивалентных уравнений

а интегрирование их приближенных версий, справедливых при малых х, дает

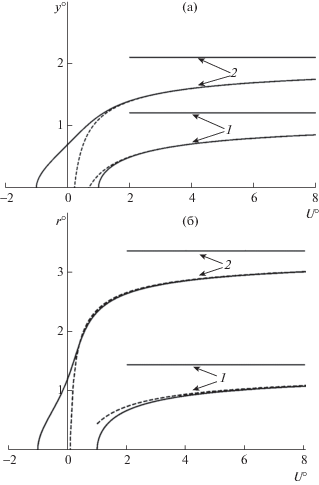
Положительные $U^\circ $, удовлетворяющие неравенствам: $0 < U^\circ \leqslant \infty $, описывают сверхзвуковые течения, заканчивающиеся центрированными волнами сжатия (при x < 0) или разрежения (при x > 0). Функции $y_{1}^{ \circ }(U^\circ )$ и $y_{2}^{ \circ }(U^\circ )$ с асимптотами $y_{{1,2}}^{ \circ } = y_{{\infty 1,2}}^{ \circ }$ представлены на фиг. 1а кривыми и горизонтальными отрезками, помеченными цифрами 1 и 2. Штриховые кривые рассчитаны по формулам из (1.12) с верхними знаками.

Разные знаки в приведенных выше формулах обычно интерпретируются как отвечающие положительным и отрицательным значениям ординаты y при положительных для решений (1.11) и отрицательных для решений (1.13) значениях х. На самом же деле все приведенные решения справедливы с обеих сторон от ПЗЛ. При отрицательных х формулы (1.11) описывают торможение сверхзвукового потока в сужающемся канале слева от ПЗЛ (газ течет слева направо). Наоборот, при положительных х формулы (1.13) описывают торможение дозвукового потока и разгон сверхзвукового.

Решения (1.11) и (1.13) допускают всевозможные комбинации. Так, объединение разгоняющихся течений (1.13) – дозвукового слева от ПЗЛ и сверхзвуковых справа от нее даст течение в симметричном относительно оси х сопле Лаваля с заостренным центральным телом, начинающимся на ПЗЛ. Очевидные симметрии решений: u(–x, y) = u(x, y), $\text{v}$(–x, y) = –$\text{v}$(x, y), справедливы не только в околозвуковом приближении, но и для решений описывающих плоскопараллельные и осесимметричные течения полных уравнений Эйлера в силу их инвариантности относительно изменения знаков координаты х и компоненты $\text{v}$ скорости газа. С другой стороны, с учетом указанной симметрии после перехода от отрицательных к положительным х нетрудно доказать невозможность изображенного в [23, с. 67] совместного течения в сужающемся канале разделенных звуковой линией тока тормозящегося сверхзвукового и разгоняющегося дозвукового потоков (см. разд. 4). Все высказанные здесь утверждения справедливы и для течений с осевой симметрией.

Для расчета методом характеристик примыкающих к ПЗЛ сверхзвуковых течений необходима начальная характеристика, построенная с привлечением решений (1.11) или (1.13), отвечающих положительным $U^\circ $. Покажем на примере начальной С^–-характеристики, как это делается.

Если b > 0, то для определения $x^\circ = x\sqrt b $ на начальной С^–-характеристике из (1.6) и (1.11) получим уравнение

с приближенным равенством для $U^\circ \gg 1$. Интегрирование при $U^\circ \gg 1$ дает решение которое с константой интегрирования $C \ll 1$ справедливо вблизи фокуса центрированной волны. При отходе от фокуса с помощью (1.16) дальнейшее построение начальной характеристики ведется численным интегрированием уравнения (1.15) до $U^\circ = 1$. В силу (1.15) и (1.16) зависимость $x^\circ $ и х от С линейная. Последнее справедливо и для течений с осевой симметрией.

Решение для b < 0 строится аналогично с заменой уравнения (1.15) на

и с по-прежнему справедливым решением (1.16). Интегрирование полного уравнения в этом случае возможно до $U^\circ = 1$, т.е. до звуковой линии тока, нормальной ПЗЛ.

Затем в согласии с равенствами (1.7) и (1.10) находятся

по формулам (1.4) осуществляется возвращение к y, y_∞k и u, а делением x и y на y_∞k нормируются переменные х и у. В переменных x, y, u и $\text{v}$ начальная характеристика готова для определения по конечным формулам прочих параметров потока и дальнейшего счета методом характеристик.

2. ПРОСТЕЙШИЕ ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ С ПРЯМОЙ ЗВУКОВОЙ ЛИНИЕЙ

Осесимметричные околозвуковые течения описывают аналоги уравнений (1.4)–(1.6)

и представлений (1.7) Подстановка этих выражений в (2.2) приводит к обыкновенным дифференциальным уравнениям

Так как на оси симметрии V = 0, то $V{\text{/}}{{r}_{ \circ }} \approx dV{\text{/}}d{{r}_{ \circ }}$ при малых ${{r}_{ \circ }}$ и система (2.5) вблизи оси симметрии сведется к уравнениям

и к их следствиям Интегрирование первого из них и подстановка во второе дают

Как и ранее, для дальнейшего интересны решения с b ≠ 0, для которых после перехода к переменным

интеграл и уравнение (2.6) принимают вид, зависящий от знака b.

Если b > 0, то |b| = b и, взяв в (2.6) с учетом положительности V и r знаки “плюс”, найдем, что у оси симметрии

Следовательно, $U^\circ \geqslant 1$, что в согласии с формулами (2.1) и (2.7) отвечает сверхзвуковому течению с разгоном (торможением) газа справа (слева) от ПЗЛ (по-прежнему газ течет слева направо).

При отходе с помощью (2.8) от оси симметрии, где $U^\circ = 1$, $V^\circ = r^\circ = 0$, дальнейший расчет ведется интегрированием до любого $U^\circ \leqslant \infty $ уравнений

являющихся следствиями уравнений (2.5), переписанных в переменных (2.7). Значению $U^\circ = \infty $ отвечает фокус центрированной волны разрежения (сжатия) справа (слева) от ПЗЛ. Для расчета параметров течения вблизи фокусов (при $U^\circ \gg 1$) привлекаются формулы (1.12) с верхними знаками и с заменой y на r. Найденная в результате величина $r_{{\infty 1}}^{ \circ } = {\text{1}}{\text{.44703}}$.

Если b < 0, то |b| = –b и для описания околозвукового потока у оси симметрии придем к уравнениям

Здесь $U^\circ \geqslant - 1$ с $U^\circ = - 1$ на оси симметрии, где $V^\circ = 0$. Поэтому при $0 \leqslant r^\circ < r_{0}^{ \circ } = r^\circ $ ($U^\circ = 0$) согласно формулам (2.1) и (2.7) к ПЗЛ могут примыкать дозвуковые потоки с разгоном (торможением) газа слева (справа) от нее. Положительным $0 < U^\circ \leqslant \infty $ и $r_{0}^{ \circ } < r^\circ \leqslant r_{{\infty 2}}^{ \circ }$ отвечают сверхзвуковые потоки с торможением (разгоном) газа слева (справа) от ПЗЛ. При отходе с помощью (2.10) от оси симметрии, где $U^\circ = - 1$, $V^\circ = r^\circ = 0$, дальнейший расчет ведется интегрированием до $U^\circ \gg 1$ уравнений (2.9).

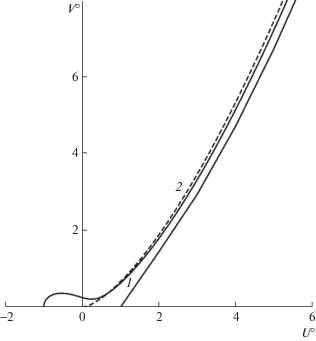
Значению $U^\circ = \infty $ по-прежнему отвечают центрированные волны разрежения или сжатия, для расчета параметров, вблизи которых привлекаются формулы (1.12) с верхними знаками и с заменой y на r. Найденные в результате величины $r_{0}^{ \circ } = 1.19262$, $r_{{\infty 2}}^{ \circ } = {\text{3}}{\text{.36664}}$. Функции $r_{1}^{ \circ }(U^\circ )$ и $r_{2}^{ \circ }(U^\circ )$ с асимптотами $r_{{1,2}}^{ \circ } = r_{{\infty 1,2}}^{ \circ }$, найденные для положительных и отрицательных b, представлены на фиг. 1б кривыми и горизонтальными отрезками, помеченными цифрами 1 и 2. Штриховые кривые рассчитаны по формулам из (1.12) с верхними знаками. Тот же смысл имеют сплошные и штриховые кривые $V_{k}^{ \circ } = V_{k}^{ \circ }(U^\circ )$ на фиг. 2.

Расчет начальной С^–-характеристики ведется аналогично плоскому случаю с заменами у на r, формул (1.4), (1.7) и (1.10) – на (2.1), (2.4) и (2.7), а уравнений (1.15) и (1.17) – на

и с сохранением решения (1.16) вблизи фокусов центрированных волн.

3. ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ С ПРЯМОЙ ЗВУКОВОЙ ЛИНИЕЙ В КАНАЛАХ С ЦЕНТРАЛЬНЫМ ТЕЛОМ

В отличие от разд. 2 в данном разделе рассматриваются течения в кольцевых каналах с центральным телом (ЦТ). ЦТ может быть цилиндрическим (${{r}_{ \circ }} = const$), сужающимся (при x > 0 – после излома на ПЗЛ) и расширяющимся (слева от ПЗЛ) с горизонтальной касательной при х = 0. Внешний контур канала может быть цилиндрическим, расширяющимся (справа от ПЗЛ) и сужающимся (слева от ПЗЛ). Как и ранее, возможны “отражения” (с изменением знаков x и $\text{v}$) перечисленных вариантов. Обтекаемые сверхзвуковым потоком звуковые ЦТ строятся в следующем разделе.

На цилиндрическом ЦТ $\text{v}$ = 0, а r = r_CB > 0. Поэтому вблизи ЦТ уравнения осесимметричного течения (2.2) и их следствия (2.5) можно заменить уравнениями плоскопараллельного течения (1.5) и их следствиями (1.8) с заменой y на r. В результате для течения в малой окрестности точки пересечения ПЗЛ с цилиндрическим ЦТ справедливы уравнения (1.9) и их следствия, получающиеся после замены переменных (2.7). В частности, теперь при b > 0 в указанной окрестности справедливы уравнения

Следовательно, $U^\circ \geqslant 1$, что в согласии с формулами (2.1) и (2.7) отвечает сверхзвуковому течению с разгоном (торможением) газа справа (слева) от ПЗЛ.

При отходе с помощью (3.1) от ЦТ, где $U^\circ = 1$, $V^\circ = 0$, $r^\circ = r_{{CB}}^{ \circ } > 0$, дальнейший расчет ведется интегрированием до любого $U^\circ \leqslant \infty $ уравнений (2.9). Значению $U^\circ = \infty $, как и ранее, отвечает центрированная волна разрежения (сжатия) справа (слева) от ПЗЛ. Для расчета параметров течения при $U^\circ \gg 1$ привлекаются формулы (1.12) с верхними знаками и с заменой y на r.

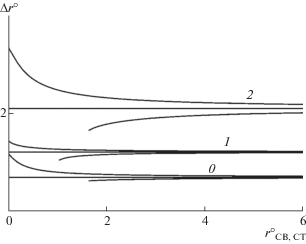
Найденная в результате расчетов зависимость $\Delta r_{{\infty 1}}^{ \circ } = r_{{\infty 1}}^{ \circ } - r_{{CB}}^{ \circ }$ от $r_{{CB}}^{ \circ }$, где $r_{{\infty 1}}^{ \circ }$ – радиус фокуса центрированной волны, представлена на фиг. 3 убывающей кривой 1. Для больших $r_{{CB}}^{ \circ }$ разность $\Delta r_{{\infty 1}}^{ \circ }$ стремится к “плоской” ординате: $y_{{\infty 1}}^{ \circ } = 1.21433$ (дана горизонтальной прямой).

При b < 0 околозвуковой поток вблизи ЦТ описывается уравнениями

Здесь $U^\circ \geqslant - 1$ с $U^\circ = - 1$ на ЦТ, где $V^\circ = 0$, а $r^\circ = r_{{CB}}^{ \circ }$. Поэтому при $r_{{CB}}^{ \circ } \leqslant r^\circ < r_{0}^{ \circ } = r^\circ $ ($U^\circ = 0$) согласно формулам (2.1) и (2.7) к ПЗЛ могут примыкать дозвуковые потоки с разгоном (торможением) газа слева (справа) от нее. Положительным $0 < U^\circ \leqslant \infty $ и $r_{0}^{ \circ } < r^\circ \leqslant r_{{\infty 2}}^{ \circ }$ отвечают сверхзвуковые потоки с торможением (разгоном) газа слева (справа) от ПЗЛ.

При отходе с помощью (3.2) от ЦТ, на котором $U^\circ = - 1$, $V^\circ = 0$, $r^\circ = r_{{CB}}^{ \circ }$, дальнейший расчет ведется интегрированием до $U^\circ \gg 1$ уравнений (2.9). Рассчитанные зависимости разностей $\Delta r_{0}^{ \circ } = r_{0}^{ \circ } - r_{{CB}}^{ \circ }$ и $\Delta r_{{\infty 2}}^{ \circ } = r_{{\infty 2}}^{ \circ } - r_{{CB}}^{ \circ }$ от радиуса ЦТ $r_{{CB}}^{ \circ }$ дают на фиг. 3 убывающие кривые 0 и 2. Для больших $r_{{CB}}^{ \circ }$ разности $\Delta r_{0}^{ \circ }$ и $\Delta r_{{\infty 2}}^{ \circ }$ стремятся к своим “плоским” величинам: $y_{0}^{ \circ } = 0.70109$ и $y_{{\infty 2}}^{ \circ } = 2.10327$.

Околозвуковое течение с ПЗЛ в кольцевом канале с цилиндрическим внешним контуром (“цилиндрической трубой”, индекс “CT”) и нецилиндрическим ЦТ рассматривается аналогичным образом. Главные отличия – знак “минус” перед правыми частями всех уравнений (3.1) и (3.2). Это связано с изменением знака радиальной компоненты скорости и с тем, что указанные уравнения справедливы вблизи цилиндрической трубы, т.е. при максимальной величине радиальной координаты $r^\circ = r_{{CT}}^{ \circ }$, а не минимальной, как для цилиндрического ЦТ.

Результаты расчетов для ПЗЛ, ограниченных сверху цилиндрическими трубами разных радиусов $r^\circ = r_{{CT}}^{ \circ }$, представлены на фиг. 3 возрастающими кривыми 0–2 с прежними асимптотами. Если с ростом $r_{{CB}}^{ \circ }$ и $r_{{CT}}^{ \circ }$ построенные кривые ведут себя одинаково, то с уменьшением радиусов ЦТ и трубы имеют место принципиальные отличия. Радиус цилиндрического ЦТ можно уменьшить до нуля, придя к задачам предыдущего раздела. В противоположность этому в задачах с цилиндрической трубой ее радиус и радиусы нецилиндрических ЦТ $r_{{\infty 1}}^{ \circ }$ и $r_{{\infty 2}}^{ \circ }$ ограничены снизу малыми, но отличными от нуля величинами. Созданная для их определения численная процедура и полученные с ее помощью результаты описаны ниже.

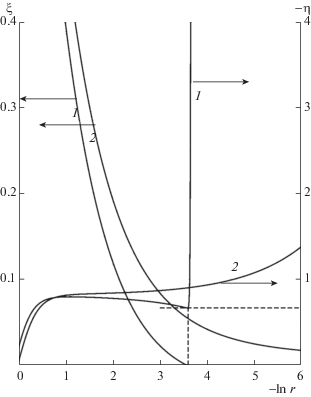
Начнем с того, что для определения с высокой точностью малых $r_{{\infty 1}}^{ \circ }$ и $r_{{\infty 2}}^{ \circ }$ интегрирование уравнений (2.9) до $U^\circ \gg 1$ с привлечением формул (1.12) было заменено интегрированием их следствий – уравнений

до сколь угодно малых $r^\circ > 0$.

Поведение интегральных кривых уравнений (3.3) зависит от значений $r_{{CT}}^{ \circ }$. Пока $r_{{CT}}^{ \circ }$ больше некоторой величины, их интегральные кривые при $r^\circ \to r_{\infty }^{ \circ } > 0$ входят в точку, в которой согласно асимптотическим формулам (1.12) ξ = 0, а η = –2/3. Можно показать, что вблизи нее без ограничений на величину $r_{\infty }^{ \circ }$

Решение (3.4) и приведенные на фиг. 4 результаты численного интегрирования – свидетельства того, что $r_{\infty }^{ \circ } > 0$. Кривые 1 и 2 на фиг. 4 получены интегрированием уравнений (3.3) для $r_{{CT}}^{ \circ } = 1.1$ и $r_{{CT}}^{ \circ } = 1.02$ соответственно. Кривые 1 приходят в точку ξ = 0, η = –2/3, а кривые 2 в нее не приходят (на штриховой горизонтали η = –2/3, штриховая вертикаль соединяет точки кривых 1 с ξ = 0 и η = –2/3). Пара и тройка найденных минимальных радиусов оказались такими:

При столь малом $r_{{\infty 1}}^{ \circ }$ возможный излом на ЦТ еще на порядок меньше. Только в этом случае реализующийся за изломом сверхзвуковой поток за счет профилирования ЦТ сможет принять на оси симметрии горизонтальное направление. При малой (порядка $r_{{\infty 1}}^{ \circ }$) длине ЦТ это невозможно в силу известных свойств локально конических течений [24].

Последняя задача данного раздела отвечает кольцевым каналам, ПЗЛ которых могут заканчиваться нижней (на нецилиндрическом ЦТ) и верхней (на нецилиндрической трубе) точками излома. Скорости $\text{v}$ в этих точках разных знаков. Поэтому в некоторой точке ПЗЛ $V^\circ = V^\circ (r_{0}^{ \circ }) = 0$. С задания радиуса $r_{0}^{ \circ }$ точки, в которой $V^\circ (r_{0}^{ \circ }) = 0$, а $U^\circ (r_{0}^{ \circ }) = 1$, начинается решение рассматриваемой задачи. Затем привлекаются две уже решенные задачи: одна с $r_{{CB}}^{ \circ } = r_{0}^{ \circ }$, другая с $r_{{CT}}^{ \circ } = r_{0}^{ \circ }$. Найденные в результате $U^\circ ({{r}^{ \circ }})$ и $V^\circ ({{r}^{ \circ }})$ позволяют построить начальные С⁺- и С^–-характеристики для дальнейшего продолжения расчета сверхзвукового течения методом характеристик.

4. ТЕЧЕНИЯ С ПРЯМОЙ ЗВУКОВОЙ ЛИНИЕЙ И НОРМАЛЬНЫМИ К НЕЙ ЗВУКОВЫМИ ЛИНИЯМИ ТОКА

Первая цель данного раздела – сравнение нескольких звуковых линий тока, нормальных ПЗЛ. Первые три из них – границы плоских критических струй, истекающих из симметричного полубесконечного насадка, образованного парой горизонтальных и наклонных стенок. Схема верхней половины насадка и струи изображена на фиг. 5а. В дополнение справа от оси у, отрезок которой – ПЗЛ, нарисован симметричный участок тормозящейся дозвуковой струи, а над ней – сверхзвуковая волна разрежения с фокусом в точке х = 0, у = у_∞2 = 3у₀. Величину у₀ возьмем за линейный масштаб задачи. Тогда для звуковых линий тока, выходящих из точки х = 0, у = у₀ = 1, в силу решения (1.14) при малых х имеем

Следовательно, у звуковых линий тока дозвукового течения снизу и сверхзвукового течения сверху на ПЗЛ совпадают только четыре производные по х.

Отличие производных более высоких порядков – естественный результат разных задач, определяющих истечение критической струи и течение газа в центрированной волне. Истечение критической струи описывается решением краевой задачи для функции тока ψ, определяемой уравнением Чаплыгина [10]

Здесь, в отличие от большей части формул предыдущих разделов, V – модуль вектора скорости (отнесенный к критической скорости ${{V}_{*}} = {{a}_{*}}$), θ – угол его наклона к оси х, а М = М(V) – число Маха. Постановку граничных условий для уравнения (4.2) поясняет фиг. 5б с теми же точками a, b, e и f, что на фиг. 5а. Особым точкам e и f плоскости переменных V и θ в плоскости ху отвечают отрезок ПЗЛ (х = 0, V = 1, θ = 0) и сечение входа (х = – ∞, 0 ≤ у ≤ у_а V = V_f < 1, θ = 0). Вместо ординаты у_а удобнее задавать скорость V_f. Сплошные кривые на фиг. 5б – линии тока, приходящие из точки f в точку е.

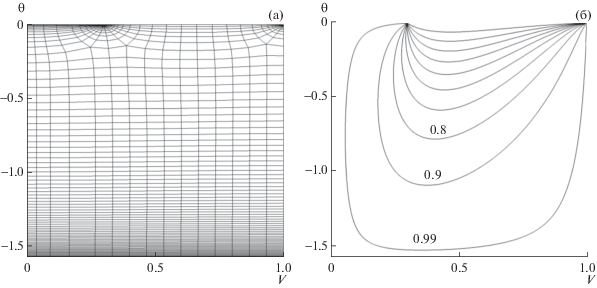
Численное решение краевой задачи для уравнения (4.2) с граничными условиями, поставленными на фиг. 5б, велось на разностной сетке, адаптированной к особенностям течения в точках e и f. Пример самой грубой сетки с числом точек N = 1920 приведен на фиг. 6а. Вблизи точек e и f функция тока задавалась на дугах окружностей радиуса δ = 10^–3 по известным формулам, справедливым вблизи этих точек [10], [25]. Кстати, из формул для течения вблизи точки е без решения краевой задачи следует равенство (4.1) с одной для разных насадок константой С. Разностная аппроксимация уравнения (4.2) проводилась на 9-ти точечном шаблоне с наилучшей среднеквадратичной аппроксимацией приращений ψ как квадратичных многочленов приращений V и θ. Получающаяся в результате линейная система уравнений для определения ψ во всех внутренних точках расчетной области решалась методом Гаусса–Зейделя. Расчеты в приводимых ниже примерах выполнены для совершенного газа с γ = 7/5.

Изолинии ψ = 0.1, 0.2, …, 0.9 и 0.99, рассчитанные для V_f = 0.3 и θ_b = –π/2 на мелкой сетке (N = 4.7 × 10⁵), приведены на фиг. 6б. По найденным вместе с функцией тока ее производным ψ_V и ψ_θ рассчитываются х и у, включая координаты границы критической струи – звуковой линии тока be. Построенные на мелких сетках для V_f = 0.3, θ_b = –0.5, –π/4, –π/2 три такие линии тока ниже сравниваются со звуковой линией тока сверхзвукового течения, для которой, как и для этих трех, справедливо уравнение (4.1) с единой константой С.

Расчет примыкающей к ПЗЛ справа центрированной волны разрежения с фокусом в точке х = 0, у = 3у₀ = 3 начинается с решения (1.13) со знаком “плюс” и 0 < $U^\circ $ ≤ ∞ и продолжается построением начальной С^–-характеристики интегрированием уравнения (1.17) с привлечением решения (1.16). При известной начальной С^–-характеристике расчет методом характеристик каждой следующей С^–-характеристики ведется сверху вниз: от новой по параметрам газа точки фокуса до точки линии тока. Последняя рассчитывается с привлечением уравнений: линии тока, С^–-характеристики с условием совместности для нее, и условия р = ${{р }_{*}}$ на звуковой линии тока. Для совершенного газа при критической плотности ${{\rho }_{*}}$ и ${{\rho }_{ * }}a_{ * }^{2}$, взятых за масштабы плотности и давления, ${{р }_{*}}$ = 1/γ.

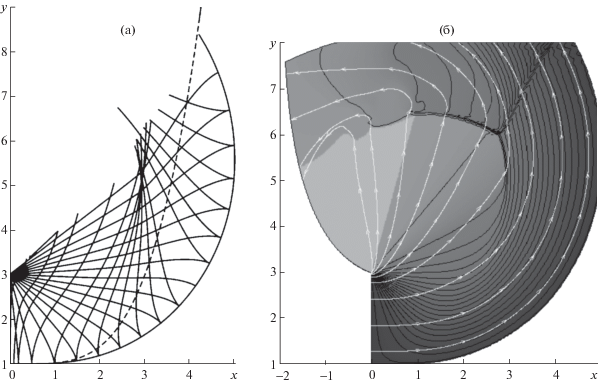
Результаты описанного расчета – построенная звуковая линия тока и многократно разреженная сетка характеристик представлены на фиг. 7а. Штриховая кривая – звуковая линия тока, определенная приближенным решением (4.1). Авторская программа метода характеристик не строит висячих скачков, возникающих из-за пересечения одноименных характеристик, однако сам факт таких пересечений устанавливается достоверно. Более того, некоторое время удается продолжать счет с построением зон неоднозначности. Подобная зона пересечения С⁺-характеристик видна и на фиг. 7а. Ее наличие, однако, может сказаться лишь на малой (правой-верхней) части рассчитанного течения, не влияя на интересную для дальнейшего сравнения его нижнюю часть. На фиг. 8а и б приведены кривые р = р(у) и θ = θ(у), дающие р и θ на С^–-характеристиках фиг. 7а. Каждая кривая начинается на вертикали у = 3 и заканчивается на звуковой линии тока, где р = ${{р }_{*}}$ = 5/7. Наличие на части этих кривых участков, близких к вертикальным, подтверждает сказанное выше о пересечениях характеристик и образовании висячего скачка.

Более полную информацию о сверхзвуковом течении в построенном плоском канале с нижней стенкой – звуковой линией тока дает численное интегрирование полных уравнений Эйлера установлением по времени со сквозным счетом возникающих разрывов. Возможности такого подхода демонстрирует фиг. 7б с результатами расчета по монотонной разностной схеме Годунова–Колгана [26] на адаптированной к особенностям течения разностной сетке с общим числом ячеек N ≈ 2.3 × 10⁵. На внешних (в основном верхних) границах расчетной области заданием параметров (прежде всего – почти нулевого давления) в присоединенном слое ячеек реализовывалось сверхзвуковое истечение. Представление о течении дает 21 черная изобара (с р от 0.01 до 0.71 с шагом 0.035) и светлые линии тока. В рассчитанном течении самостоятельный интерес представляет расщепление висячего скачка.

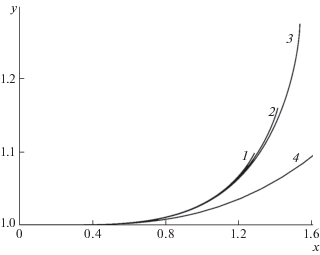
Сравнение звуковых линий тока, намеченное в начале раздела, представлено на фиг. 9. На ней в большом масштабе показаны отражения относительно оси у трех рассчитанных для разных θ_b границ критических струй (кривые 1–3 для θ_b = –0.5, –π/4, –π/2) и начальный участок звуковой линии тока сверхзвукового течения разрежения (кривая 4). Будучи в согласии со сказанным выше сначала практически неразличимыми, построенные кривые расслаиваются с ростом х, причем так, что кривая 4 оказывается ниже границ любой из трех критических струй. Результаты дальнейшего измельчения разностных и характеристических сеток в масштабе фиг. 9 незаметны.

Фиг. 9 – дополнительное к сказанному в конце разд. 1 подтверждение правильности утверждения о невозможности примыкающих к ПЗЛ дозвукового и сверхзвукового плоскопараллельных течений, разделенных звуковой линией тока. После этого правильность такого же утверждения для осесимметричных течений очевидна. Сказанное не исключает принципиальной допустимости звуковой линии, которая, отличаясь от линии тока, касалась бы ее при пересечении с ПЗЛ. Пример такого течения получен в [27] при численном решении обратной задачи о смешанном течении в осесимметричном сопле Лаваля. Некорректность обратной задачи и нестыковки в изложении расчетных и экспериментальных результатов [27] в [28], [29] требуют дополнительного изучения.

Переход к осесимметричным звуковым линиям тока, уходящим с ПЗЛ (приходящие получаются изменением знаков х и $\text{v}$), начнем с $r_{0}^{ \circ } > 0$ точки ПЗЛ, из которой выходит такая линия тока. В ней для вводимых по-прежнему равенствами (2.4) функций U и V имеем U₀ = 0, |V₀| > 0. При b = |V₀|^2/3 в формулах (2.7) получим уравнения (2.9) и начальные условия

Здесь знак “плюс” (“минус”) отвечает звуковой линии тока – внутреннему (внешнему) контуру кольцевого сопла. Численное решение задачи (4.3) начинается с задания $r_{0}^{ \circ }$ и ведется до $U^\circ \gg 1$. Значения $r_{\infty }^{ \circ }$ определяются по формулам (1.12) с r вместо y, а построение начальной С^–- или С⁺-характеристики и счет методом характеристик не отличаются от описанных выше.

Вблизи звуковой линии тока, где $U^\circ \ll 1$, уравнения (4.3) упрощаются

и интегрируются Подставив решение для $V^\circ $ в уравнение звуковой линии тока, сведем его к виду и проинтегрируем

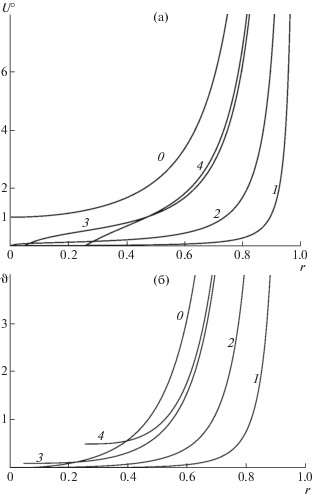
Результаты расчета течений со звуковыми ЦТ, построенными для разных $r_{0}^{ \circ }$, приведены на фиг. 10 и 11. На фиг. 10а и 10б зависимости $U^\circ $ и $\vartheta \equiv r^\circ V^\circ $ от $r = r^\circ {\text{/}}r_{\infty }^{ \circ }$ для $r_{0}^{ \circ }$ = 10^–3, 10^–2, 0.1 и 0.5 дают кривые 1–4, а для осесимметричного сопла с ПЗЛ без ЦТ – кривые 0. Сплошные кривые 1–4 на фиг. 11 – контуры звуковых ЦТ для перечисленных $r_{0}^{ \circ }$ в координатах $x = x^\circ {\text{/}}r_{\infty }^{ \circ }$, $r = r^\circ {\text{/}}r_{\infty }^{ \circ }$. В масштабе фиг. 11 сплошные кривые 1 и 2 совпадают. Штриховые кривые 1–4 определены формулой (4.5), справедливой при $x \ll 1$ и таких, что ее вторые слагаемые меньше первых. Правильность последнего утверждения подтверждает сравнение сплошных и штриховых кривых с одинаковыми номерами. К расчету методом характеристик формула (4.5) не привлекалась.

Для ЦТ 4 вместе с его контуром приведена многократно разреженная сетка С^–-характеристик. Во всех рассчитанных примерах С⁺-характеристики, как и в плоском случае, с удалением от ПЗЛ пересекаются. Возникающие из-за этого ударные волны – свидетельство невозможности реализации примыкающих к ПЗЛ слева сверхзвуковых течений со столь же интенсивными центрированными волнами сжатия.

Совпадение построенных для $r_{0}^{ \circ } = {{10}^{{ - 3}}}$ и 10^–2 сплошных кривых 1 и 2 на фиг. 11 позволяет рассчитывать на их близость к контуру звукового ЦТ, начинающегося на оси x. Для проверки этого предположения построим остроконечное (с $r_{0}^{ \circ } = 0$) звуковое ЦТ, для которого решение (4.4) теряет смысл. Вблизи ПЗЛ и ЦТ “внутреннее” решение уравнений (2.2) будем искать в форме

с пока неизвестными n и m и функцией ${{r}_{{ \circ CB}}}(x)$, дающей контур ЦТ: ${{r}_{ \circ }} = {{r}_{{ \circ CB}}}(x)$.

На ЦТ – звуковой линии тока ζ = 1, а U ⁱ(1) = 0. С учетом этого подстановка формул для u и $\text{v}$ из (4.6) в уравнение линии тока

и его интегрирование при начальном условии: ${{r}_{ \circ }}(0) = {{r}_{{ \circ CB}}}(0) = 0$ дают

Подстановка (4.6) и (4.7) в уравнения (2.2) приводит к уравнениям

При n ≠ 1 из второго уравнения получаются два. Решение одного из них U ⁱ ≡ U ⁱ(1) = 0. Как следствие, из двух оставшихся имеем V  ⁱ ≡ 0, что дает звуковой поток в цилиндрической трубе с ЦТ – осью x. Поэтому n = 1 и полученные уравнения принимают вид Их единственное решение, удовлетворяющее условию Uⁱ(1) = 0 на звуковом ЦТ, как и для n ≠ 1, тривиальное: U ⁱ ≡ V  ⁱ ≡ 0. Нетривиальное решение получается, если, учтя малость U ⁱ и х⁴ вблизи ПЗЛ и острия ЦТ, пренебречь слагаемым с kx⁴U ⁱ. Проинтегрировав получившиеся в результате уравнения, найдем

Подстановка выражений (4.6) с n = 1, m = 2 и U ⁱ из (4.8) в уравнение (2.3) со знаком “–” дает уравнения для xⁱ(ζ) и $r_{ \circ }^{i}$(ζ) на начальной С^–-характеристике:

“Внешний” отрезок начальной С^–-характеристики, как и ранее, строится с помощью функций $U({{r}_{ \circ }})$ и $V({{r}_{ \circ }})$, удовлетворяющих уравнениям (2.5):

Внутреннее решение зависит от двух констант x₁ и k, из которых ${{x}_{1}} \ll 1$ определяет близость начальной С^–-характеристики к ПЗЛ. От них же зависит и внешнее решение – непрерывное продолжение внутреннего, однако переходы

сохраняя уравнения (4.10), заменяют константу k в (4.8) и (4.9) на единицу.

В точке переключения при ${{r}_{ \circ }} = {{r}_{{ \circ i/e}}}$ с внутреннего решения (“i”) на внешнее (“e”), во-первых, нужно обеспечить непрерывность ${{u}_{ \circ }}$, $\text{v}$ и х. С учетом определений (2.2) и (4.6), решения (4.8) и k = 1 это даст

Во-вторых, на начальной С^–-характеристике должны быть непрерывны производные от ${{u}_{ \circ }}$, $\text{v}$ и х по ${{r}_{ \circ }}$. Непрерывность dx/d${{r}_{ \circ }}$ – следствие непрерывности ${{u}_{ \circ }}$ и х. Условия непрерывности производных ${{u}_{ \circ }}$ и $\text{v}$ получаются приравниванием при ${{r}_{ \circ }} = {{r}_{{ \circ i/e}}}$ их внешних и внутренних значений, найденных в рамках (4.8)–(4.11) с k = 1. Проделав необходимые выкладки, придем к равенствам Для х₁ > 0 их выполнение возможно лишь при ζ = 1. Таким образом, в согласии с (4.11) роль внутреннего решения свелась к получению начальных условий для интегрирования уравнений (4.9). Существенно то, что теперь при ${{r}_{ \circ }} = 0$ в передней точке ЦТ (на ПЗЛ) ${{r}_{{ \circ 1}}} > 0$, а V₁ велико, но конечно.

Расчет начальной С^–-характеристики начинается с задания ${{r}_{{ \circ 1}}} \ll 1$ и заканчивается переходом от ${{u}_{ \circ }}$ к u и к координатам x и r, отнесенным к радиусу лежащего на ПЗЛ фокуса центрированной волны разрежения. Расчет методом характеристик волны разрежения с фокусом в точке х = 0, r = 1 с дальнейшим построением контура звукового ЦТ ведется аналогично уже рассмотренным случаям. Обнаруженная в [17] расходимость итераций при расчете точек на ЦТ и вблизи него устраняется предложенной там же заменой θ на ϑ = rθ.

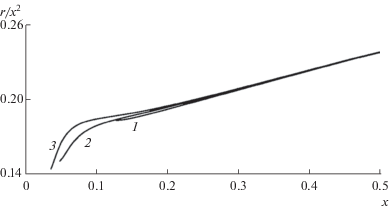
Результаты расчетов представлены на фиг. 12–14. Фиг. 12 дает отношения r/x² на звуковых ЦТ, построенных для ${{r}_{{ \circ 1}}}$= 10^–3 (1), 10^–4 (2) и 5 × 10^–5 (3). Кривые 1–3 различаются лишь вблизи начальных точек, где значения r так малы, что контуры ЦТ неразличимы с самого начала. В переменных x, r в уравнении контура ЦТ вновь появляется k: r = kx². Согласно расчетам, k зависит от выбора ${{r}_{{ \circ 1}}}$, медленно убывая с уменьшением ${{r}_{{ \circ 1}}}$:

Данные результаты расчетов, несмотря на явное замедление убывания k, не позволяют найти предел k при ${{r}_{{ \circ 1}}} \to 0$. Это, правда, в свете поведения кривых фиг. 12 непринципиально.

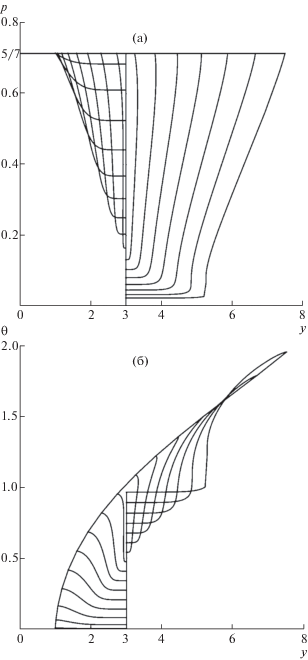
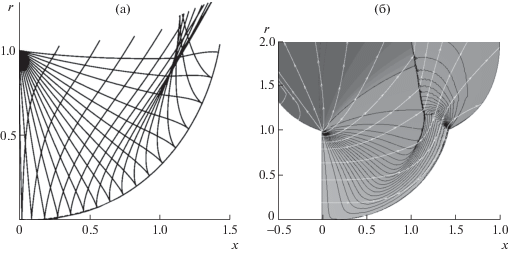
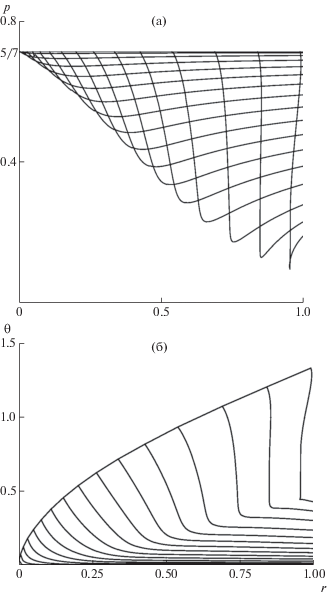
Контур звукового ЦТ и многократно разреженная сетка характеристик даны на фиг. 13а. При трехкратном отличии приведенных значений k, отвечающие им сплошные контуры в масштабе фиг. 11 и 13а неразличимы и друг от друга, и от кривой 1, 2 фиг. 11, подтверждая сделанное выше предположение. На фиг. 14а и 14б приведены кривые р = р(r) и θ = θ(r), дающие р и θ на С^–-характеристиках фиг. 13а. Все они начинаются на вертикали r = 1 и заканчиваются на звуковом ЦТ (р = 1/γ = 5/7).

На фиг. 13а С⁺-характеристики, как и ранее, пересекаются, и более полную информацию о течении в построенном осесимметричном канале дает численное интегрирование полных уравнений Эйлера на адаптированной к особенностям течения сетке со сквозным счетом разрывов. Результаты такого расчета по той же разностной схеме [26], что в плоском случае, с числом ячеек N ≈ 4.5 × 10⁴ представлены на фиг. 13б. На внешних границах расчетной области заданием почти нулевого давления в присоединенном слое ячеек реализовывалось сверхзвуковое истечение. Представление о течении дают 14 черных изобар (с p от 0.05 до 0.7 с шагом 0.05) и светлые линии тока.

ЗАКЛЮЧЕНИЕ

Прямая звуковая линия – один из интереснейших предметов изучения классической теоретической газовой динамики. В таком качестве результаты выполненного исследования представляются наиболее полными из всего, что было получено ранее, прежде всего в осесимметричном случае. К принципиально новым результатам можно отнести построение примыкающих к прямой звуковой линии сверхзвуковых течений, одна из границ которых – звуковая линия тока. Из них особенно интересно реализующееся при обтекании остроконечного звукового центрального тела, начинающегося на оси симметрии. Успех выполненного исследования обеспечило сочетание аналитических подходов с численными методами, включающими не только решение обыкновенных дифференциальных уравнений и метод характеристик, но и решение краевой задачи для уравнения Чаплыгина и построение решений полной системы уравнений Эйлера с установлением по времени и сквозным счетом разрывов.

Авторы благодарны Х.Ф. Валиеву за помощь в работе и К.С. Пьянкову за программу расчета критических струй.