Журнал вычислительной математики и математической физики, 2019, T. 59, № 4, стр. 549-565

ВВЕДЕНИЕ

В работах [1], [2] говорилось о проблемах, возникающих при численном решении дифференциально-алгебраических систем уравнений в частных производных, имеющих индекс выше единицы. Под индексом системы в алгебраическом смысле понимается максимальная в области определения степень элементарных делителей, соответствующих нулевым и бесконечным корням характеристического многочлена матричного пучка, построенного по коэффициентам дифференциально-алгебраической системы. Напомним, что при численном решении линейных дифференциально-алгебраических систем уравнений в частных производных частного вида классическими методами возникают “пограничные слои ошибок”, а при решении линейных систем общего вида или более того квазилинейных систем дифференциально-алгебраических уравнений в частных производных, применение классических методов вовсе невозможно. С целью решения этих проблем в [3] для численного решения линейных систем высокого индекса был предложен итерационный алгоритм. Он состоит в следующем. Коэффициенты системы специальным образом расщепляются, а затем к расщепленной системе применяется метод последовательных приближений. Возникающая на каждом итерационном шаге начально-краевая задача аппроксимируется устойчивой неявной сплайн-коллокационной разностной схемой [4]. Построенная таким образом неявная итерационная сплайн-коллокационная разностная схема является эффективной при определенных условиях и применяется для численного решения линейных систем. При ее реализации “пограничные слои ошибок” отсутствуют. Применить этот подход для численного решения квазилинейных дифференциально-алгебраических систем высокого индекса не представляется возможным, потому что подстановка числового ряда вместо искомой функции в коэффициенты квазилинейной системы не эффективна. В настоящей работе предлагается новый алгоритм, который также основан на расщеплении матричного пучка системы и полностью решает проблему численного решения квазилинейных дифференциально-алгебраических уравнений в частных производных индекса $(k,0)$. Предлагаемый алгоритм состоит в следующем. Выполняется расщепление матричного пучка, построенного по коэффициентам дифференциально-алгебраической системы, на два пучка: один из них имеет только простые элементарные делители, соответствующие нулевым и бесконечным корням характеристического многочлена, а другой не имеет регулярного ядра. В соответствующей расщепленной системе производные, относящиеся к регулярному пучку, аппроксимируются сплайном произвольного порядка, а производные, относящиеся к сингулярному пучку аппроксимируются сплайном меньшего порядка по каждой переменной. В результате строится нелинейная разностная схема, для решения которой применяется итерационный метод. Такая разностная схема в настоящей работе называется сплайн-коллокационной разностной схемой с расщепленным пучком. Она является достаточно эффективной и дает высокую точность во всей области решения.

Цель настоящей работы состоит в построении сплайн-коллокационной разностной схемы с расщепленным пучком, доказательстве существования ее решения и обосновании ее устойчивости.

Работа состоит из трех разделов. В первом разделе записана начально-краевая задача для квазилинейной дифференциально-алгебраической системы уравнений в частных производных. Во втором разделе построена сплайн-коллокационная разностная схема с расщепленным матричным пучком. В этом же разделе разностная схема записана в нормальной форме матрично-операторного уравнения. В третьем разделе доказана основная теорема о существовании решения разностной схемы и ее устойчивости. В четвертом разделе на одном тестовом примере с известным точным решением продемонстрирована эффективность предложенного в работе численного алгоритма. Работа снабжена необходимым списком цитируемой литературы.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим квазилинейную дифференциально-алгебраическую систему уравнений в частных производных следующего вида:

в которой $A(x,t,u)$ и $B(x,t,u)$ – заданные квадратные матрицы порядка $n$ тождественно-вырожденные во всей области определения, то есть $detA(x,t,u) = 0$ и $detB(x,t,u) = 0$ $\forall (x,t,u) \in \mathcal{U}$, где $\mathcal{U} = \{ (x,t,u)\,{\text{|}}\,(x,t) \in U,\;{{\left\| {u(x,t)} \right\|}_{{C(U)}}} < \mathcal{Q}\} $, $\mathcal{Q}$ – некоторая постоянная величина, $U = \{ (x,t)\,|\,x \in [{{x}_{0}};X],$ $t \in [{{t}_{0}};T]\} $; $F(x,t,u)$ – заданная $n$-мерная вектор-функция; $u \equiv u(x,t)$ – искомая $n$-мерная вектор-функция. Предполагается, что элементы матриц $A(x,t,u)$, $B(x,t,u)$ и вектора $F(x,t,u)$ принадлежат пространству ${{C}^{1}}(\mathcal{U})$.

Пусть для системы (2) заданы начально-краевые условия

где $\psi (t)$ и $\phi (x)$ – известные $n$-мерные вектор-функции, для которых в точке $({{x}_{0}},{{t}_{0}})$ выполнены условия согласования: $\psi ({{t}_{0}}) = \phi ({{x}_{0}})$, $\psi {\kern 1pt} '({{t}_{0}}) = \phi {\kern 1pt} '({{x}_{0}})$, $A({{x}_{0}},{{t}_{0}},u({{x}_{0}},{{t}_{0}}))\psi {\kern 1pt} '({{t}_{0}}) + B({{x}_{0}},{{t}_{0}},u({{x}_{0}},{{t}_{0}}))\phi {\kern 1pt} '({{x}_{0}})$ = = $F({{x}_{0}},{{t}_{0}},u({{x}_{0}},{{t}_{0}}))$.

Отметим, что если в каждой точке области $\mathcal{U}$ пучок матриц $\mathcal{P}(\lambda ,x,t,u) = A(x,t,u) + \lambda B(x,t,u)$, построенный по коэффициентам системы (1), является регулярным, то его индекс или индекс системы (1) определяется парой чисел $(k,0)$, где $k$ – максимальная степень элементарных делителей пучка $\mathcal{P}(\lambda ,x,t,u)$, соответствующих нулевым и бесконечным корням характеристического многочлена $det\mathcal{P}(\lambda ,x,t,u)$ во всей области $\mathcal{U}$. Второй параметр индекса равен нулю, поскольку пучок $\mathcal{P}(\lambda ,x,t,u)$ не содержит сингулярной составляющей [3]. Сформулируем достаточные условия, при выполнении которых пучок $\mathcal{P}(\lambda ,x,t,u)$ имеет индекс $(k,0)$.

Теорема 1 (см. [5]). Пусть выполнены следующие условия:

1) все корни характеристического многочлена $det(A(x) + \lambda B(x))$, где $x = ({{x}_{1}},{{x}_{2}},\; \ldots ,\;{{x}_{m}}) \in \bar {U}$, $\bar {U}$ – замыкание некоторой области, содержащейся в ${{\mathbb{R}}^{m}}$, являются вещественными и имеют постоянную кратность в области определения $\bar {U}$;

2) старший коэффициент многочлена $det(A(x) + \lambda B(x))$ относительно параметра $\lambda $ не обращается в нуль ни в одной точке $\bar {U}$;

3) ранги матриц $A(x)$ и $B(x)$ являются постоянными в каждой точке области $\bar {U}$ и меньше размерности $n$.

Тогда пучок $A(x) + \lambda B(x)$ $s$-гладко эквивалентен пучку следующего канонического вида:

где ${{E}_{d}}$ – единичная матрица порядка $d$; $M(x)$ и $N(x)$ – верхние (правые) треугольные блоки с нулевой диагональю порядка $l$ и $p$ соответственно; ${{\mathcal{O}}_{l}}$ – квадратная нулевая матрица порядка $l$; $J(x) = \operatorname{diag} \{ {{J}_{1}}(x),{{J}_{2}}(x), \ldots ,{{J}_{{\tilde {s}}}}(x)\} $ – блочно-диагональная матрица порядка $d$, в которой ${{J}_{i}}(x)$, $i = 1,2,\; \ldots ,\;\tilde {s}$ – невырожденные матрицы порядков ${{p}_{i}}$, соответственно $d = \sum\nolimits_{\nu = 1}^{\tilde {s}} {{{p}_{\nu }}} $; каждый блок ${{J}_{i}}(x)$ имеет единственное собственное значение $ - 1{\text{/}}{{\lambda }_{i}}(x)$ в области определения $\bar {U}$; ${{\lambda }_{i}}(x)$ – собственные значения характеристического многочлена $det(A(x) + \lambda B(x))$, не обращающиеся в нуль в области $\bar {U}$; $p = n - d - l$. Из теоремы 1 следует, что $M(x)$ и $N(x)$ в (3) являются нильпотентными матрицами в области определения $\bar {U}$. Пусть $\operatorname{ind} M(x) = {{k}_{1}}$ и $\operatorname{ind} N(x) = {{k}_{2}}$ в области $\bar {U}$, то есть ${{k}_{1}} = \min \{ \bar {k}:M{{(x)}^{{\bar {k}}}} = 0\,\,\forall (x) \in \bar {U}\} $. Аналогично определяется ${{k}_{2}}$. Будем предполагать, что для пучка $\mathcal{P}(\lambda ,x,t,u)$ системы (1) выполнены все условия теоремы 1. Тогда $\operatorname{ind} \mathcal{P}(\lambda ,x,t,u) = (k,0)$, где $k = \max \{ {{k}_{1}},{{k}_{2}}\} $ и соответственно индекс системы (1) также равен $(k,0)$.

Перейдем к построению сплайн-коллокационной разностной схемы.

2. РАЗНОСТНАЯ СХЕМА

В этом разделе построим сплайн-коллокационную разностную схему с расщепленным пучком и преобразуем ее к матрично-операторному уравнению в нормальной форме.

В силу сделанных в предыдущем разделе предположений существуют невырожденные в области $\mathcal{U}$ матрицы $P(x,t,u)$ и $Q(x,t,u)$, которые преобразуют пучок $\mathcal{P}(\lambda ,x,t,u)$ к каноническому виду (3), то есть

Тогда пучок $\mathcal{P}(\lambda ,x,t,u)$ можно расщепить на два пучка где и С учетом (5) запишем систему (1) в расщепленном виде Построим в прямоугольной области $U$ равномерную сетку ${{U}_{\Delta }}$ с шагами $h$ и $\tau $ соответственно по пространственной и временной переменным В области $\mathcal{U}$ будем иметь соответствующее сеточное пространство Как и в работах [3], [4], будем искать решение $u(x,t)$ задачи (6), (2) в виде сплайна ${{\delta }^{{{{m}_{1}},{{m}_{2}}}}}(x,t) \in {{C}^{1}}(\mathcal{U})$ дефекта 1 со старшими степенями, равными ${{m}_{1}}$ и ${{m}_{2}}$ по каждой независимой переменной соответственно, значения которого в узлах сетки ${{U}_{\Delta }}$ совпадают со значениями искомой функции $u(x,t)$. В каждом прямоугольнике $U_{{i,j}}^{{{{m}_{1}},{{m}_{2}}}} = [{{x}_{i}},{{x}_{i}} + {{m}_{1}}h] \times [{{t}_{j}},{{t}_{j}} + {{m}_{2}}\tau ]$ сетки ${{U}_{\Delta }}$, содержащем $({{m}_{1}} + 1)({{m}_{2}} + 1)$ узлов, где ${{m}_{1}} \leqslant {{n}_{1}}$, ${{m}_{2}} \leqslant {{n}_{2}}$, сплайн ${{\delta }^{{{{m}_{1}},{{m}_{2}}}}}(x,t)$ представляем в виде полинома Ньютона, записанного для равноотстоящих узлов. Поэтому для аппроксимации производных ${{\partial }_{t}}u(x,t)$ и ${{\partial }_{x}}u(x,t)$ на слоях $x = {{x}_{i}}$ и $t = {{t}_{j}}$ используем безразностные формулы численного дифференцирования для равноотстоящих узлов (см. [6, с. 161]). Для производных в левой части системы (6) используем аппроксимации производных, записанные по значениям искомой функции в узловых точках  области $U_{{i,j}}^{{{{m}_{1}},{{m}_{2}}}}$ (см. [3], [4]), а для аппроксимации производных в правой части системы (6) используем значения искомой функции только в узловых точках внутренней области $\tilde {U}_{{i,j}}^{{{{m}_{1}},{{m}_{2}}}} = [{{x}_{i}} + h,{{x}_{i}} + {{m}_{1}}h] \times [{{t}_{j}} + \tau ,{{t}_{j}} + {{m}_{2}}\tau ] \subseteq U_{{i,j}}^{{{{m}_{1}},{{m}_{2}}}}$.

Запишем систему (6) в узловых точках области $\tilde {U}_{{i,j}}^{{{{m}_{1}},{{m}_{2}}}}$, подставим в нее значения искомой функции $u({{x}_{i}} + {{l}_{1}}h,{{t}_{j}} + {{l}_{2}}\tau )$ и аппроксимации ее производных в этих точках. В результате получим нелинейную разностную схему

где коэффициенты ${{\gamma }_{{{{l}_{2}},{{l}_{3}}}}}$, $\mathop {\bar {\gamma }}\nolimits_{{{l}_{1}},{{l}_{3}}} $, ${{\beta }_{{{{l}_{2}},{{l}_{3}}}}}$ и $\mathop {\bar {\beta }}\nolimits_{{{l}_{1}},{{l}_{3}}} $ вычисляются по известным формулам (см. [6, с. 161]): где $C_{m}^{{{{l}_{3}}}}$ – биномиальные коэффициенты. Коэффициенты в (7) имеют следующие сокращенные обозначения: где $s = 1,2$. Разностная схема (7) в каждом узле $({{x}_{i}},{{t}_{j}})$ сетки ${{U}_{\Delta }}$ представляет собой систему нелинейных уравнений порядка $\tilde {n} = {{m}_{1}}{{m}_{2}}n$ c искомым вектором Чтобы не возникало путаницы в обозначениях, решение системы (7) в узлах $({{x}_{{i + 1}}},{{t}_{{j + 1}}})$ сетки ${{U}_{\Delta }}$ будем обозначать ${{v}_{{i + 1,j + 1}}}$, а значения искомой функции $u(x,t)$ в этих же узлах ${{u}_{{i + 1,j + 1}}} = u({{x}_{{i + 1}}},{{t}_{{j + 1}}})$. Согласно этой договоренности перепишем систему (7) следующим образом: где Разностную схему (8) назовем нелинейной сплайн-коллокационной разностной схемой с расщеплением. Система (8) представляет собой целый набор нелинейных разностных схем, порядки аппроксимации которых определяются порядками сплайнов и составляют величину, равную $O({{h}^{{{{m}_{1}} - 1}}}) + O({{\tau }^{{{{m}_{2}} - 1}}})$.

Далее мы хотим записать разностную схему (8) в нормальной форме матрично-операторного уравнения. Для этого рассмотрим функцию $F(x,t,u)$. Представим ее в следующем виде: $F(x,t,u) = {{P}^{{ - 1}}}(x,t,u)\tilde {F}(x,t,u)$, где $P(x,t,u)$ – невырожденная в $\mathcal{U}$ из (4), а $\tilde {F}(x,t,u)$ – некоторая неизвестная $n$-мерная вектор-функция. Имеем

где $\partial{ \tilde {F}}(x,t,\xi u){\text{/}}\partial \xi u = (\partial {{\tilde {F}}_{{{{s}_{1}}}}}(x,t,\xi u){\text{/}}\partial \xi {{u}_{{{{s}_{2}}}}})$ – матрица Якоби, ${{s}_{1}},{{s}_{2}} = 1,2, \ldots ,n$. Обозначим $C(x,t,u) = - \int_0^1 \,\partial{ \tilde {F}}(x,t,\xi u){\text{/}}\partial \xi ud\xi $, тогда Умножим (8) на $\tau $. Тогда в силу (9) получим следующую систему: Составим матрицу Умножим систему (10) слева на матрицу ${{\tilde {P}}_{{i + 1,j + 1}}}$ и выполним замену переменной ${{v}_{{i,j}}} = {{Q}_{{i,j}}}{{w}_{{i,j}}}$, где ${{w}_{{i,j}}} = w({{x}_{i}},{{t}_{j}})$ и ${{Q}_{{i,j}}} = Q({{x}_{i}},{{t}_{j}},{{u}_{{i,j}}})$ – матрица из (4). В результате получим систему где $i = 0,1, \ldots ,{{n}_{1}} - 1,\;j = 0,1, \ldots ,{{n}_{2}} - 1,$ ${{l}_{1}} = 1,2, \ldots ,{{m}_{1}},\;{{l}_{2}} = 1,2, \ldots ,{{m}_{2}}$ с искомым вектором Используя формулу Тейлора, представим матрицу ${{Q}_{{i + {{l}_{1}},j + {{l}_{2}}}}}$ следующим образом: где

$\sigma _{{i + {{l}_{1}},j + {{l}_{2}}}}^{1} = {{\partial }_{x}}Q({{x}_{{i + {{l}_{1}}}}} + \theta h,{{t}_{{j + {{l}_{2}}}}},w({{x}_{{i + {{l}_{1}}}}} + \theta h,{{t}_{{j + {{l}_{2}}}}}))$,       $0 < \theta < 1,$

В силу принадлежности элементов матриц $A(x,t,u)$ и $B(x,t,u)$ пространству ${{C}^{1}}(\mathcal{U})$, элементы матриц ${{\partial }_{x}}Q$ и ${{\partial }_{t}}Q$, следуя [7]–[9], непрерывны в области $\mathcal{U}$. Перепишем систему (11), используя представление матрицы ${{Q}_{{i + {{l}_{1}},j + {{l}_{2}}}}}$ из (12), а также аналогичное разложение по формуле Тейлора матрицы ${{J}_{{i + {{l}_{1}},j + {{l}_{2}}}}}$. Получим систему

где ${{\sigma }_{\nu }}$ – ограниченные в области $\mathcal{U}$ матрицы, полученные в результате разложения матриц $Q(x,t,u)$ и $J(x,t,u)$ по формуле Тейлора. В (13) матрицы ${{\hat {\Omega }}_{{i + 1,j + 1}}}$, $\hat {\mathcal{A}}$, ${{\hat {\mathcal{B}}}_{{i + 1,j + 1}}}$ и вектор ${{\tilde {f}}_{{i + 1,j + 1}}}$ имеют вид: Далее, разобьем каждую блочную компоненту ${{w}_{{i + 1,j + 1}}}$ вектора ${{\bar {w}}_{{i + 1,j + 1}}}$ на три блока ${{w}_{{i + 1,j + 1}}} = $ $ = \;{{(w_{{i + 1,j + 1}}^{1},w_{{i + 1,j + 1}}^{2},w_{{i + 1,j + 1}}^{3})}^{{\text{т }}}}$ размеров $d$, $l$ и $p$ соответственно. Пусть $T$ – матрица, которая при умножении на вектор ${{\bar {w}}_{{i + 1,j + 1}}}$ выполняет перестановку его элементов (см. [4]), то есть $T{{\bar {w}}_{{i + 1,j + 1}}} = {{(\bar {w}_{{i + 1,j + 1}}^{1},\bar {w}_{{i + 1,j + 1}}^{2},\bar {w}_{{i + 1,j + 1}}^{3})}^{{\text{т }}}},$ где блоки $\bar {w}_{{i + 1,j + 1}}^{s}$ имеют вид $\bar {w}_{{i + 1,j + 1}}^{s} = (w_{{i + 1,j + 1}}^{s}, \ldots ,w_{{i + 1,j + {{m}_{2}}}}^{s},w_{{i + 2,j + 1}}^{s}, \ldots ,$ $w_{{i + 2,j + {{m}_{2}}}}^{s}, \ldots ,w_{{i + {{m}_{1}},j + 1}}^{s}, \ldots ,w_{{i + {{m}_{1}},j + {{m}_{2}}}}^{s}{{)}^{{\text{т }}}}.$ Матрица $T$ осуществляет следующие преобразования: где матрицы

${{\bar {\Omega }}_{{i + 1,j + 1}}} = \operatorname{diag} \{ \Omega _{{i + 1,j + 1}}^{1},\Omega _{{i + 1,j + 1}}^{2},\Omega _{{i + 1,j + 1}}^{3}\} $,      $\bar {\mathcal{A}} = \operatorname{diag} \{ {{\mathcal{A}}^{1}},{{\mathcal{A}}^{2}},{{\mathcal{A}}^{3}}\} $    и

${{\bar {\mathcal{B}}}_{{_{{i + 1,j + 1}}}}} = \;\operatorname{diag} \{ \mathcal{B}_{{i + 1,j + 1}}^{1},{{\mathcal{B}}^{2}},{{\mathcal{B}}^{3}}\} $

имеют следующие блоки:

Умножим (13) слева на матрицу $T$ и выполним замену переменной ${{\bar {w}}_{{i + 1,j + 1}}} = {{T}^{{\text{т }}}}{{z}_{{i + 1,j + 1}}}$, где ${{z}_{{i + 1,j + 1}}}$ – неизвестный вектор. Тогда система (13) с учетом равенств (14) примет вид где ${{\Omega }_{{i + 1,j + 1}}} = {{\bar {\Omega }}_{{i + 1,j + 1}}} + \tau {{\tilde {\sigma }}_{1}}$ и $q({{z}_{{i + 1,j + 1}}}) = \tau T{{\tilde {f}}_{{_{{i + 1,j + 1}}}}} - (\bar {\mathcal{A}} + \tau {{\sigma }_{2}}){{z}_{{i + 1,j}}} - r({{\bar {B}}_{{_{{i + 1,j + 1}}}}} + h{{\tilde {\sigma }}_{3}}){{z}_{{i,j + 1}}}$, ${{\tilde {\sigma }}_{\nu }} = T{{\sigma }_{\nu }}$. Предположим, что в каждом узле сетки ${{\mathcal{U}}_{\Delta }}$ выполняются условия (12) леммы 1 из работы [4]. Тогда в силу леммы 1 из [4] и теоремы о спектральном разложении функции от матрицы в ряд (см. [10, теорема 5.6.3]), матрица ${{\Omega }_{{i + 1,j + 1}}}$ является невырожденной в области ${{\mathcal{U}}_{\Delta }}$. Умножим систему (15) слева на матрицу $\Omega _{{i + 1,j + 1}}^{{ - 1}}$ и после всех необходимых преобразований, аналогичных преобразованиям из [4], перейдем к системе в расщепленной по блочным компонентам форме где ${{g}_{{i + 1,j + 1}}} = \bar {\Omega }_{{i + 1,j + 1}}^{{ - 1}}T{{\bar {f}}_{{_{{i + 1,j + 1}}}}}$, ${{g}_{{i + 1,j + 1}}} = {{(g_{{i + 1,j + 1}}^{1},g_{{i + 1,j + 1}}^{2},g_{{i + 1,j + 1}}^{3})}^{{\text{т }}}}$, $g_{{i + 1,j + 1}}^{s}$ – блоки размеров ${{m}_{1}}{{m}_{2}}d$, ${{m}_{1}}{{m}_{2}}l$ и ${{m}_{1}}{{m}_{2}}p$ соответственно; здесь $\mathcal{T}$ – ортогональная матрица перестановок; Система (16) представляет собой канонический вид разностной схемы (8) . В матричной форме система (16) имеет следующий вид: где $\mathcal{V} = {{({{\mathcal{V}}^{1}},{{\mathcal{V}}^{2}},{{\mathcal{V}}^{3}})}^{{\text{т }}}}$ и ${{\mathcal{V}}^{s}} = {{(\bar {w}_{{1,1}}^{s},\bar {w}_{{2,1}}^{s}, \ldots ,\bar {w}_{{{{n}_{1}},1}}^{s},\bar {w}_{{1,2}}^{s},\bar {w}_{{2,2}}^{s}, \ldots ,\bar {w}_{{{{n}_{1}},2}}^{s}, \ldots ,\bar {w}_{{1,{{n}_{2}}}}^{s},\bar {w}_{{2,{{n}_{2}}}}^{s}, \ldots ,\bar {w}_{{{{n}_{1}},{{n}_{2}}}}^{s})}^{{\text{т }}}}$. В системе (17) матрица $L(\mathcal{V}) = \operatorname{diag} \{ {{L}^{1}}(\mathcal{V}),{{L}^{2}}(\mathcal{V}),{{L}^{3}}(\mathcal{V})\} $. Каждый ее блок является блочно-двухдиагональной матрицей ${{L}^{s}}(\mathcal{V}) = (L_{{i,j}}^{s}(\mathcal{V}))$, где $i,j = 1,2,\; \ldots ,\;{{n}_{1}}$. Блоки $L_{{i,i}}^{s}(\mathcal{V})$, расположенные на главной диагонали, имеют вид где ${{\nu }^{s}}$ принимает значения: ${{m}_{1}}{{m}_{2}}d$, ${{m}_{1}}{{m}_{2}}l$ и ${{m}_{1}}{{m}_{2}}p$, соответственно $s = 1,2,3$. Блоки $L_{{i,j}}^{s}(\mathcal{V})$, расположенные под главной диагональю, имеют блочно-диагональный вид, $\mathcal{L}_{{i,j}}^{s}(\mathcal{V}) = $ $ = \operatorname{diag} \{ \mathcal{F}_{{1,i}}^{s},\mathcal{F}_{{2,i}}^{s}, \ldots ,\mathcal{F}_{{{{n}_{1}},i}}^{s}\} $, где $i = 2,3,\; \ldots ,\;{{n}_{1}}$, $j = i - 1$. Матрица $\mathcal{L}(\mathcal{V},h,\tau ) = ({{\mathcal{L}}^{{{{\nu }_{1}},{{\nu }_{2}}}}}(\mathcal{V},h,\tau ))$, где ${{\nu }_{1}},{{\nu }_{2}} = 1,2,3$, состоит из блоков, имеющих блочно-двухдиагональный вид ${{\mathcal{L}}^{{{{\nu }_{1}},{{\nu }_{2}}}}}(\mathcal{V},h,\tau ) = (\mathcal{L}_{{i,j}}^{{{{\nu }_{1}},{{\nu }_{2}}}})$, где $i,j = 1,2,\; \ldots ,\;{{n}_{1}}$, с диагональными блоками и блоками, расположенными под главной диагональю $\mathcal{L}_{{i,j}}^{{{{\nu }_{1}},{{\nu }_{2}}}} = \operatorname{diag} \{ \tau \bar {\epsilon }_{{1,j}}^{{{{\nu }_{1}},{{\nu }_{2}}}},\tau \bar {\epsilon }_{{2,j}}^{{{{\nu }_{1}},{{\nu }_{2}}}}, \ldots ,\tau \bar {\epsilon }_{{{{n}_{1}},j}}^{{{{\nu }_{1}},{{\nu }_{2}}}}\} $. Вектор $G(\mathcal{V})$ в (17) имеет следующий вид: где $\bar {g} = (\mathop {\bar {g}}\nolimits^1 ,\mathop {\bar {g}}\nolimits^2 ,\mathop {\bar {g}}\nolimits^3 )$ – вектор размера $\bar {n} = \tilde {n}n$, $\tilde {n} = {{n}_{1}}{{n}_{2}}{{m}_{1}}{{m}_{2}}$. Блоки ${{\bar {g}}^{s}}$ имеют размеры $\tilde {n}d$, $\tilde {n}l$ и $\tilde {n}p$ соответственно значениям $s = 1,2,3$, Матрица $\mathcal{G}(\mathcal{V},h,\tau ) = ({{\mathcal{G}}^{{{{\nu }_{1}},{{\nu }_{2}}}}})$, где ${{\nu }_{1}},{{\nu }_{2}} = 1,2,3$, имеет следующие блоки: Матрица $H(\mathcal{V}) = \operatorname{diag} \{ {{H}^{1}},{{H}^{2}},{{H}^{3}}\} $ имеет блоки диагонального вида ${{H}^{s}} = \operatorname{diag} \{ H_{{1,1}}^{s},{{\mathcal{O}}_{s}}\} $, где $H_{{1,1}}^{s} = \operatorname{diag} \{ \mathcal{F}_{{1,1}}^{s},\mathcal{F}_{{2,1}}^{s}, \ldots ,\mathcal{F}_{{{{n}_{1}},1}}^{s}\} $, ${{\mathcal{O}}_{{{{\nu }^{s}}}}}$ – нулевой квадратный блок порядка ${{\nu }^{s}} = ({{n}_{2}} - 1){{n}_{1}}{{m}_{1}}{{m}_{2}}\nu $, где $\nu $ принимает значения $d$, $l$ и $p$ соответственно значениям $s = 1,2,3$. Матрица $\mathcal{H}(\mathcal{V},\tau ,h) = ({{\mathcal{H}}^{{{{\nu }_{1}},{{\nu }_{2}}}}})$ состоит из блоков ${{\mathcal{H}}^{{{{\nu }_{1}},{{\nu }_{2}}}}} = \operatorname{diag} \{ \mathcal{H}_{{1,1}}^{{{{\nu }_{1}},{{\nu }_{2}}}},{{\mathcal{O}}_{{{{\nu }^{s}}}}}\} $, где $\mathcal{H}_{{1,1}}^{{{{\nu }_{1}},{{\nu }_{2}}}} = \tau \operatorname{diag} \{ \bar {\epsilon }_{{1,1}}^{{{{\nu }_{1}},{{\nu }_{2}}}},\bar {\epsilon }_{{2,1}}^{{{{\nu }_{1}},{{\nu }_{2}}}},\; \ldots ,\;\bar {\epsilon }_{{{{n}_{1}},1}}^{{{{\nu }_{1}},{{\nu }_{2}}}}\} $. Вектор ${{w}_{0}} = {{(w_{0}^{1},w_{0}^{2},w_{0}^{3})}^{{\text{т }}}}$ имеет следующие блоки: $w_{0}^{s} = {{e}_{{{{n}_{2}}}}} \otimes {{(\bar {w}_{{1,0}}^{s},\bar {w}_{{2,0}}^{s},\; \ldots ,\;\bar {w}_{{{{n}_{1}},0}}^{s})}^{{\text{т }}}}$. Матрица $Q(\mathcal{V}) = $ $ = \operatorname{diag} \{ {{Q}^{1}},{{Q}^{2}},{{Q}^{3}}\} $ имеет диагональные блоки ${{Q}^{s}} = \operatorname{diag} \{ Q_{{1,1}}^{s},Q_{{1,2}}^{s}, \ldots ,Q_{{1,{{n}_{2}}}}^{s}\} $, где $Q_{{1,j}}^{s} = \operatorname{diag} \{ \mathcal{K}_{{1,j}}^{s},{{\mathcal{O}}_{{{{\nu }^{s}}}}}\} $, ${{\nu }^{s}} = ({{n}_{1}} - 1){{m}_{1}}{{m}_{2}}\nu $, $\nu $ принимает значения $d$, $l$ и $p$, соответственно $s = 1,2,3$. Матрица $\mathcal{Q}(\mathcal{V},h,\tau ) = ({{\mathcal{Q}}^{{{{\nu }_{1}},{{\nu }_{2}}}}})$ имеет блоки ${{\mathcal{Q}}^{{{{\nu }_{1}},{{\nu }_{2}}}}} = \operatorname{diag} \{ \mathcal{Q}_{1}^{{{{\nu }_{1}},{{\nu }_{2}}}},\mathcal{Q}_{2}^{{{{\nu }_{1}},{{\nu }_{2}}}}, \ldots ,\mathcal{Q}_{{{{n}_{2}}}}^{{{{\nu }_{1}},{{\nu }_{2}}}}\} $, где $\mathcal{Q}_{j}^{{{{\nu }_{1}},{{\nu }_{2}}}} = \tau \operatorname{diag} \{ \hat {\epsilon }_{{1,j}}^{{{{\nu }_{1}},{{\nu }_{2}}}},{{\mathcal{O}}_{{{{\nu }^{s}}}}}\} $, $j = 1,2,\; \ldots ,\;{{n}_{2}}$. Вектор ${{w}^{0}} = {{({{w}^{{0,1}}},{{w}^{{0,2}}},{{w}^{{0,3}}})}^{{\text{т }}}}$, где ${{w}^{{0,s}}} = {{({{e}_{{{{n}_{1}}}}} \otimes w_{{0,1}}^{s},{{e}_{{{{n}_{1}}}}} \otimes w_{{0,2}}^{s}, \ldots ,{{e}_{{{{n}_{1}}}}} \otimes w_{{0,{{n}_{2}}}}^{s})}^{{\text{т }}}}$.

Далее запишем систему (17) в нормальной форме. Для этого докажем существование матрицы ${{(L(\mathcal{V}) + L(\mathcal{V},h,\tau ))}^{{ - 1}}}$. Найдем ${{L}^{{ - 1}}}(\mathcal{V})$. Матрицы ${{({{L}^{s}}(\mathcal{V}))}^{{ - 1}}} = (X_{{{{\nu }_{1}},{{\nu }_{2}}}}^{s})$, где ${{\nu }_{1}},{{\nu }_{2}} = 1,2,s,{{n}_{2}}$, $s = 1,2,3,$ имеют блочную нижнюю (левую) треугольную форму, их квадратные блоки определяются равенством

где ${{\nu }^{s}} = {{n}_{1}}{{m}_{1}}{{m}_{2}}\bar {\nu }$ и $\bar {\nu }$ принимает значения $d$, $l$ и $p$, соответственно $s = 1,2,3$. В (19) символ $\prod $ обозначает левое произведение матриц. Из (19) нетрудно заметить, что $X_{{{{\nu }_{1}},{{\nu }_{2}}}}^{s}$ вычисляются также по следующим рекуррентным формулам: Матрицы ${{(L_{{{{\nu }_{2}},{{\nu }_{2}}}}^{s})}^{{ - 1}}} = (Y_{{\mathop {\tilde {\nu }}\nolimits_1 ,\mathop {\tilde {\nu }}\nolimits_2 }}^{{s,{{\nu }_{2}}}})$ имеют нижнюю (левую) треугольную форму, где $\mathop {\tilde {\nu }}\nolimits_1 ,\mathop {\tilde {\nu }}\nolimits_2 = 1,2,\; \ldots ,\;{{n}_{1}}$. Их блоки определяются следующим образом: Таким образом, ${{L}^{{ - 1}}}(\mathcal{V})$ всегда определена. В силу ограниченности матриц ${{L}^{{ - 1}}}(\mathcal{V})$ и $\mathcal{L}(\mathcal{V},h,\tau )$ на сетке ${{\mathcal{U}}_{\Delta }}$ имеем, что ${{\left\| {{{\mathcal{L}}^{{ - 1}}}(\mathcal{V})L(\mathcal{V},h,\tau )} \right\|}_{{C({{\mathcal{U}}_{\Delta }})}}} = {{c}_{1}}h + {{c}_{2}}\tau $, где ${{c}_{\nu }}$ – некоторые постоянные величины. Следовательно, существует матрица ${{(E + {{L}^{{ - 1}}}(\mathcal{V})\mathcal{L}(V,h,\tau ))}^{{ - 1}}}$, которая определяется равенством ${{(E + {{L}^{{ - 1}}}(\mathcal{V})\mathcal{L}(\mathcal{V},h,\tau ))}^{{ - 1}}} = \sum\nolimits_{\nu = 0}^\infty \,{{[ - {{L}^{{ - 1}}}(\mathcal{V})\mathcal{L}(\mathcal{V},h,\tau )]}^{\nu }}.$ Причем ${{\left\| {{{{(E + {{L}^{{ - 1}}}(\mathcal{V})\mathcal{L}(\mathcal{V},h,\tau ))}}^{{ - 1}}}} \right\|}_{{C({{\mathcal{U}}_{\Delta }})}}} = 1 + {{\tilde {c}}_{1}}h + $ $ + \,{{\tilde {c}}_{2}}h$, где ${{\tilde {c}}_{\nu }}$ – некоторые постоянные величины. Поскольку матрицу ${{(L(\mathcal{V}) + \mathcal{L}(\mathcal{V},h,\tau ))}^{{ - 1}}}$ мы можем представить в виде ${{(L(\mathcal{V}) + \mathcal{L}(\mathcal{V},h,\tau ))}^{{ - 1}}} = {{(E + {{L}^{{ - 1}}}(\mathcal{V})\mathcal{L}(\mathcal{V},h,\tau ))}^{{ - 1}}}{{L}^{{ - 1}}}(\mathcal{V})$, то тем самым мы доказали ее существование. Таким образом, перепишем систему (17) в виде где $\Pi (\mathcal{V})\;\, = \,\;{{L}^{{ - 1}}}(\mathcal{V})(\tau \bar {g}\, - \,H(\mathcal{V}){{w}_{0}}\, - \,\;Q(\mathcal{V}){{w}^{0}})\,\; + \,\;\delta (\mathcal{V},h,\tau )$ и $\delta (\mathcal{V},h,\tau )$ = $\tau {{L}^{{ - 1}}}(\mathcal{V})\mathcal{G}(\mathcal{V},h,\tau )\bar {g}$ – ${{L}^{{ - 1}}}(\mathcal{V}) \times \mathcal{H}(\mathcal{V},h,\tau ){{w}_{0}}$ – ${{L}^{{ - 1}}}(\mathcal{V})\mathcal{Q}(\mathcal{V},h,\tau ){{w}^{0}}$ + $\sum\nolimits_{\nu = 1}^\infty \,{{[ - {{L}^{{ - 1}}}(\mathcal{V})\mathcal{L}(\mathcal{V},h,\tau )]}^{\nu }}{{L}^{{ - 1}}}(\mathcal{V})G(\mathcal{V})$ + $O({{h}^{{{{m}_{1}}}}}) + O({{\tau }^{{{{m}_{2}}}}})$.

Уравнение (22) представляет собой разностную схему (17) (или (8)), записанную в нормальной форме матрично-операторного уравнения. Перейдем к доказательству существования равномерно-ограниченного на всей сетке ${{\mathcal{U}}_{\Delta }}$ решения уравнения (22).

3. УСТОЙЧИВОСТЬ РАЗНОСТНОЙ СХЕМЫ

В этом разделе докажем существование равномерно-ограниченного решения разностной схемы (22) в сеточном пространстве ${{U}_{\Delta }}$. Справедлива следующая

Теорема 2. Пусть выполнены следующие условия:

1) собственные значения $\xi _{{\mathop {\bar {\gamma }}\nolimits_{{{m}_{1}}} }}^{{{{s}_{1}}}}$, $\xi _{{{{\gamma }_{{{{m}_{2}}}}}}}^{{{{s}_{2}}}}$ и $\xi _{{{{J}_{{i,j}}}}}^{{{{s}_{3}}}}$ матриц ${{\bar {\gamma }}_{{{{m}_{1}}}}}$, ${{\gamma }_{{{{m}_{2}}}}}$ и ${{J}_{{i,j}}}$, соответственно, в каждом узле разностной сетки ${{\mathcal{U}}_{\Delta }}$ удовлетворяют условию

где ${{s}_{1}} = \overline {1,{{m}_{1}}} $, ${{s}_{2}} = \overline {1,{{m}_{2}}} $, ${{s}_{3}} = \overline {1,k} $;

2) собственные значения $\xi _{{{{J}_{{i,j}}}}}^{s}$ положительные в сеточном пространстве ${{\mathcal{U}}_{\Delta }}$;

3) отношение шагов разностной сетки $\tau {\text{/}}h$ является постоянной величиной.

Тогда разностная схема (22) в сеточном пространстве ${{\mathcal{U}}_{\Delta }}$ имеет решение равномерно-ограниченное по начально-краевым условиям и по правой части, для которого справедлива оценка (Как и прежде, в сеточном пространстве $C({{U}_{\Delta }})$ n-мерных вектор-функций используем равномерную норму ${{\left\| {{{v}_{{i,j}}}} \right\|}_{{C({{U}_{\Delta }})}}} = \mathop {max}\limits_{i,j} \left\| {{{v}_{{i,j}}}} \right\|,$ $\left\| {{{v}_{{i,j}}}} \right\| = \mathop {max}\limits_{s = 1,2, \ldots ,n} {\text{|}}v_{{i,j}}^{s}{\text{|}},$ ${{v}_{{i,j}}} = {{(u_{{i,j}}^{1},v_{{i,j}}^{2}, \ldots ,v_{{i,j}}^{n})}^{{\text{т }}}},$ согласованную с нормой n-мерной вектор-функции $v(x,t) \in C(U)$: ${{\left\| {\text{v}(x,t} \right\|}_{{C(U)}}} = \max \{ \left\| {\text{v}(x,t)} \right\|\;\;\forall (x,t) \in U\} .$)

где ${{\mathcal{M}}_{\nu }}$ – постоянные величины, $i = 1,\; \ldots ,\;{{n}_{1}}$, $j = 1,\; \ldots ,\;{{n}_{2}}$.

Доказательство. Применим к матричному уравнению (22) метод простых итераций

где $\Pi ({{\mathcal{V}}_{{k - 1}}}) = {{L}^{{ - 1}}}({{\mathcal{V}}_{{k - 1}}})(\tau \bar {g} - H({{\mathcal{V}}_{{k - 1}}}){{w}_{0}} - Q({{\mathcal{V}}_{{k - 1}}}){{w}^{0}}) + \delta ({{\mathcal{V}}_{{k - 1}}},h,\tau )$. С помощью итерационного процесса (25), начиная с некоторого стартового вектора ${{\mathcal{V}}_{0}}$, построенного по начально-краевым условиям из (8), образуем последовательность $\{ {{\mathcal{V}}_{k}}:k \geqslant 1\} $ сеточных функций. Докажем, что последовательность $\{ {{\mathcal{V}}_{k}}\} $ при $h \to 0$ и $\tau \to 0$ сходится к некоторой предельной сеточной функции $\mathcal{V}{\text{*}}$, которая является равномерно-ограниченной и удовлетворяет уравнению (22).

Составим матрицу Якоби $\partial \Pi (\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$ и выясним, при каких условиях спектр матрицы $\partial \Pi (\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$ будет находиться в круге единичного радиуса. Для удобства обозначим ${{\Pi }_{1}}(\mathcal{V}) = \tau {{L}^{{ - 1}}}(\mathcal{V})\bar {g}$, ${{\Pi }_{2}}(\mathcal{V}) = {{L}^{{ - 1}}}(\mathcal{V})H(\mathcal{V}){{w}_{0}}$, ${{\Pi }_{3}}(\mathcal{V}) = {{L}^{{ - 1}}}(\mathcal{V})Q(\mathcal{V}){{w}^{0}}$ и ${{\Pi }_{4}}(\mathcal{V}) = \delta (\mathcal{V},h,\tau )$. Исследуем спектры матриц $\partial {{\Pi }_{\nu }}(\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$.

Рассмотрим $\partial {{\Pi }_{1}}(\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$. Имеем $\partial {{\Pi }_{1}}(\mathcal{V}){\text{/}}\partial{ \mathcal{V}} = \tau \operatorname{diag} \{ \partial {{\theta }^{1}}{\text{/}}\partial {{\mathcal{V}}^{1}},\partial {{\theta }^{2}}{\text{/}}\partial {{\mathcal{V}}^{2}},\partial {{\theta }^{3}}{\text{/}}\partial {{\mathcal{V}}^{3}}\} ,$ где ${{\theta }^{s}} = \tau {{({{L}^{s}}({{\mathcal{V}}^{s}}))}^{{ - 1}}}{{\bar {g}}^{s}}$ и ${{\theta }^{s}} = {{(\theta _{1}^{s},\theta _{2}^{s}, \ldots ,\theta _{{{{n}_{2}}}}^{s})}^{{\text{т }}}}$. Компоненты вектора ${{\theta }^{s}}$ находятся из следующих равенств $\theta _{{{{\nu }_{2}}}}^{s} = \tau \sum\nolimits_{{{s}_{1}} = 1}^{{{\nu }_{2}}} \,X_{{{{\nu }_{2}},{{s}_{1}}}}^{s}\tilde {g}_{{{{s}_{1}}}}^{s}$, где ${{X}_{{{{\nu }_{2}},{{s}_{1}}}}}$ определяются по формулам (19) или (20). Обозначим $\theta _{{{{\nu }_{2}}}}^{s} = {{(\theta _{{1,{{\nu }_{2}}}}^{s},\theta _{{2,{{\nu }_{2}}}}^{s}, \ldots ,\theta _{{{{n}_{1}},{{\nu }_{2}}}}^{s})}^{{\text{т }}}}$, где ${{\nu }_{2}} = 1,2,\; \ldots ,\;{{n}_{2}}$. Тогда, принимая во внимание (18), (19) и (21), находим компоненты векторов $\theta _{{{{\nu }_{2}}}}^{s}$. Они выражаются следующими рекуррентными соотношениями:

где ${{\nu }_{1}} = 1,2,\; \ldots ,\;{{n}_{1}}$. Тогда матрицы Якоби $\partial {{\theta }^{s}}{\text{/}}\partial {{\mathcal{V}}^{s}}$ имеют следующую нижнюю (левую) треугольную форму: где $\bar {w}_{{{{\nu }_{2}}}}^{s} = {{(\bar {w}_{{1,{{\nu }_{2}}}}^{s},\bar {w}_{{2,{{\nu }_{2}}}}^{s},\; \ldots ,\;\bar {w}_{{{{n}_{1}},{{\nu }_{2}}}}^{s})}^{{\text{т }}}}$, $\mathcal{O}$ – нулевая матрица подходящего размера. Заметим, что для исследования спектра матриц (27) достаточно исследовать спектры диагональных блоков $\partial \theta _{{{{\nu }_{2}}}}^{s}{\text{/}}\partial{ \bar {w}}_{{{{\nu }_{2}}}}^{s}$. Отметим, что блоки $\partial \theta _{{{{\nu }_{2}}}}^{s}{\text{/}}\partial{ \bar {w}}_{{{{\nu }_{2}}}}^{s}$ имеют нижнюю (левую) треугольную форму. Выполним оценку по норме их диагональных блоков $\partial \theta _{{{{\nu }_{1}},{{\nu }_{2}}}}^{s}{\text{/}}\partial{ \bar {w}}_{{{{\nu }_{1}},{{\nu }_{2}}}}^{s}$, где ${{\nu }_{1}} = 1,2,\; \ldots ,\;{{n}_{1}}$, ${{\nu }_{2}} = 1,2,\; \ldots ,\;{{n}_{2}}$. Из (26) получаем необходимые оценки где Компоненты $\theta _{{{{\nu }_{1}},{{\nu }_{2}}}}^{s}$ из (28) оцениваются по следующим рекуррентным формулам: Рассмотрим первый случай, $s = 1$. Имеем где ${{c}_{\nu }}$ – постоянные величины, которые определяются следующими равенствами: ${{c}_{1}} = \mathop {\left\| {{{{(\bar {\Omega }_{{{{\nu }_{1}},{{\nu }_{2}}}}^{s})}}^{{ - 1}}}} \right\|}\nolimits_{C({{\mathcal{U}}_{\Delta }})} {{\left\| {\mathop {\tilde {f}}\nolimits_{{{\nu }_{1}},{{\nu }_{2}}} } \right\|}_{{C({{\mathcal{U}}_{\Delta }})}}}\left\| T \right\|$ и ${{c}_{2}} = \mathop {\left\| {\partial {{{(\Omega _{{{{\nu }_{1}},{{\nu }_{2}}}}^{s})}}^{{ - 1}}}e{\text{/}}\partial{ \bar {w}}_{{{{\nu }_{1}},{{\nu }_{2}}}}^{s}} \right\|}\nolimits_{C({{\mathcal{U}}_{\Delta }})} {{\left\| {\mathop {\tilde {f}}\nolimits_{{{\nu }_{1}},{{\nu }_{2}}} } \right\|}_{{C({{\mathcal{U}}_{\Delta }})}}}\left\| T \right\|$. В [4] показано, что в силу условия 2 настоящей теоремы справедливы неравенства где ${{\rho }_{1}} = {{\bar {c}}_{1}}exp( - {{\kappa }_{1}}{\text{/}}r)$, ${{\rho }_{2}} = {{\bar {с }}_{2}}exp( - {{\kappa }_{2}}r)$, ${{\bar {c}}_{\nu }}$, ${{\kappa }_{\nu }}$ – постоянные величины, $r = \tau {\text{/}}h$. Нетрудно показать, что при выполнении первого условия теоремы 1, а также в силу теоремы о глобальной структуре матрицы-функции из [9], справедливы неравенства где $\mathop {\bar {\rho }}\nolimits_1 = {{\hat {c}}_{1}}rexp( - r{{\bar {\kappa }}_{1}})$, $\mathop {\bar {\rho }}\nolimits_2 = ({{\hat {c}}_{2}}{\text{/}}r)exp( - {{\bar {\kappa }}_{2}}{\text{/}}r)$, $\mathop {\hat {c}}\nolimits_\nu $, $\mathop {\bar {\kappa }}\nolimits_\nu $ – постоянные величины. Отметим, что ${{\rho }_{1}},\mathop {\bar {\rho }}\nolimits_1 ,\mathop {\bar {\rho }}\nolimits_2 \to 0$ при $r \to 0$. Подставляя (30), (31) и (32) в (28) и (29), получаем оценки Рассмотрим второй случай, $s = 2$. В этом случае имеем $\mathcal{K}_{{i + 1,j + 1}}^{2} = {{E}_{{{{m}_{1}}{{m}_{2}}l}}} + \tilde {\mathcal{K}}_{{i + 1,j + 1}}^{2}$, где $\tilde {\mathcal{K}}_{{i + 1,j + 1}}^{2} = \sum\nolimits_{{{\nu }_{3}} = 1}^\infty \,{{( - 1)}^{{{{\nu }_{3}}}}}\mathop {\left( {\tfrac{1}{r}\bar {\gamma }_{{{{m}_{1}}}}^{{ - 1}} \otimes {{\beta }_{{{{m}_{2}}}}} \otimes {{M}_{{i + 1,j + 1}}}} \right)}\nolimits^{{{\nu }_{3}}} $. Заметим, что $\tilde {\mathcal{K}}_{{i + 1,j + 1}}^{2}$ является нильпотентной матрицей индекса ${{k}_{1}}$ на сетке ${{\mathcal{U}}_{\Delta }}$. Также в силу условий теоремы 1 где ${{\bar {c}}_{3}}$ и ${{c}_{3}}$ – постоянные величины. Рассмотрим теперь $\zeta _{{{{\nu }_{2}}}}^{2}$ из (28). Имеем где ${{c}_{4}} = \mathop {\left( {1 + {{{\left\| {\tilde {\mathcal{K}}_{{{{\nu }_{1}},{{\nu }_{2}}}}^{2}} \right\|}}_{{C({{\mathcal{U}}_{\Delta }})}}}} \right)}\nolimits^{{{k}_{1}}} $. Так как $\mathcal{F}_{{i + 1,j + 1}}^{2} = {{\mathcal{O}}_{{{{m}_{1}}{{m}_{2}}l}}}$, то с учетом оценок (30), (35) и (36) неравенства (28) и (29) имеют вид Рассмотрим  третий случай, $s = 3$. Так как $\mathcal{F}_{{i + 1,j + 1}}^{3} = {{E}_{{{{m}_{1}}{{m}_{2}}p}}} + \tilde {\mathcal{F}}_{{i + 1,j + 1}}^{3}$, где $\tilde {\mathcal{F}}_{{i + 1,j + 1}}^{3}$ – нильпотентная матрица индекса ${{k}_{2}}$ на сетке ${{\mathcal{U}}_{\Delta }}$, которая выражается равенством

$\tilde {\mathcal{F}}_{{i + 1,j + 1}}^{3} = \;\sum\nolimits_{{{\nu }_{3}} = 1}^\infty \,{{( - 1)}^{{{{\nu }_{3}}}}}\mathop {(r\mathop {\bar {\beta }}\nolimits_{{{m}_{1}}} \otimes \gamma _{{{{m}_{2}}}}^{{ - 1}} \otimes {{N}_{{i + 1,j + 1}}})}\nolimits^{{{\nu }_{3}}} ,$

то в силу условий теоремы 1 выполняются неравенства

где ${{\bar {c}}_{5}}$ и ${{c}_{5}}$ – постоянные величины. Поскольку $\mathcal{K}_{{i + 1,j + 1}}^{3} = {{\mathcal{O}}_{{{{m}_{1}}{{m}_{2}}p}}}$, то при достаточно малом $\tau $ из (28) и (29), с учетом (30) и (39), имеем неравенства Из неравенства (34), (38) и (41) следует, что уменьшая шаги разностной сетки $\tau $ и $h$ всегда можно добиться достаточной малости радиуса спектра матрицы $\partial {{\Pi }_{1}}(\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$.

Перейдем к исследованию спектра матрицы $\partial {{\Pi }_{2}}(\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$. Рассмотрим матрицу $\partial {{\Pi }_{2}}(\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$. Имеем $\partial {{\Pi }_{2}}(\mathcal{V}){\text{/}}\partial{ \mathcal{V}} = \operatorname{diag} \{ \partial {{y}^{1}}{\text{/}}\partial {{\mathcal{V}}^{1}},\partial {{y}^{2}}{\text{/}}\partial {{\mathcal{V}}^{2}},\partial {{y}^{3}}{\text{/}}\partial {{\mathcal{V}}^{3}}\} ,$ где ${{y}^{s}} = {{({{L}^{s}}({{\mathcal{V}}^{s}}))}^{{ - 1}}}{{H}^{s}}w_{0}^{s}$ и ${{y}^{s}} = {{(y_{1}^{s},y_{2}^{s}, \ldots ,y_{{{{n}_{2}}}}^{s})}^{{\text{т }}}}$. Компоненты вектора ${{y}^{s}}$ находятся из следующих равенств: $y_{{{{\nu }_{2}}}}^{s} = X_{{{{\nu }_{2}},1}}^{s}H_{{1,1}}^{s}\tilde {w}_{0}^{s}$, где ${{\nu }_{2}} = 1,2,\; \ldots ,\;{{n}_{2}}$ и $\tilde {w}_{0}^{s} = {{(\bar {w}_{{1,0}}^{s},\bar {w}_{{2,0}}^{s}, \ldots ,\bar {w}_{{{{n}_{1}},0}}^{s})}^{{\text{т }}}}$. Обозначим$y_{{{{\nu }_{2}}}}^{s} = {{(y_{{1,{{\nu }_{2}}}}^{s},y_{{2,{{\nu }_{2}}}}^{s}, \ldots ,y_{{{{n}_{1}},{{\nu }_{2}}}}^{s})}^{{\text{т }}}}$. Используя (20), находим компоненты векторов $y_{{{{\nu }_{2}}}}^{s}$. Они выражаются рекуррентными соотношениями

где ${{\nu }_{1}} = 1,2,\; \ldots ,\;{{n}_{1}}$. Следовательно, матрицы $\partial {{y}^{s}}{\text{/}}\partial {{\mathcal{V}}^{s}}$ имеют нижнюю (левую) треугольную форму Диагональные блоки $\partial y_{{{{\nu }_{2}}}}^{s}{\text{/}}\partial{ \bar {w}}_{{{{\nu }_{2}}}}^{s}$ матриц (43) также имеют нижнюю (левую) треугольную форму. Поэтому для исследования их спектра достаточно исследовать спектры диагональных блоков $\partial y_{{{{\nu }_{1}},{{u}_{2}}}}^{s}{\text{/}}\partial{ \bar {w}}_{{{{\nu }_{1}},{{\nu }_{2}}}}^{s}$. Дифференцируя $y_{{{{\nu }_{1}},{{\nu }_{2}}}}^{s}$ из (42) и оценивая их по норме, получаем Рассмотрим первый случай, $s = 1$. Оценим сначала компоненты $y_{{{{\nu }_{1}},{{\nu }_{2}}}}^{1}$. Из (20) следует, что Тогда из (45) получаем, что Так как собственные значения матриц ${{(L_{{{{\nu }_{2}},{{\nu }_{2}}}}^{1})}^{{ - 1}}}L_{{{{\nu }_{2}},{{\nu }_{2}} - 1}}^{1}$ по модулю меньше единицы, поскольку на их диагоналях расположены блоки $\mathcal{F}_{{{{\nu }_{1}},{{\nu }_{2}}}}^{1}$, то при $s = 1$ произведение матриц в правой части (46) стремится к нулю при увеличении ${{\nu }_{2}}$ и является ограниченной величиной. Следовательно, можем записать где ${{c}_{6}}$ – постоянная величина, определяемая равенством Тогда из (31), (32), (36), (44) и (47) следует Отметим, что ${{\bar {\vartheta }}_{1}} \to 0$ при уменьшении $r$.

Рассмотрим второй случай, $s = 2$. Поскольку в этом случае $\mathcal{F}_{{i + 1,j + 1}}^{2} = {{\mathcal{O}}_{{{{m}_{1}}{{m}_{2}}l}}}$, то из (42) и (44) немедленно следуют оценки

Рассмотрим третий случай, $s = 3$. В этой ситуации $\mathcal{K}_{{i + 1,j + 1}}^{3} = {{\mathcal{O}}_{{{{m}_{1}}{{m}_{2}}p}}}$. Тогда из (44) с учетом (40) имеем Для оценки по норме $y_{{{{\nu }_{1}},{{\nu }_{2}}}}^{3}$ воспользуемся равенством (46). Поскольку $\mathcal{F}_{{i + 1,j + 1}}^{3}$ является нильпотентной матрицей индекса ${{k}_{2}}$ на сетке ${{\mathcal{U}}_{\Delta }}$, то при ${{n}_{2}} \leqslant {{k}_{2}}$ выполняется Поэтому из (50) с учетом (51) получаем Таким образом, из (48), (49) и (52) получаем, что при достаточно малом $r$ спектр матрицы $\partial {{\Pi }_{3}}(\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$ будет достаточно мал. Рассмотрим матрицу $\partial {{\Pi }_{3}}(\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$. Исследуем ее спектр. Имеем $\partial {{\Pi }_{3}}(\mathcal{V}){\text{/}}\partial{ \mathcal{V}} = \operatorname{diag} \{ \partial {{z}^{1}}{\text{/}}\partial {{\mathcal{V}}^{1}},\partial {{z}^{2}}{\text{/}}\partial {{\mathcal{V}}^{2}},\partial {{z}^{3}}{\text{/}}\partial {{\mathcal{V}}^{3}}\} ,$ где ${{z}^{s}} = {{({{L}^{s}}({{\mathcal{V}}^{s}}))}^{{ - 1}}}{{Q}^{s}}{{w}_{{0,s}}}$ и ${{z}^{{0,s}}} = ({{e}_{{{{n}_{1}}}}} \otimes w_{{0,1}}^{s},{{e}_{{{{n}_{1}}}}} \otimes w_{{0,2}}^{s},\; \ldots ,$ ${{e}_{{{{n}_{1}}}}} \otimes w_{{0,{{n}_{2}}}}^{s}{{)}^{{\text{т }}}}$ при $s = 1,2,3$. Компоненты вектора ${{z}^{s}}$ определяются равенствами

$z_{{{{\nu }_{2}}}}^{s} = \;\sum\nolimits_{{{\nu }_{3}} = 1}^{{{\nu }_{2}}} \,X_{{{{\nu }_{2}},{{\nu }_{3}}}}^{s}Q_{{1,{{\nu }_{3}}}}^{s}{{e}_{{{{n}_{1}}}}} \otimes w_{{0,{{\nu }_{3}}}}^{s},$

где ${{\nu }_{2}} = 1,2,\; \ldots ,\;{{n}_{2}}$. Обозначим вектор через $z_{{{{\nu }_{2}}}}^{s} = {{(z_{{1,{{\nu }_{2}}}}^{s},z_{{2,{{\nu }_{2}}}}^{s}, \ldots ,z_{{{{n}_{1}},{{\nu }_{2}}}}^{s})}^{{\text{т }}}}$ и с помощью (20) найдем его компоненты

где ${{\nu }_{1}} = 1,2,\; \ldots ,\;{{n}_{1}}$. Таким образом, матрицы $\partial {{z}^{s}}{\text{/}}\partial {{\mathcal{V}}^{s}}$ будут иметь нижнюю (левую) треугольную форму Диагональные блоки $\partial z_{{{{\nu }_{2}}}}^{s}{\text{/}}\partial{ \bar {w}}_{{{{\nu }_{2}}}}^{s}$ матриц (54) также имеют нижнюю (левую) треугольную форму. Поэтому для исследования их спектра достаточно исследовать спектры диагональных блоков $\partial z_{{{{\nu }_{1}},{{u}_{2}}}}^{s}{\text{/}}\partial{ \bar {w}}_{{{{\nu }_{1}},{{\nu }_{2}}}}^{s}$. Дифференцируя $z_{{{{\nu }_{1}},{{\nu }_{2}}}}^{s}$ из (53) и оценивая их по норме, получаем Рассмотрим первый случай, $s = 1$. Из (55) с учетом (31) и (32) получаем оценку где ${{c}_{7}} = {{\bar {\rho }}_{1}}{{\rho }_{2}}{\text{/}}(1 - {{\rho }_{1}}) + {{\bar {\rho }}_{2}}$. Для оценки $z_{{{{\nu }_{1}},{{\nu }_{2}}}}^{1}$ воспользуемся рекуррентными соотношениями, следующими из (20): Из (57) получаем Поскольку спектр матрицы ${{(L_{{{{\nu }_{2}},{{\nu }_{2}}}}^{1})}^{{ - 1}}}L_{{{{\nu }_{2}},{{\nu }_{2}} - 1}}^{1}$ лежит внутри круга единичного радиуса, то из (58) следует, что где ${{c}_{8}}$ – постоянная величина, которая определяется равенством Подставляя (59) в (56) будем иметь Отметим, что ${{c}_{7}} \to 0$ при уменьшении $r$.

Рассмотрим второй случай, $s = 2$. Так как $\mathcal{F}_{{i + 1,j + 1}}^{2} = {{\mathcal{O}}_{{{{m}_{1}}{{m}_{2}}l}}}$, то из (55) немедленно следует, что

Выполним также оценку по норме вектора $z_{{{{\nu }_{1}},{{\nu }_{2}}}}^{2}$. Она понадобится позже. Из (53) следует, что где ${{c}_{9}} = \sum\nolimits_{{{\nu }_{3}} = 0}^{{{k}_{1}} - 1} \,C_{{{{n}_{1}}}}^{{{{\nu }_{3}}}}\mathop {\left\| {\tilde {\mathcal{K}}_{{{{\nu }_{1}},{{\nu }_{2}}}}^{2}} \right\|}\nolimits_{C({{\mathcal{U}}_{\Delta }})}^{{{\nu }_{3}}} $.

Рассмотрим третий случай, $s = 3$. Так как $\mathcal{K}_{{i + 1,j + 1}}^{3} = {{\mathcal{O}}_{{{{m}_{1}}{{m}_{2}}p}}}$, то из (53) и (55) следует, что

Из (60), (61) и (63) заключаем, что при уменьшении $r$ спектр матрицы $\partial {{\Pi }_{3}}(\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$ будет достаточно мал. Спектр матрицы $\partial {{\Pi }_{4}}(\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$ ввиду малости величины $\delta (\mathcal{V},h,\tau )$ будет значительно меньше спектра матрицы $\sum\nolimits_{s = 1}^3 \,\partial {{\Pi }_{s}}(\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$ при достаточно малых $\tau $ и $h$. Таким образом, мы доказали, что найдутся такие $\tau {\text{*}}$ и $h{\text{*}}$, удовлетворяющие условию (23), что при $\tau < \tau {\text{*}}$ и $h < h{\text{*}}$ спектр матрицы Якоби $\partial \Pi (\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$ будет расположен внутри круга единичного радиуса.

Для последовательности $\{ {{\mathcal{V}}_{k}}\} $ имеем

Из (64) по теореме о среднем получаем где ${{\tilde {\mathcal{V}}}^{k}}$ – промежуточное значение между ${{\mathcal{V}}_{k}}$ и ${{\mathcal{V}}_{{k - 1}}}$. Тогда из (65) будем иметь Так как спектр матрицы $\partial \Pi (\mathcal{V}){\text{/}}\partial{ \mathcal{V}}$ находится в круге единичного радиуса, то найдется такое число ${{n}_{\epsilon }}$, для которого будет справедливо следующее: Тогда из (66) следует неравенство гдe

Далее, в силу неравенства (67), для любых $k$ и $p$ имеем

В правой части неравенства (68) ${{\bar {\delta }}^{{\left[ {\tfrac{k}{{{{n}_{\varepsilon }}}}} \right]}}} \to 0$ при $k \to \infty $, а все другие сомножители являются ограниченными в сеточном пространстве $C({{\mathcal{U}}_{\Delta }})$, следовательно, последовательность $\{ {{\mathcal{V}}_{k}}\} $ сходится в себе и в силу полноты пространства $C({{\mathcal{U}}_{\Delta }})$ сходится к некоторому сеточному значению $\mathcal{V}{\text{*}}$, который в силу замкнутости сеточного пространства $C({{\mathcal{U}}_{\Delta }})$ будет принадлежать этому пространству [11]. Поскольку и $\{ {{\mathcal{V}}_{k}}\} \to \mathcal{V}{\text{*}}$  при  $k \to \infty $,  то ${{\mathcal{V}}_{{k + 1}}} \to \Pi (\mathcal{V}*)$. Следовательно, $\mathcal{V}{\text{*}}$ является решением уравнения (22).

Докажем равномерную ограниченность сеточного решения $\mathcal{V}{\text{*}}$ уравнения (22). Из (33), (37), (40), (47), (49), (51), (59), (62) и (63) следует, что сеточные функции ${{\mathcal{V}}_{k}}$ являются равномерно-ограниченными на сетке ${{\mathcal{U}}_{\Delta }}$ и удовлетворяют неравенству (24). Поскольку последовательность $\{ {{\mathcal{V}}_{k}}\} $ равномерно сходится к некоторой сеточной функции $\mathcal{V}{\text{*}}$, то и для предельной функции $\mathcal{V}{\text{*}}$ также будет справедлива оценка (24). Теорема доказана.

Перейдем к численным экспериментам.

4. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ РАЗНОСТНОЙ СХЕМЫ

Продемонстрируем эффективность предложенного в работе численного метода на следующем тестовом примере. Рассмотрим дифференциально-алгебраическую систему уравнений в частных производных вида (1), в которой

где ${{A}_{{1,3}}} = (0,exp(x + {{t}^{2}}),0)$, ${{B}_{{1,1}}} = exp({{u}_{1}}) + exp({{u}_{2}}{{u}_{6}}) + xt$, $\mathcal{O}$ – нулевые блоки подходящего размера, Решением системы (1) с коэффициентами (69) является вектор $u = (exp(xt),exp(x + t),$ $x + t,xt,texp(x),xexp(t),1 + x{{)}^{{\text{т }}}}$. Вектор $F(x,t,u)$ соответствует этому решению. Начально-краевые условия для такой системы будут иметь вид Очевидно,  что  матричный пучок  $\mathcal{P}(\lambda ,\;x,\;t,\;u)$, построенный по коэффициентам из (69), легко преобразуется  к каноническому виду (3) и имеет индекс, равный четырем. 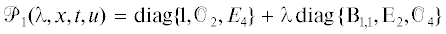Выполним следующее  расщепление пучка на два составляющих: $\mathcal{P}(\lambda ,\;x,\;t,\;u) = {{\mathcal{P}}_{1}}(\lambda ,\;x,\;t,\;u) + {{\mathcal{P}}_{2}}(\lambda ,\;x,\;t,\;u)$, где и ${{\mathcal{P}}_{2}}(\lambda ,x,t,u) = \left( {\mathcal{O},\operatorname{colon} ({{A}_{{1,3}}},{{A}_{{2,3}}},{{\mathcal{O}}_{4}})} \right) + $ $ + \;\;\lambda \operatorname{diag} \{ {{\mathcal{O}}_{3}},{{B}_{{3,3}}}\} .$ Найдем численное решение начально-краевой задачи (1), (69), (70) предложенным в работе алгоритмом с помощью специально разработанной программы. Программа написана на компьютерном языке С++ и позволяет находить численное решение начально-краевых задач (1), (2) обоснованным в настоящей работе методом. В программе пользователь задает: коэффициенты системы $A(x,t,u)$ и $B(x,t,u)$; вектор правой части $F(x,t,u)$; начально-краевые условия $\psi (t)$ и $\phi (x)$; область решения $U = [{{x}_{0}},X] \times [{{t}_{0}},T]$; порядки сплайна для каждой независимой переменной ${{m}_{1}}$ и ${{m}_{2}}$; шаги разностной сетки $h$ и $\tau $; число десятичных знаков $\kappa $, до стабилизации которых осуществляется итерационный процесс. На выходе формируется текстовый файл, в котором записаны значения сеточной функции в каждом узле разностной сетки. Программа “Численная реализация нелинейной разностной схемы с расщепленным матричным пучком для решения квазилинейной дифференциально-алгебраической системы уравнений в частных производных произвольного индекса” зарегистрирована в Федеральной регистрационной службе РОСПАТЕНТ 25 августа 2017 г. под номером № 2017619532.

Найдено численное решение задачи (1), (69), (70) в области $U = [0,1] \times [0,1]$ при $\kappa = 4$. Результаты численных расчетов представлены в таблице. Расчеты выполнены на оборудовании центра коллективного пользования “Иркутский суперкомпьютерный центр СО РАН” [12].

За результат в тестовом примере принята абсолютная погрешность $\Delta u$ как максимальное отклонение точного решения от найденного численного решения на всей разностной сетке ${{\mathcal{U}}_{\Delta }}$. Из последнего столбца таблицы видно, что численный алгоритм имеет высокую точность, которая на единицу меньше порядка аппроксимирующего сплайна. В некоторых случаях (№ 1, 5, 9) абсолютная погрешность на порядок превосходит ожидаемый результат.

ЗАКЛЮЧЕНИЕ

Предложенный в работе сплайн-коллокационный метод позволяет с высокой точностью, которая на единицу меньше порядка сплайна, численно решать рассмотренные в работе квазилинейные дифференциально-алгебраические системы индекса $(k,0)$. Особенность этого метода имеет аналитический характер и заключается в предварительном расщеплении матричного пучка системы $\mathcal{P}(\lambda ,x,t,u)$.