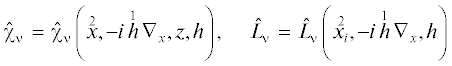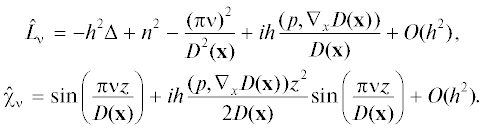Журнал вычислительной математики и математической физики, 2019, T. 59, № 4, стр. 566-578

1. ВВЕДЕНИЕ

В работе рассматривается уравнение Гельмгольца в трехмерном слое переменной толщины с локализованной правой частью

где ${\mathbf{x}} = ({{x}_{1}},{{x}_{2}})$ – горизонтальные декартовы координаты, ось $z$ направлена вверх перпендикулярно плоскости $\mathbb{R}_{x}^{2}$. Здесь задающие границу слоя функции ${{d}_{1}}({\mathbf{x}}) \leqslant z \leqslant {{d}_{2}}({\mathbf{x}})$ и задающие источник функции $F({{x}_{1}},{{x}_{2}})$, $g(z)$ предполагаются гладкими функциями всех своих аргументов. Кроме того, предполагается, что $F({\mathbf{x}})$, $g(z)$ быстро убывают на бесконечности. При этом $g(z)$ будем считать финитной функцией, ${{d}_{1}}({\mathbf{x}}) < {{z}_{0}} < {{d}_{2}}({\mathbf{x}})$, так что носитель правой части лежит внутри слоя. Для простоты считаем, что скорость звука $c$ и частота $\omega $ являются постоянными.

Предполагается, что в рассматриваемой задаче длина волны звука и вертикальный размер волновода – величины одного порядка, характерный продольный размер волновода много больше вертикального. Удобно перейти к безразмерным переменным с помощью замены $z = z{\text{'}}{{d}_{0}}$, ${{x}_{i}} = x_{i}^{'}{{l}_{0}}$, где ${{l}_{0}}$ и ${{d}_{0}}$ – характерные продольный и поперечный размеры волновода соответственно. Уравнение в новых переменных примет вид

где $h = {{d}_{0}}{\text{/}}{{l}_{0}}$ – малый параметр, здесь для простоты приняты следующие обозначения: Для наглядности мы сначала опишем метод решения уравнения (2) с одним малым параметром $h$а потом обсудим, как это уравнение обобщается для различных соотношений между параметрами $\mu $ и $h$.

Это уравнение встречается в задачах о распространении звука от источника в мелком море с неоднородным рельефом дна (см. [1], [2]). Следует отметить, однако, что часто в практических задачах дно является проницаемым для звуковых волн и, таким образом, распространение звука рассматривается в двухслойной (многослойной) среде (см. [1]–[4]). Существуют, однако, и классы задач, в которых дно можно считать полностью отражающим. Явление, когда нарушается прямолинейность распространения звука в горизонтальной плоскости, называется горизонтальной рефракцией (см. [1]–[7]) и играет значительную роль в формировании волновых полей в мелком море. Горизонтальная рефракция может быть вызвана как неоднородностями дна (см. [3], [4]), так и неоднородностями поля скорости звука в водном слое (см. [5]–[7]) (например, внутренними волнами). Задача о распространении звука в слое, одна из границ которого является неоднородной поверхностью, естественным образом возникает при моделировании распространения звука в мелком море. В подводной акустике развивается несколько методов решения уравнения Гельмгольца, которые могут быть использованы в случае однослойного волновода. Среди них можно отметить метод трехмерного параболического уравнения (см. [4], [8]–[10]), подход, основанный на трассировке лучей в трехмерном пространстве (например, [11]) или методе гауссовых пучков (см. [1], [12]), а также наиболее близкие данной работе методы, основанные на отделении вертикальной переменной и получении уравнений, описывающих изменение модовых амплитуд в горизонтальной плоскости (см. [3], [4], [13], [14]). Этот подход был впервые предложен в 70-е годы (см. [13]), где уравнения на модовые амплитуды решаются с помощью лучевой теории (в акустике океана этот подход известен как “вертикальные моды – горизонтальные лучи”). В дальнейшем для вычисления модовых амплитуд применялись, например, методы параболического уравнения (см. [14]–[16]) (впервые в задачах подводной акустики применен в [14]) и метод гауссовых пучков [17]. К уравнению Гельмгольца в слое сводятся также, например, задачи распространения света в оптических волноводах и задачи распространения радиоволн над поверхностью Земли.

Используемый нами метод, основанный на отделении вертикальной переменной, сводит трехмерную задачу в слое к двумерной во всем пространстве. Задача о коротковолновой асимптотике функции Грина для оператора Гельмгольца в ${{\mathbb{R}}^{n}}$ изучалась многими авторами, в частности, Келлером [18], Бабичем и Булдыревым [19], [20] и Кучеренко [21]. Если показатель преломления не зависит от $x \in {{\mathbb{R}}^{n}}$, то функция Грина вычисляется точно. В случае переменного показателя преломления строилась асимптотика функции Грина, для этого точное решение уравнения с постоянным показателем преломления, “замороженным” в точке источника, склеивалось с определенной вне малой окрестности этой точки лучевой асимптотикой. Если в правой части стоит функция источника, например, Гауссова экспонента, необходимо вычислять свертку этой функции с функцией Грина, что обычно является не вполне простой задачей.

Цель этой работы – построение асимптотических решений задачи (2). С помощью адиабатической редукции в операторной форме (см. [22]) и недавно развитого подхода в [23] в предположении отсутствия “ловушечных” состояний и выполнения условий излучения на бесконечности (типа условия Зоммерфельда) в работе строится асимптотическое решение сформулированной задачи при $1 \gg \mu \geqslant h$. В пределе $f({{x}_{1}},{{x}_{2}})g(z) \to \delta ({{x}_{1}})\delta ({{x}_{2}})\delta (z)$ полученные формулы описывают асимптотику функции Грина для рассматриваемого уравнения Гельмгольца, однако, в отличие от такой асимптотики, полученная формула позволяет достаточно явно описать влияние формы источника на волновую часть решения. Реализация полученных формул сводится к построению лучей (или траекторий в фазовом пространстве), концы которых определяют волновые фронты, и последующем восстановлении на них волнового поля с помощью достаточно эффективных формул. В этой работе мы уделяем основное внимание явным формулам и прикладным аспектам, рассуждения проводятся на уровне формальных асимптотических разложений. Далее для простоты мы рассматриваем слой, встречающийся в задачах подводной акустики, ${{d}_{2}}({\mathbf{x}}) = 0$, ${{d}_{1}}({\mathbf{x}}) = D({\mathbf{x}})$, $D({\mathbf{x}}) < 0$.

2. АДИАБАТИЧЕСКАЯ РЕДУКЦИЯ К ПЛОСКИМ ЗАДАЧАМ

Пусть сначала $D({\mathbf{x}}) = {\text{const}}$, тогда стандартный метод Фурье приводит к представлению в виде “разложения по вертикальным модам”

где функции ${{\psi }_{\nu }}({\mathbf{x}})$ удовлетворяют двумерным задачам где $\nu $ – натуральное число(номер моды). Здесь и далее круглые скобки обозначают скалярное произведение Если $D$ зависит от ${\mathbf{x}}$, то представление (4), (5) обобщается следующим образом [22]: где суть псевдодифференциальные операторы с символами ${{\chi }_{\nu }} = {{\chi }_{\nu }}(x,p,z,h)$, ${{L}_{\nu }} = {{L}_{\nu }}(x,p,h)$, цифры над оператором обозначают порядок действия этого оператора (см. [24], [27]). Функции ${{\chi }_{\nu }}$, ${{L}_{\nu }}$ предполагаются гладкими и допускают асимптотическое разложение по параметру $h$: В результате адиабатической редукции в операторной форме мы получили символы операторов $\mathop {\hat {\chi }}\nolimits_\nu $ и ${{\hat {L}}_{\nu }}$ с точностью до $O({{h}^{2}})$: Таким образом, задача в трехмерном слое (2) свелась к семейству задач для каждой моды в $\mathbb{R}_{x}^{2}$: Подробный вывод уравнения (10) приведен в приложении (см. ниже).

Например, для $g(z) = exp\left( {\tfrac{{ - {{{(z - {{z}_{0}})}}^{2}}}}{{2{{{(h)}}^{2}}}}} \right)$, скалярное произведение $\left( {g(z),\chi _{\nu }^{0}} \right)$ примет вид

Заметим, что аргумент функции ${\text{Erfi}}$ в (11) зависит от малого параметра $h$, поэтому в практических задачах для мод с номерами $\nu $ такими, что $\nu \ll {{h}^{{ - 2}}}$, можно использовать асимптотическое представление функции ${\text{Erfi}}$: Формула (11) с учетом асимптотического представления функции ${\text{Erfi}}$ примет следующий вид:

3. ПРЕДСТАВЛЕНИЕ БЫСТРОУБЫВАЮЩИХ ФУНКЦИЙ С ПОМОЩЬЮ КАНОНИЧЕСКОГО ОПЕРАТОРА МАСЛОВА И “ЭЛЛИПТИЧЕСКИЕ” МОДЫ

Правые части в уравнениях (10) разумно представить в виде канонического оператора Маслова, чтобы для построения асимптотического решения воспользоваться развитой теорией в [23]. Функциям такого вида соответствует лагранжево многообразие(см., например, [25])

Тогда функцию ${{F}_{\nu }}\left( {\tfrac{{{{x}_{1}} - {{\xi }_{1}}}}{h},\tfrac{{{{x}_{2}} - {{\xi }_{2}}}}{h}} \right)$ можно представить в виде где $K_{{(\Lambda ,d\mu )}}^{h}$ – канонический оператор Маслова [27].

Пусть главный символ оператора ${{\hat {L}}_{\nu }}$ не обращается в ноль при $(x,p) \in \Lambda $, т.е. ${{p}^{2}} + \tfrac{{{{{(\pi \nu )}}^{2}}}}{{{{D}^{2}}(\xi )}} - {{n}^{2}} \ne 0$, тогда согласно общим формулам из [26], [27] оператор ${{\hat {L}}_{\nu }}$ обратим на функциях ${{F}_{\nu }}$:

Функции ${{\psi }_{\nu }}$ быстро убывают и локализованы в окрестности точки $x = \xi $. При ${{\left. {{{H}_{\nu }}} \right|}_{\Lambda }} \ne 0$ решение трехмерной задачи (2) представимо в виде Это представление носит формальный характер, нужно доказывать, что соответствующий ряд сходится, и при этом суммарная поправка будет по-прежнему величиной порядка $O({{h}^{2}})$. Доказательство довольно объемное, здесь не приводится.

4. “ГИПЕРБОЛИЧЕСКИЕ” МОДЫ И ИХ АСИМПТОТИКИ

Формула (16) не работает в некоторой окрестности подмножества ${{L}_{0}} \in \Lambda $, ${{L}_{0}} = \left[ {{{p}^{2}} + \tfrac{{{{{(\pi \nu )}}^{2}}}}{{{{D}^{2}}(\xi )}} - {{n}^{2}} = 0} \right]$. Оператор ${{\hat {L}}_{\nu }}$ на ${{L}_{0}}$ становится в некотором смысле “гиперболическим” и у решения задачи возникает осциллирурующая волновая часть, связанная с новыми лагранжевыми многообразиями. Сами решения, таким образом, связаны с парой лагранжевых многообразий. Для появления “гиперболических” решений необходимо, чтобы главный символ ${{H}_{\nu }}(x,p) = {{L}_{\nu }}(x,p,0)$ оператора ${{\hat {L}}_{\nu }}$ обращался в ноль на некотором подмногообразии $\Lambda $. Равенство ${{p}^{2}} + \tfrac{{{{{(\pi \nu )}}^{2}}}}{{{{D}^{2}}(\xi )}} - {{n}^{2}} = 0$ выполняется только для конечного числа мод или не выполняется вообще. В предположении, что мода с номером $\nu $ гиперболическая, применим к построению соответствующей асимптотики метод, недавно развитый в [23].

Решение строится при следующих условиях.

1. Главный символ ${{H}_{\nu }}(x,p) = {{L}_{\nu }}(x,p,0)$ оператора ${{\hat {L}}_{\nu }}$ вещественен.

2. Гамильтоново векторное поле ${{V}_{H}} = ({{H}_{p}}, - {{H}_{x}})$ не касательно к многообразию $\Lambda $ ни в одной точке многообразия ${{L}_{0}} = ((x,p) \in \Lambda ,\;H(x,p) = 0)$.

3. Выходящая из произвольной точки $({{x}_{0}},{{p}_{0}}) \in {{L}_{0}}$ траектория $(X({{x}_{0}},{{p}_{0}},t),P({{x}_{0}},{{p}_{0}},t)) = $ $ = \;g_{H}^{t}(({{x}_{0}},{{p}_{0}}))$ поля ${{V}_{H}}$ более не возвращается на ${{L}_{0}}$ и удовлетворяет условию $li{{m}_{{t \to T}}}\left| {X({{x}_{0}},{{p}_{0}},t)} \right| = \infty $, где $t \in [0,T)$, $T \leqslant y$ – максимальный интервал существования траектории.

Пусть выполнены условия 1–3, тогда справедливо следующее

Утверждение. Пусть $\tilde {\Lambda } \in \Lambda $ – достаточно малая окрестность подмногообразия ${{L}_{0}} \in \Lambda $, ${{t}_{0}} > 0$ – достаточно малое число. Тогда при всех $t \in [0,{{t}_{0}}]$ корректно определены лагранжевы многообразия ${{\Lambda }_{t}} = g_{H}^{t}(\tilde {\Lambda })$.

Введем объекты, необходимые для определения канонического оператора на лагранжевом многообразии ${{\Lambda }_{ + }} = {{ \cup }_{{t \geqslant 0}}}g_{H}^{t}({{L}_{0}})$. Будем считать, что начальная точка $\alpha {\text{*}}$ на многообразии $\Lambda $ выбрана лежащей на ${{L}_{0}}$, тогда в качестве начальной точки на ${{\Lambda }_{ + }}$ выберем эту же точку, а на ${{\Lambda }_{t}}$ – точку $g_{H}^{t}(\alpha * )$. В точках многообразия ${{L}_{0}} \in \Lambda $ мера $d\mu $ может быть записана в виде $d\mu = dH \wedge d\sigma $, где $d\sigma $ – некоторая мера на ${{L}_{0}}$. Определим на ${{\Lambda }_{t}}$ меру $d{{\mu }_{t}} = {{(g_{H}^{{t * }})}^{{ - 1}}}d\mu $. Меру в точках многообразия ${{\Lambda }_{ + }}$ при любом $t > 0$ определим как $d{{\mu }_{ + }} = dt \wedge {{(g_{H}^{{t * }})}^{{ - 1}}}d\sigma $. На траекториях векторного поля ${{V}_{H}}$, выходящих из всевозможных точек $({{x}_{0}},{{p}_{0}}) \in \Lambda $, определим функцию $\tilde {A}$ как решение задачи Коши для уравнения переноса:

где ${{A}_{\nu }}$ – амплитуда в формуле (15), а есть субглавный символ оператора ${{\hat {L}}_{\nu }}$, ${{A}_{{ + \nu }}}$ – сужение функции ${{\hat {A}}_{\nu }}$ на многообразии ${{\Lambda }_{ + }}$. В этой задаче ${{H}_{{sub}}}(x,p) = - \tfrac{{(p,{{\nabla }_{x}}D({\mathbf{x}}))}}{{D({\mathbf{x}})}}$. Решение уравнения переноса выписывается явно: Пусть $\rho \in {{C}^{\infty }}(\Lambda )$ и $\theta \in C_{0}^{\infty }({{\mathbb{R}}^{1}})$ – срезающие функции такие, что $\rho (\alpha ) = 1$ в окрестности многообразия ${{L}_{0}}$, ${\text{supp}}\;\rho \in \Lambda $;

Определение. Функция ${{\psi }_{\nu }}(x,h)$ называется асимптотическим решением уравнения ${{\hat {L}}_{\nu }}{{\psi }_{\nu }}(x,h) = {{F}_{\nu }}$ с (асимптотическим) условием предельного поглощения (см. [28]), если существует зависящее от параметра $\varepsilon \in (0,\;1)$ семейство функций ${{\psi }_{{\nu \varepsilon }}}(x,h)$ такое, что $(\hat {L} - i\varepsilon ){{\psi }_{{\nu \varepsilon }}} = {{F}_{\nu }} + O({{h}^{\infty }})$ равномерно по $\varepsilon $ ${{\left\| {{{\psi }_{\nu }} - {{\psi }_{{\nu \varepsilon }}}} \right\|}_{{s,\Omega }}} \to 0$ равномерно по $h$ при $\varepsilon \to 0$ для любой ограниченной области $\Omega \in {{\mathbb{R}}^{2}}$ любого целого $s \geqslant 0$.

Теперь мы хотим применить следующее утверждение из [23].

Теорема. Если выполнены условия 1–3, уравнение (10) с правой частью (15) имеет асимптотическое решение ${{\psi }_{\nu }} = {{\psi }_{\nu }}(x,h)$, удовлетворяющее асимптотическому принципу предельного поглощения и представимое в главном члене формулой

где интеграл в показателе экспоненты вычисляется вдоль траектории поля ${{V}_{H}}$.

Первое слагаемое соответствует “эллиптическим” модам. Второе слагаемое – быстроосциллирующая “гиперболическая” часть решения. Третье слагаемое – сшивка этих 2 решений на многообразии ${{\Lambda }_{t}}$, которое является малой окрестностью ${{L}_{0}}$ (эта окрестность ${{L}_{0}}$ покрывается особыми картами, для особых карт представление канонического оператора Маслова интегральное, в малой окрестности ${{L}_{0}}$ соответствующий интеграл расходится, поэтому мы используем представление в таком виде).

Замечание 1. Если правая часть (15) – финитная функция, локализованная в окрестности точки $x = \xi $, асимптотическое решение уравнения (10) в области $\left| {x - \xi } \right| > C{{h}^{\beta }}$ для любых постоянных $C > 0$, $\beta \in g(1{\text{/}}2,\;1)$ для достаточно большого $L > 0$ представимо в главном члене в виде

Решение исходной задачи получается в результате суммирования по всем модам. Заметим также, что условия излучения (или предельного поглощения) для исходной задачи заменяются на парциальные соотношения (см. [29]), построенные асимптотические решения им удовлетворяют автоматически.

Замечание 2. Рассмотрим амплитуду ${{A}_{{ + \nu }}}$ (19) на многообразии ${{\Lambda }_{ + }}$. Так как справедлива формула коммутации канонического оператора с псевдодифференциальным оператором, функция $\tfrac{{\sqrt {D(\xi )} }}{{\sqrt {D({\mathbf{x}})} }}$выносится за канонический оператор. Волновая часть решения представима в виде

Амплитуда ${{A}_{\nu }}$ для конкретного источника выписывается в явном виде, поэтому можно рассчитать, для какой частоты и на каком луче функция ${{A}_{\nu }}$ имеет максимум (найти максимум функции двух переменных). Таким образом, меняя параметры источника, мы можем уменьшить или увеличить амплитуду в нужной области конфигурационного пространства (см. [23]). Из полученной формулы видно, как амплитуда зависит от координат точки, в окрестности которой расположен источник.

5. УПРОЩЕНИЕ ВОЛНОВОЙ МОДЫ И ПРИНЦИП МОПЕРТЮИ-ЯКОБИ ДЛЯ ДВУМЕРНЫХ СТАЦИОНАРНЫХ ЗАДАЧ

Ответ в двумерной задаче выражается через канонической оператор Маслова на многообразии ${{\Lambda }_{ + }} = {{ \cup }_{{t \geqslant 0}}}g_{H}^{t}({{L}_{0}})$. Применим к двумерной задаче представление канонического оператора, развитое в работе [30]. По принципу Мопертюи-Якоби [31] решения систем Гамильтона совпадают для гамильтонианов $H(x,p)$ и $F(H(x,p),x,p)$ при условии, что уравнения $H(x,p) = 0$ и $F(H(x,p),x,p) = 0$ определяют одну и ту же поверхность в фазовом пространстве. Можно перейти к гамильтониану $\tilde {H} = {{\left| p \right|} \mathord{\left/ {\vphantom {{\left| p \right|} {\sqrt { - \tfrac{{{{{(\pi \nu )}}^{2}}}}{{{{D}^{2}}(x)}} + {{n}^{2}}} }}} \right. \kern-0em} {\sqrt { - \tfrac{{{{{(\pi \nu )}}^{2}}}}{{{{D}^{2}}(x)}} + {{n}^{2}}} }} - 1$. Новая система Гамильтона связана со старой следующим образом:

где $C(x) = {1 \mathord{\left/ {\vphantom {1 {\sqrt { - {{{(\pi \nu )}}^{2}}{\text{/}}{{D}^{2}}(x) + {{n}^{2}}} }}} \right. \kern-0em} {\sqrt { - {{{(\pi \nu )}}^{2}}{\text{/}}{{D}^{2}}(x) + {{n}^{2}}} }}$ – решение уравнения $H(x,\left| p \right|) = 0$ относительно $\tfrac{1}{{\left| p \right|}}$, $R(x) = {{\left. {\left| p \right|\tfrac{{\partial H}}{{\partial \left| p \right|}}} \right|}_{{\left| p \right| = 1{\text{/}}C(x)}}} = 2{\text{/}}{{C}^{2}}(x)$. На лагранжевом многообразии ${{\Lambda }_{ + }}$ можно ввести так называемые эйконал координаты $\tau $, $\psi $ (см. [30]), где $\tau $ – собственное время новой системы Гамильтона, $\psi $ – координата на ${{L}_{0}}$: Мера на лагранжевом многообразии ${{\Lambda }_{ + }} = {{ \cup }_{{t \geqslant 0}}}g_{H}^{t}({{L}_{0}})$ имеет вид: Канонический оператор в неособых картах определен следующим образом: где ${{m}_{j}}$ – индекс Маслова неособой карты [26].

Канонический оператор в особых картах [32]:

где ${\mathbf{m}}_{j}^{s}$ – индекс Маслова особой карты [26].

Канонический оператор в эйконал координатах имеет ряд замечательных свойств, которые упрощают компьютерную реализацию канонического оператора.

1. Якобиан выражается через производную ${{\tilde {X}}_{\psi }}$

2. Фаза волновой функции – собственное время гамильтоновой системы имеет вид

Таким образом, волновые фронты – это кривые, соединяющие концы траекторий гамильтоновой системы.

6. ЗАВИСИМОСТЬ ОТ МАЛОГО ПАРАМЕТРА В ПРАВОЙ ЧАСТИ

Рассмотрим асимптотику задачи (2) с двумя малыми параметрами $\mu $ и $h$. Если $h \leqslant \mu $, можно легко свести задачу к предыдущей. Функцию ${{F}_{\nu }}\left( {\tfrac{{{{x}_{1}} - {{\xi }_{1}}}}{\mu },\tfrac{{{{x}_{2}} - {{\xi }_{2}}}}{\mu }} \right)$ можно представить через канонический оператор с малым параметром $h$:

Если $h \ll \mu $ в двумерной задаче, нужно пользоваться формулой (20). Если $\mu $ порядка $h$, волновую часть решения двумерной задачи можно представить в виде (21).

Пусть $\mu \leqslant {{h}^{2}}$, тогда представление (30) не работает. Действительно, правая часть представима через канонический оператор только с малым параметром $\mu $. В редуцированном уравнении для построения квазиклассической асимптотики вида (20) нужно сделать подстановку $\hat {p} = - i\mu {{\nabla }_{x}}$:

В приложении показано, что функция $\chi _{\nu }^{1}$, определяющая поправку $h\chi _{\nu }^{1}{{\psi }_{\nu }}$ к решению, пропорциональна $p$. Оценим эту поправку. Легко видеть, что Следовательно, при $\mu \ll h$ адиабатическое приближение не применимо. Подробнее о зависимости решения уравнений такого типа от отношения параметров $\mu $ и $h$ (см., например, [22]).

7. ПРИМЕРЫ

Рассмотрим применение полученных аналитических формул на конкретном примере. Возьмем рельеф дна, задаваемый функцией $D({\mathbf{x}}) = - 1 - exp( - (x_{1}^{2} + x_{2}^{2}))$. Источник находится в точке $\xi = ( - 3,0)$, $\mu = 0.1$, $h = 0.01$. Решена система уравнений Гамильтона (33) и построены соответствующие траектории (фиг. 2):

где ${\mathbf{n}}(\psi ) = (cos(\psi ),sin(\psi ))$.

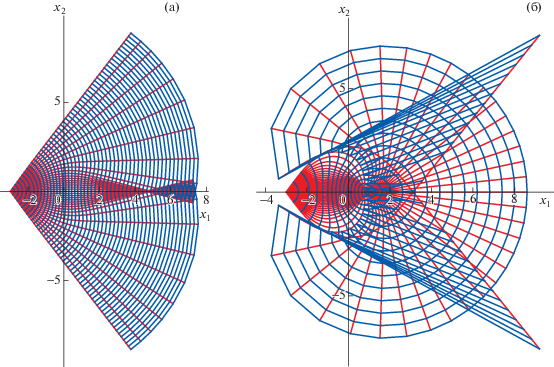
Как видно из решения (фиг. 2), каустики и фокальные точки для разных мод соответствуют разным точкам конфигурационного пространства. Решение проектируется с характеристик на конфигурационное пространство нетривиальным образом. Канонический оператор в неособых картах выражается по формуле (26). Существуют области конфигурационного пространства, которые соответствуют многолистности лангранжева многообразия ${{\Lambda }_{ + }}$. Проекция на $\mathbb{R}_{x}^{2}$ – сумма проекций с каждого листа. На фиг. 2 многолистность лагранжева многообразия соответствует областям с пересечением фронтов. Чтобы построить волновое поле в $\mathbb{R}_{x}^{2}$, нужно сложить решения на всех фронтах. При проектировании с особых карт использовалось представление интеграла (27) через функции Эйри [32], [33].

Рассмотрим два варианта правой части в уравнении (10):

соответственно, где $p = \sqrt {{{n}^{2}} - \tfrac{{{{{(\pi \nu )}}^{2}}}}{{{{D}^{2}}(\xi )}}} {\mathbf{n}}(\psi ) = \rho {\mathbf{n}}(\psi )$, амплитуду можно переписать в виде В первом случае амплитуда максимальна при $\rho \to 0$, во втором случае максимум смещается в точку $\rho = 1{\text{/}}\sqrt {{{a}^{2}}co{{s}^{2}}(\psi ) + {{b}^{2}}si{{n}^{2}}(\psi )} $, $tan(\psi ) = {{b}_{1}}{\text{/}}{{a}_{1}}$. Таким образом, меняя параметры источника, можно добиться максимума амплитуды в нужной области.

ПРИЛОЖЕНИЕ

Приведем вывод соотношений (9). Сначала рассмотрим однородное уравнение Гельмгольца, подстановка (7) приводит к уравнению

При этом будем предполагать, что функции ${{\psi }_{\nu }}$ удовлетворяют уравнению Уравнение (37) можно переписать в виде Для решения уравнения (39) перейдем от операторов к символам (см. [22]). Символ произведения операторов можно найти по формуле [22] Следовательно, уравнение (39) можно переписать в виде Решаем уравнение (41) с помощью теории возмущений, это дает где $\chi _{\nu }^{0}$ удовлетворяет граничным условиям Уравнение для $\chi _{\nu }^{0}$ имеет вид Собственные функции и собственные значения задачи (44) с граничными условиями (43) имеют вид Уравнение для $L_{\nu }^{1}$ запишем как Оператор $\left( {\mathcal{H} - L{{'}_{\nu }}} \right)$ самосопряженный, следовательно, разрешимость уравнения (45) эквивалентна ортогональности правой части и $\chi _{\nu }^{0}$: Отсюда следует, что Поэтому уравнение для модовых амплитуд с точностью до $O({{h}^{2}})$ можно переписать в виде Вычислим символ оператора $\mathop {\hat {\chi }}\nolimits_\nu ^1 $. Уравнение (45) эквивалентно следующему: Решение этого уравнения имеет вид где $\chi _{\nu }^{1}$ удовлетворяет граничным условиям поэтому ${{c}_{1}} = 0$.

Для того чтобы устранить неопределенность в выборе ${{c}_{2}}$, можно нормировать функции ${{\chi }_{\nu }}$ в виде

Уравнение (47) равносильно тому, что главный член скалярного произведения равен единице, а “поправка” порядка $h$ равна нулю. Учитывая, что $\chi _{\nu }^{0}$ не зависит от $p$, и ${{\left( {a\left( {\mathop p\limits^1 ,\mathop x\limits^2 } \right)} \right)}^{ * }} = \bar {a}\left( {\mathop p\limits^2 ,\mathop x\limits^2 } \right)$, выпишем уравнение для первой поправки: Отсюда следует, что ${{c}_{2}} = 0$.

Авторы благодарят П.С. Петрова за ценные обсуждения.