Журнал вычислительной математики и математической физики, 2019, T. 59, № 5, стр. 860-866

1. ВВЕДЕНИЕ

Бурное развитие нанотехнологий потребовало разработки специальных подходов для их численных исследований [1]. Несмотря на достигнутые успехи, микротечения являются объектом интенсивного исследования, а их изучение до сих пор вызывает различные сложности. Сосуществование разреженных и сплошносредных областей течения является характерной особенностью микротечений. Разреженные течения описываются с помощью кинетических подходов, которые являются численно затратными вследствии дискретизации кинетического уравнения в физическом и скоростном пространствах. Сплошносредные течения хорошо описываются менее дорогостоящими уравнениями Навье–Стокса, которые могут быть менее точными в критических разреженных областях течения. В пограничном слое, образующемся у поверхности твердого тела, неточность уравнений частично преодолевается введением условий скольжения и температурного скачка на твердой поверхности. Однако данные условия справедливы при числах Кнудсена Kn ≤ 0.1. Кроме того, в микротечениях разреженность играет ключевую роль и уравнения Навье–Стокса даже с учетом условий скольжения не всегда справедливы во всем поле течения.

Создание гибридных методов, использующих кинетический подход в локальных разреженных областях течения, и сплошносредное описание в остальной части течения для моделирования многомасштабных течений представляет собой важную область исследования в последние годы [2]–[10]. Наиболее популярным подходом при создании гибридного метода является разбиение физического пространства на кинетическую и сплошносредную подобласти, используя некоторый критерий. При этом в кинетической подобласти в основном используются методы Монте-Карло [2]–[7]. В разработанном гибридном подходе [8]–[10] применяется прямое численное решение кинетического уравнения, что предпочтительнее для процедуры сращивания решений, так как в этом случае и кинетический, и гидродинамический подходы используют схожие численные схемы. Для расщепление течения на подобласти используется критерий, основанный на градиентах макровеличин и локальном числе Кнудсена Kn, предложенный в [7].

В данной работе гибридный метод используется для исследования течения разреженного газа в плоском микроканале, вызванного произвольным перепадом давления. Рассматривается также предельный случай – течение через щель, когда влиянием твердых стен на течение можно пренебречь. Оценивается ускорение гибридного метода в сравнении с кинетическим подходом.

2. ПОСТАНОВКА ЗАДАЧИ

Рассматривается двумерное течение моноатомного газа в канале высоты H и длины l = 10H, соединяющего резервуары размера L_x × L_y = 5H × 3H (см. фиг. 1), заполненных газом. Также моделируется предельный случай l = 0 – течение газа через щель, расположенную на бесконечно тонкой пластине, разделяющей резервуары (см. фиг. 1). Выбор области моделирования в случае трещины обусловлен спецификой построения сетки и представляет собой полукруг радиуса R. Течение симметрично относительно y = 0, поэтому моделируется только нижняя половина области течения. Жирная линия на фиг. 1 показывает подвижную границу I_c между кинетической Ω_K и сплошносредной Ω_NS подобластями.

Предполагается, что вдали от канала (трещины) газ находится в состоянии равновесия при температуре T₀ и давление p₀ в первом резервуаре и при давлении p_e (p₀ > p_e) и той же температуре T₀ во втором. Температура стенок канала и пластины T_w совпадает с температурой газа T₀. Вследствие перепада давления между резервуарами возникает течение газа в канале (или через щель). Таким образом, течение газа определяется величиной перепада давления p₀/p_e и параметром разреженности газа δ = p₀H/μ₀${{\text{v}}_{0}}$, здесь ${{\text{v}}_{0}}$ = (2RT₀)^0.5 – тепловая скорость, μ₀ – динамическая вязкость газа при температуре T₀, R – газовая постоянная.

Основной характеристикой течения является безразмерный поток массы W = $\dot {m}$/m_fm, который нормируется на значение потока в свободномолекулярном режиме m_fm = p₀/π^0.5${{\text{v}}_{0}}$. Поток массы через канал $\dot {m}$ равен:

3. ГИБРИДНЫЙ МЕТОД

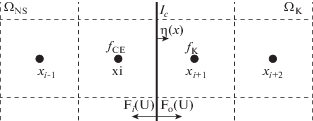
Схематичное изображение процедуры сращивания решения S-модельного кинетического уравнения с решением уравнений Навье–Стокса, выполняемой в гибридном методе, показано на фиг. 2. Для определения размера и положения кинетической подобласти Ω_K выбран критерий, основанный на оценке локального числа Кнудсена Kn и градиентов макропараметров [7], [8]:

здесь P = (ρ, |V|, T) – вектор макропараметров течения. Считается, что если Kn_GL(x) больше некоторого критического значения ε, решается кинетическое уравнение, а в остальной области течения, т.е. Kn_GL(x) < ε, решаются уравнения Навье–Стокса. В работе [10] показано, что значение ε = 0.1 гарантирует разность между гибридным и кинетическим решением около 1%.

В кинетической подобласти течения, x ∈ Ω_K, решается S-модельное кинетическое уравнение [11], которое можно записать в безразмерном виде:

здесь  f = f(t, x, ξ) – функция распределения молекул по скоростям, т.е. вероятность обнаружить частицу со скоростью ξ= (ξ_x, ξ_y, ξ_z) в точке пространства x = (x, y) в момент времени t,  f_S – стандартная локальная функция Шахова [11], c = ξ – V – собственная скорость молекул, V = (u, $\text{v}$) – массовая скорость газа. Для обезразмеривания уравнения (3) использовались равновесные параметры газа ρ₀ и T₀ и высота микроканала (трещины) H. В работе используется модель твердых шаров, тогда безразмерная вязкость вычисляется как μ = T  ^0.5.

В остальной, сплошносредной подобласти течения Ω_NS решаются вязкие сжимаемые уравнения Навье–Стокса:

Здесь U = (ρ, ρu, ρ$\text{v}$, ρe_tot)^т – вектор макровеличин, e_tot = e + V²/2 – полная энергия в единице массы, F(U) – вектор потоков, включающий конвективные и диффузионные (вязкие) компоненты.

В кинетическом подходе макровеличины плотность ρ, импульс ρV и внутренняя энергия единицы массы e вычисляются интегрированием по всему скоростному пространству:

Так как течение является двумерным, можно аналитически упростить задачу, убрав компоненту вектора скорости ξ_z [12], [13]. Кинетическое уравнение (3) дискретизируется в физическом и скоростном пространствах и решается, используя явно-неявную схему [12], [13]. Этап переноса в уравнении (3) аппроксимируется явной конечно объемной схемой. Потоки вычисляются с помощью TVD схемы с ограничителем в виде minmod.

Численное решение уравнений Навье–Стокса основано на конечно-разностном и конечно-объемном методах второго порядка точности по пространству и времени [9], [10]. Для интегрирования по времени используется схема Кранка–Николса.

Сращивание между решениями уравнений Навье–Стокса и кинетического уравнения достигается с помощью согласования полупотоков массы, импульса и энергии через границу между подобластями I_c [9], [10]

На границе I_c для молекул, входящих в подобласть Ω_K, задается функция распределения по скоростям Чепмен–Энскога f_CE(t, ξ, x) [14] с макропараметрами, вычисленными в сплошносредной подобласти течения Ω_NS. Полупотоки массы, импульса и энергии F_i(U) · η(x), входящие в подобласть Ω_NS из кинетической подобласти Ω_K, вычисляются на основе решения кинетического уравнения в Ω_K (см. фиг. 2):

где s(ξ) = (1, ξ, ξ²/2) – вектор столкновений, f(t, x, ξ) – решение кинетического уравнения (3).

Исходящие полупотоки F_o(U) · η(x) из сплошносредной подобласти Ω_NS в кинетическую Ω_K вычисляются интегрированием функции распределения Чепмен–Энскога с макропараметрами, вычисленными в Ω_NS

При таком подходе автоматически выполняется сохранение потока массы, импульса и энергии через границу I_c. Положение границы I_c между подобластями Ω_K и Ω_NS определяется на каждом шаге по времени. Если точка пространства, находящаяся в Ω_NS на предыдущем шаге по времени, перемещается в Ω_K, то функция распределения в ней задается в виде функции Чепмен–Энскога.

Если входная/выходная граница попадает в сплошносредную подобласть Ω_NS, полная температура и давление на входе задаются равными p₀ и T₀, т.е. температуре и давлению в левом резервуаре, а давление на выходе равно давлению в правом резервуаре p_e. Если входная/выходная границы находятся в кинетической подобласти Ω_K, для молекул входящих в подобласть, задается локально-максвелловская функция распределения с параметрами, соответствующими условиям в резервуарах. На твердой поверхности в кинетической подобласти Ω_K задаются диффузные граничные условия с полной аккомодацией. Если твердая поверхность попадает в Ω_NS, то задаются условия скольжения и температурный скачок.

Гибридный код написан на C++ (код для решения кинетического уравнения и процедуры сращивания) и на Fortran для решения системы уравнений Навье–Стокса. Для повышения эффективности гибридный код распараллелен с помощью MPI (message passing protocol) [15]. Расчеты выполнены на многоядерной системе, состоящей из 2 процессоров с 4 ядрами Intel(R) Xeon(R) E5520 CPU, 2.27 (2.93) GHz, 8 MB Cache.

4. ПАРАМЕТРЫ МОДЕЛИРОВАНИЯ

Численное моделирование течения газа в микроканале и микрощели проводилось для отношений давлений p₀/p_e = 1.1, 2, 10 и параметре разреженности газа δ, варьирующегося от 100 (режим скольжения) до 1 (переходный режим). Для большинства расчетов в физическом пространстве используется неоднородная структурированная криволинейная сетка с числом узлов в направлении по потоку, равным 360, и с 40 узлами в поперечном направлении. Размер минимального шага по потоку равен 0.02, в поперечном направлении – 0.008 для канала и 0.017 для щели. В случае течения со значительными градиентами макропараметров (p₀/p_e = 10) использовалась более подробная сетка размера 400 × 60.

Однородная двумерная сетка задавалась в пространстве скоростей. Размер скоростной сетки удовлетворяет условию ${{\text{v}}_{{\max }}}$ ≥ max(|u|, |v|) + 3.5$T_{{\max }}^{{0.5}}$. Для большинства расчетов число узлов по каждому направлению скорости выбиралось равным 24 и размер скоростного пространства был ограничен максимальным значением ${{\text{v}}_{{\max }}}$ = 5.2. Для максимального перепада давления p₀/p_e = 10 размер скоростного пространства и число узлов в скоростном пространстве увеличивались до ${{\text{v}}_{{\max }}}$ = 7.6 и 48 узлов (по каждому направлению) соответственно.

Влияние параметров сетки на поле течения оценивалось с помощью сравнения потока массы для расчетов на грубой сетке, состоящей из 240 × 40 узлов. Разница между результатами, полученными на грубой и более мелкой сетках, не превышала нескольких процентов. Оптимально число узлов в скоростном пространстве выбиралось таким образом, что удваивание их числа не изменяет поток массы более чем на 1–1.5%.

В гибридном методе шаг по времени выбирается из условия Δt = min(Δt_K, Δt_NS). При этом в кинетическом подходе шаг по времени Δt_K должен удовлетворять условию устойчивости Куранта–Фридрихса–Леви (CFL), где CFL = 0.4, а в сплошносредном подходе шаг может быть произвольным Δt_NS. Решение считалось установившимся, если выполнилось условие ||U^n + 1 – Uⁿ||_L2 < Δ, где L₂ – норма и Δ = 10^–7.

5. АНАЛИЗ ЧИСЛЕННЫХ РЕЗУЛЬТАТОВ

Будем считать, что кинетический подход, основанный на решении S-модельного уравнения, является эталонным методом. Оценим отклонение потока массы W, полученных гибридным методом W_h и с помощью решения уравнений Навье–Стокса W_NS от эталонного кинетического решения W_S. Для этого вычислим относительные разности ΔW_h и ΔW_NS как:

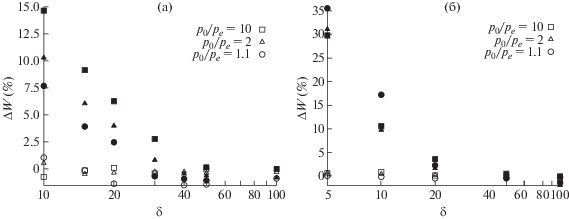
На фиг. 3 показаны относительные разности ΔW_NS и ΔW_h для течения через канал (фиг. 3а) и щель (фиг. 3б) при p₀/p_e = 10, 2 и 1.1 и параметре разреженности δ от 5 до 100. Когда газ слаборазрежен (δ ≥ 50), потоки массы, полученные кинетическим, гибридным и методами Навье–Стокса, отличаются не более чем на 2%. Начиная с δ = 20 разница между кинетическим и решением уравнений Навье–Стокса ΔW_NS становится заметной (>5%) и растет с увеличением разреженности газа. Следует отметить, что в случае течения через щель, превышение 5% порога достигается позже, при δ = 15, чем для течения в канале, вследствие более слабого воздействия твердых границ на течение через щель. Максимальное отклонение ΔW_NS = 35% для течения через щель при δ = 5 и 15% при δ = 10 для течения в канале. При этом разность между гибридным и кинетическим решением ΔW_h порядка 1–2%, во всем рассматриваемом диапазоне параметра разреженности δ.

Пример, распределение контурных линий плотности и числа Маха около щели и вдоль канала, а также положение границы I_c между кинетической областью Ω_K и сплошносредной Ω_NS показаны на фиг. 4 для δ = 10 и p₀/p_e = 2. Можно видеть, что линии, пересекающие границу I_c, демонстрируют плавный переход, что говорит о правильном сращивании кинетического и сплошносредного решений.

Время, требуемое для одного шага гибридного кода, t_h, представляет собой сумму времен, требующихся для решения S-модельного уравнения в N_K кинетических точках (подобласть Ω_K), уравнений Навье–Стокса в N_total – N_K точках (подобласть Ω_NS) и процедуры сращивания (N_total – полное число узлов в физическом пространстве). Так как время, затрачиваемое на решение уравнений Навье–Стокса и процедуру сращивания, достаточно мало, то время t_h, необходимое гибридному методу, определяется числом кинетических точек N_K, в которых решается модельное кинетическое уравнение.

Достигнутое гибридным методом ускорение оценивалось как s = t_K/t_h, где t_K – время решения кинетического уравнения во всем поле течения, т.е. в N_total точках. Максимальное ускорение, достигаемое в расчетах s ≈ 12 при δ = 100, и падает с уменьшением δ, до минимального ускорения около 2 при δ = 10, так как с увеличением разреженности газа растет число кинетических точек N_K.

ВЫВОДЫ

Гибридный метод, основанный на сращивании решений кинетического уравнения и уравнений Навье–Стокса, использовался для численного моделирования течения в микроканале и щели. Показано, что результаты, полученные гибридным методом, хорошо совпадают с кинетическими результатами, даже при тех условиях, когда сплошносредный подход (уравнения Навье–Стокса) дают полностью не корректные результаты. Гибридный метод демонстрирует ускорение от 12 до 2 раз в сравнении с решением кинетического уравнения. При этом ускорение гибридного метода зависит от степени разреженности газа.