Журнал вычислительной математики и математической физики, 2019, T. 59, № 5, стр. 867-888

ВВЕДЕНИЕ

Продолжая исследования неустойчивости течений (см. [1]–[6]) с учетом вертикальной диффузии массы и импульса, мы рассмотрим модельное течение типа Куэтта, т.е. течение с линейным вертикальным профилем скорости или с постоянным вертикальным сдвигом, которое является типичным для океана. Для описания динамики возмущений такого течения использовалось линейное уравнение потенциального вихря в квазигеострофическом приближении. Вывод основных уравнений модели подробно представлен в [3]–[5].

Особое внимание в работе уделено разработке аналитико-численного метода решения спектральных задач типа Орра–Зоммерфельда и построению асимптотического разложения собственных функций (СФ) и собственных значений (СЗ) при малых волновых числах. Это позволило создать высокоэффективный метод расчета и исследовать неустойчивость модельных течений в широком диапазоне физических параметров.

Задача ставится следующим образом. Область, в которой исследуется течение, является бесконечным (вдоль направления течения) горизонтальным слоем с верхней и нижней границами ${{z}_{0}}$ и ${{z}_{1}}$ и боковыми границами ${{y}_{0}}$ и ${{y}_{1}}$. Для описания этого слоя введем вертикальную переменную $z \in [{{z}_{0}},{{z}_{1}}]$, поперечную переменную $y \in [{{y}_{0}},{{y}_{1}}]$ и переменную $x$, направленную вдоль течения, $x \in ( - \infty ,\infty )$.

Следуя [3], [4], представим возмущение безразмерного давления $p$ в виде полуволны по оси $y$ и бегущей волны вдоль оси $x$ с неизвестной скоростью $c$,

Тогда задача нахождения профиля $F(z)$ сводится к решению на отрезке $z \in [0,1]$ уравнения для комплекснозначной функции $F = F(z)$:

Два краевых условия задают отсутствие протекания на горизонтальных границах слоя $z = 0$ и $z = 1$,

Еще два условия на этих границах задают равенство нулю потоков плавучести

Таким образом, здесь возникают две спектральные задачи на отрезке $z \in [0,1]$ для бесконечнодифференцируемых функций $F(z)$.

Задача I. Найти собственные функции (СФ) $F(z)$ и соответствующие им собственные значения (СЗ) $c$ – решения уравнения (0.2) с краевыми условиями (0.3), (0.4).

Задача II. Найти собственные функции $F(z)$ и соответствующие им СЗ $c$ – решения уравнения (0.2) с краевыми условиями (0.3), (0.5).

Необходимо отметить, что оператор задач I и II является несамосопряженным, он содержит малый параметр ${{(k{\text{R}})}^{{ - 1}}}$ при старшей производной (величина $k{\text{R}}$ для реальных течений может быть очень большой), а спектральный параметр $c$ входит как в уравнение (0.2), так и в краевое условие (0.3). Собственных функций ${{F}_{n}}(z)$ и соответствующих им СЗ ${{c}_{n}}$ будет счетное множество, а неустойчивость по времени возмущений давления $p(x,y,z;t)$ возникает для тех СФ, которым соответствует СЗ ${{c}_{n}}$, имеющее мнимую часть $\operatorname{Im} ({{c}_{n}}) > 0$, что следует из представления (0.1).

Обзор литературы и современное состояние исследований спектра подобных операторов содержатся в [7]; обзор методов вычисления СЗ таких задач дан в [8]–[10]. В [11], [4], [5] изложен метод, позволивший эффективно вычислить СФ и СЗ уравнений типа Орра–Зоммерфельда с высокой точностью. В настоящей работе этот метод использован для решения задач I и II.

1. СИММЕТРИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ

Докажем свойство симметрии СЗ ${{c}_{n}}$ задач I и II.

Tеорема. Собственные значения ${{c}_{n}}$ задачи (0.2), (0.3), (0.4) и задачи (0.2), (0.3), (0.5) при вещественных параметрах $k$, ${\text{R}}$, ${\text{Pr}}$, ${\text{Bu}}$ обладают симметрией относительно прямой $\operatorname{Re} (c) = \tfrac{1}{2}$. Если ${{c}_{n}}$ является СЗ задачи (0.2), (0.3), (0.4), то

Если ${{c}_{n}}$ является СЗ задачи (0.2), (0.3), (0.5), то

Доказательство. Рассмотрим сначала задачу (0.2), (0.3), (0.4), и пусть она имеет решение в виде СФ $F(z)$ и соответствующего СЗ $c$, причем $\operatorname{Re} (c) \ne \tfrac{1}{2}$. Обозначим вещественную и мнимую части СФ и СЗ следующим образом:

Краевые условия (0.3) в точках $z = 0$ и $z = 1$ при этом примут следующий вид:

Теперь рассмотрим другую комплекснозначную функцию $\widehat F(\tilde {z})$ и другой комплексный параметр $\hat {c}$,

Далее проводим соответствующую замену в краевых условиях (1.5) и убеждаемся в их справедливости для функций $\hat {g}(\tilde {z})$ и $\widehat h(\tilde {z})$. Таким образом, справедливость теоремы для задачи I доказана.

Аналогичная замена в задаче II с краевым условием (0.5) также доказывает справедливость теоремы. Таким образом, СФ исследуемых задач обладают симметрией относительно точки $z = \tfrac{1}{2}$, а СЗ при этом обладают симметрией относительно прямой $\operatorname{Re} (c) = \tfrac{1}{2}$. Это завершает доказательство теоремы.

2. МЕТОД РАСЧЕТА СФ И СЗ

Вычисление СФ $F(z)$ и соответствующих СЗ $c$ основано на методе (см. [11], [12], [5], [4]), который использует степенные разложения $F(z)$ в граничных точках $z = 0$, $z = 1$ и их гладкую сшивку в некоторой точке ${{z}_{ * }} \in (0,1)$.

Пусть зафиксирован спектральный параметр $c$. Тогда $F(c;z)$ – решение уравнения (0.2) – представим в виде следующих разложений в точках $z = 1$ и $z = 0$:

Подставляя ряды (2.1), (2.2) в уравнение (0.2), получаем рекуррентные соотношения для коэффициентов ${{a}_{n}}$ и ${{b}_{n}}$:

Далее учтем краевые условия. Первое из них, (0.3), задает связь коэффициентов ${{a}_{0}}$, ${{a}_{1}}$ и ${{a}_{3}}$, а также ${{b}_{0}}$, ${{b}_{1}}$ и ${{b}_{3}}$:

Сначала построим решение задачи I. Определим функцию ${{F}_{1}}(c;z)$ в виде разложения (2.1), задав $a_{0}^{{(1)}}$ и $a_{1}^{{(1)}}$ следующими:

Аналогично этому построим вторую функцию ${{F}_{2}}(c;z)$ в виде такого же разложения (2.1), но задав $a_{0}^{{(2)}}$ и $a_{1}^{{(2)}}$ следующими:

Теперь построим две функции ${{F}_{3}}(c;z)$ и ${{F}_{4}}(c;z)$ в виде разложений (2.2), задав коэффициенты $b_{0}^{{(1)}}$, $b_{1}^{{(1)}}$ и $b_{0}^{{(2)}}$, $b_{1}^{{(2)}}$ следующими:

Тогда общее решение ${{F}_{(}}c;z)$ уравнения (0.2) с краевыми условиями (0.3), (0.4) лишь в точке $z = 0$ есть линейная комбинация ${{F}_{3}}(c;z)$ и ${{F}_{4}}(c;z)$:

Для построения СФ и нахождения СЗ задачи I выберем произвольную точку ${{z}_{ * }}$ на интервале $(0,1)$ и потребуем совпадения в этой точке функций (2.8) и (2.9), а также их первых трех производных по $z$, т.е.

Нетривиальное решение системы (2.10) возможно только в случае равенства нулю вронскиана $W({{F}_{1}},{{F}_{2}},{{F}_{3}},{{F}_{4}})$:

При решении задачи II необходимо также построить две функции ${{F}_{1}}(c;z)$ и ${{F}_{2}}(c;z)$ в виде разложений (2.8) и две функции ${{F}_{3}}(c;z)$ и ${{F}_{4}}(c;z)$ в виде разложений (2.9), но вместо нулевых условий (2.6) для коэффициентов ${{a}_{2}}$ и ${{b}_{2}}$ необходимо взять условия (2.7) для ${{a}_{0}}$ и ${{b}_{0}}$ и для ${{a}_{1}},{{a}_{2}}$ положить

Необходимая для метода Ньютона производная $\partial W(...;c;{{z}_{ * }}){\text{/}}\partial c$ от вронскиана (2.11) системы (2.10) находилась с помощью явного дифференцирования по спектральному параметру $c$ всех производных $F_{1}^{{(p)}}(c;{{z}_{ * }})$, $F_{2}^{{(p)}}(c;{{z}_{ * }})$, $F_{3}^{{(p)}}(c;{{z}_{ * }})$, $F_{4}^{{(p)}}(c;{{z}_{ * }})$ для $p = 0,1,2,3$. Например, смешанные производные $\partial F_{1}^{{(p)}}(c;{{z}_{ * }}){\text{/}}\partial c$ и $\partial F_{2}^{{(p)}}(c;{{z}_{ * }}){\text{/}}\partial c$ вычислялись дифференцированием рядов (2.1),

3. АСИМПТОТИКА СФ И СЗ ЗАДАЧИ ${\text{I}}$ ПРИ $k \to 0$

Построим при $k \to 0$ асимптотическое разложение СФ и СЗ при фиксированных и ненулевых физических параметрах ${\text{Pr}}$, ${\text{Bu}}$, ${\text{Pr}}$. Здесь необходимо отдельно рассмотреть два варианта – случай конечных СЗ и случай неограниченных СЗ.

3.1. Ограниченные СЗ

Исследуем сначала асимптотическое разложение при $k \to 0$ для СФ и СЗ задачи I при условии, что СЗ имеет конечный предел.

Используя методы асимптотического анализа [13], [14], представим СФ $F(k;z)$ и соответствующее ей СЗ $c(k)$ в виде разложения по степеням малого параметра $k$:

(3.1)

$F(k;z) = {{\varphi }_{0}}(z) + k{{\varphi }_{1}}(z) + {{k}^{2}}{{\varphi }_{2}}(z) + \ldots ,$

(3.2)

$c(k) = {{\gamma }_{0}} + k{{\gamma }_{1}} + {{k}^{2}}{{\gamma }_{2}} + \ldots ,\quad k \to 0.$

Подстановка (3.1), (3.2) в уравнение (0.2) и краевые условия (0.3), (0.4) и приравнивание соответствующих слагаемых при степенях ${{k}^{p}},\;p = 0,1,\; \ldots $, приводит к цепочке краевых задач для ${{\varphi }_{p}}(z)$ на отрезке $z \in [0,1]$. Первая из них, для ${{\varphi }_{0}}(z)$, имеет вид

(3.3)

$\varphi _{0}^{{''''}}(z) - \Pr \operatorname{Bu} {{\pi }^{2}}\varphi _{0}^{{''}}(z) = 0,$

(3.4)

$\varphi _{0}^{{'''}}(0) = \varphi _{0}^{{'''}}(1) = 0,\quad \varphi _{0}^{{''}}(0) = \varphi _{0}^{{''}}(1) = 0.$

Решением (3.3), (3.4) является линейная функция

(3.5)

${{\varphi }_{0}}(z) = {{A}_{0}} + {{B}_{0}}z\quad \forall {{A}_{0}},{{B}_{0}}.$

Далее, для функции ${{\varphi }_{1}}(z)$ и константы ${{\gamma }_{0}}$ имеем уравнение

(3.6)

$\varphi _{1}^{{''''}}(z) - {\text{PrBu}}{{\pi }^{2}}\varphi _{1}^{{''}}(z) = i{\text{RBu}}{{\pi }^{2}}({{\gamma }_{0}} - z){{\varphi }_{0}}(z)$

и краевые условия

(3.7)

$\varphi _{1}^{{'''}}(z) = i{\text{R}}[(z - {{\gamma }_{0}})\varphi _{0}^{'}(z) - {{\varphi }_{0}}(z)],\quad \varphi _{1}^{{''}}(z) = 0,\quad z = \{ 0,1\} .$

Решение уравнения (3.6) ищем в виде суммы ${{\varphi }_{1}} = {{\varphi }_{h}} + {{\varphi }_{{nh}}}$, где ${{\varphi }_{h}}$ – общее решение однородного уравнения, а ${{\varphi }_{{nh}}}$ – частное решение неоднородного уравнения. Учитывая вид (3.5) для ${{\varphi }_{0}}$, выводим следующее представление для функции ${{\varphi }_{{nh}}}(z)$:

(3.8)

${{\varphi }_{{nh}}}(z) = {{D}_{2}}{{z}^{2}} + {{D}_{3}}{{z}^{3}} + {{D}_{4}}{{z}^{4}},$

где

(3.9)

${{D}_{2}} = \frac{{i{\text{R}}}}{{{\text{P}}{{{\text{r}}}^{2}}\operatorname{Bu} {{\pi }^{2}}}}{{B}_{0}} - \frac{{i{\text{R}}}}{{2{\text{Pr}}}}{{\gamma }_{0}}{{A}_{0}},\quad {{D}_{3}} = \frac{{i{\text{R}}}}{{6{\text{Pr}}}}({{A}_{0}} - {{\gamma }_{0}}{{B}_{0}}),\quad {{D}_{4}} = \frac{{i{\text{R}}}}{{12{\text{Pr}}}}{{B}_{0}}.$

Для решения ${{\varphi }_{h}}(z)$ запишем представление в удобной форме:

(3.10)

${{\varphi }_{h}}(z) = {{A}_{1}}sinh\lambda \left( {z - \frac{1}{2}} \right) + {{B}_{1}}cosh\lambda \left( {z - \frac{1}{2}} \right) + {{D}_{0}} + {{D}_{1}}z,\quad \lambda = \pi \sqrt {{\text{PrBu}}} ,$

с произвольными константами ${{A}_{1}},\;{{B}_{1}},\;{{D}_{0}}$ и ${{D}_{1}}$. Тогда, подставляя решение ${{\varphi }_{1}} = {{\varphi }_{h}} + {{\varphi }_{{nh}}}$ в краевые условия (3.7), получаем систему для искомых коэффициентов ${{A}_{1}}$ и ${{B}_{1}}$:

${{\lambda }^{2}}{{B}_{1}}cosh\frac{\lambda }{2} + 2{{D}_{2}} + 3{{D}_{3}} + 6{{D}_{4}} = 0,\quad {{\lambda }^{2}}{{A}_{1}}sinh\frac{\lambda }{2} + 3{{D}_{3}} + 6{{D}_{4}} = 0,$

${{\lambda }^{3}}{{A}_{1}}cosh\frac{\lambda }{2} + 6{{D}_{3}} + 12{{D}_{4}} + i{\text{R}}({{\gamma }_{0}}{{B}_{0}} + {{A}_{0}}) = 0,\quad {{\lambda }^{3}}{{B}_{1}}sinh\frac{\lambda }{2} + 12{{D}_{4}} = 0.$

Учитывая соотношения (3.9) и разрешая эту систему относительно ${{A}_{1}}$ и ${{B}_{1}}$, получаем систему относительно коэффициентов ${{A}_{0}}$ и ${{B}_{0}}$ в представлении ${{\varphi }_{0}}(z)$ из (3.5):

$\lambda \left( {\frac{1}{2} - {{\gamma }_{0}}} \right)sinh\frac{\lambda }{2}{{A}_{0}} + \left[ {\left( {\frac{2}{\lambda } + \frac{\lambda }{2} - \frac{\lambda }{2}{{\gamma }_{0}}} \right)sinh\frac{\lambda }{2} - cosh\frac{\lambda }{2}} \right]{{B}_{0}} = 0,$

$\left[ {\frac{\lambda }{2}cosh\frac{\lambda }{2} - (1 + {\text{Pr}})sinh\frac{\lambda }{2}} \right]{{A}_{0}} + \left[ {\frac{\lambda }{2}(1 - {{\gamma }_{0}})cosh\frac{\lambda }{2} + ({{\gamma }_{0}} - 1 - {{\gamma }_{0}}{\text{Pr}})sinh\frac{\lambda }{2}} \right]{{B}_{0}} = 0.$

Нетривиальность решения этой системы требует равенства нулю ее детерминанта, что приводит к трансцендентному уравнению для искомой величины ${{\gamma }_{0}}$:

(3.11)

$\gamma _{0}^{2} - {{\gamma }_{0}} + Q = 0,\quad Q = \frac{U}{V},$

где

(3.12)

$U = \frac{{{\text{Pr}} + 2}}{2}sinh\lambda - \frac{\lambda }{2} - \frac{{{\text{Pr}} + 1}}{2}\left( {\frac{\lambda }{2} + \frac{2}{\lambda }} \right)(cosh\lambda - 1),$

(3.13)

$V = - \frac{{{{\lambda }^{2}}}}{4}sinh\lambda - \lambda \frac{{{\text{Pr}} - 1}}{2}(cosh\lambda - 1).$

Решение уравнения (3.11) запишем в форме, учитывающей знак величины $Q - 1{\text{/}}4$:

(3.14)

${{\gamma }_{{{{0}_{{1,2}}}}}} = \frac{1}{2} \pm \sqrt {\frac{1}{4} - Q} ,\quad Q \leqslant \frac{1}{4},$

(3.15)

${{\gamma }_{{{{0}_{{1,2}}}}}} = \frac{1}{2} \pm i\sqrt {Q - \frac{1}{4}} ,\quad Q \geqslant \frac{1}{4}.$

Отсюда получаем, что при $Q > \tfrac{1}{4}$ одно из значений ${{\gamma }_{0}}$ лежит в полуплоскости $\operatorname{Im} {{\gamma }_{0}} > 0$, а значит, при малых параметрах $k$, в силу представления (3.2), обеспечивает условие $\operatorname{Im} c > 0$, что приводит к неустойчивости исследуемого течения.

При $Q < \tfrac{1}{4}$ оба значения ${{\gamma }_{{{{0}_{{1,2}}}}}}$, как видно из (3.14), лежат на оси $\operatorname{Im} {{\gamma }_{0}} = 0$, а значит, при $k \to + 0$ это практически соответствует нейтральности возмущений с точностью до первого члена разложения (3.2).

Теперь рассмотрим случай достаточно широких течений, которым соответствуют значения параметра ${\text{Bu}} \ll 1$; при этом значения ${\text{Pr}} \sim 1$. Тогда, учитывая определение $\lambda = \pi \sqrt {{\text{BuPr}}} $, введенное в (3.10), заключаем, что $\lambda \ll 1$. Разложим выражения $U$, $V$ и $Q$ из равенств (3.12), (3.13) и (3.11) в ряд по малому параметру ${\text{Bu}}$ и получим

(3.16)

$Q = \frac{1}{3} + \frac{{{{\pi }^{2}}{\text{Bu}}}}{{360}}\left( {{\text{Pr}} - 5} \right) + O(\mathop {{\text{Bu}}}\nolimits^2 ).$

Отсюда заключаем, что при малых ${\text{Bu}}$ получаем $Q > \tfrac{1}{4}$ и значения ${{\gamma }_{{{{0}_{{1,2}}}}}}$ будут вычисляться по формуле (3.15), что обеспечивает неустойчивость течения.

Отдельно рассмотрим случай $Q = \tfrac{1}{4}$, дающий кратный корень ${{\gamma }_{0}}$ в уравнении (3.11) и соответствующий пограничному режиму возмущений между неустойчивостью и нейтральностью при числах $k \to + 0$. Используя (3.11), (3.12), (3.13) и соотношение $\lambda = \pi \sqrt {{\text{PrBu}}} $, получаем параметрическую зависимость ${\text{Pr}} = {\text{Pr}}(\lambda )$ и ${\text{Bu}} = {\text{Bu}}(\lambda )$, описывающую эту границу,

(3.17)

$\Pr (\lambda ) = \frac{{8(cosh\lambda - 1) + {{\lambda }^{2}}(1 + 3cosh\lambda ) - \lambda (8 + {{\lambda }^{2}}{\text{/}}2)sinh\lambda }}{{4\lambda sinh\lambda - ({{\lambda }^{2}} + 8)(cosh\lambda - 1)}},$

(3.18)

$\operatorname{Bu} (\lambda ) = \frac{{{{\lambda }^{2}}}}{{{{\pi }^{2}}}}\frac{{4\lambda sinh\lambda - ({{\lambda }^{2}} + 8)(cosh\lambda - 1)}}{{8(cosh\lambda - 1) + {{\lambda }^{2}}(1 + 3cosh\lambda ) - \lambda (8 + {{\lambda }^{2}}{\text{/}}2)sinh\lambda }},$

а при малых значениях $\lambda $ эти зависимости ${\text{Pr}}(\lambda )$ и ${\text{Bu}}(\lambda )$ значительно упрощаются:

(3.19)

$\Pr (\lambda ) = \frac{{{{\lambda }^{2}}}}{{12}} - \frac{{{{\lambda }^{4}}}}{{720}} + O({{\lambda }^{6}}),\quad \operatorname{Bu} (\lambda ) = \frac{{12}}{{{{\pi }^{2}}}} + \frac{{{{\lambda }^{2}}}}{{5{{\pi }^{2}}}} + O({{\lambda }^{4}}).$

Если же величина $\lambda $ не является малой, то функции ${\text{Pr}}(\lambda )$ и ${\text{Bu}}(\lambda )$ значительно усложняются. Так, на фиг. 1 в координатах $({\text{Pr}},{\text{Bu}})$ представлена рассчитанная параметрическая зависимость (3.17), (3.18) для ${\text{Pr}}(\lambda )$ и ${\text{Bu}}(\lambda )$ при $\lambda \in [0,15]$.

Фиг. 1.

Зависимость Bu(Pr) для случая $Q = \frac{1}{4}$, $\lambda \in [0,\,\;15]$.

Точкам снизу под этой кривой (область ${\text{I}}$) соответствует случай $Q > 1{\text{/}}4$, а точкам сверху (область ${\text{II}}$) – случай $Q < 1{\text{/}}4$. Таким образом, в течениях с параметрами $({\text{Pr}},{\text{Bu}})$, соответствующими точкам области ${\text{I}}$, возникает неустойчивость при малых волновых числах $k$.

Течения с параметрами $({\text{Pr}},{\text{Bu}})$, соответствующими точкам области ${\text{II}}$, требуют построения разложений (3.2) для СЗ с нахождением слагаемого $k{{\gamma }_{1}}$ и выяснения знака величины $\operatorname{Im} ({{\gamma }_{1}})$, либо численных расчетов при малых $k$. Проведенные вычислительные эксперименты для этой области параметров $({\text{Pr}},{\text{Bu}})$ выявили условие ${\text{Im}}c < 0$, что обеспечивает устойчивость исследуемых возмущений течения при малых числах $k$.

Из фиг. 1 и (3.19) следует, что при значениях ${\text{Bu}} \leqslant \tfrac{{12}}{{{{\pi }^{2}}}}$ для любых параметров ${\text{Pr}}$ течение будет неустойчивым при малых $k$, а при ${\text{Bu}} > \tfrac{{12}}{{{{\pi }^{2}}}}$ будет существовать некоторый диапазон ${\text{Pr}} \in (0,{\text{P}}{{{\text{r}}}_{{{\text{Bu}}}}})$, при котором возмущения течений являются устойчивыми при малых $k$. Вне этого диапазона параметров $({\text{Pr}},{\text{Bu}})$ течение становится неустойчивым при малых $k$. Дальнейший численный анализ полностью подтвердил этот вывод.

4. АСИМПТОТИКА СФ И СЗ ЗАДАЧИ II ПРИ $k \to 0$

5. ТЕСТИРОВАНИЕ АЛГОРИТМА

Для проверки метода вычисления СЗ и СФ задач I и II были проведены многочисленные расчеты в широком диапазоне физических параметров ${\text{Pr}}$, ${\text{Bu}}$, ${\text{R}}$ и волновых чисел $k$. При этом варьировалась длина обрываемых разложений (2.1) и (2.2) и их производных по $z$ и по $c$, значительно увеличивалась мантисса ${\text{Digits}}$ в используемой арифметике, изменялась точка сшивки ${{z}_{ * }} \in (0,1)$ разложений в системе (2.10). Итерационный метод Ньютона (2.12) строился так, что начальное приближение ${{c}^{{(0)}}}$ при малых $k$ бралось из асимптотических разложений, построенных в пп. 3 и 4, а при увеличении $k$ использовался метод продолжения по параметру. Дополнительным инструментом проверки наличия СЗ в некоторой области $D$ на комплексной плоскости “c” служил обобщенный принцип аргумента (см. [15])

Помимо этого, как будет показано ниже, среди множества СЗ ${{c}_{m}}$, рассматриваемых как функции волнового числа $k$, возможно образование двойных СЗ при $\operatorname{Re} (c) = \tfrac{1}{2}$. Это означает, что есть два соседних СЗ ${{c}_{m}}(k)$ и ${{c}_{{m + 1}}}(k)$, совпадающих при некоторых величинах ${{k}_{ * }}$, а функции ${{c}_{m}}(k)$ и ${{c}_{{m + 1}}}(k)$ в точке ${{k}_{ * }}$ имеют ветвление второго порядка (2-листное ветвление). Рассматривая функции ${{c}_{m}}(k)$ и ${{c}_{{m + 1}}}(k)$ как функции комплексного числа $k$, получаем, что при обходе в плоскости $k$ вокруг точки ${{k}_{ * }}$ по кругу малого радиуса функция ${{c}_{m}}(k)$ при аналитическом продолжении переходит в ${{c}_{{m + 1}}}(k)$, а функция ${{c}_{{m + 1}}}(k)$ переходит в ${{c}_{m}}(k)$. Аналогичное поведение СЗ в задаче Орра–Зоммерфельда для течения Куэтта описано в [11], [12].

В окрестности этих значений ${{k}_{ * }}$ метод Ньютона (2.12) начинает сходиться очень медленно, что связано с тем, что и вронскиан $W(c)$ (см. (2.11)), и его производная $W'(c)$ в точке ветвления ${{c}_{m}}({{k}_{ * }})$ обращаются в ноль. Исключение этой неопределенности типа $0{\text{/}}0$ приводит к необходимости использования модификации метода Ньютона со второй производной:

Учитывая второй порядок ветвления функций ${{c}_{m}}(k)$ и ${{c}_{{m + 1}}}(k)$ в окрестности точки ${{k}_{ * }}$, их можно представить в виде

Использование (5.2) позволяет сделать вывод, что квадрат разности функций ${{c}_{m}}(k)$ и ${{c}_{{m + 1}}}(k)$ в окрестности точки ${{k}_{ * }}$ является регулярной функцией $S(k)$, имеющей в ${{k}_{ * }}$ ноль первого порядка:

Совокупность описанных методов позволила гарантированно вычислять СЗ и СФ, а также двойные СЗ ${{c}_{m}}({{k}_{ * }})$ с относительной точностью не менее 20–40 верных дес. знач. цифр.

6. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Приведем результаты расчетов спектра задач I и II для различных физических параметров ${\text{Pr}}$, ${\text{Bu}}$, ${\text{R}}$ и волновых чисел $k$. Картина траекторий СЗ ${{c}_{m}}(k)$ при изменении $k$ будет иметь много общего с траекториями СЗ задачи Орра–Зоммерфельда для течения Куэтта (см. [11], [12]).

6.1. Траектории СЗ задачи I

Как было показано в п. 3.2.1, в задаче I при $k \to 0$ существуют два конечных СЗ, описываемых асимптотикой (3.2), и счетное множество неограниченно растущих СЗ, описываемых разложением (3.46).

В зависимости от параметров ${\text{Pr}}$ и ${\text{Bu}}$ эти два конечных СЗ лежат в комплексной плоскости “c” симметрично относительно точки $c = \tfrac{1}{2}$, причем либо на вещественной оси $\operatorname{Im} (c) = 0$ (см. (3.14)), либо на прямой $\operatorname{Re} (c) = \tfrac{1}{2}$ (см. (3.15)). Первый из этих вариантов соответствует, как было отмечено в п. 3.1., устойчивым возмущениям при $k \to 0$; второй же вариант включает первое СЗ ${{c}_{1}}$ со значением $\operatorname{Im} ({{c}_{1}}) > 0$, что описывает неустойчивое по времени течение.

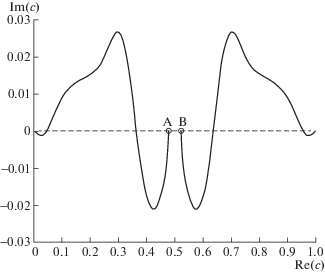
Рассмотрим траектории первых двух СЗ ${{c}_{1}}(k)$ и ${{c}_{2}}(k)$ задачи I для ${\text{Bu}} = 1.5$, ${\text{Pr}} = 1$, ${\text{R}} = 1000$ и при увеличении $k \in (0,2500]$. Как следует из фиг. 1, выбранным величинам ${\text{Bu}}$ и ${\text{Pr}}$ соответствует устойчивый характер течения при малых $k$.

На фиг. 2 в плоскости “c” приведены эти симметричные траектории ${{c}_{1}}(k)$ и ${{c}_{2}}(k)$, начинающиеся в точках $A = {{c}_{1}}(0) = 0.479...$ и $B = {{c}_{2}}(0) = 0.520...$ (отмечены кружочками), если формально положить $k = 0$ при реализации алгоритма.

Фиг. 2.

Траектории c₁(k) и c₂(k) для Bu = 1.5, Pr = 1, R = 1000 при увеличении $k \in (0,\;2500]$.

При $k \in (0,0.074)$ эти СЗ движутся в нижней полуплоскости, при $k \in (0.074,25.41)$ они переходят в верхнюю полуплоскость, а при $k \in (25.41,2500]$ эти СЗ опять движутся в нижней полуплоскости. Такое поведение СЗ показывает сложный характер устойчивых и неустойчивых возмущений для разных волновых чисел $k$, т.е. устойчивость возмущений для 1-го и 3-го интервалов изменения $k$ и неустойчивость возмущений для 2-го интервала.

Все остальные СЗ для выбранных параметров ${\text{Bu}} = 1.5$, ${\text{Pr}} = 1$ и ${\text{R}} = 1000$ при всех рассчетных числах $k \in (0,2500]$ движутся в нижней полуплоскости. При малых $k$ их поведение описывается асимптотикой (3.15), а при увеличении $k$ эти СЗ поднимаются снизу по прямой $\operatorname{Re} (c) = \tfrac{1}{2}$, причем немонотонно.

Рассмотрим поведение пары СЗ ${{c}_{3}}(k)$ и ${{c}_{4}}(k)$ на фиг. 3. При увеличении $k \in (0,0.0487]$ значение ${{c}_{3}}(k)$ поднимается до точки ${{c}_{3}} = \tfrac{1}{2} - 0.28103i$, а при дальнейшем увеличении $k \in (0.0487,{{k}_{ * }}]$, где ${{k}_{ * }} = 0.069386$, это СЗ ${{c}_{3}}(k)$ опускается до точки $A = \tfrac{1}{2} - 0.38552i$, в которой оно “сталкивается” с ${{c}_{4}}(k)$ и образует первое двойное СЗ. На фиг. 3 точка $A$ показана крестиком, прямая $\operatorname{Re} (c) = \tfrac{1}{2}$ отмечена пунктиром, а направление движения ${{c}_{3}}(k)$ и ${{c}_{4}}(k)$ по этой прямой при увеличении числа $k$ показано стрелками.

Фиг. 3.

Траектории c₃(k) и c₄(k) для Bu = 1.5, Pr = 1, R = 1000 при увеличении k.

При дальнейшем росте $k \in ({{k}_{ * }},2500]$ это двойное СЗ “распадается” на два простых СЗ, движущихся вправо и влево вдоль симметричных траекторий на фиг. 3 в направлении стрелок. Поскольку в окрестности точки ${{k}_{ * }}$ функции ${{c}_{3}}(k)$ и ${{c}_{4}}(k)$ описываются соотношением (5.2), то отсюда следует, что при переходе $k$ через точку $k = {{k}_{ * }}$ траектории ${{c}_{3}}(k)$ и ${{c}_{4}}(k)$ поворачиваются на угол $\tfrac{\pi }{2}$.

Глаголы “сталкивается” и “распадается” здесь использованы, чтобы указать, что скорости $c_{3}^{'}(k)$ и $с _{4}^{'}(k)$ движения СЗ ${{c}_{3}}(k)$ и ${{c}_{4}}(k)$ в точке $k = {{k}_{ * }}$ обращаются в бесконечность. Это следует из представления (5.2) при его дифференцировании по $k$. Нумерацию этих СЗ при $k > {{k}_{ * }}$ уже нельзя указать, если не принять дополнительных соглашений.

При стремлении $k \to + \infty $ эта пара СЗ ${{c}_{3}}(k)$ и ${{c}_{4}}(k)$ приближается к точкам $c = 0$ и $c = 1$, как показано на фиг. 3.

Все последующие пары СЗ ${{c}_{{2m + 1}}}(k)$ и ${{c}_{{2m + 2}}}(k)$, $m = 2,3,\; \ldots $, при выбранных параметрах ${\text{Bu}} = 1.5$, ${\text{Pr}} = 1$ и ${\text{R}} = 1000$ ведут себя аналогично рассмотренной паре ${{c}_{3}}(k)$ и ${{c}_{4}}(k)$.

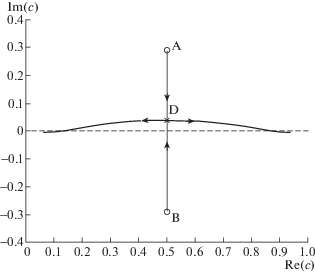
Однако при других параметрах ${\text{Bu}}$, ${\text{Pr}}$ и ${\text{R}}$ траектории ${{c}_{m}}(k)$ ведут себя иначе. На фиг. 4 показаны траектории первых двух СЗ ${{c}_{1}}(k)$ и ${{c}_{2}}(k)$ для значений ${\text{Bu}} = {{10}^{{ - 4}}}$, ${\text{Pr}} = 1$, ${\text{R}} = 1$ при изменении волнового числа $k$. Если $k \to 0$, то эти два СЗ ${{c}_{1}}(k)$ и ${{c}_{2}}(k)$ являются парой сопряженных чисел $\tfrac{1}{2} \pm 0.288656i$, отмеченных на фиг. 4 точками $A$ и $B$. При увеличении $k > 0$ эти СЗ движутся навстречу друг другу по вертикальной прямой $\operatorname{Re} (c) = \tfrac{1}{2}$, при $k = {{k}_{{ * ,2}}} = 244.9281$ они “сталкиваются” в точке $D = \tfrac{1}{2} + 0.0378i$ и образуют двойное СЗ, отмеченное на фиг. 4 крестиком. При последующем росте $k \in [244.9281,2500]$ это СЗ распадается на два простых СЗ, движущихся симметрично относительно прямой $\operatorname{Re} (c) = \tfrac{1}{2}$ и стремящихся к точкам $c = 0$ и $c = 1$.

Фиг. 4.

Траектории c₁(k) и c₂(k) для Bu = 10^–4, Pr = 1, R = 1 при увеличении $k \in (0,\;2500)$.

Последующие СЗ ${{c}_{m}}(k),$ $m = 3,4, \ldots $, при увеличении $k$ движутся по траекториям, аналогичным указанным на фиг. 3. Так, СЗ ${{c}_{3}}(k)$ и ${{c}_{4}}(k)$ сначала движутся по прямой $\operatorname{Re} (c) = \tfrac{1}{2}$ в соответствии с асимптотикой (3.46). При ${{k}_{{ * ,1}}} = 82.089$ они “сталкиваются” в точке $c = \tfrac{1}{2} - 0.36737i$ и образуют двойное СЗ. При последующем росте $k > {{k}_{{ * ,1}}}$ это СЗ “распадается” на два симметричных СЗ, а линии их движения подобны траекториям на фиг. 3. Все последующие пары СЗ ${{c}_{{2m + 1}}}(k)$ и ${{c}_{{2m + 2}}}(k)$, $m = 2,3,\; \ldots $, ведут себя аналогично СЗ ${{c}_{3}}(k)$ и ${{c}_{4}}(k)$.

Возможна также еще более сложная картина поведения траекторий ${{c}_{m}}(k)$. Пусть ${\text{Bu}} = {{10}^{{ - 4}}}$, ${\text{Pr}} = 4$ и ${\text{R}} = 1$. При $k \to 0$ имеем ${{c}_{1}}(k) \to \tfrac{1}{2} + 0.28867i$ и ${{c}_{2}}(k) \to \tfrac{1}{2} - 0.28867i$, а также множество ${{c}_{m}}(k)$, $m = 3,4,\;...$, описываемых асимптотикой (3.46). При увеличении $k$ СЗ ${{c}_{1}}(k)$ и ${{c}_{2}}(k)$ сначала движутся вниз по прямой $\operatorname{Re} (c) = \tfrac{1}{2}$, а все остальные СЗ движутся вверх.

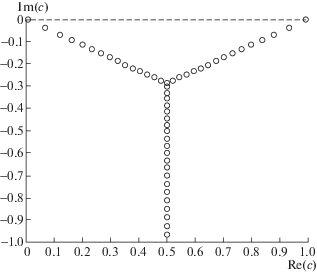
На фиг. 5 приведен фрагмент траекторий ${{c}_{2}}(k)$ и ${{c}_{3}}(k)$ при $k \in [39.2174,40.572]$ между двумя двойными СЗ; прямая $\operatorname{Re} (c) = \tfrac{1}{2}$ отмечена пунктиром. При $k = {{k}_{{ * ,1}}} = 39.2174$ СЗ ${{c}_{2}}(k)$ и ${{c}_{3}}(k)$ “сталкиваются” в точке $A = \tfrac{1}{2} - 0.2933i$ (она отмечена крестиком) и образуют первое двойное СЗ. При увеличении $k > {{k}_{{ * ,1}}}$ это СЗ “распадается” на пару простых СЗ, движущихся симметрично относительно прямой $\operatorname{Re} (c) = \tfrac{1}{2}$, но уже не по траекториям, подобным указанным на фиг. 3 или фиг. 4, а по некоторому малому овалу с поперечником $d \approx 0.0036$. При $k = {{k}_{{ * ,2}}} = 40.572$ эта пара СЗ опять “сталкивается” в точке $B = \tfrac{1}{2} - 0.2899i$ (она также отмечена крестиком на фиг. 5) и образует второе двойное СЗ.

Фиг. 5.

Траектории c₂(k) и c₃(k) для Bu = 10^–4, Pr = 4, R = 1 при увеличении $k \in [39.2174,\;40.572]$.

При дальнейшем росте $k > {{k}_{{ * ,2}}}$ это СЗ “распадется” на два простых СЗ, идущих вверх и вниз по прямой $\operatorname{Re} (c) = \tfrac{1}{2}$ . Идущее вниз СЗ при $k = {{k}_{{ * ,3}}} = 80.7106$ затем “столкнется” с ${{c}_{4}}(k)$ в точке $c = \tfrac{1}{2} - 0.3901i$ и образует третье двойное СЗ, которое при росте $k > {{k}_{{ * ,3}}}$ “распадется” на два простых СЗ, идущих по траекториям, аналогичным указанным на фиг. 3.

Идущее же вверх СЗ при $k > {{k}_{{ * ,2}}}$ затем “столкнется” при $k = {{k}_{{ * ,4}}} = 271.725$ с СЗ ${{c}_{1}}(k)$ в точке $c = \tfrac{1}{2} + 0.0458i$ и образует четвертое двойное СЗ. Его дальнейший “распад” и траектории двух симметричных СЗ аналогичны указанным на фиг. 4.

Следующее двойное СЗ образуется из пары ${{c}_{5}}(k)$ и ${{c}_{6}}(k)$ при $k = {{k}_{{ * ,5}}} = 562.786$ в точке $c = \tfrac{1}{2} - 0.34136i$, а их траектории аналогичны указанным на фиг. 3. Все последующие пары СЗ ${{c}_{{2m + 1}}}(k)$ и ${{c}_{{2m + 2}}}(k),$ $m = 3,4,\; \ldots $, ведут себя аналогично этой паре СЗ.

Таким образом, при возрастании $k$ на прямой $\operatorname{Re} (c) = \tfrac{1}{2}$ образуется и распадается конечное число двойных СЗ так, что для каждого $k$ конечное число СЗ будет лежать на плоскости “c” симметрично относительно прямой $\operatorname{Re} (c) = \tfrac{1}{2}$, а счетное множество остальных СЗ будет лежать на этой прямой с точкой сгущения $c = \tfrac{1}{2} - i\infty $.

На фиг. 6 кружочками показаны СЗ ${{c}_{m}}$ для следующих величин параметров: ${\text{R}} = 10$, ${\text{Pr}} = 1$, ${\text{Bu}} = {{10}^{{ - 2}}}$ при волновом числе $k = 2500$. Приведены первые 52 СЗ, для которых $\operatorname{Im} (c) > - 1$; 15 пар из них симметричны относительно прямой $\operatorname{Re} (c) = \tfrac{1}{2}$, а остальные 22 СЗ лежат на прямой ${\text{Re}}(c) = \tfrac{1}{2}$. Такая картина расположения СЗ аналогична распределению СЗ задачи Орра–Зоммерфельда для течения Куэтта (см. [11], [12]) и называется “спектральный галстук”.

6.2. Траектории СЗ задачи II

Фиг. 6.

Первые СЗ c_n, n = 1, 2,..., 52, для Bu = 10^–2, Pr = 1, R = 10, k = 2500.

Для задачи II траектории СЗ ${{c}_{m}}(k)$ имеют характер, аналогичный случаю задачи I, но с тем отличием, что при $k \to 0$ не существует конечных СЗ, а асимптотика всех ${{c}_{m}}(k)$ описывается соотношением (3.46). При увеличении $k > 0$, в зависимости от параметров ${\text{R}}$, ${\text{Pr}}$ и ${\text{Bu}}$, траектории ${{c}_{m}}(k)$ могут иметь такой же сложный характер, как и в задаче I.

Например, для значений ${\text{R}} = 10$, ${\text{Pr}} = 1$ и ${\text{Bu}} = {{10}^{{ - 3}}}$ при росте $k > 0$ все СЗ сначала поднимаются по прямой ${\text{Re}}(c) = \tfrac{1}{2}$ в соответствии с асимптотикой (3.46). При $k = 5.85$ первое СЗ ${{c}_{1}}(k)$ переходит в верхнюю полуплоскость ${\text{Im}}(c) > 0$, что обеспечивает неустойчивость течения. При $k = 32.01$ это СЗ достигает значения ${{c}_{1}}(k) = \tfrac{1}{2} + 0.2292i$ и затем опускается. При $k = {{k}_{{ * ,1}}} = 80.738$ пара СЗ ${{c}_{1}}(k)$ и ${{c}_{2}}(k)$ “сталкивается” в точке $c = \tfrac{1}{2} + 0.0597i$ и образует двойное СЗ. Дальнейший “распад” и симметричное движение этой пары СЗ аналогично случаю, показанному на фиг. 4.

Все последующие СЗ ${{c}_{m}}(k),\;m = 3,4,\;...,$ уже находятся в полуплоскости ${\text{Im}}(c) < 0$ и при росте $k$ образуют двойные СЗ из пар ${{c}_{{2n + 1}}}(k)$ и ${{c}_{{2n + 2}}}(k),\;n = 1,2,\;...$. Траектории их движения аналогичны указанным на фиг. 3.

Для других значений ${\text{R}} = 10$, ${\text{Pr}} = 10$ и ${\text{Bu}} = {{10}^{{ - 3}}}$ при росте $k > 0$ все СЗ опять сначала поднимаются по прямой $\operatorname{Re} (c) = \tfrac{1}{2}$ в соответствии с асимптотикой (3.46), затем ${{c}_{2}}(k)$ опускается и при ${{k}_{{ * ,1}}} = 13.598$ “сталкивается” с ${{c}_{3}}(k)$, образуя первое двойное СЗ. Затем это СЗ “распадается” на пару простых СЗ, движущихся симметрично в плоскости “c” по некоторому овалу, аналогичному показанному на фиг. 5. При ${{k}_{{ * ,2}}} = 21.135$ эта пара СЗ опять “сталкивается” и образует второе двойное СЗ. При дальнейшем росте $k$ это СЗ “распадается” на два простых СЗ, идущих вверх и вниз по прямой ${\text{Re}}(c) = \tfrac{1}{2}$. Идущее вниз СЗ “сталкивается” с ${{c}_{4}}(k)$ при ${{k}_{{ * ,3}}} = 27.928$ и образует третье двойное СЗ. А идущее вверх СЗ “сталкивается” с ${{c}_{1}}(k)$ при ${{k}_{{ * ,4}}} = 64.824$ и образует четвертое двойное СЗ.

Все последующие СЗ ${{c}_{m}}(k),\;m = 5,6,\;...,$ при росте $k$ образуют двойные СЗ из пар соседних СЗ ${{c}_{{2n + 1}}}(k)$ и ${{c}_{{2n + 2}}}(k),\;n = 2,3,\;...$, которые также “распадаются” на пары простых СЗ. При этом СЗ попадают в верхнюю полуплоскость $\operatorname{Im} (c) > 0$ лишь при $k \in (9.89,60.67)$, что обеспечивает неустойчивость течения.

При фиксированных параметрах ${\text{R}}$, ${\text{Pr}}$, ${\text{Bu}}$ и достаточно большом значении волнового числа $k$ распределение СЗ задачи II будет аналогично распределению СЗ в задаче I – конечное число симметричных СЗ будет располагаться в полуполосах $\left\{ {c:\operatorname{Im} (c) < 0,\;\operatorname{Re} (c) \in \left( {0,\tfrac{1}{2}} \right)} \right\}$, и $\left\{ {c:\operatorname{Im} (c) < 0,\;\operatorname{Re} (c) \in \left( {\tfrac{1}{2},1} \right)} \right\}$, а счетное множество СЗ будет лежать на прямой $\operatorname{Re} (c) = \tfrac{1}{2}$, аналогично спектральному портрету на фиг. 6.

7. ЗАКЛЮЧЕНИЕ

В работе проводится анализ устойчивых и неустойчивых возмущений геострофического течения с линейным вертикальным профилем скорости с учетом вертикальной диффузии плавучести и трения. Такой анализ проводится с помощью метода малых возмущений на основе уравнения эволюции потенциального вихря.

Для возникающей спектральной несамосопряженной задачи разработан и реализован эффективный аналитико-численный метод решения для ОДУ 4-го порядка с малым параметром при старшей производной и с вхождением спектрального параметра как в уравнение, так и в краевые условия. В зависимости от двух типов краевых условий рассмотрены две спектральные задачи I и II. Метод их решения основан на использовании степенных разложений для линейно-независимых решений ОДУ, удовлетворяющих части краевых условий, и на построении подходящей комбинации этих решений.

Для анализа зависимости СФ и СЗ этих задач от физических параметров ${\text{R}}$, ${\text{Pr}}$, ${\text{Bu}}$ построены асимптотики СФ и СЗ при малых значениях волнового числа $k$. Показано, что при $k \to + 0$ в задаче I существуют 2 ограниченных СЗ и счетное множество неограниченно растущих СЗ с предельной точкой $c = \tfrac{1}{2} - i\infty $. В задаче II при $k \to 0$ ограниченных СЗ нет, а все неограниченно растущие СЗ имеют главные члены асимптотического разложения, совпадающие со случаем задачи I.

Высокоточный расчет СЗ задач I и II основан на итерационном методе Ньютона с выбором начального значения, исходя из построенных асимптотик и с использованием метода продолжения по параметру $k$.

Проведенный численный анализ показал, что в обеих спектральных задачах при определенных значениях волнового числа $k$ из пар простых СЗ образуются двойные СЗ, лежащие на прямой $\operatorname{Re} (c) = \tfrac{1}{2}$. При увеличении числа $k$ эти СЗ распадаются на простые СЗ, лежащие в полосе $\operatorname{Re} (c) \in (0,1)$ и симметричные относительно прямой $\operatorname{Re} (c) = \tfrac{1}{2}$. На самой прямой $\operatorname{Re} (c) = \tfrac{1}{2}$ при этом находится счетное множество простых СЗ. Такую картину распределения СЗ можно назвать, по аналогии с задачей Орра–Зоммерфельда для течения Куэтта, “спектральный галстук”, см. [16]–[18], [11].

В окрестности двойных СЗ классический итерационный метод Ньютона теряет свою эффективность, поэтому здесь был использован модифицированный метод Ньютона с учетом второй производной. Это позволило с высокой точностью вычислить большое количество СЗ, двойных СЗ и построить траектории СЗ ${{c}_{m}}(k)$ при увеличении волнового числа $k$. Участки этих траекторий ${{c}_{m}}(k)$, попадающие в верхнюю полуплоскость ${\text{Im}}(c) > 0$, описывают неустойчивые по времени возмущения.

Суммируя сказанное, можно отметить, что диапазон изменения волнового числа $k$ неустойчивых возмущений исследуемого течения весьма сложным образом зависит от значений физических параметров задачи. Полученные результаты представляют интерес для интерпретации данных натурных наблюдений интрузий и вихрей в зонах океанских фронтальных течений, в частности, в зонах течений Арктического бассейна, см. [19], [20].