1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 1, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 1, стр. 29-38

Исследование вековых возмущений поступательно-вращательного движения в нестационарной задаче двух тел с применением компьютерной алгебры

С. Б. Бижанова 1, М. Дж. Минглибаев 1, 2, А. Н. Прокопеня 3, *

1 Казахский национальный университет им. аль-Фараби
050040 Алматы, пр-т аль-Фараби, 71, Казахстан

2 Aстрофизический институт им. В.Г. Фесенкова
050020 Алматы, Обсерватория, 23, Казахстан

3 Варшавский университет естественных наук
02-776 Варшава, ул. Новоурсыновска, 159, Польша

* E-mail: alexander_prokopenya@sggw.pl

Поступила в редакцию 29.07.2019
После доработки 29.07.2019
Принята к публикации 18.09.2019

Полный текст (PDF)

Аннотация

Рассматривается нестационарная задача двух тел, одно из которых имеет сферически симметричное распределение плотности и является “центральным”, а второе – “спутник”, обладающий осесимметричным динамическим строением, формой и переменным сжатием. Ньютоновская сила взаимодействия характеризуется приближенным выражением силовой функции с точностью до второй гармоники. Массы тел изменяются изотропно в различных темпах. Получены уравнения движения спутника в относительный системе координат. Задача исследована методами теории возмущений. Получены уравнения вековых возмущений поступательно-вращательного движения спутника в аналогах оскулирующих элементов Делоне–Андуайе. Все необходимые символьные вычисления выполнены с помощью системы компьютерной алгебры Wolfram Mathematica. Библ. 18. Фиг. 1.

Ключевые слова: переменная масса, вековые возмущения, осесимметричное тело, поступательно-вращательное движение.

1. ВВЕДЕНИЕ

Современные данные наблюдений в астрономии показывают, что реальные космические системы являются нестационарными, их массы, размеры, форма и ряд других физических характеристик изменяются с течением времени в процессе эволюции [1]–[6]. В связи с этим становится актуальным создание математических моделей движения нестационарных небесных тел.

Целью настоящей работы является получение дифференциальных уравнений поступательно-вращательного движения нестационарного осесимметричного тела переменной массы и размеров и переменного сжатия в нестационарном центральном гравитационном поле. Решение этой проблемы связано с довольно громоздкими символьными вычислениями, которые лучше всего выполнять с применением систем компьютерной алгебры (см. [7], [8]). В данной работе все необходимые вычисления выполнены с помощью системы Wolfram Mathematica [9], [10].

2. ПОСТАНОВКА ЗАДАЧИ И УРАВНЕНИЯ ДВИЖЕНИЯ В ОТНОСИТЕЛЬНОЙ СИСТЕМЕ КООРДИНАТ

Пусть первое “центральное” тело T1 с переменной массой m1 = m1(t) является шаром со сферически симметричным распределением плотности. Предположим, что второе тело T2 массой m2 = m2(t) является “спутником” тела T1 и обладает осесимметричным динамическим строением и формой, а его моменты инерции второго порядка являются заданными функциями времени. Такой “спутник” обладает переменным сжатием и его главные центральные моменты инерции A, B, C удовлетворяют соотношениям

(1)
$A(t) = B(t) \ne C(t),~\quad \frac{{C(t) - A(t)}}{{C(t)}} \ne {\text{const}}.$

Допустим, что законы изменения масс тел известны, причем массы изменяются в различных темпах, т.е. справедливо соотношение

(2)
$\frac{{{{{\dot {m}}}_{1}}}}{{{{m}_{1}}}} \ne \frac{{{{{\dot {m}}}_{2}}}}{{{{m}_{2}}}}.$
Также предположим, что массы тел изменяются изотропно и в рассматриваемой системе не появляются реактивные силы и дополнительные вращательные моменты.

Пусть нестационарное осесимметричное тело обладает экваториальной плоскостью симметрии. Тогда оно обладает тремя взаимно перпендикулярными плоскостями симметрии. Оси собственной системы координат, совпадающие с главными осями инерции тела, направим вдоль линий пересечения этих трех взаимно перпендикулярных плоскостей. Отметим, что ориентация этих осей относительно тела в ходе эволюции остается неизменной. В выражении для силовой функции ограничимся приближением с точностью до второй гармоники включительно.

Относительное поступательное движение центра масс “спутника” вокруг “центрального” тела описывается уравнениями [6]:

(3)
$\tilde {m}\ddot {x} = \frac{{\partial U}}{{\partial x}}~,~\quad \tilde {m}\ddot {y} = \frac{{\partial U}}{{\partial y}}~,~\quad \tilde {m}\ddot {z} = \frac{{\partial U}}{{\partial z}}~,$
где x, y, z – координаты центра масс тела T2 в относительной системе координат O1xyz с началом в центре тела T1, $\tilde {m} = {{m}_{1}}{{m}_{2}}{\text{/}}({{m}_{1}} + {{m}_{2}})$ – приведенная масса, силовая функция ньютоновского взаимодействия двух тел имеет вид
(4)
$U = f\frac{{{{m}_{1}}{{m}_{2}}}}{R} + \tilde {U},~\quad {{R}^{2}} = {{x}^{2}} + {{y}^{2}} + {{z}^{2}},$
(5)
$\tilde {U} = f{{m}_{1}}\frac{{2A(t) + C(t) - 3J}}{{2{{R}^{3}}}},$
а момент инерции J осесимметричного тела относительно вектора ${{{\mathbf{O}}}_{1}}{{{\mathbf{O}}}_{2}}$, соединяющего центры масс двух тел, определяется выражением
(6)
$J = A({{\alpha }^{2}} + {{\beta }^{2}}) + C{{\gamma }^{2}},$
где α, β, γ – направляющие косинусы вектора ${{{\mathbf{O}}}_{1}}{{{\mathbf{O}}}_{2}}$ с осями собственной системы координат “спутника”, совпадающими с его главными центральными осями инерции.

Вращательное движение спутника вокруг собственного центра масс в переменных Эйлера определяется уравнениями [6], [11]

$\frac{d}{{dt}}(Ap) - (A - C)qr = \frac{{\sin \varphi }}{{\sin \theta }}\left( {\frac{{\partial U}}{{\partial \psi }} - \cos \theta \frac{{\partial U}}{{\partial \varphi }}} \right) + \cos \varphi \frac{{\partial U}}{{\partial \theta }},$
(7)
$\frac{d}{{dt}}(Aq) - (C - A)rp = \frac{{\cos \varphi }}{{\sin \theta }}\left( {\frac{{\partial U}}{{\partial \psi }} - \cos \theta \frac{{\partial U}}{{\partial \varphi }}} \right) - \sin \varphi \frac{{\partial U}}{{\partial \theta }},$
$\frac{d}{{dt}}(Cr) = 0,$
(8)
$p = \dot {\psi }\sin \varphi \sin \theta + \dot {\theta }\cos \varphi ,\quad ~q = \dot {\psi }\cos \varphi \sin \theta - \dot {\theta }\sin \varphi ,~\quad r = \dot {\psi }\cos \theta + \dot {\varphi },$
где p, q, r – проекции угловой скорости спутника на оси собственной системы координат, φ, θ, ψ – углы Эйлера [12]–[14]. В рассматриваемой постановке задача является весьма сложной, поэтому для ее исследования воспользуемся методами теории возмущений [6].

3. УРАВНЕНИЯ ДВИЖЕНИЯ В ОСКУЛИРУЮЩИХ ЭЛЕМЕНТАХ ДЕЛОНЕ–АНДУАЙЕ

Поступательное движение центра масс осесимметричного тела далее опишем в оскулирующих элементах апериодического движения по квазиконическому сечению (см. [6]). Для этого перепишем уравнение (3) в виде

(9)
${\mathbf{\ddot {R}}} + f\frac{{{{m}_{1}} + {{m}_{2}}}}{{{{R}^{3}}}}~{\mathbf{R}} - b{\mathbf{R}} = {{\operatorname{grad} }_{{\mathbf{R}}}}W,$
где

(10)
$W = - \frac{1}{2}b{{R}^{2}} + \frac{{{{m}_{1}} + {{m}_{2}}}}{{{{m}_{1}}{{m}_{2}}}}\tilde {U},~\quad b = b({{t}_{0}}) = \frac{{{\ddot {v}}}}{{v}},~\quad {v} = {v}(t) = \frac{{{{m}_{1}}({{t}_{0}}) + {{m}_{2}}({{t}_{0}})}}{{{{m}_{1}}(t) + {{m}_{2}}(t)}}.$

При W = 0 уравнение (9) имеет точное решение, которое описывает апериодическое движение по квазиконическому сечению и может быть представлено в виде

(11)
$\begin{gathered} x = {v}\rho (\cos u\cos {\Omega } - \sin u\sin {\Omega }\cos i),\quad y = {v}\rho (\cos u\sin {\Omega } + \sin u\cos {\Omega }\cos i), \\ z = {v}\rho (\sin u\sin i),\quad R = {v}\rho ,\quad u = {v} + \omega , \\ \end{gathered} $
где ${v}$ – истинная аномалия,
(12)
$\rho = \frac{{a(1 - {{e}^{2}})}}{{1 + e\cos {v}}}.$
Величины a, e, i, ω, Ω являются аналогами известных кеплеровских орбитальных элементов (см. [12]). Введение эксцентрической аномалии Е согласно соотношению
(13)
$\operatorname{tg} \frac{{v}}{2} = \sqrt {\frac{{1 + e}}{{1 - e}}} \operatorname{tg} \frac{E}{2},\quad e < 1,$
приводит к известному уравнению Кеплера
(14)
$E - e\sin E = M.$
При этом зависимости эксцентрической E и средной M аномалий в (14) от времени
(15)
$E = E(t),\quad M = n[\phi (t) - \phi (\tau )],\quad n = \frac{{\sqrt {{{\mu }_{0}}} }}{{{{a}^{{3/2}}}}} = {\text{const}},\quad {{\mu }_{0}} = f[{{m}_{1}}({{t}_{0}}) + {{m}_{2}}({{t}_{0}})],$
определяются законами изменения масс тел, поскольку функция $\phi (t)$ в (15) имеет вид
(16)
$\phi (t) = \mathop \smallint \limits_{{{t}_{0}}}^t \frac{{dt}}{{{{{v}}^{2}}(t)}} = \mathop \smallint \limits_{{{t}_{0}}}^t {{\left( {\frac{{{{m}_{1}}(t) + {{m}_{2}}(t)}}{{{{m}_{1}}({{t}_{0}}) + {{m}_{2}}({{t}_{0}})}}} \right)}^{2}}dt.$
Через $\tau $ в (15) обозначено время прохождения через перицентр. Отметим, что в невозмущенном движении средняя угловая скорость не является постоянной и зависит от законов изменения масс тел:

(17)
$\dot {M} = n~\frac{1}{{{{{v}}^{2}}(t)}} = n{{\left( {\frac{{{{m}_{1}}(t) + {{m}_{2}}(t)}}{{{{m}_{1}}({{t}_{0}}) + {{m}_{2}}({{t}_{0}})}}} \right)}^{2}}.$

Для дальнейших вычислений предпочтительно использовать аналоги переменных Делоне, которые вводятся посредством соотношений (см. [6], [15])

(18)
$\begin{gathered} L = \sqrt {{{\mu }_{0}}} \sqrt a ,\quad G = \sqrt {{{\mu }_{0}}} \sqrt {a(1 - {{e}^{2}})} ,\quad H = \sqrt {{{\mu }_{0}}} \sqrt {a(1 - {{e}^{2}})} \cos i, \\ l = n[\phi (t) - \phi (\tau )],\quad g = \omega ,\quad h = \Omega . \\ \end{gathered} $

Уравнения движения центра масс осесимметричного тела, как уравнения возмущенного движения, в оскулирующих элементах Делоне имеют вид

(19)
$\begin{gathered} \dot {L} = \frac{{\partial W}}{{\partial l}},\quad \dot {G} = \frac{{\partial W}}{{\partial g}},\quad \dot {H} = \frac{{\partial W}}{{\partial h}}, \\ \dot {l} = - \frac{{\partial W}}{{\partial L}},\quad \dot {g} = - \frac{{\partial W}}{{\partial G}},\quad \dot {h} = - \frac{{\partial W}}{{\partial H}}, \\ \end{gathered} $
где
(20)
$W = \frac{1}{{\nu _{{}}^{2}(t)}}\frac{{\mu _{0}^{2}}}{{2L_{{}}^{2}}} + {{W}^{*}},$
(21)
$W* = \left( {\frac{{{{m}_{1}} + {{m}_{2}}}}{{{{m}_{1}}{{m}_{2}}}}\tilde {U} - \frac{1}{2}b{{R}^{2}}} \right).$
Учитывая соотношение ${{\alpha }^{2}} + {{\beta }^{2}} + {{\gamma }^{2}} = 1$, из формул (5), (6) и (21) получаем
(22)
$W* = \frac{{{{m}_{1}} + {{m}_{2}}}}{{{{m}_{1}}{{m}_{2}}}}\left( {\frac{{f{{m}_{1}}}}{2}\left( {C - A} \right)\left[ {\frac{1}{{{{R}^{3}}}}} \right] - \frac{{3f{{m}_{1}}}}{2}(C - A)\left[ {\frac{{{{\gamma }^{2}}}}{{{{R}^{3}}}}} \right]} \right) - \frac{1}{2}b[{{R}^{2}}].$
Величины, заключенные в квадратные скобки в правой части уравнения (22), должны быть выражены через оскулирующие элементы Делоне–Андуайе.

Вращательное движение осесимметричного тела $\left( {A = B} \right)$ вокруг его центра инерции опишем в аналогах оскулирующих элементов Андуайе. При этом невозмущенное движение является аналогом движения Эйлера-Пуансо – вращательного движения свободного нестационарного осесимметричного тела вокруг собственного центра инерции. Как было отмечено выше, оси собственной системы координат совпадают с главными центральными осями инерции тела.

В переменных Эйлера кинетическая энергия вращательного движения нестационарного осесимметричного тела имеет вид

(23)
${{T}_{{{\text{rot}}}}} = \frac{1}{2}(A({{p}^{2}} + {{q}^{2}}) + C{{r}^{2}}).$
Напомним, что угловые переменные Эйлера φ, θ, ψ и соответствующие им обобщенные импульсы Pφ, Pθ, Pψ связаны между собой соотношениями (см. [6], [16])
$Ap = \frac{1}{{\sin \theta }}({{P}_{\psi }} - {{P}_{\varphi }}\cos \theta )\sin \varphi + {{P}_{\theta }}\cos \varphi ,$
(24)
$Bq = \frac{1}{{\sin \theta }}({{P}_{\psi }} - {{P}_{\varphi }}\cos \theta )\cos \varphi - {{P}_{\theta }}\sin \varphi ,~\quad Cr = {{P}_{\varphi }},$
${{P}_{\theta }} = \frac{{\partial {{T}_{{{\text{rot}}}}}}}{{\partial{ \dot {\theta }}}} = Ap\cos \varphi - Bq\sin \varphi ,~\quad {{P}_{\varphi }} = \frac{{\partial {{T}_{{{\text{rot}}}}}}}{{\partial{ \dot {\varphi }}}} = Cr,$
(25)
${{P}_{\psi }} = \frac{{\partial {{T}_{{{\text{rot}}}}}}}{{\partial{ \dot {\psi }}}} = (Ap\sin \varphi + Bq\cos \varphi )\sin \theta + Cr\cos \theta .$
С другой стороны, в переменных Андуайе l', g', h', L', G', H' получаем (см. [6], [16]):
(26)
$Ap = \sqrt {G{\kern 1pt} {{'}^{2}}\; - L{\kern 1pt} {{'}^{2}}} ~\sin l{\kern 1pt} ',~\quad Bq = \sqrt {G{\kern 1pt} {{'}^{2}}\; - L{\kern 1pt} {{'}^{2}}} ~\cos l{\kern 1pt} ',~\quad Cr = L{\kern 1pt} '.$
Поэтому выражение для кинетической энергии (23) в переменных Андуайе в общем случае может быть записано в виде
(27)
${{T}_{{{\text{rot}}}}} = \frac{1}{2}(G{\kern 1pt} {{'}^{2}}\; - L{{'}^{2}})\left[ {\frac{{{{{\sin }}^{2}}l{\kern 1pt} '}}{A} + \frac{{{{{\cos }}^{2}}l{\kern 1pt} '}}{B}} \right] + \frac{{L{\kern 1pt} {{'}^{2}}}}{{2C}}.$
В случае осесимметричного тела выражение (27) существенно упрощается
(28)
${{T}_{{{\text{rot}}}}} = \frac{1}{{2A}}(G{\kern 1pt} {{'}^{2}}\; - L{\kern 1pt} {{'}^{2}}) + \frac{{L{\kern 1pt} {{'}^{2}}}}{{2C}}.$
Следовательно, гамильтониан вращательного движения осесимметричного тела может быть записан в виде
(29)
$F = {{F}_{{{\text{нв}}}}} + {{F}_{{{\text{воз}}}}},$
где
(30)
${{F}_{{{\text{нв}}}}} = \frac{1}{2}(G{\kern 1pt} {{'}^{2}}\; - L{\kern 1pt} {{'}^{2}})\frac{1}{A} + \frac{{L{\kern 1pt} {{'}^{2}}}}{{2C}} = \frac{1}{2}\frac{{G{\kern 1pt} {{'}^{2}}}}{A} + \frac{1}{2}\left( {\frac{1}{C} - \frac{1}{A}} \right)L{\kern 1pt} {{'}^{2}},$
(31)
${{F}_{{{\text{воз}}}}} = \tilde {U} - \frac{1}{2}b{{R}^{2}}.$
Соответственно, вращательное движение осесимметричного тела вокруг собственного центра инерции определяется уравнениями возмущенного движения в оскулирующих элементах Андуайе вида
(32)
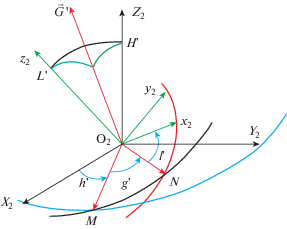
$\begin{gathered} \dot {L}{\kern 1pt} ' = - \frac{{\partial F}}{{\partial l{\kern 1pt} '}}{\text{,}}\quad \dot {G}{\kern 1pt} ' = - \frac{{\partial F}}{{\partial g{\kern 1pt} '}}{\text{,}}\quad \dot {H}{\kern 1pt} ' = - \frac{{\partial F}}{{\partial h{\kern 1pt} '}}{\text{,}} \\ \dot {l}{\kern 1pt} ' = \frac{{\partial F}}{{\partial L{\kern 1pt} '}}{\text{,}}\quad \dot {g}{\kern 1pt} ' = \frac{{\partial F}}{{\partial G{\kern 1pt} '}}{\text{,}}\quad \dot {h}{\kern 1pt} ' = \frac{{\partial F}}{{\partial H{\kern 1pt} '}}{\text{.}} \\ \end{gathered} $
Геометрический смысл элементов Андуайе выясняется из фиг. 1.

Фиг 1.

Переменные Андуайе.

На фиг. 1 приняты следующие обозначения.

1. ${{O}_{2}}{{X}_{2}}{{Y}_{2}}{{Z}_{2}}$ – невращающаяся кенигова система координат, оси которой параллельны осям абсолютной системы координат;

2. ${{O}_{2}}{{x}_{2}}{{y}_{2}}{{z}_{2}}$ – собственная система координат, оси которой направлены вдоль главных осей инерции трехосного тела, жестко связанная с телом и вращающаяся вместе с ним;

3. ${{O}_{2}}NM$ – плоскость, проходящая через начало координат (барицентр), перпендикулярная вектору кинетического момента ${\mathbf{G}}{\kern 1pt} '$;

4. ${{O}_{2}}M$ – линия пересечения плоскости ${{O}_{2}}{{X}_{2}}{{Y}_{2}}$ невращающейся системы координат ${{O}_{2}}{{X}_{2}}{{Y}_{2}}{{Z}_{2}}$ с плоскостью ${{O}_{2}}MN,$ перпендикулярной вектору кинетического момента ${\mathbf{G}}{\kern 1pt} '$, проходящей через начало координат;

5. ${{O}_{2}}N$ – линия пересечения плоскости ${{O}_{2}}{{x}_{2}}{{y}_{2}}$ вращающейся системы координат ${{O}_{2}}{{x}_{2}}{{y}_{2}}{{z}_{2}}$ с плоскостью ${{O}_{2}}MN$, перпендикулярной вектору кинетического момента ${\mathbf{G}}{\kern 1pt} '$;

6. $G{\kern 1pt} '$ – модуль вектора кинетического момента ${\mathbf{G}}{\kern 1pt} '$;

7. $L{\kern 1pt} '$ – проекция вектора кинетического момента ${\mathbf{G}}{\kern 1pt} '$ на вращающуюся ось ${{O}_{2}}{{z}_{2}}$ – одну из главных осей инерции трехосного тела;

8. $Н{\kern 1pt} '$ – проекция вектора кинетического момента ${\mathbf{G}}{\kern 1pt} '$ на ось ${{O}_{2}}{{Z}_{2}}$, сохраняющую в пространстве постоянную ориентацию;

9. $l{\kern 1pt} ' $ – угол между линией ${{O}_{2}}N$и осью ${{O}_{2}}{{х}_{2}}$;

10. $g{\kern 1pt} '$- угол между линиями ${{O}_{2}}M$ и ${{O}_{2}}N$;

11. $h{\kern 1pt} '$ – угол между осью ${{O}_{2}}{{X}_{2}}$ и линией ${{O}_{2}}M$.

Взаимная ориентация невращающейся системы координат ${{O}_{2}}{{X}_{2}}{{Y}_{2}}{{Z}_{2}}$ и вращающейся системы координат ${{O}_{2}}{{x}_{2}}{{y}_{2}}{{z}_{2}}$, связанной с осесимметричным телом, определяется следующими направляющими косинусами [15]–[18]:

${{a}_{{11}}} = \cos h{\kern 1pt} '\cos g{\kern 1pt} '\cos l{\kern 1pt} '\; - \cos h{\kern 1pt} '\cos J{\kern 1pt} '\sin g{\kern 1pt} '\sin l{\kern 1pt} '\; - \sin h{\kern 1pt} '\cos I{\kern 1pt} '\cos l{\kern 1pt} '\sin g{\kern 1pt} '\; - $
$ - \;\sin h{\kern 1pt} '\cos I{\kern 1pt} '\cos g{\kern 1pt} '\cos J{\kern 1pt} '\sin l{\kern 1pt} '\; + \sin h{\kern 1pt} '\sin I{\kern 1pt} '\sin l{\kern 1pt} '\sin J{\kern 1pt} ',$
(33)
${{a}_{{21}}} = \sin h{\kern 1pt} '\cos g{\kern 1pt} '\cos l{\kern 1pt} '\; - \sin h{\kern 1pt} '\cos J{\kern 1pt} '\sin g{\kern 1pt} '\sin l{\kern 1pt} '\; + \cos h{\kern 1pt} '\cos I{\kern 1pt} '\cos l{\kern 1pt} '\sin g{\kern 1pt} '\; + $
$ + \;\cos h{\kern 1pt} '\cos I{\kern 1pt} '\cos g{\kern 1pt} '\cos J{\kern 1pt} '\sin l{\kern 1pt} '\; - \cos h{\kern 1pt} '\sin I{\kern 1pt} '\sin l{\kern 1pt} '\sin J{\kern 1pt} ',$
${{a}_{{31}}} = \sin I{\kern 1pt} '\sin g{\kern 1pt} '\cos l{\kern 1pt} '\; + \sin I{\kern 1pt} '\cos J{\kern 1pt} '\cos g{\kern 1pt} '\sin l{\kern 1pt} '\; + \cos I{\kern 1pt} '\sin l{\kern 1pt} '\sin J{\kern 1pt} ',$
${{a}_{{12}}} = - \cos h{\kern 1pt} '\cos g{\kern 1pt} '\sin l{\kern 1pt} '\; - \cos h{\kern 1pt} '\cos J{\kern 1pt} '\sin g{\kern 1pt} '\cos l{\kern 1pt} '\; + \sin h{\kern 1pt} '\cos I{\kern 1pt} '\sin l{\kern 1pt} '\sin g{\kern 1pt} '\; - $
$ - \;\sin h{\kern 1pt} '\cos I{\kern 1pt} '\cos g{\kern 1pt} '\cos J{\kern 1pt} '\cos l{\kern 1pt} '\; + \sin h{\kern 1pt} '\sin I{\kern 1pt} '\cos l{\kern 1pt} '\sin J{\kern 1pt} ',$
(34)
${{a}_{{22}}} = - \sin h{\kern 1pt} '\cos g{\kern 1pt} '\sin l{\kern 1pt} '\; - \sin h{\kern 1pt} '\cos J{\kern 1pt} '\sin g{\kern 1pt} 'osl{\kern 1pt} '\; - \cos h{\kern 1pt} '\cos I{\kern 1pt} '\sin l{\kern 1pt} '\sin g{\kern 1pt} '\; + $
$ + \;\cos h{\kern 1pt} '\cos I{\kern 1pt} '\cos g{\kern 1pt} '\cos J{\kern 1pt} '\cos l{\kern 1pt} '\; - \cos h{\kern 1pt} '\sin I{\kern 1pt} '\cos l{\kern 1pt} '\sin J{\kern 1pt} ',$
${{a}_{{32}}} = - \sin I{\kern 1pt} '\sin g{\kern 1pt} '\sin l{\kern 1pt} '\; + \sin I{\kern 1pt} '\cos J{\kern 1pt} '\cos g{\kern 1pt} '\cos l{\kern 1pt} '\; + \cos I{\kern 1pt} '\cos l{\kern 1pt} '\sin J{\kern 1pt} ',$
${{a}_{{13}}} = \cos h{\kern 1pt} '\sin J{\kern 1pt} '\sin g{\kern 1pt} '\; - \sin h{\kern 1pt} '\sin I{\kern 1pt} '\cos J{\kern 1pt} '\; + \sin h{\kern 1pt} '\cos I{\kern 1pt} '\cos g{\kern 1pt} '\sin J{\kern 1pt} ',$
(35)
${{a}_{{23}}} = \sin h{\kern 1pt} '\sin J{\kern 1pt} '\sin g{\kern 1pt} '\; - \cos h{\kern 1pt} '\sin I{\kern 1pt} '\cos J{\kern 1pt} '\; - \cos h{\kern 1pt} '\cos I{\kern 1pt} '\cos g{\kern 1pt} '\sin J{\kern 1pt} ',$
${{a}_{{33}}} = \cos I{\kern 1pt} '\cos J{\kern 1pt} '\; - ~\sin I{\kern 1pt} '\cos g{\kern 1pt} '\sin J{\kern 1pt} ',$
где

(36)
$\cos I{\kern 1pt} ' = \frac{{H{\kern 1pt} '}}{{G{\kern 1pt} '}},\quad \sin I{\kern 1pt} ' = \sqrt {1 - \frac{{H{\kern 1pt} {{'}^{2}}}}{{G{\kern 1pt} {{'}^{2}}}}} ,\quad \cos J{\kern 1pt} ' = \frac{{L{\kern 1pt} '}}{{G{\kern 1pt} '}},\quad \sin J{\kern 1pt} ' = \sqrt {1 - \frac{{L{\kern 1pt} {{'}^{2}}}}{{G{\kern 1pt} {{'}^{2}}}}} .$

4. УРАВНЕНИЯ НЕВОЗМУЩЕННОГО ДВИЖЕНИЯ В АНАЛОГАХ ЭЛЕМЕНТОВ ДЕЛОНЕ–АНДУАЙЕ

Если возмущающая функция в уравнениях (19), (32), равна нулю, то получим уравнения невозмущенного поступательно-вращательного движения нестационарного осесимметричного тела в элементах Делоне–Андуайе.

Невозмущенное поступательное движение описывается уравнениями

(37)
$L = {{L}_{0}} = {\text{const}},\quad G = {{G}_{0}} = {\text{const}},\quad H = {{H}_{0}} = {\text{const}},$
(38)
$\begin{gathered} l = \frac{{\mu _{0}^{2}}}{{{{L}^{3}}}}\mathop \smallint \limits_{{{t}_{0}}}^t {{\left( {\frac{{{{m}_{1}}(t) + {{m}_{2}}(t)}}{{{{m}_{1}}({{t}_{0}}) + {{m}_{2}}({{t}_{0}})}}} \right)}^{2}}dt + {{l}_{0}},\quad ~{{l}_{0}} = {\text{const}},~ \\ g = {{g}_{0}} = {\text{const}},\quad h = {{h}_{0}} = {\text{const}}{\text{.}} \\ \end{gathered} $

Уравнения невозмущенного вращательного движения имеют вид

(39)
$L{\kern 1pt} ' = L_{0}^{'} = {\text{const}},\quad G{\kern 1pt} ' = G_{0}^{'} = {\text{const}},\quad H{\kern 1pt} ' = H_{0}^{'} = {\text{const}},$
(40)
$\begin{gathered} l{\kern 1pt} ' = L{\kern 1pt} {\text{'}}\mathop \smallint \limits_{{{t}_{0}}}^t \frac{{A(t) - C(t)}}{{A(t)C(t)}}dt + l_{0}^{'},\quad l_{0}^{'} = {\text{const}}, \\ g{\kern 1pt} ' = G{\kern 1pt} {\text{'}}\mathop \smallint \limits_{{{t}_{0}}}^t \frac{{dt}}{{A(t)}} + g_{0}^{'},\quad g_{0}^{'} = {\text{const}},\quad h' = h_{0}^{'} = {\text{const}}. \\ \end{gathered} $
Отметим, что угол $l{\kern 1pt} ' = l{\kern 1pt} '(t)$ описывает собственное вращение спутника. При $A(t) < C(t)$, как можно увидеть из (40), величина $\Delta l{\kern 1pt} ' = l{\kern 1pt} ' - l_{0}^{'}$ отрицательная, при $A(t) = C(t)$ эта величина равна нулю и тело останавливается, а при $A(t) > C(t)$ эта величина положительная и тело начинает вращение в обратном направлении.

5. ВЫРАЖЕНИЕ ДЛЯ СИЛОВОЙ ФУНКЦИИ ЧЕРЕЗ ОСКУЛИРУЮЩИЕ ЭЛЕМЕНТЫ ДЕЛОНЕ–АНДУАЙЕ

Перепишем выражения (20), (21) в виде

(41)
$W = \frac{1}{{{{\nu }^{2}}(t)}}\frac{{\mu _{0}^{2}}}{{2{{L}^{2}}}} + \frac{{{{m}_{1}} + {{m}_{2}}}}{{{{m}_{1}}{{m}_{2}}}}\left( {\frac{{f{{m}_{1}}}}{{2{{\nu }^{3}}}}(C - A)\left[ {\frac{1}{{{{\rho }^{3}}}}} \right] - \frac{{3f{{m}_{1}}}}{{2{{\nu }^{3}}}}(C - A)\left[ {\frac{{{{\gamma }^{2}}}}{{{{\rho }^{3}}}}} \right]} \right) - \frac{1}{2}b{{\nu }^{2}}[{{\rho }^{2}}].$
Подобным образом выражения (29)–(31) запишем в виде
(42)
$F = \frac{1}{2}\frac{{G{\kern 1pt} {{'}^{2}}}}{A} + \frac{1}{2}\left( {\frac{1}{C} - \frac{1}{A}} \right)L{\kern 1pt} {{'}^{2}}\; + \frac{{f{{m}_{1}}(C - A)}}{{2{{\nu }^{3}}}}\left[ {\frac{1}{{{{\rho }^{3}}}}} \right] - \frac{{3f{{m}_{1}}(C - A)}}{{2{{\nu }^{3}}}}\left[ {\frac{{{{\gamma }^{2}}}}{{{{\rho }^{3}}}}} \right] - \frac{1}{2}b{{\nu }^{2}}[{{\rho }^{2}}].$
Здесь
(43)
$\frac{1}{{{{\rho }^{3}}}} = \frac{{{{{(1 + e\cos {v})}}^{3}}}}{{{{a}^{3}}{{{(1 - {{e}^{2}})}}^{3}}}},$
(44)
$\gamma = c_{{13}}^{{}}\frac{x}{R} + c_{{23}}^{{}}\frac{y}{R} + c_{{33}}^{{}}\frac{z}{R},$
(45)
$\frac{x}{R} = {{\tau }_{{11}}}\sin {v} + {{\tau }_{{12}}}\cos {v},\quad \frac{y}{R} = {{\tau }_{{21}}}\sin {v} + {{\tau }_{{22}}}\cos {v},\quad \frac{z}{R} = {{\tau }_{{31}}}\sin {v} + {{\tau }_{{32}}}\cos {v}.$
(46)
$c_{{13}}^{{}} = {{\varepsilon }_{{11}}} + {{\varepsilon }_{{12}}}\sin g{\kern 1pt} '\; + {{\varepsilon }_{{13}}}\cos g{\kern 1pt} ',\quad c_{{23}}^{{}} = {{\varepsilon }_{{21}}} + {{\varepsilon }_{{22}}}\sin g{\kern 1pt} '\; + {{\varepsilon }_{{23}}}\cos g{\kern 1pt} ',\quad c_{{33}}^{{}} = {{\varepsilon }_{{31}}} + {{\varepsilon }_{{33}}}\cos g{\kern 1pt} '.$
Соответственно можно написать
(47)
$\begin{gathered} \frac{{{{\gamma }^{2}}}}{{{{\rho }^{3}}}} = \frac{{{{{(1 + e\cos {v})}}^{3}}}}{{{{a}^{3}}{{{(1 - {{e}^{2}})}}^{3}}}}\left[ {({{\varepsilon }_{{11}}} + {{\varepsilon }_{{12}}}\sin g{\kern 1pt} '\; + {{\varepsilon }_{{13}}}\cos g{\kern 1pt} ')({{\tau }_{{11}}}\sin {v} + {{\tau }_{{12}}}\cos {v}) + } \right. \\ {{\left. { + \;({{\varepsilon }_{{21}}} + {{\varepsilon }_{{22}}}\sin g{\kern 1pt} '\; + {{\varepsilon }_{{23}}}\cos g{\kern 1pt} ')({{\tau }_{{21}}}\sin {v} + {{\tau }_{{22}}}\cos {v}) + ({{\varepsilon }_{{31}}} + {{\varepsilon }_{{33}}}\cos g{\kern 1pt} ')({{\tau }_{{31}}}\sin {v} + {{\tau }_{{32}}}\cos {v})} \right]}^{2}}, \\ \end{gathered} $
где

${{\varepsilon }_{{11}}} = \frac{{L{\kern 1pt} '\sqrt {G{\kern 1pt} {{'}^{2}}\; - H{\kern 1pt} {{'}^{2}}} }}{{G{\kern 1pt} {{'}^{2}}}}~\sin h{\kern 1pt} ',\quad {{\varepsilon }_{{12}}} = \frac{{\sqrt {G{\kern 1pt} {{'}^{2}}\; - L{\kern 1pt} {{'}^{2}}} }}{{G{\kern 1pt} '}}~\cos h{\kern 1pt} ',\quad {{\varepsilon }_{{13}}} = \frac{{H{\kern 1pt} '\sqrt {G{\kern 1pt} {{'}^{2}}\; - L{\kern 1pt} {{'}^{2}}} }}{{G{\kern 1pt} {{'}^{2}}}}~\sin h{\kern 1pt} ',$
(48)
${{\varepsilon }_{{21}}} = \frac{{L{\kern 1pt} '\sqrt {G{\kern 1pt} {{'}^{2}}\; - H{\kern 1pt} {{'}^{2}}} }}{{G{\kern 1pt} {{'}^{2}}}}~\cos h{\kern 1pt} ',\quad {{\varepsilon }_{{22}}} = \frac{{\sqrt {G{\kern 1pt} {{'}^{2}}\; - L{\kern 1pt} {{'}^{2}}} }}{{G{\kern 1pt} '}}~\sin h{\kern 1pt} ',\quad {{\varepsilon }_{{23}}} = \frac{{H{\kern 1pt} '\sqrt {G{\kern 1pt} {{'}^{2}}\; - L{\kern 1pt} {{'}^{2}}} }}{{G{\kern 1pt} {{'}^{2}}}}~\cos h{\kern 1pt} ',$
${{\varepsilon }_{{31}}} = \frac{{L{\kern 1pt} 'H{\kern 1pt} '}}{{G{\kern 1pt} {{'}^{2}}}}~,\quad {{\varepsilon }_{{33}}} = - \frac{{\sqrt {G{\kern 1pt} {{'}^{2}}\; - H{\kern 1pt} {{'}^{2}}} \sqrt {G{\kern 1pt} {{'}^{2}}\; - L{\kern 1pt} {{'}^{2}}} }}{{G{\kern 1pt} {{'}^{2}}}},$
${{\tau }_{{11}}} = - \cos h\sin g - \frac{H}{G}~\sin h\cos g,\quad {{\tau }_{{12}}} = \cos h\cos g - \frac{H}{G}~\sin h\sin g,$
(49)
${{\tau }_{{21}}} = - \sin h\sin g + \frac{H}{G}~\cos h\cos g,\quad {{\tau }_{{22}}} = \sin h\cos g + \frac{H}{G}~\cos h\sin g,$
${{\tau }_{{31}}} = \cos g~\sqrt {1 - {{H}^{2}}{\text{/}}{{G}^{2}}} ,\quad {{\tau }_{{32}}} = \sin g~\sqrt {1 - {{H}^{2}}{\text{/}}{{G}^{2}}} .$

Согласно приведенным формулам аналитические выражения в квадратных скобках в (41), (42) выражаются через элементы Делоне–Андуайе. Поэтому правые части в уравнениях (19) и (32) могут быть выражены через элементы Делоне–Андуайе. Эти уравнения полностью определяют поступательно-вращательное движение нестационарного осесимметричного тела в переменных Делоне–Андуайе.

6. ОСРЕДНЕНИЕ И ПОЛУЧЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ВЕКОВЫХ ВОЗМУЩЕНИЙ

Рассмотрим нерезонансный случай. Осредняя правую часть уравнений (19) и (32) по переменным $g{\kern 1pt} '$, $l$, получаем уравнения для вековых возмущений поступательно-вращательного движения нестационарного осесимметричного тела в рассматриваемый задаче. Если вековые части возмущающих функций $W$, $F$ обозначить как ${{W}_{{{\text{век}}}}}$, ${{F}_{{{\text{век}}}}}$, то согласно схеме Гаусса имеем

(50)
${{W}_{{{\text{век}}}}} = \frac{1}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {Wdl} dg{\kern 1pt} '} ,\quad {{F}_{{{\text{век}}}}} = \frac{1}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {Fdl} dg{\kern 1pt} '} .$
Соответственно, можно записать
(51)
${{W}_{{{\text{век}}}}} = \frac{{\mu _{0}^{2}}}{{2{{\nu }^{2}}(t)}}{{\left( {\frac{1}{{{{L}^{2}}}}} \right)}_{{{\text{век}}}}} + \frac{{{{m}_{1}} + {{m}_{2}}}}{{{{m}_{1}}{{m}_{2}}}}\left( {\frac{{f{{m}_{1}}(C - A)}}{{2{{\nu }^{3}}}}{{{\left[ {\frac{1}{{{{\rho }^{3}}}}} \right]}}_{{{\text{век}}}}} - \frac{{3f{{m}_{1}}(C - A)}}{{2{{\nu }^{3}}}}{{{\left[ {\frac{{\gamma _{2}^{2}}}{{{{\rho }^{3}}}}} \right]}}_{{{\text{век}}}}}} \right) - \frac{1}{2}b{{\nu }^{2}}{{[{{\rho }^{2}}]}_{{{\text{век}}}}},$
(52)
${{F}_{{{\text{век}}}}} = \frac{1}{{2A}}{{(G{\kern 1pt} {{'}^{2}})}_{{{\text{век}}}}} + \frac{1}{2}\left( {\frac{1}{C} - \frac{1}{A}} \right){{(L{\kern 1pt} {{'}^{2}})}_{{{\text{век}}}}} + \frac{{f{{m}_{1}}(C - A)}}{{2{{\nu }^{3}}}}{{\left[ {\frac{1}{{{{\rho }^{3}}}}} \right]}_{{{\text{век}}}}} - \frac{{3f{{m}_{1}}(C - A)}}{{2{{\nu }^{3}}}}{{\left[ {\frac{{{{\gamma }^{2}}}}{{{{\rho }^{3}}}}} \right]}_{{{\text{век}}}}} - \frac{1}{2}b{{\nu }^{2}}{{[{{\rho }^{2}}]}_{{{\text{век}}}}},$
где

(53)
${{[{{\rho }^{2}}]}_{{{\text{век}}}}} = \frac{1}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {{{\rho }^{2}}dldg{\kern 1pt} '} } = {{a}^{2}}\left( {1 + \frac{3}{2}{{e}^{2}}} \right).$

При вычислении вековых возмущений следующих величин:

(54)
${{\left[ {\frac{1}{{{{\rho }^{3}}}}} \right]}_{{{\text{век}}}}} = \frac{1}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {\frac{{dldg{\kern 1pt} '}}{{{{\rho }^{3}}}}} } ,$
(55)
${{\left[ {\frac{{{{\gamma }^{2}}}}{{{{\rho }^{3}}}}} \right]}_{{{\text{век}}}}} = \frac{1}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {\left( {\frac{{{{\gamma }^{2}}}}{{{{\rho }^{3}}}}} \right)dldg{\kern 1pt} '} } ,$
удобно использовать известное соотношение [6]
(56)
$\frac{{d{v}}}{{{{{(1 + e\cos {v})}}^{2}}}} = \frac{{dl}}{{{{{(1 - {{e}^{2}})}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}.$
Используя соотношение (56), вычисляем правую часть (54)
(57)
$\frac{1}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {\frac{{dldg{\kern 1pt} '}}{{{{\rho }^{3}}}}} } = \frac{1}{{4{{\pi }^{2}}{{a}^{3}}{{{(1 - {{e}^{2}})}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {(1 + e\cos {v})d{v}} } dg{\kern 1pt} ' = \frac{1}{{{{a}^{3}}(1 - {{e}^{2}})}}.$
Используя соотношения (47) и (56), перепишем правую часть (55) в виде
(58)
$\begin{gathered} \frac{1}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {\left( {\frac{{{{\gamma }^{2}}}}{{{{\rho }^{3}}}}} \right)dldg{\kern 1pt} '} } = \frac{1}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {{{\gamma }^{2}}\frac{{{{{(1 + e\cos {v})}}^{3}}}}{{{{{(1 - {{e}^{2}})}}^{3}}}}\frac{{{{{(1 - {{e}^{2}})}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{{{{(1 + e\cos {v})}}^{2}}}}d{v}dg{\kern 1pt} '} } = \frac{1}{{4{{\pi }^{2}}{{a}^{3}}{{{(1 - {{e}^{2}})}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}} \times \\ \times \;\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {\left[ {({{\varepsilon }_{{11}}} + {{\varepsilon }_{{12}}}\sin g{\kern 1pt} '\; + {{\varepsilon }_{{13}}}\cos g{\kern 1pt} ')({{\tau }_{{11}}}\sin {v} + {{\tau }_{{12}}}\cos {v}) + ({{\varepsilon }_{{21}}} + {{\varepsilon }_{{22}}}\sin g{\kern 1pt} '\; + {{\varepsilon }_{{23}}}\cos g{\kern 1pt} ')} \right.} } \times \\ \times \;({{\tau }_{{21}}}\sin {v} + {{\tau }_{{22}}}\cos {v}) + ({{\varepsilon }_{{31}}} + {{\varepsilon }_{{33}}}\cos g{\kern 1pt} '){{\left. {({{\tau }_{{31}}}\sin {v} + {{\tau }_{{32}}}\cos {v})} \right]}^{2}}(1 + e\cos {v})d{v}dg{\kern 1pt} '. \\ \end{gathered} $
Вычисляя интегралы в (58), окончательно получаем
(59)
${{\left[ {\frac{{{{\gamma }^{2}}}}{{{{\rho }^{3}}}}} \right]}_{{{\text{век}}}}} = \frac{I}{{4{{a}^{3}}{{{(1 - {{e}^{2}})}}^{{3/2}}}}},$
где

(60)
$\begin{gathered} I = (\tau _{{11}}^{2} + \tau _{{12}}^{2})(2\varepsilon _{{11}}^{2} + \varepsilon _{{12}}^{2} + \varepsilon _{{13}}^{2}) + (\tau _{{21}}^{2} + \tau _{{22}}^{2})(2\varepsilon _{{21}}^{2} + \varepsilon _{{22}}^{2} + \varepsilon _{{23}}^{2}) + (\tau _{{31}}^{2} + \tau _{{32}}^{2})(2\varepsilon _{{31}}^{2} + \varepsilon _{{33}}^{2}) + \\ \; + \left( {{{\tau }_{{11}}}{{\tau }_{{21}}} + {{\tau }_{{12}}}{{\tau }_{{22}}}} \right)\left( {4{{\varepsilon }_{{11}}}{{\varepsilon }_{{21}}} + 2{{\varepsilon }_{{12}}}{{\varepsilon }_{{22}}} + 2{{\varepsilon }_{{13}}}{{\varepsilon }_{{23}}}} \right) + ({{\tau }_{{11}}}{{\tau }_{{31}}} + {{\tau }_{{12}}}{{\tau }_{{32}}})(4{{\varepsilon }_{{11}}}{{\varepsilon }_{{31}}} + 2{{\varepsilon }_{{13}}}{{\varepsilon }_{{33}}}) + \\ \; + ({{\tau }_{{21}}}{{\tau }_{{31}}} + {{\tau }_{{22}}}{{\tau }_{{32}}})(4{{\varepsilon }_{{21}}}{{\varepsilon }_{{31}}} + 2{{\varepsilon }_{{23}}}{{\varepsilon }_{{33}}}) = I\left( {h,H,h{\kern 1pt} ',H{\kern 1pt} '} \right). \\ \end{gathered} $

Теперь уравнения для вековых возмущений имеют следущий вид:

(61)
$\begin{gathered} {{{\dot {L}}}_{{{\text{век}}}}} = 0,\quad {{{\dot {G}}}_{{{\text{век}}}}} = 0,\quad {{{\dot {H}}}_{{{\text{век}}}}} = \frac{{\partial {{W}_{{{\text{век}}}}}}}{{\partial {{h}_{{{\text{век}}}}}}}, \\ {{{\dot {l}}}_{{{\text{век}}}}} = - \frac{{\partial {{W}_{{{\text{век}}}}}}}{{\partial {{L}_{{{\text{век}}}}}}},\quad {{{\dot {g}}}_{{{\text{век}}}}} = - \frac{{\partial {{W}_{{{\text{век}}}}}}}{{\partial {{G}_{{{\text{век}}}}}}},\quad {{{\dot {h}}}_{{{\text{век}}}}} = - \frac{{\partial {{W}_{{{\text{век}}}}}}}{{\partial {{H}_{{{\text{век}}}}}}}, \\ \end{gathered} $
(62)
$\begin{gathered} \dot {L}_{{{\text{век}}}}^{'} = 0,\quad \dot {G}_{{{\text{век}}}}^{'} = 0,\quad \dot {H}_{{{\text{век}}}}^{'} = - \frac{{\partial {{F}_{{{\text{век}}}}}}}{{\partial {{h}_{{{\text{век}}}}}}}, \\ \dot {l}_{{{\text{век}}}}^{'} = \frac{{\partial {{F}_{{{\text{век}}}}}}}{{\partial L_{{{\text{век}}}}^{'}}},\quad \dot {g}_{{{\text{век}}}}^{'} = \frac{{\partial {{F}_{{{\text{век}}}}}}}{{\partial G_{{{\text{век}}}}^{'}}},\quad \dot {h}_{{{\text{век}}}}^{'} = \frac{{\partial {{F}_{{{\text{век}}}}}}}{{\partial H_{{{\text{век}}}}^{'}}}, \\ \end{gathered} $
(63)
$\begin{gathered} {{W}_{{{\text{век}}}}} = \frac{{\mu _{0}^{2}}}{{2{{\nu }^{2}}(t)}}\left( {\frac{1}{{{{L}^{2}}}}} \right) + \frac{{{{m}_{1}} + {{m}_{2}}}}{{{{m}_{1}}{{m}_{2}}}}\left( {\frac{{f{{m}_{1}}(C - A)}}{{2{{\nu }^{3}}}}\left[ {\frac{1}{{{{a}^{3}}(1 - {{e}^{2}})}}} \right]} \right) - \\ - \;\frac{{{{m}_{1}} + {{m}_{2}}}}{{{{m}_{1}}{{m}_{2}}}}\left( {\frac{{3f{{m}_{1}}(C - A)}}{{2{{\nu }^{3}}}}\left[ {\frac{I}{{4{{a}^{3}}{{{(1 - {{e}^{2}})}}^{{3/2}}}}}} \right]} \right) - \frac{1}{2}b{{\nu }^{2}}\left[ {{{a}^{2}}\left( {1 + \frac{3}{2}{{e}^{2}}} \right)} \right] \\ \end{gathered} $
(64)
$\begin{gathered} {{F}_{{{\text{век}}}}} = \frac{1}{{2A}}(G{{'}^{2}}) + \frac{1}{2}\left( {\frac{1}{C} - \frac{1}{A}} \right)(L{\kern 1pt} {{'}^{2}}) + \frac{{f{{m}_{1}}(C - A)}}{{2{{\nu }^{3}}}}\left[ {\frac{1}{{{{a}^{3}}(1 - {{e}^{2}})}}} \right] - \\ - \;\frac{{3f{{m}_{1}}(C - A)}}{{2{{\nu }^{3}}}}\left[ {\frac{I}{{4{{a}^{3}}{{{(1 - {{e}^{2}})}}^{{3/2}}}}}} \right] - \frac{1}{2}b{{\nu }^{2}}\left[ {{{a}^{2}}\left( {1 + \frac{3}{2}{{e}^{2}}} \right)} \right], \\ \end{gathered} $
где a = L2/μ0, 1 – e2 = G 2/μ0a, I = I(H, h, H  ', h').

Таким образом, вычисление вековых возмущений сводится к системе четвертого порядка

(65)
${{\dot {H}}_{{{\text{век}}}}} = \frac{{\partial {{W}_{{{\text{век}}}}}}}{{\partial {{h}_{{{\text{век}}}}}}},\quad {{\dot {h}}_{{{\text{век}}}}} = - \frac{{\partial {{W}_{{{\text{век}}}}}}}{{\partial {{H}_{{{\text{век}}}}}}},$
(66)
$\dot {H}_{{{\text{век}}}}^{'} = - \frac{{\partial {{F}_{{{\text{век}}}}}}}{{\partial h_{{{\text{век}}}}^{'}}}{\text{,}}\quad \dot {h}_{{{\text{век}}}}^{'} = \frac{{\partial {{F}_{{{\text{век}}}}}}}{{\partial H_{{{\text{век}}}}^{'}}}.$

После решения системы (65), (66) интегрируются оставшиеся уравнения

(67)
${{\dot {L}}_{{{\text{век}}}}} = 0,\quad {{\dot {G}}_{{{\text{век}}}}} = 0,\quad \dot {L}_{{{\text{век}}}}^{'} = 0,\quad \dot {G}_{{{\text{век}}}}^{'} = 0,$
(68)
${{\dot {l}}_{{{\text{век}}}}} = - \frac{{\partial {{W}_{{{\text{век}}}}}}}{{\partial L_{{{\text{век}}}}^{'}}},\quad {{\dot {g}}_{{{\text{век}}}}} = - \frac{{\partial {{W}_{{{\text{век}}}}}}}{{\partial {{G}_{{{\text{век}}}}}}},\quad \dot {l}_{{{\text{век}}}}^{'} = \frac{{\partial {{F}_{{{\text{век}}}}}}}{{\partial L_{{{\text{век}}}}^{'}}},\quad \dot {g}_{{{\text{век}}}}^{'} = \frac{{\partial {{F}_{{{\text{век}}}}}}}{{\partial G_{{{\text{век}}}}^{'}}}.$

С учетом (63), (64) система (65), (66) принимает вид

(69)
$\begin{gathered} \dot {H} = \left( {\frac{{E(t)}}{{\tilde {m}(t)}}} \right)\left[ {\frac{{\partial I}}{{\partial h}}} \right],\quad \dot {h} = - \left( {\frac{{E(t)}}{{\tilde {m}(t)}}} \right)\left[ {\frac{{\partial I}}{{\partial H}}} \right], \\ \dot {H}{\kern 1pt} ' = E(t)\left[ {\frac{{\partial I}}{{\partial h{\kern 1pt} '}}} \right],\quad \dot {h}{\kern 1pt} ' = - E(t)\left[ {\frac{{\partial I}}{{\partial H{\kern 1pt} '}}} \right], \\ \end{gathered} $
(70)
$E(t) = - \frac{{3f{{m}_{1}}(C - A)}}{{8{{\nu }^{3}}{{a}^{3}}{{{(1 - e)}}^{{3/2}}}}},\quad \tilde {m}(t) = \frac{{{{m}_{1}}{{m}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}}.$

Заметим, что в силу равенств (67) получим

(71)
$\begin{gathered} L = {{L}_{{{\text{век}}}}} = {{L}_{0}} = {\text{const}},\quad (a = {\text{const}}),\quad G = {{G}_{{{\text{век}}}}} = {{G}_{0}} = {\text{const}},\quad (e = {\text{const}}), \\ L{\kern 1pt} ' = L_{{{\text{век}}}}^{'} = L_{0}^{'} = {\text{const}},\quad G{\kern 1pt} ' = G_{{{\text{век}}}}^{'} = G_{0}^{'} = {\text{const}}{\text{.}} \\ \end{gathered} $

Система (69) допускает первый интеграл

(72)
$I = I(H,h,H{\kern 1pt} ',h{\kern 1pt} ') = {{I}_{0}} = {\text{const}}.$

Действительно, выполняя вычисления с учетом системы (69), получаем

(73)
$\begin{gathered} \frac{{dI}}{{dt}} = \frac{{\partial I}}{{\partial H}}\dot {H} + \frac{{\partial I}}{{\partial h}}\dot {h} + \frac{{\partial I}}{{\partial H{\kern 1pt} '}}\dot {H}{\kern 1pt} ' + \frac{{\partial I}}{{\partial h{\kern 1pt} '}}\dot {h}{\kern 1pt} ' = \frac{{\partial I}}{{\partial H}}\left( {\left( {\frac{{E(t)}}{{\tilde {m}(t)}}} \right)\left[ {\frac{{\partial I}}{{\partial h}}} \right]} \right) + \frac{{\partial I}}{{\partial h}}\left( { - \left( {\frac{{E(t)}}{{\tilde {m}(t)}}} \right)\left[ {\frac{{\partial I}}{{\partial H}}} \right]} \right) + \frac{{\partial I}}{{\partial H{\kern 1pt} '}}\left( {E(t)\left[ {\frac{{\partial I}}{{\partial h{\kern 1pt} '}}} \right]} \right) + \\ \, + \frac{{\partial I}}{{\partial h{\kern 1pt} '}}\left( { - E(t)\left[ {\frac{{\partial I}}{{\partial H{\kern 1pt} '}}} \right]} \right) = \left( {\frac{{E(t)}}{{\tilde {m}(t)}}} \right)\left\{ {\frac{{\partial I}}{{\partial H}}\left[ {\frac{{\partial I}}{{\partial h}}} \right] - \frac{{\partial I}}{{\partial h}}\left[ {\frac{{\partial I}}{{\partial H}}} \right]} \right\} + \left( {E(t)} \right)\left\{ {\frac{{\partial I}}{{\partial H{\kern 1pt} '}}\left[ {\frac{{\partial I}}{{\partial h{\kern 1pt} '}}} \right] - \frac{{\partial I}}{{\partial h{\kern 1pt} '}}\left[ {\frac{{\partial I}}{{\partial H{\kern 1pt} '}}} \right]} \right\} = 0 \\ \end{gathered} $

7. ЗАКЛЮЧЕНИЕ

Поступательно-вращательное движение нестационарного осесимметричного тела в гравитационном поле нестационарного шара изучено методами теории возмущений. Получены уравнения для вековых возмущений, которые представляют собой систему дифференциальных уравнений четвертого порядка с одним первым интегралом. Далее планируется численными методами исследовать полученные эволюционные уравнения. Все аналитические вычисления выполнены с применением системы компьютерной алгебры Mathematica [9], [10].

Список литературы

  1. Omarov T.B. (Ed.). Non-Stationary Dynamical Problems in Astronomy. New-York: Nova Science Publ., 2002.

  2. Bekov A.A., Omarov T.B. The theory of orbits in non-stationary stellar systems // Astronomy and Astrophysics Transactions. 2013. V. 22. № 2. P. 145–153.

  3. Черепащук А.М. Тесные двойные звезды. Часть II. М.: Физматлит, 2013. С. 572.

  4. Eggleton P. Evolutionary processes in binary and multiple stars. London: Cambridge University Press, 2006. 332 p.

  5. Luk’yanov L.G. Dynamical evolution of stellar orbits in close binary systems with conservative mass transfer // Astron. Rep. 2008. V. 52. № 8. P. 680–693.

  6. Минглибаев М.Дж. Динамика гравитирующих тел с переменными массами и размерами. Изд-во “LAMBERT Academic Publishing ”, 2012. 229 с.

  7. Прокопеня А.Н., Минглибаев М.Дж., Маемерова Г.М. Символьные вычисления в исследованиях проблемы трех тел с переменными массами // Программирование. 2014. Т. 40. № 2. С. 51–59.

  8. Прокопеня А.Н., Минглибаев М.Дж., Шомшекова С.А. Применение компьютерной алгебры в исследованиях двухпланетной задачи трех тел с переменными массами // Программирование. 2019. Т. 45. № 2. С. 58–65.

  9. Wolfram S. An Elementary Introduction to the Wolfram Language. Champaign, IL: Wolfram Media, 2015. 324 p.

  10. Прокопеня А.Н. Решение физических задач с использованием системы Mathematica. Брест: Изд-во БГТУ, 2005. 260 с.

  11. Minglibayev M.Zh., Ahmetrassulova A.A. Secular perturbations in the problem of translational rotational motion two axisymmetric non-stationary gravitating bodies with variable oblate. In: Classical and Celestial Mechanics. Selected Papers, L. Gadomski, P. Krasilnikov, A. Prokopenya (Eds.). Siedlce: Wydawnictwo Colleguim Mazovia, 2012. P. 116–126.

  12. Дубошин Г.Н. Небесная механика. Основные задачи и методы. М.: Наука, 1975. 799 с.

  13. Белецкий В.В. Движение спутника относительно центра масс в гравитационном поле. М.: МГУ им. Ломоносова, 1975. 308 с.

  14. Видякин В.В. Поступательно-вращательное движение двух твердых тел: Учебное пособие. Архангельск: ДКПО “Норд”, 1996. 184 с.

  15. Баркин Ю.В., Демин В.Г. Поступательно-вращательное движение небесных тел // Итоги науки и техн. АН СССР. Астрономия. 1982. Т. 20. С. 115–134.

  16. Архангельский А.Ю. Аналитическая динамика твердого тела. М.: Наука, 1977. 328 с.

  17. Борисов А.В., Мамаев И.С. Динамика твердого тела. Гамильтоновы методы, интегрируемость, хаос. Москва–Ижевск: Институт компьютерных исследований, 2005. 576 с.

  18. Лидов М.Л. Курс лекций по теоретической механике. М.: Физматлит, 2010. 496 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал