1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 1, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 1, стр. 80-87

Исследование стационарных движений системы двух связанных тел на круговой орбите с применением методов компьютерной алгебры

С. А. Гутник 1, 2, *, В. А. Сарычев 3, **

1 МГИМО МИД России
119454 Москва, пр-т Вернадского, 76, Россия

2 МФТИ
141701 М. о., Долгопрудный, Институтский пер., 9, Россия

3 ИПМ им. М.В. Келдыша РАН
125047 Москва, Миусская пл., 4, Россия

* E-mail: s.gutnik@inno.mgimo.ru
** E-mail: vas31@rambler.ru

Поступила в редакцию 15.06.2019
После доработки 29.07.2019
Принята к публикации 18.09.2019

Полный текст (PDF)

Аннотация

С использованием методов компьютерной алгебры и численных методов проведено исследование свойств нелинейной алгебраической системы, определяющей равновесные ориентации системы двух тел, соединенных сферическим шарниром, движущихся по круговой орбите под действием гравитационного момента. Главное внимание уделяется изучению равновесных ориентаций связки двух тел для специальных случаев, когда одна из главных осей инерции как первого, так и второго тела совпадает с нормалью к плоскости орбиты, радиусом вектором или касательной к орбите. Для определения равновесных ориентаций связки двух тел проводилась декомпозиция системы стационарных алгебраических уравнений движения на 9 подсистем. Для решения системы алгебраических уравнений применялись алгоритмы построения базисов Гребнера. Положения равновесия определялись путем численного анализа корней алгебраических уравнений из построенного базиса Гребнера. Библ. 16. Фиг. 1.

Ключевые слова: система двух тел, круговая орбита, уравнения Лагранжа, положения равновесия, компьютерная алгебра, базис Гребнера.

ВВЕДЕНИЕ

Исследование равновесных ориентаций связки тел, движущихся в центральном ньютоновом силовом поле по круговой орбите, представляет значительный практический интерес для создания составных схем гравитационной системы ориентации спутников, которые могут функционировать на орбите продолжительное время без расходования энергии и (или) рабочего тела. Принцип работы гравитационных систем ориентации основан на том, что в центральном ньютоновом поле сил спутник с неравными главными центральными моментами инерции имеет на круговой орбите 24 положения равновесия, четыре из которых являются устойчивыми (см. [1]–[3]). Подробное рассмотрение динамики различных типов составных схем гравитационных систем ориентации представлено в [4].

Данная работа посвящена исследованию стационарных движений системы двух тел (спутник-стабилизатор), соединенных сферическим шарниром, движущихся по круговой орбите. Схема гравитационной системы ориентации, в соответствии с которой к корпусу спутника с помощью шарнира присоединяется второе тело (стабилизатор), которое выполняет роль демпфирующего устройства, была предложена Д.Е. Охоцимским в 1956 г. Общие идеи предложенной Д.Е. Охоцимским гравитационной системы ориентации спутников с использованием составной схемы спутник-стабилизатор с трехосным подвесом изложены в [4], [5]. Исследованию теории динамики гравитационной системы спутник-стабилизатор посвящен ряд работ (см. [6]–[13]). В работе [6] выведены общие нелинейные уравнения движения системы спутник-стабилизатор, получены необходимые и достаточные условия асимптотической устойчивости нулевого решения системы на круговой орбите, определены амплитуды эксцентриситетных колебаний системы двух тел, обусловленные влиянием эллиптичности орбиты, и проведено исследование переходных процессов. В [7] проведен анализ динамики системы спутник-стабилизатор с упрощенной схемой одностепенного подвеса. Динамика движения двух соединенных шарниром тел в плоскости круговой орбиты исследовалась в работах [8]–[11]. Задача нахождения всех пространственных положений равновесия двух соединенных сферическим шарниром тел на круговой орбите в общем виде до сих пор не решена. Подробное исследование задачи о пространственных положениях равновесия системы двух осесимметричных тел проведено в [12]. В [14] с использованием комбинации методов компьютерной и линейной алгебры был получен широкий класс равновесных пространственных решений системы двух тел, соединенных сферическим шарниром, на круговой орбите при определенных ограничениях на параметры задачи.

Основное внимание в данном исследовании уделяется изучению равновесных ориентаций связки двух тел для специальных случаев, когда одна из главных осей инерции как первого, так и второго тела совпадает с нормалью к плоскости орбиты, радиусом вектором или касательной к орбите. Для определения равновесных ориентаций связки двух тел проводилась декомпозиция системы стационарных алгебраических уравнений движения на 9 подсистем. Для решения системы алгебраических уравнений применялись алгоритмы построения базисов Гребнера. Положения равновесия определялись путем численного анализа корней алгебраических уравнений из построенного базиса Гребнера.

1. УРАВНЕНИЯ ДВИЖЕНИЯ

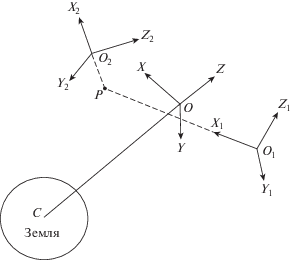
Рассмотрим задачу о движении системы двух тел, соединенных сферическим шарниром, по круговой орбите. Для записи уравнений движения системы спутник–стабилизатор введем следующие правые системы координат (фиг. 1): $OXYZ$ – орбитальная система координат; ось $OZ$ направлена вдоль радиуса-вектора, соединяющего центр масс C Земли и центр масс O системы двух тел; ось $OX$ направлена вдоль вектора линейной скорости центра масс $O$, ось $OY$ совпадает с нормалью к плоскости орбиты. Оси систем координат ${{O}_{1}}{{x}_{1}}{{y}_{1}}{{z}_{1}}$ и ${{O}_{2}}{{x}_{2}}{{y}_{2}}{{z}_{2}}$ направлены вдоль главных центральных осей инерции спутника и стабилизатора соответственно (фиг. 1). Ориентацию системы координат ${{O}_{i}}{{x}_{i}}{{y}_{i}}{{z}_{i}}$ относительно орбитальной системы координат определим с использованием самолетных углов тангажа ${{\alpha }_{i}}$, рыскания ${{\beta }_{i}}$ и крена ${{\gamma }_{i}}$ (cм. [4]) в виде

$\begin{gathered} a_{{11}}^{{(i)}} = \cos {{\alpha }_{i}}\cos {{\beta }_{i}}, \\ a_{{12}}^{{(i)}} = \sin {{\alpha }_{i}}\sin {{\gamma }_{i}} - \cos {{\alpha }_{i}}\sin {{\beta }_{i}}\cos {{\gamma }_{i}}, \\ a_{{13}}^{{(i)}} = \sin {{\alpha }_{i}}\cos {{\gamma }_{i}} + \cos {{\alpha }_{i}}\sin {{\beta }_{i}}\sin {{\gamma }_{i}}, \\ \end{gathered} $
(1.1)
$\begin{gathered} a_{{21}}^{{(i)}} = \sin {{\beta }_{i}}, \\ a_{{22}}^{{(i)}} = \cos {{\beta }_{i}}\cos {{\gamma }_{i}}, \\ a_{{23}}^{{(i)}} = - \cos {{\beta }_{i}}\sin {{\gamma }_{i}}, \\ \end{gathered} $
$\begin{gathered} a_{{31}}^{{(i)}} = - \sin {{\alpha }_{i}}\cos {{\beta }_{i}}, \\ a_{{32}}^{{(i)}} = \cos {{\alpha }_{i}}\sin {{\gamma }_{i}} + \sin {{\alpha }_{i}}\sin {{\beta }_{i}}\cos {{\gamma }_{i}}, \\ a_{{33}}^{{(i)}} = \cos {{\alpha }_{i}}\cos {{\gamma }_{i}} - \sin {{\alpha }_{i}}\sin {{\beta }_{i}}\sin {{\gamma }_{i}}. \\ \end{gathered} $
Индекс $i = 1$ $(i = 2)$ относится к телу 1 – спутнику (телу 2, стабилизатору). Рассмотрим случай, когда шарнир расположен в точке пересечения осей $O{{x}_{1}},$ $O{{x}_{2}}$. Тогда координаты сферического шарнира в связанных с телом 1 и телом 2 системах координат равны $({{a}_{1}},\;0,\;0)$ и $({{a}_{2}},\;0,\;0)$. В этом случае выражения для кинетической энергии и силовой функции системы двух тел имеют следующий вид (см. [4]):

(1.2)
$\begin{gathered} T = \frac{1}{2}[{{A}_{1}}p_{1}^{2} + ({{B}_{1}} + Ma_{1}^{2})q_{1}^{2} + ({{C}_{1}} + Ma_{1}^{2})r_{1}^{2}] + \frac{1}{2}[{{A}_{2}}p_{2}^{2} + ({{B}_{2}} + Ma_{2}^{2})q_{2}^{2} + ({{C}_{2}} + Ma_{2}^{2})r_{2}^{2}] - \\ - \;M{{a}_{1}}{{a}_{2}}[({{r}_{1}}{{a}_{{12}}} - {{q}_{1}}{{a}_{{13}}})({{r}_{2}}{{b}_{{12}}} - {{q}_{2}}{{b}_{{13}}}) + ({{r}_{1}}{{a}_{{22}}} - {{q}_{1}}{{a}_{{23}}})({{r}_{2}}{{b}_{{22}}} - {{q}_{2}}{{b}_{{23}}}) + ({{r}_{1}}{{a}_{{32}}} - {{q}_{1}}{{a}_{{33}}})({{r}_{2}}{{b}_{{32}}} - {{q}_{2}}{{b}_{{33}}})], \\ \end{gathered} $
(1.3)
$\begin{gathered} U = \frac{3}{2}\omega _{0}^{2}[({{C}_{1}} - {{A}_{1}} + Ma_{1}^{2})a_{{31}}^{2} + ({{C}_{1}} - {{B}_{1}})a_{{32}}^{2}] + \frac{3}{2}\omega _{0}^{2}[({{C}_{2}} - {{A}_{2}} + Ma_{2}^{2})b_{{31}}^{2} + ({{C}_{2}} - {{B}_{2}})b_{{32}}^{2}] + \\ \, + M{{a}_{1}}{{a}_{2}}\omega _{0}^{2}({{a}_{{11}}}{{b}_{{11}}} + {{a}_{{21}}}{{b}_{{21}}} - 2{{a}_{{31}}}{{b}_{{31}}}). \\ \end{gathered} $
Фиг. 1.

Основные системы координат.

Используя выражения для кинетической энергии (1.2) и силовой функции (1.3), определяющей действие гравитационного поля Земли на систему двух тел, уравнения движения этой системы можно записать в форме уравнений Лагранжа II рода, используя возможности символьного дифференцирования в системе Maple [16], в следующем виде:

$\begin{gathered} {{A}_{1}}{{{\dot {p}}}_{1}} + ({{C}_{1}} - {{B}_{1}}){{q}_{1}}{{r}_{1}} = 3\omega _{0}^{2}({{C}_{1}} - {{B}_{1}})a_{{32}}^{{}}a_{{33}}^{{}}, \\ ({{B}_{1}} + Ma_{1}^{2}){{{\dot {q}}}_{1}} - M{{a}_{1}}{{a}_{2}}({{a}_{{13}}}{{b}_{{13}}} + {{a}_{{23}}}{{b}_{{23}}} + {{a}_{{33}}}{{b}_{{33}}}){{{\dot {q}}}_{2}} + M{{a}_{1}}{{a}_{2}}({{a}_{{13}}}{{b}_{{12}}} + {{a}_{{23}}}{{b}_{{22}}} + {{a}_{{33}}}{{b}_{{32}}}){{{\dot {r}}}_{2}} + \\ + \;M{{a}_{1}}{{a}_{2}}\{ {{a}_{{13}}}[{{r}_{2}}({{p}_{2}}{{b}_{{13}}} - {{r}_{2}}{{b}_{{11}}}) - {{q}_{2}}({{q}_{2}}{{b}_{{11}}} - {{p}_{2}}{{b}_{{12}}})] + {{a}_{{23}}}[{{r}_{2}}({{p}_{2}}{{b}_{{23}}} - {{r}_{2}}{{b}_{{21}}}) - {{q}_{2}}({{q}_{2}}{{b}_{{21}}} - {{p}_{2}}{{b}_{{22}}})] + \\ + \;{{a}_{{33}}}[{{r}_{2}}({{p}_{2}}{{b}_{{33}}} - {{r}_{2}}{{b}_{{31}}}) - {{q}_{2}}({{q}_{2}}{{b}_{{31}}} - {{p}_{2}}{{b}_{{32}}})]\} + [({{A}_{1}} - {{C}_{1}}) - Ma_{1}^{2})]{{r}_{1}}{{p}_{1}} = 3\omega _{0}^{2}({{A}_{1}} - {{C}_{1}}){{a}_{{33}}}{{a}_{{31}}} - \\ \, - M{{a}_{1}}\omega _{0}^{2}[{{a}_{2}}({{a}_{{13}}}{{b}_{{11}}} + {{a}_{{23}}}{{b}_{{21}}} + {{a}_{{33}}}{{b}_{{31}}}) + 3{{a}_{{33}}}({{a}_{1}}{{a}_{{31}}} - {{a}_{2}}{{b}_{{31}}})], \\ \end{gathered} $
$\begin{gathered} ({{C}_{1}} + Ma_{1}^{2}){{{\dot {r}}}_{1}} + M{{a}_{1}}{{a}_{2}}[({{a}_{{12}}}{{b}_{{13}}} + {{a}_{{22}}}{{b}_{{23}}} + {{a}_{{32}}}{{b}_{{33}}}){{{\dot {q}}}_{2}} - ({{a}_{{12}}}{{b}_{{12}}} + {{a}_{{22}}}{{b}_{{22}}} + {{a}_{{32}}}{{b}_{{32}}})]{{{\dot {r}}}_{2}} - \\ - \;M{{a}_{1}}{{a}_{2}}\{ {{a}_{{12}}}[{{r}_{2}}({{p}_{2}}{{b}_{{13}}} - {{r}_{2}}{{b}_{{11}}}) - {{q}_{2}}({{q}_{2}}{{b}_{{11}}} - {{p}_{2}}{{b}_{{12}}})] + {{a}_{{22}}}[{{r}_{2}}({{p}_{2}}{{b}_{{23}}} - {{r}_{2}}{{b}_{{21}}}) - {{q}_{2}}({{q}_{2}}{{b}_{{21}}} - {{p}_{2}}{{b}_{{22}}})] + \\ + \;{{a}_{{32}}}[{{r}_{2}}({{p}_{2}}{{b}_{{33}}} - {{r}_{2}}{{b}_{{31}}}) - {{q}_{2}}({{q}_{2}}{{b}_{{31}}} - {{p}_{2}}{{b}_{{32}}})]\} + [({{B}_{1}} - {{A}_{1}}) + Ma_{1}^{2})]{{p}_{1}}{{q}_{1}} = 3\omega _{0}^{2}({{B}_{1}} - {{A}_{1}}){{a}_{{31}}}{{a}_{{32}}} + \\ \, + M{{a}_{1}}\omega _{0}^{2}[{{a}_{2}}({{a}_{{12}}}{{b}_{{11}}} + {{a}_{{22}}}{{b}_{{21}}} + {{a}_{{32}}}{{b}_{{31}}}) + 3{{a}_{{32}}}({{a}_{1}}{{a}_{{31}}} - {{a}_{2}}{{b}_{{31}}})], \\ \end{gathered} $
(1.4)
${{A}_{2}}{{\dot {p}}_{2}} + ({{C}_{2}} - {{B}_{2}}){{q}_{2}}{{r}_{2}} = 3\omega _{0}^{2}({{C}_{2}} - {{B}_{2}}){{b}_{{32}}}{{b}_{{33}}},$
$\begin{gathered} ({{B}_{2}} + Ma_{2}^{2}){{{\dot {q}}}_{2}} - M{{a}_{1}}{{a}_{2}}[({{a}_{{13}}}{{b}_{{13}}} + {{a}_{{23}}}{{b}_{{23}}} + {{a}_{{33}}}{{b}_{{33}}}){{{\dot {q}}}_{1}} - ({{a}_{{12}}}{{b}_{{13}}} + {{a}_{{22}}}{{b}_{{23}}} + {{a}_{{32}}}{{b}_{{33}}}){{{\dot {r}}}_{1}}] + \\ + \;M{{a}_{1}}{{a}_{2}}\{ {{b}_{{13}}}[{{r}_{1}}({{p}_{1}}{{a}_{{13}}} - {{r}_{1}}{{a}_{{11}}}) - {{q}_{1}}({{q}_{1}}{{a}_{{11}}} - {{p}_{1}}{{a}_{{12}}})] + {{b}_{{23}}}[{{r}_{1}}({{p}_{1}}{{a}_{{23}}} - {{r}_{1}}{{a}_{{21}}}) - {{q}_{1}}({{q}_{1}}{{a}_{{21}}} - {{p}_{1}}{{a}_{{22}}})] + \\ + \;{{b}_{{33}}}[{{r}_{1}}({{p}_{1}}{{a}_{{33}}} - {{r}_{1}}{{a}_{{31}}}) - {{q}_{1}}({{q}_{1}}{{a}_{{31}}} - {{p}_{1}}{{a}_{{32}}})]\} + [({{A}_{2}} - {{C}_{2}}) - Ma_{2}^{2}]{{r}_{2}}{{p}_{2}} = \\ = 3\omega _{0}^{2}({{A}_{2}} - {{C}_{2}}){{b}_{{33}}}{{b}_{{31}}} - M\omega _{0}^{2}{{a}_{2}}[{{a}_{1}}({{a}_{{11}}}{{b}_{{13}}} + {{a}_{{21}}}{{b}_{{23}}} + {{a}_{{31}}}{{b}_{{33}}}) + 3{{b}_{{33}}}({{a}_{2}}{{b}_{{31}}} - {{a}_{1}}{{a}_{{31}}})], \\ \end{gathered} $
$\begin{gathered} ({{C}_{2}} + Ma_{2}^{2}){{{\dot {r}}}_{2}} + M{{a}_{1}}{{a}_{2}}[({{a}_{{13}}}{{b}_{{12}}} + {{a}_{{23}}}{{b}_{{22}}} + {{a}_{{33}}}{{b}_{{32}}}){{{\dot {q}}}_{1}} - ({{a}_{{12}}}{{b}_{{12}}} + {{a}_{{22}}}{{b}_{{22}}} + {{a}_{{32}}}{{b}_{{32}}}){{{\dot {r}}}_{1}}] + \\ + \;[({{B}_{2}} - {{A}_{2}}) + Ma_{2}^{2}]{{p}_{2}}{{q}_{2}} - M{{a}_{1}}{{a}_{2}}\{ {{b}_{{12}}}[{{r}_{1}}({{p}_{1}}{{a}_{{13}}} - {{r}_{1}}{{a}_{{11}}}) - {{q}_{1}}({{q}_{1}}{{a}_{{11}}} - {{p}_{1}}{{a}_{{12}}})] + {{b}_{{22}}}[{{r}_{1}}({{p}_{1}}{{a}_{{23}}} - {{r}_{1}}{{a}_{{21}}}) - \\ - \;{{q}_{1}}({{q}_{1}}{{a}_{{21}}} - {{p}_{1}}{{a}_{{22}}})] + {{b}_{{32}}}[{{r}_{1}}({{p}_{1}}{{a}_{{33}}} - {{r}_{1}}{{a}_{{31}}}) - {{q}_{1}}({{q}_{1}}{{a}_{{31}}} - {{p}_{1}}{{a}_{{32}}})]\} = 3\omega _{0}^{2}({{B}_{2}} - {{A}_{2}}){{b}_{{31}}}{{b}_{{32}}} + \\ + \;M\omega _{0}^{2}{{a}_{2}}[{{a}_{1}}({{a}_{{11}}}{{b}_{{12}}} + {{a}_{{21}}}{{b}_{{22}}} + {{a}_{{31}}}{{b}_{{32}}}) + 3{{b}_{{32}}}({{a}_{2}}{{b}_{{31}}} - {{a}_{1}}{{a}_{{31}}})]. \\ \end{gathered} $
Здесь
$\begin{gathered} {{p}_{1}} = ({{{\dot {\alpha }}}_{1}} + {{\omega }_{0}})a_{{21}}^{{}} + {{{\dot {\gamma }}}_{1}}, \\ {{q}_{1}} = ({{{\dot {\alpha }}}_{1}} + {{\omega }_{0}})a_{{22}}^{{}} + {{{\dot {\beta }}}_{1}}\sin {{\gamma }_{1}}, \\ \end{gathered} $
(1.5)
$\begin{gathered} {{r}_{1}} = ({{{\dot {\alpha }}}_{1}} + {{\omega }_{0}})a_{{23}}^{{}} + \dot {\beta }\cos {{\gamma }_{1}}, \\ {{p}_{2}} = ({{{\dot {\alpha }}}_{2}} + {{\omega }_{0}})b_{{21}}^{{}} + {{{\dot {\gamma }}}_{2}}, \\ \end{gathered} $
$\begin{gathered} {{q}_{2}} = ({{{\dot {\alpha }}}_{2}} + {{\omega }_{0}})b_{{22}}^{{}} + {{{\dot {\beta }}}_{2}}\sin {{\gamma }_{2}}, \\ {{r}_{2}} = ({{{\dot {\alpha }}}_{2}} + {{\omega }_{0}})b_{{23}}^{{}} + {{{\dot {\beta }}}_{2}}\cos {{\gamma }_{2}}. \\ \end{gathered} $
В выражениях (1.2)–(1.5) ${{M}_{i}}$ – масса, $M = {{{{M}_{1}}{{M}_{2}}} \mathord{\left/ {\vphantom {{{{M}_{1}}{{M}_{2}}} {({{M}_{1}} + {{M}_{2}}}}} \right. \kern-0em} {({{M}_{1}} + {{M}_{2}}}})$, ${{A}_{i}},\;{{B}_{i}},\;{{C}_{i}}$ – главные центральные моменты инерции тел, $({{a}_{i}},\;0,\;0)$ – координаты шарнира в системе координат ${{O}_{i}}{{x}_{i}}{{y}_{i}}{{z}_{i}}$ (фиг. 1), $p{}_{i},\;{{q}_{i}},\;{{r}_{i}}$ – проекции абсолютной угловой скорости i-го тела на оси системы координат $O{{x}_{i}},\;O{{y}_{i}},\;O{{z}_{i}}$; ${{a}_{{ij}}},\;{{b}_{{ij}}}$ – направляющие косинусы, определяющие ориентацию первого и второго тела, соответственно, в орбитальной системе координат; ${{\omega }_{0}}$ – угловая скорость движения центра масс системы двух тел по круговой орбите. Точкой обозначено дифференцирование по времени $t$.

2. ПОЛОЖЕНИЯ РАВНОВЕСИЯ

Введем обозначения

${{m}_{1}} = {{M{{a}_{1}}{{a}_{2}}} \mathord{\left/ {\vphantom {{M{{a}_{1}}{{a}_{2}}} {[({{A}_{1}} - {{C}_{1}}) - Ma_{1}^{2}]}}} \right. \kern-0em} {[({{A}_{1}} - {{C}_{1}}) - Ma_{1}^{2}]}},\quad {{m}_{2}} = {{M{{a}_{1}}{{a}_{2}}} \mathord{\left/ {\vphantom {{M{{a}_{1}}{{a}_{2}}} {[({{A}_{2}} - {{C}_{2}}) - Ma_{2}^{2}]}}} \right. \kern-0em} {[({{A}_{2}} - {{C}_{2}}) - Ma_{2}^{2}]}},$
${{n}_{1}} = {{M{{a}_{1}}{{a}_{2}}} \mathord{\left/ {\vphantom {{M{{a}_{1}}{{a}_{2}}} {[({{B}_{1}} - {{A}_{1}}) + Ma_{1}^{2}]}}} \right. \kern-0em} {[({{B}_{1}} - {{A}_{1}}) + Ma_{1}^{2}]}},\quad {{n}_{2}} = {{M{{a}_{1}}{{a}_{2}}} \mathord{\left/ {\vphantom {{M{{a}_{1}}{{a}_{2}}} {[({{B}_{2}} - {{A}_{2}}) + Ma_{2}^{2}]}}} \right. \kern-0em} {[({{B}_{2}} - {{A}_{2}}) + Ma_{2}^{2}]}}.$
Положив в (1.4) и (1.5) ${{\alpha }_{i}} = {{\alpha }_{{i0}}} = {\text{const}}$, ${{\beta }_{i}} = {{\beta }_{{i0}}} = {\text{const}}$, ${{\gamma }_{i}} = {{\gamma }_{{i0}}} = {\text{const}}$, получим при введенных выше обозначениях уравнения
(2.1)
$\begin{gathered} {{a}_{{22}}}{{a}_{{23}}} - 3{{a}_{{32}}}{{a}_{{33}}} = 0,\quad ({{a}_{{23}}}{{a}_{{21}}} - 3{{a}_{{33}}}{{a}_{{31}}}) + {{m}_{1}}({{b}_{{21}}}{{a}_{{23}}} - 3{{b}_{{31}}}{{a}_{{33}}}) = 0, \\ ({{a}_{{21}}}{{a}_{{22}}} - 3{{a}_{{31}}}{{a}_{{32}}}) - {{n}_{1}}({{b}_{{21}}}{{a}_{{22}}} - 3{{b}_{{31}}}{{a}_{{32}}}) = 0, \\ {{b}_{{22}}}{{b}_{{23}}} - 3{{b}_{{32}}}{{b}_{{33}}} = 0,\quad ({{b}_{{23}}}{{b}_{{21}}} - 3{{b}_{{33}}}{{b}_{{31}}}) + {{m}_{2}}({{a}_{{21}}}{{b}_{{23}}} - 3{{a}_{{31}}}{{b}_{{33}}}) = 0, \\ ({{b}_{{21}}}{{b}_{{22}}} - 3{{b}_{{31}}}{{b}_{{32}}}) - {{n}_{2}}({{a}_{{21}}}{{b}_{{22}}} - 3{{a}_{{31}}}{{b}_{{32}}}) = 0, \\ \end{gathered} $
позволяющие определить положения равновесия системы спутник-стабилизатор в орбитальной системе координат. С учетом (1.1) систему (2.1) можно рассматривать как систему 6 уравнений с неизвестными ${{\alpha }_{{i0}}},\;{{\beta }_{{i0}}},\;{{\gamma }_{{i0}}}$ $(i = 1,\;2)$.

Другой, более удобный для исследования, способ замыкания уравнений (2.1) заключается в добавлении 6 условий ортогональности направляющих косинусов

(2.2)
$\begin{gathered} a_{{21}}^{2} + a_{{22}}^{2} + a_{{23}}^{2} = 1,\quad b_{{21}}^{2} + b_{{22}}^{2} + b_{{23}}^{2} = 1, \\ a_{{31}}^{2} + a_{{32}}^{2} + a_{{33}}^{2} = 1,\quad b_{{31}}^{2} + b_{{32}}^{2} + b_{{33}}^{2} = 1, \\ {{a}_{{21}}}{{a}_{{31}}} + {{a}_{{22}}}{{a}_{{32}}} + {{a}_{{23}}}{{a}_{{33}}} = 0,\quad {{b}_{{21}}}{{b}_{{31}}} + {{b}_{{22}}}{{b}_{{32}}} + {{b}_{{23}}}{{b}_{{33}}} = 0. \\ \end{gathered} $

Уравнения (2.1) и (2.2) образуют замкнутую алгебраическую систему уравнений относительно 12 направляющих косинусов, определяющих положения равновесия системы двух тел. Для этой системы уравнений ставится следующая задача: при заданных ${{m}_{1}},\;{{m}_{2}},\;{{n}_{1}},\;{{n}_{2}}$ требуется определить все 12 направляющих косинусов, т.е. все положения равновесия системы двух тел в орбитальной системе координат. После нахождения направляющих косинусов ${{a}_{{21}}},\;{{a}_{{22}}},\;{{a}_{{23}}},\;{{a}_{{31}}},\;{{a}_{{32}}},\;{{a}_{{33}}}$ и ${{b}_{{21}}},\;{{b}_{{22}}},\;{{b}_{{23}}}$ ${{b}_{{31}}},\;{{b}_{{32}}},\;{{b}_{{33}}}$ оставшиеся направляющие косинусы ${{a}_{{11}}},\;{{a}_{{12}}},\;{{a}_{{13}}},\;{{b}_{{11}}},\;{{b}_{{12}}},\;{{b}_{{13}}}$ могут быть получены из условий ортогональности.

В [14] была проведена декомпозиция системы уравнений (2.1) и (2.2) на ряд однородных подсистем, для которых были найдены решения с использованием алгоритмов построения базисов Гребнера. Решение системы 12 алгебраических уравнений (2.1) и (2.2), коэффициенты которых зависят от 4 параметров, с использованием методов построения базисов Гребнера является очень трудной алгоритмической задачей. Проводились эксперименты построения базиса Гребнера системы полиномов (2.1), (2.2) с использованием реализованного в системе компьютерной алгебры Maple [16] пакета Groebner[Basis] на персональном компьютере с 8 гигабайт оперативной памяти и процессором Intel Core i7 2.4 ГГц. Время вычисления базиса Гребнера с опцией лексикографического упорядочивания занимало более 10 ч машинного времени, после чего происходило прерывание программы из-за превышения допустимого размера памяти, который использует система Maple. Построить базис Гребнера системы полиномов (2.1), (2.2) удается только в самых простых частных случаях, когда ${{m}_{1}} = m$, ${{m}_{2}} = {{n}_{2}} = {{n}_{1}} = 1$ и когда все параметры равны между собой ${{m}_{1}} = {{m}_{2}} = {{n}_{2}} = {{n}_{1}} = m$. В первом случае для вычисления базиса Гребнера потребовалось более 4 ч машинного времени на персональном компьютере, во втором случае для вычисления базиса Гребнера потребовалось более 24 ч машинного времени на сервере с 16 процессорами Intel Xeon, с использованием системы Maple 18. В общем случае построить базис Гребнера для этой системы не удается.

3. ИССЛЕДОВАНИЕ ПОЛОЖЕНИЙ РАВНОВЕСИЯ

Проведем подробное исследование решений системы алгебраических уравнений (2.1), (2.2) для 9 специальных случаев, когда одна из главных осей инерции как первого, так и второго тела совпадает с нормалью к плоскости орбиты, радиусом вектором или касательной к орбите.

Случай 1: $a_{{22}}^{2} = 1$, $b_{{22}}^{2} = 1$. Тогда система (2.1), (2.2) при $a_{{22}}^{{}} = \pm 1$, ${{a}_{{12}}} = {{a}_{{32}}} = {{a}_{{21}}} = {{a}_{{23}}} = 0$ и $b_{{22}}^{{}} = \pm 1$, ${{b}_{{12}}} = {{b}_{{32}}} = {{b}_{{21}}} = {{b}_{{23}}} = 0$ примет вид

(3.1)
$\begin{gathered} {{a}_{{33}}}({{a}_{{31}}} + {{m}_{1}}{{b}_{{31}}}) = 0,\quad {{b}_{{33}}}({{b}_{{31}}} + {{m}_{2}}{{a}_{{31}}}) = 0, \\ a_{{31}}^{2} + a_{{33}}^{2} - 1 = 0,\quad b_{{31}}^{2} + b_{{33}}^{2} - 1 = 0. \\ \end{gathered} $
Уравнения (3.1) определяют равновесные ориентации системы двух связанных тел в плоскости орбиты. Система (3.1) имеет следующие 4 типа решений:

$\begin{gathered} 1.1.\quad {{a}_{{33}}} = 0,\quad {{a}_{{31}}} = \pm 1,\quad {{a}_{{22}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{23}}} = \;0,\quad {{a}_{{11}}} = {{a}_{{12}}} = {{a}_{{32}}} = 0, \\ {{b}_{{33}}} = 0,\quad {{b}_{{31}}} = \pm 1;\quad {{b}_{{22}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{23}}} = \;0,\quad {{b}_{{11}}} = {{b}_{{12}}} = {{b}_{{32}}} = 0; \\ \end{gathered} $

$\begin{gathered} 1.2.\quad {{a}_{{33}}} = 0,\quad {{a}_{{31}}} = \pm 1,\quad {{a}_{{22}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{23}}} = 0,\quad {{a}_{{11}}} = {{a}_{{12}}} = {{a}_{{32}}} = 0, \\ {{b}_{{31}}} = \mp {{m}_{2}},\quad {{b}_{{33}}} = \pm \sqrt {1 - m_{2}^{2}} ,\quad {{b}_{{22}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{23}}} = 0,\quad {{b}_{{12}}} = {{b}_{{32}}} = 0, \\ \end{gathered} $

$\begin{gathered} {{b}_{{11}}} = {{b}_{{22}}}{{b}_{{33}}},\quad {{b}_{{13}}} = - {{b}_{{22}}}{{b}_{{31}}},\quad {\text{|}}{{m}_{2}}{\text{|}} < 1; \\ 1.3.\quad {{a}_{{31}}} = \mp {{m}_{1}},\quad {{a}_{{33}}} = \pm \sqrt {1 - m_{1}^{2}} ,\quad {{a}_{{22}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{23}}} = 0,\quad {{a}_{{12}}} = {{a}_{{32}}} = 0, \\ \end{gathered} $

$\begin{gathered} {{a}_{{11}}} = {{a}_{{22}}}{{a}_{{33}}},\quad {{a}_{{13}}} = - {{a}_{{22}}}{{a}_{{31}}},\quad {\text{|}}{{m}_{1}}{\text{|}} < 1, \\ {{b}_{{33}}} = 0,\quad {{b}_{{31}}} = \pm 1,\quad {{b}_{{22}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{23}}} = 0,\quad {{b}_{{11}}} = {{b}_{{12}}} = {{b}_{{32}}} = 0; \\ \end{gathered} $

$\begin{gathered} 1.4.\quad {{a}_{{31}}} = {{a}_{{32}}} = 0,\quad {{a}_{{33}}} = \pm 1,\quad {{a}_{{22}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{23}}} = 0,\quad {{a}_{{11}}} = {{a}_{{12}}} = 0, \\ {{b}_{{31}}} = {{b}_{{32}}} = 0,\quad {{b}_{{33}}} = \pm 1,\quad {{b}_{{22}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{23}}} = 0,\quad {{b}_{{11}}} = {{b}_{{12}}} = 0,\quad {{m}_{1}}{{m}_{2}} \ne 1. \\ \end{gathered} $

Эти решения (3.2) при ${\text{|}}{{m}_{1}}{\text{|}} < 1,$ ${\text{|}}{{m}_{2}}{\text{|}} < 1$, ${{m}_{1}}{{m}_{2}} \ne 1$, в зависимости от знаков параметров определяют в каждом случае 16 различных положений равновесия системы двух связанных тел. В работе [8] были определены все положения равновесия, которые задаются уравнениями (3.1) в самолетных углах (1.1). С использованием интеграла энергии в качестве функции Ляпунова получены достаточные условия устойчивости положений равновесия. Рассмотрена возможность обеспечения асимптотической устойчивости положений равновесия при наличии диссипации.

Случай 2: $a_{{23}}^{2} = 1$, $b_{{23}}^{2} = 1$. В этом случае ось $O{{z}_{1}}$ спутника и ось $O{{z}_{2}}$ стабилизатора совпадают с нормалью к плоскости орбиты. Система (2.1), (2.2) при $a_{{23}}^{2} = 1$, ${{a}_{{13}}} = {{a}_{{33}}} = {{a}_{{21}}} = {{a}_{{22}}} = 0$; и $b_{{23}}^{2} = 1$, ${{b}_{{13}}} = {{b}_{{33}}} = {{b}_{{21}}} = {{b}_{{22}}} = 0$ примет вид

(3.3)
$\begin{gathered} {{a}_{{32}}}({{a}_{{31}}} - {{n}_{1}}{{b}_{{31}}}) = 0,\quad {{b}_{{32}}}({{b}_{{31}}} - {{n}_{2}}{{a}_{{31}}}) = 0, \\ a_{{31}}^{2} + a_{{32}}^{2} - 1 = 0,\quad b_{{31}}^{2} + b_{{32}}^{2} - 1 = 0. \\ \end{gathered} $
Решения системы (3.3) в случае 2 имеют вид
$\begin{gathered} 2.1.\quad {{a}_{{32}}} = 0,\quad {{a}_{{31}}} = \pm 1,\quad {{a}_{{23}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{22}}} = 0,\quad {{a}_{{11}}} = {{a}_{{13}}} = {{a}_{{33}}} = 0, \\ {{b}_{{32}}} = 0,\quad {{b}_{{31}}} = \pm 1;\quad {{b}_{{23}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{22}}} = 0,\quad {{b}_{{11}}} = {{b}_{{13}}} = {{b}_{{33}}} = 0; \\ \end{gathered} $
$\begin{gathered} 2.2.\quad {{a}_{{32}}} = 0,\quad {{a}_{{31}}} = \pm 1,\quad {{a}_{{23}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{22}}} = 0,\quad {{a}_{{11}}} = {{a}_{{13}}} = {{a}_{{33}}} = 0, \\ {{b}_{{31}}} = \pm {{n}_{2}},\quad {{b}_{{32}}} = \pm \sqrt {1 - n_{2}^{2}} ,\quad {{b}_{{23}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{22}}} = 0,\quad {{b}_{{13}}} = {{b}_{{33}}} = 0, \\ \end{gathered} $
(3.4)
$\begin{gathered} {{b}_{{11}}} = - {{b}_{{23}}}{{b}_{{32}}},\quad {{b}_{{12}}} = {{b}_{{23}}}{{b}_{{31}}},\quad {\text{|}}{{n}_{2}}{\text{|}} < 1; \\ 2.3.\quad {{a}_{{31}}} = \pm {{n}_{1}},\quad {{a}_{{32}}} = \pm \sqrt {1 - n_{1}^{2}} ,\quad {{a}_{{23}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{22}}} = 0,\quad {{a}_{{13}}} = {{a}_{{33}}} = 0, \\ \end{gathered} $
$\begin{gathered} {{a}_{{11}}} = - {{a}_{{23}}}{{a}_{{32}}},\quad {{a}_{{12}}} = {{a}_{{23}}}{{a}_{{31}}},\quad {\text{|}}{{n}_{1}}{\text{|}} < 1, \\ {{b}_{{32}}} = 0,\quad {{b}_{{31}}} = \pm 1,\quad {{b}_{{23}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{22}}} = 0,\quad {{b}_{{11}}} = {{b}_{{13}}} = {{b}_{{33}}} = 0; \\ \end{gathered} $
$\begin{gathered} 2.4.\quad {{a}_{{31}}} = {{a}_{{33}}} = 0,\quad {{a}_{{32}}} = \pm 1,\quad {{a}_{{23}}} = \pm 1,\quad {{a}_{{21}}} = {{a}_{{22}}} = 0,\quad {{a}_{{12}}} = {{a}_{{13}}} = 0, \\ {{b}_{{31}}} = {{b}_{{33}}} = 0,\quad {{b}_{{32}}} = \pm 1,\quad {{b}_{{23}}} = \pm 1,\quad {{b}_{{21}}} = {{b}_{{22}}} = 0,\quad {{b}_{{12}}} = {{b}_{{13}}} = 0,\quad {{n}_{1}}{{n}_{2}} \ne 1. \\ \end{gathered} $
Решения (3.4) при ${\text{|}}{{n}_{1}}{\text{|}} < 1$, ${\text{|}}{{n}_{2}}{\text{|}} < 1$, ${{n}_{1}}{{n}_{2}} \ne 1$ в зависимости от знаков параметров определяют в каждом случае 16 различных положений равновесия системы двух связанных тел.

Случай 3: $a_{{32}}^{2} = 1$, $b_{{32}}^{2} = 1$ и Случай 4: $a_{{33}}^{2} = 1$, $b_{{33}}^{2} = 1$ очень похожи на случаи 1 и 2.

Далее рассмотрим подробно

Случай 5: $a_{{12}}^{2} = 1$, $b_{{12}}^{2} = 1$. Тогда система (2.1), (2.2) при $a_{{12}}^{2} = 1$, ${{a}_{{11}}} = {{a}_{{13}}} = {{a}_{{22}}} = {{a}_{{32}}} = 0$ и $b_{{12}}^{2} = 1$, ${{b}_{{11}}} = {{b}_{{13}}} = {{b}_{{22}}} = {{b}_{{32}}} = 0$, когда ${{a}_{{12}}} = {{b}_{{12}}} = \;1$ или ${{a}_{{12}}} = {{b}_{{12}}} = \; - 1$ примет вид

(3.5)
$\begin{gathered} 4{{a}_{{21}}}{{a}_{{23}}} + {{m}_{1}}({{a}_{{23}}}{{b}_{{21}}} + 3{{b}_{{23}}}{{a}_{{21}}}) = 0,\quad 4{{b}_{{21}}}{{b}_{{23}}} + {{m}_{2}}({{a}_{{21}}}{{b}_{{23}}} + 3{{a}_{{23}}}{{b}_{{21}}}) = 0, \\ a_{{21}}^{2} + a_{{23}}^{2} - 1 = 0,\quad b_{{21}}^{2} + b_{{23}}^{2} - 1 = 0. \\ \end{gathered} $
Решения системы (3.5) получим с использованием алгоритма построения базиса Гребнера [15]. Для вычислений базиса Гребнера системы полиномов, представляющих собой левые части уравнений (3.5), применялся реализованный в системе компьютерной алгебры Maple 18 (см. [16]) пакет построения базисов Гребнера Groebner[Вasis] с опцией лексикографического упорядочения переменных plex. Число полиномов в построенном базисе Гребнера равнялось 9. Выпишем из построенного базиса Гребнера для системы (3.5) полином, который зависит только от одной переменной ${{a}_{{23}}}$ в виде
(3.6)
${{P}_{1}}({{a}_{{23}}}){{P}_{2}}({{m}_{1}},{{m}_{2}},{{a}_{{23}}}) = 0,$
где
(3.7)
$\begin{gathered} {{P}_{1}}({{a}_{{23}}}) = {{a}_{{23}}}(a_{{23}}^{2} - 1),\quad {{P}_{2}}({{m}_{1}},{{m}_{2}},{{a}_{{23}}}) = {{p}_{0}}a_{{23}}^{4} + {{p}_{1}}a_{{33}}^{2} + {{p}_{2}}, \\ {{p}_{0}} = 64({{m}_{1}}{{m}_{2}} - 4)({{m}_{1}}{{m}_{2}} - 1),\quad {{p}_{1}} = - 32(m_{1}^{2} + 2)({{m}_{1}}{{m}_{2}} - 4)({{m}_{1}}{{m}_{2}} - 1), \\ {{p}_{2}} = 9m_{1}^{2}({{(2{{m}_{1}}{{m}_{2}} - 4)}^{2}} - {{({{m}_{1}} + {{m}_{2}})}^{2}}). \\ \end{gathered} $
Для определения равновесных решений необходимо рассмотреть отдельно три случая:

${{a}_{{23}}} = 0,\quad a_{{23}}^{2} = 1\quad {\text{и}}\quad {{P}_{2}}({{m}_{1}},{{m}_{2}},{{a}_{{23}}}) = 0.$

В случае ${{a}_{{23}}} = 0$ из системы (3.5), получим следующие решения:

$\begin{gathered} a_{{12}}^{2} = 1,\quad a_{{21}}^{2} = 1,\quad a_{{33}}^{2} = 1,\quad {{a}_{{11}}} = {{a}_{{13}}} = {{a}_{{22}}} = {{a}_{{31}}} = {{a}_{{32}}} = 0, \\ b_{{12}}^{2} = 1,\quad b_{{21}}^{2} = 1,\quad b_{{33}}^{2} = 1,\quad {{b}_{{11}}} = {{b}_{{13}}} = {{b}_{{22}}} = {{b}_{{23}}} = {{b}_{{31}}} = {{b}_{{32}}} = 0. \\ \end{gathered} $

В случае $a_{{23}}^{2} = 1$ получим следующие решения:

$\begin{gathered} a_{{12}}^{2} = 1,\quad a_{{23}}^{2} = 1,\quad a_{{31}}^{2} = 1,\quad {{a}_{{11}}} = {{a}_{{13}}} = {{a}_{{21}}} = {{a}_{{22}}} = {{a}_{{32}}} = {{a}_{{33}}} = 0, \\ b_{{12}}^{2} = 1,\quad b_{{23}}^{2} = 1,\quad b_{{31}}^{2} = 1,\quad {{b}_{{11}}} = {{b}_{{13}}} = {{b}_{{21}}} = {{b}_{{22}}} = {{b}_{{32}}} = {{b}_{{33}}} = 0. \\ \end{gathered} $

Рассмотрим далее третий случай, когда равновесия спутника определяются действительными корнями биквадратного уравнения ${{P}_{2}}({{m}_{1}},{{m}_{2}},{{a}_{{23}}}) = 0$. Число действительных корней биквадратного уравнения четно и не превышает 4. Для каждого решения ${{a}_{{23}}}$ из третьего уравнения (3.5) можно получить два значения ${{a}_{{21}}}$ и далее значения ${{b}_{{21}}},\;{{b}_{{23}}}$.

Для каждого набора значений ${{a}_{{21}}}$, ${{a}_{{23}}}$, ${{b}_{{21}}},\;\;{{b}_{{23}}}$ можно однозначно получить из исходной системы (2.1), (2.2) соответствующие значения направляющих косинусов ${{a}_{{31}}},\;{{a}_{{33}}}$ и ${{b}_{{31}}},\;{{b}_{{33}}}$. Таким образом, каждому действительному корню биквадратного уравнения из (3.6) соответствуют два набора значений ${{a}_{{ij}}}$, ${{b}_{{ij}}}$ (две равновесные ориентации). Так как число действительных корней биквадратного уравнения из (3.6) не превышает 4, количество положений равновесия системы спутник-стабилизатор в третьем случае из случая 5 не превышает 8. Решения биквадратного уравнения из (3.6)

(3.8)
$a_{{23}}^{2} = \frac{{m_{1}^{2} + 2}}{4} \pm \frac{{(2m_{1}^{3}{{m}_{2}} - 5{{m}_{1}}({{m}_{1}} + {{m}_{2}}) + 8)\sqrt {({{m}_{1}}{{m}_{2}} - 1)({{m}_{1}}{{m}_{2}} - 4)} }}{{8({{m}_{1}}{{m}_{2}} - 1)({{m}_{1}}{{m}_{2}} - 4)}}$
существуют при выполнении условий ${{m}_{1}}{{m}_{2}} < 1$, ${{m}_{1}}{{m}_{2}} > 4$ и при условии, когда правая часть (3.8) неотрицательна и не превышает 1.

Решения $a_{{13}}^{2} = 1$, $b_{{13}}^{2} = 1$ в Случае 6 очень похожи на случай 5, если параметры ${{m}_{1}},\;{{m}_{2}}$ в случае 5 заменить на параметры ${{n}_{1}},\;{{n}_{2}}$.

В Случае 7: $(a_{{11}}^{2} = 1,\;b_{{11}}^{2} = 1)$ из системы (2.1), (2.2) получим простые уравнения, которые не зависят от параметров системы двух тел:

(3.9)
$\begin{gathered} {{a}_{{22}}}{{a}_{{23}}} = 0,\quad {{b}_{{22}}}{{b}_{{23}}} = 0, \\ a_{{22}}^{2} + a_{{23}}^{2} = 1,\quad b_{{22}}^{2} + b_{{23}}^{2} = 1. \\ \end{gathered} $

Случай 8: ($a_{{21}}^{2} = 1$, $b_{{21}}^{2} = 1$) и Случай 9: ($a_{{31}}^{2} = 1$, $b_{{31}}^{2} = 1$) рассматриваются аналогично Случаю 7.

ЗАКЛЮЧЕНИЕ

В настоящей работе проведено исследование движения системы двух тел, соединенных сферическим шарниром, движущихся по круговой орбите под действием гравитационного момента.

Главное внимание уделено изучению равновесных ориентаций системы двух тел. Предложен алгебраический метод (основанный на построении базиса Гребнера) определения положений равновесия системы двух тел в орбитальной системе координат при заданных значениях параметров системы для специальных случаев, когда одна из главных осей инерции как первого, так и второго тела совпадает с нормалью к плоскости орбиты, радиусом вектором или касательной к орбите.

Полученные результаты могут быть использованы на этапе предварительного проектирования гравитационных систем управления ориентацией искусственных спутников Земли.

Список литературы

  1. Белецкий В.В. О либрации спутника // Искусственные спутники Земли. 1959. Вып. 3. С. 13–31.

  2. Sarychev V.A. Asymptotically Stable Stationary Rotational Motions of a Satellite // Proc. 1st IFAC Symp. on Automatic Control in Space. N.Y. Plenum Press, 1966. P. 277–286.

  3. Likins P.W., Roberson R.E. Uniqueness of Equilibrium Attitudes for Earth-Pointing Satellites // J. Astronaut Sci. 1966. V. 13. № 2. P. 87–88.

  4. Сарычев В.А. Вопросы ориентации искусственных спутников. Итоги науки и техники. Сер. Исследование космического пространства. Т. 11. М.: ВИНИТИ, 1978.

  5. Охоцимский Д.Е., Сарычев В.А. Система гравитационной стабилизации искусственных спутников // Сб. Искусств. Спутники Земли. М.: Изд-во АН СССР, 1963. № 16. С. 5–9.

  6. Сарычев В.А. Исследование динамики системы гравитационной стабилизации // Сб. Искусств. спутники Земли. М.: Изд-во АН СССР. 1963. № 16. С. 10–33.

  7. Пеньков В.И., Сарычев В.А. Гравитационная система стабилизации спутников с одностепенным шарнирным подвесом // Космические исследования. 1977. Т. 15. № 4. С. 499–510.

  8. Сарычев В.А. Положения относительного равновесия двух тел, соединенных сферическим шарниром, на круговой орбите // Космические исследования. 1967. Т. 5. № 3. С. 360–364.

  9. Сарычев В.А., Сазонов В.В. Оптимальные параметры пассивных систем ориентации спутников // Космические исследования. 1976. Т. 14. № 2. С. 198–208.

  10. Сарычев В.А., Мирер С.А. Оптимальные параметры гравитационной системы спутник–стабилизатор // Космические исследования. 1976. Т. 14. № 2. С. 209–219.

  11. Sarychev V.A., Mirer S.A., Sazonov V.V. Plane oscillations of a gravitational system satellite-stabilizer with maximal speed of response // Acta Astronautica. 1976. V. 3. № 9–10. P. 651–669.

  12. Сарычев В.А. Положения равновесия системы двух соединенных сферическим шарниром осесимметричных тел на круговой орбите // Космические исследования. 1999. Т. 3. № 2. С. 176–181.

  13. Zajac E.E. Damping of a gravitationally oriented two-body satellite // ARS Journal. 1962. V. 32. № 12. P. 1871–1875.

  14. Гутник С.А., Сарычев В.А. Применение методов компьютерной алгебры для исследования динамики системы двух связанных тел на круговой орбите // Программирование. 2019. Т. 45. № 2. С. 32–40.

  15. Бухбергер Б. Базисы Гребнера. Алгоритмический метод в теории полиномиальных идеалов // Компьютерная алгебра. Символьные и алгебраические вычисления. М.: Мир, 1986. С. 331–372.

  16. Maple online help: http: // www.maplesoft.com/support/help/

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал