1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 1, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 1, стр. 88-95

Расчет вероятностей перехода в квантовой механике с неотрицательной функцией распределения в системе компьютерной алгебры MAPLE

А. В. Зорин 1, *, Н. П. Третьяков 1

1 РУДНРоссийская академия народного хозяйства и гос. службыРоссийский гос. социальный ун-т
117198 129226 119571 Москва, Москва, Москва, ул. Миклухо-Маклая, 6пр-т Вернадского, 82-2ул. Вильгельма Пика, 4-1, Россия

* E-mail: trn11-2011@mail.ru

Поступила в редакцию 15.06.2019
После доработки 19.08.2019
Принята к публикации 18.09.2019

Полный текст (PDF)

Аннотация

В системе компьютерной алгебры MAPLE реализован алгоритм символьно-численных вычислений для определения вероятностей переходов для водородоподобных атомов в квантовой механике с неотрицательной функцией распределения вероятностей (QDF). Квантовая механика с неотрицательной QDF эквивалентна стандартной теории квантовых измерений. Однако наличие в ней вероятностной квантовой теории на фазовом пространстве дает дополнительные возможности вычисления и интерпретации результатов квантовых измерений. Методы компьютерной алгебры представляются необходимыми для проведения соответствующих расчетов. Вычисление матричных элементов операторов необходимо для определения уровней энергии, сил осцилляторов и параметров радиационного перехода для атомов и ионов с открытой оболочкой. Переходные вероятности рассчитываются и сравниваются с экспериментальными данными. Для их расчета используется метод Галеркина с функциями Штурма атома водорода в качестве координатных функций. Проведенная верификация модели показала высокую точность совпадения вычисленных и экспериментально измеренных переходных вероятностей. Библ. 20. Фиг. 3.

Ключевые слова: компьютерная алгебра, MAPLE, квантовая механика, энергетические уровни, квантование, вероятности перехода, водородоподобные атомы.

1. ВВЕДЕНИЕ

Квантовая механика с неотрицательной функцией распределения (QDF), известная в отечественной литературе еще как квантовая механика Курышкина (КМК) (см. [1]–[4]), на современном этапе ее развития требует решения целого ряда вспомогательных задач, часть из которых допускает решение в символьном виде, а часть может быть решена только численно. К числу задач, допускающих аналитическое решение, следует отнести построение штурмовских функций и вычисление интегралов, содержащих эти функции. К числу задач, требующих численного решения, следует отнести прежде всего алгебраическую задачу на собственные значения для матриц, размер которых составляет несколько десятков, такие задачи возникают в этой теории при применении метода Ритца для отыскания спектров атомов. Задачи эти весьма громоздки, поэтому естественным шагом в развитии КМК является создание специализированного программного обеспечения (ПО) для решения этих задач.

Интересующие нас задачи КМК, допускающие символьное решение, могут быть с успехом решены в любой системе компьютерной алгебры. Следует заметить, что многие такие системы, в том числе Maple и Sage, уже содержат модули для работы с ортогональными полиномами, что, вообще говоря, должно было упростить построение штурмовских функций. Однако нормировки, принятые в квантовой механике, отличаются от принятых по умолчанию в англоязычных курсах ортогональных полиномов, поэтому при разработке специализированного ПО мы решили создать такой модуль с нуля, используя лишь стандартные средства системы, как то дифференцирование и интегрирование символьных выражений. Отказавшись от использования встроенных модулей для работы с классическими ортогональными полиномами, мы имели весьма большой выбор среди систем компьютерной алгебры.

Численное решение задач на собственные значения для матриц размером в несколько десятков реализовано как в виде отдельных программ и библиотек на C и Fortran, так и во многих средах, ориентированных на научные и инженерные вычисления, в том числе Matlab иMathematica. Уже довольно давно разработчики систем компьютерной алгебры стали дополнять их функционалом, связанным с численным решением популярных задач, в том числе задач на собственные значения. Так, например, ПО Maple, разработанная изначально как система компьютерной алгебры, позиционирует себя как среда для символьных и численных вычислений (symbolic and numeric computing environment), а также как язык программирования [5]. Мы выбрали именно эту среду для разработки своего ПО, поскольку в ней можно было решать задачи КМК как аналитически, так и численно, и при этом собрать ПО в виде пакета (package), написанного на языке Maple.

В настоящей статье мы хотим представить наш пакет SourceFunctions под Maple, созданный на основе методов и алгоритмов, разработанных для нужд КМК А.В. Зориным, Л.А. Севастьяновым и Н.П. Третьяковым [6]–[9], уделив особое внимание не квантово-механическим аспектам, как это было сделано в названных публикациях, а моментам, связанным с реализацией этих методов в Maple. Пакет размещен в открытый доступ [10].

2. ПОСТРОЕНИЕ ЯВНОГО ВИДА ОПЕРАТОРА ГАМИЛЬТОНА И СООТВЕТСТВУЮЩИХ МАТРИЦ РИТЦА ЗАДАЧИ КЕПЛЕРА В КМК, А ТАКЖЕ ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИХ СПЕКТРА С ПОМОЩЬЮ Maple

Теория измерений в квантовой механике хорошо описывается с помощью так называемой стандартной модели квантовых измерений Холево [11]. В работах Курышкина [1], [2] была построена модель квантовой механики с неотрицательной квантовой функцией распределения. Л. Коэн и Ю.И. Запарованный [12] показали, что она эквивалентна операциональной модели квантовых измерений Вудкевича [13]. В свою очередь, Озава [14] показал, что область применения операционной модели квантовых измерений имеет непустое пересечение с областью применения стандартной модели квантовых измерений. Именно в этой области действует модель квантовых измерений Курышкина-Вудкевича.

Структура квантовой механики с неотрицательной функцией распределения значительно превосходит по своей сложности традиционную квантовую механику и требует привлечения символьных вычислений наряду с применением численных методов. Процедура расчета операторов наблюдаемых величин в QDF включает в себя вычисление многомерных интегралов, а полученные выражения операторов слишком громоздки для вычисления вручную и требуют привлечения численных методов. Был проведен численный расчет спектра водорода и некоторых щелочных металлов с использованием метода Ритца с матрицами размерности 55 × 55. Это соответствует использованию базиса из функций со значениями главного квантового числа $n = 1,2,3,4,5$. Полученные значения затем сравнивались с экспериментальными данными для нахождения оптимальных параметров, обеспечивающих наилучшее согласование данных. Кроме того, был разработан алгоритм численного расчета переходных вероятностей для водородоподобных атомов и процедура сравнения этих данных с теми, что были получены экспериментальным путем.

2.1. Явный вид решений задачи Кеплера в общепринятой квантовой механике

Водородоподобный атом – это ядро с зарядом $( - Ze)$, где $e$ – отрицательный заряд электрона, и одиночный электрон в связанном состоянии. На классическом уровне водородоподобный атом описывается трехмерной задачей Кеплера, которая является вполне интегрируемой и обладает тремя первыми интегралами, находящимися в инволюции относительно скобок Пуассона. Первые интегралы соответствуют:

1) функции Гамильтона, описывающей полную энергию системы $H({\mathbf{r}},{\mathbf{p}}) = {{({\mathbf{p}})}^{2}}{\text{/}}2\mu - (Z{{e}^{2}}){\text{/|}}{\mathbf{r}}{\text{|}}$;

2) проекции момента импульса ${\mathbf{L}} = \left[ {{\mathbf{r}} \times {\mathbf{p}}} \right]$ на ось $Oz$: ${{L}_{z}} = x{{p}_{y}} - y{{p}_{x}}$;

3) квадрату момента импульса $\mathop {\left( {\mathbf{L}} \right)}\nolimits^2 = \mathop {(y{{p}_{z}} - z{{p}_{y}})}\nolimits^2 + \mathop {(z{{p}_{x}} - x{{p}_{z}})}\nolimits^2 + \mathop {(x{{p}_{y}} - y{{p}_{x}})}\nolimits^2 $.

На квантово-механическом уровне описания трем первым интегралам в инволюции соответствуют три эрмитовых дифференциальных оператора $\hat {H}$, ${{\hat {L}}_{z}}$ и $\mathop {({\mathbf{\hat {L}}})}\nolimits^2 $, коммутирующих между собой, образующих полную систему наблюдаемых и обладающих собственными векторами с совместным простым спектром

(1)
${{\hat {L}}_{z}}{{\psi }_{{nlm}}} = \hbar m{{\psi }_{{nlm}}},\quad m = - l, - l + 1,...,l - 1,l;$
(2)
$\mathop {({\mathbf{\hat {L}}})}\nolimits^2 {{\psi }_{{nlm}}} = - \hbar l(l + 1){{\psi }_{{nlm}}},\quad l = 0,1,...,n - 1;$
(3)
$\hat {H}{{\psi }_{{nlm}}} = {{E}_{n}}{{\psi }_{{nlm}}},\quad n = 1,2,3,...,$
где ${{E}_{n}} = - {{E}_{0}}{\text{/}}{{n}^{2}},$ ${{E}_{0}} = ({{Z}^{2}}{{e}^{4}}\mu ){\text{/}}(2{{\hbar }^{2}}) = {{e}^{2}}{\text{/}}(2{{r}_{0}})$, где ${{r}_{0}} = {{\hbar }^{2}}{\text{/}}(\mu {{e}^{2}})$ – первый боровский радиус электрона в атоме водорода.

Собственные векторы ${{\psi }_{{nlm}}}$ в конфигурационном пространстве ${{L}_{2}}({{R}^{3}})$ факторизуются в произведение радиальных ${{R}_{{nl}}}(r)$ и сферических функций ${{Y}_{{lm}}}(\vartheta ,\varphi )$ в сферических координатах $({\mathbf{r}}) = (r,\vartheta ,\varphi )$:

(4)
${{\psi }_{{nlm}}}(r,\vartheta ,\varphi ) = {{R}_{{nl}}}(r){{Y}_{{lm}}}(\vartheta ,\varphi ).$
Радиальная нормированная функция имеет вид
(5)
${{R}_{{nl}}}(r) = {{C}_{{nl}}}\mathop {\left( {2{{\rho }_{0}}{\text{/}}n} \right)}\nolimits^l {{e}^{{ - {{\rho }_{0}}/n}}}L_{{n - l - 1}}^{{(2l + 1)}}\left( {2{{\rho }_{0}}{\text{/}}n} \right),$
где $L_{k}^{{(s)}}$ – присоединенные полиномы Лагерра, ${{\rho }_{0}} = r{\text{/}}{{r}_{0}}$, а коэффициенты нормировки рассчитываются по формуле
(6)
${{C}_{{nl}}} = \frac{1}{{\sqrt \pi }}\mathop {\left( {\frac{2}{n}} \right)}\nolimits^{3/2} \sqrt {\frac{{(n - l - 1)!}}{{2n(n + l)!}}} .$
Нормированные сферические функции имеют вид
(7)
${{Y}_{{lm}}}(\vartheta ,\varphi ) = {{\tilde {C}}_{{lm}}}P_{l}^{{(m)}}(\cos \vartheta ){{e}^{{im\varphi }}},$
где $P_{l}^{{(m)}}$ – присоединенные полиномы Лежандра, и коэффициенты нормировки равны

(8)
${{\tilde {C}}_{{lm}}} = \sqrt {\frac{{(2l + 1)(l - m)!}}{{2{{\varepsilon }_{m}}(l + m)!}}} ,\quad {{\varepsilon }_{m}} = \left\{ \begin{gathered} 2\quad {\text{при}}\quad m = 0, \hfill \\ 1\quad {\text{при}}\quad m \ne 0. \hfill \\ \end{gathered} \right.$

2.2. Структура вспомогательных функций для задачи Кеплера в квантовой механике с неотрицательной функцией распределения

Операторы квантовой механики с неотрицательной квантовой функцией распределения (КФР) действуют в том же гильбертовом пространстве ${{L}_{2}}({{R}^{3}})$, базис в котором задается штурмовскими функциями $\Psi _{{nlm}}^{{st}} = {{S}_{{nl}}}\left( r \right){{Y}_{{lm}}}(\vartheta ,\varphi )$ [15]. Радиальные штурмовские функции ${{S}^{{nl}}}(r)$, порожденные кулоновским потенциалом $V(r) = - \tfrac{2}{r}$, являются решениями уравнения

(9)
$\left( { - \frac{{{{d}^{2}}}}{{d{{r}^{2}}}} + \frac{{l(l + 1)}}{{{{r}^{2}}}} + {{a}_{{nl}}}V(r) - {{E}_{0}}} \right){{S}_{{nl}}}(r) = 0$
с граничными условиями ${{S}_{{nl}}}(0) = 0$, ${{S}_{{nl}}}(r) \to 0$ при $r \to \infty $; здесь $n = 1,2,3,...$; $l = 0,1,...,n - 1$; ${{E}_{0}}$ – фиксированное отрицательное число; ${{a}_{{nl}}} = kn$, где $k = \sqrt { - {{E}_{0}}} $. Функции ${{S}_{{nl}}}(r)$ ортогональны с весом $V(r) = - \tfrac{2}{r}$:

(10)
$\int\limits_0^\infty {{{S}_{{nl}}}V(r){{S}_{{n'l'}}}(r)dr} = - {{\delta }_{{nn'}}}.$

В квантовой механике с неотрицательной КФР правило квантования задается с помощью вспомогательных функций $\{ {{\psi }_{j}}\} $, моделирующих смешанное состояние измерительного прибора

$\mathop {\hat {\rho }}\nolimits_{ap} = \sum\limits_j {{{a}_{j}}\left| {{{\psi }_{j}}} \right\rangle \left\langle {{{\psi }_{j}}} \right|} .$
В качестве вспомогательных функций удобно выбрать первые пять модифицированных штурмовских функций
$\Psi _{{nlm}}^{{st}} = {{S}_{{nl}}}\left( {r{\text{/}}b} \right){{Y}_{{lm}}}(\vartheta ,\varphi )\quad n = 1,2.$
Здесь $b$ – масштабирующий подгоночный коэффициент, другими подгоночными коэффициентами являются ${{E}_{0}},{{a}_{1}},...,{{a}_{5}}$, а также, в случае щелочных металлов, эффективный заряд ядра $Z$ [6].

2.3. Вычисления явного вида оператора Гамильтона водородоподобного атома в QDF с помощью Maple

Оператор полной энергии

${{O}_{\rho }}(H) = \sum\limits_{j = 1}^5 {{{a}_{j}}{{O}_{j}}(H)} ,\quad {\text{где}}\quad {{O}_{j}}(H) = {{O}_{j}}\left( {\tfrac{{{{{\mathbf{p}}}^{2}}}}{{2\mu }}} \right) + {{O}_{j}}\left( { - \tfrac{{Z{{e}^{2}}}}{r}} \right).$
В работе [6] показано, что
(11)
${{O}_{j}}\left( {\frac{{{{{\mathbf{p}}}^{2}}}}{{2\mu }}} \right) = \frac{1}{{2\mu }}\int {{{{(\eta - i\hbar \nabla )}}^{2}}{\text{|}}\tilde {\Psi }(\eta ){{{\text{|}}}^{2}}{{d}^{3}}\eta } ,$
где
$\mathop {\tilde {\psi }}\nolimits_j (\eta ) = \tfrac{1}{{{{{(2\pi \hbar )}}^{{3/2}}}}}\int {{{\psi }_{j}}({\mathbf{r}}){{e}^{{\tfrac{i}{\hbar }(\eta ,{\mathbf{r}})}}}{{d}^{3}}{\mathbf{r}}} .$
Аналогично,

(12)
${{O}_{j}}\left( { - \frac{{Z{{e}^{2}}}}{r}} \right) = - Z{{e}^{2}}\smallint \frac{{\mathop {\left| {{{\psi }_{j}}(\xi )} \right|}\nolimits^2 }}{{\left| {{\mathbf{r}} + \xi } \right|}}{{d}^{3}}\xi .$

Для вычисления операторов ${{O}_{j}}( - Z{{e}^{2}}{\text{/|}}{\mathbf{r}}{\text{|}})$ потенциальной энергии возникает необходимость воспользоваться разложениями по сферическим гармоникам, например:

(13)
$\frac{1}{{\left| {{\mathbf{q}} - {\mathbf{s}}} \right|}} = 4\pi \sum\limits_{l = 0}^\infty \,\frac{1}{{2l + 1}}\frac{{r_{ - }^{l}}}{{r_{ + }^{{l + 1}}}}\sum\limits_{m = - l}^l \,{{Y}_{{lm}}}({{\vartheta }_{q}},{{\varphi }_{q}})Y_{{lm}}^{*}({{\vartheta }_{s}},{{\varphi }_{s}}),$
где
${{r}_{ - }} = \min ({\text{|}}{\mathbf{q}}{\text{|}},{\text{|}}{\mathbf{s}}{\text{|}}),\quad {{r}_{ + }} = \max ({\text{|}}{\mathbf{q}}{\text{|}},{\text{|}}{\mathbf{s}}{\text{|}}),$
а также известными формулами для произведения сферических функций.

В рамках Maple символьно вычисляются матрицы операторов кинетической и потенциальной энергии водородоподобного атома в базисе штурмовских функций. Аналитические вычисления операторов с помощью Maple дают, в соответствии с (11), (12) и (13), выражения следующего вида:

(14)
${{O}_{j}}\left( {\frac{{{{{\mathbf{p}}}^{2}}}}{{2\mu }}} \right) = - \frac{{{{\hbar }^{2}}}}{{2\mu }}{{\nabla }^{2}} + \frac{{{{\hbar }^{2}}}}{{2\mu b_{i}^{2}}},\quad i = 1...5;$
(15)
${{O}_{1}}\left( { - \frac{{Z{{e}^{2}}}}{r}} \right) = - \frac{{Z{{e}^{2}}}}{r} + Z{{e}^{2}}\exp \left( { - \frac{{2r}}{{{{b}_{1}}{{r}_{0}}}}} \right)\left( {\frac{1}{{{{r}_{0}}}} + \frac{1}{{{{b}_{1}}{{r}_{0}}}}} \right);$
(16)
${{O}_{2}}\left( { - \frac{{Z{{e}^{2}}}}{r}} \right) = - \frac{{Z{{e}^{2}}}}{r} + \frac{{Z{{e}^{2}}}}{{{{b}_{2}}{{r}_{0}}}}\exp \left( { - \frac{{2r}}{{{{b}_{2}}{{r}_{0}}}}} \right)\left( {\frac{3}{4} + \frac{{{{b}_{2}}{{r}_{0}}}}{r} + \frac{1}{4}\frac{r}{{{{b}_{2}}{{r}_{0}}}} + \frac{1}{8}\mathop {\left( {\frac{r}{{{{b}_{2}}{{r}_{0}}}}} \right)}\nolimits^2 } \right);$
остальные выражения ${{O}_{3}},\;{{O}_{4}},\;{{O}_{5}}$ имеют аналогичную структуру [10]. Они используются для построения матриц Ритца и вычисления спектра. С их помощью мы приближенно вычисляем в Maple спектр оператора $O(H)$. А именно, нами написана процедура вычисления спектра с использованием матрицы Ритца размерности 55, что соответствует первым пяти главным квантовым числам $n$ [10].

3. ПРОГРАММА

Созданный авторами подпакет “SourceFunctions” состоит из вычисления базовых функций (10), в частности, производится расчет сферических гармоник, их произведений, полиномов Лежандра с использованием формулы Родрига, вычисление коэффициентов Клебша-Гордана $SO(3)$. В качестве примера приведем код подпрограммы для вычисления штурмовских функций по приведенным выше формулам.

Sturm:=proc(np,lp,b)

local kk,alpha_nl,N_nl,altLaguerreL;

kk:=1/b: alpha_nl:=kk*np: N_nl:=-sqrt((np-lp-1)!/((np+lp)!)^3/2):

altLaguerreL := (n,a,x) -> (-1)^a*n!*LaguerreL(n-a,a,x):

N_nl*exp(-kk*r)*(2*kk*r)^(lp+1)*

simplify(altLaguerreL(np+lp,2*lp+1,2*kk*r) ): end proc;

Далее эти функции необходимо нормировать

R:=proc(n,l,b)

subs(r=r, Sturm(n,l,b) /r )/sqrt(int(subs(r=r,Sturm(n,l,b)^2/r^2)

*r^2, r=0..infinity)): end proc;

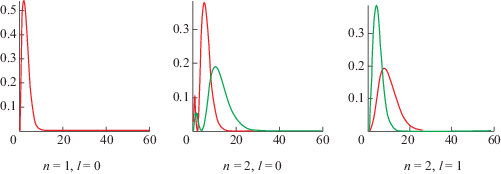
Сравним поведение радиальных частей штурмовских и обычных кулоновских волновых функций при различных значениях $n,\;l$. Из фиг. 1 видно, что в случае $n = 1$, $l = 0$ обе функции точно совпадают, но с ростом $n$ амплитуда и число гармоник штурмовских функций отличаются от кулоновских.

Фиг. 1.

Поведение штурмовской и кулоновской радиальных частей волновых функций при различных значениях n и l.

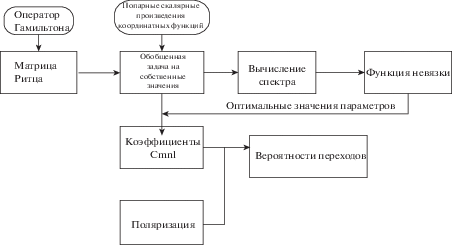
Пакет “SourceFunctions” загружается обычным способом:

>with(SourceFunctions_Sturm);

Отметим, что в соответствии с методом Ритца, собственные значения матриц Ритца представляют спектральные значения исследуемой величины, то есть энергии. Элементы матрицы Ритца рассчитываются по формуле:

(17)
$M_{{kl}}^{j} = \int {\mathop {\bar {\psi }}\nolimits_k^{{{E}_{0}}} ({\mathbf{r}})} \left[ {{{O}_{j}}\left( {\frac{{{{{\mathbf{p}}}^{2}}}}{{2\mu }}} \right) + {{O}_{j}}\left( { - \frac{{{{Z}_{{eff}}}{{e}^{2}}}}{r}} \right)} \right]\psi _{l}^{{{{E}_{0}}}}({\mathbf{r}})d{\mathbf{r}}.$

Однако из-за неортогональности множества координатных функций необходимо решить обобщенную проблему собственных значений $Mx = \lambda Bx$, где $M$ – матрица Ритца, а $B$ – матрица парных скалярных произведений координатных функций. Отсюда следует процедура расчета спектров операторов Гамильтона. Она включает в себя варьирование входящих в модель параметров (${{E}_{0}},\;{{a}_{j}},\;{{b}_{j}},\;Z$), вычисление значений уровней энергии (из некоторого множества $\Omega $), построение квадратичной невязки (штрафной функции) между вычисленными значениями ${{E}_{k}} = {{E}_{k}}({{E}_{0}},{{a}_{j}},{{b}_{j}},Z)$ и экспериментальными уровнями энергии $E_{k}^{{{\text{exp}}}}$ [16]

(18)
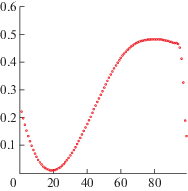
${{F}_{\Omega }} = \sum\limits_{k \in \Omega } \,\mathop {({{E}_{k}} - E_{k}^{{\exp }})}\nolimits^2 {\text{/}}\mathop {(E_{k}^{{\exp }})}\nolimits^2 $
и нахождение ее минимума. Пример зависимости функции невязки от параметра ${{E}_{0}}$ приведен ниже на фиг. 3. Значения параметров, соответствующих такому минимуму, считаются оптимальными и могут использоваться для вычисления других характеристик, например, переходных вероятностей.

Фиг. 2.

Структура блока программы для вычисления переходных вероятностей.

Фиг. 3.

График квадратичной невязки по параметру ${{E}_{0}}$ для первых восьми энергетических уровней атома лития (от $2S$ до $3P$).

Следует отметить, что получение значений энергии производится численно, с некоторой заданной точностью. Таким образом, в данной программе сполна используется упомянутая выше способность Maple выполнять не только символьные, но и численные расчеты.

Расчеты проводились с использованием матрицы Ритца размерности 55, что соответствует первым пяти главным квантовым числам n [9]. Тем не менее даже для такой ограниченной размерности удалось получить спектр водорода и некоторых щелочных металлов с высокой точностью. Отметим, что ключевой момент, т.е. вычисление собственных значений, производится с помощью функции Maple “eigenvals”:

eigen_vls:=eigenvals(MM):

Отметим однако, что модель зависит от достаточно большого числа свободных параметров. Поэтому мы не претендуем на то, что в настоящем варианте программы находятся глобальные минимумы штрафных функций. Тем не менее для атома водорода (в отличие от щелочных металлов) единственным чувствительным параметром оказалось значение ${{E}_{0}}$. Это можно утверждать на основании многочисленных расчетов. Так, для параметров ${{a}_{j}}$ в случае атома водорода оптимальным значением, вне зависимости от количества спектральных значений в невязке, оказалось значение ${{a}_{1}} = 1$, а остальные коэффициенты при оптимизации обращались в ноль.

3.1. Верификация компьютерной модели на соответствующих экспериментальных данных

Для проверки качества модели и правильности выбора вспомогательных функций был проведен расчет переходных вероятностей. В работе [7] описан формализм расчета переходных вероятностей методом Галеркина со штурмовскими функциями атома водорода в качестве координатных, что позволяет свести вычисления к алгебраическим операциям с матричными элементами, которые вычисляются аналитически. Отметим, что в основе лежит выражение для вероятности перехода из состояния $\alpha $ в состояние $\beta $ с испусканием кванта с поляризацией ${{{\mathbf{e}}}_{\rho }}$ в направлении ${\mathbf{k}}$:

(19)
$d{{W}_{{\rho {\mathbf{k}}}}}(\alpha ,\beta ) = \frac{{{{e}^{2}}{{\omega }^{3}}}}{{2\pi \hbar {{c}^{3}}}}\mathop {\left| {{{{\mathbf{e}}}_{{\rho {\mathbf{k}}}}}\left\langle {{{\psi }_{\alpha }}} \right|{\mathbf{r}}\left| {{{\psi }_{\beta }}} \right\rangle } \right|}\nolimits^2 .$

В данной работе символьный расчет переходных вероятностей с помощью данной формулы и описанного в [7] формализма был реализован в рамках программного комплекса Maple. Структура соответствующего блока программы приведена на фиг. 2. На этой схеме верхняя часть соответствует описанному выше алгоритму вычисления спектра. Необходимость использования коэффициентов Клебша-Гордана связана с разложением выражения под знаком модуля в (19) по штурмовским функциям:

(20)
${{{\mathbf{e}}}_{{\rho {\mathbf{k}}}}}\left\langle {{{\psi }_{\alpha }}} \right|{\mathbf{r}}\left| {{{\psi }_{\beta }}} \right\rangle = \sum\limits_{nlm} \,C_{{nlm}}^{\alpha }\sum\limits_{pqs} \,\bar {C}_{{pqs}}^{\beta }\left\langle {nlm} \right|{{{\mathbf{e}}}_{{\rho {\mathbf{r}}}}}{\mathbf{r}}\left| {pqs} \right\rangle .$

Отметим, что в составленной нами процедуре вычисления коэффициентов Клебша-Гордана (текст программы приведен в [10]) основное содержание кода соответствует перебору различных значений индексов, что успешно решается с помощью функции $if$. Финальное вычисление вероятности перехода производится с помощью формулы (19).

4. ЗАКЛЮЧЕНИЕ

Алгоритм расчета для конкретных атомов (водорода, лития, натрия) включает построение штрафных функций (квадратичных невязок) для нескольких первых уровней энергии (между расчетными и экспериментальными значениями). Нахождение минимумов этих штрафных функций позволяет определить значения настраиваемых параметров (наиболее важным из которых является ${{E}_{0}}$). Оказывается, что такие функции имеют четкие минимумы (примеры приведены, например, в [6], [18]). На фиг. 3 показан новый пример: график квадратичного расхождения по параметру ${{E}_{0}}$ в случае первых восьми энергетических уровней атома лития. Отметим, что наличие таких ярко выраженных минимумов само по себе можно рассматривать как качественное подтверждение QDF и ее физической значимости. Переходные вероятности могут затем рассматриваться как метод проверки расчетов, когда параметры, полученные из минимизации энергетического штрафа, затем используются для вычисления этих вероятностей. Например, для вероятности перехода атома водорода из состояния $(n = 1,\;l = 0)$ в состояние ($n = 2$, $l = 1$) получается значение $6.264 \times {{10}^{8}}$ сек–1, что хорошо согласуется с экспериментальным значением $6.2649 \times {{10}^{8}}$ сек–1 (см. [19], [20]):

tp:=dW_alf_bet(-0.21935, 0,0,0,0,0, 1,0,0, 1, 1, 55, 1,0, 2,1);

    9

           tp := 0.6264033351 10.

Аналогично, для других вероятностей перехода между несколькими уровнями атома водорода значения отличаются от экспериментальных не более чем на 1%, а для лития – не более чем на 2%. Это еще раз подтверждает, что QDF перестает быть некой формальной теорией и становится реальной расчетной схемой.

Авторы признательны Л.А. Севастьянову за плодотворные обсуждения и постоянное внимание к их работе.

Список литературы

  1. Kuryshkin V.V. Some problems of quantum mechanics possessing a non-negative phase-space distribution function // Int. J. Theor. Phys. 1973. V. 7. № 6. P. 451.

  2. Kuryshkin V.V. La mechanique quantique avec une function nonnegative de distribution dans l’espace des phases // Annales Inst. Henri Poincare. 1972. V. 17, № 1. P. 81.

  3. Zorin A.V., Sevastianov L.A. Hydrogen-like atom with nonnegative quantum distribution function // Physics of Atomic Nuclei. 2007. V. 70. P. 792.

  4. Zorin A.V. The Operational Model of Quantum Measurement of Kuryshkin–Wodkiewicz // Bull. PFUR. Ser. Math. Phys. 2012. № 2. P. 43.

  5. Аладьев В.З. Основы программирования в Maple. Таллинн, 2006.

  6. Зорин А.В., Севастьянов Л.А., Третьяков Н.П. Компьютерное моделирование водородоподобных атомов в квантовой механике с неотрицательной функцией распределения // Программирование. 2007. Т. 33. № 2. С. 50.

  7. Zorin A.V. Transition probabilities in Kuryshkin’s quantum mechanics // Bull. PFUR, Ser. Math. Phys. 2008. № 4. P. 108.

  8. Sevastianov L., Zorin A., Gorbachev A. Pseudo-Differential Operators in the Operational Model of a Quantum Measurement of Observables // LNCS. 2012. V. 7125. P. 174.

  9. Zorin A.V., Tretyakov N.P. MAPLE program for modelling hydrogen-like atoms in quantum mechanics with non-negative distribution function // Bull. PFUR. Ser. Math. Phys. 2018. № 4. P. 343.

  10. Zorin A.V., Sevastianov A.L., Tretyakov N.P. QDF code. Computer Modelling of Hydrogen-Like Atoms in Quantum Mechanics with Nonnegative Distribution Function. 2019. Located at: https://bitbucket.org/yamadharma/articles-2019-zorin-qdf

  11. Holevo A.S. Statistical structure of quantum theory // Lecture Notes in Physics. Monographs, 67. Berlin: Springer-Verlag, 2001.

  12. Cohen L., Zaparovanny Y.I. Positive quantum joint distributions // Journal of Mathematical Physics. 1980. V. 21. P. 794.

  13. Wodkiewicz K. Operational Approach to Phase-Space Measurements in Quantum Mechanics // Phys. Rev. Lett. 1984. V. 52. P. 1064.

  14. Ozawa M. Mathematical foundations of quantum information: measurement and foundations // Sugaku Expositions. 2014. V. 27. P. 195.

  15. Rotenberg M. Theory and application of sturmian functions // Advances in Atomic and Molecular Physics. 1970. V. 6 P. 233. Elsevier, 1970.

  16. Basic Atomic Spectroscopic Data. Located at: http://physics.nist.gov/PhysRefData

  17. Sevastianov L.A., Zorin A.V. The Computer-Based Model of Quantum Measurement // Physics of Atomic Nuclei. 2017. V. 80. № 4. P. 774.

  18. Zorin A.V., Sevastianov L.A., Tretyakov N.P. Application of the noncommutative theory of statistical decisions to the modeling of quantum communication channels // International Congress on Ultra Modern Telecommunications and Control Systemsand Workshops. 2017. 2018. P. 26.

  19. Jitrik O., Bunge C.F. Transition probabilities for hydrogen-like atoms // J. Phys. Chem. Ref. Data. 2004. V. 33. P. 1059.

  20. Jitrik O., Bunge C.F. Salient features of electric and magnetic multipole transition probabilities of hydrogen-like systems // Physica Scripta. 2004. V. 69. P. 196.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал