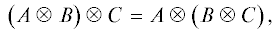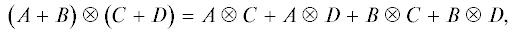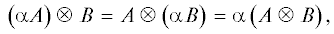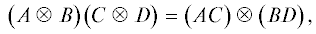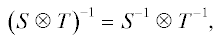Журнал вычислительной математики и математической физики, 2020, T. 60, № 1, стр. 96-108

Вычисление неприводимых разложений перестановочных представлений сплетений конечных групп

В. В. Корняк

ОИЯИ
141980 М.о., Дубна, ул. Жолио Кюри, 6, Россия

Поступила в редакцию 24.07.2019
После доработки 24.07.2019
Принята к публикации 18.09.2019

DOI: 10.31857/S0044466920010123

Аннотация

Описан алгоритм вычисления полного множества примитивных ортогональных идемпотентов централизаторного кольца перестановочного представления сплетения конечных групп. Это множество определяет разложение представления на неприводимые компоненты. В формализме квантовой механики примитивные идемпотенты являются операторами проекции в неприводимые инвариантные подпространства гильбертова пространства, описывающего состояния многочастичной квантовой системы. Предлагаемый алгоритм использует методы компьютерной алгебры и вычислительной теории групп. Реализация алгоритма на языке Си способна строить разложения на неприводимые компоненты представлений высоких размерностей и рангов. Библ. 15. Фиг. 3.

Ключевые слова: сплетение групп, перестановочное представление, централизаторное кольцо, примитивные идемпотенты, разложение на неприводимые подпредставления, вычислительная теория групп.

1. ВВЕДЕНИЕ

Описание физической системы обычно включает геометрическое пространство $X$, на котором действует группа пространственных симметрий $G = G(X)$, и множество локальных состояний $V$ с группой локальных (или внутренних) симметрий $F = F(V)$. Множества $X$, $V$ и группу $F$ можно рассматривать, соответственно, как базу, типичный слой и структурную группу расслоения. Состояния системы в целом описываются функциями из $X$ в $V$, то есть сечениями расслоения. Естественной группой симметрий, действующей на множестве сечений ${{V}^{X}}$ с сохранением структуры расслоения, является комбинация локальной $F$ и пространственной $G$ групп, называемая сплетением [1], [2]. Сплетение, обозначаемое символом $F\wr G$, имеет структуру полупрямого произведения [3] множества функций ${{F}^{X}}$ на точках пространства со значениями в локальной группе и пространственной группы:

(1)

$\widetilde W = F\wr G \cong {{F}^{X}} \rtimes G.$

Действие сплетения $\widetilde W$ на множестве сечений ${{V}^{X}}$ описывается формулой

(2)

$v(x)(f(x),g) = v(x{{g}^{{ - 1}}})f(x{{g}^{{ - 1}}}),$

где $v \in {{V}^{X}}$, $f \in {{F}^{X}}$, $g \in G$. В формуле (2) и далее мы записываем действия групп справа, как это принято в теории групп. Приведем несколько примеров приложений сплетений.

1. Универсальная теорема вложения (теорема Калужнина–Краснера) утверждает, что любое расширение группы $A$ с помощью группы $B$ изоморфно некоторой подгруппе сплетения $A\wr B$, т.е., сплетение представляет собой универсальный объект, содержащий все расширения.

2. Сплетения играют важную роль в описании всех максимальных подгрупп симметрической группы (теорема О’Нэна–Скотта) [4].

3. Сплетение ${{{\text{S}}}_{m}}\wr {{{\text{S}}}_{n}}$ является группой автоморфизмов гиперкубического графа или схемы Хэмминга $H\left( {n,m} \right)$ в теории кодирования [5].

4. Унитарные представления сплетений возникают естественно при описании многочастичных квантовых систем.

При изучении представлений групп и их приложений естественным начальным шагом является разложение представлений на неприводимые подпредставления. Ранее мы предложили алгоритм разложения представлений конечных групп [6], [7], основанный на построении полного множества взаимно ортогональных инвариантных проекторов. Это множество является частным случаем конструкции, которая в общей теории колец называется полным множеством примитивных ортогональных идемпотентов. Любое кольцо с единицей содержит такое множество (возможно, тривиальное, т.е., состоящее из одной единицы). Кольцо, содержащее нетривиальное полное множество примитивных ортогональных идемпотентов, может быть представлено в виде прямой суммы неразложимых колец. Это представление называется разложением Пирса [8], [9]. В нашем случае неприводимые инвариантные проекторы являются примитивными идемпотентами централизаторного кольца рассматриваемого представления группы. Централизаторное кольцо определяется как кольцо матриц, коммутирующих со всеми матрицами представления. Централизаторное кольцо можно рассматривать как алгебру над полем, содержащим элементы матриц. Эта алгебра называется централизаторной алгеброй, а ее размерность называется рангом представления, который мы будем обозначать символом $R$.

Подход, описанный в [6], [7], вкратце сводится к следующему. Пусть у нас имеется группа $G$ и ее представление $\mathcal{U}\left( G \right)$ в некотором пространстве. Вначале мы вычисляем базис централизаторной алгебы $\{ {{A}_{1}}, \ldots ,{{A}_{R}}\} $. Это несложная задача линейной алгебры, поскольку матрицы ${{A}_{1}}, \ldots ,{{A}_{R}}$ являются решениями системы линейных уравнений $\mathcal{U}({{g}^{{ - 1}}})A\mathcal{U}(g) = A$, $g \in G$. Предположим, что централизаторное кольцо содержит $L$ примитивных ортогональных идемпотентов ${{B}_{1}}, \ldots ,{{B}_{L}}$. Условия ортогональности и идемпотентности можно записать в виде системы квадратных уравнений

(3)

${{B}_{k}}{{B}_{\ell }} = {{\delta }_{{k\ell }}}{{B}_{\ell }}.$

Записав идемпотенты в общем виде в базисе централизаторной алгебы

(4)

${{B}_{\ell }} = \sum\limits_{r = 1}^R \,{{b}_{{r\ell }}}{{A}_{r}}$

и подставив (4) в (3), мы получаем систему квадратных уравнений относительно неизвестных ${{b}_{{r\ell }}}$. Из общей теории представлений групп следует, что корни этой системы полиномиальных уравнений принадлежат к абелевым расширениям (aбелевым расширением называется расширение поля рациональных чисел $\mathbb{Q}$ с помощью корней полинома, имеющего абелеву группу Галуа. Согласно теореме Кронекера–Вебера любое абелево расширение является подполем некоторого циклотомического поля – расширения $\mathbb{Q}$ с помощью примитивного корня некоторой степени из единицы) и поэтому, в принципе, всегда могут быть вычислены алгоритмически. В нашем случае число переменных в полиномах равно рангу и наш опыт показывает, что современные системы компьютерной алгебры легко справляются лишь с задачами невысоких рангов, обычно $R \leqslant 17$ (в отдельных случаях удается решить задачи с рангами 18 и 19). Это связано с тем, что алгоритмы работы с полиномами по своей природе являются трудными (имеют двойную экспоненциальную сложность по числу переменных).

Многие важные представления имеют невысокие ранги. Например, около 96% представлений простых групп (и “небольших” расширений простых групп, имеющих нетривиальный мультипликатор Шура и/или нетривиальную группу внешних автоморфизмов), содержащихся в известном Атласе представлений конечных групп [10], удовлетворяют условию $R \leqslant 17$. Компьютерная реализация алгоритма, описанного в [6], [7], расщепляет представления из [10], имеющие размерности в сотни тысяч, в наиболее трудном для вычислений случае полей характеристики нуль.

Сплетения, поскольку они содержат все возможные расширения, весьма “далеки” от простых групп и их представления имеют высокие ранги. Поэтому в данной статье предлагается другой подход. Компьютерная реализация этого подхода расщепляет представления сплетений размерностей в квадриллионы и рангов в сотни миллионов.

2. ЦЕНТРАЛИЗАТОРНОЕ КОЛЬЦО ПЕРЕСТАНОВОЧНОГО ПРЕДСТАВЛЕНИЯ СПЛЕТЕНИЯ

Мы предполагаем, что $\left| X \right| = N$ и $\left| V \right| = M$, и, следовательно, пространственная и локальная группы являются подгруппами соответствующих симметрических групп: $G(X) \leqslant {{{\text{S}}}_{N}}$ и $F(V) \leqslant {{{\text{S}}}_{M}}$. Перестановочное представление $\widetilde P = \widetilde P(\widetilde W)$ сплетения $\widetilde W$ реализуется $(0,1)$-матрицами размера ${{M}^{N}} \times {{M}^{N}}$, имеющими вид

(5)

$\widetilde P\mathop {(\tilde {w})}\nolimits_{u,v} = {{\delta }_{{u\tilde {w},v}}},\quad {\text{где}}\quad \tilde {w} \in \widetilde W;\quad u,v \in {{V}^{X}};\quad \delta \; - \;{\text{дельта}}\;{\text{Кронекера}}.$

Мы предполагаем, что пространством представления является ${{M}^{N}}$-мерное гильбертово пространство

над некоторым абелевым расширением $\mathcal{F}$ поля $\mathbb{Q}$, являющимся расщепляющим полем (расщепляющим полем для конечной группы называется поле, над которым любое линейное представление этой группы может быть полностью разложено на неприводимые компоненты) для локальной группы $F$. Обозначим базис централизаторной алгебры представления $\widetilde P$ через

(6)

$\{ {{\widetilde A}_{1}}, \ldots ,{{\widetilde A}_{{\widetilde R}}}\} ,$

где $\widetilde R$ означает ранг представления. Элементы множества (6) являются решениями системы уравнений, выражающих условия инвариантности

(7)

$\widetilde P({{\tilde {w}}^{{ - 1}}})\widetilde A\widetilde P(\tilde {w}) = \widetilde A,\quad \tilde {w} \in \widetilde W.$

Более детальный анализ соотношения (7) показывает, что базисные элементы из множества (6) находятся во взаимно однозначном соответствии с орбитами действия группы $\widetilde W$ на декартовом квадрате ${{V}^{X}} \times {{V}^{X}}$. Такие орбиты называются орбиталами. Для удобства представим этот декартов квадрат в виде $\mathop {\left( {V \times V} \right)}\nolimits^X $, то есть в виде массива

(8)

$\left[ {\mathop {(V \times V)}\nolimits_1 , \ldots ,\mathop {(V \times V)}\nolimits_N } \right].$

Для вычисления орбиталов рассмотрим структуру группы $\widetilde W = F\wr G$ более подробно. Ее подгруппа

(9)

$\widetilde {{{F}^{X}}} = ({{F}^{X}};\;{{{\mathbf{1}}}_{G}}) \cong {{F}^{X}}$

называется базовой группой сплетения. Группа $\widetilde {{{F}^{X}}}$ является нормальным делителем (или инвариантной подгруппой) группы $\widetilde W$. Это означает, что ${{\tilde {w}}^{{ - 1}}}\widetilde {{{F}^{X}}}\tilde {w} = \widetilde {{{F}^{X}}}$ для любого $\widetilde w \in \widetilde W$ и обозначается символически отношением $\widetilde {{{F}^{X}}}\; \triangleleft \;\widetilde W$. Подгруппа

(10)

$\widetilde G = ({\mathbf{1}}_{F}^{X};\;G) \cong G$

является дополнением к $\widetilde {{{F}^{X}}}$ в $\widetilde W$, т.е.

$\widetilde W = \widetilde {{{F}^{X}}}\widetilde G\quad {\text{и}}\quad \widetilde {{{F}^{X}}} \cap \widetilde G = {{{\mathbf{1}}}_{{\widetilde W}}} \equiv ({\mathbf{1}}_{F}^{X};\;{{{\mathbf{1}}}_{G}}).$

Таким образом, мы можем построить орбиты множества $\mathop {\left( {V \times V} \right)}\nolimits^X $, действуя сначала элементами базовой группы (9), а затем элементами дополнения (10). Поскольку ${{F}^{X}}$ является прямым произведением $N$ копий $F$, т.е. ${{F}^{X}} = {{F}_{1}} \times \cdots \times {{F}_{N}}$, мы можем действовать группой ${{F}^{X}}$ на массив (8) покомпонентно.

Действие локальной группы $F$ разбивает множество $V \times V$ на $R$ орбит ${{\Delta }_{1}}, \ldots ,{{\Delta }_{R}},$ которые мы будем называть локальными орбиталами. Вычисление локальных орбиталов – простая задача, поскольку локальная группа “экспоненциально меньше” сплетения. Пусть $\overline R = \left\{ {1, \ldots ,R} \right\}$, а ${{\bar {R}}^{X}}$ обозначает множество всех отображений из $X$ в $\bar {R}$. Определим действие $g \in G$ на отображение $r \in {{\bar {R}}^{X}}$ следующим образом:

(11)

$rg = [{{r}_{{1g}}}, \ldots ,{{r}_{{Ng}}}].$

Орбитал сплетения в терминах локальных орбиталов имеет вид

${{\widetilde \Delta }_{r}} = \mathop \sqcup \limits_{q \in rG} \,{{\Delta }_{{{{q}_{1}}}}} \times \cdots \times {{\Delta }_{{{{q}_{N}}}}},$

где $rG$ обозначает орбиту отображения $r$ относительно действия (11). Для перевода с языка множеств на язык матриц мы должны заменить локальные орбиталы базисными элементами локальной централизаторной алгебры, объединение – суммированием и декартовы произведения – тензорными. В результате мы получаем следующее выражение для базисного элемента централизаторной алгебры сплетения:

(12)

${{\widetilde A}_{r}} = \sum\limits_{q \in rG} \,{{A}_{{{{q}_{1}}}}} \otimes \cdots \otimes {{A}_{{{{q}_{N}}}}},$

где ${{A}_{1}}, \ldots ,{{A}_{R}}$ – базисные элементы локальной централизаторной алгебры. Легко проверить, что базисные элементы (12) образуют полную систему, т.е.

$\sum\limits_{i = 1}^{\widetilde R} \,{{\widetilde A}_{{{{r}^{{(i)}}}}}} = {{\mathbb{J}}_{{{{M}^{N}}}}},$

где ${{\mathbb{J}}_{{{{M}^{N}}}}}$ обозначает матрицу размера ${{M}^{N}} \times {{M}^{N}}$, все элементы которой равны единице; ${{r}^{{(i)}}}$ обозначает некоторую нумерацию орбит группы $G$ на множестве ${{\bar {R}}^{X}}$.

3. ПОЛНОЕ МНОЖЕСТВО ПРИМИТИВНЫХ ОРТОГОНАЛЬНЫХ ИДЕМПОТЕНТОВ

Полное множество примитивных ортогональных идемпотентов является подмножеством централизаторного кольца, выделяемым условиями идемпотентности и взаимной ортогональности. Для выделения этого подмножества мы использовали свойства тензорного (кронекерова) произведения. Наиболее важными для наших целей являются следующие тождества [11]:

(13)

где $A$, $B$, $C$ и $D$ – матрицы, $S$ и $T$ – обратимые матрицы и $\alpha $ – скаляр. Непосредственно из этих тождеств следует, что

1) если $A$ и $B$ инвариантны, то $A \otimes B$ также инвариантная матрица;

2) если $A$ и $B$ идемпотенты, то $A \otimes B$ – идемпотент;

3) если $A{\kern 1pt} ' = {{S}^{{ - 1}}}AS$ и $B{\kern 1pt} ' = {{T}^{{ - 1}}}BT$, то

$A{\kern 1pt} '\; \otimes B{\kern 1pt} ' = \mathop {\left( {S \otimes T} \right)}\nolimits^{ - 1} \left( {A \otimes B} \right)\left( {S \otimes T} \right) \equiv \left( {A \otimes B} \right){\kern 1pt} {\kern 1pt} '.$

Это соотношение позволяет независимо выбирать наиболее удобные базисы в каждом множителе тензорного произведения.

Используя приведенные выше тождества, их следствия и некоторые дополнительные соображения технического характера, мы получаем основной результат этого раздела.

Пусть ${{B}_{1}}, \ldots ,{{B}_{L}}$ – полное множество примитивных ортогональных идемпотентов перестановочного представления локальной группы $F$. Обозначим символом ${{\bar {L}}^{X}}$ множество всех отображений из $X$ в $\bar {L}$, где $\bar {L} = \left\{ {1, \ldots ,L} \right\}$. Действие $g \in G$ на отображение $\ell \in {{\bar {L}}^{X}}$ определяется как $\ell g = [{{\ell }_{{1g}}}, \ldots ,{{\ell }_{{Ng}}}]$. Тогда мы имеем

Предложение. Примитивный ортогональный идемпотент централизаторного кольца перестановочного представления сплетения имеет вид

(14)

${{\widetilde B}_{k}} = \sum\limits_{\ell \in kG} \,{{B}_{{{{\ell }_{1}}}}} \otimes \cdots \otimes {{B}_{{{{\ell }_{N}}}}},$

где $kG$ обозначает $G$-орбиту отображения $k$ на множестве ${{\bar {L}}^{X}}$.

Легко проверить, что выполняется условие полноты $\sum\nolimits_{i = 1}^{\widetilde K} {{{{\widetilde B}}_{{{{k}^{{(i)}}}}}}} = {{1}_{{{{M}^{N}}}}}$. Здесь $\widetilde K$ обозначает число примитивных ортогональных идемпотентов, равное числу неприводимых подпредставлений перестановочного представления сплетения; ${{1}_{{{{M}^{N}}}}}$ – единичная матрица в перестановочном пространстве; ${{k}^{{(i)}}}$ обозначает некоторую нумерацию орбит пространственной группы $G$ на множестве отображений ${{\bar {L}}^{X}}$.

Для вычисления базисных элементов (12) централизаторной алгебры и примитивных ортогональных идемпотентов (14) мы написали программу на языке Си. Входными данными для программы являются порождающие элементы пространственной и локальной групп, а также полное множество примитивных ортогональных идемпотентов локальной группы (полученное, например, с помощью программы, описанной в [6], [7]).

4. ПРИМЕРЫ ВЫЧИСЛЕНИЙ

Для иллюстрации работы программы приведем примеры вычислений примитивных идемпотентов для сплетений, построенных из групп симметрий октаэдра, икосаэдра и додекаэдра. Полная группа симметрий для октаэдра изоморфна прямому произведению ${{{\text{S}}}_{4}} \times {{{\text{S}}}_{2}}$, а полные группы икосаэдра и додекаэдра изоморфны группе ${{{\text{A}}}_{5}} \times {{{\text{S}}}_{2}}$. Здесь ${{{\text{S}}}_{n}}$ обозначает симметрическую группу, т.е. группу всех перестановок $n$ объектов; ${{{\text{A}}}_{n}}$ обозначает знакопеременную группу – группу всех четных перестановок $n$ объектов. Заметим, что ${{{\text{A}}}_{5}}$ – наименьшая некоммутативная простая конечная группа. Заметим также, что полная группа симметрий октаэдра сама по себе имеет структуру сплетения: ${{{\text{S}}}_{4}} \times {{{\text{S}}}_{2}} \cong {{{\text{S}}}_{2}}\wr {{{\text{S}}}_{3}}$. Множитель ${{{\text{S}}}_{2}}$ в полных группах симметрий рассматриваемых многогранников описывает отражения, а дополнительные к ${{{\text{S}}}_{2}}$ множители описывают вращательные (или сохраняющие ориентацию, или хиральные) симметрии. Чтобы убрать несущественные технические усложнения, мы будем рассматривать только вращательные симметрии. Далее для краткости мы будем называть их просто “симметриями”, опуская слово “вращательные”. Для начала опишем реализации вращательных симметрий, как групп перестановок вершин указанных многогранников, а также неприводимые разложения их представлений. Неприводимые представления обозначаются их размерностями в жирном шрифте, а перестановочные – размерностями в жирном шрифте с подчеркиванием. Перестановки приводятся в формате произведений непересекающихся циклов [3]. Символы ${{0}_{n}}$ и ${{1}_{n}}$ обозначают соответственно нулевую и единичную матрицы размера $n \times n$.

Фиг. 1.

Октаэдр.

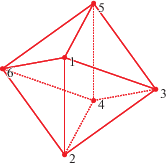
4.1. Октаэдр

• Для указанной нумерации вершин группу симметрий октаэдра ${{G}_{{\text{O}}}} \cong {{{\text{S}}}_{4}}$ можно породить, например, следующими двумя перестановками:

$a = \left( {1,3,5} \right)\left( {2,4,6} \right)\quad {\text{и}}\quad b = \left( {1,2,4,5} \right).$

• Шестимерное перестановочное представление ${{G}_{{\text{O}}}}$, которое мы обозначаем символом $\underline {\mathbf{6}} $, имеет ранг $3$.

• Базис централизаторной алгебры представления $\underline {\mathbf{6}} $ имеет вид

(15)

${{A}_{1}} = {{1}_{6}},\quad {{A}_{2}} = \left( {\begin{array}{*{20}{c}} {\mathop 0\nolimits_3 }&{\mathop 1\nolimits_3 } \\ {\mathop 1\nolimits_3 }&{\mathop 0\nolimits_3 } \end{array}} \right),\quad {{A}_{3}} = \left( {\begin{array}{*{20}{c}} Y&Y \\ Y&Y \end{array}} \right),\quad {\text{где}}\quad Y = \left( {\begin{array}{*{20}{c}} 0&1&1 \\ 1&0&1 \\ 1&2&0 \end{array}} \right).$

• Разложение на неприводимые подпредставления имеет вид

$\underline {\mathbf{6}} \cong {\mathbf{1}}\; \otimes \;{\mathbf{2}}\; \otimes \;{\mathbf{3}}.$

• Полное множество примитивных ортогональных идемпотентов в базисе (15) имеет вид

${{B}_{{\mathbf{1}}}} = \frac{1}{6}({{A}_{1}} + {{A}_{2}} + {{A}_{3}}),$

(16)

${{B}_{{\mathbf{2}}}} = \frac{1}{3}\left( {{{A}_{1}} + {{A}_{2}} - \frac{1}{2}{{A}_{3}}} \right),$

${{B}_{{\mathbf{3}}}} = \frac{1}{2}({{A}_{1}} - {{A}_{2}}).$

Фиг. 2.

Икосаэдр.

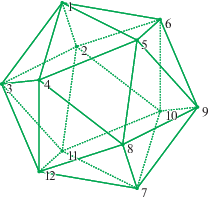
4.2. Икосаэдр

• Перестановки, порождающие группу симметрий икосаэдра ${{G}_{{\text{I}}}} \cong {{{\text{A}}}_{5}}$:

$a = (1,7)(2,8)(3,12)(4,11)(5,10)(6,9),\quad b = (2,3,4,5,6)(8,9,10,11,12).$

• Ранг перестановочного представления $\underline {{\mathbf{12}}} $ группы ${{G}_{{\text{I}}}}$ равен $4$.

• Ввиду громоздкости мы не приводим в явном виде базис централизаторной алгебры, состоящий из четырех симметричных матриц ${{A}_{1}} = {{1}_{{12}}},$ ${{A}_{2}},$ ${{A}_{3}}$ и ${{A}_{4}}$ размера $12 \times 12$.

• Разложение на неприводимые подпредставления:

$\underline {{\mathbf{12}}} \cong {\mathbf{1}}\; \otimes \;{\mathbf{3}}\; \otimes \;{\mathbf{3}}{\kern 1pt} '\; \otimes \;{\mathbf{5}}.$

Здесь ${\mathbf{3}}$ и ${\mathbf{3}}{\kern 1pt} '$ обозначают два неэквивалентных неприводимых трехмерных представления группы ${{{\text{A}}}_{5}}$.

• Полное множество примитивных ортогональных идемпотентов:

$\begin{gathered} {{B}_{1}} = \frac{1}{{12}}({{A}_{1}} + {{A}_{2}} + {{A}_{3}} + {{A}_{4}}), \\ {{B}_{3}} = \frac{1}{4}\left( {{{A}_{1}} - {{A}_{2}} + \frac{{\sqrt 5 }}{5}{{A}_{3}} - \frac{{\sqrt 5 }}{5}{{A}_{4}}} \right), \\ {{B}_{{3'}}} = \frac{1}{4}\left( {{{A}_{1}} - {{A}_{2}} - \frac{{\sqrt 5 }}{5}{{A}_{3}} + \frac{{\sqrt 5 }}{5}{{A}_{4}}} \right), \\ {{B}_{5}} = \frac{5}{{12}}\left( {{{A}_{1}} + {{A}_{2}} - \frac{1}{5}{{A}_{3}} - \frac{1}{5}{{A}_{4}}} \right). \\ \end{gathered} $

Фиг. 3.

Додекаэдр.

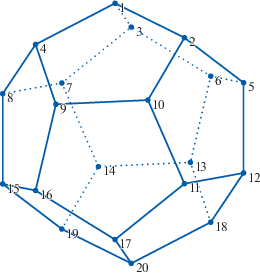
4.3. Додекаэдр

• Группа симметрий додекаэдра ${{G}_{{\text{D}}}} \cong {{{\text{A}}}_{5}}$ порождается перестановками:

$\begin{gathered} a = (2,3,4)(5,7,9)(6,8,10)(11,13,15)(12,14,16)(17,18,19), \\ b = (1,2,5,6,3)(4,10,12,13,7)(8,9,11,18,14)(15,16,17,20,19). \\ \end{gathered} $

• Ранг перестановочного представления $\underline {{\mathbf{20}}} $ группы ${{G}_{{\text{D}}}}$ равен $8$.

• Базис централизаторной алгебры состоит из восьми матриц размера $20 \times 20$:

$\overbrace {{{A}_{1}} = {{1}_{{20}}},{{A}_{2}},{{A}_{3}},{{A}_{4}},{{A}_{5}},{{A}_{6}}}^{{\text{симметричные}}\;{\text{матрицы}}},{{A}_{7}},{{A}_{8}} = A_{7}^{{\text{т}}}.$

• Разложение на неприводимые подпредставления:

$\underline {{\mathbf{20}}} \cong {\mathbf{1}} \otimes {\mathbf{3}} \otimes {\mathbf{3}}{\kern 1pt} '\; \otimes \underbrace {{\mathbf{4}} \otimes {\mathbf{4}}}_ \otimes {\mathbf{5}}.$

Нижней фигурной скобкой мы подчеркнули тот факт, что перестановочное представление $\underline {{\mathbf{20}}} $ содержит четырехмерное неприводимое подпредставление ${\mathbf{4}}$ c кратностью два.

• Полное множество примитивных ортогональных идемпотентов:

$\begin{gathered} {{B}_{{\mathbf{1}}}} = \frac{1}{{20}}({{A}_{1}} + {{A}_{2}} + {{A}_{3}} + {{A}_{4}} + {{A}_{5}} + {{A}_{6}} + {{A}_{7}} + {{A}_{8}}), \\ {{B}_{{\mathbf{3}}}} = \frac{3}{{20}}\left( {{{A}_{1}} - {{A}_{2}} + \frac{{\sqrt 5 }}{3}{{A}_{3}} - \frac{{\sqrt 5 }}{3}{{A}_{4}} - \frac{{{{A}_{5}}}}{3} - \frac{{{{A}_{6}}}}{3} + \frac{{{{A}_{7}}}}{3} + \frac{{{{A}_{8}}}}{3}} \right), \\ \end{gathered} $

$\begin{gathered} {{B}_{{{\mathbf{3'}}}}} = \frac{3}{{20}}\left( {{{A}_{1}} - {{A}_{2}} - \frac{{\sqrt 5 }}{3}{{A}_{3}} + \frac{{\sqrt 5 }}{3}{{A}_{4}} - \frac{{{{A}_{5}}}}{3} - \frac{{{{A}_{6}}}}{3} + \frac{{{{A}_{7}}}}{3} + \frac{{{{A}_{8}}}}{3}} \right), \\ B_{{\mathbf{4}}}^{{(1)}} = \frac{1}{5}\left( {{{A}_{1}} - \frac{{{{A}_{3}}}}{3} - \frac{{{{A}_{4}}}}{3} + \frac{{2{{A}_{6}}}}{3} - \frac{{1 - {\text{i}}\sqrt {11} }}{6}{{A}_{7}} - \frac{{1 + {\text{i}}\sqrt {11} }}{6}{{A}_{8}}} \right), \\ \end{gathered} $

$\begin{gathered} B_{{\mathbf{4}}}^{{(2)}} = \frac{1}{5}\left( {{{A}_{1}} - \frac{{{{A}_{3}}}}{3} - \frac{{{{A}_{4}}}}{3} + \frac{{2{{A}_{6}}}}{3} - \frac{{1 + {\text{i}}\sqrt {11} }}{6}{{A}_{7}} - \frac{{1 - {\text{i}}\sqrt {11} }}{6}{{A}_{8}}} \right), \\ {{B}_{{\mathbf{5}}}} = \frac{1}{4}\left( {{{A}_{1}} + {{A}_{2}} + \frac{{{{A}_{3}}}}{3} + \frac{{{{A}_{4}}}}{3} - \frac{{{{A}_{5}}}}{3} - \frac{{{{A}_{6}}}}{3} - \frac{{{{A}_{7}}}}{3} - \frac{{{{A}_{8}}}}{3}} \right). \\ \end{gathered} $

Заметим, что примитивные идемпотенты, соответствующие четырехмерному неприводимому подпредставлению, из-за нетривиальной кратности, образуют бесконечное двухпараметрическое семейство. Выражения $B_{{\mathbf{4}}}^{{(1)}}$ и $B_{{\mathbf{4}}}^{{(2)}}$ представляют собой достаточно произвольно выбранную пару взаимно ортогональных представителей этого семейства.

4.4. Компьютерные вычисления

В этом разделе представлены результаты применения программы, написанной на языке Си, полученные с помощью персонального компьютера с частотой процессора 3.30GHz и оперативной памятью 16GB. Мы рассмотрим три примера, в которых пространством $X$ всегда будет икосаэдр с соответствующей пространственной группой, а множествами локальных состояний $V$ будут, в порядке возрастания трудности вычислений, октаэдр, икосаэдр и додекаэдр с их группами симметрий. В случае октаэдра мы приведем подробный вывод программы с комментариями. В остальных случаях ограничимся сжатой информацией о результатах вычислений.

4.4.1. Сплетение ${{{\text{S}}}_{4}}\left( {octahedron} \right)\wr {{{\text{A}}}_{5}}\left( {icosahedron} \right)$.

1. Программа считывает порождающие элементы пространственной и локальной групп и печатает сопутствующую информацию: ‘Name’ – имя файла, содержащего порождающие перестановки, ‘Number of points’ – число точек множества $X$ или $V$ (размерность перестановочного представления) и т.д.

Space G(X) group:

Name = “A5_on_icosahedron”

Number of points = 12

Comment = “Action of A_5 on 12 vertices of icosahedron”

Size = “60"

Number of generators = 2

Local F(V) group:

Name = “S4_on_octahedron”

Number of points = 6

Comment = “Action of S_4 on 6 vertices of octahedron”

Size = “24"

Number of generators = 2

2. Программа из порождающих элементов пространственной и локальной групп строит порождающие элементы сплетения и записывает их в отдельный файл. Этот шаг предназначен для исследования сплетений другими средствами и может быть пропущен, поскольку не требуется для дальнейших вычислений.

Whole F(V).wr.G(X) group:

Name = “S4_on_octahedron_wr_A5_on_icosahedron”

Number of points V^X = 2 176 782 336

Size = “24^12*60"

Number of generators = 4

3. Программа печатает общий заголовок для вывода дальнейшей информации в формате LATEX:

Wreath product ${{{\text{S}}}_{4}}\left( {{\text{octahedron}}} \right)\wr {{{\text{A}}}_{5}}\left( {{\text{icosahedron}}} \right)$

Representation dimension: ${\mathbf{2}}\,{\mathbf{176}}\,{\mathbf{782}}\,{\mathbf{336}}$

4. Программа вычисляет базисные элементы централизаторной алгебры перестановочного представления сплетения. Этот шаг не требуется для вычисления идемпотентов и может быть пропущен. Если он включен, то вычисляются следующие элементы:

(а) Ранг представления (размерность централизаторной алгебры).

(б) Множество длин подорбит. Для группы перестановок подорбитами называются орбиты стабилизатора одной точки переставляемого множества [4]. Подорбиты находятся во взаимно однозначном соответствии с орбиталами. Размеры орбиталов равны длинам подорбит, умноженным на размерность представления. Сумма длин подорбит равна размерности представления и мы используем этот факт для контроля возможных ошибок вычисления, выводя значение переменной ‘Checksum’. Мы печатаем только различные длины подорбит, указывая кратности длин в виде верхнего индекса.

(в) Базисные элементы централизаторной алгебры представления сплетения. Выражения для базисных элементов представляют собой тензорные полиномы от матриц (15). Мы выводим здесь только по три элемента из начала, середины и конца большого массива.

Rank: ${\mathbf{122}}\,{\mathbf{776}}$

Number of different suborbit lengths: $46$

Wreath suborbit lengths:

1³⁵, 2²⁴⁹, 3¹¹, 4²⁵⁸, 5¹⁶, 6⁴⁰³, 8¹⁴⁴², 16¹⁸⁹⁰, 24²⁴¹⁸, 32³⁹⁴³, 48⁴³, 64⁵⁰⁸², 80⁵¹, 96⁶⁴⁸², 128⁶⁶²⁹, 256⁸⁸⁵⁸, 384¹⁰⁷³⁵, 512⁷²³⁷, 768⁶⁷, 1024⁹⁹⁰¹, 1280⁵⁸, 1536¹²⁰⁰⁶, 2048⁵⁶¹¹, 4096⁸²⁰⁹, 6144⁹⁶⁰³, 8192³⁰⁹³, 12 288³⁹, 16 384⁴⁷⁹⁵, 20 480⁴⁶, 24 576⁵⁵⁵⁸, 32 768¹²²⁵, 65 536²¹⁷¹, 98 304²³⁸⁹, 131 072³¹⁰, 196 608¹⁵, 262 144⁶⁷⁴, 327 680¹⁴, 393 216⁷⁴³, 524 288⁷⁷, 1 048 576¹⁴⁶, 1 572 864¹⁷⁷, 2 097 152¹⁸, 4 194 304¹⁶, 5 242 880², 6 291 456²⁴, 16 777 216⁷

Checksum = $2\,176\,782\,336$ Maximum multiplicity = $12\,006$

Wreath invariant basis forms:

$\begin{gathered} {{\widetilde A}_{1}} = A_{1}^{{ \otimes 12}} \\ {{\widetilde A}_{2}}\; = \;A_{1}^{{ \otimes 5}} \otimes {{A}_{2}} \otimes A_{1}^{{ \otimes 2}} \otimes {{A}_{2}} \otimes A_{1}^{{ \otimes 3}} \\ {{\widetilde A}_{3}}\; = \;A_{1}^{{ \otimes 4}} \otimes A_{2}^{{ \otimes 2}} \otimes A_{1}^{{ \otimes 2}} \otimes A_{2}^{{ \otimes 2}} \otimes A_{1}^{{ \otimes 2}} \\ \vdots \\ \end{gathered} $

$\begin{gathered} {{\widetilde A}_{{61387}}} = A_{2}^{{ \otimes 3}} \otimes {{A}_{1}} \otimes {{A}_{3}} \otimes A_{1}^{{ \otimes 2}} \otimes A_{3}^{{ \otimes 2}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{3}} + {{A}_{2}} \otimes {{A}_{1}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{1}} \otimes {{A}_{3}} \otimes {{A}_{1}} \otimes {{A}_{2}} \otimes A_{3}^{{ \otimes 3}} \otimes {{A}_{2}} + \\ \, + {{A}_{1}} \otimes A_{2}^{{ \otimes 2}} \otimes A_{3}^{{ \otimes 3}} \otimes {{A}_{2}} \otimes {{A}_{1}} \otimes {{A}_{3}} \otimes {{A}_{1}} \otimes A_{2}^{{ \otimes 2}} + {{A}_{1}} \otimes A_{3}^{{ \otimes 2}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{3}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{1}} \otimes {{A}_{3}} \otimes {{A}_{1}} \otimes {{A}_{2}} \\ {{\widetilde A}_{{61388}}} = {{A}_{2}} \otimes {{A}_{1}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{1}} \otimes {{A}_{3}} \otimes {{A}_{1}} \otimes A_{2}^{{ \otimes 2}} \otimes A_{3}^{{ \otimes 3}} + A_{2}^{{ \otimes 2}} \otimes {{A}_{3}} \otimes {{A}_{1}} \otimes {{A}_{2}} \otimes A_{1}^{{ \otimes 2}} \otimes A_{3}^{{ \otimes 2}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{3}} + \\ \, + {{A}_{1}} \otimes A_{3}^{{ \otimes 2}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{3}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{1}} \otimes {{A}_{2}} \otimes {{A}_{1}} \otimes {{A}_{3}} + {{A}_{1}} \otimes {{A}_{2}} \otimes A_{3}^{{ \otimes 3}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{1}} \otimes {{A}_{3}} \otimes {{A}_{1}} \otimes A_{2}^{{ \otimes 2}} \\ {{\widetilde A}_{{61389}}} = {{A}_{2}} \otimes {{A}_{1}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{1}} \otimes {{A}_{3}} \otimes A_{2}^{{ \otimes 3}} \otimes A_{3}^{{ \otimes 3}} + A_{2}^{{ \otimes 2}} \otimes {{A}_{3}} \otimes A_{2}^{{ \otimes 2}} \otimes A_{1}^{{ \otimes 2}} \otimes A_{3}^{{ \otimes 2}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{3}} + \\ \, + {{A}_{1}} \otimes A_{3}^{{ \otimes 2}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{3}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{1}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{3}} + A_{2}^{{ \otimes 2}} \otimes A_{3}^{{ \otimes 3}} \otimes A_{2}^{{ \otimes 2}} \otimes {{A}_{1}} \otimes {{A}_{3}} \otimes {{A}_{1}} \otimes A_{2}^{{ \otimes 2}} \\ \vdots \\ \end{gathered} $

$\begin{gathered} {{\widetilde A}_{{122774}}} = A_{3}^{{ \otimes 2}} \otimes {{A}_{2}} \otimes A_{3}^{{ \otimes 9}} + A_{3}^{{ \otimes 3}} \otimes {{A}_{2}} \otimes A_{3}^{{ \otimes 8}} + A_{3}^{{ \otimes 10}} \otimes {{A}_{2}} \otimes {{A}_{3}} + A_{3}^{{ \otimes 11}} \otimes {{A}_{2}} \\ {{\widetilde A}_{{122775}}} = A_{3}^{{ \otimes 4}} \otimes {{A}_{2}} \otimes A_{3}^{{ \otimes 7}} + A_{3}^{{ \otimes 5}} \otimes {{A}_{2}} \otimes A_{3}^{{ \otimes 6}} + A_{3}^{{ \otimes 8}} \otimes {{A}_{2}} \otimes A_{3}^{{ \otimes 3}} + A_{3}^{{ \otimes 9}} \otimes {{A}_{2}} \otimes A_{3}^{{ \otimes 2}} \\ {{\widetilde A}_{{122776}}} = {{A}_{2}} \otimes A_{3}^{{ \otimes 11}} + {{A}_{3}} \otimes {{A}_{2}} \otimes A_{3}^{{ \otimes 10}} + A_{3}^{{ \otimes 6}} \otimes {{A}_{2}} \otimes A_{3}^{{ \otimes 5}} + A_{3}^{{ \otimes 7}} \otimes {{A}_{2}} \otimes A_{3}^{{ \otimes 4}} \\ \end{gathered} $

5. Основная часть программы вычисляет полное множество примитивных ортогональных идемпотентов (14). Приведенный ниже вывод содержит следующее.

(а) Информация о том, содержит ли разложение на неприводимые подпредставления нетривиальные кратности.

(б) Полное число примитивных ортогональных идемпотентов.

(в) Число различных неприводимых размерностей.

(г) Полный список неприводимых размерностей. Верхние индексы представляют числа идемпотентов соответствующей размерности. Сумма всех размерностей должна совпадать с размерностью представления сплетения, что проверяется прямым вычислением величины ‘Checksum’.

(д) Несколько выражений для примитивных ортогональных идемпотентов (неприводимых проекторов), которые представляют собой тензорные полиномы от матриц локальных идемпотентов (16).

Wreath product decomposition is multiplicity free

Number of irreducible components: $122\,776$

Number of different dimensions: $134$

Irreducible dimensions:

1, 4⁶, 6³, 8⁶, 9³, 12¹⁵, 16³², 18⁷, 20, 24⁷⁰, 32⁴¹, 36⁸⁶, 45, 48¹⁹¹, 54²⁶, 64⁸⁴, 72²⁹⁸, 80⁴, 81⁷, 96⁴¹², 108²²³, 128¹¹⁴, 144⁹¹³, 162⁵⁴, 180⁸, 192⁷⁰⁴, 216⁹²⁶, 243⁴, 256¹⁰⁴, 288¹⁸⁰⁴, 320⁷, 324⁵⁰⁴, 384⁷⁷², 405⁴, 432²⁵¹⁷, 486⁹⁹, 512⁷⁶, 576²⁵⁰⁸, 648¹⁹⁰⁹, 720¹⁷, 729⁹, 768⁷⁰⁵, 864⁴³⁰³, 972⁸¹⁸, 1024⁵¹, 1152²⁵⁶², 1280³, 1296⁴⁴⁵⁵, 1458¹⁴¹, 1536⁴⁷⁹, 1620¹⁶, 1728⁵³²², 1944²⁷¹², 2048²⁰, 2187⁴, 2304¹⁹³⁵, 2592⁶⁷⁰⁸, 2880¹⁴, 2916⁹⁶¹, 3072²²³, 3456⁴⁵⁷⁵, 3645⁷, 3888⁵⁴⁹⁵, 4096⁴, 4374¹³⁶, 4608¹⁰⁰⁴, 5120, 5184⁶⁹²⁴, 5832²⁷⁵⁴, 6144⁵⁹, 6480¹⁸, 6561⁹, 6912²⁷¹⁹, 7776⁶⁹⁶⁶, 8192³, 8748⁸²², 9216³²⁹, 10 368⁴⁷⁶⁰, 11 520¹⁰, 11 664⁴⁶⁹⁵, 12 288¹⁹, 13 122⁹⁸, 13 824¹⁰¹¹, 14 580¹³, 15 552⁵⁷⁸¹, 17 496¹⁹⁹⁹, 18 432⁸³, 19 683³, 20 736²⁰⁸⁵, 23 328⁴⁸²⁶, 25 920¹⁶, 26 244⁵¹¹, 27 648²⁶⁰, 31 104²⁹⁶⁴, 32 805³, 34 992²⁷⁷⁵, 36 864⁵, 39 366⁵⁵, 41 472⁵³⁴, 46 080, 46 656³⁰¹², 52 488¹⁰²³, 55 296¹⁵, 58 320¹⁹, 59 049⁵, 62 208⁸⁷⁷, 69 984²¹⁷³, 78 732²⁴², 82 944⁴⁸, 93 312¹⁰³⁸, 103 680⁴, 104 976¹⁰⁷⁹, 118 098²⁷, 124 416¹⁰², 131 220⁸, 139 968⁹⁰⁵, 157 464³⁵⁵, 186 624¹³⁰, 209 952⁵⁶⁸, 233 280⁷, 236 196⁸⁴, 279 936¹⁴⁸, 295 245, 314 928²⁵⁴, 354 294⁶, 419 904¹¹⁶, 472 392⁷⁹, 524 880³, 531 441, 629 856⁶², 708 588¹⁵; 944 784²⁶; 1 180 980; 1 417 176⁹

Checksum = $2\,176\,782\,336$ Maximum number of equal dimensions = $6966$

Wreath irreducible projectors:

$\begin{gathered} {{\widetilde B}_{1}} = B_{1}^{{ \otimes 12}} \\ {{\widetilde B}_{2}} = B_{1}^{{ \otimes 3}} \otimes {{B}_{2}} \otimes B_{1}^{{ \otimes 6}} \otimes {{B}_{2}} \otimes {{B}_{1}} \\ {{\widetilde B}_{3}} = B_{1}^{{ \otimes 9}} \otimes {{B}_{2}} \otimes B_{1}^{{ \otimes 2}} + B_{1}^{{ \otimes 4}} \otimes {{B}_{2}} \otimes B_{1}^{{ \otimes 7}} \\ \vdots \\ \end{gathered} $

$\begin{gathered} {{\widetilde B}_{{61387}}} = {{B}_{2}} \otimes {{B}_{3}} \otimes {{B}_{1}} \otimes B_{2}^{{ \otimes 2}} \otimes B_{1}^{{ \otimes 3}} \otimes B_{3}^{{ \otimes 2}} \otimes {{B}_{2}} \otimes {{B}_{3}} + \\ \, + {{B}_{3}} \otimes {{B}_{2}} \otimes {{B}_{1}} \otimes {{B}_{2}} \otimes {{B}_{1}} \otimes {{B}_{3}} \otimes {{B}_{1}} \otimes {{B}_{2}} \otimes {{B}_{3}} \otimes {{B}_{1}} \otimes {{B}_{3}} \otimes {{B}_{2}} + \\ \, + B_{1}^{{ \otimes 2}} \otimes {{B}_{3}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 2}} \otimes {{B}_{2}} \otimes {{B}_{3}} \otimes {{B}_{1}} \otimes B_{2}^{{ \otimes 2}} \otimes {{B}_{1}} + \\ \, + {{B}_{1}} \otimes B_{2}^{{ \otimes 2}} \otimes {{B}_{3}} \otimes {{B}_{1}} \otimes B_{3}^{{ \otimes 2}} \otimes {{B}_{2}} \otimes {{B}_{3}} \otimes {{B}_{1}} \otimes {{B}_{2}} \otimes {{B}_{1}} \\ \end{gathered} $

$\begin{gathered} {{\widetilde B}_{{61388}}} = B_{2}^{{ \otimes 2}} \otimes {{B}_{3}} \otimes B_{1}^{{ \otimes 2}} \otimes {{B}_{3}} \otimes {{B}_{1}} \otimes {{B}_{2}} \otimes {{B}_{3}} \otimes B_{2}^{{ \otimes 2}} \otimes {{B}_{3}} + \\ \, + {{B}_{1}} \otimes {{B}_{2}} \otimes {{B}_{3}} \otimes B_{2}^{{ \otimes 2}} \otimes {{B}_{3}} \otimes B_{2}^{{ \otimes 2}} \otimes {{B}_{3}} \otimes B_{1}^{{ \otimes 2}} \otimes {{B}_{3}} \\ \end{gathered} $

$\begin{gathered} {{\widetilde B}_{{61389}}} = B_{1}^{{ \otimes 2}} \otimes B_{2}^{{ \otimes 3}} \otimes {{B}_{1}} \otimes {{B}_{2}} \otimes {{B}_{3}} \otimes {{B}_{2}} \otimes {{B}_{1}} \otimes B_{3}^{{ \otimes 2}} + \\ \, + {{B}_{2}} \otimes {{B}_{1}} \otimes {{B}_{2}} \otimes {{B}_{3}} \otimes {{B}_{2}} \otimes {{B}_{1}} \otimes {{B}_{3}} \otimes {{B}_{2}} \otimes B_{1}^{{ \otimes 2}} \otimes {{B}_{2}} \otimes {{B}_{3}} + \\ \, + {{B}_{1}} \otimes {{B}_{3}} \otimes {{B}_{2}} \otimes B_{1}^{{ \otimes 3}} \otimes {{B}_{3}} \otimes B_{2}^{{ \otimes 3}} \otimes {{B}_{3}} \otimes {{B}_{2}} + \\ + \;{{B}_{3}} \otimes {{B}_{2}} \otimes {{B}_{3}} \otimes {{B}_{2}} \otimes B_{1}^{{ \otimes 2}} \otimes {{B}_{2}} \otimes B_{1}^{{ \otimes 2}} \otimes {{B}_{2}} \otimes {{B}_{3}} \otimes {{B}_{2}} + {{B}_{2}} \otimes B_{3}^{{ \otimes 3}} \otimes {{B}_{1}} \otimes {{B}_{2}} \otimes B_{1}^{{ \otimes 3}} \otimes B_{2}^{{ \otimes 3}} + \\ \, + {{B}_{3}} \otimes B_{2}^{{ \otimes 2}} \otimes {{B}_{3}} \otimes B_{2}^{{ \otimes 2}} \otimes {{B}_{1}} \otimes {{B}_{3}} \otimes B_{1}^{{ \otimes 3}} \otimes {{B}_{2}} \\ \vdots \\ \end{gathered} $

$\begin{gathered} {{\widetilde B}_{{122774}}} = B_{3}^{{ \otimes 2}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 9}} + B_{3}^{{ \otimes 3}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 8}} + B_{3}^{{ \otimes 10}} \otimes {{B}_{2}} \otimes {{B}_{3}} + B_{3}^{{ \otimes 11}} \otimes {{B}_{2}} \\ {{\widetilde B}_{{122775}}} = B_{3}^{{ \otimes 2}} \otimes {{B}_{2}} \otimes {{B}_{3}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 7}} + B_{3}^{{ \otimes 2}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 2}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 6}} + B_{3}^{{ \otimes 3}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 4}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 3}} + \\ \, + B_{3}^{{ \otimes 5}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 4}} \otimes {{B}_{2}} \otimes {{B}_{3}} + B_{3}^{{ \otimes 8}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 2}} \otimes {{B}_{2}} + B_{3}^{{ \otimes 9}} \otimes {{B}_{2}} \otimes {{B}_{3}} \otimes {{B}_{2}} \\ {{\widetilde B}_{{122776}}} = B_{3}^{{ \otimes 3}} \otimes B_{2}^{{ \otimes 2}} \otimes B_{3}^{{ \otimes 7}} + {{B}_{2}} \otimes B_{3}^{{ \otimes 4}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 6}} + {{B}_{3}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 3}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 6}} + \\ \, + B_{3}^{{ \otimes 6}} \otimes {{B}_{2}} \otimes {{B}_{3}} \otimes {{B}_{2}} \otimes B_{3}^{{ \otimes 3}} + B_{3}^{{ \otimes 7}} \otimes B_{2}^{{ \otimes 2}} \otimes B_{3}^{{ \otimes 3}} + B_{3}^{{ \otimes 9}} \otimes B_{2}^{{ \otimes 2}} \otimes {{B}_{3}} \\ \end{gathered} $

Time: 0.58 sec

Maximum number of tensor monomials: 531 441

4.4.2. Сплетение ${{{\text{A}}}_{5}}\left( {icosahedron} \right)\wr {{{\text{A}}}_{5}}\left( {icosahedron} \right)$.

Wreath product ${{{\text{A}}}_{5}}\left( {{\text{icosahedron}}} \right)\wr {{{\text{A}}}_{5}}\left( {{\text{icosahedron}}} \right)$

Representation dimension: ${\mathbf{8}}\,{\mathbf{916}}\,{\mathbf{100}}\,{\mathbf{448}}\,{\mathbf{256}}$

Rank: ${\mathbf{3}}\,{\mathbf{875}}\,{\mathbf{157}}$

Wreath product decomposition is multiplicity free

Number of irreducible components: $3\;875\;157$

Number of different dimensions: $261$

Time: 7.35 sec

Maximum number of tensor monomials: 16 777 216

4.4.3. Сплетение ${{{\text{A}}}_{5}}\left( {dodecahedron} \right)\wr {{{\text{A}}}_{5}}\left( {icosahedron} \right)$.

Wreath product ${{{\text{A}}}_{5}}\left( {{\text{dodecahedron}}} \right)\wr {{{\text{A}}}_{5}}\left( {{\text{icosahedron}}} \right)$

Representation dimension: ${\mathbf{4}}\,{\mathbf{096}}\,{\mathbf{000}}\,{\mathbf{000}}\,{\mathbf{000}}\,{\mathbf{000}}$

Rank: $ > {\kern 1pt} {\mathbf{502}}\,{\mathbf{985}}\,{\mathbf{717}}$

Wreath product decomposition has non-trivial multiplicities

Number of irreducible components: $502\,985\,717$

Number of different dimensions: $1065$

Time: 26 min 46.16 sec

Maximum number of tensor monomials: 2 176 782 336

5. ЗАМЕЧАНИЯ О МОДЕЛИРОВАНИИ МНОГОЧАСТИЧНЫХ КВАНТОВЫХ СИСТЕМ

Квантовое описание можно сделать конструктивным, если заменить в квантовом формализме непрерывные группы унитарных операторов эволюции унитарными представлениями конечных групп. Известно, что любое линейное (автоматически унитарное) представление конечной группы является подпредставлением некоторого перестановочного представления. В частности, так называемое регулярное представление, т.е. перестановочное представление действия группы на своих собственных элементах, содержит все возможные неприводимые представления данной группы. Таким образом, мы можем вложить любую конструктивную квантовую модель в подходящее инвариантное подпространство некоторого перестановочного представления [12], [13].

Пространством состояний составной (многокомпонентной) квантовой системы является тензорное произведение пространств состояний входящих в нее компонент. Состояния составной системы, представимые в виде взвешенной суммы тензорных произведений состояний компонент, называются сепарабельными. Состояния, не являющиеся сепарабельными, называются запутанными. Фактически, из-за экспоненциальной зависимости размерности пространства состояний составной системы от числа компонент, подавляющее большинство состояний составной системы являются запутанными. Понятие запутанности лежит в основе квантовой информатики. Запутанность приводит к таким экспериментально наблюдаемым явлениям, как квантовая телепортация, нелокальные квантовые корреляции (нарушение неравенств Белла) и т.д. Более того, в последнее время все большую популярность приобретает идея (см., например, [14], [15]), что само геометрическое пространство не является фундаментальной сущностью, а возникает как феноменологическая (“эмерджентная”) структура внутри большого гильбертова пространства за счет его приближенного разложения (для данного “квантового состояния Вселенной”) в тензорное произведение большого числа факторов, которые интерпретируются как точки (или области) геометрического пространства, расстояния между которыми (метрика) определяются мерами запутанности, типичным примером которых является квантовая взаимная информация.

Одной из основных наших целей была разработка средств изучения моделей составных квантовых систем. Операторы проектирования, получаемые нашей программой, предполагается использовать для вычислений в таких моделях. Эти операторы представляют собой матрицы огромных размерностей (например, четыре квадриллиона в примере $4.4.3$). Очевидно, явное вычисление таких матриц невозможно и не нужно. Представление проекторов для сплетений в виде тензорных полиномов позволяет свести вычисление квантовых корреляций к последовательности вычислений с маленькими матрицами локальных проекторов. Рассмотрим, например, вычисление скалярного произведения. Пусть $\left\{ {\left| 1 \right\rangle , \ldots ,\left| M \right\rangle } \right\}$ – ортонормальный базис в локальном гильбертовом пространстве $\mathcal{H}$. Тогда ортонормальный базис в гильбертовом пространстве сплетения 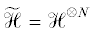образуют элементы вида

$\left| {{{m}_{1}}} \right\rangle \otimes \cdots \otimes \left| {{{m}_{N}}} \right\rangle ,\quad m = \left[ {{{m}_{1}}, \ldots ,{{m}_{N}}} \right] \in {{\bar {M}}^{{\bar {N}}}}.$

Здесь $M = \left| V \right|,N = \left| X \right|$, $\bar {M} = \left\{ {1, \ldots ,M} \right\}$, $\bar {N} = \left\{ {1, \ldots ,N} \right\}$. Векторы общего вида в гильбертовом пространстве сплетения можно записать следующим образом:

$\widetilde \Phi = \sum\limits_{m \in {{V}^{X}}} \,{{\varphi }_{m}}\left| {{{m}_{1}}} \right\rangle \otimes \cdots \otimes \left| {{{m}_{N}}} \right\rangle \quad {\text{и}}\quad \widetilde \Psi = \sum\limits_{n \in {{V}^{X}}} \,{{\psi }_{n}}\left| {{{n}_{1}}} \right\rangle \otimes \cdots \otimes \left| {{{n}_{N}}} \right\rangle ,$

где ${{\varphi }_{m}}$ и ${{\psi }_{n}}$ – произвольные скаляры из базового поля $F$. (Можно ограничиться натуральными ${{\varphi }_{m}}$ и ${{\psi }_{n}}$, если придерживаться идеологии подхода [12], [13].) Скалярное произведение этих векторов в инвариантном подпространстве, определяемом проектором (14), имеет вид

$\left\langle {\widetilde \Phi \left| {{{{\widetilde B}}_{k}}} \right|\widetilde \Psi } \right\rangle = \sum\limits_{m \in {{V}^{X}}} \,\sum\limits_{n \in {{V}^{X}}} \,\sum\limits_{\ell \in kG} \,{{\bar {\varphi }}_{m}}{{\psi }_{n}}{{A}_{{m,n,\ell }}},$

где

(17)

${{A}_{{m,n,\ell }}} = \left\langle {{{m}_{1}}\left| {\; \otimes \cdots \otimes \left\langle {{{m}_{N}}\left| {{{B}_{{{{\ell }_{1}}}}} \otimes \cdots \otimes {{B}_{{{{\ell }_{N}}}}}} \right|{{n}_{1}}} \right\rangle \otimes \cdots \otimes \;} \right|{{n}_{N}}} \right\rangle = $

(18)

$ = \left\langle {{{m}_{1}}\left| {{{B}_{{{{\ell }_{1}}}}}} \right|{{n}_{1}}} \right\rangle \cdots \left\langle {{{m}_{N}}\left| {{{B}_{{{{\ell }_{N}}}}}} \right|{{n}_{N}}} \right\rangle .$

Последнее выражение (18), полученное применением тождества (13) к (17), представляет собой просто произведение $N$ скаляров.

Анализ всевозможных сценариев вычислений, которые могут возникнуть в конструктивных моделях многокомпонентных квантовых систем, показывает, что вычисления могут включать длинные циклы суммирования вида $\sum\nolimits_{m \in {{{\overline M }}^{{\bar {N}}}}} $, короткие циклы суммирования $\sum\nolimits_{\ell \in kG} \,$, а также циклы умножения длины $N$. Величины, обрабатываемые внутри циклов, можно вычислить предварительно и собрать в таблицы небольших размеров. Этими величинами являются скаляры

$\left\langle {p\left| {{{B}_{r}}} \right|q} \right\rangle \equiv \mathop {\left( {{{B}_{r}}} \right)}\nolimits_{pq} \quad {\text{и}}\quad tr\left( {{{B}_{r}}\left| p \right\rangle \left\langle q \right|{{B}_{r}}} \right) \equiv \overline {\left\langle {p\left| {{{B}_{r}}} \right|q} \right\rangle } \equiv \mathop {\left( {{{B}_{r}}} \right)}\nolimits_{qp} ,$

считываемые непосредственно из явных выражений для матриц локальных проекторов, и $M \times M$ матрицы вида ${{B}_{r}}\left| p \right\rangle \left\langle q \right|{{B}_{s}}$, образующие таблицу размера ${{L}^{2}}{{M}^{2}}$, где $p,q \in \left\{ {1, \ldots ,M} \right\}$ и $r,s \in \left\{ {1, \ldots ,L} \right\}.$

Автор благодарен Ю.А. Блинкову за помощь в подготовке статьи и В.П. Гердту за плодотворные обсуждения и полезные советы.

Список литературы

Meldrum J.D.P. Wreath products of groups and semigroups. New York: John Wiley & Sons Inc., 1995.
James G.D., Kerber A. The representation theory of the symmetric group. Encyclopedia of Math. and its Applicat., vol. 16. Reading: Addison-Wesley, 1981.
Холл М. Теория групп. М.: Изд-во иностр. лит., 1962. 460 с.
Cameron P.J. Permutation groups. Cambridge: Cambridge University Press, 1999.
Bannai Eiichi, Ito Tatsuro. Algebraic combinatorics I: Association schemes. Menlo Park, CA: The Benjamin/Cummings Publishing Co., Inc. 1984.
Kornyak V.V. Splitting permutation representations of finite groups by polynomial algebra methods. In: Gerdt V.P. (Eds.): CASC 2018, LNCS. V. 11077. P. 304–318. Cham: Springer, 2018.
Kornyak V.V. A new algorithm for irreducible decomposition of representations of finite groups // J. Phys.: Conf. Ser. 2019. V. 1194. P. 012060.
Jacobson N. Structure of rings. Vol. 37. Amer. Math. Soc. Providence, R.I.: AMS, 1956.
Rowen L.H. Ring theory. Boston: Academic Press, Inc., 1991.
Wilson R., Walsh P., Tripp J., Suleiman I., Parker R., Norton S., Nickerson S., Linton S., Bray J., Abbott R. Atlas of finite group representations.
Steeb W.-H. Matrix Calculus and the Kronecker Product with Applications and C++ Programs. River Edge, NJ, USA: World Scientific Publishing Co., Inc., 1997.
Kornyak V.V. Modeling Quantum Behavior in the Framework of Permutation Groups // EPJ Web of Conferences. 2018. V. 173. P. 01007.
Kornyak V.V. Quantum models based on finite groups // IOP Conf. Series: Journal of Physics: Conf. Series. 2018. V. 965. P. 012023.
Van Raamsdonk M. Building up spacetime from quantum entanglement // Gen. Relativ. Grav. 2010. V. 42. P. 2323–2329.
Cao C., Carroll S.M., Michalakis S. Space from Hilbert space: recovering geometry from bulk entanglement // Phys. Rev. D. 2017. V. 95. P. 024031.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал