1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 2, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 2, стр. 267-280

Об одном подходе к интегрированию по времени системы уравнений Навье–Стокса

В. Т. Жуков 1, *, Н. Д. Новикова 1, **, О. Б. Феодоритова 1, ***

1 ИПМатем. им. М.В. Келдыша РАН
125047 Москва, Миусская пл., 4, Россия

* E-mail: zhukov@kiam.ru
** E-mail: nn@kiam.ru
*** E-mail: feodor@kiam.ru

Поступила в редакцию 02.07.2019
После доработки 02.07.2019
Принята к публикации 17.10.2019

Полный текст (PDF)

Аннотация

Разработан подход к интегрированию по времени системы нестационарных уравнений динамики сжимаемого теплопроводного газа. В его основе лежит принцип расщепления алгоритма решения уравнений Навье–Стокса на конвективный и диффузионный этапы. Конвективный этап представляет собой явную схему годуновского типа. Диффузионный этап реализуется с помощью чебышёвской явно-итерационной схемы. Результирующая схема обеспечивает на разностном уровне выполнение основных законов сохранения, а ее алгоритмическая структура гарантирует эффективность параллельной реализации. Библ. 27. Фиг. 6.

Ключевые слова: численное моделирование, уравнения Навье–Стокса, расщепление по физическим процессам, чебышёвская явно-итерационная схема.

1. ВВЕДЕНИЕ

Нашей перспективной целью является разработка подхода для расчета нестационарных многокомпонентных течений, математическая модель которых приведена в [1]. В данной работе основные элементы нового подхода демонстрируются и исследуются в однокомпонентном случае на примере интегрирования по времени системы трехмерных уравнений Навье–Стокса динамики сжимаемого теплопроводного газа [2] для случая пространственной дискретизации на неструктурированных сетках [3]. Предлагаемый подход основан на принципе расщепления по физическим процессам: расчет одного временного шага всей системы уравнений состоит в последовательном выполнении конвективного и диффузионного этапов. На конвективном этапе учитываются собственно конвективные потоки, а также потоки, обусловленные действием сил давления, на диффузионном этапе – диссипативные потоки (вязкие члены в уравнениях движения и члены с теплопроводностью в уравнении энергии).

Построение алгоритмов решения уравнений Навье–Стокса на основе расщепления по физическим процессам естественным образом отражает природу течений и наиболее полно изложено в [4]. В общем случае двухэтапные схемы расщепления обеспечивают первый порядок точности на гладких решениях [4]–[6]. Для получения более высокого порядка точности используются многоэтапные схемы. Например, второй порядок точности обеспечивает трехэтапная схема [6].

Одно из основных преимуществ метода расщепления состоит в том, что гиперболическая и параболическая подзадачи имеют разную природу и могут быть решены различными численными методами. В нашем подходе гиперболическая подсистема, получающаяся из исходной системы в отсутствие вязкости и теплопроводности, реализуется по явной схеме годуновского типа. Поэтому шаг по времени ${{\tau }_{{{\text{conv}}}}}$ ограничен критерием Куранта–Фридрихса–Леви. При наличии зон доминирования диффузионных процессов (т.е. в данном случае вязких и теплопроводных) проводить расчеты по явной схеме с шагом ${{\tau }_{{{\text{conv}}}}}$ практически невозможно. В этом случае для параболических уравнений, отвечающих диффузионному этапу, можно записать неявную схему и решать ее одним из итерационных алгоритмов, требующих, как правило, подбор эмпирических элементов (предобусловливателей, критерия окончания итераций и др.). Чтобы избежать известных трудностей использования неявной схемы, мы предлагаем новую схему. Эта схема, будем называть ее LINS (Local Iterations for Navier-Stokes equations), основана на явно-итерационной схеме интегрирования параболических уравнений ЛИ-М [7], [8]. Схема LINS наследует основные свойства схемы ЛИ-М, в силу которых результирующая схема для всей системы уравнений обеспечивает выполнение законов сохранения.

При использовании явно-итерационных схем для решения параболических уравнений может возникать ограничение на число итераций снизу, см. теорему Гельфанда–Локуциевского [9, с. 275–282]. Класс схем, удовлетворяющих этому ограничению, включает итерационные схемы, эквивалентные некоторой двухслойной явной схеме с увеличенным сеточным шаблоном. Для схемы ЛИ-М, используемой в данной работе в качестве прототипа схемы LINS, реализующей диффузионный этап, упомянутая теорема выполняется. Число итераций определяется шагом по времени ${{\tau }_{{{\text{conv}}}}}$ и верхней границей сеточного диффузионного оператора. Преимуществами схемы LINS являются алгоритмическая простота, отсутствие как диффузионного ограничения на шаг по времени, так и эмпирических параметров, эффективность при параллельной реализации.

Отметим, что прототипная схема ЛИ-М [7] построена на основе схемы [10]. Теоретическое обоснование этих схем проведено для многомерных линейных параболических уравнений, но схема может быть использована и для более общих эволюционных уравнений и систем. В частности, в [11] в рамках газодинамической модели схема ЛИ-М применена для решения нелинейного уравнения теплопроводности и обеспечивает выполнение баланса тепла для каждой ячейки сетки и исходных законов сохранения, что важно при расчетах высокотемпературных процессов.

В разд. 2 приведено описание схемы ЛИ-М для линейного параболического уравнения, в разд. 3 изложена схема LINS, сочетающая метод расщепления для сеточных аппроксимаций уравнений Навье–Стокса с использованием схемы ЛИ-М, в разд. 4 демонстрируется работоспособность алгоритма при решении модельных задач.

2. СХЕМА ЛОКАЛЬНЫХ ИТЕРАЦИЙ ЛИ-М

Для простоты изложения алгоритм схемы ЛИ-М приведем для начально-краевой задачи для линейного дифференциального уравнения параболического типа:

(1)
$\frac{{\partial u}}{{\partial t}} = - Lu + f(x,t),\quad x \in G \subset {{R}^{d}},\quad t \in [0,T].$
На границе $\partial G$ области $G$ задано условие $u(x,t) = \varphi (x,t),$ $x \in \partial G,$ $t \in [0,T]$, при $t = 0$ – начальное условие $u(x,0) = {{u}^{0}}(x),$ $x \in G$. В (1) $L$ – линейный эллиптический самосопряженный неотрицательно-определенный оператор, Функции $f,\,\,\varphi ,\,\,{{u}^{0}}$ – заданы, функция $u$ является искомой. Типичным примером служит оператор $Lu = - {\text{div}}(k(x,t){\text{grad }}u)$ при краевых условиях I, II или III рода. Вопросы пространственной дискретизации в данной работе не обсуждаются. Считаем, что в области $G \times [0,T]$ построена пространственно-временная сетка ${{\Omega }_{{\,h,\,\tau }}} = {{\Omega }_{h}} \times {{\Omega }_{\tau }}$, где ${{\Omega }_{\tau }} = \{ {{t}_{n}} = n\tau ,\;0 \leqslant n \leqslant {{N}_{\tau }}\} $ – сетка по времени с шагом $\tau = T{\text{/}}{{N}_{\tau }}$ (может быть переменным), ${{\Omega }_{h}} = \left\{ {{{x}_{i}} \in G,\;0 \leqslant i \leqslant {{N}_{h}}} \right\}$ – неструктурированная сетка в $G$, зависящая от параметра $h$ – шага сетки, характеризующего средний диаметр ячеек. Узлы сетки ${{\Omega }_{h}}$ будем записывать также в виде ${{x}_{h}}$, опуская в записи узла его номер. Обозначим через $\partial \,{{\Omega }_{h}}$ теоретико-множественную границу ${{\Omega }_{h}}$. Введем сеточные функции обычным образом: значения сеточной функции $u$ на $n$-м временном слое ${{t}_{n}}$ обозначим как ${{u}^{n}}$ или ${{u}^{n}}(x) = u(x,t_{n}^{{}})$, $x \in {{\Omega }_{h}}$, а значения функции на сетке ${{\Omega }_{{h,\tau }}}$ как $u_{i}^{n}(x) = u({{x}_{i}},t_{n}^{{}})$ или в безындексном виде, как $u(x,t)$, $x,t \in {{\Omega }_{{h,\tau }}}$. В подпространстве ${{U}_{h}}$ сеточных функций, заданных на ${{\Omega }_{h}}$ и обращающихся в нуль на $\partial \,{{\Omega }_{h}}$, определим сеточный оператор ${{L}_{h}}$, аппроксимирующий исходный дифференциальный оператор $L$ на классе гладких функций, определенных на $G$ и обращающихся в нуль на $\partial G$. Конкретный вид оператора ${{L}_{h}}$ и его порядок аппроксимации не являются принципиальными, для определенности считаем, что его точность $O\,({{h}^{2}})$. Предполагаем, что оператор ${{L}_{h}}$ – самосопряженный, его собственные значения $\lambda $ неотрицательны и лежат на отрезке $\left[ {0;{{\lambda }_{{\max }}}} \right]$ вещественной оси.

Схема ЛИ-М является двухслойной по времени, алгоритм перехода от слоя ${{t}_{n}}$ к слою ${{t}_{{n + 1}}}$ явно-итерационный. Число итераций $q$ зависит от шага $\tau $ и верхней границы спектра ${{\lambda }_{{\max }}}$ оператора ${{L}_{h}}$ на данном слое ${{t}_{n}}$. Конструкция схемы основана на использовании оптимальных многочленов Чебышёва I рода. Нужный алгебраической многочлен Чебышёва определяется параметрами $\tau $ и ${{\lambda }_{{\max }}}$, а его степень $p \approx \sqrt {{{C}_{{{\text{dif}}}}}} $, где ${{C}_{{{\text{dif}}}}} = \tau {{\lambda }_{{\max }}}$ – “диффузионное” число Куранта. При задании сеточного оператора матрицей или шаблонными коэффициентами оценку максимального собственного числа ${{\lambda }_{{\max }}}$ можно получить по теореме Гершгорина [12].

Одной из ключевых особенностей схемы ЛИ-М является правильный расчет эволюции во времени первых, низкочастотных компонентов разностного решения. Главная идея ЛИ-М отличается от обычного чебышёвского ускорения итераций: конструкция схемы диктуется требованиями аппроксимации, устойчивости, сохранения монотонности и положительности решений, а не оптимизацией сходимости итераций к решению неявной схемы. Контроль сходимости итераций в схеме ЛИ-М не нужен, точность $O(\tau + {{h}^{2}})$ обеспечивается конструкцией схемы. Нижняя граница спектра оператора ${{L}_{h}}$, обычно неизвестная, не участвует в определении алгоритма.

2.1. Алгоритм схемы ЛИ-М

1. Находим верхнюю границу ${{\lambda }_{{{\text{max}}}}}$ спектра оператора ${{L}_{h}}$ и определяем степень $p$ чебышёвского многочлена Чебышёва I рода ${{T}_{p}}(x) = \cos \left( {p~\arccos ~x} \right)$ формулой

(2)
$p = \left\lceil {0.25\pi \sqrt {\tau {{\lambda }_{{{\text{max}}}}} + 1} } \right\rceil ,$
где функция $\left\lceil s \right\rceil $ – это наименьшее целое, большее или равное $s$.

2. Берем упорядоченное для устойчивости [13], [14] множество нулей многочлена Чебышёва ${{T}_{p}}(x)\,$

${{K}_{p}} = \left\{ {cos\frac{{2i - 1}}{{2p}}\pi ,\;i = 1,2,...,p} \right\},$
выделяя в качестве первого корень ${{z}_{1}} = {{\beta }_{1}} = cos\left( {{{0.5\pi } \mathord{\left/ {\vphantom {{0.5\pi } p}} \right. \kern-0em} p}} \right)$. По упорядоченному множеству ${{\beta }_{m}} \in {{K}_{p}}$ находим параметры

(3)
${{a}_{m}} = \frac{{{{\lambda }_{{{\text{max}}}}}}}{{1 + {{z}_{1}}}}\left( {{{z}_{1}} - {{\beta }_{m}}} \right),\quad m = 1,...,p.$

Окончательно набор итерационных параметров состоит из $q = 2p - 1$ чисел $\left\{ {{{b}_{1}},...,{{b}_{q}}} \right\} \equiv \left\{ {{{a}_{p}},...,{{a}_{2}},{{a}_{p}},...,{{a}_{2}},{{a}_{1}}} \right\}$. В этом наборе параметры ${{a}_{p}},...,{{a}_{2}}$ повторяются дважды, а параметр ${{a}_{1}} = 0$ – один раз; вместо обратного можно взять прямой порядок, это не имеет значения.

3. Задаем начальное приближение ${{y}^{{(0)}}} = {{u}^{n}}$ на слое n и вычисляем

(4)
${{y}^{{(l)}}} = {{(1 + \tau {{b}_{l}})}^{{ - 1}}}({{y}^{{(0)}}} + \tau {{b}_{l}}{{y}^{{(l - 1)}}} - \tau {{L}_{h}}{{y}^{{(l - 1)}}} + \tau {{f}^{{n + 0.5}}}),\quad l = 1,2, \ldots ,q,$
где ${{f}^{{n + 0.5}}} = f(x,\,\,{{t}_{n}} + 0.5\tau )$. Результат – функция на верхнем слое ${{u}^{{n + 1}}} = {{y}^{{(q)}}}$.

4. Если $n + 1 < {{N}_{\tau }}$, то переходим на следующий слой ${{t}_{{n + 1}}}$ с новыми данными.

Выбор ${{\beta }_{1}} = cos\left( {{{0.5\pi } \mathord{\left/ {\vphantom {{0.5\pi } p}} \right. \kern-0em} p}} \right)$ в (3) обеспечивает равенство ${{a}_{1}} = 0$, поэтому последняя итерация на каждом шаге по времени эквивалентна счету по явной схеме ${{u}^{{n + 1}}} = {{u}^{n}} - \tau {{L}_{h}}{{u}^{n}} + \tau {{f}^{{n + 0.5}}}$, что хорошо вписывается в структуру “предиктор-корректор” схем, основанных на законах сохранения.

Дадим операторное описание схемы, вводя с этой целью операторный многочлен

(5)
${{F}_{p}}\left( {{{L}_{h}}} \right) = {{{{H}_{p}}\left( {{{L}_{h}}} \right)} \mathord{\left/ {\vphantom {{{{H}_{p}}\left( {{{L}_{h}}} \right)} {{{H}_{p}}\left( { - 1{\text{/}}\tau } \right)}}} \right. \kern-0em} {{{H}_{p}}\left( { - 1{\text{/}}\tau } \right)}},$
где
${{H}_{p}}\left( \lambda \right) = \prod\limits_{m = p}^{m = 1} \,\left( {{{a}_{m}} - \lambda } \right) \equiv {{T}_{p}}\left( {{{z}_{1}} - \left( {{{z}_{1}} + 1} \right){\lambda \mathord{\left/ {\vphantom {\lambda {{{\lambda }_{{\max }}}}}} \right. \kern-0em} {{{\lambda }_{{\max }}}}}} \right)$
есть алгебраический многочлен степени $p$, полученный с помощью многочлена Чебышёва ${{T}_{p}}(x)$, наименее уклоняющегося от 0 на отрезке $[ - 1;1]$:
(6)
${{T}_{p}}\left( x \right) = \left\{ {\begin{array}{*{20}{l}} {\cos \left( {p\arccos x} \right),\quad ~\left| x \right| \leqslant 1,} \\ {\operatorname{ch} \left( {p\operatorname{arch} x} \right),\quad \left| x \right| > 1.} \end{array}} \right.{\text{\;}}$
В приведенных и нижеследующих формулах присутствуют алгебраические и операторные многочлены от ${{L}_{h}}$ над полем вещественных чисел. Заметим, что так как ${{L}_{h}}$ – самосопряженный оператор, то и операторные многочлены от ${{L}_{h}}$ являются самосопряженными операторами. Для представления о структуре многочлена ${{F}_{p}}\left( {{{L}_{h}}} \right)$ введем вспомогательные операторы
(7)
$B = I + \tau {{L}_{h}},\quad {{Z}_{{p - 1}}} = \prod\limits_{m = p}^{m = 2} \,(I - {{(1 + \tau {{a}_{m}})}^{{ - 1}}}B),$
здесь $I$ – тождественный оператор. Так как ${{a}_{1}} = 0$, то ${{F}_{p}} = - \tau {{L}_{h}}{{Z}_{{p - 1}}}$. После исключения из (4) промежуточных итераций схему ЛИ-М можно записать с помощью введенных обозначений в операторной форме:

(8)
$\begin{gathered} {{y}^{{n + 1}}} = {{S}^{ + }}{{y}^{n}} + \tau {{Q}^{n}},\quad 0 \leqslant n < {{N}_{\tau }},\quad {{y}^{0}} = {{u}^{0}},{\text{ }} \\ {{S}^{ + }} = (I - F_{p}^{2}){{B}^{{ - 1}}},\quad {{Q}^{n}} = (I - {{F}_{p}}Z_{{p - 1}}^{{}}){{B}^{{ - 1}}}{{f}^{{n + 0.5}}}. \\ \end{gathered} $

В (8) выражение ${{B}^{{ - 1}}}$ носит формальный характер, в явном виде обращение оператора не выполняется. Схема (8) детально исследована в [7]: показано, что при условии устойчивости $p \geqslant 0.25\,\pi \,\,\sqrt {\tau {{\lambda }_{{{\text{max}}}}} + 1} $ выполнены неравенства $\left\| {{{F}_{p}}} \right\| \leqslant 1$ и $\left\| {{{S}^{ + }}} \right\| \leqslant 1$, обеспечивающие сходимость схемы ЛИ-М со скоростью $O\,(\tau + {{h}^{2}})$ в сеточной ${{L}_{2}}$-норме. Существуют модификации [7], позволяющие считать с точностью $O({{\tau }^{2}} + {{h}^{2}})$, но для решения нелинейных уравнений хорошо зарекомендовала себя именно схема ЛИ-М.

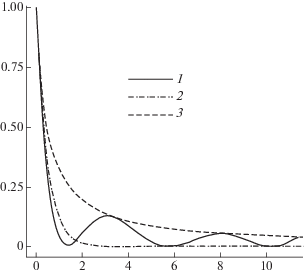
В (8) ${{S}^{ + }}$ – это оператор послойного перехода схемы. Дадим качественную характеристику его свойств. Для этого рассмотрим в единичном кубе на кубической сетке c шагом $h$ полудискретное уравнение ${{u}_{t}} = - {{L}_{h}}\,u$ с нулевыми граничными значениями; здесь ${{L}_{h}}$ – дискретный оператор Лапласа. Его максимальное собственное значение ${{\lambda }_{{\max }}} \approx {{12} \mathord{\left/ {\vphantom {{12} {{{h}^{2}}}}} \right. \kern-0em} {{{h}^{2}}}}$. Вместо отрезка $[0;{{\lambda }_{{\max }}}]$ рассмотрим нормированный отрезок $[0;~{{h}^{2}}{{\lambda }_{{\max }}}] \approx [0;12]$. Спектр оператора ${{S}^{ + }}$ на этом отрезке показан на фиг. 1 (сплошная линия 1), там же показаны спектры операторов послойного перехода чисто неявной схемы ${{B}^{{ - 1}}} = (1 + \tau {{L}_{h}})$ и точной схемы $\exp \,( - \tau {{L}_{h}})$. Видим, что спектр ${{S}^{ + }}$ неотрицателен и его начальный участок близок к спектру точного оператора. Это объясняет причину высокой реальной точности схемы ЛИ-М, так как согласно известному принципу [15], [16, с. 122] важен правильный расчет эволюции во времени первых низкочастотных компонентов разностного решения.

Фиг. 1.

Спектры операторов перехода схем: ЛИ-М (сплошная линия 1), точной (штрихпунктир 2) и неявной (штриховая линия 3).

Итак, на шаге по времени схема ЛИ-М выполняет $q = 2p - 1 \geqslant 1$ итераций. Если формально исключить промежуточные итерации, то схему ЛИ-М можно представить как явную схему с увеличенным шаблоном узлов сетки по пространству. Причем расширение шаблона дает возможность увеличить шаг счета по времени в ${{p}^{2}}$ раз по сравнению с явной схемой. Рассмотрим для примера на единичном отрезке на сетке с достаточно малым шагом $h$ полудискретное уравнение ${{u}_{t}} = {{L}_{h}}u$ с нулевыми граничными значениями. Вдали от концов отрезка расширенный шаблон для схемы ЛИ-М состоит из $2q + 1$ узлов и решение на верхнем слое ${\text{ }}{{\bar {u}}_{i}}{\text{ }}$ определяется по значениям функции ${{u}_{{i + m}}}$, $m = 0, \pm 1,..., \pm q$ с нижнего слоя, т.е. схему ЛИ-М можно в этом узле записать в явном виде:

(9)
${\text{ }}{{\bar {u}}_{i}}{\text{ }} = \sum\limits_{m = - q}^{m = q} \,{{G}_{m}}{{u}_{{i + m}}},$
где $\{ {{G}_{m}},\,\,m = 0,\,\, \pm 1,...,\,\, \pm q\} $ – шаблонные коэффициенты. В расчетах [7] показано, что функция $\{ {{G}_{m}}\} $ положительна, ${{G}_{m}} > 0$, и близка на шаблоне к функции $G_{m}^{P} = {{\left( {4\pi r} \right)}^{{ - 0.5}}}exp[ - {{0.25{{m}^{2}}} \mathord{\left/ {\vphantom {{0.25{{m}^{2}}} r}} \right. \kern-0em} r}]$, $r = {\tau \mathord{\left/ {\vphantom {\tau {{{h}^{2}}}}} \right. \kern-0em} {{{h}^{2}}}}$, возникающей при сеточной аппроксимации представления решения в виде интеграла Пуассона [17, с. 225]. Условие ${{G}_{m}} > 0$ обеспечивает сохранение положительности решений.

Схему ЛИ-М можно отнести к классу схем Рунге–Кутта на основе многочленов Чебышёва [18, с. 43]. К этому классу относятся схемы [19], [20]. Однако в схеме ЛИ-М выбор параметров подчинен аппроксимации точного оператора послойного перехода $\exp \,( - \tau {{L}_{h}})$ на начальном участке спектра, а не расширению области устойчивости. Как показано в [21], формальное использование многочленов Чебышёва может приводить к нежелательным конструкциям, например, к зависимости константы в оценке точности $O(\tau + {{h}^{2}})$ от степени многочлена Чебышёва. Пример такой схемы приведен в [21]; в ее эквивалентной записи (9) для любого числа итераций $p$ только три коэффициента ${{G}_{m}}$ являются ненулевыми (средний и два крайних), т.е. схема превращается в простейшую явную схему с шагом по пространству $ph$.

В данной работе на основе схемы ЛИ-М мы строим схему LINS расчета нестационарных течений в рамках модели Навье–Стокса. В будущем предполагается реализация схемы LINS для моделирования вязких, теплопроводных и диффузионных процессов в многокомпонентных химически реагирующих газовых средах.

3. ИНТЕГРИРОВАНИЕ ПО ВРЕМЕНИ УРАВНЕНИЙ НАВЬЕ–СТОКСА

3.1. Постановка задачи

Рассмотрим систему трехмерных уравнений Навье–Стокса, записанную в декартовой системе координат ${{x}_{k}}$, $k = 1,2,3$. При отсутствии внешних сил эта система может быть записана в виде законов сохранения относительно вектора $U = (\rho ,\rho {{u}_{1}},\rho {{u}_{2}},\rho {{u}_{3}},E)_{{}}^{{\text{т}}}$ основных переменных состояния сплошной среды [2]:

$\frac{{\partial U}}{{\partial t}} + \frac{{\partial {{F}_{1}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{F}_{2}}}}{{\partial {{x}_{2}}}} + \frac{{\partial {{F}_{3}}}}{{\partial {{x}_{3}}}} = 0.$
Здесь ${{F}_{k}}(U) = F_{k}^{{{\text{conv}}}}(U) + F_{k}^{\mu }(U) + F_{k}^{\lambda }(U)$ и $F_{k}^{{{\text{conv}}}}(U) = {{u}_{k}}U + {{\left( {0,p{{\delta }_{{k1}}},p{{\delta }_{{k2}}},p{{\delta }_{{k3}}}} \right)}^{{\text{т}}}}$– вектор потока и его невязкая составляющая соответственно, $F_{k}^{\mu }(U) = - {{\left( {0,{\text{ }}{{\tau }_{{k1}}},{{\tau }_{{k2}}},{{\tau }_{{k3}}},0} \right)}^{{\text{т}}}}$, $F_{k}^{\lambda }(U) = - (0,{\text{0}},0,0,{{u}_{1}}{{\tau }_{{k1}}} + $ $ + \;{{u}_{2}}{{\tau }_{{k2}}} + {{u}_{3}}{{\tau }_{{k3}}} + {{q}_{k}}{{)}^{{\text{т}}}}$ – векторы диссипативных потоков, обусловленных вязкостью и теплопроводностью соответственно,
(10)
${{\tau }_{{ij}}} = \mu \left[ {\left( {\frac{{\partial {{u}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{u}_{j}}}}{{\partial {{x}_{i}}}}} \right) - \frac{2}{3}{{\delta }_{{ij}}}\frac{{\partial {{u}_{k}}}}{{\partial {{x}_{k}}}}} \right]$
суть компоненты тензора вязких напряжений (по повторяющимся индексам производится суммирование), ${{\delta }_{{ij}}} - $ символ Кронекера, $i,\,\,j = 1,\,\,2,\,\,3$, ${{q}_{k}}$ – компоненты вектора теплового потока $q = \lambda ~\nabla T$, ${{\left( {{{u}_{1}},{{u}_{2}},{{u}_{3}}} \right)}^{{\text{т}}}}$ – декартовы компоненты вектора скорости $u$, $\rho $ – плотность, $p$ – давление, ${\text{ }}E = \rho (e + 0.5{{u}^{2}})$ – полная энергия, отнесенная к единице объема; здесь и далее ${{u}^{2}} = u_{1}^{2} + u_{2}^{2} + u_{3}^{2}$. Используется модель совершенного газа $p = e\rho \left( {\gamma - 1} \right) = \rho RT$; $e = e(T) = {{C}_{V}}\,T$ – удельная внутренняя энергия, $\gamma $ – показатель адиабаты, $R$ – газовая постоянная, $T$ – температура, ${{C}_{V}}$ – теплоемкость при постоянном объеме. В общем случае коэффициент теплопроводности $\lambda $ является тензором. Для частного случая молекулярной теплопроводности $\lambda = {{\mu {{C}_{p}}} \mathord{\left/ {\vphantom {{\mu {{C}_{p}}} {{\text{Pr}}}}} \right. \kern-0em} {{\text{Pr}}}}$, где ${\text{Pr}}$ – число Прандтля, а зависимости вязкости $\mu $ и теплоемкости при постоянном давлении ${{C}_{p}}$ от температуры известны: $\mu = \mu (T)$, ${{C}_{p}} = {{C}_{p}}(T)$.

Для трехмерных нестационарных уравнений Навье–Стокса строится схема LINS с использованием геометрических и аппроксимационных построений кода [3]. В этом коде предполагается, что все сеточные функции заданы в узлах неструктурированной сетки. При этом используется смешанный метод аппроксимации: члены конвективного переноса аппроксимируются с использованием метода конечных объемов, а диссипативная часть – методом конечных элементов. Для каждого узла сетки строится дуальная ячейка, объем и грани которой являются геометрическими конструкциями схемы.

Интегрированием по дуальным ячейкам строится дифференциально-разностная схема (дискретная по пространству, непрерывная по времени)

(11)
$\Omega \frac{{dU}}{{dt}} + F_{{}}^{{{\text{conv}}}}(U) + F_{{}}^{\mu }(U) + F_{{}}^{\lambda }(U) = 0,$
где $\Omega $ – диагональная матрица, элементами которой являются объемы дуальных ячеек, $F_{{}}^{{{\text{conv}}}}$, $F_{{}}^{\mu }$, $F_{{}}^{\lambda }$ – сеточные аналоги конвективного, вязкого и теплового потоков через границы дуальных ячеек. Конвективные потоки определяем с помощью решения элементарных задач Римана на гранях дуальных ячеек. Диффузионные потоки представляют собой разностные соотношения, полученные на гранях дуальных ячеек с помощью конечно-элементного восполнения сеточных функций.

Проинтегрируем уравнение (11) по времени на интервале $[{{t}_{n}},{{t}_{{n + 1}}}]$, где ${{t}_{{n + 1}}} = {{t}_{n}} + \tau $, $\tau > 0$ – некоторый временной шаг. Запишем этапы расчета основных переменных ${{U}^{{n + 1}}}$ на верхнем слое по времени$\,\,\,{{t}_{{n + 1}}}$ по значениям ${{U}^{n}} = (\rho ,\rho {{u}_{1}},\rho {{u}_{2}},\rho {{u}_{3}},E)_{{}}^{{\text{т}}}$ с нижнего временного слоя ${{t}_{n}}.$ Мы строим схему LINS на основе принципа расщепления алгоритма перехода на слой по времени$\,\,\,{{t}_{{n + 1}}}$ на конвективный и диффузионный этапы. Конвективный этап представляет собой явную схему годуновского типа.

Диффузионный этап реализуется с помощью чебышёвской явно-итерационной схемы. Как будет показано ниже, результирующая схема обеспечивает на разностном уровне выполнение основных законов сохранения. Так как шаг по времени определен на гиперболическом этапе, то для работы схемы LINS достаточно найти оценки верхних границ сеточных операторов вязкости и теплопроводности. Дополнительно мы накладываем на схему LINS требование автоматического перехода к явной схеме для всей системы (11) в случае выполнения условия устойчивости явной схемы. Поэтому в следующем пункте приводится анализ устойчивости явной схемы, а также схемы LINS.

3.2. Анализ устойчивости

Полный линейный анализ устойчивости с учетом взаимодействия конвективных и диссипативных членов в уравнениях Навье–Стокса очень сложен, см. [22, с. 384]. Рассмотрим, как можно получить условие устойчивости явной схемы

(12)
$\Omega \frac{{{{U}^{{n + 1}}} - {{U}^{n}}}}{\tau } + F_{{}}^{{{\text{conv}}}}({{U}^{n}}) + F_{{}}^{\mu }({{U}^{n}}) + F_{{}}^{\lambda }({{U}^{n}}) = 0.$

Для гиперболических (конвективных) процессов ограничение на шаг по времени выбирается из условия Куранта–Фридрихса–Леви вида ${{a\tau } \mathord{\left/ {\vphantom {{a\tau } {h \leqslant 1}}} \right. \kern-0em} {h \leqslant 1}}$, где $a$ – скорость распространения возмущений в ячейке диаметром $h$. Описание процедуры выбора ${{\tau }_{{{\text{conv}}}}}$ для схемы Годунова можно найти в [23, с. 198]. Пусть максимально допустимый шаг ${{\tau }_{{{\text{conv}}}}}$ выбран, тогда расчетный шаг $\tau $ обычно берется меньшим, $\tau \leqslant {{\tau }_{{{\text{conv}}}}}$. Отношение $Cu = {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{{{\text{conv}}}}}}}} \right. \kern-0em} {{{\tau }_{{{\text{conv}}}}}}} \leqslant 1$ является гиперболическим числом Куранта.

Для оценки “диффузионного” числа Куранта нужно вычислить верхние границы $\lambda _{{\max }}^{\mu }$, $\lambda _{{\max }}^{\lambda }$ спектров дискретных операторов, отвечающих аппроксимациям процессов диффузионного переноса за счет вязкости и теплопроводности. В соответствии с теоремой Гершгорина о кругах [12] величины $\lambda _{{\max }}^{\mu }$, $\lambda _{{\max }}^{\lambda }$ можно оценить, вычисляя для каждого узла сетки сумму модулей коэффициентов разностных аппроксимаций диссипативных членов, поэтому будем считать эти величины известными.

Положим $\lambda _{{\max }}^{{}} = \lambda _{{\max }}^{\mu } + \,\,\lambda _{{\max }}^{\lambda }$. Оценку максимального шага времени для явного расчета процессов диффузии можно взять в виде ${{\tau }_{{{\text{dif}}}}} = \lambda _{{\max }}^{{ - 1}}$, подчинив выбор шага ограничению ${{\tau }_{{{\text{dif}}}}}\lambda _{{\max }}^{{}} \leqslant 1,$ в два раза более жесткому, чем следует из известного условия устойчивости $ - 1 \leqslant 1 - {{\tau }_{{{\text{dif}}}}}\lambda \leqslant 1$, получающегося из оценки нормы оператора послойного перехода. Условие $\tau \leqslant \min ({{\tau }_{{{\text{conv}}}}},{{\tau }_{{{\text{dif}}}}})$ не всегда работоспособно, см. [24]. Поэтому для обеспечения корректного перехода схемы LINS в чисто явную схему мы берем за основу достаточное условие устойчивости противопотоковой явной схемы для линейного уравнения конвекции-диффузии [25]

(13)
$\tau \leqslant {{(\tau _{{{\text{conv}}}}^{{ - 1}} + \tau _{{{\text{dif}}}}^{{ - 1}})}^{{ - 1}}}.$

Вводя диффузионное число Куранта $Cd = {\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{{{\text{dif}}}}}}}} \right. \kern-0em} {{{\tau }_{{{\text{dif}}}}}}}$, перепишем (13) в виде $\tau \cdot (\tau _{{{\text{conv}}}}^{{ - 1}} + \tau _{{{\text{dif}}}}^{{ - 1}}) = Cu + Cd \leqslant 1$ $\tau \cdot (\tau _{{{\text{conv}}}}^{{ - 1}} + \tau _{{{\text{dif}}}}^{{ - 1}}) = Cu + Cd \leqslant 1$.

Это условие выполнено, в частности, при одновременном выполнении неравенств $Cu \leqslant 0.5$, $Cd \leqslant 0.5$. Для их справедливости достаточно взять шаг ${{\tau }_{s}}$ явного интегрирования всей системы из условия

(14)
${{\tau }_{s}} \leqslant 0.5\min ({{\tau }_{{{\text{conv}}}}};{{\tau }_{{{\text{dif}}}}}).$

При доминировании конвекции, т.е. при условии${{\tau }_{{{\text{conv}}}}} < {{\tau }_{{{\text{dif}}}}}$, ограничение (14) определяет максимальный допустимый шаг ${{\tau }_{s}} = 0.5{{\tau }_{{{\text{conv}}}}}$. За этим новым шагом оставим прежнее обозначение, $\tau _{{{\text{сonv}}}}^{{}}: = 0.5{{\tau }_{{{\text{conv}}}}}$. При доминировании диффузии, т.е. при ${{\tau }_{{{\text{conv}}}}} > {{\tau }_{{{\text{dif}}}}}$, расчет по явной схеме проводить нельзя  в силу нарушения условия (14), поэтому расчет проведем по схеме LINS с шагом $\tau _{{{\text{сonv}}}}^{{}}$. При преобладании конвекции выполнено неравенство $Cd \leqslant \,0.5$ и в силу конструкции схемы LINS это неравенство обеспечивает автоматический переход к явной схеме для всей системы (12).

3.3. Конвективный и диффузионный этапы расчета

Конвективный этап состоит в расчете по явной схеме годуновского типа с нахождением потоков $F_{{}}^{{{\text{conv}}}}({{U}^{n}})$ на гранях дуальных ячеек с помощью решения задачи Римана о распаде произвольного разрыва. Запишем конвективный этап в виде

(15)
$\Omega \frac{{\bar {U} - {{U}^{n}}}}{{{{\tau }_{{{\text{conv}}}}}}} + F_{{}}^{{{\text{conv}}}}({{U}^{n}}) = 0.$

Результат расчета отметим верхней чертой: $\bar {U} = (\bar {\rho },\bar {\rho }{{\bar {u}}_{1}},\bar {\rho }{{\bar {u}}_{2}},\bar {\rho }{{\bar {u}}_{3}},\bar {E})_{{}}^{{\text{т}}}$, ${\text{ }}\bar {E} = \bar {\rho }(\bar {e} + 0.5\bar {u}_{{}}^{2})$. Сеточные функции ${\text{ }}\bar {u},\;\bar {E},\;\bar {e}$ являются предварительными и уточняются на диффузионном этапе, функция $\bar {\rho }$ является окончательной, т.е. ${{\rho }^{{n + 1}}} = \bar {\rho }$.

Диффузионный этап состоит из двух явно-итерационных процедур, примененных последовательно к редуцированным (без учета конвективных потоков) уравнениям импульса и энергии. Такое разделение удобно для будущего включения в схему уравнений диффузии химических компонентов смеси, так как уравнение энергии является замыкающим законом сохранения с учетом суммарного теплового потока.

Явно-итерационная процедура выглядит одинаково для вязкой и теплопроводной параболических подсистем. Нам важен случай доминирования диффузии, ${{\tau }_{{{\text{conv}}}}} > {{\tau }_{{{\text{dif}}}}}$. При измельчении сетки доминирование диффузии усиливается, ${{\tau }_{{{\text{conv}}}}} \gg {{\tau }_{{{\text{dif}}}}}$. Использование на диффузионном этапе явной схемы ведет к большим вычислительным затратам, поэтому мы строим процедуру, пригодную при любом соотношении масштабов ${{\tau }_{{{\text{conv}}}}}$, ${{\tau }_{{{\text{dif}}}}}$ и переходящую при доминировании конвекции (${{\tau }_{{{\text{conv}}}}} < {{\tau }_{{{\text{dif}}}}}$) в явную схему для системы уравнений (11).

Запишем каждую из параболических задач в виде

(16)
${{dH} \mathord{\left/ {\vphantom {{dH} {dt}}} \right. \kern-0em} {dt}} + {{D}_{h}}V = {{g}_{h}},$
где ${{D}_{h}}$ – сеточный диффузионный оператор, определяемый аппроксимациями потоков $F_{{}}^{\mu }({{U}^{n}})$, $F_{{}}^{\lambda }({{U}^{n}})$, ${{g}_{h}}$ – правая часть. Например, для уравнения энергии ${{D}_{h}}$ – это аппроксимация эллиптического оператора $ - \operatorname{div} (\lambda \nabla T)$. Оператор ${{D}_{h}}$ является самосопряженным неотрицательно-определенным оператором в сеточном скалярном произведении. Предполагаем, что $H = H(\,V)$ и переменную $V$ можно выразить через $H:V = V(H)$. Для вязкого случая

$H = (\rho {{u}_{1}},\rho {{u}_{2}},\rho {{u}_{3}})_{{}}^{{\text{т}}},\quad V = ({{u}_{1}},{{u}_{2}},{{u}_{3}})_{{}}^{{\text{т}}}.$

При расчете теплопроводности аналогами $H,\;V$ являются полная энергия ${\text{ }}E = \rho (e + 0.5u_{{}}^{2})$ и температура $T$, связанная с внутренней энергией уравнением состояния $e = e\,(T)$.

Для параболических подсистем вида (16) число итераций и итерационные параметры берутся одинаковыми; они определяются значениями ${{\tau }_{{{\text{conv}}}}}$ и $\lambda _{{\max }}^{{}}$, как и в разд. 2. Для каждой подсистемы итерационный цикл ($m = 1,...,2p - 1$) проводится в соответствии с формулой

(17)
${{H}^{m}} = {{(1 + {{\tau }_{{{\text{conv}}}}}{{b}_{m}})}^{{ - 1}}}\{ {{H}^{0}} + {{\tau }_{{{\text{conv}}}}}{{b}_{m}}{{H}^{{m - 1}}} - {{\tau }_{{{\text{conv}}}}}({{D}_{h}}{{V}^{{m - 1}}} - {{g}_{h}})\} .$

В качестве начального приближения ${{V}^{0}}$ берутся значения с нижнего слоя по времени, а ${{H}^{0}}$ определяется данными с предыдущего шага расщепления. Поэтому при ${{b}_{m}} = 0$ формула (17) превращается в явную схему для вязкой и теплопроводной подсистем сответственно. Условие ${{b}_{m}} = 0$ реализуется при $m = 2p - 1$, см. разд. 2.

Применим процедуру (17) к уравнениям импульса (в отсутствие конвекции) с переменными

${{H}^{0}} = H_{{}}^{{{\text{conv}}}} = (\bar {\rho }{{\bar {u}}_{1}},\bar {\rho }{{\bar {u}}_{2}},\bar {\rho }{{\bar {u}}_{3}})_{{}}^{{\text{т}}},$

полученными на конвективном этапе. Плотность “заморожена” на интервале $[{{t}_{n}},{{t}_{n}} + {{\tau }_{{{\text{conv}}}}}]$ – берется ее значение $\bar {\rho }$. В ходе итераций (17) на предпоследней итерации, т.е. при $m = 2p - 2$, получаем вектор $\,{{H}^{m}}$ и отвечающие ему компоненты вектора скорости $({{\tilde {u}}_{1}},{{\tilde {u}}_{2}},{{\tilde {u}}_{3}})_{{}}^{{\text{т}}}$. Тем самым определен вектор основных переменных ${{\tilde {U}}^{n}} = (\bar {\rho },\bar {\rho }{{\tilde {u}}_{1}},\bar {\rho }{{\tilde {u}}_{2}},\bar {\rho }{{\tilde {u}}_{3}},\bar {E})_{{}}^{{\text{т}}}$ и поток вязкого трения $F_{{}}^{\mu }({{\tilde {U}}^{n}})$. Тогда завершающая итерация $m = 2p - 1$ эквивалентна расчету уравнений импульса с учетом только вязких членов в соответствии с законом сохранения

(18)
$\Omega \frac{{H_{{}}^{{n + 1}} - H_{{}}^{{{\text{conv}}}}}}{{{{\tau }_{{{\text{conv}}}}}}} + F_{{}}^{\mu }({{\tilde {U}}^{n}}) = 0.$

Результат расчета – переменные $H_{{}}^{{n + 1}} = (\bar {\rho }{{\bar {\bar {u}}}_{1}},\bar {\rho }{{\bar {\bar {u}}}_{2}},\bar {\rho }{{\bar {\bar {u}}}_{3}})_{{}}^{{\text{т}}}$ на верхнем слое по времени. С помощью $H_{{}}^{{n + 1}}$ находим новые значения вектора скорости $\bar {\bar {u}} = {{({{\bar {\bar {u}}}_{1}},{{\bar {\bar {u}}}_{2}},{{\bar {\bar {u}}}_{3}})}^{{\text{т}}}} = {{H_{{}}^{{n + 1}}} \mathord{\left/ {\vphantom {{H_{{}}^{{n + 1}}} {\bar {\rho }}}} \right. \kern-0em} {\bar {\rho }}}$, отвечающие данному этапу, затем обновляем с их помощью основные переменные $\bar {\bar {U}} = (\bar {\rho },\bar {\rho }{{\bar {\bar {u}}}_{1}},\bar {\rho }{{\bar {\bar {u}}}_{2}},\bar {\rho }{{\bar {\bar {u}}}_{3}},\bar {E})_{{}}^{{\text{т}}}$. Суммируя уравнения (15) и (18), получаем разностное уравнение, выражающее законы сохранения массы и импульса.

Аналогично, применим процедуру (17) к уравнению энергии (в отсутствие конвекции) с функцией ${{H}^{0}} \equiv \bar {E} = \bar {\rho }(\bar {e} + 0.5\bar {u}_{{}}^{2})$, определенной на конвективном этапе. В ходе итераций (17) получаем на предпоследней итерации $m = 2p - 2$ функцию $\,{{H}^{m}}$, т.е. полную энергию $\tilde {E} = {{H}^{m}}$ (и соответствующие величины $\tilde {e}$, $\tilde {T}$). Тем самым определен вектор основных переменных ${{\tilde {U}}^{n}} = (\bar {\rho },\bar {\rho }{{\bar {u}}_{1}},\bar {\rho }{{\bar {u}}_{2}},\bar {\rho }{{\bar {u}}_{3}},\tilde {E})_{{}}^{{\text{т}}}$ и тепловой поток $F_{{}}^{\lambda }({{\tilde {U}}^{n}})$. Тогда завершающая итерация $m = 2p - 1$ эквивалентна закону сохранения энергии с учетом теплопроводности и диссипации тепла за счет трения

(19)
${{\Omega }_{{}}}\frac{{E_{{}}^{{n + 1}} - \bar {E}}}{{{{\tau }_{{{\text{conv}}}}}}} + {{F}^{\lambda }}({{\tilde {U}}^{n}}) = f.$
В уравнении (19) правая часть $f = {{\partial ({{u}_{i}}{{\tau }_{{ij}}})} \mathord{\left/ {\vphantom {{\partial ({{u}_{i}}{{\tau }_{{ij}}})} {\partial {{x}_{j}}}}} \right. \kern-0em} {\partial {{x}_{j}}}}$представляет собой энергию, диссипируемую в виде тепла благодаря вязкости, и определяется по значениям переменных с нижнего слоя по времени. Находим из (19) полную энергию $\bar {\bar {E}} \equiv {{E}^{{n + 1}}} = \bar {\rho }(\bar {\bar {e}} + 0.5\bar {\bar {u}}_{{}}^{2})$. Тем самым вектор переменных ${{U}^{{n + 1}}} = (\bar {\rho },\bar {\rho }{{\bar {\bar {u}}}_{1}},\bar {\rho }{{\bar {\bar {u}}}_{2}},\bar {\rho }{{\bar {\bar {u}}}_{3}},\bar {\bar {E}})_{{}}^{{\text{т}}}$ определен. В его обозначениях одна черта означает, что на шаге по времени переменная изменялась один раз, две черты – два раза. По существу, уравнение (19) служит для нахождения внутренней энергии $e$ и температуры $T$, связанных уравнением состояния: $e = e(T)$, $T = T(e)$. Суммируя уравнения (17), (18) и (19), получаем разностное уравнение для вектора основных переменных, выражающее исходные законы сохранения.

Алгоритм LINS можно представить следующим образом.

Шаг 1. Находим значения временных шагов${{\tau }_{{{\text{conv}}}}}$, ${{\tau }_{{{\text{dif}}}}}$. Если диффузия не доминирует (${{\tau }_{{{\text{conv}}}}} \cdot {{\lambda }_{{\max }}} = {{{{\tau }_{{{\text{conv}}}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{{\text{conv}}}}}} {{{\tau }_{{{\text{dif}}}}}}}} \right. \kern-0em} {{{\tau }_{{{\text{dif}}}}}}} \leqslant 0.5$, тогда $p = \left\lceil {0.25\pi \sqrt {{{\tau }_{{{\text{conv}}}}}{{\lambda }_{{{\text{max}}}}} + 1} } \right\rceil = 1$), то расчет по схеме LINS автоматически перейдет в явную схему с шагом ${{\tau }_{{{\text{conv}}}}}$ для всей системы уравнений Навье–Стокса. Если диффузия доминирует, т.е. ${{{{\tau }_{{{\text{conv}}}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{{\text{conv}}}}}} {{{\tau }_{{{\text{dif}}}}}}}} \right. \kern-0em} {{{\tau }_{{{\text{dif}}}}}}} > 0.5$, то гиперболический и диффузионный этапы выполняются с шагом ${{\tau }_{{{\text{conv}}}}}$, но на диффузионом этапе затрачивается $q = 2p - 1 > 1$ итераций для решения каждой параболической системы.

Шаг 2. Выполняем конвективный этап (15).

Шаг 3. Выполняем диффузионный этап, решая две системы вида (16) с помощью алгортима (17).

Заметим, что законы сохранения массы, импульса и полной энергии выполняются на разностном уровне для каждой дуальной ячейки. Из локальной консервативности следует выполнение законов сохранения по всей расчетной области. При доминировании конвекции, точнее при ${{{{\tau }_{{{\text{conv}}}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{{\text{conv}}}}}} {{{\tau }_{{{\text{dif}}}}}}}} \right. \kern-0em} {{{\tau }_{{{\text{dif}}}}}}} \leqslant 0.5$, в соответствии с (2) число итераций $p = 1$, следовательно, схема LINS эквивалента явной схеме. Т.е. в случае $\lambda _{{\max }}^{\mu } \leqslant 1$ и $\lambda _{{\max }}^{\lambda } \leqslant 1$ локальная консервативность обеспечена конструкциями явных схем. При нарушении одного из этих неравенств выполнено условие $p > 1$. Тогда схему LINS можно интерпретировать как схему предиктор-корректор, в которой на этапе предиктора сначала выполняется расчет по схеме (17) с числом итераций $r = 2p - 2$ и находится предварительное значение ${{V}^{r}}$ с обновлением вектора скорости или температуры. После этого выполняется корректор по схемам (18) и (19) с вычислением вязкого и теплового потоков по новым значениям. Тем самым локальная консервативность обеспечена. Устойчивость и аппроксимация такой расчетной схемы следует из доказанных свойств схемы ЛИ-М.

Заметим, что не все схемы типа предиктор-корректор, построенные на основе устойчивого предиктора, при использовании явного корректора для консервативного замыкания являются устойчивыми. Например, для простейшего двумерного уравнения теплопроводности ${{u}_{t}} = {{u}_{{xx}}} + {{u}_{{yy}}}$ на прямоугольной сетке продольно-поперечная прогонка устойчива, но явный корректор устойчивость нарушает.

4. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Продемонстрируем возможности схемы LINS. Шаг интегрирования по времени будем брать с ограничением $\tau \leqslant {{\tau }_{{{\text{conv}}}}}$, включая случай ${{\tau }_{{{\text{conv}}}}} > {{\tau }_{{{\text{dif}}}}}$ доминирования диффузии над конвекцией. Обычно мы берем $\tau = {{{\text{K}}}_{{{\text{conv}}}}}{{\tau }_{{{\text{conv}}}}}$ с числом Куранта ${{{\text{K}}}_{{{\text{conv}}}}} = 0.125{\kern 1pt} - {\kern 1pt} 0.5$.

Задача 1. Рассмотрим задачу о тепловой конвекции [26] – нестационарном течении газа при постоянном нагреве границы. Пусть газ с постоянными начальными плотностью ${{\rho }_{0}}$, температурой ${{T}_{0}}$ и скоростью ${{u}_{0}} = 0$, ${{v}_{0}} = 0$ заключен в замкнутую область между двумя стенками, одна из которых нагрета до температуры ${{T}_{1}} > {{T}_{0}}$ и в дальнейшем не изменяется во времени, а вторая поддерживается при постоянной температуре ${{T}_{0}}$. Найдем распространение тепла и движение газа в последующие моменты времени. Будем рассматривать совершенный газ с коэффициентами теплопроводности и вязкости, зависящими от температуры по формуле Сазерленда. Проведем расчеты на конечном отрезке времени от начального состояния до момента столкновения волн температуры, скорости, плотности и давления с противоположной стенкой. Рассмотрим начально-краевую задачу в двумерной области $0 < x < 1$; $0 < y < 1$. Для моделирования одномерного течения на нижней и верхней границах области ставятся условия периодичности. Краевые условия на вертикальных стенках: $u(0,t) = 0$, $u(1,t) = 0$, $T(0,t) = 10$, $T(1,t) = 1$. Начальные условия при $t = 0$: $u(x,0) = 0$, $\rho (x,0) = 1$, $T(x,0) = 1$. Уравнение состояния при выбранном обезразмеривании имеет вид $p = \rho T$. Расчеты проведены на прямоугольных сетках с числом ячеек ${{N}_{x}} \times {{N}_{y}}$. Число шагов ${{N}_{x}}$ по оси $Ox$ изменялось, по оси $Oy$ оставалось постоянным (задача одномерная). Динамика волн плотности и давления до момента столкновения с противоположной стенкой показана на фиг. 2. Графики показаны для 6 моментов времени ${{t}_{i}} = 0.05 \cdot i$, $i = 1,...,6$, и отмечены цифрами 1, 2, …, 6.

Фиг. 2.

Профили плотности (слева) и давления (справа).

В момент времени ${{t}_{6}}\,\, = 0.3$ возмущения достигают правой холодной стенки. Эти результаты получены на сетке $320 \times 10$ по схеме LINS с конвективным числом Куранта ${{{\text{K}}}_{{{\text{conv}}}}} = 0.125$, выбранным из соображений точности. Число итераций схемы LINS с ростом времени возрастало с 9 до 15. Отметим, что условие продвижения волны за шаг по времени не более, чем на шаг по пространству, выполняется при ${{{\text{K}}}_{{{\text{conv}}}}} = 0.5$.

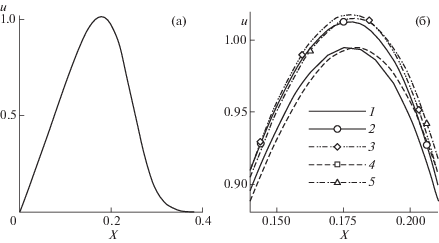
Расчеты на сетках с числом узлов ${{N}_{x}} = 160$ и ${{N}_{x}} = 320$ по оси $Ox$ дают одинаковые результаты с различием в пределах 1%. На фиг. 3, 4 показаны графики давления и скорости в момент времени ${{t}_{1}} = 0.05\,$. В реальном масштабе графики практически неразличимы (левые рисунки); поэтому справа показаны фрагменты графиков, где отличия заметны – для давления вблизи горячей стенки, для скорости – вблизи точки максимума. По схеме LINS расчеты проведены на сетке с числом узлов ${{N}_{x}} = 160$ и фиксированным шагом $\tau = 5 \times {{10}^{{ - 4}}}$, что соответствует числу ${{K}_{{{\text{conv}}}}} \approx 0.3$, а на сетке с ${{N}_{x}} = 320$ – с шагами $\tau = 2.5 \times {{10}^{{ - 4}}}$ и $\tau = 5 \times {{10}^{{ - 4}}}$, с ${{K}_{{{\text{conv}}}}} \approx 0.3$ и ${{K}_{{{\text{conv}}}}} \approx 0.6$ соответственно; на фиг. 3 и 4 эти графики обозначены цифрами 1, 2, 3. Численные эксперименты показывают, что расчеты по явной схеме с числом Куранта ${{K}_{{\exp l}}}$, вычисленным для полной системы с учетом совместного конвективно-диффузионного ограничения, являются успешными при ${{K}_{{\exp l}}}\,\, \leqslant \,\,\,0.25$. Указанное ограничение определяет шаг интегрирования по времени $\tau \approx {{10}^{{ - 5}}}$. Это означает, что расчеты по схеме LINS проведены с более крупными шагами по времени (в 25 и 50 раз). Результаты по точности удовлетворительны, см. фиг. 3–4, цифрами обозначены результаты: 1, 2, 3 – LINS, 4, 5 – явная схема с ${{N}_{x}} = 160$ и ${{N}_{x}} = 320$ соответственно.

Фиг. 3.

Профили давления при $t = 0.05$.

Фиг. 4.

Профили скорости при $t = 0.05$.

Для сетки с ${{N}_{x}} = 320$ расчет по схеме LINS с шагом $\tau = 5 \times {{10}^{{ - 4}}}$ требует в 5 раз меньше времени, чем явная схема. На интервале $[0;\,\,0.05]$ явная схема делает 4172 шага по времени, схема LINS – 100 шагов, но в этой схеме на каждом шаге по времени в среднем $q = 2p - 1 = 21$ раз происходит пересчет теплого и вязких потоков, что соответствует степени $p = 11$ чебышёвского многочлена, лежащего в основе конструкции схемы LINS.

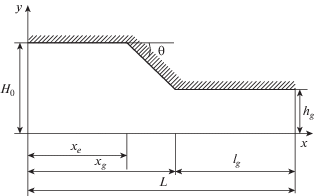
Задача 2. Расчет сверхзвукового течения в канале переменного сечения [27]. Геометрия канала показана на фиг. 5. Для расчетов система уравнений динамики вязкого теплопроводного газа приводится к безразмерному виду путем деления декартовых координат на характерный линейный размер $D$, компонентов вектора скорости – на скорость ${{V}_{\infty }}$, давления – на удвоенный скоростной напор $2{{q}_{\infty }} = {{\rho }_{\infty }}{\text{ }}V_{\infty }^{2}$, времени – на характерное время пребывания частицы около тела ${{t}_{*}} = D{\text{/}}{{V}_{\infty }}$. В качестве характерного линейного размера принято расстояние $D = {{H}_{0}}$ от оси симметрии до передней кромки входа в канал. В выходном сечении канала расстояние от оси симметрии до задней кромки равно ${{h}_{g}}{{H}_{0}} = 0.75\,{{H}_{0}}$. Входной участок с постоянной площадью поперечного сечения имеет относительную длину ${{x}_{e}}$. Длина канала подбирается из условия, чтобы в выходном сечении при заданном числе Рейнольдса ${\text{Re}}$ не наблюдалось возвратное течение. Переходной участок канала имеет форму клина с углом полураствора $\theta $ и длину $({{x}_{g}} - {{x}_{e}}){{H}_{0}} = 0.25{{H}_{0}}{\text{ctg}}\theta $. Общая длина канала равна $L{{H}_{0}}$. Геометрические характеристики канала взяты из [27]: ${{H}_{0}} = 1$, $\theta = {{10}^{{^{ \circ }}}}$, $\,{{x}_{e}} = 1$, ${{l}_{g}} = 4.0823$, $L = 6.5$, ${{l}_{g}}{\text{/}}{{h}_{g}} = 5.443$.

Фиг. 5.

Геометрия модельной задачи.

Систематические расчеты на разных сетках выполнены для канала с адиабатическими (теплоизолированными) стенками с числом Маха на входе ${{M}_{\infty }} = 4$ и с числом Рейнольдса ${\text{Re}} = {{10}^{4}}$ (вычисляется по параметрам невозмущенного потока и характерному линейному размеру).

Для построения сеток область расчета разбивается на три подобласти (слева направо – прямоугольник, трапеция и прямоугольник, см. фиг. 5). В каждой подобласти число шагов ${{N}_{y}}$ по вертикальной оси Oy взято одинаковым. По оси $Ox$ в первой и второй подобластях сетки равномерные с числом шагов $N_{x}^{1}$, $N_{x}^{2}$ соответственно. В третьей подобласти сетка по оси $Ox$ с числом узлов $N_{x}^{3}$ укрупняется в направлении выхода по геометрической прогрессии. При измельчении сетки отношение ${{g}_{x}} = {{h_{x}^{{\max }}} \mathord{\left/ {\vphantom {{h_{x}^{{\max }}} {h_{x}^{{\min }}}}} \right. \kern-0em} {h_{x}^{{\min }}}}$ остается неизменным (${{g}_{x}} = 4$). Здесь $h_{y}^{{\max }}$ и $h_{y}^{{\min }}$ – максимальная и минимальная толщины ячеек соответственно.

Для построения сетки в пограничных слоях используется аналогичный подход. Выделяются зоны толщиной 20% от высоты области по оси $Oy$ и строится сетка, сгущающаяся к соответствующей твердой стенке по геометрической прогрессии. При этом отношение максимальной и минимальной толщин ячеек в зоне каждого пограничного слоя ${{g}_{y}} = {{h_{y}^{{\max }}} \mathord{\left/ {\vphantom {{h_{y}^{{\max }}} {h_{y}^{{\min }}}}} \right. \kern-0em} {h_{y}^{{\min }}}}$ остается постоянным (${{g}_{y}} = 8$) при измельчении сетки. В центральной части области сетка взята равномерной с числом узлов ${{N}_{y}}{\text{/}}2$. Расчеты проведены на трех сетках с общим числом узлов $N = 10\,000,\;40\,000,\;160\,000$. Расстановка узлов по зонам задана следующая: 1) $N_{x}^{1} = N_{x}^{2} = 30$, $N_{x}^{3} = 40$, ${{N}_{y}} = 100$; 2) $N_{x}^{1} = N_{x}^{2} = 60$, $N_{x}^{3} = 80$, ${{N}_{y}} = 200$; 3) $N_{x}^{1} = N_{x}^{2} = 120$, $N_{x}^{3} = 160$, ${{N}_{y}} = 400$. На всех указанных сетках безразмерный параметр $y + $, характеризующий расстояние от стенки до первого узла сетки, меняется вдоль стенки в допустимых пределах $0.1{\kern 1pt} - {\kern 1pt} 1$, т.е. пограничный слой хорошо разрешен.

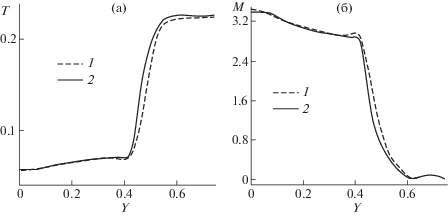
В расчетах подтверждены приведенные в [27] особенности установившегося ламинарного течения. Его структура достаточно сложна, включает взаимодействующие ударные волны и веера волн разрежения. При заданном числе Рейнольдса ${\text{Re }} = {\text{ }}{{10}^{4}}$ на стенках канала формируется толстый пограничный слой с зоной отрывного течения. Появление такой зоны обусловлено ударной волной, отраженной от оси (плоскости) симметрии. На фиг. 6 показаны профили температуры (слева) и числа Маха (справа) в сечении $x = 4.6$ (в зоне отрыва) для верхней половины канала $0\,\, \leqslant \,\,y\,\, \leqslant \,\,0.75$. Приведены результаты для сеток 1 и 2, графики для сеток 2 и 3 неразличимы. Поэтому можно предполагать, что расчеты на указанных сетках являются удовлетворительными.

Фиг. 6.

Профили температуры (слева) и числа Маха (справа) в сечении $x = 4.6$.

Заметим, что схема LINS разрабатывается для расчетов в основном нестационарных процессов. При использовании неявной схемы шаг по времени можно регулировать автоматически, увеличивая или уменьшая его в зависимости от некоторых индикаторов. Большие шаги по времени обычно используют, когда нестационарная постановка служит для определения стационарного решения и не требуется сохранять физическую адекватность промежуточных решений в процессе установления.

Схема LINS разрабатывается для расчетов в основном нестационарных процессов. При использовании неявной схемы шаг по времени можно регулировать автоматически, увеличивая или уменьшая его в зависимости от некоторых индикаторов. Большие шаги по времени обычно используют, когда нестационарная постановка служит для определения стационарного решения и не требуется сохранять физическую адекватность промежуточных решений в процессе установления. Данная задача рассматривается в методических целях, поэтому мы используем неявную схему в режиме расчета эволюционных задач – шаг по времени фиксирован и близок к максимальному шагу, допускаемому гиперболическим ограничением устойчивости явной схемы с ${{K}_{{{\text{conv}}}}} = 1$. На сетке 3 это значение примерно в 4 раза больше границы устойчивости явной схемы для полной системы уравнений. Кроме того, для неявной схемы фиксируются основные вычислительные процедуры: делается одна ньютоновская итерация, линейная система решается стабилизированным методом бисопряженных градиентов с предобусловливателем ILU(0) с относительной точностью $\varepsilon = 0.01$ в ${{L}_{2}}$ – норме. Для явной схемы шаг по времени вычисляется с учетом совместного гиперболического и диффузионного ограничений с коэффициентом запаса ${{K}_{{\exp l}}} = 0.5$ (счет по явной схеме с ${{K}_{{\exp l}}} = 1$ на сетках 2 и 3 приводит к авосту). Для схемы LINS шаг по времени взят равным шагу неявной схемы. В этом расчете взят предельно-допустимый шаг (разумно брать вдвое меньший шаг). Отсутствие негативных эффектов связано с тем, что, по-видимому, наличие в процедуре LINS итераций на этапе решения диффузионных подсистем положительно влияет на качество решения. Число итераций схемы LINS определяется в соответствии с (2) и на сетке 3 в зависимости от шага и текущих значений коэффициентов молекулярной вязкости и теплопроводности составляет 7–9 итераций. При измельчении сетки число итераций будет возрастать (примерно обратно пропорционально квадратному корню из шагу сетки).

6. ЗАКЛЮЧЕНИЕ

В данной работе приведен новый алгоритм интегрирования по времени системы уравнений Навье–Стокса динамики сжимаемой теплопроводной среды. Он основан на расщеплении расчета одного временного шага на гиперболический и параболический этапы. Для гиперболической подсистемы расчет выполнен по явной схеме. На диффузионном этапе используется явно-итерационная чебышёвская схема, обладающая алгоритмической простотой и отсутствием настроечных параметров. Результирующая схема обеспечивает выполнение законов сохранения, расчеты демонстрируют хорошую эффективность по точности и объему вычислительных затрат, хорошую масштабируемость в параллельной реализации.

Авторы выражают признательность и благодарность А.В. Горобцу и П.В. Бахвалову за помощь в работе и ценные замечания.

Список литературы

  1. Жуков В.Т., Рыков Ю.Г., Феодоритова О.Б. Математическая модель течения многокомпонентной смеси газов с учетом возможности возникновения жидкой фазы // Препринты ИПМ им. М.В. Келдыша. 2018. № 183. 36 с.

  2. Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1987. 840 с.

  3. Абалакин И.В., Бахвалов П.А., Горобец А.В., Дубень А.П., Козубская Т.К. Параллельный программный комплекс NOISEtte для крупномасштабных расчетов задач аэродинамики и аэроакустики // Вычисл. методы и программирование. 2012. Т. 13. № 3. С. 110–125.

  4. Марчук Г.И. Методы расщепления. М.: Наука, 1988.

  5. Strang G. On the construction and comparison of difference schemes // SIAM J. Numer. Anal. 1968. № 5. P. 506–517.

  6. Chertock A., Kurganov A. On splitting-based numerical methods for convection-diffusion equations. In: Numerical Methods for Balance Laws, Quaderni di Matematica, Dept. Math., Seconda Univ. Napoli, Caserta. 2009. № 24. P. 303–343.

  7. Жуков В.Т. О явных методах численного интегрирования для параболических уравнений // Матем. моделирование. 2010. Т. 22. № 10. С. 127–158.

  8. Жуков В.Т., Новикова Н.Д., Феодоритова О.Б. О решении эволюционных уравнений многосеточным и явно-итерационным методами // Ж. вычисл. матем. и матем. физ. 2015. Т. 55. № 8. С. 1305–1319.

  9. Гельфанд И.М., Локуциевский О.В. О разностных схемах для решения уравнения теплопроводности. В кн.: Годунов С.К., Рябенький B.C. Введение в теорию разностных схем. М.: Физматгиз, 1962.

  10. Локуциевский В.О., Локуциевский О.В. О численном решении краевых задач для уравнений параболического типа // Докл. АН СССР. 1986. Т. 291. № 3. С. 540–544.

  11. Жуков В.Т., Забродин А.В., Феодоритова О.Б. Метод решения двумерных уравнений динамики теплопроводного газа в областях сложной формы // Журн. вычисл. матем. и матем. физ. 1993. Т. 33. № 8. С. 1240–1250.

  12. Гантмахер Ф.Р. Теория матриц. М.: Наука, 1966.

  13. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. М.: Наука, 1978.

  14. Лебедев В.И., Финогенов С.А. О порядке выбора итерационных параметров в чебышёвском циклическом методе // Журн. вычисл. матем. и матем. физ. 1971. Т. 11. № 2. С. 425–438.

  15. Люстерник Л.А. О разностных аппроксимациях оператора Лапласа // Успехи матем. наук, 1954. Т. IX. Вып. 2(60). С. 3–66.

  16. Федоренко Р.П. Введение в вычислительную физику. 2-е изд., испр. и доп.– Долгопрудный: “Интеллект”, 2008.

  17. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1977.

  18. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. М.: Мир, 1999.

  19. Лебедев В.И. Как решать явными методами жесткие системы дифференциальных уравнений // В кн.: Вычислительные процессы и системы. Вып. 8 / Под. ред. Г.И. Марчука. М.: Наука, 1991.

  20. Verwer J.G., Sommeijer B.P., Hundsdorfe L.F. RKC time-stepping for advection-diffusion-reaction problems. J. of Computational Physics. 2004. V. 201. № 1. P. 61–79.

  21. Shvedov A.S., Zhukov V.T. Explicit iterative difference schemes for parabolic equations // Russian J. Numer. Anal. Math. Modelling. 1998. V. 13. №. 2. C. 133–148. [In English]

  22. Роуч П. Вычислительная гидродинамика. М.: Мир, 1980.

  23. Численное решение многомерных задач газовой динамики. Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н., Прокопов Г.П. М.: Наука, 1976.

  24. Власенко В.В. Расчетно-теоретические модели высокоскоростных течений газа с горением и детонацией в каналах // Дисс. на соискание ученой степени доктора физ.-мат. наук. Жуковский: ЦАГИ, 2017.

  25. Самарский А.А., Вабищевич П.Н. Численные методы решения задач конвекции-диффузии. М.: ЛИБРОКОМ, 2015.

  26. Полежаев В.И. Численное решение уравнений Навье–Стокса для течения и теплообмена в замкнутой двумерной области // Дисс. ... канд. техн. наук. М.: НИИТП, 1967.

  27. Башкин В.А., Егоров И.В. Численное исследование задач внешней и внутренней аэродинамики. М.: Физматлит, 2013.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал