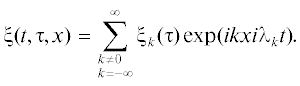1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 2, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 2, стр. 253-266

Асимптотики регулярных решений в задаче Камасса–Холма

С. А. Кащенко *

Ярославский гос. университет им. П.Г. Демидова Национальный исследовательский ядерный университет “МИФИ”
150000 Ярославль, ул. Советская, 14, Россия

* E-mail: kasch@uniyar.ac.ru

Поступила в редакцию 16.07.2019
После доработки 16.07.2019
Принята к публикации 17.10.2019

Полный текст (PDF)

Аннотация

Рассматривается периодическая краевая задача для модернизированного уравнения Камасса–Холма, которое отличается от известного классического уравнения наличием еще нескольких квадратичных слагаемых. Сформулированы три важных условия на коэффициенты уравнения, выполнение которых относит исходное уравнение к уравнениям типа Камасса–Холма. Исследуется вопрос о динамических свойствах так называемых регулярных решений в окрестностях всех состояний равновесия. Для определения “главных” составляющих решений строятся специальные нелинейные краевые задачи. Получены асимптотические формулы для множества периодических решений и конечномерных торов. Изучается вопрос о бесконечномерных торах. Показано, что компактная запись в виде уравнения в частных производных нормализованного уравнения в задаче о таких торах возможна лишь для классического уравнения Камасса–Холма. Приведен асимптотический анализ в случаях, когда один из коэффициентов линейной части уравнения является достаточно малым и когда значение периода в граничных условиях является достаточно большим. Библ. 16.

Ключевые слова: нормальная форма, асимптотическое разложение, периодическое решение, уравнение Камасса–Холма.

1. ВВЕДЕНИЕ

1. Описание краевой задачи. При $x \in ( - \infty ,\infty )$, $t \geqslant {{t}_{0}}$ рассматриваем уравнение

(1)
$\frac{{\partial {v}}}{{\partial t}} = {{a}_{1}}\frac{{{{\partial }^{3}}{v}}}{{\partial t\partial {{x}^{2}}}} + {{a}_{2}}\frac{{\partial {v}}}{{\partial x}} + {{a}_{3}}{v}\frac{{\partial {v}}}{{\partial x}} + {{a}_{4}}\frac{{\partial {v}}}{{\partial x}}\frac{{{{\partial }^{2}}{v}}}{{\partial {{x}^{2}}}} + {{a}_{5}}{v}\frac{{{{\partial }^{3}}{v}}}{{\partial {{x}^{3}}}}.$
В классическом уравнении Камасса–Холма для коэффициентов ${{a}_{j}}$ выполнены равенства
(2)
${{a}_{1}} = 1,\quad {{a}_{3}} = - 3,\quad {{a}_{4}} = 2,\quad {{a}_{5}} = 1.$
В дальнейшем считаем, что ${{a}_{1}} > 0$.

Уравнение (1) исследовалось многими авторами (см. [1]–[9]). Основные результаты посвящены вопросам интегрируемости и нахождению решений.

Вместе с уравнением (1) будем рассматривать $L$-периодические краевые условия

(3)
${v}(t,x + L) \equiv {v}(t,x).$

Сначала сформулируем три важных вывода о решениях краевой задачи (1), (3).

Вывод 1. Каждое стационарное значение функции ${v}$: ${v}(t,x) \equiv d$ $(d \in ( - \infty ,\infty ))$ является состоянием равновесия краевой задачи (1), (3).

Положим в (1)

(4)
${v}(t,x) = u(t,x) + d$
и будем рассматривать все такие функции ${v}(t,x)$, которые при $t \geqslant {{t}_{0}}$, $x \in ( - \infty ,\infty )$ удовлевoряют условию (3) и соотношению

(5)
$M({v}) \equiv d,\quad {\text{где}}\quad M(\varphi (x)) = \frac{1}{L}\int\limits_0^L {\varphi (x)dx} .$

Вывод 2. Из условия $M({v}({{t}_{0}},x)) = d$ следует, что $M({v}(t,x)) \equiv d$ для всех таких значений $t > {{t}_{0}}$, для которых решение ${v}(t,x)$ существует.

Произведем в (1), (3), (5), замену (4) и перейдем к “движущейся” переменной

(6)
$x \to x + d{{a}_{5}}a_{1}^{{ - 1}}t.$

В результате получаем уравнение

(7)
$\frac{{\partial u}}{{\partial t}} = \alpha \frac{{{{\partial }^{3}}u}}{{\partial t\partial {{x}^{2}}}} + \kappa \frac{{\partial u}}{{\partial x}} + au\frac{{\partial u}}{{\partial x}} + b\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + cu\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}}$
с краевыми условиями
(8)
$u(t,x + L) \equiv u(t,x),\quad M(u) = 0.$
В (7) приняты обозначения
$\alpha = {{a}_{1}}(\alpha > 0),\quad \kappa = {{a}_{2}} - d{{a}_{5}}a_{1}^{{ - 1}},\quad a = {{a}_{3}},\quad b = {{a}_{4}},\quad c = {{a}_{5}}.$
Отметим, что в результате другой замены в (1)
$x \to x + ({{a}_{2}} + {{a}_{3}}d)t$
получаем уравнение с третьей пространственной производной в линейном слагаемом
(9)
$\frac{{\partial u}}{{\partial t}} = \alpha \frac{{{{\partial }^{3}}u}}{{\partial t\partial {{x}^{2}}}} + \delta \frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + au\frac{{\partial u}}{{\partial x}} + b\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + cu\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}},$
где $\delta = {{a}_{1}}({{a}_{2}} + d{{a}_{3}})$.

Поставим задачу исследования локального – в достаточно малой окрестности нулевого состояния равновесия – поведения всех решений краевой задачи (7), (8) при каждом $d \in ( - \infty ,\infty )$. Основу асимптотического исследования составляет построение уравнений для главных членов асимптотических представлений решений. Такое представление часто называют нормализацией.

Важную роль играет характер расположения корней ${{\lambda }_{k}}$ характеристического уравнения для линеаризованной в нуле краевой задачи (7), (8): ${{\lambda }_{k}} = i\lambda ({{z}_{k}}),$ где

$\lambda (z) = - \kappa {{(1 + \alpha {{z}^{2}})}^{{ - 1}}}z,\quad {{z}_{k}} = 2\pi k{{L}^{{ - 1}}},\quad k = \pm 1, \pm 2,...\;.$

Вывод 3. При всех значениях параметра $d$ все корни характеристического уравнения являются чисто мнимыми, а значит, в задаче об устойчивости нулевого решения краевой задачи (7), (8) при всех $d \in ( - \infty ,\infty )$ реализуется критический случай бесконечной размерности.

Обозначим через $F(u)$ квадратичное выражение, содержащие величины $u,\;\tfrac{{\partial u}}{{\partial x}},\;\tfrac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}},\;u\tfrac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}}$:

$\begin{gathered} F(u) = {{f}_{1}}{{u}^{2}} + {{f}_{2}}u\frac{{\partial u}}{{\partial x}} + {{f}_{3}}u\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + {{f}_{4}}u\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + {{f}_{5}}\mathop {\left( {\frac{{\partial u}}{{\partial x}}} \right)}\nolimits^2 + {{f}_{6}}\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + \\ \, + {{f}_{7}}\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + {{f}_{8}}\mathop {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}} \right)}\nolimits^2 + {{f}_{9}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + {{f}_{{10}}}\mathop {\left( {\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}}} \right)}\nolimits^2 . \\ \end{gathered} $

Рассмотрим более общую по сравнению с (7) краевую задачу

(10)
$\frac{{\partial u}}{{\partial t}} = \alpha \frac{{{{\partial }^{3}}u}}{{\partial t\partial {{x}^{2}}}} + \kappa \frac{{\partial u}}{{\partial x}} + F(u) - M(F(u)),$
(11)
$u(t,x + L) \equiv u(t,x),\quad M(u) = 0.$
Для этой краевой задачи тоже верны выводы 1 и 2. Потребуем, чтобы для краевой задачи (10), (11) был верен и вывод 3. Произведем в (10), (11) замену (4) и рассмотрим вопрос о корнях ${{\lambda }_{k}}(k = \pm 1, \pm 2,...)$ получающегося характеристического уравнения для линеаризованной в нуле краевой задачи. Для ${{\lambda }_{k}}$ тогда приходим к формуле

${{\lambda }_{k}}\left( {1 + \alpha \mathop {\left( {\frac{{2\pi k}}{{L\alpha }}} \right)}\nolimits^2 } \right) = \kappa 2\pi ik{{L}^{{ - 1}}} + 2{{f}_{1}}d + \frac{{2\pi ikd}}{L}{{f}_{2}} - \left( {\frac{{2\pi k}}{L}} \right)d{{f}_{3}} - {{f}_{4}}di\mathop {\left( {\frac{{2\pi k}}{L}} \right)}\nolimits^3 .$

Согласно выводу 3 из условия $\operatorname{Re} {{\lambda }_{k}} = 0$, $k = \pm 1, \pm 2,...$, вытекает, что ${{f}_{1}} = {{f}_{3}} = 0$.

В ряде задач, например, в задачах об асимптотике периодических по времени решений полезно рассмотреть уравнение, которое отличается от (10) наличием линейных членов со второй и четвертой производными по пространственной переменной и с малым множителем $\mu $:

(12)
$\mu \left( {{{b}_{1}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + {{b}_{2}}\frac{{{{\partial }^{4}}u}}{{\partial {{x}^{4}}}}} \right),\quad {{b}_{2}} < 0,\quad 0 < \mu \ll 1.$
Здесь прослеживаются аналогии в вопросе изучения уравнения Кортевега–де Вриза и Кортевега–де Вриза–Бюргерса (см., например, [10]–[12]).

Итак, после замены (4) и $x \to x + d{{f}_{4}}{{\alpha }^{{ - 1}}}t$ и с учетом выражения (12) приходим к краевой задаче

(13)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} = \alpha \frac{{{{\partial }^{3}}u}}{{\partial t\partial {{x}^{2}}}} + {{\kappa }_{0}}\frac{{\partial u}}{{\partial x}} + {{g}_{1}}u\frac{{\partial u}}{{\partial x}} + {{g}_{2}}u\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + {{g}_{3}}\left( {\mathop {\left( {\frac{{\partial u}}{{\partial x}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{\partial u}}{{\partial x}}} \right)}\nolimits^2 } \right)} \right) + \\ + \;{{g}_{4}}\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + {{g}_{5}}\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + {{g}_{6}}\left( {\mathop {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}} \right)}\nolimits^2 } \right)ght) + {{g}_{7}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + } \right. \\ \, + {{g}_{8}}\left( {\mathop {\left( {\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}}} \right)}\nolimits^2 } \right)} \right) + \mu \left( {{{b}_{1}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + {{b}_{2}}\frac{{{{\partial }^{4}}u}}{{\partial {{x}^{4}}}}} \right). \\ \end{gathered} $
(14)
$u(t,x + L) \equiv u(t,x),\quad M(u) = 0.$
Здесь приняты обозначения

${{\kappa }_{0}} = \kappa + d{{f}_{2}},\quad {{g}_{1}} = {{f}_{2}},\quad {{g}_{2}} = {{f}_{4}},\quad {{g}_{3}} = {{f}_{5}},$
${{g}_{4}} = {{f}_{6}},\quad {{g}_{5}} = {{f}_{7}},\quad {{g}_{6}} = {{f}_{8}},\quad {{g}_{7}} = {{f}_{9}},\quad {{g}_{8}} = {{f}_{{10}}}.$

Для этой краевой задачи можно предложить другую – эквивалентную запись. Сначала введем одно обозначение. Пусть $w(x)$ – есть ($2\pi {\text{/}}L$)-периодические функции с нулевым средним:

$w(x) = \sum\limits_{k = - \infty ,k \ne 0}^\infty \,{{w}_{k}}exp\left( {\frac{{ik2\pi }}{L}x} \right).$
Через $J(w)$ обозначен оператор “интегрирования”
$J(w) = \sum\limits_{k = - \infty ,k \ne 0}^\infty \,\mathop {\left( {i\frac{{2\pi k}}{L}} \right)}\nolimits^{ - 1} {{w}_{k}}exp\left( {\frac{{2\pi ki}}{L}x} \right).$
Отметим, что для произвольной (дифференцируемой) периодической функции $z(x)$ имеем соотношение

(15)
$J\left( {\frac{{\partial z}}{{\partial x}}} \right) = z(x) - M(z(x)).$

Продифференцируем (13) и (14) по $x$ и положим $w = \tfrac{{\partial u}}{{\partial x}}$, т.е. $u = J(w)$. Тогда приходим к уравнению, не содержащему оператор усреднения:

(16)
$\begin{gathered} \frac{{\partial w}}{{\partial t}} = \alpha \frac{{{{\partial }^{3}}w}}{{\partial t\partial {{x}^{2}}}} + {{\kappa }_{0}}\frac{{\partial w}}{{\partial x}} + {{g}_{1}}\left[ {{{w}^{2}} + J(w)\frac{{\partial w}}{{\partial x}}} \right] + {{g}_{2}}\left[ {w\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + J(w)\frac{{{{\partial }^{3}}w}}{{\partial {{x}^{3}}}}} \right] + \\ \, + 2{{g}_{3}}w\frac{{\partial w}}{{\partial x}} + {{g}_{4}}\left[ {\mathop {\left( {\frac{{\partial w}}{{\partial x}}} \right)}\nolimits^2 + w\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}}} \right] + \left[ {\frac{{\partial w}}{{\partial x}}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + w\frac{{{{\partial }^{3}}w}}{{\partial {{x}^{3}}}}} \right] + \\ \, + 2({{g}_{6}} + {{g}_{8}})\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}}\frac{{{{\partial }^{3}}w}}{{\partial {{x}^{3}}}} + {{g}_{7}}\frac{{\partial w}}{{\partial x}}\frac{{{{\partial }^{3}}w}}{{\partial {{x}^{3}}}} + \kappa \left[ {{{b}_{1}}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + {{b}_{2}}\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}}} \right]. \\ \end{gathered} $
Краевые условия имеют вид
(17)
$w(t,x + L) \equiv w(t,x),\quad M(w) = 0.$
Здесь ${{\kappa }_{0}} = \kappa + d({{g}_{1}} - {{g}_{2}}{{\alpha }^{{ - 1}}})$.

Важно отметить, что краевые задачи (13), (14) и (16), (17) зависят от параметра $d \in ( - \infty ,\infty )$ и от “внутреннего” параметра $L \in (0,\infty )$.

Ниже вводится еще один малый параметр $\varepsilon $, который учитывает варьирования значения периода $L$. Предполагаем, что значение ${{L}_{0}} > 0$ как-то фиксировано и для некоторого ${{L}_{1}}$ выполнено равенство

(18)
$L = {{L}_{0}} + \varepsilon {{L}_{1}},\quad 0 < \varepsilon \ll 1.$

В работе рассматриваются так называемые регулярные решения (см. [12]–[14]). Регулярность означает, что эти решения и их производные являются ограниченными по $x \in [0,L]$ функциями при каждом фиксированном $t$. В частности, верно асимптотическое представление

$u(t,x + \varepsilon ) = u(t,x) + \varepsilon u{\text{'}}(t,x) + \frac{1}{2}{{\varepsilon }^{2}}u{\text{''}}(t,x) + ...\;.$

Отметим, что пространственные производные нерегулярных решений могут достигать больших значений при стремлении к нулю малого параметра. Результаты исследования нерегулярных решений существенно отличаются от приводимых ниже. Им будет посвящена отдельная публикация.

Поставим задачу исследования поведения всех решений этих краевых задач из достаточно малой окрестности нулевого состояния равновесия. При условии (18) в разд. 2 изучается асимптотика периодических по $t$ решений и одномерных торов в рассматриваемых краевых задачах. Соответствующие построения можно применить и к рассмотрению асимптотики торов большей размерности. Для бесконечномерных торов методика оказывается неэффективной, поскольку приводит к бесконечной системе нелинейных обыкновенных дифференциальных уравнений, которую, вообще говоря, нельзя упростить.

В связи с этим возникает задача определения таких коэффициентов краевой задачи (13), (14) ((16), (17)), для которых соответствующую бесконечномерную систему удается записать в компактной форме в виде уравнения в частных производных. Решению этой задачи посвящен разд. 3.

Наконец, отметим, что без ограничения общности можно считать, что выполнено условие

(19)
$\alpha = 1.$
Это равенство (при $\alpha > 0$) достигается нормировкой пространственной переменной и очевидными переобозначениями параметров краевой задачи. Возникает, конечно, необходимость асимптотического изучения рассматриваемых краевых задач отдельно при условиях
(20)
$0 < \alpha \ll 1$
и
(21)
$\alpha \gg 1.$
Кроме этого, весьма важно изучение решений в предположении, что значение параметра $L$ в краевых условиях достаточно велико:

(22)
$L \gg 1.$

Этому случаю и случаю (20) посвящен разд. 4. Случай (21) будет изучен в отдельной публикации, посвященной нерегулярным решениям.

2. ПОСТРОЕНИЕ АСИМПТОТИКИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ И ТОРОВ

Во всех приведенных выше краевых задачах фигурирует “внутренний” параметр $L$, входящий в периодические краевые условия. Будем варьировать этот параметр и изучать зависимость от него асимптотики решений.

Фиксируем произвольно ${{L}_{0}} > 0$ и ${{L}_{1}}$, а через $\varepsilon $ обозначим малый положительный параметр. Положим

(23)
$L = {{L}_{0}} + \varepsilon {{L}_{1}},\quad 0 \leqslant \varepsilon \leqslant 1.$

Еще один малый параметр $\mu $, фигурирующий в (13) и (16), удобно представить в виде

(24)
$\mu = \delta \varepsilon \quad (\delta > 0).$

Остановимся для определенности на рассмотрении при условии (19) краевой задачи (13), (14). Для того чтобы период по пространственной переменной у решений не зависел от $\varepsilon $, в (13), (14) произведем замену

(25)
$x \to (1 + \varepsilon {{L}_{1}}L_{0}^{{ - 1}})x.$

В результате приходим к краевой задаче

(26)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} = \alpha (\varepsilon )\frac{{{{\partial }^{3}}u}}{{\partial t\partial {{x}^{2}}}} + \kappa (\varepsilon )\frac{{\partial u}}{{\partial x}} + {{g}_{1}}(\varepsilon )u\frac{{\partial u}}{{\partial x}} + {{g}_{2}}(\varepsilon )u\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + {{g}_{3}}(\varepsilon )\left[ {\mathop {\left( {\frac{{\partial u}}{{\partial x}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{\partial u}}{{\partial x}}} \right)}\nolimits^2 } \right)} \right] + \\ \, + {{g}_{4}}(\varepsilon )\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + {{g}_{5}}(\varepsilon )\frac{{\partial u}}{{lx}}\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + {{g}_{6}}(\varepsilon )\left[ {\mathop {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}} \right)}\nolimits^2 } \right)} \right] + {{g}_{7}}(\varepsilon )\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + \\ \, + {{g}_{8}}\left[ {\mathop {\left( {\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}}} \right)}\nolimits^2 } \right)} \right] + \varepsilon \left[ {{{b}_{1}}(\varepsilon )\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + {{b}_{2}}(\varepsilon )\frac{{{{\partial }^{4}}u}}{{\partial {{x}^{4}}}}} \right], \\ \end{gathered} $
(27)
$u(t,x + {{L}_{0}}) = u(t,x) < M(u) = 0.$
Здесь приняты обозначения

$\alpha (\varepsilon ) = (1 + \varepsilon {{L}_{1}}L_{0}^{{ - 1}}) = (1 - 2\varepsilon {{L}_{1}}L_{0}^{{ - 1}} + {\text{O}}({{\varepsilon }^{2}})),$
$\kappa (\varepsilon ) = \kappa (1 - \varepsilon {{L}_{1}}L_{0}^{{ - 1}} + {\text{O}}({{\varepsilon }^{2}})),\quad {{g}_{j}}(\varepsilon ) = {{g}_{j}}(1 + {\text{O}}(\varepsilon )),\quad (j = 1,...\,,8),$
${{b}_{j}}(\varepsilon ) = \delta {{b}_{j}}(1 + {\text{O}}(\varepsilon ))\quad (j = 1,2).$

2.1. Построение асимптотики периодических решений

Фиксируем произвольно целое ${{k}_{0}} > 0$ и положим ${{z}_{0}} = 2\pi {{k}_{0}}L_{0}^{{ - 1}}$. Отметим, что выполнены условия

(28)
$\lambda (2{{z}_{0}}) \ne z\lambda ({{z}_{0}})\quad {\text{и}}\quad \lambda (3{{z}_{0}}) \ne 3\lambda ({{z}_{0}}).$

Линеаризованная в нуле краевая задача (26), (27) имеет, в частности, периодические решения

$\xi exp\left( {i{{z}_{0}}x + i\lambda ({{z}_{0}})t} \right) + \overline \xi exp\left( { - i{{z}_{0}}x - i\lambda ({{z}_{0}})t} \right),$
где $\xi $ – произвольная комплексная постоянная.

Введем в рассмотрение формальный ряд

(29)
$u = {{\varepsilon }^{{1/2}}}[\xi (\tau )exp[i{{z}_{0}}x + i\lambda ({{z}_{0}})t] + \overline \xi (\tau )exp( - i{{z}_{0}}x - i\lambda ({{z}_{0}})t)] + \varepsilon {{u}_{2}}(t,\tau ,x) + {{\varepsilon }^{{3/2}}}{{u}_{3}}(t,\tau ,x) + ...\;.$
Здесь $\tau = \varepsilon t$ – “медленное” время, функции ${{u}_{j}}(t,\tau ,x)$ являются $2\pi {{\lambda }^{{ - 1}}}({{z}_{0}})$-периодическими по $t$ и $2\pi z_{0}^{{ - 1}} = {{L}_{0}}$ – периодическими по $x$. Подставим (29) в (26) и будем приравнивать коэффициенты при одинаковых степенях $\varepsilon $. Тогда для определения ${{u}_{2}}(t,\tau ,x)$ получаем уравнение
$\frac{{\partial {{u}_{2}}}}{{\partial t}} = \frac{{{{\partial }^{3}}{{u}_{2}}}}{{\partial t\partial {{x}^{2}}}} + {{\kappa }_{0}}\frac{{\partial {{u}_{2}}}}{{\partial x}} + A{{\xi }^{2}}exp(2i{{z}_{0}}x + 2i\lambda ({{z}_{0}})t) + \overline A {{\bar {\xi }}^{2}}exp( - 2i{{z}_{0}} - 2i\lambda ({{z}_{0}})t),$
в котором
$A = i{{z}_{0}}{{g}_{1}} - iz_{0}^{3}{{g}_{2}} - z_{0}^{2}{{g}_{3}} - iz_{0}^{3}{{g}_{4}} + ({{g}_{5}} + {{g}_{6}})z_{0}^{4} - iz_{0}^{5}{{g}_{7}} - z_{0}^{6}{{g}_{8}}.$
Отсюда находим, что
(30)
${{u}_{2}}(t,\tau ,x) = B{{\xi }^{2}}exp(2i{{z}_{0}}x + 2i\lambda ({{z}_{0}})t) + \overline B \overline \xi exp( - 2i{{z}_{0}}x - 2i\lambda ({{z}_{0}})t),$
где

$B = {{(6{{\kappa }_{0}}z_{0}^{3})}^{{ - 1}}}(1 + z_{0}^{2})A.$

На следующем шаге, собирая в формальном тождестве коэффициенты при ${{\varepsilon }^{{3/2}}}$, получаем уравнение для ${{u}_{3}}(t,\tau ,x)$. Из условия его разрешимости в указанном классе функций приходим к уравнению для определения $\xi (\tau )$:

(31)
$\frac{{d\xi }}{{d\tau }} = \beta \xi + \delta \xi {{\xi }^{2}}.$
Для коэффициентов $\beta $ и $\delta $ имеем равенства
$\beta = {{[1 + z_{0}^{2}]}^{{ - 1}}}(\delta {{b}_{2}}z_{0}^{4} - \delta {{b}_{1}}z_{0}^{2} - i{{z}_{0}}{{\kappa }_{0}}{{L}_{1}}L_{0}^{{ - 1}} + 2iz_{0}^{2}\lambda ({{z}_{0}}){{L}_{1}}L_{0}^{{ - 1}}),$
$\delta = [1 + z_{0}^{2}]B[i{{z}_{0}}{{g}_{1}} - i7z_{0}^{3}{{g}_{2}} + 4z_{0}^{4}{{g}_{3}} + 2iz_{0}^{3}{{g}_{4}} - z_{0}^{4}(6{{g}_{5}} - 8{{g}_{6}}) + 4iz_{0}^{5}{{g}_{7}} + 16z_{0}^{6}{{g}_{8}}].$
Сформулируем итоговое утверждение.

Теорема 1. Пусть ${{\xi }_{0}}(\tau )$ – ограниченное при $\tau \to \infty $ решение уравнения (29). Тогда краевая задача (26), (27) имеет асимптотическое по невязке с точностью до O(${{\varepsilon }^{{3/2}}}$) периодическое решение ${{u}_{0}}(t,\tau ,x)$, для которого

$\begin{gathered} {{u}_{0}}(t,\tau ,x) = {{\varepsilon }^{{1/2}}}[{{\xi }_{0}}(\tau )exp(i{{z}_{0}}x + i\lambda ({{z}_{0}})t) + {{{\bar {\xi }}}_{0}}(\tau )exp( - i{{z}_{0}}x - i\lambda ({{z}_{0}})t)] + \\ \, + \varepsilon [B\xi _{0}^{2}(\tau )exp(2i{{z}_{0}}x + 2i\lambda ({{z}_{0}})t) + \overline B \bar {\xi }_{0}^{2}(\tau )exp( - 2i{{z}_{0}}x - 2i\lambda ({{z}_{0}})t)]. \\ \end{gathered} $

Сделаем ряд выводов. Сначала отметим, что при $\delta = {{g}_{3}} = {{g}_{5}} = {{g}_{6}} = {{g}_{8}} = 0$ коэффициенты в уравнении (31) являются чисто мнимыми. Поэтому все его решения периодические (негрубые). Это дает основание говорить о том, что в малой окрестности нуля краевая задача (26), (27) имеет континуальное семейство асимптотических по невязке решений. Их асимптотика определяется по решениям $\xi (\tau )$ уравнения (31) из формулы (29).

Уравнение (31) интегрируется в явном виде при любых значениях коэффициентов $\beta $ и $\delta $. Например, при условии $\operatorname{Re} \beta \cdot \operatorname{Re} \delta < 0$ это уравнение имеет устойчивый цикл

$\xi (\tau ) = {{\rho }_{0}}\exp (i{{\varphi }_{0}}\tau ),\quad {{\rho }_{0}} = {{( - \operatorname{Re} \beta \cdot {{(\operatorname{Re} \delta )}^{{ - 1}}})}^{{1/2}}},\quad {{\varphi }_{0}} = \operatorname{Im} \beta + {{\rho }^{2}}\operatorname{Im} \delta .$
Краевая задача (26), (27) тогда имеет периодическое решение
${{u}_{0}}(t,x,\varepsilon ) = 2{{\varepsilon }^{{1/2}}}{{\rho }_{0}}cos(i{{z}_{0}}x + \lambda ({{z}_{0}}) + \varepsilon {{\varphi }_{0}} + O({{\varepsilon }^{2}})) + O(\varepsilon ).$
Отметим, что устойчивость решения ${{\xi }_{0}}(\tau )$ уравнения (31) – лишь необходимое условие устойчивости решения ${{u}_{0}}(t,x,\varepsilon )$ в (26), (27).

Обратим внимание, что произвольно фиксированный (континуальный) параметр ${{L}_{1}}$ и параметр ${{k}_{0}}$, принимающий целые значения, являются “внутренними” параметрами: само уравнение (26) от них не зависит. Поэтому формулы (29) дают представление для довольно богатого множества асимптотических по невязке решений в (26), (27).

2.2. Построение 2-мерных торов

Фиксируем произвольно два различных целых положительных значения ${{k}_{1}}$ и ${{k}_{2}}$. Рассмотрим формальный ряд

(32)
$\begin{gathered} u = {{\varepsilon }^{{1/2}}}[\xi (\tau )exp(i{{z}_{1}}x + i{{\lambda }_{1}}t) + \overline \xi (\tau )exp( - i{{z}_{1}}x - i{{\lambda }_{1}}) + \eta (\tau )exp(i{{z}_{2}}x + i{{\lambda }_{2}}t) + \\ \, + \bar {\eta }(\tau )exp( - i{{z}_{2}}x - i{{\lambda }_{2}}t)] + \varepsilon {{u}_{2}}(t,\tau ,x) + {{\varepsilon }^{{3/2}}}{{u}_{3}}(t,\tau ,x) + \ldots ,\quad \tau = \varepsilon t, \\ \end{gathered} $
где ${{u}_{j}}(t,\tau ,x)$ суть $2\pi L_{0}^{{ - 1}}$-периодичны по $x$ и почти периодичны по $t$, ${{z}_{j}} = 2\pi {{k}_{j}}L_{0}^{{ - 1}}$, ${{\lambda }_{j}} = \lambda ({{z}_{j}})$. Подставим (32) в (26). Производя стандартные действия, сначала определяем функцию ${{u}_{2}}(t,\tau ,x)$. Затем, собирая коэффициенты при ${{\varepsilon }^{{3/2}}}$, учитывая дополнительно некоторые соотношения типа общности положения (аналогичные (28)), приходим к уравнению для ${{u}_{3}}(t,\tau ,x)$. Из условия его разрешимости получаем систему уравнений относительно комплексных величин $\xi (\tau )$ и $\eta (\tau )$:
(33)
$\begin{gathered} \dot {\xi } = {{{\tilde {B}}}_{1}}\xi + \xi [{{D}_{1}}{{\xi }^{2}} + {{D}_{2}}{{\eta }^{2}}], \\ \dot {\eta } = {{{\tilde {B}}}_{2}}\eta + \eta [{{D}_{3}}{{\xi }^{2}} + {{D}_{4}}{{\eta }^{2}}]. \\ \end{gathered} $
Явные формулы для коэффициентов (33) довольно громоздкие, поэтому здесь их не приводим. Отметим лишь, что при $\delta = {{g}_{3}} = {{g}_{5}} = {{g}_{6}} = {{g}_{8}} = 0$ все коэффициенты в (33) – чисто мнимые. Это означает что все решения (33) – негрубые двумерные торы. Из (32) вытекает, что и рассматриваемая краевая задача (26), (27) имеет континуальное семейство асимптотических по невязке двумерных торов с соответствующей асимптотикой.

2.3. О более общих случаях

По аналогии с (32) можно рассмотреть вопрос об асимптотике 3, 4-мерных торов. В общем случае формальные выражения имеют вид

(34)
$u = {{\varepsilon }^{{1/2}}}\sum\limits_{k \ne 0\;k = - \infty }^\infty \,{{\xi }_{k}}(\tau )exp(i{{z}_{k}}x + i{{\lambda }_{k}}t) + \varepsilon {{u}_{2}}(t,\tau ,x) + {{\varepsilon }^{{3/2}}}{{u}_{3}}(t,\tau ,x) + \ldots ({{\xi }_{{ - k}}} = {{\bar {\xi }}_{k}}(\tau )),$
${{\lambda }_{k}} = \lambda ({{z}_{k}})$, ${{z}_{k}} = 2\pi kL_{0}^{{ - 1}}$. Действуя по аналогии с предыдущими построениями, для определения всех величин ${{\xi }_{k}}(\tau )$ получаем бесконечную систему обыкновенных дифференциальных уравнений (ОДУ) и по ее решениям формулируем выводы об асимптотических по невязке решениях исходной краевой задачи (26), (27). Отметим, что эту бесконечную систему ОДУ, вообще говоря, не удается записать в компактной форме. В следующем разделе будет получено такое уравнение вида (26), которое допускает компактное представление для уравнения первого приближения.

3. АСИМПТОТИКА БЕСКОНЕЧНОМЕРНЫХ ТОРОВ

Остановимся подробнее на схеме построения асимптотики решений этой краевой задачи, базирующейся на формальном ряде (34).

3.1. Построение функций ${{u}_{2}}(t,\tau ,x)$

Ниже для простоты будем предполагать, что $\delta = 0$, значение $L$ не зависит от малого параметра $\varepsilon $, а варьируется только параметр $\kappa :\kappa = {{\kappa }_{0}} + \varepsilon {{\kappa }_{1}}$, $0 < \varepsilon \ll 1$. Таким образом, рассматривается краевая задача

(35)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} = \alpha \frac{{{{\partial }^{3}}u}}{{\partial t\partial {{x}^{2}}}} + ({{\kappa }_{0}} + \varepsilon {{\kappa }_{1}})\frac{{\partial u}}{{\partial x}} + {{g}_{1}}u\frac{{\partial u}}{{\partial x}} + {{g}_{2}}u\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + {{g}_{3}}\left( {\mathop {\left( {\frac{{\partial u}}{{\partial x}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{\partial u}}{{\partial x}}} \right)}\nolimits^2 } \right)} \right) + {{g}_{4}}\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + \\ \, + {{g}_{5}}\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + {{g}_{6}}\left( {\mathop {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}} \right)}\nolimits^2 } \right)} \right) + {{g}_{7}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + {{g}_{8}}\left( {\mathop {\left( {\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}}} \right)}\nolimits^2 } \right)} \right), \\ \end{gathered} $
(36)
$u(t,x + L) \equiv u(t,x),\quad M(u) = 0.$

Положим здесь

(37)
Отметим, для примера, что запись
(38)
$\sum\limits_{k = - \infty ,k \ne 0}^\infty \,\sum\limits_{p = - \infty \;k + p \ne 0,p \ne 0}^\infty \,{{(k + p)}^{s}}{{k}^{m}}{{p}^{n}}{{\xi }_{k}}{{\xi }_{p}}$
при целых неотрицательных $m$ и $n$ эквивалентны выражению
(39)
$\frac{{{{\partial }^{s}}}}{{\partial {{x}^{s}}}}\left( {\left( {\frac{{{{\partial }^{m}}\xi }}{{\partial {{x}^{m}}}}} \right)\left( {\frac{{{{\partial }^{n}}\xi }}{{\partial {{x}^{n}}}}} \right)} \right)$
при целом $s \geqslant 0$ и выражению
${{J}^{{ - s}}}\left( {\left( {\frac{{{{\partial }^{m}}\xi }}{{\partial {{x}^{m}}}}} \right)\left( {\frac{{{{\partial }^{n}}\xi }}{{\partial {{x}^{n}}}}} \right)} \right)$
при целых $s < 0$ и $m \ne n$.

Подставим (34) в (26). Тогда для ${{u}_{2}}(t,\tau ,x)$ приходим к уравнению

(40)
$\frac{{\partial {{u}_{2}}}}{{\partial t}} = \frac{{{{\partial }^{3}}{{u}_{2}}}}{{\partial t\partial {{x}^{2}}}} + {{\kappa }_{0}}\frac{{\partial {{u}_{2}}}}{{\partial x}} + \sum\limits_{k = - \infty }^\infty \,\sum\limits_{p = - \infty }^\infty \,R({{z}_{k}},{{z}_{p}}){{\xi }_{k}}(\tau ){{\xi }_{p}}(\tau )exp[i({{z}_{k}} + {{z}_{p}})x + i(\lambda ({{z}_{k}}) + \lambda ({{z}_{p}}))t],$
в котором

$\begin{gathered} R(k,p) = \frac{{i{{g}_{1}}}}{2}(k + p) - \frac{{i{{g}_{2}}}}{2}({{k}^{3}} + {{p}^{3}}) - {{g}_{3}}kp - \frac{{i{{g}_{4}}}}{2}kp(k + p) + \\ \, + \frac{{{{g}_{5}}}}{2}kp({{k}^{2}} + {{p}^{2}}) + {{g}_{6}}{{k}^{2}}{{p}^{2}} + \frac{{i{{g}_{7}}}}{2}{{k}^{2}}{{p}^{2}}(k + p) - {{g}_{8}}{{k}^{3}}{{p}^{3}}. \\ \end{gathered} $

Функцию ${{u}_{2}}(t,\tau ,x)$ ищем в виде

(41)
${{u}_{2}} = \sum\limits_{k = - \infty }^\infty \,\sum\limits_{p = - \infty }^\infty \,{{u}_{{kp}}}{{\xi }_{k}}{{\xi }_{p}}exp[i({{z}_{k}} + {{z}_{p}})x + i(\lambda ({{z}_{k}}) + \lambda ({{z}_{p}}))].$
Из (40) тогда получаем, что
${{u}_{{kp}}} = {{\xi }_{k}}{{\xi }_{p}}R({{z}_{k}},{{z}_{p}}){{N}^{{ - 1}}}({{z}_{k}},{{z}_{p}}),$
где

(42)
$N(k,p) = i\kappa (k + p)kp[3 + ({{k}^{2}} + {{p}^{2}} + kp)]{{[(1 + {{k}^{2}})(1 + {{p}^{2}})]}^{{ - 1}}}.$

Поставим задачу определения всех таких коэффициентов ${{g}_{i}}$, при которых функцию ${{u}_{2}}(t,\tau ,x)$ из (41) можно записать, не используя бесконечное суммирование, а используя только производные и интегралы от $\xi (\tau ,x)$ и от их квадратичных произведений. Ниже удобно нормировать функцию $u(t,x)$ так, чтобы выполнялось равенство

(43)
${{g}_{2}} = 1,$
а коэффициент ${{g}_{6}}$ переобозначить через $g:{{g}_{6}} = g$.

Сформулируем основной результат

Теорема 2. Функцию ${{u}_{2}}(t,x)$ можно выразить через $\xi (\tau ,x)$, не используя бесконечные суммирования, в том и только в том случае, когда выполнены равенства

(44)
${{g}_{7}} = {{g}_{8}} = 0,$
(45)
${{g}_{1}} = {{g}_{2}} = - 3,\quad {{g}_{4}} = 2,$
(46)
${{g}_{3}} = - g,\quad {{g}_{5}} = 2g,\quad {{g}_{6}} = g.$

Доказательство. Положим в (40) $kp = x$ и $(k + p) = y$. Выражение $N(k,p)$ можно тогда записать в виде

$N(x,y) = i\kappa xy{{(1 + {{y}^{2}} - 2x + {{x}^{2}})}^{{ - 1}}}(3 - x + {{y}^{2}}),$
а выражение $R(k,p)$ имеет вид $P(x,y)$, где

$P(x,y) = \frac{i}{2}{{g}_{1}}y - \frac{i}{2}{{g}_{2}}y({{y}^{2}} - 3x) - {{g}_{3}}x - \frac{i}{2}{{g}_{4}}xy + \frac{1}{2}{{g}_{5}}x({{y}^{2}} - 2x) + {{g}_{6}}{{x}^{2}} + \frac{i}{2}{{g}_{7}}{{x}^{2}}y - {{g}_{8}}{{x}^{3}}.$

Согласно (36) и (37), условие представления ${{u}_{2}}$ через функции $\xi $ и через производные и “интегралы” от нее состоит в том, чтобы выражение $P(x,y)$ было представимо в виде

$P(x,y) = {{x}^{{{{s}_{1}}}}}{{y}^{{{{s}_{2}}}}}[3 - x + {{y}^{2}}].$
Тем самым при $x = 3 + {{y}^{2}}$ функция ${{P}_{0}}(y) = P(3 + {{y}^{2}},y)$ должна тождественно обращаться в нуль. Тем самым из равенства нулю тождественно многочлена 6-й степени относительно $y$
$\begin{gathered} \frac{i}{2}{{g}_{1}}y + \frac{i}{2}{{g}_{2}}y(2{{y}^{2}} + 9) - {{g}_{3}}({{y}^{2}} + 3) - \frac{i}{2}{{g}_{4}}y({{y}^{2}} + 3) - \\ \, - \frac{i}{2}{{g}_{5}}({{y}^{2}} + 3)({{y}^{2}} + 6) + {{g}_{6}}{{({{y}^{2}} + 3)}^{2}} + \frac{i}{2}{{g}_{7}}y({{y}^{2}} + 3) - {{g}_{8}}({{y}^{2}} + 3) \equiv 0 \\ \end{gathered} $
следует, что коэффициенты при всех степенях этой функции нулевые. Тем самым приходим к равенствам (43)–(46). Теорема доказана.

В порядке обобщения теоремы 2 заметим, что при условии $g = 0$ на основании равенств (43)–(46) получаем классическое уравнение Камасса–Холма, а если бы вместо (43) принять условие ${{g}_{2}} = 0$, то имеем уравнение

(47)
$\frac{{\partial u}}{{\partial t}} = \frac{{{{\partial }^{3}}u}}{{\partial t\partial {{x}^{2}}}} + \kappa \frac{{\partial u}}{{\partial x}} - 3g\left[ {\mathop {\left( {\frac{{\partial u}}{{\partial x}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{\partial u}}{{\partial x}}} \right)}\nolimits^2 } \right)} \right] + 2g\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + g\left[ {\mathop {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}} \right)}\nolimits^2 } \right)} \right].$
После дифференцирования по $x$ в (47) и переобозначения $\tfrac{{\partial u}}{{\partial x}} \to u$ снова приходим к уравнению Камасса–Холма.

В общем случае из теоремы 2 получаем уравнение (без учета слагаемого с множителем $\kappa $)

(48)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} = \frac{{{{\partial }^{3}}u}}{{\partial t\partial {{x}^{2}}}} + \kappa \frac{{\partial u}}{{\partial x}} - 3u\frac{{\partial u}}{{\partial x}} + 2u\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} - 3g\left[ {\mathop {\left( {\frac{{\partial u}}{{\partial x}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{\partial u}}{{\partial x}}} \right)}\nolimits^2 } \right)} \right] + \\ \, + 2\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + 2g\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + g\left[ {\mathop {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}} \right)}\nolimits^2 } \right)} \right]. \\ \end{gathered} $

Приведем явный вид функции ${{u}_{2}}(t,x)$ при условиях (44)–(46). В случае ${{g}_{0}} = 0$, т.е. для уравнения Камасса–Холма, имеет равенство ${{u}_{2}}(t,\tau ,x) = U(t,\tau ,x)$, где

(49)
$U(t,\tau ,x) = - \frac{\kappa }{2}\left[ {\mathop {\left( {J(\xi )} \right)}\nolimits^2 - M(\mathop {(J(\xi ))}\nolimits^2 ) + \mathop {\left( {\frac{{\partial \xi }}{{\partial x}}} \right)}\nolimits^2 - M\left( {\mathop {\left( {\frac{{\partial \xi }}{{\partial x}}} \right)}\nolimits^2 } \right) + 2J(\xi )\frac{{\partial \xi }}{{\partial x}}} \right].$
Соответственно при ${{g}_{2}} = 0$ имеем
(50)
${{u}_{2}}(t,x) = gJ\left( {U(t,\tau ,x)} \right),$
а при условии (38) и $g \ne 0$ получаем

(51)
${{u}_{2}}(t,x) = U(t,\tau ,x) + gJ\left( {U(t,\tau ,x)} \right).$

3.2. Построение нормализованного уравнения

На следующем шаге, подставляя ряд (34) в (26) соберем коэффициенты при ${{\varepsilon }^{{3/2}}}$. В результате с учетом (48) проходим к уравнению

(52)
$\frac{{\partial {{u}_{3}}}}{{\partial t}} - \frac{{{{\partial }^{3}}{{u}_{3}}}}{{\partial t\partial {{x}^{2}}}} - \kappa \frac{{\partial {{u}_{3}}}}{{\partial x}} = - \frac{1}{2}\frac{\partial }{{\partial x}}\left[ {3{{u}_{2}}\frac{{\partial \xi }}{{\partial x}} + 16\frac{{\partial \xi }}{{\partial x}}\frac{{\partial {{u}_{2}}}}{{lx}} - 2\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}(\xi {{u}_{2}})} \right].$
Ограничимся рассмотрением случая, когда $g = 0$, т.е. классического уравнения Камасса–Холма. При $g \ne 0$ новых сложностей не возникает, только соответствующие построения более громоздкие.

Критерий разрешимости (52) относительно ${{u}_{3}}(t,\tau ,x)$ в указанном классе функций состоит в отсутствии в правой части гармоник вида $exp(ikx + i{{\lambda }_{k}}t)$. Отсюда, учитывая формулы (49) и (37), для величин ${{\xi }_{k}}(\tau )$ приходим к бесконечной системе обыкновенных дифференциальных уравнений

(53)
$\frac{{d{{\xi }_{k}}}}{{d\tau }} = {{\Phi }_{k}}( \ldots ,{{\xi }_{{ - 2}}},{{\xi }_{{ - 1}}},{{\xi }_{1}},{{\xi }_{2}}, \ldots ),\quad l = \pm 1, \pm 2, \ldots .$
Основной результат состоит в том, что эту систему можно записать в компактной форме в виде специальной краевой задачи. Чтобы показать это, сначала введем несколько обозначений. Положим
(54)
$z(\tau ,x) = \sum\limits_{k = - \infty ,k \ne 0}^\infty \,{{\xi }_{k}}(\tau )exp(ikx),\quad {{\xi }_{{ - k}}} = {{\bar {\xi }}_{k}},$
где коэффициенты Фурье ${{\xi }_{k}}(\tau )$ – те же, что и в (37) и (53). Далее, через $K(z)$ обозначим бесконечномерный вектор ($ \ldots ,{{\xi }_{{ - 1}}}exp( - ix),{{\xi }_{1}}exp(ix),{{\xi }_{2}}exp(ix), \ldots $). Произведение двух бесконечномерных векторов $K(z)$ и $\overline K (z)$ – покоординатное, т.е. $K(z)\bar {K}(z) = ( \ldots ,\xi _{1}^{2},\xi _{1}^{2},\xi _{2}^{2}, \ldots )$. Тогда для скалярного произведения ($K(z)\overline K (z),K(z)$) верна формула
$(K(z)\bar {K}(z),K(z)) = \sum\limits_{k = - \infty ,k \ne 0}^\infty \,{{\xi }_{k}}\xi _{k}^{2}exp(ikx).$
Введем в рассмотрение краевую задачу
(55)
$\frac{{\partial z}}{{\partial \tau }} - \frac{{{{\partial }^{3}}z}}{{\partial \tau \partial {{x}^{2}}}} = {{\kappa }^{{ - 1}}}[{{\kappa }_{1}}(z) + {{\kappa }_{2}}(z)],$
(56)
$z(\tau ,x + L) \equiv z(\tau ,x),\quad M(z) = 0,$
где

$\begin{gathered} {{\kappa }_{1}}(z) = \frac{1}{2}M\left( {(J({{z}^{2}}) - M({{z}^{2}})) + \mathop {\left( {\frac{{\partial z}}{{\partial x}}} \right)}\nolimits^2 } \right)\frac{{\partial z}}{{\partial x}} + 8M({{z}^{2}})\left( {\frac{{\partial z}}{{\partial x}} - \frac{{{{\partial }^{3}}z}}{{\partial {{x}^{3}}}}} \right) - \\ \, - 16M\left( {\mathop {\left( {\frac{{\partial z}}{{\partial x}}} \right)}\nolimits^2 } \right)\left( {\frac{{\partial z}}{{\partial x}} + \frac{{{{\partial }^{3}}z}}{{\partial {{x}^{3}}}}} \right) - M\left( {\left( {J({{z}^{2}}) - \mathop {\left( {\frac{{\partial z}}{{\partial x}}} \right)}\nolimits^2 - {{z}^{2}}} \right)} \right)\frac{{{{\partial }^{3}}z}}{{\partial {{x}^{3}}}}, \\ \end{gathered} $
$\begin{gathered} {{\kappa }_{2}}(z) = i\left\{ {\frac{1}{4}(JK(z),K(z)\bar {K}(z) + \frac{1}{4}\left( {\frac{{{{\partial }^{3}}K(z)}}{{\partial {{x}^{3}}}},K(z)\bar {K}(z)} \right) - } \right. \\ \left. { - \;8\left( {\frac{{{{\partial }^{3}}K(z)}}{{\partial {{x}^{3}}}} - \frac{{{{\partial }^{5}}K(z)}}{{\partial {{x}^{5}}}},K(z)\bar {K}(z)} \right) + \frac{1}{2}\left( {\frac{{\partial K(z)}}{{\partial x}} + \frac{{{{\partial }^{5}}K(z)}}{{\partial {{x}^{5}}}},K(z)\bar {K}(z} \right)} \right\}. \\ \end{gathered} $

Будем говорить, что уравнение из (55) эквивалентно бесконечной системе разностных уравнений (53), если при подстановке в (55) ряда Фурье функции $z(\tau ,x)$ для коэффициентов Фурье получаем систему (53).

Из приведенных выше построений вытекает

Теорема 3. Уравнение (55) эквивалентно системе (53).

Сделаем важное замечание. Уравнение (55) можно существенно упростить, “убрав” слагаемые, содержащие функции $K(z)$. Для этого в системе (51) произведем замены

(57)
${{\xi }_{k}}(\tau ) = {{w}_{k}}(\tau )exp\left( {i{{{(\kappa (1 + {{k}^{2}}))}}^{{ - 1}}}C(k\int\limits_0^\tau {{{{\left| {{{\xi }_{k}}(\tau )} \right|}}^{2}}} d\tau } \right),$
где
$C(k) = - \frac{1}{4}\left( {{{k}^{{ - 1}}} - \frac{1}{2}k - 31{{k}^{3}} - 34{{k}^{5}}} \right).$
Тогда для величин ${{w}_{k}}(\tau )$ получим бесконечную систему, которой эквивалентно уравнение
(58)
$\frac{{\partial w}}{{\partial \tau }} - \frac{{{{\partial }^{3}}w}}{{\partial \tau \partial {{x}^{2}}}} - {{\kappa }_{1}}\frac{{\partial w}}{{\partial x}} + {{\kappa }^{{ - 1}}}{{\kappa }_{1}}(w)$
с краевыми условиями

(59)
$w(\tau ,x + L) \equiv w(\tau ,x),\quad M(w) = 0.$

4. АСИМПТОТИКА РЕГУЛЯРНЫХ РЕШЕНИЙ ПРИ УСЛОВИЯХ $\alpha \ll 1$ И ПРИ $L \gg 1$

Обратим внимание, что с помощью функций $w(\tau ,x)$ определяются, согласно формуле (34), коэффициенты Фурье ${{\xi }_{k}}(\tau )$ функции $u(t,x,\varepsilon )$, а не сама эта функция.

В этом разделе коротко остановимся на построении нормализованных уравнений для двух случаев: когда $0 < \alpha \ll 1$ и когда $L \gg 1$.

4.1. Здесь предполагаем, что коэффициент $\alpha $ является малым параметром: $\alpha = \varepsilon $ и $0 < \varepsilon \ll 1$. Формально при $\varepsilon = 0$ главная часть уравнения (7) имеет вид

(60)
$\frac{{\partial u}}{{\partial t}} = \kappa \frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + au\frac{{\partial u}}{{\partial x}} + b\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + c\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}}.$
Для того, чтобы (60) действительно являлось главной частью (7), необходимо выполнение условия регулярности. Оно состоит в том, что при каждом из рассматриваемых значений $\varepsilon $-периодические по $x$ функции ${{\partial }^{n}}u{\text{/}}\partial {{x}^{n}}$ являются ограниченными при $\varepsilon \to 0$. Тем самым выражение $\varepsilon {{\partial }^{n}}u{\text{/}}\partial {{x}^{n}}$ $(n = 1,2, \cdots )$ есть $O(\varepsilon )$ при $\varepsilon \to 0$.

Учитывая условие регулярности и формулу (60), из (7) приходим к более точной, порядка $O(\varepsilon )$, записи уравнения (7)

(61)
$\frac{{\partial u}}{{\partial t}} = \kappa \frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + \ldots + \varepsilon \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}\left( {\kappa \frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + \ldots } \right) + \ldots \;.$
Формально асимптотический ряд для правой части (61) можно получить и из условия регулярности, и из выражения
$\frac{{\partial u}}{{\partial t}} = \mathop {\left( {1 + \varepsilon \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}} \right)}\nolimits^{ - 1} \left[ {\kappa \frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + \ldots } \right],$
$\mathop {\left( {1 + \varepsilon \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}} \right)}\nolimits^{ - 1} = 1 - \varepsilon \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{1}{2}{{\varepsilon }^{2}}\frac{{{{\partial }^{4}}}}{{\partial {{x}^{4}}}} - \frac{1}{6}{{\varepsilon }^{3}}\frac{{{{\partial }^{6}}}}{{\partial {{x}^{6}}}} + \ldots \;.$
Уравнение (60) лишь последним слагаемым отличается от одной из разновидностей классического уравнений Кортевега–де Вриза (см., например [10]–[12]). В [13]–[16] исследовались асимптотические свойства решений обобщенного уравнения Кортевега–де Вриза с периодическими краевыми условиями. Кратко остановимся на этих результатах применительно к уравнению (61) с добавлением в его правую часть последних слагаемых, соответствующих правой части (9):
(62)
$\frac{{\partial u}}{{\partial t}} = \kappa \frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + au\frac{{\partial u}}{{\partial x}} + b\frac{{\partial u}}{{\partial x}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + cu\frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}} + \varepsilon \delta \left[ {{{b}_{1}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + {{b}_{2}}\frac{{{{\partial }^{4}}u}}{{\partial {{x}^{4}}}}} \right] + \varepsilon \kappa \frac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}},$
(63)
$u(t,x + L) \equiv u(t,x),\quad M(u) = 0.$
Корни ${{\lambda }_{k}}$ характеристического уравнения для линеаризованной в нуле краевой задачи (62), (63) с точностью O($\varepsilon $) имеют вид
${{\lambda }_{k}} = - i{{k}^{3}},\quad k = \pm 1, \pm 2, \cdots .$
Фиксируем произвольно ${{k}_{0}} \ne 0$, как и в предыдущем разделе подставим в (62) формальное выражение
(64)
$\begin{gathered} u = {{\varepsilon }^{{1/2}}}[\xi (\tau )exp(2i{{k}_{0}}x - ik_{0}^{3}t) + \bar {\xi }(\tau )exp( - i{{k}_{0}}x + ik_{0}^{3}t)] + \\ + \;\varepsilon [Aexp(2i{{k}_{0}}x - 2ik_{0}^{3}t) + \bar {A}exp( - 2i{{k}_{0}}x + 2ik_{0}^{3}t)] + {{\varepsilon }^{{3/2}}}{{u}_{3}}(t,\tau ,x) + \ldots , \\ \end{gathered} $
где $\tau = \varepsilon t$, зависимость от $t$ и $x$ функции ${{u}_{3}}(t,\tau ,x)$ периодическая. Для коэффициента $A$ получаем выражение
$A = {{\xi }^{2}}(\tau ){{(6\kappa k_{0}^{3})}^{{ - 1}}}[{{k}_{0}}a - (b + c)k_{0}^{3} - i{{a}_{0}}].$
Из условия разрешимости уравнения для ${{u}_{3}}(t,\tau ,x)$ имеем равенство
(65)
$\frac{{d\xi }}{{d\tau }} = {{A}_{1}}\xi + {{A}_{2}}\xi {{\left| \xi \right|}^{2}},$
в котором

${{A}_{1}} = - \delta {{b}_{1}}k_{0}^{2} + \delta {{b}_{2}}k_{0}^{4} - i\kappa k_{0}^{3},$
${{A}_{2}} = A[ia + 6ik_{0}^{3}b - 7ik_{0}^{3}c].$

И здесь при $\delta = 0$ и ${{a}_{0}} = 0$ все коэффициенты в (65) являются чисто мнимыми, а значит все асимптотические по невязке решения (62), (63) согласно (64) тоже периодические. При $\delta \ne 0$ речь может идти об одном периодическом решении.

Как и выше, можно рассмотреть вопрос о построении асимптотики конечномерных асимптотических по невязке торов. Более интересен вопрос о бесконечномерных торах. В отличие от уравнения (7), здесь удается получить компактную запись системы уравнений, которая играет роль нормальной формы. Покажем это.

Рассмотрим формальный ряд

(66)
$u = {{\varepsilon }^{{1/2}}}\left[ {\sum\limits_{k = - \infty ,k \ne 0}^\infty \,{{\xi }_{k}}(\tau )exp(ikx - i{{k}^{3}}t)} \right] + \varepsilon {{u}_{2}}(t,\tau .x) + {{\varepsilon }^{{3/2}}}{{u}_{3}}(t,\tau ,x) + \ldots ,$
где $\tau = \varepsilon t$, а зависимость от $t$ и $x$ периодическая, а для ${{u}_{1}}(t,\tau ,x)$ имеем формулу
${{u}_{1}}(t,\tau ,x) = \sum\limits_{k = - \infty ,k \ne 0}^\infty \,{{\xi }_{k}}(\tau )exp(ikx - i{{k}^{3}}t).$
Подставим его в (62) и будем приравнивать коэффициенты при одинаковых степенях $\varepsilon $. На первом шаге получаем верное тождество (для ${{u}_{1}}(t,\tau ,x)$). На втором шаге приходим к уравнению для ${{u}_{2}}(t,\tau ,x)$:

(67)
$\frac{{\partial {{u}_{2}}}}{{\partial t}} = \kappa \frac{{{{\partial }^{3}}{{u}_{2}}}}{{\partial {{x}^{3}}}} + \frac{1}{2}a\frac{\partial }{{\partial x}}u_{1}^{2} + \frac{1}{2}b\frac{\partial }{{\partial x}}\mathop {\left( {\frac{{\partial {{u}_{1}}}}{{\partial x}}} \right)}\nolimits^2 + \frac{1}{2}c\frac{\partial }{{\partial x}}\left[ {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}(u_{1}^{2}) - 3\mathop {\left( {\frac{{\partial {{u}_{1}}}}{{\partial x}}} \right)}\nolimits^2 } \right].$

Это уравнение разрешимо в указанном классе функций при выполнении условия равенства нулю коэффициентов при всех гармониках вида $exp(ikx - i\kappa {{k}^{3}}t)$ в его правой части:

${{u}_{2}} = - \frac{i}{{3\kappa }}\left\{ {\frac{a}{2}({{{(J({{u}_{2}}))}}^{2}} - M({{{(J({{u}_{1}}))}}^{2}}) + \frac{1}{2}b(b - 9c)(u_{1}^{2} - M(u_{1}^{2})) + \left. {\frac{1}{2}c\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}({{{(J({{u}_{2}}))}}^{2}})} \right\}} \right..$

На следующем шаге соберем коэффициенты при ${{\varepsilon }^{{3/2}}}$. В результате получим уравнение для определения ${{u}_{3}}(t,\tau ,x)$:

(68)
$\begin{gathered} \frac{{\partial {{u}_{3}}}}{{\partial t}} - \kappa \frac{{{{\partial }^{3}}{{u}_{3}}}}{{\partial t\partial {{x}^{2}}}} = - \frac{{\partial {{u}_{1}}}}{{\partial \tau }} + \delta \left[ {{{b}_{1}}\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{x}^{2}}}} + {{b}_{2}}\frac{{{{\partial }^{4}}{{u}_{1}}}}{{\partial {{x}^{4}}}}} \right] + \kappa \frac{{{{\partial }^{5}}{{u}_{1}}}}{{\partial {{x}^{5}}}} + \Phi ({{u}_{1}},{{u}_{2}}), \\ {{u}_{3}}(t,\tau ,x + 2\pi ) \equiv {{u}_{1}}(t,\tau ,x), \\ \end{gathered} $
где

$\Phi ({{u}_{1}},{{u}_{2}}) * \frac{\partial }{{\partial x}}({{u}_{1}}{{u}_{2}}) + 2b\frac{\partial }{{\partial x}}\left( {\frac{{\partial {{u}_{1}}}}{{\partial x}}\frac{{\partial {{u}_{2}}}}{{\partial x}}} \right) + 2c\left( {{{u}_{1}}\frac{{{{\partial }^{3}}{{u}_{2}}}}{{\partial {{x}^{3}}}} + {{u}_{2}}\frac{{{{\partial }^{3}}{{u}_{1}}}}{{\partial {{x}^{3}}}}} \right).$

Эта система допускает компактную запись подобно тому, как согласно теореме 3 систему (52) удалось записать в компактной форме (54). Соответствующее выражение для функции

$w(\tau ,x) = \sum\limits_{k \ne 0\;k = - \infty }^\infty \,{{\xi }_{k}}(\tau )exp(ikx)$
не сложное, но достаточно громоздкое. Линейной части в (68) отвечает для $w(\tau ,x)$ выражение
$\frac{{\partial w}}{{\partial \tau }} = \kappa \frac{{{{\partial }^{5}}w}}{{\partial {{x}^{5}}}} + \delta \left[ {{{b}_{1}}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + {{b}_{2}}\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}}} \right],$
а для нелинейной части ограничимся здесь только тем, что приведем один (в некотором смысле – основной) фрагмент соответствующего выражения в нормализованном уравнении, полученном из (68). Так выражению $u_{1}^{3}$, входящему в функцию $\Phi ({{u}_{1}},{{u}_{2}})$, отвечает выражение

$6\xi M({{\xi }^{2}}) - 3(K(\xi )\bar {K}(\xi ),K(\xi )).$

4.2. Асимптотика решений при условии достаточно больших значений параметра $L$.

Кратко остановимся на исследовании регулярных решений в случае, когда

(69)
$L = {{\varepsilon }^{{ - 1}}}\quad {\text{и}}\quad 0 < \varepsilon \ll 1.$

Рассматривается модернизированное уравнение Камасса–Холма, которое отличается от формы записи в (10) тем, что вместо слагаемого $\kappa \tfrac{{\partial u}}{{\partial x}}$ имеем (как и в (9)) слагаемое $\kappa \tfrac{{{{\partial }^{3}}u}}{{\partial {{x}^{3}}}}$. Предполагается, конечно, что выполнены условия ${{f}_{1}} = {{f}_{3}} = 0$ на коэффициенты функции $F(u)$.

Произведем формализующие замены

$x \to Lx,\quad \tau = {{\varepsilon }^{2}}t\quad {\text{и}}\quad u = {{\varepsilon }^{2}}{v}.$
В результате приходим к краевой задаче
(70)
$\frac{{\partial {v}}}{{\partial \tau }} = \kappa \frac{{{{\partial }^{3}}{v}}}{{\partial {{x}^{3}}}} + {{f}_{2}}{v}\frac{{\partial {v}}}{{\partial x}} + O({{\varepsilon }^{2}}),$
(71)
${v}(\tau ,x + 1) \equiv {v}(\tau ,x).$
Осталось заметить, что с точностью до величины $O({{\varepsilon }^{2}})$ уравнение (70) совпадает с классическим уравнением Кортевега–де Вриза. Результаты изучения асимптотики регулярных периодических решений и торов для уравнения Кортевега–де Вриза приведены в [15].

ВЫВОДЫ

Представлен класс модернизированных уравнений Камасса–Холма, который существенно обобщает классическое уравнение Камасса–Холма и сохраняет ряд его основополагающих свойств. Эти уравнения с периодическими ограниченными условиями имеют однопараметрическое семейство состояний равновесия, в окрестности каждого из которых реализуется критический случай бесконечной размерности в задаче об устойчивости стационаров.

Рассмотрено поведение так называемых регулярных решений в малых окрестностях состояний равновесия. Приведены асимптотические формулы для семейств периодических по времени решений и конечномерных торов.

Исследован вопрос о построении в окрестности состояний равновесия нормализованных уравнений, играющих роль нормальных форм. Эти нормальные формы представляют собой бесконечно мерные системы специальных нелинейных обыкновенных дифференциальных уравнений. Решена задача о компактной записи таких бесконечномерных систем в виде нелинейного уравнения в частных производных. В частности, показано, что такая запись возможна только для классического уравнения Камасса–Холма.

Изучены асимптотические свойства решений при условиях, когда коэффициент $\alpha $ в (7) является достаточно малым параметром или значение периода $L$ в граничных условиях (8) является достаточно большим. В обоих случаях исходная краевая задача сводится в главном к уравнению Кортевега–де Вриза.

Отметим, что построенные выше нормализованные уравнения, как правило, обладают тем свойством, что в окрестности их состояний равновесия тоже реализуется критический в задаче об устойчивости случай бесконечной размерности. Поэтому можно запустить процесс повторной нормализации.

Список литературы

  1. Fokas A.S., Fuchssteiner B. On the structure of symplectic operators and hereditary symmetries // Lettere al nuvo cimento. 1980. № 28. P. 299–303.

  2. Fokas A.S., Fuchssteiner B. Symplectic structure. Their Bäcklund transformations and hereditary symmetries // Phisica D. 1981. № 4. P. 47–66.

  3. Camassa R., Holm D.D. An integrable shallow water equation with Peaked solitons // Phys, Rev. Lett. 1993. № 71. P. 1661–1664.

  4. Camassa R., Hyman J., Holm D. A new integrable shallow water equation // Advances In Applied Mechanics. 1994. V. 31. P. 1–31.

  5. Lakshmanan M. Integrable nonlinear wave equations and possible connections to tsunami dynamics // Tsunami and Nonlinear Waves. Springer. 2007.

  6. Johnson R. Camassa-Holm, Korteweg-de Vries and related models for water waves // J. of Fluid Mechanics 2002. V. 455. P. 63–82.

  7. Constantine A., Lannes D. The hydrodynamical relevance of the Camassa-Holm and degaperis procesi equation // Archive for Rational Mechanics and Analysis. 2009. V. 192. P. 165–186.

  8. Dias F., Milewski P. On the fully-nonlinear shallow-water generalized serre equations // Physics Letters A. 2010 V. 374. P. 1049–1053.

  9. Bhatt R., Mikhailov A.V. On the inconsistency of the Camassa-Holm model with the shallow water theory. arXiv:1010.1932v1.

  10. Korteweg D.J., de Vries G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves // Phil. Mag. 1895. V. 5. № 39. P. 422–443.

  11. Kudryashov N.A. On “new travelling wave solutions” of the KdV and KdV-Burgers equotions // Commun. Nonlinear Sci. Numer. Simul. 2009. V. 14. № 5. P. 1891–1900.

  12. Кудряшов Н.А. Методы нелинейной математической физики. М.: “Интеллект”. 2010.

  13. Кащенко С.А. Регулярные и нерегулярные решения в задаче о дислокациях в твердом теле // Теор. и матем. физ. 2018. Т. 195. № 3. С. 362–380.

  14. Kashchenko S.A. Dynamics of a delay logistic equation with slowly varying coefficients // Comput. Math. and Math. Phys. 2018. V. 58. № 12. P. 1926–1936.

  15. Кащенко С.А. Бифуркации в уравнении Курамото–Сивашинского // Теор. и матем. физ. 2017. Т. 192. № 1. С. 23–40.

  16. Кащенко С.А., Преображенская М.М. Бифуркации в обобщенном уравнении Кортевега-де Вриза // Известия в. уч. з. Математика. 2018. № 2. С. 54–68.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал