Журнал вычислительной математики и математической физики, 2020, T. 60, № 3, стр. 391-404

1. ПОСТАНОВКА ЗАДАЧИ

В последние два десятилетия вышел ряд публикаций, в которых исследуются свойства вырожденного квадратичного функционала с линейными связями в виде обыкновенных дифференциальных уравнений (ОДУ). Под вырожденным функционалом понимается функционал, у которого усиленное условие Лежандра (УЛ) тождественно нарушено на отрезке задания интеграла [1]–[4] или некотором его подмножестве [6]–[8]. Обычно из необходимых условий экстремума (уравнений, вытекающих из принципа максимума) находится вектор-функция, которую затем проверяют на выполнение достаточных условий, например, условий выпуклости. В данной работе авторы, опираясь на достижения последних лет в теории вырожденных систем ОДУ, применяют другую схему исследования.

Рассмотрим квадратичный функционал

со связями где $A \equiv A(t)$ есть $(m \times m)$-матрица, $B \equiv B(t)$ есть $(n \times m)$-матрица, $C \equiv C(t)$ есть $(n \times n)$-матрица, ${{A}_{1}} \equiv {{A}_{1}}(t)$, ${{A}_{0}} \equiv {{A}_{1}}(t)$ суть $(n \times n)$-матрицы, $H \equiv H(t)$ есть $(n \times m)$-матрицa, $x \equiv x(t)$ – гладкая на $T$ $n$-мерная вектор-функция состояния системы, $\dot {x} \equiv dx{\text{/}}dt$, $u \equiv u(t)$ есть $m$-мерная вектор-функция управления, $\left\langle {.,.} \right\rangle $ – скалярное произведение в пространствах ${{{\mathbf{R}}}^{n}}$, $n = 1,2,\; \ldots $ .

Множество допустимых управлений имеет вид

где число $q$ определено ниже, ${{u}^{{(i)}}}(t) = {{(d{\text{/}}dt)}^{i}}u(t)$, ${{u}^{{(0)}}}(t) = u(t)$. Предполагается, что и входные данные в формулах (1), (2) обладают гладкостью, необходимой при дальнейших рассуждениях, a матрицы $A$, $C$ в формуле (1) симметричные. Для любой квадратной матрицы $\tilde {G}$ справедливо соотношение $\left\langle {\tilde {G}y,y} \right\rangle = \left\langle {0.5(\tilde {G} + {{{\tilde {G}}}^{{\text{т}}}})y,y} \right\rangle $ $\forall y \in {{{\mathbf{R}}}^{\nu }}$, где ${\text{т}}$ – символ транспонирования, предположение о симметричности не уменьшает общности. При выполнении условий (5) произвольно малым изменениям функционала $\Phi (u)$ могут соответствовать произвольно большие изменения его аргумента (см., например, [9]).

В ряде работ (см., например, [1]–[3]) предполагается выпуклость подынтегрального выражения в (1), что эквивалентно выполнению соотношения

Авторы данной статьи отказываются от этого условия и исследуют задачу общего вида.

Замечание. 1. Для упрощения записи указание зависимости от $t$ иногда опускается, если это не вызывает путаницы. Включения $V(t) \in {{{\mathbf{C}}}^{i}}(T)$, $i > 1$, где $V(t)$ – матрица или вектор-функция, означают, что все производные ее элементов непрерывны до порядка $i$ включительно. Непрерывность обозначаем в виде $V(t) \in {\mathbf{C}}(T)$. Запись $V(t) \in {{{\mathbf{L}}}_{2}}(T),$ означает, что элементы $V(t)$ являются функциями, суммируемыми с квадратом на $T$.

В работе используются нормы $n$-мерного вектора $b = {{({{b}_{1}},{{b}_{2}},\; \ldots ,\;{{b}_{n}})}^{{\text{т}}}} \in {{{\mathbf{R}}}^{n}}$, и вектор-функции $b(t) = {{({{b}_{1}}(t),{{b}_{2}}(t),\; \ldots ,\;{{b}_{n}}(t))}^{{\text{т}}}}$, $t \in T$, вычисляемые по правилам

Основными задачами работы являются следующие:

1) поиск условий, при выполнении которых $\Phi (u) \geqslant 0$ $\forall u \in {\mathbf{U}}$;

2) поиск условий, при которых из неравенства $\Phi (u) \leqslant \varepsilon ,$ вытекают соотношения:

где $\varepsilon \in [0,{{\varepsilon }_{0}}]$, ${{\varepsilon }_{0}}$ – некоторое положительное число, $\kappa = {\text{const}} > 0$.

Иначе говоря, ищутся условия, при выполнении которых малым изменениям функционала $\Phi (u)$ соответствуют малые изменения управления или траектории.

2. СВЕДЕНИЯ ИЗ ТЕОРИИ ВЫРОЖДЕННЫХ СИСТЕМ УРАВНЕНИЙ

Ниже нам потребуются сведения о системах уравнений вида

где ${{A}_{i}}(t)$ есть $(n \times n)$-матрицы, $\lambda $ – скалярный параметр, ${\text{K}}(t,s)$ есть $(n \times n)$-матрица, определенная в области $T \times T$, $x(t)$, $z(t)$, $f(t)$ – искомые и известная вектор-функции, соответственно, ${{x}^{{(i)}}}(t) = {{(d{\text{/}}dt)}^{i}}x(t)$, ${{x}^{{(0)}}}(t) = x(t)$, Заданы начальные условия где ${{a}_{i}},{{b}_{i}}$ – заданные векторы из ${{{\mathbf{R}}}^{n}}$.

Под решением систем (6), (7) мы будем понимать любые $k$-раз дифференцируемые на $T$ вектор-функции $x(t)$, $z(t)$, которые обращают системы (6), (7) в тождество на $T$ при подстановке. Если вектор-функции $x(t)$, $z(t)$, являются решениями и удовлетворяют условиям (9), то они являются решением задач (6), (7), (9).

Системы вида (6), удовлетворяющие условию (8), называют в настоящее время дифференциально-алгебраическими уравнениями (ДАУ) [5]. Используются также термины “сингулярные системы” [12], “алгебро-дифференциальные системы” (АДС) [13], “дескрипторные системы” [14].

Определение 1 (см., например, [11]).  Полуобратной  матрицей к $(m \times n)$-матрице $M(t)$, $t \in T$, называется $(n \times m)$-матрица ${{M}^{ - }}(t)$, удовлетворяющая для любых $t \in T$ уравнению $M(t){{M}^{ - }}(t)M(t) = M(t).$

Полуобратная матрица определена для любого $t \in T$ и любой $(m \times n)$-матрицы $M(t)$ (см., например, [12]). Если матрица $M(t)$ квадратная и неособенная, то ${{M}^{{ - 1}}}(t) = {{M}^{ - }}(t)$. Согласно [11], существует матрица ${{M}^{ - }}(t) \in {{{\mathbf{C}}}^{q}}(T)$, если $M(t) \in {{{\mathbf{C}}}^{q}}(T),$ $\operatorname{rank} M(t) = r = {\text{const}}$ $\forall t \in T$. Если $\operatorname{rank} M(t) \ne {\text{const}}$, $t \in T$, то хотя один элемент любой матрицы ${{M}^{ - }}(t)$ имеет разрыв II рода на $T$. Матрица ${{M}^{ - }}(t)$ определена неединственным образом (ее частным случаем является псевдообратная матрица ${{M}^{ + }}(t)$).

Система линейных уравнений $M(t)\chi = \vartheta (t)$, $\operatorname{rank} M(t) = r = {\text{const}}$ $\forall t \in T$ разрешима тогда и только тогда, когда выполнено условие $[{{E}_{m}} - M(t){{M}^{ - }}(t)]\vartheta (t) = 0$, $t \in T$, и ее решение имеет вид

где $\omega (t)$ – произвольная вектор-функция (см. [11, с. 40], [12, с. 33]).

Из формулы Лейбница для дифференцирования произведений вытекает формула

где $M \equiv M(t)$, $F \equiv F(t)$ некоторые матрицы подходящей размерности из ${{{\mathbf{C}}}^{i}}(T)$, суть биномиальные коэффициенты.

Введем следующие понятия.

Определение 2. Пространство решений (ПР) однородного ДАУ (6) конечномерно, если все произведения ${{\tilde {X}}_{d}}(t)c$, где ${{\tilde {X}}_{d}}(t)$ – $(n \times d)$-матрица из ${{{\mathbf{C}}}^{k}}(T)$, c – вектор произвольных постоянных, являются решениями ДАУ (6), и на отрезке $T$ нет других решений.

Минимально возможное значение целочисленного параметра $d$ называется размерностью ПР системы (6). ПР однородного ДАУ (6) бесконечномерно, если оно содержит бесконечное количество линейно-независимых решений.

Подчеркнем, что основным условием, налагаемым на матрицу ${{\tilde {X}}_{d}}(t)$, является требование: при минимальном $d$ различным $c \in {{{\mathbf{R}}}^{d}}$ соответствуют различные решения (см. пример 2).

Определение 3. Система (6) имеет решение типа Коши на отрезке $T$, если она разрешима для любой вектор-функции $f(t) \in {{{\mathbf{C}}}^{{kn}}}(T)$ и ее решения представимы в виде линейной комбинации

где ${{X}_{d}}(t)$ есть $(n \times d)$-матрица из ${{{\mathbf{C}}}^{k}}(T)$, со свойством $\operatorname{rank} {{{\text{d}}}_{{k - 1}}}[{{X}_{d}}(t)] = d$ $\forall t \in T$, ${{{\text{d}}}_{{k - 1}}}[.]$ – оператор из формул (11), c – вектор произвольных постоянных, $\psi (t)$ – вектор-функция со свойством ${{\Lambda }_{k}}\psi (t) = f(t)$, $t \in T$, и на любом подотрезке $[{{\alpha }_{0}},{{\beta }_{0}}] \subseteq T$ нет решений, отличных от $x(t,c)$.

Определение 4. Если существуют операторы

где ${{L}_{j}}(t)$, ${{R}_{j}}(t)$ суть $(n \times n)$-матрицы из ${\mathbf{C}}(T)$, обладающие свойствами где $y \equiv y(t) \in {{{\mathbf{C}}}^{{\nu + k}}}(T)$ – произвольная вектор-функция, $\nu = {\text{\{ }}l\;{\text{или}}\;r{\text{\} }}$, ${{\tilde {A}}_{i}}(t)$, ${{\tilde {A}}_{i}}(t)$ суть $(n \times n)$-некоторые матрицы из ${\mathbf{C}}(T)$, $\det {{\tilde {A}}_{k}}(t) \ne 0$, $\det {{\bar {A}}_{k}}(t) \ne 0$ $\forall t \in T$, то они называются левым и правым регуляризирующими операторами (ЛРО и ПРО) для системы (6), а наименьшие возможные $l$, $r$ называются ее индексами (левым и правым).

Определение 5. Если существует оператор ${{\tilde {\Omega }}_{l}}$, для которого определен ЛРО, обладающий свойством

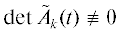где , $t \in T$, то изолированные точки ${{t}_{\nu }} \in T$, в которых $\det {{\tilde {A}}_{k}}({{t}_{\nu }}) = 0$, называются особыми точками системы (6).

Пример 1. Пусть имеем ДАУ

где $x = {{({{x}_{1}}{{x}_{2}})}^{{\text{т}}}}$, $f = {{({{f}_{1}}{{f}_{2}})}^{{\text{т}}}}$, $z(t) = sin(\omega (t))$, $\gamma (t)$, $\omega (t)$ – некоторые заданные функции из ${{{\mathbf{C}}}^{1}}(T).$ Ранг ${{A}_{1}}(t)$ может произвольно меняться на $T$. Здесь ${{x}_{2}} = - t{{x}_{1}} + {{f}_{2}}(t)$. Из первого уравнения следует: $w(t){{x}_{1}} = {{f}_{1}}(t) - z(t)f_{2}^{{(1)}}(t)$, где ${\mathbf{w}}(t) = \gamma (t) - z(t)$. Тогда имеем Если $\left| {\gamma (t)} \right| > 1$ $\forall t \in T$, $f \in {{{\mathbf{C}}}^{2}}(T)$, то вектор-функция $x \equiv x(t)$ является решением типа Коши ДАУ. Индекс $l = 2$, размерность ПР $d = 0$. В качестве ЛРО можно принять оператор ${{\Omega }_{2}} = (d{\text{/}}dt){{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Lambda } }_{1}}$. Любая точка ${{t}_{ * }} \in T$, ${\mathbf{w}}({{t}_{ * }}) = 0$ является особой: существуют $f \in {{{\mathbf{C}}}^{2}}(T)$ такие, что норма решения $\mathop {\left\| {x(t)} \right\|}\nolimits_{{\mathbf{C}}(T)} \to \infty $ при $t \to {{t}_{ * }}$.

При ${\mathbf{w}}(t) = 0$ $\forall t \in T$ подстановкой проверяется, что любая вектор-функция вида ${{( - y(t)\;\,ty(t))}^{{\text{т}}}}$, где $y(t)$ – произвольная функция из ${{{\mathbf{C}}}^{1}}(T)$, является решением системы, а вектор-функции ${{\phi }_{j}} = {{( - {{t}^{j}}\;{{t}^{{j + 1}}})}^{{\text{т}}}}$, $j = 0,1,\; \cdots $, образуют базис в ПР: ${\text{dim}}\;{\text{ker}}{{\Lambda }_{1}} = \infty $.

Пример 2. Пусть имеем ДАУ

где $x = {{({{x}_{1}}{{x}_{2}})}^{{\text{т}}}}$, $f = {{({{f}_{1}}{{f}_{2}})}^{{\text{т}}}}$, ${\text{rank}}\;A(t) = {\text{const}} = 1$ $\forall t \in T$. Если $\lambda \ne 2$, то система имеет особую точку в смысле определения 5, где Элементарными преобразованиями система расщепляется на дифференциальное и алгебраическое уравнения На любом отрезке ${{T}_{0}} = [{{\alpha }_{0}},{{\beta }_{0}}] \subset T$, не содержащем нуля, оператор ${{\tilde {\Omega }}_{l}}$ является ЛРО и на ${{T}_{0}}$ определено решение типа Коши (размерность ПР $d = 1$), исходя из формул (14).

При $\lambda = 2$ решение типа Коши нашего ДАУ существует и единственно на $T$:

где $f \in {{{\mathbf{C}}}^{2}}(T)$. ДАУ имеет индекс $l = 2$. Размерность ПР $d = 0$.

Изучим случай $\lambda \ne 2$ подробнее. Однородная система (14) при $\lambda = 1$ имеет вид $ - t{{\dot {x}}_{1}}(t) + 2{{x}_{1}}(t) = 0$, $ - t{{x}_{1}}(t) + {{x}_{2}}(t) = 0$, $t \in T$. Подстановкой проверяется, что

В определении 2 имеем

Через особую точку $t = 0,$ при начальном условии $x(0) = 0$ проходит бесконечное число решений, но фиксированным ${{c}_{1}}$, ${{c}_{2}}$ соответствует только одно решение.

Итак, ЛРО для линейного ДАУ не существует в двух случаях: 1) ПР однородной системы (6) бесконечномерно; 2) на $T$ существуют особые точки (см. примеры 1, 2). Изменения рангов матриц, задающих ДАУ в общем случае не дает информации о наличии на $T$ особых точек и структуре ПР. Здесь может быть полезным такое понятие.

Определение 6. Ненулевой многочлен $\det [\lambda {\text{A}}(t) + {\text{B}}(t)]$, $t \in T$, где ${\text{A}}(t)$, ${\text{B}}(t)$ – квадратные матрицы, удовлетворяет критерию “ранг-степень” на $T$, если:

$1)\;r = max{\text{\{ }}\operatorname{rank} {\text{A}}(t),\;t \in T{\text{\} }};\quad 2)\det [\lambda {\text{A}}(t) + {\text{B}}(t)] = {{{\mathbf{a}}}_{0}}(t){{\lambda }^{r}} + \ldots ,\quad {{{\mathbf{a}}}_{0}}(t) \ne 0\quad \forall t \in T.$

Условия 1),  2)  эквивалентны  равенствам:  $\operatorname{rank} {\text{A}}(t) = \deg \det [\lambda {\text{A}}(t) + {\text{B}}(t)] = r = {\text{const}}$, $t \in T.$ Этот критерий для многочлена $det[\lambda {{A}_{k}}(t) + {{A}_{{k - 1}}}(t)]$, $t \in T$, выполнен тогда и только тогда, когда ДАУ (6) имеет индекс $l = 1$ [20] или существует решение типа Коши, где $d = kr + (k - 1)(n - r) = (k - 1)n + r$. Любая изолированная точка $\mu \in T:{{{\mathbf{a}}}_{0}}(\mu ) = 0$, является особой точкой (см., пример 2 при $\lambda \ne 2$ и общий случай в [11, с. 133]).

Для вычисления ЛРО нам потребуются ниже следующие понятия.

Определение 7. Совокупность самой системы (6) и ее производных до порядка $i$ включительно: ${{{\text{d}}}_{i}}[{{\Lambda }_{k}}x - f] = 0$, $t \in T$, где ${{{\text{d}}}_{i}}[.]$ – оператор из формул (11), называется $i$-продолженной системой (6).

С использованием формулы (11) $i$-продолженную систему запишем в виде соотношения

где ${\mathbf{A}} = \left( {\begin{array}{*{20}{c}} {{{A}_{k}}}&{{{A}_{{k - 1}}}}& \ldots &{{{A}_{0}}} \end{array}} \right)$, матрица ${{D}_{i}}[{\mathbf{A}}(t)]$ имеет размерность $[(i + 1)n \times (i + k + 1)n]$, нулевые матрицы ${{O}_{j}},\;{{\tilde {O}}_{j}}$ имеют размерности $[(i + 1)n \times jn]$, $[(i + 1)n \times (k - j)n]$, $j = \overline {0,k} $, соответственно, ${{{\text{x}}}_{{i + k}}} = {{{\text{d}}}_{{i + k}}}[x]$, ${{\Gamma }_{i}}[{\mathbf{A}}(t)]$ – блочно-треугольная квадратная матрица с блоками ${{A}_{k}}(t)$ на диагонали.

Далее нам потребуется сводка результатов (теоремы 1, 2, леммы 4, 5) из работы [16].

Теорема 1. Пусть в ДАУ (6): 1) ${{A}_{i}}(t) \in {{{\mathbf{C}}}^{{\text{m}}}}(T)$, $i = \overline {0,k} $, ${\text{m}} = max{\text{\{ }}(k - 1)n + {\text{r}} + 1,\;2l{\text{\} }}$, $f(t) \in {{{\mathbf{C}}}^{l}}(T)$, $r = max{\text{\{ }}\operatorname{rank} {{A}_{k}}(t),\;t \in T{\text{\} }}$; 2) индекс (6) равен $l$. Тогда:

1. существует решение типа Коши и в формуле (12)

где $K(t,s)$, ${{C}_{j}}(t)$ – некоторые $(n \times n)$-матрицы, $t \in T$, $(t,s) \in T \times T$ (при достаточной гладкости матриц ${{A}_{i}}(t)$ из существования решения типа Коши на $T$ следует существование ЛРО);

2. если в формуле (12) $d = 0$, то

3. начиная с некоторого $i = l$, справедливы равенства

где ${{Z}_{{21}}}(t)$, ${{Z}_{{22}}}(t)$ – некоторые блоки подходящей размерности, причем первые $n$ строк матрицы $\Gamma _{l}^{ - }[{\mathbf{A}}(t)]$, разбитые на $(n \times n)$-блоки, можно принять в качестве коэффициентов ЛРО.

4. при выполнении условия $l \leqslant k$ система (7) разрешима при произвольном $\lambda $ и ее общее решение имеет структуру вида $z(t,c) = {{Z}_{d}}(t)c + \phi (t)$, $t \in T$, где ${{Z}_{d}}(t) = ({{E}_{n}} + \lambda {\mathbf{W}}){{X}_{d}}(t)$, $\phi (t) = ({{E}_{n}} + \lambda {\mathbf{W}})\psi (t)$, ${\mathbf{W}}$ – некоторый оператор Вольтерра.

Поясним смысл условия $l \leqslant k$ в пятом пункте утверждения теоремы 1.

Пример 3. Рассмотрим две системы уравнений:

где $A = \left( {\begin{array}{*{20}{c}} 0&1 \\ 0&0 \end{array}} \right)$. ${{A}^{2}} = 0$. Используя формулу $x = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Lambda } }_{1}}f = [{{E}_{2}} - A(d{\text{/}}dt)]f$ из примера 2, получим уравнение $z + \lambda {{\hat {\Lambda }}_{1}}[Vz] = {{\hat {\Lambda }}_{1}}f$, из которого следуют соотношения Итак, при невыполнении условия $l \leqslant k$ возмущение оператора ДАУ оператором Вольтерра может приводить к существенным изменениям свойств исходного оператора. Например, при $\lambda = 1$ оператор ${{\Lambda }_{1}} + \lambda V$ имеет бесконечномерное ПР и в нем можно выбрать базис вида ${{\phi }_{j}} = {{( - {{(t - \alpha )}^{j}},{{(t - \alpha )}^{{j + 1}}}{\text{/}}(j + 1))}^{{\text{т}}}}$, $j = 0,1,2,\; \ldots $, где $({{\Lambda }_{1}} + V){{\phi }_{j}} = 0,$ $t \in T$.

Приведем очевидные условия разрешимости начальных задач.

Лемма 1. Начальные задачи (6), (9) в условиях теоремы 1 имеют единственное решение $x(t)$, $z(t) \in {{{\mathbf{C}}}^{k}}(T)$ тогда и только тогда, когда разрешимы системы

где ${{\hat {X}}_{{k - 1}}}(t) = {{{\text{d}}}_{{k - 1}}}[{{X}_{d}}(t)]$, ${{\psi }_{{k - 1}}}(t) = {{{\text{d}}}_{{k - 1}}}[\psi (t)]$, ${{\hat {Z}}_{{k - 1}}}(t) = {{{\text{d}}}_{{k - 1}}}[{{Z}_{d}}(t)]$, ${{\phi }_{{k - 1}}}(t) = {{{\text{d}}}_{{k - 1}}}[\phi (t)],$ относительно вектора $c$.

Замечание 2. Если ДАУ (6) имеет решение типа Коши, то сохраняются важнейшие свойства линейных систем ОДУ в нормальной форме (форме Коши): 1) множества решений на отрезках $T$ и ${{T}_{0}} = [{{\alpha }_{0}},{{\beta }_{0}}] \subset T$ совпадают (отсутствует “память”); 2) если через заданную точку ($b \in {{{\mathbf{R}}}^{{kn}}}$, ${{t}_{ * }} \in T$) проходит решение ДАУ, то оно единственно на $T$, так как решение системы ${{\hat {X}}_{{k - 1}}}({{t}_{ * }})c = b - {{\psi }_{{k - 1}}}({{t}_{ * }})$ относительно вектора $c$ единственно: ${\text{rank}}\;{{\hat {X}}_{{k - 1}}}({{t}_{ * }}) = d < kn$ $\forall {{t}_{ * }} \in T$. Это и обусловило появление термина “решение типа Коши”. Для уравнений с последействием, например, для уравнения Фредгольма $\varsigma (t) = \int_\alpha ^\beta \,t\varsigma (s)ds + 1,t \in T,$ решение $\varsigma (t) = 2\tau t{\text{/}}(2 - {{\tau }^{2}}) + 1$, $\tau = \beta - \alpha $ меняется (или может вообще не существовать) на сужениях ${{T}_{0}} \subset T$.

Рассмотрим задачи (7), (9) с возмущениями свободного члена и начальных данных:

где ${{\tilde {b}}_{j}}$ – заданные векторы из ${{{\mathbf{R}}}^{n}}$.

Теорема 2 (cм. [17]). Пусть: 1. Выполнены условия теоремы 1; 2. $l \leqslant k$; 3. 3адачи (7), (9) и (18), (19) удовлетворяют условиям леммы 2.

Тогда справедливы оценки

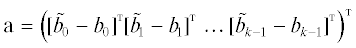где $y(t) = z(t) - \tilde {z}(t)$, , $\varphi (t) = f(t) - \tilde {f}(t)$, ${{\kappa }_{j}}$, ${{\tilde {\kappa }}_{j}}$ – некоторые положительные константы $j = 2,3$.

Условие $l \leqslant k$ теоремы 2 очень важно. В примере 3 $l > k$ и решение $z(t)$ зависит от $\dot {f}(t)$ при $\lambda \ne 1$. Вектор-функция $\tilde {f}(t) = f(t) + {{(01)}^{{\text{т}}}}\varepsilon sin(t{\text{/}}{{\varepsilon }^{2}})$ обладает свойством

где символ $ * $ соответствует пространствам ${{{\mathbf{L}}}_{2}}(T)$ или ${\mathbf{C}}(T)$.

3. ОБЩИЕ СВОЙСТВА ЛИНЕЙНО-КВАДРАТИЧНОЙ ЗАДАЧИ

Ниже рассматривается самый простой класс связей (ПР ДАУ (2) конечномерно и отсутствуют на $T$ особые точки), а именно для ДАУ выполнены условия теоремы 1. Тогда существует решение типа Коши и мы можем записать соотношение

где $({{\mathcal{C}}_{0}}(t){{\mathcal{C}}_{1}}(t) \ldots ,{{\mathcal{C}}_{{\text{p}}}}(t)) = ({{C}_{0}}(t){{C}_{1}}(t), \ldots ,{{C}_{{\text{p}}}}(t)){{\mathcal{M}}_{{\text{p}}}}[H(t)]$, ${{\mathcal{M}}_{{\text{p}}}}[.]$ – оператор из формул (11). Если в формулах (4) принять $q \geqslant {\text{p}}$, то из равенств (3), (21) следует, что $c = 0$. С учетом этого факта подставим выражение (21) в функционал (1). Получим где Несложные выкладки позволяют записать функционал в следующем виде: где учтено, что матрица $C$ симметричная,

Лемма 2. Пусть решение системы (2) представимо в виде формулы (21).

Тогда для выполнения условия $\Phi (u) \geqslant 0$ $\forall и \in {\mathbf{U}}$ необходимо, чтобы для матриц из формулы (23) выполнялись неравенства

Доказательство. Рассмотрим функцию Иначе говоря, функция $\tau (t)$ нулевая на отрезке $T$, кроме интервала $({{t}_{0}},{{t}_{1}})$, на котором она имеет вид “шапочки”. Простые выкладки показывают, что справедливы оценки Пусть условие (24) нарушается в точке ${{t}_{ * }} \in T$: существует вектор $w \in {{{\mathbf{R}}}^{m}}$ со свойством $\left\langle {{{\mathcal{A}}_{{{\text{p}},{\text{p}}}}}({{t}_{ * }})w,w} \right\rangle < 0$. Так как матрица ${{\mathcal{A}}_{{{\text{p}},{\text{p}}}}}(t)$, по крайней мере непрерывна, справедливо неравенство $\left\langle {{{\mathcal{A}}_{{{\text{p}},{\text{p}}}}}(t)w,w} \right\rangle < 0$, $t \in ({{t}_{2}},{{t}_{3}}) \subset ({{t}_{ * }} - \varepsilon ,{{t}_{ * }} + \epsilon )$, $\epsilon $ – некоторое положительное число. В интервале $({{t}_{2}},{{t}_{3}})$ по непрерывности найдется отрезок $[{{t}_{4}},{{t}_{5}}] \subset ({{t}_{2}},{{t}_{3}})$, на котором стандартной процедурой (см., например, [23, с. 258]) можно произвести разложение где $Q(t)$ – ортогональная матрица $Q(t){{Q}^{{\text{т}}}}(t) = {{E}_{m}}$, ${{\sigma }_{j}}(t)$ – собственные значения матрицы ${{\mathcal{A}}_{{{\text{p}},{\text{p}}}}}(t)$, $r = \operatorname{rank} {{\mathcal{A}}_{{{\text{p}},{\text{p}}}}}(t) = {\text{const}}$, $t \in [{{t}_{4}},{{t}_{5}}]$. Матрица $Q(t)$ имеет ту же гладкость, что и матрица ${{\mathcal{A}}_{{{\text{p}},{\text{p}}}}}(t)$. Примем: $Q(t) = Q({{t}_{4}})$, $t \in [\alpha ,{{t}_{4}})$, $Q(t) = Q({{t}_{5}})$, $t \in [{{t}_{5}},\beta ]$. Стандартным приемом матрицу $Q(t)$ можно доопределить в точках ${{t}_{4}}$, ${{t}_{5}}$ сколь угодно гладким образом. При предположении отрицательности формы $\left\langle {{{\mathcal{A}}_{{{\text{p}},{\text{p}}}}}(t)w,w} \right\rangle $, $t \in [{{t}_{4}},{{t}_{5}}]$, по крайней мере одно из собственных значений ${{\sigma }_{j}}(t) < 0$, $j \in {\text{\{ }}1,2,\; \ldots ,\;r{\text{\} }}$, $t \in [{{t}_{4}},{{t}_{5}}]$. Выберем пробную вектор-функцию $u(t) = {{Q}^{{ - 1}}}(t){{(0,0,\; \ldots ,\;v(t),0,0,\; \ldots ,\;0)}^{{\text{т}}}}$, $t \in T$, где $[{{t}_{0}},{{t}_{1}}] \subset ({{t}_{4}},{{t}_{5}})$, и вычислим на ней функционал (23). Имеем так как для произвольного вектора $w$ справедливы соотношения где $\tilde {w} = [Q(t)w]$. Учет условия ${{\sigma }_{j}}(t) < 0,$ и оценок (25) завершает доказательство.

Одним из способов проверки функционала $\Phi (u)$ на неотрицательность является приведение его к полному квадрату: поиск функционала $\hat {\Phi }(u)$ со свойством

где ${{\mathcal{X}}_{i}}(t)$, $\mathcal{Y}(t,s)$ – некоторые $(m \times m)$-матрицы, достаточно гладкие в своих областях определения. Эта идея восходит еще к Лежандру (см., например, [18], а также [11, с. 241], [21], [22]).

Множество ${\mathbf{U}}$ из формулы (4) является выпуклым, так как $\mu {{u}_{1}} + (1 - \mu ){{u}_{2}} \in {\mathbf{U}}$ при всех ${{u}_{1}},{{u}_{2}} \in {\mathbf{U}}$ и всех $\mu \in [0,1]$. В силу стандартного определения нормы, функционал $\Phi (u)$ из формулы (26) также является выпуклым:

при всех ${{u}_{1}},{{u}_{2}} \in {\mathbf{U}}$ и всех $\mu \in [0,1]$. Предположим, что в ДАУ (2) ${\text{rank}}\;H(t) = {{m}_{1}} = {\text{const}} \leqslant n$ $\forall t \in T$ (если элементы $H(t)$ вещественно-аналитических функций, то это условие можно снять). Согласно [11], существует матрица $Q(t)$ той же гладкости, что и $H(t)$ со свойствами $\det Q(t) \ne 0$, $\forall t \in T$, $H(t)Q(t){{Q}^{{ - 1}}}(t)u = ({{H}_{1}}(t)0){{Q}^{{ - 1}}}(t)u$, где блок ${{H}_{1}}(t)$ имеет размерность $({{m}_{1}} \times n)$. Поэтому мы полагаем, что ниже $m \leqslant n$, ${\text{rank}}\;H(t) = m$ $\forall t \in T$, в силу чего уравнение $H(t)u = 0$, $t \in T$, имеет только нулевое решение. Функционал $\Phi (u)$ является строго выпуклым: неравенство (28) является строгим.

При обосновании градиентных методов, применяемых для поиска минимума выпуклых функционалов $\tilde {\Phi }(u)$ одним из условий сходимости является ограниченность множества $\mathcal{U} = {\text{\{ }}u:\tilde {\Phi }(u) \leqslant \mathop {\tilde {\varepsilon }}\nolimits_0 {\text{\} }}$, $\mathop {\tilde {\varepsilon }}\nolimits_0 $ – некоторое число [19]. Для наших задач это не всегда так.

Пример 4. Рассмотрим функционал

Если $x(t) = \varepsilon \sin ([t - $ $ - \;\alpha ]{\text{/}}{{\varepsilon }^{2}})$, то $\Phi (u) < \varepsilon $, $0 < \varepsilon < {{\varepsilon }_{0}}$ – некоторое число. Здесь соответствующее множество $\mathcal{U} = $ $ = {\text{\{ }}u:\tilde {\Phi }(u) \leqslant {{\varepsilon }_{0}}{\text{\} }}$ неограниченно: ${{\left\| {u(t)} \right\|}_{{{{{\mathbf{L}}}_{2}}(T)}}} \to \infty $, $\varepsilon \to 0$.

В общем случае выразим управление $u$ из уравнения (2) по формуле (10). Получим

так как $m \leqslant n$, ${\text{rank}}\;H(t) = m$ $\forall t \in T$ и в силу этого $[{{E}_{m}} - {{H}^{ - }}(t)H(t)] = 0$. Подставляя выражение для $u$ в (2) и приводя подобные, получаем задачу минимизации вида где $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} $, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{B} $, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} $ суть $(n \times n)$-матрицы, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }_{0}}$, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{A} }_{1}}$ суть $([n - m] \times n)$-матрицы, так как $m \leqslant n$, ${\text{rank}}[{{E}_{n}} - H(t){{H}^{ - }}(t)] = $ $ = n - m$. Для исследования задачи (29) можно применять методику, развитую в работе [22]. Рассмотрим случай, когда $n = m$ (дифференциальные связи отсутствуют) и функционал приводим к полному квадрату: найдутся $(n \times n)$-матрицы $F$, $G$ со свойством Если для оператора ${{\Lambda }_{1}}$ определен индекс $l \geqslant 1$, то уже при $l = 1$ для функционала $\Phi (x) < \varepsilon $ возможны ситуации ${{\left\| {u(t)} \right\|}_{{{{{\mathbf{L}}}_{2}}(T)}}} = {{\left\| {\dot {x}(t)} \right\|}_{{{{{\mathbf{L}}}_{2}}(T)}}} \to \infty $, $\varepsilon \to 0$. При этом с необходимостью $\left\| {x(t)} \right\|_{{{{{\mathbf{L}}}_{2}}(T)}}^{2} \leqslant \kappa \varepsilon $. При $l \geqslant 2$ найдутся вектор-функции $x(t)$ со свойствами: $\varepsilon \to 0,$Но выполняется неравенство $\left\| {\int_\alpha ^t {{{{(t - s)}}^{{\text{p}}}}} x(s)ds} \right\|_{{{{{\mathbf{L}}}_{2}}(T)}}^{2} \leqslant \kappa \varepsilon $. Здесь индекс $l = 1$ тогда и только тогда, когда выполняется критерий “ранг-степень” для многочлена $det[\lambda F(t) + G(t)]$, $t \in T$ (см. определение 6). В общем случае возможно, что малое значение $\Phi (u)$ гарантирует малые значения нормы управления $u$. Из теоремы 2 вытекает такое утверждение.

Лемма 3. Пусть для оператора ${{\hat {\Lambda }}_{{\text{p}}}}$ из формулы (26) определен индекс $\varrho \leqslant {\text{p}}$.

Тогда, из условия $\Phi (u) \leqslant \varepsilon $ $\forall u \in {\mathbf{U}}$, следует неравенство $\left\| {u(t)} \right\|_{{{{{\mathbf{L}}}_{2}}(T)}}^{2} \leqslant \kappa \varepsilon $ где $\varepsilon \in [0,{{\varepsilon }_{0}}]$, $\kappa = {\text{const}} > 0$.

Заметим, что в примере 5 оператор ${{\hat {\Lambda }}_{{\text{p}}}}$ нулевой, индекс для него не определен (условие леммы 3 не выполнено). Заканчивая этот раздел, отметим следующее обстоятельство. Для вычислений матриц ${{C}_{j}}(t)$, $j = \overline {0,{\text{p}}} $, входящих в равенство (21), в частном случае ДАУ (2) можно использовать пункт 2 утверждения теоремы 1. В случае задания ДАУ (2) постоянными матрицами ${{A}_{0}}$, ${{A}_{1}}$, соответствующие матрицы постоянные и способы их нахождения даны в монографии [3]. В общей постановке проблема пока не решена.

4. ИССЛЕДОВАНИЕ СВОЙСТВ ЧАСТНОГО СЛУЧАЯ

Предположим, что ядро оператора ДАУ (2) нулевое и согласно пункту 2 утверждения теоремы 1 в формуле (21)

где с необходимостью ${\text{p}} \geqslant 1$, ${\text{p}} = l - 1$. Таким образом, функционал (23) после приведения подобных имеет вид где ${{\mathcal{A}}_{{i,j}}}(t)$ – соответствующие $(m \times m)$-матрицы, в частности, ${{\mathcal{A}}_{{{\text{p}},{\text{p}}}}}(t) = {{{\mathbf{S}}}_{{{\text{p}},{\text{p}}}}}(t)$ и в формуле (27) ${{\hat {\Lambda }}_{{\text{p}}}}u = \sum\nolimits_{i = 0}^{\text{p}} {{{\mathcal{X}}_{i}}} (t){{u}^{{(i)}}}(t)$. Уравнение Эйлера–Пуассона [18] имеет у нас вид системы линейных ОДУ где ${{{\text{A}}}_{i}}(t)$ – соответствующие $(m \times m)$-матрицы, после приведения подобных. Эту систему будем называть ниже уравнением Якоби–Пуассона.

Определение 8. Пусть существует точка ${{t}_{ * }} \in (\alpha ,\beta ) \subset T$ со свойством: краевая задача для ДАУ (32) с условиями ${{u}^{{(j)}}}(\alpha ) = 0$, ${{u}^{{(j)}}}({{t}_{ * }}) = 0$, $j = \overline {0,{\text{p}}} $, имеет на $T$ ненулевое решение. Тогда точку ${{t}_{ * }}$ мы назовем сопряженной к точке $\alpha $.

Допустим, что функционал (30) удовлетворяет условию

Сравнивая матрицы ${{\mathcal{A}}_{{i,j}}}(t)$, $i,j \in {\text{\{ }}0,1,\; \ldots ,\;{\text{p\} }}$, в равенстве (30) с произведениями матриц ${{\mathcal{X}}_{i}}(t){{\mathcal{X}}_{j}}(t)$ в (33), получаем систему уравнений для определения последних. Но число матриц ${{\mathcal{A}}_{{i,j}}}(t)$ превосходит число искомых матриц ${{\mathcal{X}}_{i}}(t)$ уже в случае $l = 2$. Чтобы избежать решения переопределенных систем, рассмотрим функционал где ${{\mathcal{W}}_{{i,j}}}(t)$, ${{\mathcal{X}}_{i}}(t)$ – неизвестные $(m \times m)$-матрицы. Предполагая, что в определении множества допустимых функций (4) $q \geqslant l - 2$, мы видим, что $\hat {\Phi }(u) = \Phi (u)$ $\forall u \in {\mathbf{U}}$. Получается замкнутая (число неизвестных равно числу уравнений) система относительно неизвестных матриц. Для примера выпишем эти системы при $l = 2$ и $l = 3$.

В случае $l = 2$ имеем систему для определения матриц ${{\mathcal{W}}_{{0,0}}}(t)$, ${{\mathcal{X}}_{0}}(t)$, ${{\mathcal{X}}_{1}}(t)$ вида

Вопросы разрешимости матричного ДАУ (35) рассматривались в работах [11], [21]. В частности, там показано, что из системы (35) можно вывести матричное уравнение Риккати. В [22] показана его эквивалентность уравнению Риккати из монографии [8].

В случае $l = 3$ аналог системы (35) состоит из шести уравнений

Ниже мы будем предполагать, что существуют матрицы ${{\mathcal{W}}_{{i,j}}}(t)$ и ${{\mathcal{X}}_{i}}(t)$, удовлетворяющие равенству (34). Тогда уравнение Якоби–Пуассона, построенное по формуле (31), имеет вид

Определение 9. Оператор, действующий на вектор-функцию $f$ по правилу

мы будем называть сопряженным к оператору ${{\hat {\Lambda }}_{{\text{p}}}} = \sum\nolimits_{i = 0}^{\text{p}} {{{\mathcal{X}}_{i}}} (t){{(d{\text{/}}dt)}^{i}}$, $t \in T$.

Введем обозначение $\zeta = {{\left( {{{u}^{{\text{т}}}}{{{\dot {u}}}^{{\text{т}}}}\; \ldots \;\left( {{{u}^{{({\text{p}} - 1)}}}} \right)} \right)}^{{\text{т}}}}$. Тогда мы можем поставить в соответствие системе ${{\hat {\Lambda }}_{{\text{p}}}}u = \sum\nolimits_{i = 0}^{\text{p}} {{{\mathcal{X}}_{i}}} (t){{u}^{{(i)}}} = 0$, $t \in T$, эквивалентное ДАУ первого порядка

где $\eta = ({\text{p}} - 1)m$, $\tilde {\mathcal{X}}(t) = \left( {\begin{array}{*{20}{c}} {{{X}_{1}}(t)}&{{{\mathcal{X}}_{2}}(t)}& \ldots &{{{\mathcal{X}}_{{{\text{p}} - 1}}}(t)} \end{array}} \right)$.

Лемма 4. Пусть в равенстве (37) ${{\mathcal{X}}_{i}}(t) \in {{C}^{\nu }}(T)$, $\nu \geqslant {\text{p}}$. Тогда:

1. ДАУ, сопряженное системе $\hat {\Lambda }_{{\text{p}}}^{ * }y = \sum\nolimits_{i = 0}^{\text{p}} {{{{( - d{\text{/}}dt)}}^{i}}} \left[ {\mathcal{X}_{i}^{{\text{т}}}(t)y} \right] = 0$, $t \in T$, совпадает с исходной системой ${{\hat {\Lambda }}_{{\text{p}}}}h = \sum\nolimits_{i = 0}^{\text{p}} {{{\mathcal{X}}_{i}}} (t){{h}^{{(i)}}} = 0$, $t \in T$;

2. справедливо равенство $\left\langle {\xi ,{\text{A}}(t)\zeta } \right\rangle = c$, где $\zeta \equiv \zeta (t)$, $\xi \equiv \xi (t)$ – решения системы (38) и сопряженной к ней соответственно, $c$ – постоянный вектор;

3. уравнения Якоби–Пуассона (32) и (36) совпадают.

Доказательство. Система, сопряженная к ДАУ (38), имеет вид

Из элементарных выкладок следует, что сопряженная к ней равна ${\text{A}}(t)\dot {\zeta } + {\text{B}}(t)\zeta = 0.$ Рассмотрим равенство, следующее из второго пункта утверждения леммы Так как $\xi $ и $\zeta $ являются решениями соответствующих систем, из правой части равенства следует, что Докажем третий пункт утверждения. Функционалы (33), (34) совпадают при любом значении аргумента. Поэтому соответствующие уравнения Якоби–Пуассона также совпадают. Для ${\text{p}} = 1,2$ это можно проверить прямым вычислением (см., например, [22]).

Теорема 3. Пусть: 1) в равенствах (1), (2) ${{A}_{0}}(t)$, ${{A}_{1}}(t)$, $H(t)$, $A(t)$, $B(t)$, $C(t) \in {{{\mathbf{C}}}^{\nu }}(T)$; 2) для оператора уравнения Якоби–Пуассона ${{\Lambda }_{J}}$ определен индекс на $T$. Тогда:

1. в уравнении Якоби–Пуассона (32) матрицы ${{{\text{A}}}_{i}}(t) \in {{{\mathbf{C}}}^{{\nu - 2{\text{p}}}}}(T)$, $i = \overline {0,2{\text{p}}} $;

2. для операторов ${{\hat {\Lambda }}_{{\text{p}}}}$, $\hat {\Lambda }_{{\text{p}}}^{ * }$ из формулы (36) определены индексы, равные $\varrho $;

3. индекс уравнения Якоби–Пуассона (36) равен $2\varrho $ (индекс является четным числом);

4. на полуинтервале $(\alpha .\beta ]$ отсутствуют сопряженные точки (см. определение 8).

Доказательство. Первый пункт утверждения следует из формулы (15) и пункта 2 утверждения теоремы 1. В монографиях [11], [13] показано, что в произведении ${{\Lambda }_{J}} = \hat {\Lambda }_{{\text{p}}}^{ * } \circ \hat {\Lambda }_{{\text{p}}}^{{}}$ (при достаточной гладкости входных данных) из существования ЛРО для оператора ${{\Lambda }_{J}}$ следует существование ЛРО и для сомножителей. Верно и обратное утверждение. Отсюда следует конечномерность ПР для соответствующих уравнений. Поэтому (см., например, [13, с. 147]) любой отрезок ${{T}_{0}} \subset T$ содержит подотрезок ${{T}_{1}} = [{{\alpha }_{1}},{{\beta }_{1}}] \subset {{T}_{0}}$, на котором для ДАУ (38) определены матрицы $P,Q \in {{{\mathbf{C}}}^{1}}({{T}_{1}})$ со свойствами: $detPQ \ne 0$ $\forall t \in {{T}_{1}}$,

где ${\mathbf{Q}} = {\text{diag\{ }}{{E}_{\chi }},\;{{({{E}_{{\eta - \chi }}} + {{\dot {N}}^{{\text{т}}}})}^{{ - 1}}}{\text{\} }}{{Q}^{{\text{т}}}}$, $\zeta = Qv$, $N$ – верхнетреугольная матрица с нулевой диагональю, $\tilde {N} = {{({{E}_{{\eta - \chi }}} + {{\dot {N}}^{{\text{т}}}})}^{{ - 1}}}{{N}^{{\text{т}}}}$, ${{N}^{\varrho }} \equiv 0$, ${{\tilde {N}}^{\varrho }} \equiv 0,$ ${{N}^{{\varrho - 1}}} = \mathcal{N}$, ${{\tilde {N}}^{{\varrho - 1}}} = {{\mathcal{N}}^{{\text{т}}}}$.

Решения подсистем ДАУ (39): $N{{\dot {v}}_{2}} + {{v}_{2}} = g$, $\tilde {N}{{\dot {w}}_{2}} + {{w}_{2}} = g$, где $v = {{(v_{1}^{{\text{т}}}v_{2}^{{\text{т}}})}^{{\text{т}}}}$, $w = {{(w_{1}^{{\text{т}}}w_{2}^{{\text{т}}})}^{{\text{т}}}}$, имеют вид

где $\mathcal{T} = - N(t)(d{\text{/}}dt)$, $\tilde {\mathcal{T}} = \tilde {N}(t)(d{\text{/}}dt)$, $g(t)$ – произвольная вектор-функция из ${{{\mathbf{C}}}^{\varrho }}({{T}_{1}})$.

Искусственно вводя неоднородность ${\text{f}} \equiv {\text{f}}(t) \in {{{\mathbf{C}}}^{\infty }}({{T}_{1}})$, перепишем уравнения Якоби–Пуассона в такой форме

Введем замены $\xi = {{P}^{{\text{т}}}}{{(w_{1}^{{\text{т}}}w_{2}^{{\text{т}}})}^{{\text{т}}}}$, $\zeta = Q{{(v_{1}^{{\text{т}}}v_{2}^{{\text{т}}})}^{{\text{т}}}}$. Согласно формулам (39), (40), получим где ${{({\text{f}}_{1}^{{\text{т}}}{\text{f}}_{2}^{{\text{т}}})}^{{\text{т}}}} = {\mathbf{Q}}{\text{f}}$, ${\text{V}}{{{\text{f}}}_{1}} = \int_\alpha ^t {\text{Y}} (t){{{\text{Y}}}^{{ - 1}}}(s){{{\text{f}}}_{1}}(s)ds$, ${\text{W}}{{\xi }_{1}} = \int_\alpha ^t {\text{Z}} (t){{{\text{Z}}}^{{ - 1}}}(s){{\xi }_{1}}(s)ds$, ${\text{Y}}(t)$, ${\text{Z}}(t)$ – матрицанты (см., например, [23]) систем ${{\dot {v}}_{1}} = - J{{v}_{1}}$, ${{\dot {w}}_{1}} = {{J}^{{\text{т}}}}{{w}_{1}}$, ${{c}_{1}}$, ${{c}_{2}}$ – вектора произвольных постоянных, $c = {{(c_{1}^{{\text{т}}},c_{2}^{{\text{т}}})}^{{\text{т}}}}$.

Раскрывая выражения (42) с учетом формул (39) и (40), видим, что уравнение Якоби–Пуассона имеет решение типа Коши:

где ${{{\text{X}}}_{d}}(t)$, ${\text{K}}(t,s)$, ${{{\text{C}}}_{j}}(t)$ – матрицы соответствующих размерностей, $d = 2\chi $, $t \in {{T}_{1}}$, матрица

${{{\mathbf{Q}}}_{2}}$ – блок, образованный из последних $\eta - \chi $ строк матрицы ${\mathbf{Q}}$. Так как $detP \ne 0$ $\forall t \in {{T}_{1}}$, имеем неравенства ${{P}^{{\text{т}}}}P > 0$, ${{P}_{{22}}} > 0$, 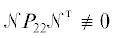, , 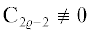$t \in {{T}_{1}}$. Ввиду эквивалентности условий существования ЛРО и решения типа Коши (см., например, [13]), для уравнения Якоби–Пуассона определен индекс, равный $2\varrho $.

Допустим, что существует точка на ${{t}_{ * }} \in T$, которая не попадает ни в один из отрезков с определенными на них каноническими формами (39) (см., например, пример 1 из [16]) со свойством: старший коэффициент ${{{\text{C}}}_{{{{\varrho }_{1}}}}}({{t}_{ * }}) \ne 0$, где ${{\varrho }_{1}}$ нечетно. По непрерывности существует отрезок $[{{t}_{ * }} - \varepsilon {{t}_{ * }} + \varepsilon ]$, на котором мы можем повторить приведенные выше рассуждения. Получили противоречие.

Осталось доказать последний пункт утверждения теоремы. Предположим, что сопряженные точки существуют на $T$. По условию для оператора ${{\hat {\Lambda }}_{{\text{p}}}}$, определен ЛРО и задачи

имеют только нулевые решения (см. замечание 2). Получили противоречие.

Замечание 3. Размерность ядра произведения операторов ДАУ равна сумме размерностей ядер сомножителей (размерности ПР соответствующих операторам уравнений суммируются), если для сомножителей определены ЛРО. Индекс же произведения операторов может меняться довольно произвольным образом. Например, произведение $[{{E}_{n}} + N(d{\text{/}}dt)] \circ [{{E}_{n}} - N(d{\text{/}}dt)] = {{E}_{n}}$ имеет индекс $l = 0$, произведение $[{{E}_{n}} - N(d{\text{/}}dt)] \circ [{{E}_{n}} - N(d{\text{/}}dt)] = {{E}_{n}} - 2N(d{\text{/}}dt)$ имеет индекс $l = 2$, причем сомножители имеют индекс 2, где $N$ – постоянная матрица, ${{N}^{2}} = 0$. В настоящее время правила сложения индексов операторов ДАУ не удалось установить.

В заключение работы отметим следующие моменты. Сейчас для авторов важной задачей является проблема обращения теоремы 3 в следующей форме. Если для функционала (30) выполнены условия: 1) $\Phi (u) \geqslant 0$ $\forall u \in {\mathbf{U}}$; 2) на $T$ определен индекс уравнения Якоби–Пуассона (32), то функционал приводим к полному квадрату: существуют матрицы ${{\mathcal{W}}_{{i,j}}}(t)$ и ${{\mathcal{X}}_{i}}(t)$, удовлетворяющие равенству (34). Интерес представляют также поиски соответствия полученных результатов с известными в теории оптимального управления условиями вырождения типа Келли и их аналогами. Для анализа случаев с особыми точками у уравнений Якоби–Пуассона авторам представляется перспективным синтез развитой теории с методами из работ [6], [7]. В последних положение особых точек задано явно, тогда как в нашем случае задача и их поиска сама по себе очень непроста.