Журнал вычислительной математики и математической физики, 2020, T. 60, № 3, стр. 405-412

1. ВВЕДЕНИЕ

Одной из проблем при решении систем нелинейных уравнений является выбор начального приближения. Подходящее начальное приближение можно получить методом продолжения по параметру, который восходит к работам [1], [2] (подробнее см., например, [3]–[5]). Метод состоит в решении системы уравнений ${\mathbf{F}}({\mathbf{x}},\lambda ) = 0$ относительно ${\mathbf{x}} \in {{\mathbb{R}}^{n}}$ при значениях параметра $\lambda $ из некоторого интервала. Во многих практических задачах решение системы легко получить при некотором $\lambda $ из этого интервала, которое может служить стартовым значением. Изменяя параметр $\lambda $ с малым шагом и используя в качестве начального приближения решение системы с предыдущего шага, можно вычислить зависимость ${\mathbf{x}}(\lambda )$ (фиг. 1а). При подходе к особой точке, где якобиан $det\left( {\partial {\mathbf{F}}{\text{/}}\partial {\mathbf{x}}} \right)$ системы уравнений обращается в нуль, вычисления замедляются из-за того, что необходимо делать все более мелкий шаг по параметру $\lambda $ для достижения сходимости. В невырожденной особой точке кривая ${{x}_{i}}(\lambda )$ для каждой координаты находится по одну сторону от вертикальной касательной (фиг. 1б). Дальнейшее продолжение по $\lambda $ становится невозможным, поэтому вблизи особой точки необходима замена параметра. Вместо $\lambda $ можно использовать одну из компонент вектора ${\mathbf{x}}$. (Замены параметра можно избежать, если с самого начала использовать в качестве параметра длину дуги [5], [6]. Однако такой подход требует вычисления производных $\partial {\mathbf{F}}{\text{/}}\partial {\mathbf{x}}$ и $\partial {\mathbf{F}}{\text{/}}\partial \lambda $, что не всегда удобно в реальных задачах. По той же причине не всегда удобно использовать переход к системе дифференциальных уравнений по параметру [2].)

В настоящей работе метод продолжения по параметру используется для нелинейной системы, состоящей из скалярных и функциональных уравнений. Под скалярными уравнениями мы понимаем алгебраические или трансцендентные уравнения, а в качестве функциональных уравнений могут выступать интегральные или интегродифференциальные уравнения, а также краевые задачи для дифференциальных уравнений. При наличии двух групп переменных в системе нелинейных уравнений: скалярных переменных и неизвестных функций, для решения системы при фиксированном значении параметра удобно использовать методы типа Якоби и Гаусса–Зейделя (см., например, [3]). Преимущество такого подхода заключается в том, что каждую из подсистем: скалярных и функциональных уравнений, можно решать методами, учитывающими специфику задачи. Например, можно использовать методы без производных для решения системы скалярных уравнений и специализированные методы для решения интегральных уравнений или краевых задач. Предлагаемый нами метод решения при фиксированном значении параметра является более экономным вариантом метода Гаусса–Зейделя: решение системы скалярных уравнений вычисляется подходящим итерационным методом, а неизвестные функции обновляются на каждой итерации этого метода из системы функциональных уравнений.

Метод продолжения по параметру применен для вычисления температурной зависимости магнитных характеристик металлов в динамической теории спиновых флуктуаций (ДТСФ) [7]. Мы продолжаем решение системы нелинейных уравнений ДТСФ по температуре от нуля, где уравнения имеют простой вид. При высоких температурах система уравнений ДТСФ становится близка к вырожденной, и ее решение может стать неустойчивым [8]. Предложенный метод продолжения по параметру используется для уменьшения числа итераций при самосогласованном вычислении когерентного потенциала в ДТСФ. Самосогласованное вычисление и его ускорение являются важными проблемами в расчетах электронной структуры в рамках теории функционала плотности (см., например, [9], [10]), в описании процессов агрегационной кинетики (см., например, [11]) и др. В качестве иллюстрации предложенного метода мы вычисляем температурную зависимость магнитных характеристик железа, где вычислительные проблемы наиболее существенны.

Изложение построено следующим образом. В разд. 2 описан модифицированный метод Гаусса–Зейделя для решения нелинейной системы, состоящей из скалярных и функциональных уравнений, при фиксированном значении параметра. В разд. 3 обсуждается вычисление температурной зависимости магнитных характеристик в ДТСФ. В разд. 4 приведены результаты расчетов и их обсуждение. Разд. 5 суммирует результаты работы.

2. МОДИФИЦИРОВАННЫЙ МЕТОД ГАУССА–ЗЕЙДЕЛЯ

Рассмотрим нелинейную систему с параметром $\lambda $, состоящую из скалярных и функциональных уравнений. В результате дискретизации функциональных уравнений мы получаем систему нелинейных уравнений

Здесь ${\mathbf{F}} = ({{F}_{1}}, \ldots ,{{F}_{n}})$, где $n$ – число скалярных переменных ${\mathbf{x}}$, а ${\mathbf{G}} = ({{G}_{1}}, \ldots ,{{G}_{N}})$, где $N$ – число значений функций в узлах дискретизации ${\mathbf{y}}$. Размерность ${\mathbf{x}}$ значительно меньше размерности ${\mathbf{y}}$: $n \ll N$. Задача состоит в вычислении зависимостей ${\mathbf{x}}(\lambda )$ и ${\mathbf{y}}(\lambda )$ при изменении $\lambda $ в некотором интервале.

При фиксированном значении параметра $\lambda $ для решения системы нелинейных уравнений с двумя и более группами переменных можно использовать блочные методы Якоби или Гаусса–Зейделя. Блочный метод Якоби для решения системы (1) работает следующим образом. Пусть $({{{\mathbf{x}}}^{k}},{{{\mathbf{y}}}^{k}})$ – результат выполнения $k$-й итерации. Тогда, решая систему уравнений ${\mathbf{F}}({\mathbf{x}},{{{\mathbf{y}}}^{k}},\lambda ) = 0$, находим ${{{\mathbf{x}}}^{{k + 1}}}$, а решая систему ${\mathbf{G}}({{{\mathbf{x}}}^{k}},{\mathbf{y}},\lambda ) = 0$, находим ${{{\mathbf{y}}}^{{k + 1}}}$. Блочный метод Гаусса–Зейделя позволяет использовать новое значение вектора ${\mathbf{x}}$ для вычисления вектора ${\mathbf{y}}$. А именно, ${{{\mathbf{y}}}^{{k + 1}}}$ вычисляется как решение системы уравнений ${\mathbf{G}}({{{\mathbf{x}}}^{{k + 1}}},{\mathbf{y}},\lambda ) = 0$. В обратном методе Гаусса–Зейделя сначала решается система ${\mathbf{G}}({{{\mathbf{x}}}^{k}},{\mathbf{y}},\lambda ) = 0$ относительно ${\mathbf{y}}$, а затем полученное значение ${{{\mathbf{y}}}^{{k + 1}}}$ используется для вычисления ${{{\mathbf{x}}}^{{k + 1}}}$ из системы ${\mathbf{F}}({\mathbf{x}},{{{\mathbf{y}}}^{{k + 1}}},\lambda ) = 0$. Итерационный процесс во всех методах продолжается до тех пор, пока норма невязки в системе (1) не станет меньше заданной точности $\delta $.

Мы используем более экономный вариант обратного метода Гаусса–Зейделя. Стартуя с $({{{\mathbf{x}}}^{k}},{{{\mathbf{y}}}^{k}})$, на следующей итерации:

Итерационный процесс продолжается до достижения точности ${{\delta }_{x}}$ в системе ${\mathbf{F}}({\mathbf{x}},{\mathbf{y}},\lambda ) = 0$. Часто переменная ${\mathbf{y}}$ имеет вспомогательный характер, в этом случае значение ${{\delta }_{y}}$ может быть выбрано много большим, чем ${{\delta }_{x}}$.

3. СИСТЕМА НЕЛИНЕЙНЫХ УРАВНЕНИЙ ДТСФ

Основной вклад в магнетизм металлов дают коллективизированные электроны в кристаллической решетке. В ДТСФ электронное взаимодействие описывается как взаимодействие электронов с обменным полем ${{V}_{j}}(\tau )$, которое может принимать случайные значения на разных узлах решетки $j$, а вследствие квантового характера задачи зависит от переменной $\tau $, имеющей размерность времени. Любая магнитная характеристика $A$ в ДТСФ вычисляется в два этапа: сначала вычисляется ее значение $A(V)$ для фиксированной конфигурации поля, а затем вычисляется среднее по всем конфигурациям:

где ${\text{D}}V$ указывает на функциональное интегрирование. Плотность вероятности обменного поля $p(V)$ вычисляется самосогласованно в гауссовом приближении при каждом значении температуры $T$. В результате для вычисления зависимости магнитных характеристик металлов от температуры в ДТСФ необходимо решить нелинейную систему, состоящую из скалярных и функционального уравнений при каждом $T$ (явный вид уравнений см. в [7]).

В принятых нами обозначениях систему уравнений ДТСФ можно записать следующим образом. Функция ${\mathbf{F}} = ({{F}_{1}},{{F}_{2}},{{F}_{3}},{{F}_{4}})$ задает систему из $n = 4$ скалярных уравнений. Вектор ${\mathbf{x}} = (\mu ,{{\bar {V}}^{z}},{{\zeta }^{x}},{{\zeta }^{z}})$ состоит из четырех величин: химического потенциала $\mu $, среднего поля $\mathop {\bar {V}}\nolimits^z $ и двух среднеквадратических флуктуаций обменного поля ${{\zeta }^{x}} \equiv \left\langle {\Delta V_{x}^{2}} \right\rangle $ и ${{\zeta }^{z}} \equiv \left\langle {\Delta V_{z}^{2}} \right\rangle $. Функциональное уравнение на когерентный потенциал $\Delta {{\Sigma }_{\sigma }}(z)$ имеет вид

где есть локальная функция Грина, которая, в свою очередь, зависит от когерентного потенциала. Здесь $\sigma $ – спиновый индекс, принимающий значения $ \uparrow ,\; \downarrow $ или $ \pm 1$ ($\bar {\sigma } = - \sigma $), а $\nu (\varepsilon {\text{'}})$ есть плотность электронных состояний конкретного металла. Интеграл в правой части (3) определяется как предел из нижней комплексной полуплоскости: $z = \varepsilon - i{{0}^{ + }}$. Поэтому функция Грина и когерентный потенциал комплексны. После дискретизации по переменной $z$ уравнения (2) и (3) задают функцию ${\mathbf{G}} = ({{G}_{1}}, \ldots ,{{G}_{N}})$, где вектор ${\mathbf{y}}$ составлен из значений когерентного потенциала в точках разбиения $\Delta {{\Sigma }_{\sigma }}({{z}_{l}})$, $l = 1, \ldots ,N$. Задача сводится к системе нелинейных уравнений (1), где в качестве параметра $\lambda $ выступает температура $T$. При $T = 0$ флуктуации ${{\zeta }^{x}}$ и ${{\zeta }^{z}}$ и когерентный потенциал $\Delta {{\Sigma }_{\sigma }}(z)$ обращаются в ноль. Система относительно двух оставшихся переменных сравнительно легко решается. Полученные значения используются в качестве стартовых для продолжения по $T$. В окрестности особой точки происходит замена параметра $T$ на среднее поле ${{\bar {V}}_{z}}$. Для решения системы уравнений при фиксированном значении параметра мы используем предложенный в предыдущем разделе модифицированный метод Гаусса–Зейделя.

Решение системы скалярных уравнений ${\mathbf{F}} = 0$ сводится к решению задачи оптимизации

с подходящими масштабирующими коэффициентами ${{c}_{i}}$ и покоординатными ограничениями на ${\mathbf{x}}$. Задача оптимизации (4) очень чувствительна к конечно-разностным аппроксимациям. Попытки использовать квазиньютоновские методы дают неудовлетворительные результаты [8]. Поэтому мы решаем (4) методами оптимизации без производных [12]. В нашем программном комплексе [13] используются три таких метода оптимизации: симплекс-метод Нелдера–Мида [14], метод покоординатного линейного поиска [15] и метод доверительных областей с квадратичной аппроксимацией [16].

Для решения системы функциональных уравнения ${\mathbf{G}} = 0$ мы используем метод простой итерации (индекс l у аргумента $z$ для краткости опускаем):

где функция Грина на $k$-м шаге вычисляется по формуле

Численные методы для преобразования Гильберта, интегралов с функцией Ферми и ее производной, интегралов по зоне Бриллюэна и другие методы, необходимые для вычислений в ДТСФ, описаны в [7, приложение H ].

4. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

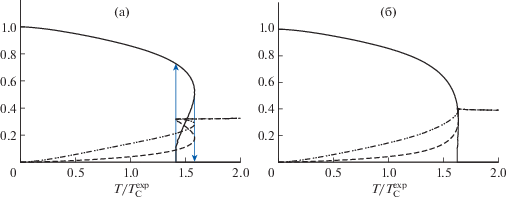
Ранее в ДТСФ [7] функции $\Delta {{\Sigma }_{\sigma }}(z)$ и ${{g}_{\sigma }}(z)$ вычислялись по формулам (5) и (6), но лишь с одной итерацией, а в качестве начального приближения использовалось значение $\Delta \Sigma _{\sigma }^{0}(z) = 0$ при всех $T$. На фиг. 2a приведены соответствующие результаты расчета для железа с точностью ${{\delta }_{x}} = {{10}^{{ - 8}}}$. Входные данные для железа взяты из работы [17], расчет выполнен в гауссовом приближении ДТСФ, температура приведена в единицах экспериментальной температуры Кюри $T_{C}^{{\exp }} = 1044$ K. При высоких температурах возникает невырожденная особая точка системы. Если продолжать решение по температуре, возникает скачок намагниченности из ферромагнитного состояния (${{m}^{z}} \ne 0$) в парамагнитное состояние $({{m}^{z}} = 0)$, а при уменьшении температуры происходит обратный скачок из пара- в ферромагнитное состояние, но при меньшем значении температуры (в полном согласии с результатами работы [8]). Поэтому вблизи особой точки мы заменяем параметр $T$ на среднее поле ${{\bar {V}}_{z}}$ (которое пропорционально намагниченности ${{m}^{z}}$). За счет этого нам удается построить промежуточную ветвь решения между ферромагнитным и парамагнитным решениями. Таким образом, в данном расчете имеет место температурный гистерезис, вопреки эксперименту.

В рамках метода, предложенного в настоящей работе, функция $\Delta {{\Sigma }_{\sigma }}(z)$ вычисляется самосогласованно до достижения необходимой точности, то есть уравнения (2) и (3) решаются с заданной точностью ${{\delta }_{y}}$. Для этого мы выполняем итерации по формулам (5) и (6) до тех пор, пока не выполнится критерий сходимости

На фиг. 2б приведены результаты расчетов с самосогласованием по $\Delta {{\Sigma }_{\sigma }}(z)$ до достижения точности ${{\delta }_{y}} = {{10}^{{ - 2}}}$ (расчеты с меньшими значениями ${{\delta }_{y}}$ не меняют результатов для ${\mathbf{x}}$ в пределах выбранной точности ${{\delta }_{x}} = {{10}^{{ - 8}}}$). Как видно из фиг. 2б, самосогласованное решение уравнений ДТСФ устраняет температурный гистерезис и приводит к непрерывному фазовому переходу из ферро- в парамагнитное состояние. Таким образом, самосогласованный расчет до достижения необходимой точности дает правильный ход температурной зависимости без использования членов старших порядков в разложении свободной энергии [18].

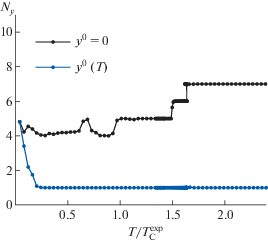
Сходимость метода решения ${\mathbf{G}} = 0$ значительно ускоряется, если использовать в качестве начального приближения для ${\mathbf{y}}$ значение с предыдущего шага по параметру так же, как это делается для скалярных переменных ${\mathbf{x}}$. Для оценки скорости сходимости метода простых итераций при самосогласованном вычислении $\Delta {{\Sigma }_{\sigma }}(z)$ до достижения заданной точности, мы подсчитываем среднее число итераций (5) на каждом шаге по параметру (температуре или среднему полю). Среднее число итераций ${{N}_{y}}$ определяется как отношение числа итераций (5) к числу вычислений целевой функции ${{N}_{f}}$ в задаче минимизации (4). Как видно из фиг. 3, если начинать итерации (5) с нулевого начального приближения, величина ${{N}_{y}}$ увеличивается с ростом температуры. Так, ${{N}_{y}}$ возрастает с 4 до 7 итераций в парамагнитной области. Это связано с тем, что чем выше температура, тем больше функция $\Delta {{\Sigma }_{\sigma }}(z)$ отличается от нуля и тем больше итераций требуется для ее вычисления. Если использовать значение с предыдущего шага по параметру в качестве начального приближения для $\Delta {{\Sigma }_{\sigma }}(z)$, величина ${{N}_{y}}$ сохраняется примерно на уровне одной итерации при всех температурах (фиг. 3). Этот результат показывает, что продолжение функции $\Delta {{\Sigma }_{\sigma }}(z)$ по параметру позволяет устранить гистерезис с помощью всего одной итерации при решении функционального уравнения.

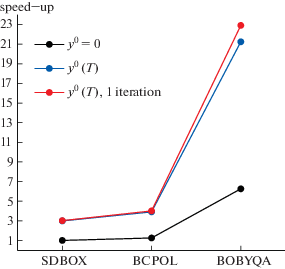
Для проверки численных результатов мы провели расчеты для железа с использованием трех различных солверов для оптимизации без вычисления производных: солвера BCPOL из библиотеки IMSL, реализующего метод Нелдера–Мида [14]; солвера SDBOX из библиотеки DFL, реализующего метод покоординатного линейного поиска [15]; солвера BOBYQA, реализующего метод доверительных областей [16]. Для каждого из солверов точность по целевой функции в задаче (4) выбрана равной ${{\delta }_{f}} = {{10}^{{ - 11}}}$. Результаты всех трех солверов дают одинаковые значения (с точностью до 4–5 значащих цифр). В табл. 1 приведены результаты для магнитных характеристик железа, а также число вычислений целевой функции ${{N}_{f}}$ в зависимости от температуры. Как видно из таблицы, солвер BOBYQA требует в несколько раз меньшее число вычислений целевой функции по сравнению с двумя другими. Выбор начального приближения ${{{\mathbf{y}}}^{0}}$ с предыдущего значения параметра и солвера BOBYQA позволяют получить выигрыш в быстродействии более 20 раз по сравнению с наиболее медленным вариантом, использующим начальное приближение ${{{\mathbf{y}}}^{0}} = 0$ и солвер SDBOX (фиг. 4).

5. ЗАКЛЮЧЕНИЕ

Метод продолжения по параметру использован для решения нелинейной системы, состоящей из скалярных и функциональных уравнений. Для решения системы при фиксированном значении параметра предложен модифицированный метод Гаусса–Зейделя: функциональное уравнение решается самосогласованно на каждом шаге итерационного метода решения системы скалярных уравнений. Преимущество такого подхода состоит в том, что система разбивается на две части по группам переменных, и для решения каждой из частей используется подходящий численный метод, который зависит от конкретной задачи. В частности, наш метод применим в задачах, где вычисление частных производных приводит к потере точности.

Предложенный метод продолжения по параметру применен для вычисления температурной зависимости магнитных характеристик в ДТСФ и проиллюстрирован на примере железа, где вычислительные трудности наиболее существенны. При помощи замены параметра в расчете с одной итерацией по когерентному потенциалу получена неустойчивая ветвь решения между ферро- и парамагнитной ветвями решения. Показано, что самосогласованное решение функционального уравнения на когерентный потенциал устраняет гистерезис и дает правильный ход температурной зависимости магнитных характеристик железа. Использование современных методов оптимизации без производных позволяет быстро и эффективно решать систему скалярных уравнений в ДТСФ. А продолжение когерентного потенциала по параметру значительно ускоряет сходимость и позволяет всего один раз обновлять решение функционального уравнения на каждом шаге итерационного процесса по скалярным переменным.

Авторы признательны участникам международной конференции “Современные проблемы вычислительной математики и математической физики”, посвященной 100-летию со дня рождения академика А.А. Самарского, за доброжелательное обсуждение результатов и полезные замечания. Авторы также признательны рецензенту за полезные замечания.