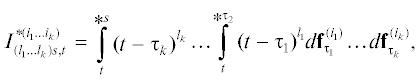Журнал вычислительной математики и математической физики, 2020, T. 60, № 3, стр. 379-390
Явный одношаговый численный метод с порядком сильной сходимости 2.5 для стохастических дифференциальных уравнений Ито с многомерным неаддитивным шумом, основанный на разложении Тейлора–Стратоновича
Д. Ф. Кузнецов *
Санкт-Петербургский Политехнический
Университет Петра Великого
195251 С.-Петербург, Политехническая ул., 29, Россия
* E-mail: sde_kuznetsov@inbox.ru
Поступила в редакцию 29.08.2018
После доработки 29.08.2018
Принята к публикации 18.11.2019
Аннотация
Статья посвящена построению численного метода с порядком сильной сходимости 2.5 для стохастических дифференциальных уравнений Ито с многомерным неаддитивным шумом, основанного на унифицированном разложении Тейлора–Стратоновича. Основное внимание уделено подходам и методам среднеквадратической аппроксимации повторных стохастических интегралов Стратоновича кратностей 1–5, численное моделирование которых представляет собой главную проблему при реализации рассмотренного численного метода. Библ. 17.
1. ВВЕДЕНИЕ
Хорошо известно [1]–[5], что численное интегрирование стохастических дифференциальных уравнений (СДУ) Ито, исходя из сильного критерия сходимости приближений [1], широко применяется при численном моделировании выборочных траектории решений СДУ (что необходимо при построении новых математических моделей на основе данных уравнений), численном решении задачи фильтрации сигнала на фоне случайной помехи в различных постановках (линейная фильтрация Калмана-Бьюси, нелинейная оптимальная фильтрация, фильтрация марковской цепи с непрерывным временем и конечным пространством состояний и т.д.), задачи стохастического оптимального управления (в том числе по неполным данным), задач тестирования процедур оценивания параметров стохастических систем и некоторых других задач.
В настоящей статье применяется перспективный подход [1], [2], [6]–[8] к численному интегрированию СДУ Ито, основанный на стохастическом аналоге формулы Тейлора (разложении Тейлора–Стратоновича) [1], [9], [10] для решений СДУ Ито. Этот подход подразумевает конечную дискретизацию временнóй переменной и численное моделирование решения СДУ Ито в дискретные моменты времени с помощью указанного стохастического аналога формулы Тейлора.
В ряде работ [1], [2], [6], [7] содержатся численные схемы с порядками сильной сходимости 1.5, 2.0 и 2.5 для СДУ Ито, однако без эффективных процедур среднеквадратической аппроксимации входящих в них повторных стохастических интегралов (ПСИ) для случая многомерного неаддитивного шума.
В настоящей работе особое внимание уделяется заполнению указанного пробела, т.е. методам численного моделирования ПСИ Стратоновича кратностей 1–5, входящих в рассматриваемый численный метод. Также поясняются достоинства и недостатки применения унифицированного разложения Тейлора–Стратоновича [10] к постороению численных методов для СДУ Ито в сравнении с его аналогом – унифицированным разложением Тейлора–Ито [11].
В статье применяется так называемое, унифицированное разложение Тейлора–Стратоновича [10], позволяющее (в отличие от своего классического аналога [9]) использовать минимальную совокупность ПСИ Стратоновича, что является упрощающим фактором на стадии реализации численного метода. Для аппроксимации ПСИ Стратоновича, входящих в рассматриваемую численную схему с порядком сильной сходимости 2.5, используется метод кратных рядов Фурье–Лежандра, рассмотренный в ряде работ автора [8], [12]–[15]. Важно отметить, что указанный метод кратных рядов Фурье не приводит к дроблению промежутка интегрирования $[t,T]$ упомянутых ПСИ Стратоновича, который представляет собой шаг интегрирования численных методов для СДУ Ито и поэтому является уже достаточно малой величиной без дополнительного дробления.
Ряд численных экспериментов показывает [8], что применение методов численного моделирования ПСИ (в которых применяется дробление промежутка $[t,T]$) приводит к неприемлемо большим вычислительным затратам и накоплению ошибок вычислений.
Пусть задано фиксированное вероятностное пространство ($\Omega $, ${\text{F}}$, ${\text{P}}$) неубывающая совокупность $\sigma $-алгебр ${\text{\{ }}{{{\text{F}}}_{t}},\;t \in [0,T]{\text{\} }}$ на нем и ${{{\text{F}}}_{t}}$-измеримый при всех $t \in [0,T]$ $m$-мерный стандартный винеровский процесс ${{{\mathbf{f}}}_{t}}$ с независимыми компонентами ${\mathbf{f}}_{t}^{{(i)}}$, $i = 1,\; \ldots ,\;m$.
Рассмотрим СДУ Ито в интегральной форме:
(1)
${{{\mathbf{x}}}_{t}} = {{{\mathbf{x}}}_{0}} + \int\limits_0^t {\mathbf{a}} ({{{\mathbf{x}}}_{\tau }},\tau )d\tau + \int\limits_0^t B ({{{\mathbf{x}}}_{\tau }},\tau )d{{{\mathbf{f}}}_{\tau }},\quad {{{\mathbf{x}}}_{0}} = {\mathbf{x}}(0,\omega ),$2. ЯВНАЯ ОДНОШАГОВАЯ ЧИСЛЕННАЯ СХЕМА С ПОРЯДКОМ СИЛЬНОЙ СХОДИМОСТИ 2.5, ОСНОВАННАЯ НА УНИФИЦИРОВАННОМ РАЗЛОЖЕНИИ ТЕЙЛОРА–СТРАТОНОВИЧА
Дадим определение сильной сходимости численного метода для СДУ Ито [1], [7].
Рассмотрим разбиение ${\text{\{ }}{{\tau }_{p}}{\text{\} }}_{{p = 0}}^{N}$ промежутка $[0,T]$ с рангом дробления ${{\Delta }_{N}}$ такое, что $0 = {{\tau }_{0}} < {{\tau }_{1}} < \ldots < {{\tau }_{N}} = T$. Через ${{{\mathbf{y}}}_{{{{\tau }_{p}}}}}\mathop = \limits^{{\text{def}}} {{{\mathbf{y}}}_{p}}$; $p = 0,1,\; \ldots ,\;N$ обозначим дискретную аппроксимацию процесса ${{{\mathbf{x}}}_{t}}$, $t \in [0,T]$ (решение СДУ Ито (1)), соответствующую максимальному шагу дискретизации ${{\Delta }_{N}}$.
Определение 1 (см. [1], [7]). Будем говорить, что дискретная аппроксимация (численный метод) ${{{\mathbf{y}}}_{p}}$; $p = 0,\;1,\; \ldots ,\;N$, соответствующая максимальному шагу дискретизации ${{\Delta }_{N}},$ сходится сильно с порядком $\gamma > 0$ к процессу ${{{\mathbf{x}}}_{t}}$, $t \in [0,T]$, если существуют постоянная $C > 0,$ которая не зависит от ${{\Delta }_{N}}$ и $p$ ($p = 0,1,\; \ldots ,\;N$), а также число $\delta > 0$ такие, что
(2)
${\text{M\{ }}\left| {{{{\mathbf{x}}}_{p}} - {{{\mathbf{y}}}_{p}}} \right|{\text{\} }} \leqslant C{{({{\Delta }_{N}})}^{\gamma }},\quad p = 0,1,\; \ldots ,\;N,$В (2) мы положили ${{{\mathbf{x}}}_{{{{\tau }_{p}}}}}\mathop = \limits^{{\text{def}}} {{{\mathbf{x}}}_{p}}$, $p = 0,1,\; \ldots ,\;N$.
В ряде публикаций [2], [6] авторы рассматривают вместо сильной сходимости среднеквадратическую сходимость, которая в силу неравенства Ляпунова влечет сильную сходимость.
Достаточно нетривиален вопрос, какие ПСИ (Ито или Стратоновича) целесообразно применять для численного моделирования решений СДУ Ито. В разд. 3 настоящей статьи приведен ряд теорем, сформулированных и доказанных автором в [8], [12]–[15], которые демонстрируют, что аппроксимации ПСИ Стратоновича (в рамках метода кратных рядов Фурье–Лежандра [8], [12]–[15]) существенно проще, чем соответствующие аппроксимации ПСИ Ито. Однако процедура оценки среднеквадратической погрешности аппроксимации, наоборот, оказывается проще для ПСИ Ито, нежели для ПСИ Стратоновича.
Рассмотрим явную одношаговую численную схему для СДУ Ито, основанную на унифицированном разложении Тейлора–Стратоновича [10] и имеющую при стандартных условиях [1] порядок сильной сходимости, равный 2.5:
(3)
$\begin{gathered} + \;{{G}_{{{{i}_{2}}}}}{{G}_{{{{i}_{1}}}}}{\mathbf{\bar {a}}}\left. {\left( {I_{{(01){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{2}}{{i}_{1}})q}} + \Delta I_{{(00){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{2}}{{i}_{1}})q}}} \right)} \right) + \sum\limits_{{{i}_{1}},{{i}_{2}},{{i}_{3}},{{i}_{4}} = 1}^m {{{G}_{{{{i}_{4}}}}}} {{G}_{{{{i}_{3}}}}}{{G}_{{{{i}_{2}}}}}{{B}_{{{{i}_{1}}}}}I_{{(0000){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{4}}{{i}_{3}}{{i}_{2}}{{i}_{1}})q}} + \\ + \;\sum\limits_{{{i}_{1}} = 1}^m {\left( {{{G}_{{{{i}_{1}}}}}\bar {L}{\mathbf{\bar {a}}}\left( {\frac{1}{2}I_{{(2){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}})}} + \Delta I_{{(1){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}})}} + \frac{{{{\Delta }^{2}}}}{2}I_{{(0){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}})}}} \right)} \right.} + \\ \end{gathered} $Известно [1], что при стандартных условиях численная схема (3) имеет порядок сильной сходимости 2.5. Отметим здесь лишь условие, которому должны удовлетворять аппроксимации ПСИ Стратоновича, входящие в численную схему (3) :
(5)
${\text{M}}\left\{ {{{{\left( {I_{{({{l}_{1}} \ldots {{l}_{k}}){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}} \ldots {{i}_{k}})}} - I_{{({{l}_{1}} \ldots {{l}_{k}}){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}} \ldots {{i}_{k}})q}}} \right)}}^{2}}} \right\} \leqslant C{{\Delta }^{6}},$На основе численной схемы (3) можно строить ее неявные или многошаговые аналоги [1], [2], [6], [7]. При этом набор ПСИ Стратоновича, необходимый для реализации указанных численных методов, будет таким же, как и для численной схемы (3) .
Отметим, что усеченное унифицированное разложение Тейлора–Стратоновича (на основе которого построена численная схема (3) ) [10] содержит 12 различных типов ПСИ Стратоновича, которые не могут быть связаны линейными соотношениями [10]. Аналогичное классическое разложение Тейлора–Стратоновича [1], [9] содержит уже 17 различных типов ПСИ Стратоновича, часть из которых связаны друг с другом линейными соотношениями и часть имеют большую кратность, нежели ПСИ Стратоновича из (3). Данное обстоятельство обусловливает мотивацию применения численной схемы (3) на основе унифицированного разложения Тейлора–Стратоновича [10].
Основной проблемой на стадии реализации численной схемы (3) является проблема совместного численного моделирования ПСИ Стратоновича, входящих в (3).
В следующем разделе рассмотрим эффективный метод численного моделирования ПСИ Стратоновича.
3. ТЕОРЕМЫ О РАЗЛОЖЕНИЯХ И ОЦЕНКЕ СРЕДНЕКВАДРАТИЧЕСКОЙ ПОГРЕШНОСТИ АППРОКСИМАЦИИ ПСИ СТРАТОНОВИЧА И ИТО
В настоящем разделе приведены формулировки теорем о разложениях и оценке среднеквадратической погрешности аппроксимации ПСИ Стратоновича и Ито методом кратных рядов Фурье–Лежандра и тригонометрических рядов Фурье, сформулированных и доказанных автором в [8], [12]–[15].
Введем в рассмотрение следующие ПСИ Стратоновича и Ито:
(6)
$J{\text{*}}{{[{{\psi }^{{(k)}}}]}_{{T,t}}} = \int\limits_t^{ * T} {{{\psi }_{k}}} ({{t}_{k}}) \ldots \int\limits_t^{ * {{t}_{2}}} {{{\psi }_{1}}} ({{t}_{1}})d{\mathbf{w}}_{{{{t}_{1}}}}^{{({{i}_{1}})}} \ldots d{\mathbf{w}}_{{{{t}_{k}}}}^{{({{i}_{k}})}},$(7)
$J{{[{{\psi }^{{(k)}}}]}_{{T,t}}} = \int\limits_t^T {{{\psi }_{k}}} ({{t}_{k}}) \ldots \int\limits_t^{{{t}_{2}}} {{{\psi }_{1}}} ({{t}_{1}})d{\mathbf{w}}_{{{{t}_{1}}}}^{{({{i}_{1}})}} \ldots d{\mathbf{w}}_{{{{t}_{k}}}}^{{({{i}_{k}})}},$Введем в рассмотрение следующую функцию:
Рассмотрим разбиение ${\text{\{ }}{{\tau }_{j}}{\text{\} }}_{{j = 0}}^{N}$ промежутка $[t,T]$ такое, что
(8)
$t = {{\tau }_{0}} < \ldots < {{\tau }_{N}} = T,\quad {{\Delta }_{N}} = \mathop {{\text{max}}}\limits_{0 \leqslant j \leqslant N - 1} \Delta {{\tau }_{j}} \to 0\quad {\text{при}}\quad N \to \infty ,$Теорема 3.1 (см. [8]). Пусть выполнены следующие условия:
1. ${{\psi }_{i}}(\tau )$; $i = 1,\;2,\; \ldots ,\;k$ – непрерывные на промежутке $[t,T]$ функции;
2. ${\text{\{ }}{{\phi }_{j}}(x){\text{\} }}_{{j = 0}}^{\infty }$ – полная ортонормированная система полиномов Лежандра или тригонометрических функций в пространстве ${{L}_{2}}([t,T]).$
Тогда ПСИ Ито $J{{[{{\psi }^{{(k)}}}]}_{{T,t}}}$ вида (7) разлагается в сходящийся в среднеквадратическом смысле кратный ряд
(9)
$J{{[{{\psi }^{{(k)}}}]}_{{T,t}}} = \mathop {{\text{l}}.{\text{i}}.{\text{m}}.}\limits_{{{p}_{1}}, \ldots ,{{p}_{k}} \to \infty } \sum\limits_{{{j}_{1}} = 0}^{{{p}_{1}}} \ldots \sum\limits_{{{j}_{k}} = 0}^{{{p}_{k}}} {{{C}_{{{{j}_{k}} \ldots {{j}_{1}}}}}} \left( {\prod\limits_{l = 1}^k {\zeta _{{{{j}_{l}}}}^{{({{i}_{l}})}}} - \mathop {{\text{l}}.{\text{i}}.{\text{m}}.}\limits_{N \to \infty } \sum\limits_{({{l}_{1}}, \ldots ,{{l}_{k}}) \in {{\mathcal{G}}_{k}}} {{{\phi }_{{{{j}_{1}}}}}} ({{\tau }_{{{{l}_{1}}}}})\Delta {\mathbf{w}}_{{{{\tau }_{{{{l}_{1}}}}}}}^{{({{i}_{1}})}} \ldots {{\phi }_{{{{j}_{k}}}}}({{\tau }_{{{{l}_{k}}}}})\Delta {\mathbf{w}}_{{{{\tau }_{{{{l}_{k}}}}}}}^{{({{i}_{k}})}}} \right){\kern 1pt} ,$Выпишем в несколько преобразованной и более удобной для применения на практике форме частные случаи теоремы 3.1 для $k = 1,\; \ldots ,\;5$:
(10)
$J{{[{{\psi }^{{(1)}}}]}_{{T,t}}} = \mathop {{\text{l}}.{\text{i}}.{\text{m}}.}\limits_{{{p}_{1}} \to \infty } \sum\limits_{{{j}_{1}} = 0}^{{{p}_{1}}} {{{C}_{{{{j}_{1}}}}}} \zeta _{{{{j}_{1}}}}^{{({{i}_{1}})}},$(11)
$J{{[{{\psi }^{{(2)}}}]}_{{T,t}}} = \mathop {{\text{l}}.{\text{i}}.{\text{m}}.}\limits_{{{p}_{1}},{{p}_{2}} \to \infty } \sum\limits_{{{j}_{1}} = 0}^{{{p}_{1}}} {\sum\limits_{{{j}_{2}} = 0}^{{{p}_{2}}} {{{C}_{{{{j}_{2}}{{j}_{1}}}}}} } \left( {\zeta _{{{{j}_{1}}}}^{{({{i}_{1}})}}\zeta _{{{{j}_{2}}}}^{{({{i}_{2}})}} - {{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{1}} = {{i}_{2}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{1}} = {{j}_{2}}{\text{\} }}}}}} \right),$(12)
$\begin{gathered} J{{[{{\psi }^{{(3)}}}]}_{{T,t}}} = \mathop {{\text{l}}.{\text{i}}.{\text{m}}.}\limits_{{{p}_{1}}, \ldots ,{{p}_{3}} \to \infty } \sum\limits_{{{j}_{1}} = 0}^{{{p}_{1}}} \ldots \sum\limits_{{{j}_{3}} = 0}^{{{p}_{3}}} {{{C}_{{{{j}_{3}}{{j}_{2}}{{j}_{1}}}}}\left( {\zeta _{{{{j}_{1}}}}^{{({{i}_{1}})}}\zeta _{{{{j}_{2}}}}^{{({{i}_{2}})}}\zeta _{{{{j}_{3}}}}^{{({{i}_{3}})}}} \right.} - \\ - \;{{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{1}} = {{i}_{2}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{1}} = {{j}_{2}}{\text{\} }}}}}\zeta _{{{{j}_{3}}}}^{{({{i}_{3}})}} - {{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{2}} = {{i}_{3}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{2}} = {{j}_{3}}{\text{\} }}}}}\zeta _{{{{j}_{1}}}}^{{({{i}_{1}})}} - \left. {{{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{1}} = {{i}_{3}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{1}} = {{j}_{3}}{\text{\} }}}}}\zeta _{{{{j}_{2}}}}^{{({{i}_{2}})}}} \right), \\ \end{gathered} $(13)
$\begin{gathered} - \;{{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{1}} = {{i}_{4}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{1}} = {{j}_{4}}{\text{\} }}}}}\zeta _{{{{j}_{2}}}}^{{({{i}_{2}})}}\zeta _{{{{j}_{3}}}}^{{({{i}_{3}})}} - {{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{2}} = {{i}_{3}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{2}} = {{j}_{3}}{\text{\} }}}}}\zeta _{{{{j}_{1}}}}^{{({{i}_{1}})}}\zeta _{{{{j}_{4}}}}^{{({{i}_{4}})}} - \\ - \;{{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{2}} = {{i}_{4}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{2}} = {{j}_{4}}{\text{\} }}}}}\zeta _{{{{j}_{1}}}}^{{({{i}_{1}})}}\zeta _{{{{j}_{3}}}}^{{({{i}_{3}})}} - {{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{3}} = {{i}_{4}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{3}} = {{j}_{4}}{\text{\} }}}}}\zeta _{{{{j}_{1}}}}^{{({{i}_{1}})}}\zeta _{{{{j}_{2}}}}^{{({{i}_{2}})}} + \\ \end{gathered} $(14)
$\begin{gathered} + \;{{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{1}} = {{i}_{2}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{1}} = {{j}_{2}}{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{3}} = {{i}_{4}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{3}} = {{j}_{4}}{\text{\} }}}}}\zeta _{{{{j}_{5}}}}^{{({{i}_{5}})}} + {{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{1}} = {{i}_{2}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{1}} = {{j}_{2}}{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{3}} = {{i}_{5}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{3}} = {{j}_{5}}{\text{\} }}}}}\zeta _{{{{j}_{4}}}}^{{({{i}_{4}})}} + \\ + \;{{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{1}} = {{i}_{2}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{1}} = {{j}_{2}}{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{4}} = {{i}_{5}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{4}} = {{j}_{5}}{\text{\} }}}}}\zeta _{{{{j}_{3}}}}^{{({{i}_{3}})}} + {{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{1}} = {{i}_{3}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{1}} = {{j}_{3}}{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{i}_{2}} = {{i}_{4}} \ne 0{\text{\} }}}}}{{{\mathbf{1}}}_{{{\text{\{ }}{{j}_{2}} = {{j}_{4}}{\text{\} }}}}}\zeta _{{{{j}_{5}}}}^{{({{i}_{5}})}} + \\ \end{gathered} $В ряде работ автора [13]–[15] теорема 3.1 адаптирована для ПСИ Стратоновича вида (6) кратности 2–5 при различных условиях гладкости функций ${{\psi }_{l}}(\tau )$, $l = 1,\; \ldots ,\;k$, и различных способах суммирования рядов в (11)–(14). Сформулируем некоторые из этих результатов в виде следующей теоремы.
Теорема 3.2 (см. [13]–[15]). Пусть ${\text{\{ }}{{\varphi }_{j}}(x){\text{\} }}_{{j = 0}}^{\infty }$ – полная ортонормированная система полиномов Лежандра или система тригонометрических функций в пространстве ${{L}_{2}}([t,T])$. При этом ${{\psi }_{2}}(s)$ – непрерывно дифференцируемая на интервале $[t,T]$ функция, а ${{\psi }_{1}}(s)$, ${{\psi }_{3}}(s)$ – дважды непрерывно дифференцируемые на интервале $[t,T]$ функции. Тогда имеем
(15)
$J{\text{*}}{{[{{\psi }^{{(k)}}}]}_{{T,t}}} = \mathop {{\text{l}}.{\text{i}}.{\text{m}}.}\limits_{p \to \infty } \sum\limits_{{{j}_{1}}, \ldots ,{{j}_{k}} = 0}^p {{{C}_{{{{j}_{k}} \ldots {{j}_{1}}}}}} \zeta _{{{{j}_{1}}}}^{{({{i}_{1}})}} \ldots \zeta _{{{{j}_{k}}}}^{{({{i}_{k}})}},$Несмотря на относительную сложность разложений (11)–(14) (в сравнении с разложениями ПСИ Стратоновича (теорема 3.2)), именно для ПСИ Ито удается эффективно оценить и даже вычислить точно среднеквадратическую погрешность аппроксимаций вида
(16)
$J[{{\psi }^{{(k)}}}]_{{T,t}}^{q} = \sum\limits_{{{j}_{1}}, \ldots ,{{j}_{k}} = 0}^q {{{C}_{{{{j}_{k}} \ldots {{j}_{1}}}}}} \left( {\prod\limits_{l = 1}^k {\zeta _{{{{j}_{l}}}}^{{({{i}_{l}})}}} - \mathop {{\text{l}}.{\text{i}}.{\text{m}}.}\limits_{N \to \infty } \sum\limits_{({{l}_{1}}, \ldots ,{{l}_{k}}) \in {{\mathcal{G}}_{k}}} {{{\phi }_{{{{j}_{1}}}}}} ({{\tau }_{{{{l}_{1}}}}})\Delta {\mathbf{w}}_{{{{\tau }_{{{{l}_{1}}}}}}}^{{({{i}_{1}})}} \ldots {{\phi }_{{{{j}_{k}}}}}({{\tau }_{{{{l}_{k}}}}})\Delta {\mathbf{w}}_{{{{\tau }_{{{{l}_{k}}}}}}}^{{({{i}_{k}})}}} \right),$В частности справедлива
Теорема 3.3 (см. [12]). Пусть выполнены условия теоремы 3.1 при ${{i}_{1}},\; \ldots ,\;{{i}_{k}} = 1,\; \ldots ,\;m$. Тогда получаем
(17)
$\begin{gathered} {\text{M}}\{ {{(J{{[{{\psi }^{{(k)}}}]}_{{T,t}}} - J[{{\psi }^{{(k)}}}]_{{T,t}}^{q})}^{2}}\} = \int\limits_{{{{[t,T]}}^{k}}} {{{K}^{2}}} ({{t}_{1}},\; \ldots ,\;{{t}_{k}})d{{t}_{1}} \ldots d{{t}_{k}} - \\ - \;\sum\limits_{{{j}_{1}}, \ldots ,{{j}_{k}} = 0}^q {{{C}_{{{{j}_{k}} \ldots {{j}_{1}}}}}} {\text{M}}\left\{ {J{{{[{{\psi }^{{(k)}}}]}}_{{T,t}}}\sum\limits_{({{j}_{1}}, \ldots ,{{j}_{k}})} {\int\limits_t^T {{{\phi }_{{{{j}_{k}}}}}} ({{t}_{k}}} ) \ldots \int\limits_t^{{{t}_{2}}} {{{\phi }_{{{{j}_{1}}}}}} ({{t}_{1}})d{\mathbf{f}}_{{{{t}_{1}}}}^{{({{i}_{1}})}} \ldots d{\mathbf{f}}_{{{{t}_{k}}}}^{{({{i}_{k}})}}} \right\}, \\ \end{gathered} $Поскольку
(18)
${\text{M}}\{ {{(J{{[{{\psi }^{{(k)}}}]}_{{T,t}}} - J[{{\psi }^{{(k)}}}]_{{T,t}}^{q})}^{2}}\} = \int\limits_{{{{[t,T]}}^{k}}} {{{K}^{2}}} ({{t}_{1}},\; \ldots ,{{t}_{k}})d{{t}_{1}} \ldots d{{t}_{k}} - \sum\limits_{{{j}_{1}}, \ldots ,{{j}_{k}} = 0}^q {C_{{{{j}_{k}} \ldots {{j}_{1}}}}^{2}} .$Следует отметить, что ПСИ Стратоновича и Ито вида (6) и (7) совпадают с вероятностью 1 при попарно различных ${{i}_{1}},\; \ldots ,\;{{i}_{k}} = 1,\; \ldots ,\;m$. Этот факт означает, что формула (18) может применяться для вычисления среднеквадратической погрешности аппроксимации ПСИ Стратоновича вида (6) при попарно различных ${{i}_{1}},\; \ldots ,\;{{i}_{k}} = 1,\; \ldots ,\;m$. Заметим также, что правая часть (18) стремится к нулю при $q \to \infty $ в силу равенства Парсеваля.
При фиксированном $k$ и различных сочетаниях ${{i}_{1}},\; \ldots ,\;{{i}_{k}} = 1,\; \ldots ,\;m$ формула (17) порождает достаточно большое количество своих частных случаев, отвечающих конкретным значениям ${{i}_{1}},\; \ldots ,\;{{i}_{k}}$. В связи с этим может оказаться полезной следующая оценка [12], [14]:
4. АППРОКСИМАЦИЯ ПСИ СТРАТОНОВИЧА С ПОМОЩЬЮ КРАТНЫХ РЯДОВ ФУРЬЕ–ЛЕЖАНДРА
Отметим, что в [12] показано преимущество системы полиномов Лежандра перед системой тригонометрических функций при аппроксимации ПСИ Стратоновича и Ито в рамках метода кратных рядов Фурье (теоремы 3.1, 3.2).
Рассмотрим аппроксимации ПСИ Стратоновича, входящие в численную схему (3) , с помощью кратных рядов Фурье–Лежандра (теорема 3.2):
(19)
$\begin{gathered} I_{{(1){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}})}} = - \frac{{{{\Delta }^{{3/2}}}}}{2}\left( {\zeta _{0}^{{({{i}_{1}})}} + \frac{1}{{\sqrt 3 }}\zeta _{1}^{{({{i}_{1}})}}} \right), \\ I_{{(2){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}})}} = \frac{{{{\Delta }^{{5/2}}}}}{3}\left( {\zeta _{0}^{{({{i}_{1}})}} + \frac{{\sqrt 3 }}{2}\zeta _{1}^{{({{i}_{1}})}} + \frac{1}{{2\sqrt 5 }}\zeta _{2}^{{({{i}_{1}})}}} \right), \\ \end{gathered} $(20)
$\begin{gathered} I_{{(01){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}})q}} = - \frac{\Delta }{2}I_{{(00){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}})q}} - \frac{{{{\Delta }^{2}}}}{4}\left( {\frac{1}{{\sqrt 3 }}\zeta _{0}^{{({{i}_{1}})}}\zeta _{1}^{{({{i}_{2}})}}} \right. + \\ + \;\left. {\sum\limits_{i = 0}^q {\left( {\frac{{(i + 2)\zeta _{i}^{{({{i}_{1}})}}\zeta _{{i + 2}}^{{({{i}_{2}})}} - (i + 1)\zeta _{{i + 2}}^{{({{i}_{1}})}}\zeta _{i}^{{({{i}_{2}})}}}}{{\sqrt {(2i + 1)(2i + 5)} (2i + 3)}} - \frac{{\zeta _{i}^{{({{i}_{1}})}}\zeta _{i}^{{({{i}_{2}})}}}}{{(2i - 1)(2i + 3)}}} \right)} } \right), \\ \end{gathered} $(21)
$\begin{gathered} I_{{(10){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}})q}} = - \frac{\Delta }{2}I_{{(00){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}})q}} - \frac{{{{\Delta }^{2}}}}{4}\left( {\frac{1}{{\sqrt 3 }}\zeta _{0}^{{({{i}_{2}})}}\zeta _{1}^{{({{i}_{1}})}}} \right. + \\ + \;\sum\limits_{i = 0}^q {\left. {\left( {\frac{{(i + 1)\zeta _{{i + 2}}^{{({{i}_{2}})}}\zeta _{i}^{{({{i}_{1}})}} - (i + 2)\zeta _{i}^{{({{i}_{2}})}}\zeta _{{i + 2}}^{{({{i}_{1}})}}}}{{\sqrt {(2i + 1)(2i + 5)} (2i + 3)}} + \frac{{\zeta _{i}^{{({{i}_{1}})}}\zeta _{i}^{{({{i}_{2}})}}}}{{(2i - 1)(2i + 3)}}} \right)} \right)} , \\ \end{gathered} $(22)
$I_{{(000){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}})q}} = \sum\limits_{i,j,k = 0}^q {{{C}_{{kji}}}\zeta _{i}^{{({{i}_{1}})}}\zeta _{j}^{{({{i}_{2}})}}\zeta _{k}^{{({{i}_{3}})}}} ,$(23)
$I_{{(100){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}})q}} = \sum\limits_{i,j,k = 0}^q {C_{{kji}}^{{100}}} \zeta _{i}^{{({{i}_{1}})}}\zeta _{j}^{{({{i}_{2}})}}\zeta _{k}^{{({{i}_{3}})}},$(24)
$I_{{(010){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}})q}} = \sum\limits_{i,j,k = 0}^q {C_{{kji}}^{{010}}} \zeta _{i}^{{({{i}_{1}})}}\zeta _{j}^{{({{i}_{2}})}}\zeta _{k}^{{({{i}_{3}})}},$(25)
$I_{{(001){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}})q}} = \sum\limits_{i,j,k = 0}^q {C_{{kji}}^{{001}}} \zeta _{i}^{{({{i}_{1}})}}\zeta _{j}^{{({{i}_{2}})}}\zeta _{k}^{{({{i}_{3}})}},$(26)
$I_{{(0000){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}}{{i}_{4}})q}} = \sum\limits_{i,j,k,l = 0}^q {{{C}_{{lkji}}}} \zeta _{i}^{{({{i}_{1}})}}\zeta _{j}^{{({{i}_{2}})}}\zeta _{k}^{{({{i}_{3}})}}\zeta _{l}^{{({{i}_{4}})}},$(27)
$I_{{(00000){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}}{{i}_{4}}{{i}_{5}})q}} = \sum\limits_{i,j,k,l,r = 0}^q {{{C}_{{rlkji}}}} \zeta _{i}^{{({{i}_{1}})}}\zeta _{j}^{{({{i}_{2}})}}\zeta _{k}^{{({{i}_{3}})}}\zeta _{l}^{{({{i}_{4}})}}\zeta _{r}^{{({{i}_{5}})}},$В работах [8], [12], [14] отмечалось, что коэффициенты Фурье ${{\bar {C}}_{{kji}}}$, ${{\bar {C}}_{{lkji}}}$, $\bar {C}_{{kji}}^{{001}}$, $\bar {C}_{{kji}}^{{010}}$, $\bar {C}_{{kji}}^{{100}}$, ${{\bar {C}}_{{rlkji}}}$ могут быть вычислены точно с помощью компьютерных пакетов символьных преобразований таких, как, например, DERIVE или MAPLE. В монографии [8] составлены таблицы точно вычисленных с помощью пакета DERIVE указанных коэффициентов Фурье. Отметим, что указанные коэффициенты Фурье не зависят от шага интегрирования ${{\tau }_{{p + 1}}} - {{\tau }_{p}}$ численного метода, который может быть и переменным.
Вообще говоря, минимальные числа $q$, обеспечивающие выполнение условия (5) для каждой из аппроксимаций (19)–(27), различны и резко убывают с ростом порядка малости (в среднеквадратическом смысле) аппроксимации ПСИ Стратоновича по величине $\Delta $.
Рассмотрим более подробно вопрос выбора указанных чисел $q$.
В силу стандартных соотношений между стохастическими интегралами Стратоновича и Ито [1] с вероятностью 1 справедливы следующие равенства:
Это означает, что среднеквадратические погрешности аппроксимации ПСИ Стратоновича $I_{{(00){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}})}}$, $I_{{(01){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}})}}$, $I_{{(10){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}})}}$ будут равны соответствующим среднеквадратическим погрешностям аппроксимации ПСИ Ито $I_{{(00){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{({{i}_{1}}{{i}_{2}})}}$, $I_{{(01){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{({{i}_{1}}{{i}_{2}})}}$, $I_{{(10){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{({{i}_{1}}{{i}_{2}})}}$, которые могут быть вычислены по теореме 3.3 [12]–[14]:
(28)
${\text{M}}\left\{ {{{{\left( {I_{{(00){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{({{i}_{1}}{{i}_{2}})}} - I_{{(00){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{({{i}_{1}}{{i}_{2}})q}}} \right)}}^{2}}} \right\} = \frac{{{{\Delta }^{2}}}}{2}\left( {\frac{1}{2} - \sum\limits_{i = 1}^q {\frac{1}{{4{{i}^{2}} - 1}}} } \right),$(29)
$\begin{gathered} {\text{M}}\left\{ {{{{\left( {I_{{(10){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{({{i}_{1}}{{i}_{2}})}} - I_{{(10){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{({{i}_{1}}{{i}_{2}})q}}} \right)}}^{2}}} \right\}{\text{M}} = \left\{ {{{{\left( {I_{{(01){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{({{i}_{1}}{{i}_{2}})}} - I_{{(01){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{({{i}_{1}}{{i}_{2}})q}}} \right)}}^{2}}} \right\} = \\ = \;\frac{{{{\Delta }^{4}}}}{{16}}\left( {\frac{5}{9} - 2\sum\limits_{i = 2}^q {\frac{1}{{4{{i}^{2}} - 1}}} } \right. - \sum\limits_{i = 1}^q {\frac{1}{{{{{(2i - 1)}}^{2}}{{{(2i + 3)}}^{2}}}}} - \left. {\sum\limits_{i = 0}^q {\frac{{{{{(i + 2)}}^{2}} + {{{(i + 1)}}^{2}}}}{{(2i + 1)(2i + 5){{{(2i + 3)}}^{2}}}}} } \right),\quad {{i}_{1}} \ne {{i}_{2}}, \\ \end{gathered} $(30)
$\begin{gathered} {\text{M}}\left\{ {{{{\left( {I_{{(10){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{({{i}_{1}}{{i}_{1}})}} - I_{{(10){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{({{i}_{1}}{{i}_{1}})q}}} \right)}}^{2}}} \right\} = {\text{M}}\left\{ {{{{\left( {I_{{(01){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{({{i}_{1}}{{i}_{1}})}} - I_{{(01){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{({{i}_{1}}{{i}_{1}})q}}} \right)}}^{2}}} \right\} = \\ = \;\frac{{{{\Delta }^{4}}}}{{16}}\left( {\frac{1}{9} - \sum\limits_{i = 0}^q {\frac{1}{{(2i + 1)(2i + 5){{{(2i + 3)}}^{2}}}}} - 2\sum\limits_{i = 1}^q {\frac{1}{{{{{(2i - 1)}}^{2}}{{{(2i + 3)}}^{2}}}}} } \right). \\ \end{gathered} $Рассмотрим вопрос об оценке среднеквадратических погрешностей аппроксимации ПСИ Стратоновича 3–5 кратности, входящих в численную схему (3) .
Согласно (28) имеем
(31)
$\begin{gathered} {\text{M}}\left\{ {{{{\left( {I_{{(00){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}})}} - I_{{(00){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}})q}}} \right)}}^{2}}} \right\} = \frac{{{{\Delta }^{2}}}}{2}\sum\limits_{i = q + 1}^\infty {\frac{1}{{4{{i}^{2}} - 1}}} \leqslant \\ \leqslant \;\frac{{{{\Delta }^{2}}}}{2}\int\limits_q^\infty {\frac{1}{{4{{x}^{2}} - 1}}} dx = - \frac{{{{\Delta }^{2}}}}{8}{\text{ln}}\left| {1 - \frac{2}{{2q + 1}}} \right| \leqslant {{C}_{1}}\frac{{{{\Delta }^{2}}}}{q}, \\ \end{gathered} $Поскольку (как уже отмечалось ранее) величина $\Delta $ играет роль шага интегрирования в численных методах для СДУ Ито, то эта величина достаточно мала. Принимая во внимание это обстоятельство, нетрудно заметить, что существует такая постоянная ${{K}_{1}}$, что
(32)
${\text{M}}\left\{ {{{{\left( {I_{{({{l}_{1}} \ldots {{l}_{k}}){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}} \ldots {{i}_{k}})}} - I_{{({{l}_{1}} \ldots {{l}_{k}}){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}} \ldots {{i}_{k}})q}}} \right)}}^{2}}} \right\} \leqslant {{K}_{1}}{\text{M}}\left\{ {{{{\left( {I_{{(00){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}})}} - I_{{(00){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}})q}}} \right)}}^{2}}} \right\},$Из (31) и (32) мы окончательно получаем
(33)
${\text{M}}\left\{ {{{{\left( {I_{{({{l}_{1}} \ldots {{l}_{k}}){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}} \ldots {{i}_{k}})}} - I_{{({{l}_{1}} \ldots {{l}_{k}}){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}} \ldots {{i}_{k}})q}}} \right)}}^{2}}} \right\} \leqslant K\frac{{{{\Delta }^{2}}}}{q},$Заметим, что оценка типа (33) была получена в [1], [2], [6], [17] для случая тригонометрической системы базисных функций и метода аппроксимации ПСИ Стратоновича, основанного на тригонометрических разложениях Фурье компонент векторного винеровского процесса, по которым строится ПСИ Стратоновича [2], [6].
Отметим, что существенно больше информации о числах $q$, входящих в формулы (22)–(27), можно получить с помощью (18) при попарно различных ${{i}_{1}},\; \ldots ,\;{{i}_{5}}$. В частности, уже при $q = 6$ в (22), $q = 2$ в (23)–(26) и $q = 1$ в (27) имеем
(34)
${\text{M}}\left\{ {{{{\left( {I_{{(000){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}})}} - I_{{(000){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}})6}}} \right)}}^{2}}} \right\} = \frac{{{{\Delta }^{3}}}}{6} - \sum\limits_{i,j,k = 0}^6 {C_{{kji}}^{2}} \approx 0.01956000{{\Delta }^{3}},$(35)
${\text{M}}\left\{ {{{{\left( {I_{{(100){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}})}} - I_{{(100){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}})2}}} \right)}}^{2}}} \right\} = \frac{{{{\Delta }^{5}}}}{{60}} - \sum\limits_{i,j,k = 0}^2 {{{{(C_{{kji}}^{{100}})}}^{2}}} \approx 0.00815429{{\Delta }^{5}},$(36)
${\text{M}}\left\{ {{{{\left( {I_{{(010){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}})}} - I_{{(010){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}})2}}} \right)}}^{2}}} \right\} = \frac{{{{\Delta }^{5}}}}{{20}} - \sum\limits_{i,j,k = 0}^2 {{{{(C_{{kji}}^{{010}})}}^{2}}} \approx 0.01739030{{\Delta }^{5}},$(37)
${\text{M}}\left\{ {{{{\left( {I_{{(001){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}})}} - I_{{(001){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}})2}}} \right)}}^{2}}} \right\} = \frac{{{{\Delta }^{5}}}}{{10}} - \sum\limits_{i,j,k = 0}^2 {{{{(C_{{kji}}^{{001}})}}^{2}}} \approx 0.02528010{{\Delta }^{5}},$(38)
${\text{M}}\left\{ {{{{\left( {I_{{(0000){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}}{{i}_{4}})}} - I_{{(0000){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}}{{i}_{4}})2}}} \right)}}^{2}}} \right\} = \frac{{{{\Delta }^{4}}}}{{24}} - \sum\limits_{i,j,k,l = 0}^2 {C_{{lkji}}^{2}} \approx 0.02360840{{\Delta }^{4}},$(39)
${\text{M}}\left\{ {{{{\left( {I_{{(00000){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}}{{i}_{4}}{{i}_{5}})}} - I_{{(00000){{\tau }_{{p + 1}}},{{\tau }_{p}}}}^{{ * ({{i}_{1}}{{i}_{2}}{{i}_{3}}{{i}_{4}}{{i}_{5}})1}}} \right)}}^{2}}} \right\} = \frac{{{{\Delta }^{5}}}}{{120}} - \sum\limits_{i,j,k,l,r = 0}^1 {C_{{rlkji}}^{2}} \approx 0.00759105{{\Delta }^{5}}.$Отметим, что в формулах (34)–(39) коэффициенты Фурье вычислялись точно с помощью пакета DERIVE [8]. Соотношения (34)–(39) показывают, что достижение приемлемой точности среднеквадратических аппроксимаций (22)–(27) для ПСИ Стратоновича 3–5 кратности достигается уже при небольших значениях $q$.
Список литературы
Kloeden P.E., Platen E. Numerical solution of stochastic differential equations. Berlin: Springer, 1992.
Milstein G.N., Tretyakov M.V. Stochastic numerics for mathematical physics. Berlin: Springer, 2004.
Arato M. Linear stochastic systems with constant coefficients. A statistical approach. Berlin, Heidelberg, N.Y.: Springer, 1982.
Ширяев А.Н. Основы стохастической финансовой математики. М.: Фазис, 1998. Т. 1, 2.
Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов: Нелинейная фильтрация и смежные вопросы. М.: Наука, 1974. 696 с.
Мильштейн Г.Н. Численное интегрирование стохастических дифференциальных уравнений. Свердловск: Изд-во Уральск. ун-та, 1988.
Kloeden P.E., Platen E., Schurz H. Numerical solution of SDE through computer experiments. Berlin: Springer, 1994.
Кузнецов Д.Ф. Численное интегрирование стохастических дифференциальных уравнений. 2. СПб: Изд-во Политехн. ун-та, 2006. 764 с. http://doi.org/10.18720/SPBPU/2/s17-227
Kloeden P.E., Platen E. The Stratonovich and Ito–Taylor expansions // Math. Nachr. 1991. V. 151. P. 33–50.
Кузнецов Д.Ф. Новые представления разложения Тейлора–Стратоновича // Зап. научн. семинаров ПОМИ РАН. Вероятность и статистика 4. СПб., 2001. Т. 278. С. 141–158.
Кульчицкий О.Ю., Кузнецов Д.Ф. Унифицированное разложение Тейлора–Ито // Зап. науч. сем. ПОМИ им. В.А. Стеклова. 1997. Т. 244. С. 186–204.
Кузнецов Д.Ф. Разработка и применение метода Фурье к численному интегрированию стохастических дифференциальных уравнений Ито // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 7. С. 1108–1120.
Kuznetsov D.F. Strong approximation of multiple Ito and Stratonovich stochastic integrals: Multiple Fourier series approach. 2nd Ed. [In English]. St.-Petersburg: Polytechnical University Publishing House, 2011, 284 p. https://doi.org/10.18720/SPBPU/2/s17-233
Кузнецов Д.Ф. Стохастические дифференциальные уравнения: теория и практика численного решения. С программами в среде MatLab. Изд. 5-е // Электронный Журнал “Дифференциальные Уравнения и Процессы Управления”. 2017. № 2. 1000 с. http://www.math.spbu.ru/diffjournal/pdf/kuznetsov_book3.pdf
Kuznetsov D.F. Expansion of multiple Stratonovich stochastic integrals of fifth multiplicity, based on generalized multiple Fourier series. arXiv:1802.00643 [math.PR]. 2018, 21 p.
Гихман И.И., Скороход А.В. Стохастические дифференциальные уравнения и их приложения. Киев: Наук. думка, 1982.
Kloeden P.E., Platen E., Wright I.W. The approximation of multiple stochastic integrals // Stoch. Anal. Appl. 1992. V. 10. № 4. P. 431–441.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики