1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 3, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 3, стр. 451-461

Асимптотически устойчивые периодические решения в одной задаче атмосферной диффузии примесей: асимптотика, существование, единственность

М. А. Давыдова 1, *, А. Л. Нечаева 1, **

1 Московский государственный университет им. М.В. Ломоносова, физический факультет, кафедра математики
119991 Москва, Ленинские горы, 1, стр. 2., Россия

* E-mail: m.davydova@physics.msu.ru
** E-mail: nechaeva.al15@physics.msu.ru

Поступила в редакцию 31.07.2019
После доработки 23.08.2019
Принята к публикации 18.11.2019

Полный текст (PDF)

Аннотация

Основу настоящей работы составляет использование современных методов асимптотического анализа в задачах реакция-диффузия-адвекция с целью описания классического периодического решения погранслойного типа одной сингулярно возмущенной задачи для нелинейного уравнения диффузии с адвекцией. Рассматривается построение асимптотического приближения произвольного порядка точности такого решения и обоснование формальных построений. Доказывается теорема единственности, устанавливаются асимптотическая устойчивость по Ляпунову и локальная область притяжения периодического решения погранслойного типа. В статье обсуждается одно из приложений этого результата в задачах атмосферной диффузии, а именно: математическое моделирование процессов переноса и химической трансформации антропогенных примесей в пограничном слое атмосферы с учетом периодических, например суточных или сезонных, изменений. Развиваемые аналитические алгоритмы, в том числе для данной задачи, составят основу для нового метода расчета ежедневно корректируемых эмиссионных потоков антропогенных примесей от городских источников, что позволит разработать улучшенные методики определения ежедневных интегральных эмиссий со всей территории города или городской агломерации, основанные на применении аналитических решений модельных задач в сочетании с информацией, полученной на сети станций мониторинга атмосферы. Библ. 15. Фиг. 1.

Ключевые слова: задачи атмосферной диффузии, периодические задачи типа реакция-диффузия-адвекция, нелинейное уравнение диффузии примесей, антропогенное загрязнение атмосферы, фотохимические процессы в атмосфере.

ВВЕДЕНИЕ

В настоящей работе на основе современных асимптотических методов исследуются периодические решения погранслойного типа сингулярно возмущенной задачи для нелинейного уравнения диффузии с адвекцией. В работах [1], [2] рассматривались периодические решения погранслойного типа и контрастные структуры в сингулярно возмущенных параболических задачах реакция–диффузия. Дальнейшие исследования в этом направлении продолжились в работе [3], где с использованием результатов работы [4] исследовалась достаточно общая периодическая задача для одномерного сингулярно возмущенного параболического уравнения с нелинейно входящей в уравнение производной от неизвестной функции. Идеи этой работы, а также работы [4], получили свое дальнейшее развитие в работах [5], [6], направленных на изучение вопроса о существовании контрастных структур в задачах с малой адвекцией.

В данной статье сформулированы достаточные условия существования и единственности классического периодического решения погранслойного типа одной задачи для нелинейного уравнения диффузии с переносом. Асимптотическое приближение решения произвольного порядка точности получается с использованием алгоритма А.Б. Васильевой [7], [8], составляющего основу метода пограничных функций. Обоснование формальных построений основано на использовании принципа сравнения [9], [10] в периодических задачах типа реакция-диффузия-адвекция. Применение методов работы [2] позволяет доказать асимптотическую устойчивость по Ляпунову периодического решения с описанием локальной области притяжения такого решения.

Одним из приложений результатов этой работы являются периодические задачи атмосферной диффузии примесей, описывающие перенос и химическую трансформацию антропогенных примесей в пограничном слое атмосферы. Использование математических моделей реакция–диффузия–адвекция и аналитических решений соответствующих задач направлено на улучшение качества метеорологических прогнозов, позволяющих заблаговременно выявлять предпосылки образования экстремальных ситуаций. В частности, использование периодических аналитических решений соответствующих модельных задач позволит получить более качественную информацию о пространственно-временной структуре распределения эмиссий и о вертикальной стратификации примесей над крупными городами с учетом суточной или сезонной изменчивости в дополнение к информации, полученной по данным наблюдений на сети станций мониторинга атмосферы (см., например, [11]). Развиваемые аналитические алгоритмы, в том числе для данной задачи, составят основу для новых методов расчета ежедневно корректируемых эмиссионных потоков антропогенных примесей от городских источников, что позволит разработать улучшенные методики определения ежедневных интегральных эмиссий со всей территории города или городской агломерации, основанные на применении аналитических решений модельных задач в сочетании с информацией, полученной на сети станций мониторинга атмосферы.

Потребность в улучшенных методах расчета эмиссионных потоков антропогенных примесей также связана с осознанным завышением значений химически активных соединений в атмосфере над российскими городами в глобальных и региональных инвентаризациях EDGAR v 4.2; TNO-MACC и TNO-MACC_II, проводимых группами зарубежных экспертов [12]. Это сильно искажает представление о влиянии российских городов на состояние атмосферы и климат Земли (см., например, [11], [13]). В частности, глобальная инвентаризация EDGAR v 4.2, являющаяся основой для прогноза изменений состава глобальной атмосферы и климата Земли, завышает антропогенные выбросы ${\text{N}}{{{\text{O}}}_{x}}$ от Московского мегаполиса в 2.5 раза, ${\text{C}}{{{\text{H}}}_{4}}$ в 10 раз, ${\text{S}}{{{\text{O}}}_{2}}$ в 30 раз и т.д.

Изменение концентрации примеси $u(x,t)$ с течением времени описывается нелинейным уравнением типа реакция-диффузия-адвекция следующего вида:

(1)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} = \sum\limits_{i = 1}^3 {\frac{\partial }{{\partial {{x}_{i}}}}} \left( {{{k}_{i}}(x,t)\frac{{\partial u}}{{\partial {{x}_{i}}}}} \right) - \sum\limits_{i = 1}^3 {\frac{\partial }{{\partial {{x}_{i}}}}} (u{{\mathcal{A}}_{i}}(x,t)) + F(u,x,t), \\ x \in D \subset {{\mathbb{R}}^{3}},\quad t > 0, \\ \end{gathered} $
где ${{k}_{i}}(x,t)$ – коэффициент турбулентной диффузии в направлении оси ${{x}_{i}}$, ${{\mathcal{A}}_{i}}(x,t)$ – компоненты скорости переноса вещества, $F(u,x,t)$ – объемная плотность источников вещества. Наличие последнего слагаемого в уравнении (1) может быть обусловлено, например, производственными выбросами, фотохимическими процессами, распадом вещества. С учетом того, что частное
$\tfrac{{{{k}_{3}}}}{{L{{v}_{x}}}} = {{({\text{P}}{{{\text{r}}}_{D}}{\text{Re}})}^{{ - 1}}} \sim {{40}^{{ - 1}}} \approx 0.02$
для приземного слоя атмосферы, где ${\text{P}}{{{\text{r}}}_{D}}$ – диффузионное турбулентное число Прандтля, ${\text{Re}}$ – число Рейнольдса, $L$ – характерный пространственный масштаб, ${{v}_{x}}$ – характерная скорость, ${{T}_{x}} = L{\text{/}}{{v}_{x}}$ – характерный временной масштаб, имеем (см. [14])
$\tfrac{{{{k}_{i}}(Lx{\text{'}},{{T}_{x}}t{\text{'}})}}{{L{{v}_{x}}}}: = \varepsilon {{k}_{i}}(x{\text{'}},t{\text{'}}),\quad {{k}_{i}}(x{\text{'}},t{\text{'}}) \sim 1,\quad \varepsilon \sim 0.01.$
Если в качестве ${{v}_{x}}$ положить $\tfrac{{\left\langle {{{k}_{i}}} \right\rangle {\text{P}}{{{\text{r}}}_{D}}{\text{Re}}}}{L}$, где $\left\langle {{{k}_{i}}} \right\rangle $ – среднее значение коэффициента турбулентной диффузии, то в приближении несжимаемой среды получаем уравнение в безразмерных переменных:
(2)
$\frac{{\partial u{\text{'}}}}{{\partial t'}} = \varepsilon \sum\limits_{i = 1}^3 {{{k}_{i}}} (x{\text{'}},t{\text{'}})\frac{{{{\partial }^{2}}u{\text{'}}}}{{\partial x_{i}^{{'2}}}} + \varepsilon \sum\limits_{i = 1}^3 {\frac{{\partial {{k}_{i}}}}{{\partial x_{i}^{'}}}} \frac{{\partial u{\text{'}}}}{{\partial x_{i}^{'}}} - \sum\limits_{i = 1}^3 {\mathcal{A}_{i}^{'}} (x{\text{'}},t{\text{'}})\frac{{\partial u{\text{'}}}}{{\partial x_{i}^{'}}} + \frac{{F(Uu{\text{'}},Lx{\text{'}},{{T}_{x}}t{\text{'}}){{L}^{2}}}}{{U\left\langle {{{k}_{i}}} \right\rangle {\text{P}}{{{\text{r}}}_{D}}{\text{Re}}}},$
где $U$ – характерная величина концентрации примеси. Соответствующий выбор пространственного масштаба приводит к уравнению
(3)
$\begin{gathered} \varepsilon \frac{{\partial u}}{{\partial t}} = {{\varepsilon }^{2}}\sum\limits_{i = 1}^3 {{{k}_{i}}} (x,t)\frac{{{{\partial }^{2}}u}}{{\partial \mathop {{{x}_{i}}}\nolimits^2 }} + {{\varepsilon }^{2}}\sum\limits_{i = 1}^3 {\frac{{\partial {{k}_{i}}}}{{\partial {{x}_{i}}}}} \frac{{\partial u}}{{\partial {{x}_{i}}}} - \varepsilon \sum\limits_{i = 1}^3 \,{{\mathcal{A}}_{i}}(x,t)\frac{{\partial u}}{{\partial {{x}_{i}}}} + f(u,x,t), \\ x \in D \subset {{\mathbb{R}}^{3}},\quad t > 0, \\ \end{gathered} $
где штрихи опущены в целях удобства.

1. ПОСТАНОВКА ЗАДАЧИ. ТЕОРЕМА ЕДИНСТВЕННОСТИ

Пусть скорость переноса по горизонтали много меньше скорости переноса по вертикали, например, рассматривается перенос конвективными потоками в безветренную погоду. С целью получения информации о вертикальной стратификации примеси с учетом суточной или сезонной изменчивости рассматривается периодическая задача для одномерного уравнения:

(4)
$\begin{gathered} \varepsilon \frac{{\partial u}}{{\partial t}} = {{\varepsilon }^{2}}\frac{\partial }{{\partial z}}\left( {k(z,t)\frac{{\partial u}}{{\partial z}}} \right) - \varepsilon \mathcal{A}(z,t)\frac{{\partial u}}{{\partial z}} + f(u,z,t), \\ {{z}_{0}} < z < {{H}_{0}},\quad - {\kern 1pt} \infty < t < \infty , \\ \mathop {\left. u \right|}\nolimits_{z = {{z}_{0}}} = {{u}_{1}}(t),\quad \mathop {\left. {{{u}_{z}}} \right|}\nolimits_{z = {{H}_{0}}} = 0,\quad - {\kern 1pt} \infty < t < \infty , \\ u(z,t) = u(z,t + T),\quad {{z}_{0}} \leqslant z \leqslant {{H}_{0}},\quad - {\kern 1pt} \infty < t < \infty , \\ \end{gathered} $
где $k(z,t) > 0$ – безразмерный коэффициент турбулентной диффузии, $A(z,t)$ – безразмерная скорость переноса по вертикали. Функции $k(z,t)$, $f(u,z,t)$, ${{u}_{1}}(t)$, $A(z,t)$ являются достаточно гладкими T-периодическими функциями, причем $A({{H}_{0}},t)$ = 0.

С целью доказательства единственности классического решения задачи (4) рассмотрим функцию $v = {{u}_{2}} - {{u}_{1}}$, где ${{u}_{1}}$, ${{u}_{2}}$ – несовпадающие классические решения задачи (4). Тогда

(5)
$\begin{gathered} \varepsilon \frac{{\partial v}}{{\partial t}} = \frac{\partial }{{\partial z}}\left( {{{\varepsilon }^{2}}k(z,t)\frac{{\partial v}}{{\partial z}}} \right) - \varepsilon \mathcal{A}(z,t)\frac{{\partial v}}{{\partial z}} + v(z,t)\int\limits_0^1 {\frac{{\partial f}}{{\partial u}}} ({{u}_{\lambda }},z,t)d\lambda , \\ {{z}_{0}} < z < {{H}_{0}},\quad - {\kern 1pt} \infty < t < \infty , \\ \mathop {\left. v \right|}\nolimits_{z = {{z}_{0}}} = 0,\quad \mathop {\left. {{{v}_{z}}} \right|}\nolimits_{z = {{H}_{0}}} = 0,\quad - {\kern 1pt} \infty < t < \infty , \\ v(z,t) = v(z,t + T),\quad {{z}_{0}} \leqslant z \leqslant {{H}_{0}},\quad - {\kern 1pt} \infty < t < \infty , \\ \end{gathered} $
${\text{где}}\;{\kern 1pt} {{u}_{\lambda }} = \lambda {{u}_{2}}(z,t) + (1 - \lambda ){{u}_{1}}(z,t)$.

Домножив равенство (5) на функцию $v(z,t)$ и проинтегрировав по $z$ в пределах от ${{z}_{0}}$ до ${{H}_{0}}$, с учетом граничных условий, имеем

(6)
$\frac{1}{2}\varepsilon \int\limits_{{{z}_{0}}}^{{{H}_{0}}} {\frac{{\partial {{v}^{2}}}}{{\partial t}}} dz = - {{\varepsilon }^{2}}\int\limits_{{{z}_{0}}}^{{{H}_{0}}} k (z,t)\mathop {\left( {\frac{{\partial v}}{{\partial z}}} \right)}\nolimits^2 dz + \frac{\varepsilon }{2}\int\limits_{{{z}_{0}}}^{{{H}_{0}}} {{{v}^{2}}\frac{{\partial A}}{{\partial z}}} dz + \int\limits_{{{z}_{0}}}^{{{H}_{0}}} {{{v}^{2}}} \int\limits_0^1 {{{f}_{u}}} ({{u}_{\lambda }},z,t)d\lambda dz,$
где учтено, что $A({{H}_{0}},t)$ = 0, поскольку перенос вещества на границе z = H0 обусловлен только диффузией. Проинтегрировав равенство (6) по периоду, находим

(7)
${{\varepsilon }^{2}}\int\limits_0^T {\int\limits_{{{z}_{0}}}^{{{H}_{0}}} k } (z,t)\mathop {\left( {\frac{{\partial v}}{{\partial z}}} \right)}\nolimits^2 dzdt - \frac{\varepsilon }{2}\int\limits_0^T {\int\limits_{{{z}_{0}}}^{{{H}_{0}}} {{{v}^{2}}\frac{{\partial A}}{{\partial z}}dzdt} } - \int\limits_0^T {\int\limits_{{{z}_{0}}}^{{{H}_{0}}} {{{v}^{2}}} } (z,t)\int\limits_0^1 {{{f}_{u}}} ({{u}_{\lambda }},z,t)d\lambda dzdt = 0.$

Пусть ${{f}_{u}}(u,z,t) \leqslant 0$ при $z \in [{{z}_{0}},{{H}_{0}}]$, $ - \infty < t < \infty $. Поскольку $k(z,t) > 0$, то из равенства (7) следует, что $v(z,t) \equiv 0$ при $z \in [{{z}_{0}},{{H}_{0}}]$, $t \in [0,T]$, если ${{A}_{z}}(z,t) \leqslant 0$, $z \in [{{z}_{0}},{{H}_{0}}]$, $t \in [0,T]$. В силу непрерывности функции $v(z,t)$ с учетом дополнительных условий (5), имеем $v(z,t) \equiv 0$, $z \in [{{z}_{0}},{{H}_{0}}]$, $ - \infty < t < \infty $.

Таким образом, справедлива

Теорема 1. Задача (4) не может иметь более одного классического решения, если ${{f}_{u}}(u,z,t) \leqslant 0$, ${{A}_{z}}(z,t) \leqslant 0$ при $z \in [{{z}_{0}},{{H}_{0}}]$, $ - \infty < t < \infty $.

Замечание. Ограничения на поведение функции A(z, t) являются естественными, так как скорость воздушных потоков уменьшается с увеличением высоты и на границе атмосферного пограничного слоя обращается в ноль. Их можно ослабить, если при доказательстве теоремы 1 воспользоваться принципом максимума.

2. ФОРМАЛЬНАЯ АСИМПТОТИКА

Введeм обозначения $A(z,t,\varepsilon ): = \mathcal{A}(z,t) - \varepsilon \tfrac{{\partial k}}{{\partial z}}$, $B(u,z,t): = - f(u,z,t)$ и рассмотрим задачу

(8)
$\begin{gathered} \varepsilon \frac{{\partial u}}{{\partial t}} = {{\varepsilon }^{2}}k(z,t)\frac{{{{\partial }^{2}}u}}{{\partial {{z}^{2}}}} - \varepsilon A(z,t,\varepsilon )\frac{{\partial u}}{{\partial z}} - B(u,z,t), \\ {{z}_{0}} < z < {{H}_{0}},\quad - {\kern 1pt} \infty < t < \infty , \\ {{\left. {u{\kern 1pt} } \right|}_{{z = {{z}_{0}}}}} = {{u}_{1}}(t),\quad \mathop {\left. {\frac{{\partial u}}{{\partial z}}{\kern 1pt} } \right|}\nolimits_{z = {{H}_{0}}} = 0,\quad - {\kern 1pt} \infty < t < \infty ,\quad u(z,t) = u(z,t + T),\quad {{z}_{0}} \leqslant z \leqslant {{H}_{0}},\quad - {\kern 1pt} \infty < t < \infty , \\ \end{gathered} $
при условии

Условие 1. Вырожденное уравнение $B(u,z,t) = 0$ имеет $T$ – периодическое решение $u = \varphi (z,t)$ такое, что ${{B}_{u}}(\varphi (z,t),z,t) > 0$ при $z \in [{{z}_{0}},{{H}_{0}}]$, $t \in ( - \infty , + \infty )$.

Требуемый порядок гладкости коэффициентов устанавливается в процессе построения асимптотики.

Далее будем исследовать вопрос о существовании решения погранслойного типа задачи (8), которое близко к решению $u = \varphi (z,t)$ вырожденного уравнения внутри интервала $({{z}_{0}},{{H}_{0}})$, а в точках $z = {{z}_{0}}$ и $z = {{H}_{0}}$ удовлетворяет соответствующим граничным условиям.

В соответствии с методом пограничных функций А.Б. Васильевой асимптотику решения погранслойного типа ищем в виде

(9)
$u(z,t,\varepsilon ) = \bar {u}(z,t,\varepsilon ) + {{\Pi }^{{( + )}}}u({{\rho }_{{( + )}}},t,\varepsilon ) + {{\Pi }^{{( - )}}}u({{\rho }_{{( - )}}},t,\varepsilon ),$
где $\bar {u}(z,t,\varepsilon ) = \varphi (z,t) + \varepsilon {{\bar {u}}_{1}}(z,t) + \ldots $ – регулярное разложение, ${{\Pi }^{{( \pm )}}}u({{\rho }_{{( \pm )}}},t,\varepsilon ) = \Pi _{0}^{{( \pm )}}u({{\rho }_{{( \pm )}}},t) + $ $ + \;\varepsilon \Pi _{1}^{{( \pm )}}u({{\rho }_{{( \pm )}}},t) + \ldots $ – погранслойные разложения, описывающие пограничные слои в окрестности точек $z = {{z}_{0}}$ и $z = {{H}_{0}}$, ${{\rho }_{{( + )}}} = \tfrac{{z - {{H}_{0}}}}{\varepsilon }$, ${{\rho }_{{( - )}}} = \tfrac{{z - {{z}_{0}}}}{\varepsilon }$. Подставляя разложение (9) в задачу (8), получаем задачи для определения коэффициентов разложения (9).

Коэффициенты регулярного разложения определяются как решения конечных уравнений:

(10)
$\begin{gathered} {{{\bar {u}}}_{1}}(z,t) = - \frac{{{{\varphi }_{t}}(z,t) + A(z,t,0){{\varphi }_{z}}(z,t)}}{{{{B}_{u}}(\varphi (z,t),z,t)}}, \\ \ldots \\ {{{\bar {u}}}_{n}}(z,t) = \frac{{k(z,t)\tfrac{{{{\partial }^{2}}{{{\bar {u}}}_{{n - 2}}}}}{{\partial {{z}^{2}}}} - {{g}_{n}}(z,t)}}{{{{B}_{u}}(\varphi (z,t),z,t)}},\quad n \geqslant 2, \\ \end{gathered} $
где функции ${{g}_{n}}(z,t)$ известны.

В окрестности граничной точки $z = {{z}_{0}}$ в нулевом приближении приходим к нелинейной краевой задаче для системы уравнений:

(11)
$\begin{gathered} \frac{{\partial {{{\tilde {z}}}^{{( - )}}}}}{{\partial {{\rho }_{{( - )}}}}} = \frac{{A({{z}_{0}},t,0)}}{{k({{z}_{0}},t)}}\mathop {\tilde {z}}\nolimits^{( - )} + \frac{{B({{{\tilde {u}}}^{{( - )}}},{{z}_{0}},t)}}{{k({{z}_{0}},t)}}, \\ \frac{{\partial {{{\tilde {u}}}^{{( - )}}}}}{{\partial {{\rho }_{{( - )}}}}} = {{{\tilde {z}}}^{{( - )}}},\quad 0 < {{\rho }_{{( - )}}} < \infty , \\ {{{\tilde {u}}}^{{( - )}}}(0,t) = {{u}_{1}}(t),\quad {{{\tilde {u}}}^{{( - )}}}(\infty ,t) = \varphi ({{z}_{0}},t), \\ \end{gathered} $
где ${{\tilde {u}}^{{( - )}}}({{\rho }_{{( - )}}},t) = \varphi ({{z}_{0}},t) + \Pi _{0}^{{( - )}}u({{\rho }_{{( - )}}},t)$. Разрешимость задачи (11) обеспечивается принадлежностью граничного условия ${{\tilde {u}}^{{( - )}}}(0,t) = {{u}_{1}}(t)$ области влияния точки покоя $(\varphi ({{z}_{0}},t),0)$ при любом $t$:

Условие 2. Прямая ${{\tilde {u}}^{{( - )}}} = {{u}_{1}}(t)$ на плоскости (${{\tilde {u}}^{{( - )}}}$, ${{\tilde {z}}^{{( - )}}}$) пересекает сепаратрису, входящую в седло ($\varphi ({{z}_{0}},t)$, 0) при ${{\rho }_{{( - )}}} \to + \infty $.

Для определенности положим ${{u}_{1}}(t) - \varphi ({{z}_{0}},t) > 0$.

Справедлива следующая

Лемма. При фиксированном параметре $t \in ( - \infty ,\infty )$ функции $\Pi _{0}^{{( - )}}u({{\rho }_{{( - )}}},t)$ и ${{\tilde {z}}^{{( - )}}}$ удовлетворяют неравенствам

(12)
$Cexp\left[ {({{\lambda }_{2}}(t) - \sigma (t)){{\rho }_{{( - )}}}} \right] \leqslant \left| {\Pi _{0}^{{( - )}}u({{\rho }_{{( - )}}},t)} \right| \leqslant Cexp\left[ {({{\lambda }_{2}}(t) + \sigma (t)){{\rho }_{{( - )}}}} \right],$
(13)
$Cexp\left[ {({{\lambda }_{2}}(t) - \sigma (t)){{\rho }_{{( - )}}}} \right] \leqslant \left| {{{{\tilde {z}}}^{{( - )}}}({{\rho }_{{( - )}}},t)} \right| \leqslant Cexp\left[ {({{\lambda }_{2}}(t) + \sigma (t)){{\rho }_{{( - )}}}} \right],$
где функция $\sigma (t) > 0$ – достаточно малая, $t \in ( - \infty , + \infty )$, $0 < {{\rho }_{{( - )}}} < \infty $, $C > 0$, ${{\lambda }_{2}}(t)$ – отрицательное собственное значение матрицы

(14)
$\left( {\begin{array}{*{20}{c}} {\frac{{A({{z}_{0}},t,0)}}{{k({{z}_{0}},t)}}}&{\frac{{{{B}_{u}}(\varphi ({{z}_{0}},t),{{z}_{0}},t)}}{{k({{z}_{0}},t)}}} \\ 1&0 \end{array}} \right).$

Не зависящие от $\varepsilon $ положительные постоянные величины, значения которых не являются существенными, здесь и далее обозначаются символом $C$.

Доказательство леммы аналогично соответствующему доказательству из работы [15].

Функции $\Pi _{n}^{{( - )}}u\left( {{{\rho }_{{( - )}}},t} \right)$, $n \geqslant 1$, определяются как решения линейных задач следующего вида:

(15)
$\begin{gathered} \frac{{{{\partial }^{2}}\Pi _{n}^{{( - )}}u}}{{\partial \rho _{{( - )}}^{2}}} - \frac{{A({{z}_{0}},t,0)}}{{k({{z}_{0}},t)}}\frac{{\partial \Pi _{n}^{{( - )}}u}}{{\partial {{\rho }_{{( - )}}}}} - \frac{{{{B}_{u}}({{{\tilde {u}}}^{{( - )}}},{{z}_{0}},t)}}{{k({{z}_{0}},t)}}\Pi _{n}^{{( - )}}u = g_{n}^{{( - )}}\left( {{{\rho }_{{( - )}}},t} \right), \\ \Pi _{n}^{{( - )}}u(0,t) = - {{{\bar {u}}}_{n}}({{z}_{0}},t),\quad \Pi _{n}^{{( - )}}u(\infty ,t) = 0. \\ \end{gathered} $
В частности, используя уравнения (16), находим

$\begin{gathered} g_{1}^{{( - )}}({{\rho }_{{( - )}}},t) = \frac{1}{{k({{z}_{0}},t)}}\left[ {{{B}_{u}}({{{\tilde {u}}}^{{( - )}}},{{z}_{0}},t)\left( {{{{\bar {u}}}_{1}}({{z}_{0}},t) + {{\rho }_{{( - )}}}\frac{{\partial \varphi }}{{\partial z}}({{z}_{0}},t)} \right)} \right. + \\ + \;\left( {\frac{{\partial A}}{{\partial z}}({{z}_{0}},t,0){{\rho }_{{( - )}}} + \frac{{\partial A}}{{\partial \varepsilon }}({{z}_{0}},t,0)} \right)\frac{{\partial {{{\tilde {u}}}^{{( - )}}}}}{{\partial {{\rho }_{{( - )}}}}} + \left( {{{B}_{z}}({{{\tilde {u}}}^{{( - )}}},{{z}_{0}},t) - {{k}_{z}}({{z}_{0}},t)\frac{{{{\partial }^{2}}{{{\tilde {u}}}^{{( - )}}}}}{{\partial \rho _{{( - )}}^{2}}}} \right){{\rho }_{{( - )}}} + \\ + \;A({{z}_{0}},t,0)\frac{{\partial \varphi }}{{\partial z}}({{z}_{0}},t) + \left. {\frac{{\partial {{{\tilde {u}}}^{{( - )}}}}}{{\partial t}}} \right]. \\ \end{gathered} $

Решения задач (15) выписываются в явном виде по аналогии с работой [15]:

(16)
$\begin{gathered} \Pi _{n}^{{( - )}}u({{\rho }_{{( - )}}},t) = - \frac{{{{{\bar {u}}}_{n}}({{z}_{0}},t)}}{{{{{\tilde {z}}}^{{( - )}}}(0,t)}}{{{\tilde {z}}}^{{( - )}}}({{\rho }_{{( - )}}},t) - {{{\tilde {z}}}^{{( - )}}}({{\rho }_{{( - )}}},t) \times \\ \times \;\int\limits_0^{{{\rho }_{{( - )}}}} {\frac{{exp\left( {\tfrac{{A({{z}_{0}},t,0)}}{{k({{z}_{0}},t)}}\tau } \right)d\tau }}{{{{{\tilde {z}}}^{{( - )2}}}(\tau ,t)}}\int\limits_\tau ^{ + \infty } {{{{\tilde {z}}}^{{( - )}}}(s,t)exp\left( { - \frac{{A({{z}_{0}},t,0)}}{{k({{z}_{0}},t)}}s} \right)} } g_{n}^{{( - )}}(s,t)ds. \\ \end{gathered} $

Поскольку в задачу (15) переменная $t$ входит в качестве параметра, то по аналогии с работой [15] при фиксированном $t$ имеем

$\left| {g_{n}^{{( - )}}({{\rho }_{{( - )}}},t)} \right| \leqslant C(t)exp( - \mathop {\tilde {\chi }}\nolimits_n (t){{\rho }_{{( - )}}}),\mathop {\quad \tilde {\chi }}\nolimits_n (t) > 0.$
Используя формулы (16) и применяя лемму, получаем оценки:

$\left| {\Pi _{n}^{{( - )}}u({{\rho }_{{( - )}}},t)} \right| \leqslant C(t)exp( - {{\chi }_{n}}(t){{\rho }_{{( - )}}}),\quad {{\chi }_{n}}(t) > 0,\quad n \geqslant 1.$
Фиг. 1.

Схематичное изображение фазовой плоскости (${{\tilde {u}}^{{( - )}}}$, ${{\tilde {z}}^{{( - )}}}$) с сепаратрисами седла ($\varphi ({{z}_{0}},t)$, 0).

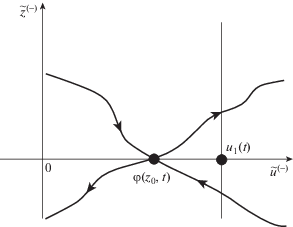
При построении асимптотических приближений решений погранслойного типа в сингулярно возмущенных задачах с граничными условиями Неймана, член нулевого порядка в погранслойном разложении полагают равным нулю для того, чтобы решение с построенной асимптотикой обладало свойством устойчивости (см., например, [16]). Поэтому, положим $\Pi _{0}^{{( + )}}u({{\rho }_{{( + )}}},t) = 0,\;\, - \infty < {{\rho }_{{( + )}}} \leqslant 0,\;\, - \infty < t < \infty $. При $n \geqslant 1$ имеем последовательность линейных задач:

(17)
$\begin{gathered} \frac{{{{\partial }^{2}}\Pi _{n}^{{( + )}}u}}{{\partial \rho _{{( + )}}^{2}}} - \frac{{A({{H}_{0}},t,0)}}{{k({{H}_{0}},t)}}\frac{{\partial \Pi _{n}^{{( + )}}u}}{{\partial {{\rho }_{{( + )}}}}} - \frac{{{{B}_{u}}(\varphi ({{H}_{0}},t),{{H}_{0}},t)}}{{k({{H}_{0}},t)}}\Pi _{n}^{{( + )}}u = g_{n}^{{( + )}}({{\rho }_{{( + )}}},t), \\ \frac{{\partial \Pi _{n}^{{( + )}}u}}{{\partial {{\rho }_{{( + )}}}}}(0,t) = - \frac{{\partial {{{\bar {u}}}_{{n - 1}}}}}{{\partial z}}({{H}_{0}},t),\quad \Pi _{n}^{{( + )}}u( - \infty ,t) = 0, \\ \end{gathered} $
где $g_{n}^{{( + )}}({{\rho }_{{( + )}}},t)$ – известные функции. Например, $g_{1}^{{( + )}}({{\rho }_{{( + )}}},t) = 0$. Решения задач (17) выписываются в явном виде с использованием метода функции Грина:
(18)
$\begin{gathered} \Pi _{n}^{{( + )}}u({{\rho }_{{( + )}}},t) = - \frac{1}{{{{{\tilde {\lambda }}}_{2}}(t)}}\frac{{\partial {{{\bar {u}}}_{{n - 1}}}}}{{\partial z}}({{H}_{0}},t)exp({{{\tilde {\lambda }}}_{2}}(t){{\rho }_{{( + )}}}) + \frac{{{{{\tilde {\lambda }}}_{1}}(t)}}{{{{{\tilde {\lambda }}}_{2}}(t) - {{{\tilde {\lambda }}}_{1}}(t)}} \times \\ \times \;\int\limits_{ - \infty }^{{{\rho }_{{( + )}}}} {\left[ {exp({{{\tilde {\lambda }}}_{2}}(t){{\rho }_{{( + )}}} - {{{\tilde {\lambda }}}_{1}}(t)s) - \frac{{{{{\tilde {\lambda }}}_{2}}(t)}}{{{{{\tilde {\lambda }}}_{1}}(t)}}exp({{{\tilde {\lambda }}}_{1}}(t)({{\rho }_{{( + )}}} - s))} \right]} {\kern 1pt} g_{n}^{{( + )}}(s,t)ds + \frac{{{{{\tilde {\lambda }}}_{1}}(t)}}{{{{{\tilde {\lambda }}}_{2}}(t) - {{{\tilde {\lambda }}}_{1}}(t)}} \times \\ \times \;\int\limits_{{{\rho }_{{( + )}}}}^0 {\left[ {exp({{{\tilde {\lambda }}}_{2}}(t){{\rho }_{{( + )}}} - {{{\tilde {\lambda }}}_{1}}(t)s) - \frac{{{{{\tilde {\lambda }}}_{2}}(t)}}{{{{{\tilde {\lambda }}}_{1}}(t)}}exp({{{\tilde {\lambda }}}_{2}}(t)({{\rho }_{{( + )}}} - s))} \right]} {\kern 1pt} g_{n}^{{( + )}}(s,t)ds, \\ \end{gathered} $
где

${{\tilde {\lambda }}_{{1,2}}}(t) = \frac{{A({{H}_{0}},t,0) \mp \sqrt {{{A}^{2}}({{H}_{0}},t,0) + 4{{B}_{u}}(\varphi ({{H}_{0}},t),t)k({{z}_{0}},t)} }}{{2k({{H}_{0}},t)}}.$

Поскольку функции $g_{n}^{{( + )}}({{\rho }_{{( + )}}},t)$ выражаются через члены асимптотики порядков $k < n$, то при $n \geqslant 2$

$\left| {g_{n}^{{( + )}}} \right| \leqslant C(t)exp\left( {{{\eta }_{{n - 1}}}(t){{\rho }_{{( + )}}}} \right),\quad 0 < {{\eta }_{{n - 1}}} < {{\eta }_{{n - 2}}} < \ldots < {{\eta }_{2}} < {{\eta }_{1}} = {{\tilde {\lambda }}_{2}}(t).$
Используя это и формулу (18), получаем оценки

$\left| {\Pi _{n}^{{( + )}}u\left( {{{\rho }_{{( + )}}},t} \right)} \right| \leqslant C(t)exp\left( {{{{\bar {\eta }}}_{n}}(t){{\rho }_{{( + )}}}} \right),\quad 0 < {{\bar {\eta }}_{n}}(t) < {{\tilde {\lambda }}_{2}}(t).$

3. СУЩЕСТВОВАНИЕ И АСИМПТОТИЧЕСКАЯ УСТОЙЧИВОСТЬ РЕШЕНИЙ ПОГРАНСЛОЙНОГО ТИПА

Доказательство существования решения задачи (8) с асимптотикой (9) базируется на идеях асимптотического метода дифференциальных неравенств (см., например, [1]), основанного на использовании принципа сравнения [9], [10].

Функции ${{\alpha }^{{( \mp )}}}(z,t,\varepsilon ) \in {{C}^{{2,1}}}(D) \cap {{C}^{{1,0}}}(D \cup S)$ суть $T$-периодические по переменной $t$ в области $D: = \left\{ {(z,t):{{z}_{0}} < z < {{H}_{0}},\; - \infty < t < \infty } \right\}$, $S$ – граница области $D$, называются соответственно нижним и верхним решениями задачи (8), если они удовлетворяют неравенствам

$\begin{gathered} {{L}_{\varepsilon }}[{{\alpha }^{{( + )}}}]: = {{\varepsilon }^{2}}\frac{\partial }{{\partial z}}\left( {k(z,t)\frac{{\partial {{\alpha }^{{( + )}}}}}{{\partial z}}} \right) - \varepsilon \mathcal{A}(z,t)\frac{{\partial {{\alpha }^{{( + )}}}}}{{\partial z}} - \varepsilon \frac{{\partial {{\alpha }^{{( + )}}}}}{{\partial t}} - B({{\alpha }^{{( + )}}},z,t) \leqslant 0 \leqslant {{L}_{\varepsilon }}[{{\alpha }^{{( - )}}}], \\ z \in ({{z}_{0}},{{H}_{0}}),\quad - {\kern 1pt} \infty < t < \infty ; \\ {{\alpha }^{{( - )}}}(z,t,\varepsilon ) \leqslant {{\alpha }^{{( + )}}}(z,t,\varepsilon ),\quad z \in [{{z}_{0}},{{H}_{0}}],\quad - {\kern 1pt} \infty < t < \infty ; \\ {{\alpha }^{{( - )}}}({{z}_{0}},t,\varepsilon ) \leqslant {{u}^{1}}(t) \leqslant {{\alpha }^{{( + )}}}({{z}_{0}},t,\varepsilon ),\quad \alpha _{z}^{{( - )}}({{H}_{0}},t,\varepsilon ) \leqslant 0 \leqslant \alpha _{z}^{{( + )}}({{H}_{0}},t,\varepsilon ),\quad - {\kern 1pt} \infty < t < \infty . \\ \end{gathered} $

В качестве ${{\alpha }^{ \pm }}(z,t,\varepsilon )$ в соответствии с [1], [2] выберем следующие функции:

$\begin{gathered} \alpha _{{n + 1}}^{{( \pm )}}(z,t,\varepsilon ) = \pm {{\varepsilon }^{{n + 1}}}\gamma + \sum\limits_{k = 0}^{n + 1} {{{\varepsilon }^{k}}{{{\bar {u}}}_{k}}} (z,t) + \sum\limits_{k = 0}^{n + 1} {{{\varepsilon }^{k}}} \Pi _{k}^{{( - )}}u({{\rho }_{{( - )}}},t) + \\ + \;{{\varepsilon }^{{n + 1}}}\Pi _{\alpha }^{{( \pm )}}u({{\rho }_{{( - )}}},t) + \sum\limits_{k = 0}^{n + 2} {{{\varepsilon }^{k}}} \Pi _{k}^{{( + )}}u({{\rho }_{{( + )}}},t), \\ \end{gathered} $
где $\gamma > 0$, а функции $\Pi _{\alpha }^{{( \pm )}}u$ определяются как решения следующих задач:
$\begin{gathered} \frac{{{{\partial }^{2}}\Pi _{\alpha }^{{( \pm )}}u}}{{\partial \rho _{{( - )}}^{2}}} - \frac{{A({{z}_{0}},t,0)}}{{k({{z}_{0}},t)}}\frac{{\partial \Pi _{\alpha }^{{( \pm )}}u}}{{\partial {{\rho }_{{( - )}}}}} - \frac{{{{B}_{u}}({{{\tilde {u}}}^{{( - )}}},{{z}_{0}},t)}}{{k({{z}_{0}},t)}}\Pi _{\alpha }^{{( \pm )}}u = \\ = \; \pm {\kern 1pt} \frac{\gamma }{{k({{z}_{0}},t)}}({{B}_{u}}({{{\tilde {u}}}^{{( - )}}},{{z}_{0}},t) - {{B}_{u}}(\varphi ({{z}_{0}},t),{{z}_{0}},t)) \mp \Psi ({{\rho }_{{( - )}}},t), \\ \Pi _{\alpha }^{{( \pm )}}u(0,t) = 0,\quad \Pi _{\alpha }^{{( \pm )}}u(\infty ,t) = 0. \\ \end{gathered} $
Здесь функция $\Psi ({{\rho }_{{( - )}}},t)$ удовлетворяет неравенствам:

(19)
$\begin{gathered} 0 < \Psi ({{\rho }_{{( - )}}},t) \leqslant {{C}_{\Psi }}(t)exp( - \bar {\sigma }(t){{\rho }_{{( - )}}}), \\ {{C}_{\Psi }}(t) > 0,\quad t \in ( - \infty , + \infty ),\quad \bar {\sigma }(t) > 0. \\ \end{gathered} $

Докажем выполнение дифференциальных неравенств. Рассмотрим разность

$\alpha _{{n + 1}}^{{( + )}}(z,t,\varepsilon ) - \alpha _{{n + 1}}^{{( - )}}(z,t,\varepsilon ) = 2{{\varepsilon }^{{n + 1}}}\gamma + {{\varepsilon }^{{n + 1}}}V\left( {{{\rho }_{{( - )}}},t} \right),$
где функция $V\left( {{{\rho }_{{( - )}}},t} \right) = \Pi _{\alpha }^{{( + )}}u\left( {{{\rho }_{{( - )}}},t} \right) - \Pi _{\alpha }^{{( - )}}u\left( {{{\rho }_{{( - )}}},t} \right)$ является решением краевой задачи

(20)
$\begin{gathered} \frac{{{{\partial }^{2}}V}}{{\partial \rho _{{( - )}}^{2}}} - \frac{{A({{z}_{0}},t,0)}}{{k({{z}_{0}},t)}}\frac{{\partial V}}{{\partial {{\rho }_{{( - )}}}}} - \frac{{{{B}_{u}}({{{\tilde {u}}}^{{( - )}}},{{z}_{0}},t)}}{{k({{z}_{0}},t)}}V = \\ = - {\kern 1pt} 2\Psi ({{\rho }_{{( - )}}},t) + \frac{{2\gamma }}{{k({{z}_{0}},t)}}({{B}_{u}}({{{\tilde {u}}}^{{( - )}}},{{z}_{0}},t) - {{B}_{u}}(\varphi ({{z}_{0}},t),{{z}_{0}},t)), \\ V(0,t) = 0,\quad V(\infty ,t) = 0. \\ \end{gathered} $

Решение задачи (20) выписывается в явном виде и дается формулой, аналогичной формуле (16):

(21)
$\begin{gathered} V\left( {{{\rho }_{{( - )}}},t} \right) = - 2{{{\tilde {z}}}^{{( - )}}}({{\rho }_{{( - )}}},t)\int\limits_0^{{{\rho }_{{( - )}}}} {\frac{{exp(A({{z}_{0}},t,0){{k}^{{ - 1}}}({{z}_{0}},t)\tau )d\tau }}{{{{{\tilde {z}}}^{{( - )2}}}(\tau ,t)}}} \int\limits_\tau ^\infty {{{{\tilde {z}}}^{{( - )}}}} (s,t) \times \\ \times \;exp( - A({{z}_{0}},t,0){{k}^{{ - 1}}}({{z}_{0}},t)s)\left[ {\frac{\gamma }{{k({{z}_{0}},t)}}({{B}_{u}}({{{\tilde {u}}}^{{( - )}}},{{z}_{0}},t) - {{B}_{u}}(\varphi (t),{{z}_{0}},t)) - \Psi (s,t)} \right]ds. \\ \end{gathered} $

Поскольку ${{\tilde {z}}^{{( - )}}}({{\rho }_{{( - )}}},t) = \tfrac{{\partial {{{\tilde {u}}}^{{( - )}}}}}{{\partial {{\rho }_{{( - )}}}}} < 0$, то, выбирая параметры ${{C}_{\Psi }}(t)$ и $\bar {\sigma }(t)$ в неравенствах (19) таким образом, чтобы выражение в квадратных скобках в интеграле (21) оказалось отрицательным, окончательно получаем

$\alpha _{{n + 1}}^{{( + )}}(z,t,\varepsilon ) - \alpha _{{n + 1}}^{{( - )}}(z,t,\varepsilon ) \geqslant 0,\quad z \in [{{z}_{0}},{{H}_{0}}],\quad t \in ( - \infty ,\infty ).$

Далее находим, что

${{L}_{\varepsilon }}[\alpha _{{n + 1}}^{{( + )}}] = - {{\varepsilon }^{{n + 1}}}\gamma {{B}_{u}}(\varphi (z,t),z,t) - {{\varepsilon }^{{n + 1}}}\Psi ({{\rho }_{{( - )}}},t) + O({{\varepsilon }^{{n + 1}}}) < 0.$

Выполнение неравенства обеспечивается условием 2, выбором $\gamma $ и $\Psi ({{\rho }_{{( - )}}},t)$.

В граничных точках функция $\alpha _{{n + 1}}^{{( + )}}(z,t,\varepsilon )$ удовлетворяет условиям

$\frac{{\partial \alpha _{{n + 1}}^{{( + )}}}}{{\partial z}}({{H}_{0}},t,\varepsilon ) = 0,\quad \alpha _{{n + 1}}^{{( + )}}({{z}_{0}},t,\varepsilon ) = {{\varepsilon }^{{n + 1}}}\gamma + {{u}^{1}}(t) \geqslant {{u}^{1}}(t).$

Аналогично проверяется выполнение дифференциальных неравенств в случае нижнего решения. Таким образом, справедлива

Теорема 2. Пусть выполнены условия 1, 2. Тогда существует классическое T-периодическое решение $u(z,t,\varepsilon )$ задачи (8) такое, что

$\left| {u(z,t,\varepsilon ) - {{U}_{n}}(z,t,\varepsilon )} \right| \leqslant C{{\varepsilon }^{{n + 1}}},\quad z \in [{{z}_{0}},{{H}_{0}}],\quad t \in ( - \infty , + \infty ),$
где
${{U}_{n}}(z,t,\varepsilon ) = \varphi (z,t) + \sum\limits_{k = 1}^n {{{\varepsilon }^{k}}{{{\bar {u}}}_{k}}} (z,t) + \sum\limits_{k = 0}^n {{{\varepsilon }^{k}}} (\Pi _{k}^{{( - )}}u\left( {{{\rho }_{{( - )}}},t} \right) + \Pi _{k}^{{( + )}}u({{\rho }_{{( + )}}},t))$
есть частичная сумма $n$-го порядка асимптотического ряда (9), постоянная $C$ не зависит от $\varepsilon $.

Оценку остаточного члена легко получить, если воспользоваться неравенством треугольника

$\left| {u(z,t,\varepsilon ) - {{U}_{n}}(z,t,\varepsilon )} \right| \leqslant \left| {u(z,t,\varepsilon ) - \alpha _{{n + 1}}^{{( + )}}(z,t,\varepsilon )} \right| + \left| {\alpha _{{n + 1}}^{{( + )}}(z,t,\varepsilon ) - {{U}_{n}}(z,t,\varepsilon )} \right| \leqslant C{{\varepsilon }^{{n + 1}}}.$

Периодические решения задачи (8) можно рассматривать как решения соответствующей начально-краевой задачи на полубесконечном интервале времени:

(22)
$\begin{gathered} {{\varepsilon }^{2}}k(z,t)\frac{{{{\partial }^{2}}v}}{{\partial {{z}^{2}}}} - \varepsilon A(z,t,\varepsilon )\frac{{\partial v}}{{\partial z}} - \varepsilon \frac{{\partial v}}{{\partial t}} - B(v,z,t) = 0, \\ {{z}_{0}} < z < {{H}_{0}},\quad 0 < t < \infty , \\ {{\left. v \right|}_{{z = {{z}_{0}}}}} = {{u}_{1}}(t),\quad \mathop {\left. {\frac{{\partial v}}{{\partial z}}{\kern 1pt} } \right|}\nolimits_{z = {{H}_{0}}} = 0,\quad 0 \leqslant t < \infty , \\ {{\left. v \right|}_{{t = 0}}} = {{v}^{0}}(z),\quad {{z}_{0}} \leqslant z \leqslant {{H}_{0}}, \\ \end{gathered} $
где
$\mathop {\left. {\tfrac{{\partial {{v}_{0}}}}{{\partial z}}{\kern 1pt} } \right|}\nolimits_{z = {{H}_{0}}} = 0,\quad {{v}^{0}}({{z}_{0}}) = {{u}_{1}}(0).$
Если ${{v}^{0}}(z) = u(z,0,\varepsilon )$, где $u(z,t,\varepsilon )$ – решение задачи (8) с асимптотикой (9), то задача (22) имеет решение $v(z,t,\varepsilon ) = u(z,t,\varepsilon )$. Исследование его на наличие асимптотической устойчивости по Ляпунову основано на использовании асимптотического метода дифференциальных неравенств и принципа сравнения [2], [9], [10].

В качестве верхнего и нижнего решений задачи (22) выберем функции:

$\begin{gathered} {{{\bar {\alpha }}}^{{( - )}}}(z,t,\varepsilon ) = u(z,t,\varepsilon ) + exp( - \lambda (\varepsilon )t)(\alpha _{1}^{{( - )}}(z,t,\varepsilon ) - u(z,t,\varepsilon )), \\ {{{\bar {\alpha }}}^{{( + )}}}(z,t,\varepsilon ) = u(z,t,\varepsilon ) + exp( - \lambda (\varepsilon )t)(\alpha _{1}^{{( + )}}(z,t,\varepsilon ) - u(z,t,\varepsilon )), \\ \end{gathered} $
где $\lambda (\varepsilon ) > 0$ определим ниже.

Очевидно, что функции ${{\bar {\alpha }}^{{( - )}}}$ и ${{\bar {\alpha }}^{{( + )}}}$ удовлетворяют соответствующим неравенствам на границе области:

$\begin{gathered} {{{\bar {\alpha }}}^{{( - )}}}({{z}_{0}},t,\varepsilon ) \leqslant {{u}_{1}}(t) \leqslant {{{\bar {\alpha }}}^{{( + )}}}({{z}_{0}},t,\varepsilon ),\quad \bar {\alpha }_{z}^{{( - )}}({{H}_{0}},t,\varepsilon ) \leqslant 0 \leqslant \bar {\alpha }_{z}^{{( + )}}({{H}_{0}},t,\varepsilon ),\quad 0 \leqslant t < \infty ; \\ {{{\bar {\alpha }}}^{{( - )}}}(z,0,\varepsilon ) \leqslant {{v}^{0}}(z) \leqslant {{{\bar {\alpha }}}^{{( + )}}}(z,0,\varepsilon ),\quad z \in [{{z}_{0}},{{H}_{0}}], \\ \end{gathered} $
и ${{\bar {\alpha }}^{{( - )}}} < {{\bar {\alpha }}^{{( + )}}}$ (см. [8]). Докажем, что ${{L}_{\varepsilon }}\left[ {{{{\bar {\alpha }}}^{{( - )}}}} \right] > 0$, ${{L}_{\varepsilon }}[{{\bar {\alpha }}^{{( + )}}}] < 0$. Например,
$\begin{gathered} {{L}_{\varepsilon }}[{{{\bar {\alpha }}}^{{( + )}}}] = exp( - \lambda t)\left\{ {\left[ {{{\varepsilon }^{2}}k(z,t)\frac{{{{\partial }^{2}}\alpha _{1}^{{( + )}}}}{{\partial {{z}^{2}}}}} \right.} \right. - \varepsilon A(z,t,\varepsilon )\frac{{\partial \alpha _{1}^{{( + )}}}}{{\partial z}} - \left. {\varepsilon \frac{{\partial \alpha _{1}^{{( + )}}}}{{\partial t}} - B(\alpha _{1}^{{( + )}},z,t)} \right] + \\ \left. {\mathop + \limits_{}^{} \;[B(\alpha _{1}^{{( + )}},z,t) - B(u,z,t) - {{B}_{u}}(u + \theta exp( - \lambda t)(\alpha _{1}^{{( + )}} - u),z,t)(\alpha _{1}^{{( + )}} - u)] + \varepsilon \lambda (\alpha _{1}^{{( + )}} - u)} \right\} = \\ = \;exp( - \lambda t)\{ L\alpha _{1}^{{( + )}}\, + \,B_{{uu}}^{ * }(z,t){{(\alpha _{1}^{{( + )}}\, - \,u)}^{2}}\, + \,\varepsilon \lambda (\alpha _{1}^{{( + )}}\, - \,u)\} \, = \,exp( - \lambda t)\left\{ { - \varepsilon \gamma {{B}_{u}}(\varphi (z,t),z,t)\, + \,O(\varepsilon )} \right\}\, \leqslant \,0 \\ \end{gathered} $
при достаточно большом $\gamma $, $0 < \theta < 1$, $B_{{uu}}^{ * }(z,t)$ – производная в некоторой промежуточной точке. Здесь учтено, что $(\alpha _{1}^{{( + )}} - u) = O(\varepsilon )$, $\lambda (\varepsilon ) = {{\lambda }_{0}}$.

Аналогично проверяется неравенство ${{L}_{\varepsilon }}[{{\bar {\alpha }}^{{( - )}}}] > 0$. Итак, справедлива

Теорема 3. При выполнении условий 1, 2 классическое $T$-периодическое решение $u(z,t,\varepsilon )$ задачи (8) с асимптотикой (9), как решение задачи (22), асимптотически устойчиво по Ляпунову с областью притяжения

${{v}^{0}}(z) \in [\alpha _{1}^{{( - )}}(z,0,\varepsilon ),\alpha _{1}^{{( + )}}(z,0,\varepsilon )],\quad z \in [{{z}_{0}},{{H}_{0}}].$

4. ПРИМЕРЫ

В качестве примеров рассмотрим наиболее интересные, с точки зрения приложения, частные случаи, для которых коэффициенты асимптотического ряда (9) выписываются в явном виде.

4.1. Периодическое изменение поля концентрации в задаче без переноса

Пусть скорость переноса равна нулю: $\mathcal{A}(z,t) \equiv 0$. Тогда $A(z,t,\varepsilon ) = - \varepsilon \tfrac{{\partial k}}{{\partial z}}$. Следовательно, дифференциальное уравнение фазовых траекторий системы (11) интегрируется в квадратурах, причем сепаратрисы седла ($\varphi ({{z}_{0}},t)$, 0) описываются уравнениями:

(23)
${{\tilde {z}}^{{( - )}}}({{\tilde {u}}^{{( - )}}},t) = \pm \sqrt {2\int\limits_{\varphi ({{z}_{0}},t)}^{{{{\tilde {u}}}^{{( - )}}}} {\frac{{B(\xi ,{{z}_{0}},t)}}{{k({{z}_{0}},t)}}} d\xi } .$

Учитывая второе уравнение системы (11), а также то, что ${{u}_{1}}(t) > \varphi ({{z}_{0}},t)$ по условию, с использованием представления (23) получаем решение нелинейной задачи нулевого приближения:

(24)
$\int\limits_{{{u}_{1}}(t)}^{{{{\tilde {u}}}^{{( - )}}}} {\mathop {\left( {2\int\limits_{\varphi ({{z}_{0}},t)}^u {\frac{{B(\xi ,{{z}_{0}},t)}}{{k({{z}_{0}},t)}}} d\xi } \right)}\nolimits^{ - 1/2} } du = - {{\rho }_{{( - )}}}.$

В этом случае асимптотическое решение погранслойного типа нулевого порядка задачи (8) имеет вид

$u(z,t,\varepsilon ) = \varphi (z,t) - \varphi ({{z}_{0}},t) + {{\tilde {u}}^{{( - )}}}\left( {\frac{{z - {{z}_{0}}}}{\varepsilon },t} \right) + O(\varepsilon ),$
где функция ${{\tilde {u}}^{{( - )}}}$ описывается квадратурной формулой (24).

4.2. Поле концентрации линейного стока вещества

Наличие в атмосфере активных антропогенных примесей, водяных паров, а также солнечного света способствует протеканию химических реакций, скорость которых зависит от степени освещенности. Таким образом, интенсивность фотохимических процессов в атмосфере имеет периодический характер и связана с естественной сменой дня и ночи.

Пусть плотность стоков вещества описывается линейной функцией [14]:

$F(u,z,t) = - \gamma (t)(u - {{u}^{0}}(z,t)),$
где $\gamma (t) > 0$ – скорость распада, $\gamma (t)$, ${{u}^{0}}(z,t)$ – функции, периодические по переменной $t$ с периодом $T$. Тогда $B(u,z,t) = \gamma (t)(u - {{u}^{0}}(z,t))$. Получим формальную асимптотику нулевого порядка програнслойного периодического решения задачи (8) в этом случае.

Вырожденное уравнение $B(u,z,t) = 0$ имеет $T$-периодическое решение $u = {{u}^{0}}(z,t)$, при этом ${{B}_{u}}({{u}^{0}}(z,t),z,t) = \gamma (t) > 0$, $t \in ( - \infty , + \infty )$, то есть выполнено условие устойчивости соответствующего корня.

В нулевом приближении приходим к линейной задаче:

$\begin{gathered} \frac{{{{\partial }^{2}}\Pi _{0}^{{( - )}}u}}{{\partial \rho _{{( - )}}^{2}}} - \frac{{A({{z}_{0}},t,0)}}{{k({{z}_{0}},t)}}\frac{{\partial \Pi _{0}^{{( - )}}u}}{{\partial {{\rho }_{{( - )}}}}} = \frac{{\gamma (t)\Pi _{0}^{{( - )}}u}}{{k({{z}_{0}},t)}}, \\ \Pi _{0}^{{( - )}}u(0,t) + \varphi ({{z}_{0}},t) = {{u}_{1}}(t),\quad \Pi _{0}^{{( - )}}u(\infty ,t) = 0, \\ \end{gathered} $
с решением в явном виде:
(25)
$\Pi _{0}^{{( - )}}({{\rho }_{{( - )}}},t) = ({{u}_{1}}(t) - {{u}^{0}}(z,t))exp({{\lambda }_{2}}(t){{\rho }_{{( - )}}}),$
где

${{\lambda }_{2}}(t) = \tfrac{{A({{z}_{0}},t,0) - \sqrt {{{A}^{2}}({{z}_{0}},t,0) + 4\gamma (t)k({{z}_{0}},t)} }}{{2k({{z}_{0}},t)}}.$

Таким образом, поле концентрации линейного стока вещества описывается функцией

$u(z,t,\varepsilon ) = {{u}^{0}}(z,t) + ({{u}_{1}}(t) - {{u}^{0}}(z,t))exp\left( {{{\lambda }_{2}}(t)\frac{{(z - {{z}_{0}})}}{\varepsilon }} \right) + O(\varepsilon ).$
Авторы благодарят проф. В.Ф. Бутузова за обсуждение результатов работы и полезные рекомендации по ее улучшению.

Список литературы

  1. Нефедов Н.Н. Метод дифференциальных неравенств для некоторых сингулярно возмущенных задач в частных производных // Дифференц. ур-ния. 1995. Т. 31. № 4. С. 719–722.

  2. Нефедов Н.Н. Асимптотический метод дифференциальных неравенств в исследовании периодических контрастных структур: существование, асимптотика, устойчивость // Дифференц. ур-ния. 2000. Т. 36. № 2. С. 262–269.

  3. Нефедов Н.Н., Давыдова М.А. Периодические контрастные структуры в системах типа реакция–диффузия–адвекция // Дифференц. ур-ния. 2010. Т. 46. № 9. С 1300–1312.

  4. Васильева А.Б., Давыдова М.А. О контрастной структуре типа ступеньки для одного класса нелинейных сингулярно возмущенных уравнений второго порядка // Ж. вычисл. матем. и матем. физ. 1998. Т. 38. № 6. С. 938–947.

  5. Nefedov N.N., Nikulin E.I. Existence and stability of periodic contrast structures in the reaction–advection–diffusion problem // Rus. J. Math. Phys. 2015. V. 22. № 2. P. 215–226.

  6. Nefedov N.N., Nikulin E.I., Recke L. On the existence and asymptotic stability of periodic contrast structures in quasilinear reaction–advection–diffusion equations // Rus. J. Math. Phys. 2019. V. 26. № 1. P. 55–69.

  7. Васильева А.Б., Бутузов В.Ф. Асимптотические методы в теории сингулярных возмущений. Научн.-теор. пособие. М.: Высш. школа, 1990.

  8. Васильева А.Б., Бутузов В.Ф., Нефедов Н.Н. Сингулярно возмущенные задачи с пограничными и внутренними слоями // Труды Мат. ин-та им. В.А. Стеклова РАН. 2010. № 268. С. 268.

  9. Amann H. Periodic solutions of semilinear parabolic equations // Nonlinear Analysis. 1978. P. 1–29.

  10. Hess P. Periodic-parabolic boundary value problems and positivity // Pitman research notes in mathematics series. 1991. P. 62–80.

  11. Elansky N.F., Lavrova O.V., Skorokhod A.I., Belikov I.B. Trace gases in the atmosphere over Russian cities // Atmospheric Environment. 2016. V. 143. P. 108–119.

  12. Gurjar B.R., Butler T.M., Lawrence M.G., Lelieveld J. Evaluation of emissions and air qualities in megacities // Atm. Envr. 2008. V. 42. P. 1593–1606.

  13. Elansky N. Air quality and CO emissions in the Moscow megacity // Urban Climate. 2014. V. 8. P. 42–56.

  14. Берлянд М.Е. Прогноз и регулирование загрязнения атмосферы. Гидрометеоиздат, 1985.

  15. Davydova M.A. Existence and stability of solutions with boundary layers in multidimensional singularly perturbed reaction–diffusion–advection problems // Math. Notes. V. 98. P. 909–919.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал