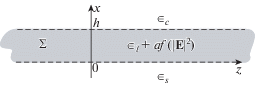Журнал вычислительной математики и математической физики, 2020, T. 60, № 3, стр. 429-450

1. ФОРМУЛИРОВКА ЗАДАЧИ И ВВОДНЫЕ ЗАМЕЧАНИЯ

Пусть $\Sigma = \{ (x,y,z) \in {{\mathbb{R}}^{3}}:0 \leqslant x \leqslant h,(y,z) \in {{\mathbb{R}}^{2}}\} $ – слой, расположенный между двумя полупространствами в ${{\mathbb{R}}^{3}}$, см. фиг. 1.

Рассмотрим распространение монохроматической ТЕ-волны $({\mathbf{E}},{\mathbf{H}}){{e}^{{ - i\omega }}}$ в слое $\Sigma $, где

компоненты полей (1.1) имеют вид здесь $\omega $ – круговая частота, $\gamma $ – неизвестный вещественный параметр (постоянная распространения).

Поля (1.1), (1.2) удовлетворяют уравнениям Максвелла

условию непрерывности касательных компонент поля на границах $x = 0$, $x = h$ и условию излучения на бесконечности: электромагнитное поле экспоненциально затухает при $\left| x \right| \to \infty $; значение ${{\left. {{{e}_{x}}} \right|}_{{x = 0 - 0}}} = A \ne 0$ предполагается фиксированным (без потери общности $A > 0$).

Диэлектрическая проницаемость пространства имеет вид

где $a > 0$ – вещественный параметр, ${{\epsilon }_{s}},\;{{\epsilon }_{l}},\;{{\epsilon }_{c}}$ – положительные вещественные постоянные такие, что а $f \in {{C}^{2}}[0, + \infty )$ – монотонно возрастающая функция и $f(0) = 0$. Во всем пространстве $\mu = {{\mu }_{0}} > 0$ – магнитная проницаемость вакуума.

В сформулированной задаче искомыми являются значения параметра $\gamma $, которые отвечают распространяющимся в $\Sigma $ волнам (1.1), (1.2). Отметим, что зависимость диэлектрической проницаемости от модуля поля и выбор компонент поля в виде (1.2) естественно приводят к требованию о вещественности $\gamma $. Далее будет показано, что параметр $\gamma $ удовлетворяет некоторому (трансцендентному) уравнению, которое называется дисперсионным уравнением. Исследование этого уравнения позволяет получить результаты о разрешимости изучаемой задачи.

Условие (1.5) означает, что в линейном случае среда в слое является оптически более плотной по сравнению со средами, заполняющими полупространства. Такое условие необходимо для существования распространяющихся волн вида (1.1), (1.2) в слое $\Sigma $ при $a = 0$ (см. разд. 3).

Зависимость от модуля поля в (1.4) отвечает эффектам самовоздействия в нелинейной оптике [1]–[3]. Функция $f$ наделена свойствами, которые позволяют применять развитую ниже теорию для изучения широкого круга нелинейностей, отвечающих средам с центром инверсии [1], [2], [4]. Свойствам, наложенным на функцию $f$, в частности, удовлетворяют полиномы по четным степеням с положительными коэффициентами, степенная функция с произвольным положительным показателем степени, логарифмическая нелинейность, различные типы ограниченных нелинейностей [1]–[3], [5]–[12]. Дальнейшие комментарии по поводу постановки задачи см. в п. 1 работы [13].

В нелинейной оптике волноведущих структур многие используемые нелинейные зависимости имеют числовой множитель, который в силу физических ограничений является малым параметром [1], [2], [5]. Это позволяет применить метод возмущений и доказать существование решений нелинейной задачи, близких к решениям соответствующей линейной задачи (см., например, [14], [15]). Необходимо отметить, что метод возмущений, использующий в качестве невозмущенной линейную задачу, позволяет найти только те решения нелинейной задачи, которые близки к решениям (невозмущенной) линейной задачи. Ниже доказано, что для некоторых важнейших нелинейностей возникают решения, не связанные с решениями соответствующей линейной задачи. Аналогичные результаты имеют место и в случае задачи о ТЕ-волнах в нелинейной среде, см., например, [8]–[10], [13], [16]. Другими словами, по крайней мере для некоторых прикладных задач метод возмущений, использующий в качестве невозмущенной линейную задачу, не позволяет получить полные результаты.

Первая достаточно строгая формулировка изучаемой здесь задачи, насколько известно автору, появилась в работе [17]. Результаты, накопившиеся к 1991 г. в этой области, изложены в работе [5], где имеется обширная библиография, см. также работы [6], [18]. Отметим, что даже для простейшей нелинейности $f({{\left| {\mathbf{E}} \right|}^{2}}) = {{\left| {\mathbf{E}} \right|}^{2}}$ существенный прогресс в обсуждаемой задаче для полей (1.1)–(1.2) был достигнут относительно недавно, см. работы [19], [20].

Здесь рассматривается скалярная диэлектрическая проницаемость. Такой подход оправдан в случае распространения ТЕ-волны [13]. При изучении распространения ТМ-волн полная строгость достигается при использовании тензорной (анизотропной) диэлектрической проницаемости, см., например, [21]. Однако, как видно из работы [21], в наиболее общем виде тензорная диэлектрическая проницаемость приводит к чрезвычайно громоздким формулам, которые едва ли могут быть эффективно исследованы в общем случае. Уже случай анизотропной кубической (керровской) нелинейности показывает, сколь громоздкими становятся выкладки [22]. Тем не менее общность развиваемого здесь подхода и глубина полученных результатов, а также во многих случаях возможность использования скалярной проницаемости, являются достаточным основанием для разработки теории в скалярном случае. В связи с обсуждением тензорной диэлектрической проницаемости упомянем работу [23].

В настоящей работе построен общий математический аппарат, позволяющий исследовать сформулированную задачу для широкого круга нелинейностей. Статья имеет следующую структуру: в разд. 2 физическая задача сведена к нелинейной задаче на собственные значения на отрезке; в разд. 3 кратко изложены известные результаты о разрешимости линейной задачи; в разд. 4 получено и исследовано дисперсионное уравнение; в разд. 5 получены достаточные условия существования собственных значений; в разд. 6 получены дальнейшие результаты для нелинейности со степенным ростом и ограниченных нелинейностей; доказательства полученных результатов представлены в разд. 7.

2. НЕЛИНЕЙНАЯ ЗАДАЧА НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ

Подставив поля (1.1), (1.2) в систему (1.3) и обозначив $(\, \cdot \,){\text{'}} = \tfrac{d}{{dx}}$, получаем

Отсюда после простейших преобразований находим при этом ${{h}_{y}}(x) = \tfrac{\omega }{\gamma }\epsilon {{e}_{x}}(x)$.

Обозначив $u(x): = i{{e}_{x}}(x)$, $v(x): = {{e}_{z}}(x)$, из найденного получаем

где $\varepsilon : = {{\omega }^{2}}\mu \epsilon $, $\alpha : = {{\omega }^{2}}\mu a$, а ${{\varepsilon }_{j}}: = {{\omega }^{2}}\mu {{\epsilon }_{j}}$. и $j \in \{ s,l,c\} $.

В полупространствах $x < 0$ и $x > h$ система (2.1) является линейной; ее решения, с учетом условий на бесконечности, имеют вид

где ${{k}_{s}} = \sqrt {{{\gamma }^{2}} - {{\varepsilon }_{s}}} > 0$, ${{k}_{c}} = \sqrt {{{\gamma }^{2}} - {{\varepsilon }_{c}}} > 0$ и ${{\varepsilon }_{s}} \geqslant {{\varepsilon }_{c}}$.

Внутри слоя $\Sigma $ система (2.1) принимает вид

где $u \equiv u(x;\gamma )$, $v \equiv v(x;\gamma )$, $x \in [0,h]$; при этом $\gamma $ – (вещественный) спектральный параметр, $\alpha > 0$ – постоянная, а $f \in {{C}^{2}}[0, + \infty )$ – монотонно возрастающая функция и $f(0) = 0$. Кроме того, если $f$ – ограниченная функция, то дополнительно предполагаем, что $sf{\text{'}}(s)$ ограничена при $s \in [0, + \infty )$.

Известно, что касательные компоненты электромагнитного поля непрерывны на границе раздела сред [24], [25]. Здесь таковыми являются ${{h}_{y}}$ и ${{e}_{z}}$. Из непрерывности этих компонент следуют условия сопряжения

где $\mathop {\left. {[p]} \right|}\nolimits_{x = {{x}_{0}}} = li{{m}_{{x \to {{x}_{0}} - 0}}}p(x) - li{{m}_{{x \to {{x}_{0}} + 0}}}p(x)$.

Используя найденные для полупространств $x < 0$ и $x > h$ решения и условия сопряжения, получаем краевые условия

где ${{u}_{0}}: = u(0 + 0)$, ${{u}_{h}}: = u(h - 0)$, ${{v}_{0}} = {{k}_{s}}{{\gamma }^{{ - 1}}}A$, ${{v}_{h}} = - {{k}_{c}}{{\gamma }^{{ - 1}}}B$ – предельные значения функций $u$ и $v$ на границах слоя, а величина является фиксированной (известной). Предполагаем, что

Из условий ${{k}_{s}},{{k}_{c}} > 0$ и ${{\varepsilon }_{s}} \geqslant {{\varepsilon }_{c}}$ следует, что

Из (2.2), (2.3) видно, что если $(u,v,\hat {\gamma })$ – решение изучаемой задачи для $A > 0$, то $(u, - v, - \hat {\gamma })$ и $( - u,v, - \hat {\gamma })$ – также ее решения для $A > 0$ и $A < 0$ соответственно. Отсюда следует, что достаточно изучить случай $A > 0$ и $\gamma > \sqrt {{{\varepsilon }_{s}}} $.

Итак, задача о распространении волн сведена к нелинейной задаче на собственные (2.2)–(2.6).

Введем необходимое

Определение 1. Число $\gamma = \hat {\gamma }$, удовлетворяющее условию (2.6), и такое, что при фиксированном значении $u(0 - 0) \ne 0$ (без потери общности $u(0 - 0) > 0$) существуют функции $u \equiv u(x;\hat {\gamma })$, $u \equiv v(x;\hat {\gamma })$, которые удовлетворяют системе уравнений (2.2) и условиям (2.3)–(2.5), будем называть собственным значением задачи (2.2)–(2.6), а функции $u(x;\hat {\gamma })$, $v(x;\hat {\gamma })$, соответствующие собственному значению $\widehat \gamma $, – собственными функциями задачи (2.2)–(2.6).

Задачу (2.2)–(2.6) назовем задачей $\mathcal{Q}$, а ее собственные значения обозначим $\hat {\gamma }$ и ${{\hat {\gamma }}_{i}}$; в последнем случае предполагается, что собственные значения упорядочены по возрастанию.

Замечание 1. Определение 1 является неклассическим аналогом известного определения характеристического числа линейной оператор-функции, нелинейно зависящей от спектрального параметра [26].

Подчеркнем, что всюду ниже, когда речь идет о собственных значениях, имеются в виду собственные значения, удовлетворяющие определению 1. Другими словами, приводимые ниже утверждения и теоремы не относятся к понятию собственного значения в общеупотребительном смысле.

Отметим, что многие задачи нелинейной теории волноводов остаются вне пределов досягаемости известных подходов нелинейного анализа, см., например, [8]–[10], [14]–[16]. В частности, ни вариационные методы, ни методы теории ветвления решений [27]–[30] не применимы для полного исследования задачи $\mathcal{Q}$ в случае неограниченной функции $f$ (см. теорему 6 ниже).

3. ЛИНЕЙНАЯ ЗАДАЧА

Линейную задачу (при $\alpha = 0$) назовем задачей ${{\mathcal{Q}}_{0}}$, а ее собственные значения обозначим через $\tilde {\gamma }$ и ${{\tilde {\gamma }}_{i}}$; в последнем случае предполагается, что собственные значения упорядочены по возрастанию. Задача ${{\mathcal{Q}}_{0}}$ является классической в электродинамике и хорошо изучена [31], [32]. А именно, справедливо

Утверждение 1. Существует постоянная ${{h}_{0}} > 0$ такая, что для любого $h > {{h}_{0}}$ задача ${{\mathcal{Q}}_{0}}$ имеет конечное число (не менее одного) положительных и простых собственных значений ${{\tilde {\gamma }}_{i}} \in (\sqrt {{{\varepsilon }_{s}}} ,\sqrt {{{\varepsilon }_{l}}} )$. Если ${{\varepsilon }_{s}} = {{\varepsilon }_{c}}$, то ${{h}_{0}} = 0$.

Собственные значения $\gamma = {{\tilde {\gamma }}_{i}}$ задачи ${{\mathcal{Q}}_{0}}$ являются (однократными) корнями дисперсионного уравнения

где ${{k}_{l}} = \sqrt {{{\varepsilon }_{l}} - {{\gamma }^{2}}} > 0$ [24].

Замечание 2. Если ${{\varepsilon }_{l}} < {{\varepsilon }_{s}}$, то задача ${{\mathcal{Q}}_{0}}$ не имеет решений.

4. ДИСПЕРСИОННОЕ УРАВНЕНИЕ

Для сокращения записи обозначим $f \equiv f({{u}^{2}} + {{v}^{2}})$, $f{\kern 1pt} {\text{'}} \equiv {{\left. {\tfrac{{df(s)}}{{ds}}} \right|}_{{s = {{u}^{2}} + {{v}^{2}}}}}$.

Приведем систему (2.2) к нормальной форме. Дифференцируя по $x$ второе уравнение системы (2.2), получаем

Используя полученное соотношение, систему (2.2) перепишем в виде

Из условий (2.3) и (2.4) следуют условия

где ${{u}_{0}}$ является решением уравнения ${{\varepsilon }_{s}}A = ({{\varepsilon }_{l}} + \alpha f(u_{0}^{2} + v_{0}^{2})){{u}_{0}}$, а ${{v}_{0}} = \tfrac{{{{k}_{s}}}}{\gamma }A$, которые составляют начальные данные задачи Коши для системы уравнений (4.1). Таким образом, изучение задачи $\mathcal{Q}$ естественно начать с изучения вопроса о глобальной однозначной разрешимости указанной задачи Коши.

Из системы (4.1) получаем уравнение $Mdu + Ndv = 0$, где

Поскольку $\tfrac{{\partial M}}{{\partial v}} = \tfrac{{\partial N}}{{\partial u}}$, то найденное уравнение является уравнением в полных дифференциалах. Его решение имеет вид где

Так как постоянная $A$ предполагается известной, то ${{u}_{0}}$ определяется из первого уравнения (2.3). При условиях, наложенных на функцию $f$ и параметры, указанное уравнение имеет единственное решение ${{u}_{0}}$. Это решение удовлетворяет неравенству $0 < {{u}_{0}} < \tfrac{{{{\varepsilon }_{s}}}}{{{{\varepsilon }_{l}}}}A < A$.

Подставляя $x = 0$ в (4.3), находим

где ${{f}_{0}}: = f(u_{0}^{2} + v_{0}^{2})$ и ${{F}_{0}}: = F(u_{0}^{2} + v_{0}^{2})$.

Ниже понадобится следующее

Утверждение 2. Определенная формулой (4.4) величина $C \equiv C(\gamma )$ является положительной при $\gamma \in (\sqrt {{{\varepsilon }_{s}}} , + \infty )$ и справедлива формула

где ${{\beta }_{1}} = ({{\varepsilon }_{l}} - {{\varepsilon }_{s}})(u_{0}^{2} + {{A}^{2}}) + {{\varepsilon }_{s}}{{({{u}_{0}} - A)}^{2}} + \alpha {{F}_{0}}$, ${{\beta }_{2}} = - {{\varepsilon }_{s}}({{\varepsilon }_{l}} - {{\varepsilon }_{s}}){{A}^{2}}$.

Используя (4.3), (4.4) и утверждение 2, можно показать, что задача Коши (2.2), (4.2) имеет единственное непрерывное решение $u \equiv u(x;\gamma )$, $v \equiv v(x;\gamma )$, определенное при $x \in [0,h]$. В деталях этот подход будет реализован в доказательстве утверждения 3, сформулированного ниже.

Введем новые переменные

В переменных (4.6) имеем $f \equiv f(\tau )$ и $f{\kern 1pt} {\text{'}} = df(\tau ){\text{/}}d\tau $.

Учитывая непрерывность $\varepsilon u$ и $v$ и используя условия (2.3), находим

Система (4.1) в переменных (4.6) имеет вид

Интеграл (4.3) примет вид

где постоянная $C$ определена формулой (4.4), $f \equiv f(\tau )$, $F \equiv F(\tau )$.

Поскольку формула (4.9) неявно определяет функцию $\tau \equiv \tau (\eta ;\gamma )$, то второе уравнение системы (4.8) можно переписать в виде $\eta {\text{'}} = w(\eta ;\gamma )$, где

Можно проверить, что $w(\eta ;\gamma ) > 0$ для всех $\gamma $, удовлетворяющих условию (2.6). Действительно, пусть $w$ в какой-то точке обращается в нуль. Из равенства $w = 0$ находим

Подставляя это выражение в (4.9), получаем Легко видеть, что ${{\varepsilon }_{l}} + \alpha f - 2{{\gamma }^{2}} \ne 0$. Действительно, пусть ${{\varepsilon }_{l}} + \alpha f = 2{{\gamma }^{2}}$, тогда ${{\eta }^{2}} = - 4{{\gamma }^{4}} < 0$. Найденное противоречие показывает, что верно первоначальное заключение.

Поделив полученное равенство на ${{\varepsilon }_{l}} + \alpha f - 2{{\gamma }^{2}}$, находим

Поскольку $f$ монотонно возрастает, то $f{\kern 1pt} {\text{'}} > 0$ и, значит, $C < 0$. Но из утверждения 2 известно, что $C > 0$ для всех $\gamma > \sqrt {{{\varepsilon }_{s}}} $. Полученное противоречие показывает, что $w(\eta ;\gamma ) > 0$ для $\gamma > \sqrt {{{n}_{s}}} $.

Итак, $\eta {\text{'}} = w(\eta ;\gamma ) > 0$ и, следовательно, функция $\eta (x)$ монотонно возрастает. Из второй формулы (4.6) следует, что $\eta $ непрерывна если и только если $v$ не обращается в нуль. Предположим, что $v(x)$ имеет $n \geqslant 0$ нулей ${{x}_{1}}, \ldots ,{{x}_{n}} \in (0,h)$, тогда $\eta (x)$ имеет $n$ точек разрыва ${{x}_{1}}, \ldots ,{{x}_{n}}$. Очевидно, что есл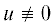и и 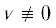, то $u({{x}_{i}}) \ne 0$ для всех $i = \overline {1,n} $. Действительно, если функции $u,\;v$, являющиеся непостоянным решением системы уравнений (4.1), обращаются в нуль в некоторой (одной и той же) точке, то из классических результатов о (локальном) существовании и единственности решения задачи Коши для системы обыкновенных дифференциальных уравнений следует, что $u \equiv 0$, $v \equiv 0$ [33]. Таким образом, все точки разрыва являются точками разрыва II рода.

Из монотонного возрастания $\eta (x)$ и формул (4.7) следует, что

Теперь осталось проинтегрировать уравнение $\eta ' = w(\eta ;\gamma )$ на каждом из (полу) интервалов $[0,{{x}_{1}})$, $({{x}_{1}},{{x}_{2}})$, …, $({{x}_{n}},h]$ и использовать условия (4.11), чтобы получить

Утверждение 3. Задача Коши (4.1), (4.2) глобально и однозначно разрешима, а ее (классическое) решение $u \equiv u(x;\gamma )$, $v \equiv v(x;\gamma )$ непрерывно зависит от точки $(x,\gamma ,\alpha ) \in [0,h] \times (\sqrt {{{\varepsilon }_{s}}} , + \infty ) \times (0, + \infty )$; при этом если функция $v \equiv v(x;\gamma )$ имеет $n \geqslant 0$ нулей при $x \in (0,h)$, то для такого решения справедлива формула

где значение $\eta (h)$, вообще говоря, не фиксировано.

Учитывая знаки выражений (4.7), получаем, что $\eta (x)$ не может быть дифференцируемой на всем интервале $(0,h)$, а необходимо имеет точку разрыва. Подчеркнем, что этот вывод справедлив только если $\eta (x)$ удовлетворяет обоим условиям (4.7). Теперь дисперсионное уравнение задачи $\mathcal{Q}$ получается из соотношения (4.12) при использовании второго из условий (4.7) и имеет вид

где $n = 1,2, \ldots $

Соотношение $\Phi (\gamma ;n) = h$ является семейством (но не системой) уравнений при различных $n$. Функция $\Phi (\gamma ;n)$ не зависит от $h$.

Результатом, позволяющим перейти от изучения задачи $\mathcal{Q}$ к изучению дисперсионного уравнения (4.13), является

Теорема 1 (об эквивалентности). Дисперсионное уравнение (4.13) эквивалентно задаче $\mathcal{Q}$ в том смысле, что число $\hat {\gamma }( > \sqrt {{{\varepsilon }_{s}}} )$ является собственным значением задачи $\mathcal{Q}$ если и только если существует целое число $\hat {n} \geqslant 1$ такое, что $\gamma = \hat {\gamma }$ удовлетворяет уравнению $\Phi (\gamma ;\hat {n}) = h$; при этом собственная функция $v(x;\hat {\gamma })$ имеет $\hat {n}$ (простых) нулей

где $i = \overline {1,\hat {n}} $.

В связи с теоремой 1 естественно ввести

Определение 2. Собственное значение $\hat {\gamma }$ задачи $\mathcal{Q}$ имеет кратность $p$, если $\gamma = \hat {\gamma }$ является корнем кратности $p$ уравнения (4.13).

Принимая во внимание теорему 1, уравнение (4.13) естественно называть интегральным характеристическим уравнением, а функцию $\Phi (\gamma ;n)$ называем h-интегральной характеристической функцией задачи $\mathcal{Q}$.

Вывод уравнения (4.13) основан на том, что функция $w(s;\gamma )$, определенная формулой (4.10), является знакопостоянной. Сохранение знака обеспечивает необращение в нуль знаменателя подынтегрального выражения в (4.13), при условии, что знаменатель существует. Однако функция $\tau \equiv \tau (s;\gamma )$, определенная формулой (4.9), может не существовать при некоторых $\gamma $, а значит, при таких $\gamma $ не существует и функция $w(s;\gamma )$. Обозначим через ${{\gamma }_{{max}}}$ такое наименьшее значение $\gamma > \sqrt {{{\varepsilon }_{s}}} $, при котором не существует (положительной) функции $\tau $. Если $\tau > 0$ существует для любого $\gamma > \sqrt {{{\varepsilon }_{s}}} $, то ${{\gamma }_{{max}}} = + \infty $. Далее будем использовать обозначение $\Gamma : = (\sqrt {{{\varepsilon }_{s}}} ,{{\gamma }_{{max}}})$.

Заметим, что рассуждения предыдущего абзаца не противоречат утверждению 3, поскольку когда речь идет об уравнении (4.13), то выполняются оба условия (4.7), в этом случае $n \geqslant 1$ и, следовательно, $\eta $ принимает все значения из $( - \infty ,\eta (h)) \cup (\eta (0), + \infty )$. В случае обсуждаемой задачи Коши выполняется лишь первое из этих условий, и, таким образом, функция $v$ не обращается в нуль, а функция $\eta (x)$ принимает значения лишь из ограниченного подмножества $\mathbb{R}$ (подробности см. в доказательстве утверждений 3 и 5).

Имеет место

Утверждение 4. Определенная формулой (4.13) функция $\Phi \equiv \Phi (\gamma ;n)$ существует, непрерывна и положительна для всех $\gamma \in \Gamma $.

Из теоремы 1 и утверждения 4 вытекает

Следствие 1. Дисперсионное уравнение (4.13) эквивалентно (в смысле теоремы 1) задаче $\mathcal{Q}$ для всех $\gamma \in \Gamma $.

Ниже получены оценки на ${{\gamma }_{{max}}}$, позволяющие точно определить множество $\Gamma $, на котором имеет место установленная в теореме 1 эквивалентность. А именно, справедливо

Утверждение 5. Если $f$ – неограниченная функция, то ${{\gamma }_{{max}}} = + \infty $; если же $f$ – ограниченная функция, то ${{\gamma }_{{max}}} = \sqrt {{{\varepsilon }_{l}} + \alpha {{f}_{{max}}}} $, где ${{f}_{{max}}} = li{{m}_{{\tau \to + \infty }}}f(\tau )$.

Определенный интерес представляет

Теорема 2 (о периодичности). Пусть $\gamma = \hat {\gamma }$ – собственное значение задачи $\mathcal{Q}$, а $u \equiv u(x;\hat {\gamma })$ и $v \equiv v(x;\hat {\gamma })$, где $x \in [0,h]$, отвечающие ему собственные функции. Если функция $v(x;\hat {\gamma })$ имеет более двух нулей при $x \in (0,h)$, то она периодическая с периодом $\Theta = 2\int_{ - \infty }^{ + \infty } \,\tfrac{{ds}}{{w(s;\hat {\gamma })}}$.

Из теоремы 2, учитывая, что функции $u$ и $v$ связаны соотношением (4.3), получаем такое

Следствие 2. Если собственная функция $v \equiv v(x;\hat {\gamma })$ задачи $\mathcal{Q}$ является периодической, то таковой же является и собственная функция $u \equiv u(x;\hat {\gamma })$; причем периоды обеих собственных функций совпадают.

По поводу периодических решений см. замечание 2 в работе [13].

5. ДОСТАТОЧНЫЕ УСЛОВИЯ СУЩЕСТВОВАНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ

Пусть

где $k = 1,2, \ldots $, а $\Phi (\gamma ;k)$ определена в (4.13).

Поскольку $\Phi (\gamma ;k) > 0$, то $h_{{inf}}^{{(k)}}$ всегда существует и имеет конечное значение. Если существует $\gamma \in \Gamma $, в окрестности которого функция $\Phi (\gamma ;k)$ стремится к бесконечности, то считаем $h_{{sup}}^{{(k)}} = + \infty $. Заметим, что $h_{{sup}}^{{(k)}}$ может стремиться к бесконечности только если $\gamma \to {{\gamma }_{{max}}}$.

Достаточное условие существования по крайней мере одного собственного значения задачи $\mathcal{Q}$ дает

Теорема 3. Пусть $h_{{inf}}^{{(p)}} < h_{{sup}}^{{(p)}}$ для некоторого $p = p{\text{'}}$, и $h$ таково, что $h_{{inf}}^{{(p{\text{'}})}} < h < h_{{sup}}^{{(p{\text{'}})}}$, тогда задача $\mathcal{Q}$ имеет, по крайней мере, одно решение.

Пусть $\Delta = [0, + \infty ) \subset \mathbb{R}$, ${{B}_{\delta }}(x)$ – открытый шар радиуса $\delta $ с центром в точке $x$, $\delta > 0$ фиксированное число. Обозначим через $R_{\Delta }^{\delta } = \bigcup\nolimits_{x \in \Delta } \,{{B}_{\delta }}(x)$ – (открытую) окрестность множества $\Delta $ на комплексной плоскости $\mathbb{C}$. Тогда имеет место

Утверждение 6. Функция $\tau (\eta ;\gamma )$, неявно заданная формулой (4.9), существует, непрерывна и положительна для всех $(\eta ,\gamma ) \in \mathbb{R} \times \Gamma $. Если при этом $f \equiv f(z)$ является аналитической функцией $z$ при $z \in R_{\Delta }^{\delta } \subset \mathbb{C}$, то $\tau (\eta ;\gamma )$ аналитически зависит от $\gamma $ при $\gamma \in \Gamma $.

Из результатов следствия 1 и утверждения 6 вытекает

Теорема 4. Пусть $h_{{inf}}^{{(p)}} < h_{{sup}}^{{(p)}}$ для всех $p$, функция $f(z)$ является аналитической функцией $z$ при $z \in R_{\Delta }^{\delta } \subset \mathbb{C}$ в $\mathbb{C}$ и $h$ таково, что для некоторого $p = p{\text{'}}$ выполняется неравенство $h_{{inf}}^{{(p{\text{'}})}} < h < h_{{sup}}^{{(p{\text{'}})}}$, тогда множество собственных значений задачи $\mathcal{Q}$ не пусто и является дискретным на $\Gamma $, то есть на каждом отрезке $\Gamma {\text{'}} \subset \Gamma $ содержится не более конечного числа (изолированных) собственных значений.

Величины $h_{{inf}}^{{(k)}}$ и $h_{{sup}}^{{(k)}}$ можно находить численно.

Пусть параметры задачи $\mathcal{Q}$ таковы, что отвечающая ей (линейная) задача ${{\mathcal{Q}}_{0}}$ имеет $k$ собственных значений. В этих условиях можно доказать существование собственных значений задачи $\mathcal{Q}$, близких к решениям задачи ${{\mathcal{Q}}_{0}}$, если постоянная $\alpha ( > 0)$ достаточно мала.

Сначала докажем, что имеет место

Утверждение 7. Если $\sqrt {{{\varepsilon }_{s}}} < \gamma < \sqrt {{{\varepsilon }_{l}}} $, то $li{{m}_{{\alpha \to + 0}}}\Phi (\gamma ;n) = {{\Phi }_{0}}(\gamma ;n)$, где $n \geqslant 1$ – целое число, и имеет место уравнение

С помощью утверждения 7 можно показать, что справедлива

Теорема 5. Пусть задача ${{\mathcal{Q}}_{0}}$ имеет $k$ решений ${{\tilde {\gamma }}_{i}}$ $(i = \overline {1,k} )$, тогда найдется постоянная $\alpha {\text{''}} > 0$ такая, что для любого положительного $\alpha = \alpha {\text{'}} < \alpha {\text{''}}$ существует по крайней мере $k$ собственных значений ${{\hat {\gamma }}_{i}}$ $(i = \overline {1,k} )$ задачи $\mathcal{Q}$ и верно, что ${{\hat {\gamma }}_{i}} \in (\sqrt {{{\varepsilon }_{s}}} ,\sqrt {{{\varepsilon }_{l}}} )$, при этом $li{{m}_{{\alpha {\text{'}} \to + 0}}}{{\hat {\gamma }}_{i}} = {{\tilde {\gamma }}_{i}}$ $(i = \overline {1,k} )$.

Доказательство этой теоремы по существу представляет собой вариант метода возмущений и основано на использовании уравнений (4.13) и (5.1). Аналогичный результат может быть доказан с использованием принципиально иного подхода, основанного на полуобращении с помощью функции Грина линейной части дифференциального оператора, определенного уравнениями системы (2.2). Такой подход в случае двухпараметрических задач на собственные значения реализован, например, в работах [14], [15].

Вычислив интегралы в (5.1) и упростив, получим уравнение

где ${{k}_{l}} = \sqrt {{{\varepsilon }_{l}} - {{\gamma }^{2}}} $, $n = 1,2, \ldots $ Взяв $tan$ от полученного уравнения, приходим к (3.1).

Дальнейшие результаты о собственных значениях задачи $\mathcal{Q}$ получены в разд. 6 при дополнительных условиях на функцию $f$ и без предположения о малости $\alpha $.

Замечание 3. Из теоремы 1 следует, что если $\gamma = \hat {\gamma }$ является решением уравнения $\Phi (\gamma ;\hat {n}) = h$, то собственная функция $v(x;\hat {\gamma })$ имеет $\hat {n}$ нулей. В задаче $\mathcal{Q}$ могут существовать собственные функции, отвечающие различным собственным значениям, но имеющие одно и то же число нулей. В задаче ${{\mathcal{Q}}_{0}}$, для всякого допустимого целого $n \geqslant 1$ существует не более одной собственной функции, которая имеет $n$ нулей.

6. ПРИМЕРЫ И ПРИЛОЖЕНИЯ

Из формулы (4.13) следует неравенство

где $n = 1,2, \ldots $,

Неравенство (6.1) позволяет свести изучение разрешимости задачи $Q$ к изучению поведения $T(\gamma )$ при $\gamma \to {{\gamma }_{{max}}}$.

Если нелинейность $f$ является ограниченной функцией, то уравнение (4.13) вместе с интегралом позволяет выяснить разрешимость соответствующей нелинейной задачи, см. п. 6.2.

Для удобства введем обозначения

В случае когда нелинейность $f$-неограниченная функция, то полезным может оказаться

Утверждение 8. Справедлива формула

где $\tau = {{\tau }_{0}}$ – (единственный) положительный корень уравненияа $\tau = {{\tau }_{\infty }}$ – (единственный) положительный корень уравнения $Q(\tau ) - P(\tau ) = 0$.

7. ДОКАЗАТЕЛЬСТВА

Доказательство утверждения 2. Формулу (4.4) можно привести к виду

Отсюда очевидно, что $C > 0$ при ${{\gamma }^{2}} \leqslant {{\varepsilon }_{l}}$.

Принимая во внимание первую формулу (2.3) и то, что ${{v}_{0}} = \tfrac{{{{k}_{s}}}}{\gamma }A$, выражение (4.4) можно записать в виде

Отсюда ясно, что $C > 0$ при ${{\gamma }^{2}} \geqslant {{\varepsilon }_{l}}$.

Формула (4.5) элементарно следует из (4.4).

Доказательство утверждения 3. Если функции $f(s)$ и $sf{\kern 1pt} {\text{'}}(s)$ являются ограниченными при $s \in [0, + \infty )$, то известно, что задача Коши (2.2), (4.2) имеет единственное непрерывное решение $u \equiv u(x;\gamma )$, $v \equiv v(x;\gamma )$, определенное при $x \in [0,h]$ [44].

Если $f$ не ограничена, то воспользуемся следующей процедурой. Итак, пусть $v(x)$ имеет $n \geqslant 0$ нулей ${{x}_{1}}, \ldots ,{{x}_{n}} \in (0,h)$, тогда $\eta (x)$ имеет $n$ точек разрыва ${{x}_{1}}, \ldots ,{{x}_{n}}$; причем все точки разрыва являются точками разрыва II рода.

Интегрируя уравнение $\eta {\text{'}} = w(\eta ;\gamma )$ на каждом из (полу) интервалов $[0,{{x}_{1}})$, $({{x}_{1}},{{x}_{2}})$, …, $({{x}_{n}},h]$, получаем

Подставляя $x = 0$, $x = {{x}_{{i + 1}}} - 0$, $x = h$ в (первую, вторую и третью соответственно) строки (7.1), находим С учетом найденных ${{c}_{i}}$ формулы (7.1) принимают вид

Подставляя $x = {{x}_{1}} - 0$, $x = {{x}_{i}} + 0$, $x = {{x}_{n}} + 0$ в (первую, вторую и третью соответственно) строки предыдущей формулы, получаем

Отсюда, принимая во внимание первую формулу (4.7) и формулы (4.11), находим

Формулы (7.2) дают явные выражения для расстояний между нулями функции ${v}$, в частности, отсюда легко получить явную формулу для $i$-го нуля ${{x}_{i}}$ функции $v$. Кроме того, из формул (7.2) следует сходимость всех рассматриваемых несобственных интегралов.

Далее, складывая все соотношения (7.2), получаем соотношение

которое есть (4.12).

Проведенные построения позволяют утверждать, что задача Коши (2.2), (4.2) глобально и однозначно разрешима при $x \in [0,h]$. Ее решение $u \equiv u(x;\gamma )$, $v \equiv v(x;\gamma )$ непрерывно зависит от $x$ и параметров $\gamma ,\;\alpha $ при $(x,\gamma ,\alpha ) \in [0,h] \times (\sqrt {{{\varepsilon }_{s}}} , + \infty ) \times (0, + \infty )$. Этот результат следует из непрерывности правых частей системы уравнений (2.2) и условий (4.2) по переменным $x,u,{v}$ и параметрам.

Рассмотрим решение $u \equiv u(x;\gamma )$, $v \equiv v(x;\gamma )$ задачи Коши (2.2), (4.2). В случае если выполняются только условия (4.2), величина $\eta $ не обязательно изменяется от $ - \infty $ до $ + \infty $. Например, если $f$ ограничена и $\gamma > {{\gamma }_{{max}}}$, то решение $u$ не обращается в нуль. Это приводит к тому, что переменная $\eta $ изменяется в области $(\eta (0),\delta )$, где $\delta \equiv \delta (\gamma )$ и $\delta < + \infty $.

Доказательство теоремы 1. Поскольку уравнение (4.13) является следствием задачи $\mathcal{Q}$, то всякое собственное значение этой задачи является также и корнем этого уравнения. Докажем обратное. Пусть $\gamma = \hat {\gamma }$ – решение дисперсионного уравнения (4.13) при $n = \hat {n}$ и выполняются условия (4.2). Заметим, что соотношения (4.2) дают первое из условий (2.3).

Рассмотрим задачу Коши для системы уравнений (4.1) с условиями (4.2). Существование единственного непрерывного решения $u \equiv u(x;\gamma )$, $v \equiv v(x;\gamma )$ этой задачи, определенного при $x \in [0,h]$, следует из утверждения 3.

Используя найденное решение $u,v$ задачи Коши, построим функции $\tau = {{u}^{2}} + {{{v}}^{2}}$ и $\eta = ({{\varepsilon }_{l}} + \alpha f)\tfrac{u}{v}$. Ясно, что $\eta (0;\hat {\gamma }) = \tfrac{{{{\varepsilon }_{s}}\hat {\gamma }}}{{{{k}_{s}}}}$. Предположим, что $\eta (h;\hat {\gamma }) \ne - \tfrac{{{{\varepsilon }_{s}}\hat {\gamma }}}{{{{k}_{c}}}}$. Для определенности пусть $\eta (h;\hat {\gamma }) = - a < - \tfrac{{{{\varepsilon }_{s}}\hat {\gamma }}}{{{{k}_{c}}}}$.

При помощи $\tau $ и $\eta $ построим выражение

аналогичное (4.13). Последнее соотношение есть в точности Поскольку $\gamma = \hat {\gamma }$ является решением уравнения (4.13) при $n = \hat {n}$, то

Вычислив разность двух последних выражений, получаем

Поскольку $w(s;\gamma ) > 0$, то очевидно, что допущение $ - a < - \tfrac{{\widehat \gamma {{\varepsilon }_{c}}}}{{{{k}_{c}}}}$ неверно. Также неверно и допущение $ - a > - \tfrac{{\hat {\gamma }{{\varepsilon }_{c}}}}{{{{k}_{c}}}}$. Стало быть $ - a = - \tfrac{{\hat {\gamma }{{\varepsilon }_{c}}}}{{{{k}_{c}}}}$.

По построению функции $u,\;v$ удовлетворяют первому из условий (2.3). Выполнение условия $\eta (h) = - \tfrac{{\hat {\gamma }{{\varepsilon }_{c}}}}{{{{k}_{c}}}}$ означает, что $u,\;v$ удовлетворяют и второму из условий (2.3). Но тогда $u,\;v$ являются собственными функциями, а $\gamma = \hat {\gamma }$ – собственным значением. Таким образом, (спектральная) эквивалентность задачи $\mathcal{Q}$ и уравнения (4.13) доказана.

Формулы (7.2) дают явные выражения для расстояний между нулями функции $v$, в частности, отсюда получается формула для $i$-го нуля ${{x}_{i}}$ функции $v$.

Доказательство утверждения 4. По определению множества $\Gamma $ функция $\tau \equiv \tau (\eta ;\gamma ) > 0$ существует при всех $\gamma \in \Gamma $ и непрерывно зависит от $(\eta ,\gamma ) \in \mathbb{R} \times \Gamma $. Поскольку функция $w(\eta ;\gamma ) > 0$ и непрерывно зависит от $\gamma \in \Gamma $, то отсюда следует результат утверждения.

Доказательство утверждения 5. Запишем интеграл (4.9) в виде ${{g}_{1}}(\tau ;\eta ,\gamma ) = {{g}_{2}}(\tau ;\eta ,\gamma )$, где

и $f \equiv f(\tau )$, $F \equiv F(\tau )$, а $\tau \geqslant 0$.

Начиная с некоторой точки $\tau = {{\tau }_{*}}$, функция ${{g}_{2}}$ монотонно убывает до $ - \infty $; при $\tau = 0$ она принимает значение $(\varepsilon _{l}^{2} + {{\eta }^{2}})C > 0$. Напомним, что $C > 0$ в силу утверждения 2.

Функция ${{g}_{1}}$ принимает нулевое значение при $\tau = 0$, а ее поведение характеризуется следующим образом:

1) если $f$ неограничена и

$ \bullet $ ${{\varepsilon }_{l}} - 2{{\gamma }^{2}} \geqslant 0$, то ${{g}_{1}}$ монотонно возрастает до $ + \infty $;

$ \bullet $ ${{\varepsilon }_{l}} - 2{{\gamma }^{2}} \leqslant 0$, то ${{g}_{1}}$ монотонно убывает до некоторой точки, после которой монотонно возрастает до $ + \infty $;

2) если $f$ ограничена и

$ \bullet $ ${{\varepsilon }_{l}} - 2{{\gamma }^{2}} \geqslant 0$, то ${{g}_{1}}$ монотонно возрастает до $ + \infty $;

$ \bullet $ ${{\varepsilon }_{l}} - 2{{\gamma }^{2}} \leqslant 0$, а ${{\varepsilon }_{l}} + \alpha ma{{x}_{\tau }}f(\tau ) - 2{{\gamma }^{2}} > 0$, то ${{g}_{1}}$ монотонно убывает до некоторой точки, после которой монотонно возрастает до $ + \infty $;

$ \bullet $ ${{\varepsilon }_{l}} + \alpha ma{{x}_{\tau }}f(\tau ) - 2{{\gamma }^{2}} \leqslant 0$, то ${{g}_{1}}$ монотонно убывает до $ - \infty $.

Принимая во внимание проведенный анализ, можно заключить, что если $f$ неограничена, то функция $\tau \equiv \tau (\eta ;\gamma ) > 0$, определенная неявно соотношением (4.9), существует для любых $\eta $ и ${{\gamma }^{2}} > {{\varepsilon }_{s}}$. Это означает, что ${{\gamma }_{{max}}} = + \infty $.

Если $f$ ограничена, то функции ${{g}_{1}}$ и ${{g}_{2}}$ при достаточно больших $\tau $ “почти” линейны по $\tau $ . Ясно, что искомой функции $\tau (\eta ;\gamma )$ не существует, если ${{g}_{1}}$ и ${{g}_{2}}$ не пересекаются. Подставив ${{f}_{{max}}} = ma{{x}_{{\tau \to \infty }}}f(\tau )$ вместо $f$ и ${{f}_{{max}}}\tau $ вместо $F$ в уравнение ${{g}_{1}} = {{g}_{2}}$, получим

Полученные прямые не пересекаются, как только их угловые коэффициенты совпадают. Приравнивая эти коэффициенты, находим Минимальное положительное значение ${{\gamma }^{2}}$ достигается при $\eta \to \infty $ и равно ${{\varepsilon }_{l}} + \alpha {{f}_{{max}}}$. Таким образом, ${{\gamma }_{{max}}} = \sqrt {{{\varepsilon }_{l}} + \alpha {{f}_{{max}}}} $.

Пусть $u \equiv u(x;\gamma )$, $v \equiv v(x;\gamma )$ – решение задачи Коши (2.2), (4.2). Как было отмечено при доказательстве утверждения 3, величина $\eta $ не обязательно изменяется от $ - \infty $ до $ + \infty $. А именно, если $f$ ограничена и $\gamma > {{\gamma }_{{max}}}$, то решение $v$ не обращается в нуль, а значит, переменная $\eta $ изменяется в области $(\eta (0),\delta )$, где $\delta \equiv \delta (\gamma )$ и $\delta < + \infty $. Таким образом, уравнение ${{g}_{1}} = {{g}_{2}}$ всегда имеет решение.

Доказательство теоремы 2. Пусть пара $(u(x),v(x))$ – решение системы (4.1) и функция $v(x)$ имеет три нуля ${{x}_{1}},{{x}_{2}},{{x}_{3}} \in (0,h)$, причем ${{x}_{1}} < {{x}_{2}} < {{x}_{3}}$. Из формул (7.2) следует, что ${{x}_{2}} - {{x}_{1}} = {{x}_{3}} - {{x}_{2}} = \Theta {\text{/}}2$. Легко проверить, что если $(u(x),v(x))$ – решение, то $(u(\Theta + 2{{x}_{1}} - x), - v(\Theta + 2{{x}_{1}} - x))$ – также решение.

Пусть

Используя систему (4.1), легко проверить, что функции $u(x)$ и $u(\Theta + 2{{x}_{1}} - x)$, а также ${v}(x)$ и $ - v(\Theta + 2{{x}_{1}} - x)$ в точке $x = {{x}_{2}}$ склеены с первым порядком гладкости. Учитывая полученный результат, из системы (2.2) видим, что функции $v(x)$ и $ - v(\Theta + 2{{x}_{1}} - x)$ склеены со вторым порядком гладкости.

Пусть теперь $k \geqslant 3$ и ${{x}_{1}},{{x}_{2}}, \ldots ,{{x}_{k}} \in (0,h)$ – нули функции ${v}(x)$. Тогда для любой точки $x{\text{*}} \in (0,h)$ существует целое число $q \geqslant - 1$ такое, что $x{\text{*}} = x{\text{'}} + q\Theta $, где $x{\text{'}} \in [{{x}_{1}},{{x}_{3}}]$. Теперь положим

Другими словами, $(\tilde {u}(x),\tilde {v}(x))$ – периодическое решение системы (4.1) с периодом $\Theta $. В силу классических результатов о (локальном) существовании и единственности решения системы обыкновенных дифференциальных уравнений [33] других решений нет.

Доказательство теоремы 3. Для всех $\gamma \leqslant \gamma _{{max}}^{*} < {{\gamma }_{{max}}}$, где $\gamma _{{max}}^{*} > 0$ – постоянная, интегралы в уравнении (4.13) сходятся, а значит, $h_{{inf}}^{{(p)}}$ и $h_{{sup}}^{{(p)}}$ существуют и имеют конечные значения.

В силу теоремы 4 функция $\Phi (\gamma ;k)$ непрерывна по параметру $\gamma \in \Gamma $. Отсюда получаем, что для всякого $h_{{inf}}^{{(p')}} < h < h_{{sup}}^{{(p')}}$ существует, по крайней мере, одно решение уравнения (4.13), которое по теореме 1 является собственным значением задачи $\mathcal{Q}$.

Доказательство утверждения 6. Существование неотрицательной непрерывной функции $\tau \equiv \tau (\eta ;\gamma )$ для $(\eta ,\gamma ) \in \mathbb{R} \times \Gamma $ следует из доказательства теоремы 4. Остается доказать аналитичность этой функции по $\gamma $ при $\gamma \in \Gamma $. Функция $\tau \equiv \tau (s;\gamma )$ определена соотношением (4.9). Учитывая, что в окрестности каждой точки $(s{\text{*}},\gamma {\text{*}}) \in \mathbb{R} \times \Gamma $ существует функция $\tau \equiv \tau (s{\text{*}};\gamma {\text{*}})$ и $f(z)$ аналитична по $z$ при $z \in R_{\Delta }^{\delta }$, то по теореме о неявной функции $\tau $ зависит аналитически от $\gamma $ при $\gamma \in \Gamma $ [45].

Доказательство теоремы 4. Существование, по крайней мере, одного собственного значения для $h_{{inf}}^{{(p{\text{'}})}} < h < h_{{sup}}^{{(p{\text{'}})}}$ следует из теоремы 3.

Пусть $f(z)$ – аналитическая функция, тогда в силу утверждения 6 функция $\tau \equiv \tau (s;\gamma )$ аналитически зависит от $\gamma $ при $\gamma \in \Gamma $, но тогда и функция $\Phi (\gamma ,k)$ также является аналитической функцией параметра $\gamma $ при $\gamma \in \Gamma $. Поскольку неравенство $h_{{inf}}^{p} < h_{{sup}}^{p}$ справедливо для всех $p$, то отсюда, в силу аналитичности функции $\Phi (\gamma ,k)$ по $\gamma $, следует, что $\Phi (\gamma ,k)$ не может оставаться постоянной на любом открытом множестве $\gamma \in \Gamma {\text{''}} \subset \Gamma $. Как известно, аналитическая функция на любом ограниченном подмножестве области аналитичности всякое свое значение принимает конечное число раз [45]. Отсюда следует, что на каждом отрезке $\Gamma {\text{'}} \subset \Gamma $ содержится не более конечного числа (изолированных) собственных значений задачи $Q$.

Доказательство утверждения 7. Пусть $\gamma \in [\sqrt {{{\varepsilon }_{s}}} + \delta ,\sqrt {{{\varepsilon }_{l}}} - \delta ]$, где $\delta > 0$ достаточно мало. Пусть ${{w}_{0}}: = \tfrac{{{{\gamma }^{2}}\varepsilon _{l}^{2} + ({{\varepsilon }_{l}} - {{\gamma }^{2}}){{s}^{2}}}}{{\gamma {{\varepsilon }_{l}}}}$. В этом случае $\tfrac{1}{w}$ стремится к $\tfrac{1}{{{{w}_{0}}}}$ равномерно относительно $\gamma $ при $\alpha \to + 0$. Переходя к пределу $\alpha \to + 0$ в уравнении (4.13), получаем дисперсионное уравнение линейной задачи (5.1), где можно положить $\gamma \in (\sqrt {{{\varepsilon }_{s}}} ,\sqrt {{{\varepsilon }_{l}}} )$.

Доказательство теоремы 5. Рассмотрим уравнение (5.1) и предположим, что оно имеет $k$ решений ${{\tilde {\gamma }}_{i}}$ $(i = \overline {1,k} )$. Из утверждения 1 следует, что все решения ${{\tilde {\gamma }}_{i}} \in (\sqrt {{{\varepsilon }_{s}}} ,\sqrt {{{\varepsilon }_{l}}} )$ и являются однократными корнями уравнения (5.1).

Обратимся к уравнению (4.13). Вычтем из обеих частей этого уравнения величину ${{\Phi }_{0}}(\gamma ;n)$, определенную в (5.1), получим

После приведения левой части к общему знаменателю имеем где при этом $f \equiv f(\tau )$ и $\tau \equiv \tau (s;\gamma )$ определяется из уравнения (4.9) при $\eta = s$.

Нули правой части полученного уравнения являются однократными собственными значениями $\mathop {\widetilde \gamma }\nolimits_i $ линейной задачи; при этом все собственные значения ${{\tilde {\gamma }}_{i}}$ лежат внутри интервала $(\sqrt {{{\varepsilon }_{s}}} ,\sqrt {{{\varepsilon }_{l}}} )$. Отсюда следует, что существует отрезок $\Delta = [\sqrt {{{\varepsilon }_{s}}} + \delta ,\sqrt {{{\varepsilon }_{l}}} - \delta ]$, где число $\delta > 0$ достаточно мало, такой, что ${{\tilde {\gamma }}_{i}} \in \Delta $ при $i = \overline {1,k} $. Это значит, что найдутся отрезки ${{\Gamma }_{i}}$ такие, что ${{\tilde {\gamma }}_{i}} \in {{\Gamma }_{i}} \subset \Delta $ при $i = \overline {1,k} $ и на концах каждого из отрезков ${{\Gamma }_{i}}$ непрерывная функция $h - {{\Phi }_{0}}(\gamma ;n)$ принимает значения разных знаков.

При условии $\gamma \in \Delta $ знаменатели подынтегральных выражений положительны и превосходят ${{\delta }^{4}}\varepsilon _{l}^{4} > 0$. Это значит, что интегралы в полученном выше уравнении не имеют особенностей. Поскольку $\gamma \in \Delta $, то функция $\tau \equiv \tau (s;\gamma )$ ограничена, а значит ограничена и функция $f \equiv f(\tau )$. Также ясно, что если $\gamma \in \Delta $, то несобственные интегралы сходятся. Отсюда следует, что левая часть полученного уравнения может быть сделана как угодно малой, если достаточно мало $\alpha $. Принимая во внимание, что правая часть меняет знак при переходе через $\gamma = {{\tilde {\gamma }}_{i}}$, получаем, что найдется $\alpha {\text{'}} > 0$ такое, что при $\alpha = \alpha {\text{'}}$ в окрестности всякого $\gamma = {{\tilde {\gamma }}_{i}}$ уравнение (4.13) имеет, по крайней мере, один корень $\gamma = {{\tilde {\gamma }}_{i}}$; при этом $\alpha {\text{'}}$ можно выбрать так, что ${{\hat {\gamma }}_{i}} \in {{\Gamma }_{i}}$.

Доказательство утверждения 8. Принимая во внимание формулу (4.9), ясно, что

Далее, используя систему (4.8), выразим $d\eta $ через $d\tau $. Положив $\eta = s$ и используя формулу (4.9), получим подынтегральное выражение формулы (6.2).

Пределы интегрирования в (6.2) определяются из (4.9) при $s = 0$ и $s = + \infty $.

Объединяя результаты, получаем формулу (6.2).

Доказательство утверждения 9. Поскольку справедлива теорема 4, а для функции $f(s) \equiv s$ справедливо утверждение 5, то неотрицательная функция $\tau \equiv \tau (s;\gamma )$, определяемая из формулы (4.9), существует при $(s,\gamma ) \in \mathbb{R} \times \Gamma $, где $\Gamma = (\sqrt {{{\varepsilon }_{s}}} , + \infty )$. Из формулы (4.9) ясно, что эта функция непрерывно зависит от $\gamma $. Поскольку $w(\eta ;\gamma ) > 0$ для всех $\gamma > \sqrt {{{\varepsilon }_{s}}} $ и непрерывна по $\gamma $, то интеграл $T$ непрерывен и имеет конечное значение для всех конечных $\gamma > \sqrt {{{\varepsilon }_{s}}} $.

В дальнейшем мы будем анализировать функцию $T$, заданную формулой (6.2). Заменив в формуле (6.2) переменную $\tau $ на ${{\gamma }^{{2/q}}}\bar {\tau }$, получаем

где и ${{\bar {\varepsilon }}_{l}} = {{\varepsilon }_{l}}{{\gamma }^{{ - 2}}}$, $\bar {C} = C{{\gamma }^{{ - 4 - 2/q}}}$. При этом $\bar {\tau } = {{\bar {\tau }}_{0}}$ – (единственный) положительный корень уравнения $\bar {P}(\bar {\tau }) = 0$, а $\bar {\tau } = {{\bar {\tau }}_{\infty }}$ – (единственный) положительный корень уравнения

Вычислим ${{\bar {\tau }}_{0}}$ и ${{\bar {\tau }}_{\infty }}$ при больших значениях $\gamma $.

Принимая во внимание формулу (4.5) из уравнения (6.3), видим, что решение $\tau = {{\tau }_{0}}$ является ограниченной величиной при любых $\gamma $. Поскольку ${{\bar {\tau }}_{0}} = {{\gamma }^{{ - 2/q}}}{{\tau }_{0}}$, то при больших $\gamma $ получаем ${{\bar {\tau }}_{0}} = O({{\gamma }^{{ - 2/q}}})$.

Теперь рассмотрим уравнение (7.4). Считая, что $\bar {\tau }$ достаточно велико и используя формулы (6.4) и (6.5), перейдем к пределу по $\gamma \to + \infty $ в (7.4). Отсюда получаем

Вычислив положительное решение полученного уравнения, находим первое приближение $\bar {\tau }_{\infty }^{0} = {{\left( {\tfrac{{2q + 1}}{{\alpha (q + 1)}}} \right)}^{{1/q}}}$ к искомому значению ${{\bar {\tau }}_{\infty }}$. Итак, где ${{r}_{q}} > 0$.

Пусть

Тогда $T(\gamma )$ можно записать в виде $T(\gamma ) = {{\gamma }^{{ - 1}}}({{T}_{1}}(\gamma ) + {{T}_{2}}(\gamma ))$, где ${{T}_{j}}(\gamma ) = \int_{\mathop {\bar {\tau }}\nolimits_0 }^{\mathop {\bar {\tau }}\nolimits_\infty } \,{{g}_{j}}(\bar {\tau })d\bar {\tau }$, $j = 1,2$.

Преобразуем ${{T}_{j}}(\gamma )$ следующим образом:

где $g_{j}^{0}(s) = li{{m}_{{\gamma \to + \infty }}}{{g}_{j}}(s)$ при условиях (6.4), (6.5), а $j = 1,2$.

Итак, используя (6.4), (6.5) и переходя к пределу при $\gamma \to + \infty $, получаем

Для первого слагаемого в правой части формулы (7.6) получаем

Интеграл в правой части полученной формулы элементарно вычисляется. Нетрудно проверить, что каждый из двух указанных интегралов является (конечной) постоянной, не зависящей от $\gamma $.

Вычисляя второе слагаемое в правой части формулы (7.6), получаем

и аналогично

Объединяя полученные результаты, приходим к формуле (6.6).

Доказательство теоремы 6. Из формулы (6.6) следует, что $li{{m}_{{\gamma \to + \infty }}}T(\gamma ) = 0$. Из этого факта, принимая во внимание неравенство (6.1), получаем, что существует целое число ${{n}_{0}}1$ такое, что дисперсионное уравнение (4.13) имеет, по крайней мере, одно решение для каждого $n = {{n}_{0}},$ ${{n}_{0}} + 1, \ldots $ Таким образом, задача $\mathcal{Q}$ имеет бесконечно много собственных значений ${{\hat {\gamma }}_{i}}$, где, очевидно, $li{{m}_{{i \to \infty }}}{{\hat {\gamma }}_{i}} = + \infty $.

Неравенство (6.7) следует из формул (6.1) и (6.6).

Из формулы (6.6) видно, что главный член асимптотического разложения не зависит от $\alpha $ и, следовательно, для любого $\alpha > 0$ существует бесконечное число собственных значений, которые не сводятся к какому-либо решению соответствующей линейной задачи.

Из рассуждений, проведенных при получении формулы (7.3), следует, что $ma{{x}_{{\gamma \in \Gamma }}}\bar {\tau } = li{{m}_{{\gamma \to + \infty }}}\bar {\tau } = {{\bar {\tau }}_{\infty }}$. Принимая во внимание формулу (7.5), получаем, что $ma{{x}_{{\gamma \in \Gamma }}}\bar {\tau } = {{\left( {\tfrac{{2q + 1}}{{\alpha (q + 1)}}} \right)}^{{1/q}}}$. Напомним,  что значение ${{\bar {\tau }}_{\infty }} = {{\gamma }^{{ - 2/q}}}{{\tau }_{\infty }}$ вычисляется из формулы (4.9) при $\eta \to \infty $. Из второй формулы (4.6) ясно, что $\eta $ стремится к $\infty $ при $v \to 0$. Тогда $ma{{x}_{{\gamma \in \Gamma }}}\bar {\tau } = ma{{x}_{{\gamma \in \Gamma }}}{{\gamma }^{{ - 2/q}}}{{u}^{2}} = {{\left( {\tfrac{{2q + 1}}{{\alpha (q + 1)}}} \right)}^{{1/q}}}$. Из полученного соотношения следует первая часть утверждения (ii).

Имея в виду результат теоремы 2 и доказанный выше факт существования бесконечного числа собственных значений с точкой накопления на бесконечности, естественно искать $max{{v}^{2}}$ при условии $v{\text{'}} = 0$. Из второго уравнения системы (4.1) следует, что $v\tilde {u}$ обращается в нуль, если либо $u = 0$, либо ${{\varepsilon }_{l}} - {{\gamma }^{2}} + \alpha f({{u}^{2}} + {{v}^{2}}) = 0$. Первое условие дает ограниченное значение для $max{{v}^{2}}$. Рассмотрим второе условие. Сначала заменим $u$ и $v$ на ${{\gamma }^{{1/q}}}\bar {u}$ и ${{\gamma }^{{1/q}}}\bar {v}$ соответственно. Считаем, что значение ${{u}^{2}} + {{v}^{2}}$ достаточно велико, используем формулы (6.4) и перейдем к пределу при $\gamma \to + \infty $. Тогда формула ${{\varepsilon }_{l}} - {{\gamma }^{2}} + \alpha f({{u}^{2}} + {{v}^{2}}) = 0$ преобразуется в

Теперь перейдем к $\bar {u}$ и $\bar {v}$ в формуле (4.3). Также как и выше, считаем, что значение ${{u}^{2}} + {{v}^{2}}$ достаточно велико. Используя формулы (6.4), получаем из (4.3) следующее выражение: где постоянная $C$ определена выражением (4.5). Переходя к пределу при $\gamma \to + \infty $ в полученном выражении, приходим к формуле Теперь используя (7.7), из последнего уравнения находим ${{\bar {v}}^{2}} = {{\alpha }^{{ - 1/q}}}\tfrac{q}{{q + 1}}$. Возвращаясь к переменной $v$, получаем вторую часть утверждения (ii).

Более слабый результат можно получить непосредственно из системы (2.2) и условий (2.3). Умножая первое уравнение системы (2.2) на $v$ и интегрируя, получаем

где $f \equiv f({{u}^{2}} + {{{v}}^{2}})$. Выражая $v' = - \tfrac{1}{\gamma }({{\varepsilon }_{l}} - {{\gamma }^{2}} + \alpha f)u$ из второго уравнения системы (2.2) и подставляя это выражение в предыдущую формулу, находим Полученную формулу можно преобразовать к виду Используя условия (2.3), окончательно получаем Правая часть полученного соотношения стремится к $\infty $ при $\gamma \to + \infty $, а значит, также ведет себя и левая часть. Отсюда следует, что $ma{{x}_{\gamma }}({{u}^{2}} + {{v}^{2}})$ неограниченно возрастает вместе с $\gamma $.

Доказательство теоремы 10. Имеет место оценка

Отсюда находим Интегралы в левой и правой частях полученной формулы элементарно вычисляются и дают Из полученной формулы следуют искомые оценки.

Неограниченность $\Phi (\gamma ;n)$ при $\gamma \to {{\gamma }_{{max}}}$ получается из следующих рассуждений. Пусть $\delta {\text{'}} > 0$ – фиксированное достаточно большое число. Тогда уравнение (4.13) при любом целом $n \geqslant 1$ содержит слагаемое

Пусть ${{U}_{{{{\gamma }_{{max}}}}}}$ – достаточно малая окрестность (на вещественной оси $R$) точки ${{\gamma }_{{max}}}$. Рассмотрим уравнение (4.9) при $s \in [\delta {\text{'}}, + \infty )$ и таких $\gamma \in {{U}_{{{{\gamma }_{{max}}}}}}$, что решение $\tau \equiv \tau (s;\gamma )$ уравнения (4.9) существует. Из доказательства утверждения 5 следует, что при достаточно большом $\delta '$ решение $\tau (s;\gamma )$ удовлетворяет неравенствам ${{\tau }_{ - }} \leqslant \tau (s;\gamma ) \leqslant {{\tau }_{ + }}$, где ${{\tau }_{ - }}$ и ${{\tau }_{ + }}$ достаточно большие постоянные. Отсюда следует, что $f(s) \leqslant f({{\tau }_{ + }})$, где $f({{\tau }_{ + }})$ тем меньше отличается от ${{f}_{{max}}}$, чем больше $\delta {\text{'}}$. Очевидно, имеет место оценка

Вычисляя интеграл в левой части, получаем

Если ${{\gamma }^{2}} \to - \delta {{{\text{'}}}^{{ - 2}}} + {{\varepsilon }_{l}} + \alpha f({{\tau }_{ + }})$, то

где $c$ – постоянная, не зависящая от $\delta {\text{'}}$. Но если $\delta {\text{'}} \to \infty $, то $f({{\tau }_{ + }}) \to {{f}_{{max}}}$, а значит, левая часть полученного выше неравенства стремится $\infty $. Отсюда следует, что левая часть полученного выше неравенства неограниченно возрастает при ${{\gamma }^{2}} \to {{\varepsilon }_{l}} + \alpha {{f}_{{max}}}$. Но тогда и $li{{m}_{{\gamma \to {{\gamma }_{{max}}}}}}\Phi (\gamma ;n) = + \infty $.