1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 3, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 3, стр. 462-475

Стохастическая модель переноса тепла в приземном слое атмосферы

В. Г. Задорожний 1, 2, *, В. С. Ножкин 2, **, М. Е. Семенов 1, 2, 3, ***, И. И. Ульшин 2, ****

1 Воронежский гос. ун-т
394006 Воронеж, Университетская пл., 1, Россия

2 ВУНЦ ВВС “ВВА им. Н.Е. Жуковского и Ю.А. Гагарина”
394064 Воронеж, ул. Старых большевиков, 54а, Россия

3 ФИЦ ЕГС РАН
249035 Обнинск, пр-т Ленина, 189, Россия

* E-mail: zador@amm.vsu.ru
** E-mail: nozhkin-v@list.ru
*** E-mail: mkl150@mail.ru
**** E-mail: ulshin@rambler.ru

Поступила в редакцию 10.02.2019
После доработки 10.02.2019
Принята к публикации 18.11.2019

Полный текст (PDF)

Аннотация

В работе предлагается новая стохастическая модель переноса тепла в приземном слое атмосферы. В основе модели лежит экспериментально подтвержденный факт, позволяющий трактовать значение горизонтальной компоненты скорости ветра как случайный процесс. Поэтому модель формализуется в рамках дифференциального уравнения со случайными коэффициентами. Приводятся явные формулы математического ожидания и второй моментной функции решения уравнения переноса тепла со случайными коэффициентами. Получена оценка, позволяющая оценить погрешность, получающуюся при замене случайного коэффициента уравнения его математическим ожиданием. Приведен пример, демонстрирующий эффективность предлагаемого подхода в случае гауссова распределения горизонтальной компоненты скорости ветра, позволяющий определить математическое ожидание и вторую моментную функцию в рамках модельных представлений. Библ. 23. Фиг. 1.

Ключевые слова: уравнение притока тепла, вариационная производная, случайный процесс, математическое ожидание, вторая моментная функция, характеристический функционал.

ВВЕДЕНИЕ

Влага в атмосфере может находиться в различных агрегатных состояниях. Образование облачности и выпадение осадков связаны с переходом влаги из одного состояния в другое. При прогнозировании осадков и связанных с повышенным влагосодержанием опасных метеорологических явлений, моделирование процессов конденсации и влагопереноса является определяющим. В связи с этим отметим работы, посвященные этой тематике [1]–[13].

Модели прогноза опасных явлений, связанных с повышенным содержанием водяного пара, в свою очередь непосредственно включают в себя уравнения переноса и конденсации влаги. Определяющим фактором фазовых переходов влаги в атмосфере является температурный режим, который в свою очередь связан с теплопереносом.

В частности динамика изменения влажности с учетом фазовых переходов описывается уравнением (см. [14])

(0.1)
$\frac{{\partial {{s}_{m}}}}{{\partial t}} + u\frac{{\partial {{s}_{m}}}}{{\partial x}} + v\frac{{\partial {{s}_{m}}}}{{\partial y}} + w\frac{{\partial {{s}_{m}}}}{{\partial z}} = - \frac{m}{\rho },$
где $u$, $v$, $w$ – проекции скорости ветра на соответствующие оси локальной системы координат; sm – максимальная массовая доля водяного пара (которая возможна при заданной температуре); $\rho $ – плотность воздуха; $m$ – скорость конденсации водяного пара в единице объема воздуха.

С помощью уравнения притока тепла, записанного с учетом теплоты конденсации, и уравнения Клапейрона–Клаузиуса, можно найти выражение для скорости конденсации, которая оказывается пропорциональной вертикальной скорости и некоторой функции давления и температуры $F{\text{(}}U,p{\text{)}}$ [14]. Тогда последнее соотношение можно записать в виде

(0.2)
$\frac{{\partial {{s}_{m}}}}{{\partial t}} + u\frac{{\partial {{s}_{m}}}}{{\partial x}} + v\frac{{\partial {{s}_{m}}}}{{\partial y}} + w\frac{{\partial {{s}_{m}}}}{{\partial z}} = F{\text{(}}U{\text{, }}p{\text{)}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} ,$
где
$F{\text{(}}U{\text{,}}p{\text{)}} = \frac{{\frac{{{{s}_{m}}}}{p}\left( {\frac{R}{{{{c}_{p}}}} - \frac{Q}{{{{c}_{p}}U}}\frac{R}{{{{R}_{П}}}}} \right)}}{{1 + \frac{{{{s}_{m}}Q(Q - {{R}_{П}}U)}}{{{{c}_{p}}{{R}_{П}}{{U}^{2}}}}}};$
здесь U – температура воздуха; $Q$ – скрытая теплота конденсации (сублимации); ${{R}_{П}}$ – удельная газовая постоянная водяного пара; $R$ – удельная газовая постоянная сухого воздуха; ${{c}_{p}}$ – удельная теплоемкость воздуха при постоянном давлении; $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} $ – аналог вертикальной скорости в p-системе координат.

В случае достижения состояния насыщения, для расчета изменения массовой доли водяного пара используется выражение (0.2). Поскольку ${{s}_{m}}$ является функцией температуры, то необходимо одновременно прогнозировать и температуру, используя уравнение притока тепла в виде

(0.3)
$\frac{{\partial U}}{{\partial t}} + u\frac{{\partial U}}{{\partial x}} + v\frac{{\partial U}}{{\partial y}} = \frac{{({{\gamma }_{a}} - \gamma )}}{{g\rho }}\tau ,$
где ${{\gamma }_{a}}$ – сухоадиабатический градиент температуры; $\gamma $ – вертикальный градиент температуры; $g$ – ускорение свободного падения.

1. ПОСТАНОВКА ЗАДАЧИ

Как правило, в гидродинамических моделях используются лишь усредненные значения метеорологических величин, допускающие лишь незначительные пространственно-временные изменения [9]–[13] и др. Такой подход представляется вполне оправданным при моделировании крупно и среднемасштабных процессов, имеющих характерный пространственный масштаб, превышающий десятки километров. Однако реальные метеорологические значения (например, направление и скорость ветра), как показывают наблюдения, подвержены неупорядоченным хаотическим возмущениям, учет которых необходим при рассмотрении мелкомасштабных явлений. Предлагаемый ниже подход связан с учетом турбулентных свойств атмосферы в рамках стохастических методов [15]–[18]. В связи с этим отметим цикл работ, посвященных различным аспектам стохастических дифференциальных уравнений [21]–[23] и др. и прежде всего фундаментальную монографию [18], в которой систематизированы основные результаты в области дифференциальных уравнений со случайными параметрами. В рассматриваемом случае естественно трактовать проекцию вектора скорости как случайный процесс. Косвенным доказательством правомерности такого подхода служит серия экспериментов, проведенных на метеостанции, имеющей географические координаты 51°40′33,7″ с.ш., 39°15′00,6″ в.д. в декабре 2017 г. На фиг. 1 приведены примеры графиков изменения значений проекции вектора скорости при интервалах усреднения 15, 60 и 180 с (для удобства представления приведены результаты проекции вектора скорости в течение 21 мин.). Отметим, что пространственные изменения скорости ветра в приземном слое также весьма значительны.

Фиг. 1.

(а) усредненные значения проекции вектора скорости за 15 с; (б) усредненные значения проекции вектора скорости за 60 с; (в) усредненные значения проекции вектора скорости за 180 с.

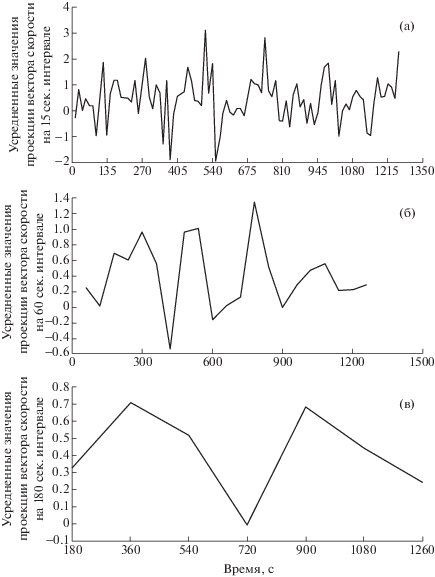
Из приведенного рисунка видно, что скорость ветра, рассматриваемая на малых интервалах времени, никак нельзя считать постоянной.

Для построения модели, во избежание громоздких выкладок, во внимание не принимаются вертикальные движения воздуха, ось x соответствует направлению преимущественного переноса воздушной массы и вводится обозначение

$f(x) = \frac{{({{\gamma }_{a}} - \gamma )}}{{g\rho }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} (x).$

Таким образом, уравнение (0.3) запишем в виде

(1.1)
$\frac{{\partial U}}{{\partial t}} + \varepsilon (t)\frac{{\partial U}}{{\partial x}} = f(x),$
где $\varepsilon (t)$ – случайный процесс, характеристики которого идентифицируются по наблюдениям пространственно-временного распределения скорости ветра. Начальное условие для уравнения (1.1) определяется равенством

(1.2)
$U(0,x) = {{U}_{0}}(x);\quad --{\kern 1pt} \infty < x < \infty .$

Случайный процесс будем считать заданным характеристическим функционалом [15]–[17]

(1.3)
$\varphi (\nu ) = M\left[ {\exp \left( {i\int\limits_T {\varepsilon (\tau )\nu (\tau )d\tau } } \right)} \right],$
где функция v принадлежит пространству L1(T) суммируемых на отрезке Т функций с нормой
$\left\| \nu \right\| = \int\limits_T {\left| {\nu (\tau )} \right|d\tau } ;$
и М – математическое ожидание по функции распределения процесса $\varepsilon (t)$; Т – отрезок времени, на котором изучается процесс [0; t1].

Задача состоит в нахождении первых двух моментных функций решения уравнения (1.1) с начальным условием (1.2).

2. ПЕРЕХОД К ДЕТЕРМИНИРОВАННОЙ ЗАДАЧЕ

Один из методов решения указанной выше задачи связан с переходом к детерминированному уравнению на основе подхода, развитого в работах [15–17] и связанного с понятием вариационной производной.

Приведем базовые определения этого метода. Пусть $y:{{L}_{1}}(T) \to {\text{C}}{\kern 1pt} |$ – функционал, определенный на множестве интегрируемых с квадратом функций, определенных на конечном временном промежутке, а $y:{{L}_{1}}(T) \to {\text{C}}{\kern 1pt} |$ обозначает множество комплексных чисел. Если для приращения функционала верно равенство

$y(\nu + h) - y(\nu ) = \int\limits_T {\psi (t,\nu )h(t)dt + o(h)} ,$
где интеграл понимается в смысле Лебега и является линейным ограниченным относительно $h \in {{L}_{1}}(T)$ функционалом, $o(h)$ обозначает бесконечно малую высшего порядка относительно $h$, то $\psi :T \times {{L}_{1}}(T) \to {\text{C}}{\kern 1pt} |$ называется вариационной (функциональной) производной функционала y и обозначается $\delta y(\nu ){\text{/}}\delta \nu (t)$. Подробное описание вариационной производной, ее свойств, а также приложение аппарата вариационного исчисления к решению уравнений со стохастическими коэффициентами содержится в [15]–[17].

Умножим уравнение (1.1) на $\exp \left( {i\int_T {\varepsilon (\tau )\nu (\tau )d\tau } } \right)$ и применим операцию математического ожидания по функции распределения случайного процесса $\varepsilon (t)$ к полученному равенству

(2.1)
$\begin{gathered} M\left[ {\frac{{\partial U}}{{\partial t}}\exp \left( {i\int\limits_T {\varepsilon (\tau )\nu (\tau )d\tau } } \right)} \right] = M\left[ { - \varepsilon (t)\frac{{\partial U}}{{\partial x}}\exp \left( {i\int\limits_T {\varepsilon (\tau )\nu (\tau )d\tau )} } \right)} \right] + \\ + \;f(x)M\left[ {\exp \left( {i\int\limits_T {\varepsilon (\tau )\nu (\tau )d\tau )} } \right)} \right]. \\ \end{gathered} $
Для дальнейших построений введем вспомогательное отображение:
(2.2)
$y(t,x,\nu ) = M\left[ {U(t,x)\exp \left( {i\int\limits_T {\varepsilon (\tau )\nu (\tau )d\tau } } \right)} \right],$
где $x \in R$; $v(t) \in {{L}_{1}}(T)$.

Тогда уравнение (2.1) можно записать в виде

(2.3)
$\frac{{\partial y(t,x,\nu )}}{{\partial t}} = i\frac{\delta }{{\delta \nu (t)}}\frac{\partial }{{\partial x}}y(t,x,\nu ) + f(x)\varphi (\nu )$.
с начальным условием

(2.4)
$y(0,x,\nu ) = {{U}_{0}}(x)\varphi (\nu ).$

3. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ПЕРЕНОСА ТЕПЛА

Непосредственно из определений следует, что математическое ожидание решения уравнения (1.1) с начальным условием (1.2) может быть получено из соотношения (2.2), в котором функцию $\nu $ следует положить равной нулю. Иными словами, имеет место равенство

(3.1)
$y(t,x,0) = M\left[ {U(t,x)} \right].$

Таким образом, для нахождения математического ожидания решения уравнения (1.1) с начальным условием (1.2) достаточно найти решение уравнения с вариационной и обычной производными (2.3) при условии (2.4) в некоторой окрестности точки $\nu = 0$.

Применив к обеим частям выражений (2.3) и (2.4) преобразование Фурье [19], [20], получим

(3.2)
$\frac{\partial }{{\partial t}}{{F}_{x}}\left[ {y(t,x,\nu )} \right](\xi ) = i\frac{\delta }{{\delta \nu (t)}}( - i\xi ){{F}_{x}}\left[ {y(t,x,\nu )} \right](\xi ) + {{F}_{x}}\left[ {f(x)} \right](\xi )\varphi (\nu ),$
(3.3)
${{F}_{x}}\left[ {y(0,x,\nu )} \right](\xi ) = {{F}_{x}}\left[ {{{U}_{0}}(x)} \right](\xi )\varphi (\nu ),$
где ${{F}_{x}}$ – преобразование Фурье по переменной x, а $\xi $ – двойственная к x переменная. Пусть
$Y(t,\xi ,\nu ) = {{F}_{x}}\left[ {y(t,x,\nu )} \right](\xi );\quad b(\xi ,\nu ) = {{F}_{x}}\left[ {f(x)} \right](\xi )\varphi (\nu ).$
Тогда соотношения (3.2) и (3.3) перепишутся в виде

(3.4)
$\frac{\partial }{{\partial t}}Y(t,\xi ,\nu ) = \xi \frac{\delta }{{\delta \nu (t)}}Y(t,\xi ,\nu ) + b(\xi ,\nu ),$
(3.5)
${{Y}_{0}}(0,\xi ,\nu ) = {{F}_{x}}\left[ {{{U}_{0}}(x)} \right](\xi )\varphi (\nu ).$

Введем вспомогательную функцию, зависящую от трех переменных $\chi (\tau ,t,w)$ следующим образом $\chi (\tau ,t,w) = {\text{sign}}(w - \tau )$ при $w$, принадлежащем отрезку с концами $\tau $, $t$, и $\chi (\tau ,t,w) = 0$ в противном случае. Нам потребуется лемма [15], [16].

Лемма 3.1. Пусть $a(t)$ – непрерывная функция на отрезке Т и функционал $y:{{L}_{1}}(T) \to \not {C}$ имеет вариационную производную $\frac{{\delta y(\nu + a\chi (\tau ,t))}}{{\delta \nu (t)}}$. Тогда почти при всех $\,t \in T$ существует производная $\frac{{\partial y(\nu + a\chi (\tau ,t))}}{{\partial t}}$ и выполняется равенство

$\frac{{\partial y(\nu + a\chi (\tau ,t))}}{{\partial t}} = a(t)\frac{{\delta y(\nu + a\chi (\tau ,t))}}{{\delta \nu (t)}}.$

Теорема 3.2. Если существует вариационная производная $\frac{{\delta \varphi (\nu + \xi \chi (\tau ,t))}}{{\delta \nu (t)}}$, то

(3.6)
$Y(t,\xi ,\nu ) = {{Y}_{0}}(0,\xi ,\nu + \xi \chi (0,t)) + \int\limits_0^t {b(v + \xi \chi (\tau ,t))} d\tau $
является решением задачи (3.4), (3.5).

Доказательство. Получается подстановкой (3.6) в (3.4) и (3,5) с использованием леммы 3.1.

Теорема 3.3. В условиях теоремы 3.1

(3.7)
$y(t,x,\nu ) = {{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\varphi (\nu + \xi \chi (0,t))} \right](x) + f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\varphi (\nu + \xi \chi (\tau ,t))d\tau } } \right](x)$
является решением задачи (2.3), (2.4).

Доказательство. Применим обратное преобразование Фурье [19], [20] к (3.6), получим (3.7). Теорема доказана.

Теорема 3.4. Пусть выполняются условия предыдущей теоремы, тогда

(3.8)
$M\left[ {U(t,x)} \right] = {{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\varphi (\xi \chi (0,t))} \right](x) + f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\varphi (\xi \chi (\tau ,t))d\tau } } \right](x)$
является математическим ожиданием решения уравнения (1.1), при начальном условии (1.2).

Доказательство. Поскольку $y(t,x,0) = M\left[ {U(t,x)} \right]$, то из (3.7) при $\nu = 0$ получаем (3.8). Теорема доказана.

Оценим степень влияния случайных факторов на поведение системы, описываемой задачей (1.1), (1.2). Заменим уравнение (1.1) детерминированным уравнением

$\frac{{\partial U}}{{\partial t}} + M\left[ {\varepsilon (t)} \right]\frac{{\partial U}}{{\partial x}} = f(x).$

Легко проверить, что

${{U}_{d}}(t,x) = {{U}_{0}}(x - \int\limits_0^t {M\left[ {\varepsilon (s)} \right]ds) + } \int\limits_0^t {f(x - \int\limits_s^t {M\left[ {\varepsilon (\tau )d\tau } \right])} } ds$
является решением этого уравнения с начальным условием (1.2). Тогда функция
$I(t,x) = \left| {{{U}_{d}}(t,x) - M\left[ {U(t,x)} \right]} \right| = \left| {{{U}_{0}}\left( {x - \int\limits_0^t {M\left[ {\varepsilon (s)} \right]ds)} } \right) + \int\limits_0^t {f\left( {x - \int\limits_s^t {M\left[ {\varepsilon (\tau )d\tau } \right]} } \right)ds} - } \right.$
$\left. { - \;{{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\varphi (\xi \chi (0,t))} \right](x) + f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\varphi (\xi \chi (\tau ,t))d\tau } } \right](x)} \right|$
дает оценку погрешности решений при отказе от учета случайных факторов.

4. ВТОРАЯ МОМЕНТНАЯ ФУНКЦИЯ РЕШЕНИЯ УРАВНЕНИЯ ПЕРЕНОСА ТЕПЛА

Для получения второй моментной функции решения задачи (1.1) введем в рассмотрение отображение

(4.1)
$z(t,x,\gamma ,{{x}_{1}},\nu ) = M\left[ {U(t,x)U(\gamma ,{{x}_{1}})\exp \left( {i\int\limits_T {\varepsilon (\tau )\nu (\tau )d\tau )} } \right)} \right].$
Отметим, что отображение $z(t,x,\gamma ,{{x}_{1}},\nu )$ симметрично по парам переменных $t$, $x$ и $\gamma $, ${{x}_{1}}$.

Умножим уравнения (1.1), (1.2) на $U(\gamma ,{{x}_{1}})\exp \left( {i\int_T {\varepsilon (\tau )\nu (\tau )d\tau } } \right)$ и применим операцию математического ожидания по функции распределения случайного процесса $\varepsilon (t)$, получим

(4.2)
$\begin{gathered} M\left[ {\frac{{\partial U}}{{\partial t}}U(\gamma ,{{x}_{1}})\exp \left( {i\int\limits_T {\varepsilon (\tau )\nu (\tau )d\tau } } \right)} \right] = M\left[ { - \varepsilon (t)\frac{{\partial U}}{{\partial x}}U(\gamma ,{{x}_{1}})\exp \left( {i\int\limits_T {\varepsilon (\tau )\nu (\tau )d\tau } } \right)} \right] + \\ + \;f(x)M\left[ {U(\gamma ,{{x}_{1}})\exp \left( {i\int\limits_T {\varepsilon (\tau )\nu (\tau )d\tau } } \right)} \right]. \\ \end{gathered} $
(4.3)
$M\left[ {U(0,x)U(\gamma ,{{x}_{1}})\exp \left( {i\int\limits_T {\varepsilon (\tau )\nu (\tau )d\tau } } \right)} \right] = M\left[ {{{U}_{0}}(x)U(\gamma ,{{x}_{1}})\exp \left( {i\int\limits_T {\varepsilon (\tau )\nu (\tau )d\tau } } \right)} \right].$

Используя вспомогательное отображение $z(t,x,\gamma ,{{x}_{1}},\nu )$, соотношения (4.2), (4.3) запишем в виде

(4.4)
$\frac{\partial }{{\partial t}}z(t,x,\gamma ,{{x}_{1}},\nu ) = i\frac{\delta }{{\delta \nu (t)}}\frac{\partial }{{\partial x}}z(t,x,\gamma ,{{x}_{1}},\nu ) + f(x)y(\gamma ,{{x}_{1}},\nu ),$
(4.5)
$z(0,x,\gamma ,{{x}_{1}},\nu ) = {{U}_{0}}(x)y(\gamma ,{{x}_{1}},\nu ).$

Определение 4.1. Второй моментной функцией решения задачи (1.1) с детерминированным начальным условием (1.2) называется $z(t,x,\gamma ,{{x}_{1}},0)$, где $z(t,x,\gamma ,{{x}_{1}},\nu )$ – симметричное по переменным $t$, $x$ и $\gamma $, ${{x}_{1}}$ решение задачи (4.4), (4.5) и обозначается через $M\left[ {U(t,x)U(\gamma ,{{x}_{1}})} \right]$.

Теорема 4.1. Если существует вариационная производная $\frac{{\delta \varphi (\nu + \xi \chi (\tau ,t))}}{{\delta \nu (t)}}$, то решение задачи (4.4), (4.5) имеет вид

(4.6)
$z(t,x,\gamma ,{{x}_{1}},\nu ) = {{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {y(\gamma ,{{x}_{1}},\nu + \xi \chi (0,t))} \right](x) + f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {y(\gamma ,{{x}_{1}},\nu + \xi \chi (\tau ,t))d\tau } } \right](x),$
где $y(\gamma ,{{x}_{1}},\nu )$ определяется соотношением (3.7).

Доказательство. Задача (4.4), (4.5) имеет вид задачи (2.3), (2.4). Используя формулу (3.6), получаем (4.6). Теорема доказана.

Воспользовавшись равенством (3.7) и подставив его в (4.6), получим решение, представленное с использованием начального условия и характеристического функционала φ

$z(t,x,\gamma ,{{x}_{1}},\nu ) = {{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {{{U}_{0}}({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\varphi (\nu + {{\xi }_{1}}\chi (0,\gamma ) + \xi \chi (0,t))} \right]({{x}_{1}}) + } \right.$
(4.7)
$\begin{gathered} \left. { + \;f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\int\limits_0^\gamma {\varphi (\nu + {{\xi }_{1}}\chi (\tau ,\gamma ) + \xi \chi (0,t))d\tau } } \right]({{x}_{1}})} \right](x) + \\ + \;f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\left( {{{U}_{0}}({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\varphi (\nu + {{\xi }_{1}}\chi (0,\gamma ) + \xi \chi ({{\tau }_{1}},t))} \right]({{x}_{1}}) + } \right.} } \right. \\ \end{gathered} $
$\left. {\left. { + \;f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\int\limits_0^\gamma {\varphi (\nu + {{\xi }_{1}}\chi (\tau ,\gamma ) + \xi \chi ({{\tau }_{1}},t))d\tau } } \right]({{x}_{1}})} \right)d{{\tau }_{1}}} \right](x).$

Теорема 4.2. В условиях предыдущей теоремы вторая моментная функция решения уравнения (4) имеет вид

$M\left[ {U(t,x)U(\gamma ,{{x}_{1}})} \right] = {{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {{{U}_{0}}({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\varphi ({{\xi }_{1}}\chi (0,\gamma ) + \xi \chi (0,t))} \right]} \right.({{x}_{1}}) + $
(4.8)
$\begin{gathered} \left. { + \;f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\int\limits_0^\gamma {\varphi ({{\xi }_{1}}\chi (\tau ,\gamma ) + \xi \chi (0,t))d\tau } } \right]({{x}_{1}})} \right](x) + \\ + \;f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\left( {{{U}_{0}}({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\varphi ({{\xi }_{1}}\chi (0,\gamma ) + \xi \chi ({{\tau }_{1}},t))} \right]({{x}_{1}}) + } \right.} } \right. \\ \end{gathered} $
$\left. {\left. { + \;f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\int\limits_0^\gamma {\varphi ({{\xi }_{1}}\chi (\tau ,\gamma ) + \xi \chi ({{\tau }_{1}},t))d\tau } } \right]({{x}_{1}})} \right)d{{\tau }_{1}}} \right](x).$

Доказательство. Поскольку $z(t,x,\gamma ,{{x}_{1}},0) = M\left[ {U(t,x)U(\gamma ,{{x}_{1}})} \right]$, то из (4.7) при $\nu = 0$, получаем (4.8). Теорема доказана.

Важной статистической характеристикой случайного процесса является дисперсионная функция $D\left[ {U(t,x)} \right] = M[{{U}^{2}}(t,x)] - {{(M[U(t,x)])}^{2}}$.

Теорема 4.3. Пусть выполняются условия теоремы 4.1, тогда дисперсионная функция решения задачи (1.1), (1.2) имеет вид

$D\left[ {U(t,x)} \right] = \left( {{{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {{{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\exp \left[ {2i\xi \int\limits_0^t {M\left[ {\varepsilon (\tau )} \right]d\tau } } \right. - } \right.} \right.} \right.$
$\left. { - \;\left. {{{\xi }^{2}}\int\limits_0^t {\int\limits_0^t {b({{\tau }_{1}},{{\tau }_{2}})} } d{{\tau }_{1}}d{{\tau }_{2}}} \right]} \right](x) + f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\left( {\exp \left[ {i\xi \int\limits_\tau ^t M \left[ {\varepsilon (\tau )} \right]d\tau } \right. + } \right.} } \right.$
$ + \;i\xi \int\limits_0^t M \left[ {\varepsilon (\tau )} \right]d\tau - \frac{1}{2}{{\xi }^{2}}\int\limits_\tau ^t {\int\limits_\tau ^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}} - \;} } {{\xi }^{2}}\int\limits_\tau ^t {\int\limits_0^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}} - } } $
$\left. { - \;\left. {\left. {\frac{1}{2}{{\xi }^{2}}\int\limits_0^t {\left. {\int\limits_0^t b ({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} \right]} } \right)d\tau } \right](x)} \right](x) + f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\left( {{{U}_{0}}(x)\mathop * \limits^x } \right.} } \right.$
$\mathop * \limits^x \;F_{\xi }^{{ - 1}}\left[ {\exp \left[ {i\xi \int\limits_0^t M \left[ {\varepsilon (\tau )} \right]d\tau } \right. + } \right.i\xi \int\limits_{{{\tau }_{1}}}^t M \left[ {\varepsilon (\tau )} \right]d\tau - \frac{1}{2}{{\xi }^{2}}\int\limits_0^t {\int\limits_0^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}} - } } $
(4.9)
$\left. { - \;{{\xi }^{2}}\int\limits_0^t {\int\limits_{{{\tau }_{1}}}^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}} - } } \frac{1}{2}{{\xi }^{2}}\left. {\int\limits_{{{\tau }_{1}}}^t {\int\limits_{{{\tau }_{1}}}^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } } \right]} \right](x) + f(x)\mathop * \limits^x $
$\mathop * \limits^x \;F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\left( {\exp \left[ {i\xi \int\limits_\tau ^t M } \right.\left[ {\varepsilon (\tau )} \right]d\tau } \right.} } \right. + i\xi \int\limits_{{{\tau }_{1}}}^t M \left[ {\varepsilon (\tau )} \right]d\tau - \frac{1}{2}{{\xi }^{2}}\int\limits_\tau ^t {\int\limits_\tau ^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}} - } } $
$\left. {\left. {\left. {\left. {\left. { - \;{{\xi }^{2}}\int\limits_\tau ^t {\int\limits_{{{\tau }_{1}}}^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}} - } } \frac{1}{2}{{\xi }^{2}}\left. {\int\limits_{{{\tau }_{1}}}^t {\int\limits_{{{\tau }_{1}}}^t b ({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } \right]} \right)d\tau } \right](x)} \right)d{{\tau }_{1}}} \right](x)} \right) - $
$ - \;\left( {{{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\exp \left( {i\xi \int\limits_0^t {M\left[ {\varepsilon (\tau )} \right]d\tau } } \right.} \right. - } \right.$
$\left. { - \;\left. {\frac{1}{2}{{\xi }^{2}}\int\limits_0^t {\int\limits_0^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } } \right)} \right](x) + f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\exp \left( {i\xi \int\limits_\tau ^t {M\left[ {\varepsilon ({{\tau }_{1}})} \right]d{{\tau }_{1}}} } \right.} } \right. - $
${{\left. {\left. { - \;\left. {\frac{1}{2}{{\xi }^{2}}\int\limits_\tau ^t {\int\limits_\tau ^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } } \right)d\tau } \right](x)} \right)}^{2}}.$

Доказательство. Подставив в формулу определения дисперсионной функции равенства (3.8) и (4.8), положив в последнем выражении $\gamma = t$, ${{x}_{1}} = x$, получим (4.9). Теорема доказана.

5. УРАВНЕНИЕ ПРИТОКА ТЕПЛА С ГАУССОВЫМ СЛУЧАЙНЫМ ПРОЦЕССОМ

Одним из наиболее распространенных в технических и иных приложениях является гауссов случайный процесс. Проведенная серия экспериментов, упомянутых выше, не всегда соответствует характеристикам данного распределения (соответствующая гипотеза не отвергалась в 60% случаев и отвергалась в 40% на статистическом значимом уровне). Тем не менее идентификация количественных характеристик решения уравнения переноса тепла со случайными коэффициентами представляется весьма важной в условиях, когда соответствующий коэффициент допускает трактовку, как гауссов случайный процесс.

Характеристический функционал гауссова случайного процесса определяется соотношением [15]–[17]

(5.1)
$\varphi (\nu ) = \exp \left( {i\int\limits_0^{{{t}_{1}}} {M\left[ {\varepsilon (\tau )} \right]\nu (\tau )d\tau } - \frac{1}{2}\int\limits_0^{{{t}_{1}}} {\int\limits_0^{{{t}_{1}}} {b({{\tau }_{1}},{{\tau }_{2}})\nu ({{\tau }_{1}})\nu ({{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } } \right),$
где
$b({{\tau }_{1}},{{\tau }_{2}}) = M\left[ {\varepsilon ({{\tau }_{1}})\varepsilon ({{\tau }_{2}})} \right] - M\left[ {\varepsilon ({{\tau }_{1}})} \right]M\left[ {\varepsilon ({{\tau }_{2}})} \right]$
есть ковариационная функция процесса $\varepsilon $.

Для упрощения дальнейших громоздких выкладок введем обозначения

$A = \int\limits_0^\gamma {M\left[ {\varepsilon (\tau )} \right]d\tau } ;\quad {{A}_{1}} = \int\limits_0^\gamma {\int\limits_0^\gamma {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } ;\quad B = \int\limits_0^t {M\left[ {\varepsilon (\tau )} \right]d\tau } ;$
${{B}_{1}} = \int\limits_0^t {\int\limits_0^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } ;\quad C = \int\limits_0^\gamma {\int\limits_0^t {\xi b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } ;\quad D = \int\limits_\tau ^\gamma {M\left[ {\varepsilon (\tau )} \right]d\tau } ;$
${{D}_{1}} = \int\limits_\tau ^t {\int\limits_\tau ^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } ;\quad E = \int\limits_\tau ^\gamma {\int\limits_0^t {\xi b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } ;\quad {{E}_{1}} = \int\limits_{{{\tau }_{1}}}^t {M\left[ {\varepsilon (\tau )} \right]d\tau } ;$
$G = \int\limits_0^\gamma {\int\limits_{{{\tau }_{1}}}^t {\xi b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } ;\quad {{G}_{1}} = \int\limits_{{{\tau }_{1}}}^t {\int\limits_{{{\tau }_{1}}}^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } ;\quad K = \int\limits_\tau ^\gamma {\int\limits_{{{\tau }_{1}}}^t {\xi b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } ;$
${{K}_{1}} = \int\limits_\tau ^t M \left[ {\varepsilon (\tau )} \right]d\tau ;\quad N = \int\limits_\tau ^t {\int\limits_0^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } ;$
${{N}_{1}} = \int\limits_0^t {\int\limits_{{{\tau }_{1}}}^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } ;\quad S = \int\limits_\tau ^t {\int\limits_{{{\tau }_{1}}}^t {b({{\tau }_{1}},{{\tau }_{2}})d{{\tau }_{1}}d{{\tau }_{2}}} } .$

Теорема 5.1. Пусть $\varepsilon (t)$ – гауссов случайный процесс, тогда математическое ожидание $M\left[ {U(t,x)} \right]$ решения уравнения (1.1) с начальным условием (1.2) имеет вид

(5.2)
$M\left[ {U(t,x)} \right] = {{U}_{0}}(x)\mathop * \limits^x \frac{1}{{\sqrt {2\pi {{B}_{1}}} }}\exp \left( { - \frac{{{{{(x - B)}}^{2}}}}{{2{{B}_{1}}}}} \right) + f(x)\mathop * \limits^x \int\limits_0^t {\frac{1}{{\sqrt {2\pi {{D}_{1}}} }}\exp \left( { - \frac{{{{{(x - {{K}_{1}})}}^{2}}}}{{2{{D}_{1}}}}} \right)d\tau } .$

Доказательство. Подставив характеристический функционал (5.1) в соотношение (3.8) и воспользовавшись определением функции $\chi (\tau ,t)$, получим

$M\left[ {U(t,x)} \right] = {{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\exp \left( {i\xi B - \frac{1}{2}{{\xi }^{2}}{{B}_{1}}} \right)} \right] + f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\exp } \left( {i\xi {{K}_{1}} - \frac{1}{2}{{\xi }^{2}}{{D}_{1}}} \right)d\tau } \right] = $
$ = {{U}_{0}}(x)\mathop * \limits^x \frac{1}{{\sqrt {2\pi {{B}_{1}}} }}\exp \left( { - \frac{{{{{(x - B)}}^{2}}}}{{2{{B}_{1}}}}} \right) + f(x)\mathop * \limits^x \int\limits_0^t {\frac{1}{{\sqrt {2\pi {{D}_{1}}} }}\exp \left( { - \frac{{{{{(x - {{K}_{1}})}}^{2}}}}{{2{{D}_{1}}}}} \right)d\tau } .$

Теорема доказана.

Влияние случайных факторов на систему оценивается функцией (см. разд. 3)

$\begin{gathered} I(t,x) = \left| {{{U}_{0}}(x - \int\limits_0^t {B(s)ds) + } \;\int\limits_0^t {f(x - \int\limits_s^t {B(\tau )d\tau )} )ds} - } \right. \\ \left. { - \;{{U}_{0}}(x)\mathop * \limits^x \frac{1}{{\sqrt {2\pi {{B}_{1}}} }}\exp \left( { - \frac{{{{{(x - B)}}^{2}}}}{{2{{B}_{1}}}}} \right) + f(x)\mathop * \limits^x \int\limits_0^t {\frac{1}{{\sqrt {2\pi {{D}_{1}}} }}\exp \left( { - \frac{{{{{(x - {{K}_{1}})}}^{2}}}}{{2{{D}_{1}}}}} \right)d\tau } } \right|. \\ \end{gathered} $
Отметим, что при ${{B}_{1}}(t) \to 0$ выражение
$\frac{1}{{\sqrt {\pi {{B}_{1}}} }}\exp \left( { - \frac{{{{{(x - B)}}^{2}}}}{{2{{B}_{1}}}}} \right)$
стремится к δ-функции Дирака и $I(t,x) \to 0$. Таким образом, при ${{B}_{1}}(t) \to 0$ формула (5.2) переходит в формулу решения детерминированной задачи.

Теорема 5.2. Пусть выполняются условия предыдущей теоремы, тогда вторая моментная функция имеет вид

$M\left[ {U(t,x)U(\gamma ,{{x}_{1}})} \right] = {{U}_{0}}(x)\mathop * \limits^x \left[ {\frac{1}{{\sqrt {\pi {{B}_{1}}} }}\exp \left( { - \frac{{{{{(x - B)}}^{2}}}}{{2{{B}_{1}}}}} \right) \times } \right.$$ \times \;{{U}_{0}}({{x}_{1}})\mathop * \limits^{{{x}_{1}}} \left[ {\frac{1}{{\sqrt {\pi {{A}_{1}}} }}\exp \left( { - \frac{{{{{({{x}_{1}} - A)}}^{2}}}}{{2{{A}_{1}}}}} \right)\exp \left[ {i({{x}_{1}} - A)\frac{C}{{{{A}_{1}}}}} \right]\exp \left[ {\frac{C}{{2{{A}_{1}}}}} \right]} \right]({{x}_{1}}) + $
$ + \;f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} \left[ {\int\limits_0^\gamma {\left( {\frac{1}{{\sqrt {\pi {{B}_{1}}} }}\exp \left( { - \frac{{{{{(x - B)}}^{2}}}}{{2{{B}_{1}}}}} \right)\frac{1}{{\sqrt {\pi {{D}_{1}}} }}\exp \left( { - \frac{{{{{({{x}_{1}} - D)}}^{2}}}}{{2{{D}_{1}}}}} \right) \times } \right.} } \right.$
(5.3)
$\begin{gathered} \left. {\left. {\left. { \times \;\exp \left[ {i({{x}_{1}} - D)\frac{E}{{{{D}_{1}}}}} \right]\exp \left[ {\frac{E}{{2{{D}_{1}}}}} \right]} \right)d\tau } \right]({{x}_{1}})} \right](x) + \\ + \;f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\left( {\frac{1}{{\sqrt {\pi {{G}_{1}}} }}\exp \left( { - \frac{{{{{(x - {{E}_{1}})}}^{2}}}}{{2{{G}_{1}}}}} \right){{U}_{0}}({{x}_{1}})\mathop * \limits^{{{x}_{1}}} } \right.} } \right. \\ \end{gathered} $
$\left. {\mathop * \limits^{{{x}_{1}}} \;\left[ {\frac{1}{{\sqrt {\pi {{A}_{1}}} }}\exp \left( { - \frac{{{{{({{x}_{1}} - A)}}^{2}}}}{{2{{A}_{1}}}}} \right)} \right.\exp \left[ {i({{x}_{1}} - A)\frac{G}{{{{A}_{1}}}}} \right]\exp \left[ {\frac{G}{{2{{A}_{1}}}}} \right]} \right]({{x}_{1}}) + $
$ + \;f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} \left[ {\int\limits_0^\gamma {\frac{1}{{\sqrt {\pi {{G}_{1}}} }}\exp \left( { - \frac{{{{{(x - {{E}_{1}})}}^{2}}}}{{2{{G}_{1}}}}} \right)} } \right.\frac{1}{{\sqrt {\pi {{D}_{1}}} }}\exp \left( { - \frac{{{{{({{x}_{1}} - D)}}^{2}}}}{{2{{D}_{1}}}}} \right) \times $
$\left. {\left. {\left. { \times \;\exp \left[ {i({{x}_{1}} - D)\frac{K}{{{{D}_{1}}}}} \right]\exp \left[ {\frac{K}{{2{{D}_{1}}}}} \right]\mathop {d\tau }\limits_{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}^{} } \right]({{x}_{1}})} \right)\mathop {d{{\tau }_{1}}}\limits_{_{{_{{_{{_{{_{{}}}}}}}}}}}^{} } \right](x).$

Доказательство. Подставив характеристический функционал (5.1) в равенство (4.8), используя свойства функции $\chi (\tau ,t)$, получим

$M\left[ {U(t,x)U(\gamma ,{{x}_{1}})} \right] = {{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\mathop {{{U}_{0}}({{x}_{1}})}\limits_{_{{_{{_{{_{{}}}}}}}}}^{} \mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}} \right.\left[ {\exp \left[ {i{{\xi }_{1}}A + i\xi B - \frac{1}{2}} \right.} \right.\xi _{1}^{2}{{A}_{1}} - {{\xi }_{1}}C - \left. {\left. {\frac{1}{2}{{\xi }^{2}}{{B}_{1}}} \right]} \right]({{x}_{1}}) + $
(5.4)
$\begin{gathered} + \;f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left. {\left[ {\int\limits_0^\gamma {\exp \left[ {i{{\xi }_{1}}D + i\xi B - \frac{1}{2}\xi _{1}^{2}{{D}_{1}} - {{\xi }_{1}}E - \frac{1}{2}{{\xi }^{2}}{{B}_{1}}} \right]d\tau } } \right]({{x}_{1}})} \right](x) + \\ + \;f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\left( {{{U}_{0}}({{x}_{1}})\mathop * \limits^{{{x}_{1}}} } \right.} } \right.F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\exp \left[ {i{{\xi }_{1}}A + i\xi {{E}_{1}} - \frac{1}{2}\xi _{1}^{2}{{A}_{1}} - {{\xi }_{1}}G - \frac{1}{2}{{\xi }^{2}}{{G}_{1}}} \right]} \right]({{x}_{1}}) + \\ \end{gathered} $
$ + \;f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left. {\left. {\left[ {\int\limits_0^\gamma {\left( {\exp \left[ {i{{\xi }_{1}}D + i\xi {{E}_{1}} - \frac{1}{2}\xi _{1}^{2}{{D}_{1}} - {{\xi }_{1}}K - \frac{1}{2}{{\xi }^{2}}{{G}_{1}}} \right]} \right)d\tau } } \right]({{x}_{1}})} \right)d{{\tau }_{1}}} \right](x).$

В силу очевидной громоздкости последнего выражения дальнейшие преобразования будем производить по частям.

Определим первое слагаемое

${{U}_{0}}({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\exp \left[ {i{{\xi }_{1}}A + i\xi B - \frac{1}{2}\xi _{1}^{2}{{A}_{1}} - {{\xi }_{1}}C - \frac{1}{2}{{\xi }^{2}}{{B}_{1}}} \right]} \right]({{x}_{1}}) = $
$ = \;\exp \left( {i\xi B - \frac{1}{2}{{\xi }^{2}}{{B}_{1}}} \right){{U}_{0}}({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\exp [i{{\xi }_{1}}A - \frac{1}{2}\xi _{1}^{2}{{A}_{1}} - {{\xi }_{1}}C]} \right]({{x}_{1}}) = $
$ = \;\exp \left( {i\xi B - \frac{1}{2}{{\xi }^{2}}{{B}_{1}}} \right){{U}_{0}}({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\exp [i{{\xi }_{1}}A]\exp \left[ { - \frac{1}{2}{{A}_{1}}{{{\left( {\xi + \frac{C}{{{{A}_{1}}}}} \right)}}^{2}}} \right]} \right. \times $
$\left. {\mathop \times \limits_{_{{_{{_{{_{{_{{}}}}}}}}}}}^{} \;\exp \left[ {\frac{C}{{2{{A}_{1}}}}} \right]} \right]({{x}_{1}}) = \exp \left( {i\xi B - \frac{1}{2}{{\xi }^{2}}{{B}_{1}}} \right) \times $
$ \times \;{{U}_{0}}({{x}_{1}})\mathop *\limits^{{{x}_{1}}} \left[ {\frac{1}{{\sqrt {\pi {{A}_{1}}} }}\exp \left( { - \frac{{{{{({{x}_{1}} - A)}}^{2}}}}{{2{{A}_{1}}}}} \right)\exp [i({{x}_{1}} - A)\left. {\frac{C}{{{{A}_{1}}}}} \right]\exp \left[ {\frac{C}{{2{{A}_{1}}}}} \right]} \right]({{x}_{1}}).$

Второе слагаемое

$f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\int\limits_0^\gamma {\exp \left[ {i{{\xi }_{1}}D + i\xi B - \frac{1}{2}\xi _{1}^{2}{{D}_{1}} - {{\xi }_{1}}E - \frac{1}{2}{{\xi }^{2}}{{B}_{1}}]d\tau } \right]} } \right.({{x}_{1}}) = $
$ = \;f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left. {\left[ {\int\limits_0^\gamma {\left( {\exp \left( {i\xi B - \frac{1}{2}{{\xi }^{2}}{{B}_{1}}} \right)\exp \left[ {i{{\xi }_{1}}D - \frac{1}{2}\xi _{1}^{2}{{D}_{1}} - {{\xi }_{1}}E} \right]} \right)d\tau } } \right.} \right]({{x}_{1}}) = $
$ = \;f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} \left[ {\int\limits_0^\gamma {\left( {\exp \left( {i\xi B - \frac{1}{2}{{\xi }^{2}}{{B}_{1}}} \right)\frac{1}{{\sqrt {\pi {{D}_{1}}} }}\exp \left( { - \frac{{{{{({{x}_{1}} - D)}}^{2}}}}{{2{{D}_{1}}}}} \right) \times } \right.} } \right.$
$ \times \;\left. {\left. {\exp \left[ {i({{x}_{1}} - D)\frac{E}{{{{D}_{1}}}}} \right]\exp \left[ {\frac{E}{{2{{D}_{1}}}}} \right]} \right)\mathop {d\tau }\limits_{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}^{} } \right]({{x}_{1}}).$

Третье слагаемое

${{U}_{0}}({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\exp \left[ {i{{\xi }_{1}}A + i\xi {{E}_{1}} - \frac{1}{2}\xi _{1}^{2}{{A}_{1}} - {{\xi }_{1}}G - \frac{1}{2}{{\xi }^{2}}{{G}_{1}}} \right]} \right]({{x}_{1}}) = $
$ = \;\exp \left( {i\xi {{E}_{1}} - \frac{1}{2}{{\xi }^{2}}{{G}_{1}}} \right){{U}_{0}}({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\exp \left[ {i{{\xi }_{1}}A - \frac{1}{2}\xi _{1}^{2}{{A}_{1}} - {{\xi }_{1}}G} \right]} \right]({{x}_{1}}) = $
$ = \;\exp \left( {i\xi {{E}_{1}} - \frac{1}{2}{{\xi }^{2}}{{G}_{1}}} \right){{U}_{0}}({{x}_{1}})\mathop * \limits^{{{x}_{1}}} \left[ {\frac{1}{{\sqrt {\pi {{A}_{1}}} }}\exp \left( { - \frac{{{{{({{x}_{1}} - A)}}^{2}}}}{{2{{A}_{1}}}}} \right)} \right. \times $
$\left. { \times \;\exp \left[ {i({{x}_{1}} - A)\frac{G}{{{{A}_{1}}}}} \right]\exp \left[ {\frac{G}{{2{{A}_{1}}}}} \right]} \right]({{x}_{1}}).$

Четвертое слагаемое

$f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\int\limits_0^\gamma {\left( {\exp \left[ {i{{\xi }_{1}}D + i\xi {{E}_{1}} - \frac{1}{2}} \right.} \right.} \xi _{1}^{2}{{D}_{1}} - {{\xi }_{1}}K - \left. {\left. {\frac{1}{2}{{\xi }^{2}}{{G}_{1}}} \right]} \right)d\tau } \right]({{x}_{1}}) = $
$ = f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} F_{{{{\xi }_{1}}}}^{{ - 1}}\left[ {\int\limits_0^\gamma {\left( {\left. {\exp \left( {i\xi {{E}_{1}} - \frac{1}{2}{{\xi }^{2}}{{G}_{1}}} \right)\exp \left[ {i{{\xi }_{1}}D - \frac{1}{2}\xi _{1}^{2}{{D}_{1}} - {{\xi }_{1}}K} \right]d\tau } \right)} \right.} } \right]({{x}_{1}}) = $
$ = \;f({{x}_{1}})\mathop * \limits^{{{x}_{1}}} \left[ {\int\limits_0^\gamma {\exp \left( {i\xi {{E}_{1}} - \frac{1}{2}{{\xi }^{2}}{{G}_{1}}} \right)} } \right.\frac{1}{{\sqrt {\pi {{D}_{1}}} }}\exp \left( { - \frac{{{{{({{x}_{1}} - D)}}^{2}}}}{{2{{D}_{1}}}}} \right) \times $
$\left. { \times \exp \left[ {i({{x}_{1}} - D)\frac{K}{{{{D}_{1}}}}} \right]\exp [\frac{K}{{2{{D}_{1}}}}]{\kern 1pt} \mathop {d\tau }\limits_{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}^{} } \right]({{x}_{1}}).$

Подставив получившиеся выражения в (5.4) и взяв обратное преобразование Фурье по $\xi $, получим (5.3). Теорема доказана.

Теорема 5.3. Пусть выполняются условия теорем 5.1 и 5.2, тогда дисперсионная функция имеет вид

$D\left[ {U(t,x)} \right] = \left( {{{U}_{0}}(x)\mathop * \limits^x \left[ {\frac{1}{{2\pi }}F_{\xi }^{{ - 1}}\left[ {{{U}_{0}}(\xi )} \right](x)} \right.} \right.\left( {\exp \left[ { - 2ixB - {{x}^{2}}{{B}_{1}}} \right]} \right) + $
$ + \;\frac{1}{{2\pi }}F_{\xi }^{{ - 1}}\left[ {f(\xi )} \right](x)\int\limits_0^t {\left( {\exp \left[ { - ix({{K}_{1}} + B) - \frac{1}{2}{{x}^{2}}({{D}_{1}} + 2N + {{B}_{1}})} \right]} \right)} {\kern 1pt} d\tau (x) + $
$ + \;f(x)\mathop * \limits^x \left[ {\frac{1}{{2\pi }}\int\limits_0^t {\left( {F_{\xi }^{{ - 1}}\left[ {{{U}_{0}}(\xi )} \right](x)\left( {\exp \left[ { - ix(B + {{E}_{1}}) - \frac{1}{2}{{x}^{2}}({{B}_{1}} + 2{{N}_{1}} + {{G}_{1}})} \right]} \right)} \right.} } \right. + $
$ + \;F_{\xi }^{{ - 1}}\left[ {f(\xi )} \right](x)\left. {\left. {\left. {\left[ {\frac{1}{{2\pi }}\int\limits_0^t {\left( {\exp \left[ { - ix({{K}_{1}} + {{E}_{1}}) - \frac{1}{2}{{x}^{2}}({{D}_{1}} + 2S + {{G}_{1}})} \right]} \right)d\tau } } \right]} \right)d{{\tau }_{1}}} \right](x)} \right) - $
$ - \;{{\left( {{{U}_{0}}(x)\mathop * \limits^x \frac{1}{{\sqrt {2\pi {{B}_{1}}} }}\exp \left( { - \frac{{{{{(x - B)}}^{2}}}}{{2{{B}_{1}}}}} \right)(x) + f(x)\mathop * \limits^x \int\limits_0^t {\frac{1}{{\sqrt {2\pi {{D}_{1}}} }}\exp \left( { - \frac{{{{{(x - {{K}_{1}})}}^{2}}}}{{2{{D}_{1}}}}} \right)d\tau (x)} } \right)}^{2}}.$

Доказательство. Подставив характеристический функционал (5.1) в равенство (4.9), использовав свойства функции $\chi (\tau ,t)$, получим

$D\left[ {U(t,x)} \right] = \left( {{{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {{{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}} \right.} \right.\left[ {\exp [2i\xi B - {{\xi }^{2}}{{B}_{1}}]} \right](x) + $
$ + \;f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left. {\left. {\left[ {\int\limits_0^t {\left( {\exp \left[ {i\xi {{K}_{1}} + i\xi B - \frac{1}{2}{{\xi }^{2}}{{D}_{1}} - {{\xi }^{2}}N - \frac{1}{2}{{\xi }^{2}}{{B}_{1}}} \right]} \right)} d\tau } \right.} \right](x)} \right](x) + $
$ + \;f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\left( {{{U}_{0}}(x)\mathop * \limits^x } \right.} } \right.F_{\xi }^{{ - 1}}\left[ {\exp \left[ {i\xi B + i\xi {{E}_{1}} - \frac{1}{2}{{\xi }^{2}}{{B}_{1}} - {{\xi }^{2}}{{N}_{1}} - \frac{1}{2}{{\xi }^{2}}{{G}_{1}}} \right]} \right](x) + $
$ + \;f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left. {\left. {\left. {\left. {\left[ {\int\limits_0^t {} \left( {\exp \left[ {i\xi {{K}_{1}} + i\xi {{E}_{1}} - \frac{1}{2}{{\xi }^{2}}{{D}_{1}} - {{\xi }^{2}}S - \frac{1}{2}{{\xi }^{2}}{{G}_{1}}} \right]} \right)} \right.d\tau } \right](x)} \right)d{{\tau }_{1}}} \right](x)} \right) - $
$ - \;{{\left( {{{U}_{0}}(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\exp \left( {i\xi B - \frac{1}{2}{{\xi }^{2}}{{B}_{1}}} \right)} \right] + f(x)\mathop * \limits^x F_{\xi }^{{ - 1}}\left[ {\int\limits_0^t {\exp } \left( {i\xi B - \frac{1}{2}{{\xi }^{2}}{{B}_{1}}} \right)d\tau } \right]} \right)}^{2}} = $
$ = \;\left( {{{U}_{0}}(x)\mathop * \limits^x \left[ {\frac{1}{{2\pi }}F_{\xi }^{{ - 1}}\left[ {{{U}_{0}}(\xi )} \right](x)} \right.} \right.\left( {\exp [ - 2ixB - {{x}^{2}}{{B}_{1}}]} \right) + $
$ + \frac{1}{{2\pi }}F_{\xi }^{{ - 1}}\left[ {f(\xi )} \right](x)\int\limits_0^t {\left( {\left. {\exp \left. {\left[ { - ix({{K}_{1}} + B) - \frac{1}{2}{{x}^{2}}({{D}_{1}} + 2N + {{B}_{1}})} \right]} \right)d\tau } \right]} \right.} (x) + $
$ + \;f(x)\mathop * \limits^x \left[ {\frac{1}{{2\pi }}\int\limits_0^t {\left( {F_{\xi }^{{ - 1}}\left[ {{{U}_{0}}(\xi )} \right](x)\left( {\exp \left[ { - ix(B + {{E}_{1}}) - \frac{1}{2}{{x}^{2}}({{B}_{1}} + 2{{N}_{1}} + {{G}_{1}})} \right]} \right)} \right.} } \right. + $
$ + \;F_{\xi }^{{ - 1}}\left[ {f(\xi )} \right](x)\left. {\left. {\left. {\left[ {\frac{1}{{2\pi }}\int\limits_0^t {\left( {\exp [ - ix({{K}_{1}} + {{E}_{1}}) - \frac{1}{2}{{x}^{2}}({{D}_{1}} + 2S + {{G}_{1}})]} \right)d\tau } } \right]} \right)} \right](x)} \right) - $
$ - \;{{\left( {{{U}_{0}}(x)\mathop * \limits^x \frac{1}{{\sqrt {2\pi {{B}_{1}}} }}\exp \left( { - \frac{{{{{(x - B)}}^{2}}}}{{2{{B}_{1}}}}} \right)(x) + f(x)\mathop * \limits^x \int\limits_0^t {\frac{1}{{\sqrt {2\pi {{D}_{1}}} }}\exp \left( { - \frac{{{{{(x - {{K}_{1}})}}^{2}}}}{{2{{D}_{1}}}}} \right)d\tau (x)} } \right)}^{2}}.$

Теорема доказана.

ЗАКЛЮЧЕНИЕ

В статье исследована новая модель переноса тепла, учитывающая влияние случайных факторов, а именно неконтролируемые пульсации скорости ветра, связанных с турбулентностью. В соответствующих уравнениях переноса проекции вектора скорости трактуются как случайные процессы с заданным характеристическим функционалом. Получены аналитические выражения математического ожидания, второй моментной функции, дисперсионной функции решения дифференциального уравнения, в рамках сформулированного модельного представления, позволяющие учитывать турбулентные (стохастические) свойства атмосферы. В качестве примера рассмотрен случай гауссова случайного процесса, для которого получены явные формулы решения и моментные функции. Приводится оценка, позволяющая оценить погрешность, получающуюся при замене случайного коэффициента уравнения его математическим ожиданием.

Возможные приложения предложенного в статье подхода применительно к задачам метеорологии сосредоточены, прежде всего, в области прогнозирования погодных явлений малого пространственно-временного масштаба (на расстояниях до нескольких километров и временных интервалов порядка нескольких часов). Именно на таких интервалах учет случайных составляющих в моделях переноса представляется вполне оправданным, поскольку неконтролируемые отклонения скорости ветра могут вносить существенные изменения в распределения метеорологических величин. Отметим также, что возможные приложения метода не ограничиваются метеорологией, поскольку явления переноса широко распространены в различных технологических процессах и производствах.

Список литературы

  1. Denisov A.M. Uniqueness and nonuniqueness of the solution to the problem of determining the source in the heat equation // Computational mathematics and mathematical physics. 2016. V. 56. № 10. P. 1737–1742.

  2. Трощиев В.Е., Трощиев Ю.В. Монотонные разностные схемы с весом для уравнения переноса в плоском слое // Матем. моделирование. 2003. Т. 15. № 1. С. 3–13.

  3. Nozhkin V.S. et al. Stochastic model of moisture motion in atmosphere // J. Phys.: Conf. Ser. 2018. V. 1096.012167. https://doi.org/10.1088/1742-6596/1096/1/012167

  4. Абрамов А.А., Юхно Л.Ф. О решении некоторых задач для систем линейных обыкновенных дифференциальных уравнений с избыточными условиями // Ж. вычисл. матем. и матем. физ. 2017. Т. 57. № 8. С. 1285–1293.

  5. Bogomolov S.V., Dorodnitsyn L.V. Equations of stochastic quasi-gas dynamics: Viscous gas case // Mathematical models and computer simulations. 2011. V. 3. № 4. P. 457–467.

  6. Bayev A.Zh., Bogomolov S.V. On the stability of the discontinuous particle method for the transfer equation // Mathematical models and computer simulations. 2018. V. 10. № 2. P. 186–197.

  7. Denisov A.M. Inverse problem for a quasilinear system of partial differential equations with a nonlocal boundary condition // Computational mathematics and mathematical physics. 2014. V. 54. № 10. P. 1513–1521.

  8. Germider O.V., Popov V.N., Yushkanov A.A. Heat transfer process in an elliptical channel // Mathematical models and computer simulations. 2017. V. 9. № 4. P. 521–528.

  9. Dzierzbicka-Głowacka L., Jakacki J., Janecki M., Nowicki A. Activation of the operational ecohydrodynamic model (3D CEMBS) – the hydrodynamic part // Oceanologia. 2013. V. 55. № 3. P. 519–541.

  10. Gimeno L., Dominguez F., Nieto R. Major mechanisms of atmospheric moisture transport and their role in extreme precipitation events // Review in Advance. 2016. V. 41. P. 3.1–3.25.

  11. Hadfield M.G., Rickard G.J., Uddstrom M.J. A hydrodynamic model of Chatham Rise, New Zealand // New Zealand journal of Marine and Freshwater Research. 2007. V. 41. P. 239–264.

  12. Mo K.C., Chelliah M., Carrera M.L. Atmospheric moisture transport over the united states and mexico as evaluated in the NCEP regional reanalysis // Journal of hydrometeorology. 2005. V. 6. P. 710–728.

  13. Дмитриева-Арраго Л.Р. Методы краткосрочного прогноза неконвективной облачности и осадков на основе модели преобразования влаги с учетом параметризации микрофизических процессов. 1. Модель преобразования влаги в атмосфере и прогноз неконвективной облачности // Метеорология и гидрология. 2004. № 2. С. 5–26.

  14. Белов Я.Н., Борисенков Е.П., Панин Б.Д. Численные методы прогноза погоды. Л.: Гидрометеоиздат, 1989. 376 с.

  15. Zadorozhniy V.G. Linear chaotic resonance in vortex motion // Computational mathematics and mathematical physics. 2013. V. 53. № 4. P. 486–502.

  16. Zadorozhniy V.G. Stabilization of Linear Systems by a Multiplicative Random Noise // Differential Equations.2018. V. 54. № 6. P. 728–747.

  17. Задорожний В.Г. Методы вариационного анализа. М.–Ижевск: РХД, 2006. 316 с.

  18. Oksendal B. Stochastic differential equations. Berlin: Springer, 2003. 379 p.

  19. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. 6-е изд., исправл. М.: Наука, 1989. 624 с.

  20. Шилов Г.Е. Математический анализ. Второй специальный курс. М.: Физматлит, 1965. 328 с.

  21. Allen E.J., Huff C. Derivation of stochastic differential equations for sunspot activity // Astronomy and astrophysics. 2010. V. 516. https://doi.org/10.1051/0004-6361/200913978

  22. Kozlov R. Random Lie symmetries of Ito stochastic differential equations // J. Phys. A.: Mathematical and Theoretical. 2018. V. 51. № 30. 305203.

  23. Mao W., Hu L., Mao X. Approximate solutions for a class of doubly perturbed stochastic differential equations // Advances in Difference Equations. 2018. https://doi.org/10.1186/s13662-018-1490-5

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал