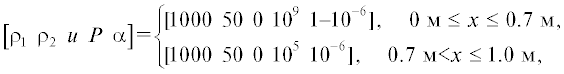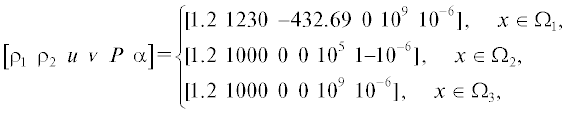Журнал вычислительной математики и математической физики, 2020, T. 60, № 3, стр. 476-488

Метод сквозного расчета межфазных границ в двухфазных течениях на основе уравнения Кана–Хилларда

И. С. Меньшов^{1, 2, 3, *}, Ч. Чжан^4, **

¹ ИПМатем. РАН
125047 Москва, Миусская пл., 4, Россия

² ФГУП ВНИИА
127055 Москва, Сущевская ул., 22, Россия

³ Ин-т системных исследований РАН
117218 Москва, Нахимовский пр-т, 36/1, Россия

⁴ МГУ
119992 Москва, Ленинские горы, Россия

^* E-mail: menshov@kiam.ru
^** E-mail: zhang-c@mail.ru

Поступила в редакцию 13.06.2019
После доработки 13.06.2019
Принята к публикации 18.11.2019

DOI: 10.31857/S0044466920030126

Полный текст (PDF)

Аннотация

Рассматривается численный метод для течений неоднородных двухфазных сжимаемых сред. Основная задача, возникающая при построении такого метода, связана с определением межфазных границ (интерфейсов), разделяющих компоненты с различными физико-механическими свойствами. Для решения этой задачи предлагается эффективный метод, обеспечивающий высокое пространственное разрешение межфазных границ. Метод основан на применении уравнения Кана–Хилларда. Для описания течения двухфазной среды используется односкоростная модель пяти уравнений, в которой в качестве уравнения функции порядка применяется уравнение Кана–Хилларда. Это позволяет существенно уменьшить область численного размазывания интерфейсов. Результаты численных экспериментов показывают точность и эффективность предложенного метода. Библ. 22. Фиг. 5. Табл. 2.

Ключевые слова: двухфазное течение, уравнение Кана–Хилларда, разрешение межфазных границ.

1. ВВЕДЕНИЕ

При моделировании течения многоматериальной гетерогенной среды одной из важных задач является определение положения межфазной границы (интерфейса), разделяющей компоненты с различными физическими свойствами. Численные методы расчета течения неоднородной среды с интерфейсом можно разделить на две основные группы. К первой группе относятся методы, в которых положение интерфейса явно отслеживается специальным образом так, что в каждый момент времени интерфейс представляется поверхностью [1]–[5]. Вторая группа – это так называемые методы диффузной границы [6]–[11], в которых интерфейс определяется узкой областью в пространстве с резким изменением характеристической функции или параметра порядка, задающего пространственное распределение компонент.

В рамках каждого из подходов в настоящее время предложен целый ряд моделей для описания динамики межфазной границы. В методах первой группы межфазная граница представляет собой поверхность разрыва характеристической функции; ее положение на каждом временном шаге рассчитывается. Это относительно просто сделать, если межфазная граница совпадает с линией вычислительной сетки. Однако это может приводить к сильному искажению ячеек расчетной сетки, если интерфейс претерпевает большие деформации. Альтернативные подходы не привязывают явно способ отслеживания границы к расчетной сетке. Среди них отметим лагранжево-эйлеров метод (ALE – Arbitrary Lagrangian–Eulerian) [1], метод уровней (level-set) [2], метод маркеров (front-tracking) [3]. Основной недостаток этих подходов состоит в нарушении консервативности метода в окрестности интерфейса.

Методы второй группы позволяют обойти основные недостатки методов прямого расчета интерфейса. В литературе эта группа получила название “Методы диффузной границы” [6]–[11]. Суть этих методов состоит в том, что среда из разных материалов рассматривается как некоторая однородная эффективная среда, свойства которой зависят от характеристической функции – параметра порядка, определяющего пространственное распределение составляющих компонент. В качестве такой функции может использоваться, например, объемная доля компонента. В этом случае граница между фазами специально не выделяется и представляется зоной, где значение объемной доли непрерывно меняется от нуля до единицы.

Следует отметить, что помимо моделей на основе характеристической функции [6], [7], [9]–[11] разрабатываются также подходы, в которых не предполагается рассмотрение специальных уравнений для описания межфазной границы. В них используются уравнения для массовых концентраций отдельных компонент и балансовые соотношения для суммарного импульса и энергии смеси [12], [13].

Область размазывания интерфейса в методах диффузной границы из-за наличия численной диссипации неизбежно увеличивается со временем. Даже схемы высокого порядка на фиксированных сетках не могут полностью устранить численную диссипацию; начальный скачок в распределении объемной доли со временем приобретает гладкий профиль. В этой области среда представляет собой смесь разных компонент, и движение интерфейса определяется принятой физической моделью смеси. При этом, чем меньше будет эта зона, тем меньше влияние численной модели смеси и тем точнее определение положения интерфейса. Поэтому при разработке метода диффузной границы необходимо искать определенный компромисс, допуская контролируемое размазывание интерфейса, т.е. разрешать численное размазывание, но в определенных границах.

Целью настоящей работы является построение такой технологии контролируемого разрешения для моделей диффузной границы. Основная идея состоит в использовании уравнения Кана–Хилларда [14], [15] для коррекции размазывания функции порядка.

Уравнениe Кана–Хилларда выводится из термодинамических положений для параметра порядка, определяющего фазовый переход в двухфазной системе. Оно основывается на предположении о свободной энергии системы вида

(1)

$\psi \left( {\phi ,\nabla \phi } \right) = f\left( \phi \right) + \frac{{{{\chi }^{2}}}}{2}{{\left| {\nabla \phi } \right|}^{2}},$

где $\psi $ – плотность свободной энергии, $\phi $ – параметр порядка (обычно выбирается как разность концентраций фаз), $\chi $ – положительная константа, связанная с линейным размером области диффузионной границы, $f\left( \phi \right)$ – однородная (“coarse-grain”) составляющая свободной энергии, отвечающая за разделение фаз.

Полная свободная энергия определяется по формуле

(2)

$\Psi \left( \phi \right) = \int\limits_\Omega {\psi \left( {\phi ,\nabla \phi } \right)} d{\mathbf{x}},$

где $\Omega $ – область пространства, занятая системой.

Формальная вариация $\Psi \left( \phi \right)$ относительно параметра порядка $\phi $ имеет следующий вид:

(3)

$\delta \Psi \left( \phi \right) = \int\limits_\Omega {[f{\kern 1pt} '\left( \phi \right) - {{\chi }^{2}}\Delta \phi ]\delta \phi {\text{d}}{\mathbf{x}}} = \int\limits_\Omega \mu \delta \phi d{\mathbf{x}},$

где

$\mu \left( \phi \right): = \frac{{\delta \Psi \left( \phi \right)}}{{\delta \phi }} = f{\kern 1pt} '\left( \phi \right) - {{\chi }^{2}}\Delta \phi $

обозначает первую вариацию свободной энергии системы и имеет смысл химического потенциала.

Процесс релаксации в направлении равновесия определяется следующим балансовым уравнением [14], [15]:

(4)

$\frac{{\partial \phi }}{{\partial t}} = \nabla \cdot \left( {M\left( \phi \right)\nabla \mu } \right),$

где положительная функция$M\left( \phi \right) \geqslant 0$ называется мобильностью системы. В настоящей работе мы полагаем ее равной 1.

Однородная составляющая свободной энергии $f\left( \phi \right)$ имеет вид функции с двумя локальными минимумами и в большинстве работ аппроксимируется многочленом четвертого порядка

(5)

$f\left( \phi \right) = \frac{1}{4}{{({{\phi }^{2}} - 1)}^{2}}.$

Аппроксимация (5) не гарантирует физически допустимый диапазон изменения $\phi $. Решение (4) при этом может выходить за пределы интервала [–1, 1], что будет соответствовать отрицательному значению плотности фаз. Поэтому в настоящей работе используется логарифмическая аппроксимация Флори–Хаггинса [16]:

(6)

$f\left( \phi \right) = {{f}_{0}}\left( \phi \right) - \frac{{{{\theta }_{0}}}}{2}{{\phi }^{2}},\quad {{f}_{0}}\left( \phi \right) = \left( {1 + \phi } \right)\ln \left( {1 + \phi } \right) + \left( {1 - \phi } \right)\ln \left( {1 - \phi } \right),$

где ${{\theta }_{0}}$ – параметр, управляющий зоной разделения фаз и связанный с толщиной межфазной границей.

Таким образом, получается уравнение для эволюции параметра порядка $\phi $, которое в дальнейшем мы будем использовать в модели диффузной границы для течений двухфазных сред:

(7)

$\begin{gathered} \frac{{\partial \phi }}{{\partial t}} = \Delta \mu \left( \phi \right), \\ \mu \left( \phi \right) = \ln \left( {1 + \phi } \right) - \ln \left( {1 - \phi } \right) - {{\theta }_{0}}\phi - {{\chi }^{2}}\Delta \phi . \\ \end{gathered} $

В модели (7) размер диффузионной зоны межфазной границы будет контролироваться двумя параметрами $\chi $ и ${{\theta }_{0}}$. Зависимость равновесного распределения $\phi $ от параметров $\chi $ и ${{\theta }_{0}}$ будет показана ниже в разделе, где обсуждаются численные результаты.

Статья организована следующим образом. В разд. 2 рассматриваются определяющие уравнения математической модели, используемой для описания течения двухфазной гетерогенной среды. В разд. 3 обсуждается модель разрешения межфазного интерфейса на основе решения уравнения Кана–Хилларда. В разд. 4 описывается численный метод решения системы определяющих уравнений и уравнения функции порядка. Разд. 5 посвящен результатам численных тестов для верификации предложенных методов. В заключение статьи делаются краткие выводы.

2. ОПРЕДЕЛЯЮЩИЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Рассматривается течение двухфазной гетерогенной смеси, состоящей из двух несмешивающихся жидкостей. Для описания такого течения мы используем односкоростную модель пяти уравнений [9]–[11], которая может быть записана в следующем виде:

$\begin{gathered} \frac{{\partial {{\alpha }_{1}}{{\rho }_{1}}}}{{\partial t}} + {\text{div}}\left( {{{\alpha }_{1}}{{\rho }_{1}}u} \right) = {{\rho }_{1}}R\left( \alpha \right), \\ \frac{{\partial {{\alpha }_{2}}{{\rho }_{2}}}}{{\partial t}} + {\text{div}}\left( {{{\alpha }_{2}}{{\rho }_{2}}u} \right) = - {{\rho }_{2}}R\left( \alpha \right), \\ \end{gathered} $

(8)

$\frac{{\partial \rho u}}{{\partial t}} + {\text{div}}\left( {\rho uu + PI} \right) = R\left( \alpha \right)\left( {{{\rho }_{1}} - {{\rho }_{2}}} \right)u,$

$\begin{gathered} \frac{{\partial \rho e}}{{\partial t}} + {\text{div}}\left( {\rho Hu} \right) = R\left( \alpha \right)\left[ {\left( {{{\rho }_{1}} - {{\rho }_{2}}} \right)k + \left( {{{\rho }_{1}}{{\varepsilon }_{1}} - {{\rho }_{2}}{{\varepsilon }_{2}}} \right)} \right], \\ \frac{{\partial \alpha }}{{\partial t}} + u \cdot \operatorname{grad} \alpha = H\left( \alpha \right) + R\left( \alpha \right), \\ \end{gathered} $

где α_i – объемная доля компоненты i, плотность смеси $\rho = \sum\nolimits_{i = 1}^2 {{{\alpha }_{i}}{{\rho }_{i}}} $, давление смеси $P = \sum\nolimits_{i = 1}^2 {{{\alpha }_{i}}{{P}_{i}}} $, внутренняя энергия смеси $\rho \varepsilon = \sum\nolimits_{i = 1}^2 {{{\alpha }_{i}}{{\rho }_{i}}{{\varepsilon }_{i}}} $, энтальпия смеси $\rho h = \sum\nolimits_{i = 1}^2 {{{\alpha }_{i}}{{\rho }_{i}}{{h}_{i}}} $, удельная полная энергия смеси $e = \varepsilon + {{{{{\left| {\mathbf{u}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {\mathbf{u}} \right|}}^{2}}} 2}} \right. \kern-0em} 2}$, $k = {{{{{\left| {\mathbf{u}} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {\mathbf{u}} \right|}}^{2}}} 2}} \right. \kern-0em} 2}$ – удельная кинетическая энергия, удельная суммарная энтальпия смеси H = e + P/ρ, $\alpha = {{\alpha }_{1}}$, $H\left( \alpha \right) = {{{{\alpha }_{1}}{{\alpha }_{2}}\left( {{{C}_{2}} - {{C}_{1}}} \right)} \mathord{\left/ {\vphantom {{{{\alpha }_{1}}{{\alpha }_{2}}\left( {{{C}_{2}} - {{C}_{1}}} \right)} {\left( {{{\alpha }_{1}}{{C}_{2}} + {{\alpha }_{2}}{{C}_{1}}} \right)}}} \right. \kern-0em} {\left( {{{\alpha }_{1}}{{C}_{2}} + {{\alpha }_{2}}{{C}_{1}}} \right)}}$, ${{C}_{i}} = {{\rho }_{i}}{{c}_{i}}^{2}$, с_i – скорость звука компоненты i.

Введение неконсервативных членов с $R\left( \alpha \right)$ в правую часть системы уравнений (8) было предложено в работе [10] и представляет собой специальную численную регуляризацию для обеспечения более точного разрешения межфазной границы. Фактически эта неконсервативная добавка работает только в узкой области вблизи интерфейса. С измельчением сетки эта область стягивается к поверхности интерфейса, и эффект неконсервативной добавки должен исчезать. Основная цель работы – попробовать вывести выражение для $R\left( \alpha \right)$ из рассмотрения аналогии с термодинамикой межфазной границы Кана–Хилларда. Заметим, что регуляризованные уравнения газовой динамики используются достаточно часто, например, в работах [17], [18].

Сделаем несколько замечаний касательно определяющих уравнений. Система уравнений (8) является гиперболической и описывает равновесную по скорости и давлению гидродинамическую модель двухфазной среды. Эта модель может быть формально выведена из более общей неравновесной модели Байера–Нунзиато на основе асимптотического анализа по релаксационным параметрам, описывающим выход на механическое равновесие двухфазной системы по скорости и давлению. В теории, если рассматривается течениe двух несмешивающихся жидкостей, ${{\alpha }_{i}} = 1$, ${\mathbf{x}} \in {{\Omega }_{i}}$ и ${{\alpha }_{i}} = 0$, ${\mathbf{x}} \notin {{\Omega }_{i}}$, и в этом случае $H\left( \alpha \right) = 0$. Но при использовании уравнений (7) для сквозного расчета течения двухфазной жидкости $H\left( \alpha \right) \ne 0$ в диффузной области интерфейса. Вместе с тем в работе [9] была проведена оценка члена $H\left( \alpha \right)$ в правой части уравнения для объемной доли и показано, что им можно пренебречь и использовать упрощенную модель с $H\left( \alpha \right) = 0$. Ниже мы используем это приближение.

Для описания термодинамических свойств фаз применяется обобщенное уравнение состояния Ван-дер-Ваальса, которое записывается в виде

(9)

${{P}_{i}}\left( {{{\rho }_{i}},{{\rho }_{i}}{{\varepsilon }_{i}}} \right) = \left( {\frac{{{{\gamma }_{i}} - 1}}{{1 - {{b}_{i}}{{\rho }_{i}}}}} \right)({{\rho }_{i}}{{\varepsilon }_{i}} - {{\pi }_{i}} + {{a}_{i}}\rho _{i}^{2}) - ({{\pi }_{i}} + {{a}_{i}}\rho _{i}^{2}),\quad i = 1,2,$

где ${{\gamma }_{i}}$ – коэффициент адиабаты, коэффициент a_i учитывает силы притяжения между молекулами, (Па м⁶)/моль², поправка b_i – суммарный объем молекул газа, м³/моль, ${{\pi }_{i}}$ – полуэмпирическая константа, которая получается из анализа экспериментальных данных, Па.

Изобарическое замыкание системы уравнений (8), P₁ = P₂ = P, приводит к уравнению состояния смеси следующего вида:

(10)

$P\left( {{{\rho }_{1}},{{\rho }_{2}},\rho \varepsilon ,z} \right) = {{\left[ {\sum\limits_{i = 1}^2 {{{z}_{i}}{{\xi }_{i}}({{\rho }_{i}})} } \right]}^{{ - 1}}}\left\{ {\rho \varepsilon + \sum\limits_{i = 1}^2 {{{z}_{i}}\left[ {({{a}_{i}}\rho _{i}^{2} - {{\pi }_{i}}) - {{\xi }_{i}}({{\rho }_{i}})({{a}_{i}}\rho _{i}^{2} + {{\pi }_{i}})} \right]} } \right\},$

где

${{\xi }_{i}}\left( {{{\rho }_{i}}} \right) = \frac{{1 - {{b}_{i}}{{\rho }_{i}}}}{{{{\gamma }_{i}} - 1}}.$

Фазовые скорости звука рассчитываются по формуле

(11)

${{c}_{i}} = \sqrt {\left( {{{h}_{i}} - {{\delta }_{i}}} \right){\text{/}}{{\xi }_{i}}} ,$

где

${{\delta }_{i}}\left( {{{\rho }_{i}}} \right) = 2{{a}_{i}}{{\rho }_{i}}\left[ {{{\xi }_{i}}\left( {{{\rho }_{i}}} \right) - 1} \right] - \frac{{{{b}_{i}}}}{{{{\gamma }_{i}} - 1}}\left( {{{P}_{i}} + {{\pi }_{i}} + {{a}_{i}}\rho _{i}^{2}} \right).$

Смесевая скорость звука в рассматриваемой модели определяется соотношением

(12)

$c = \sqrt {{{\sum\limits_{i = 1}^2 {{{y}_{i}}{{\xi }_{i}}\left( {{{\rho }_{i}}} \right){{c}_{i}}^{2}} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^2 {{{y}_{i}}{{\xi }_{i}}\left( {{{\rho }_{i}}} \right){{c}_{i}}^{2}} } {\xi \left( {{{\rho }_{1}},{{\rho }_{2}},z} \right)}}} \right. \kern-0em} {\xi \left( {{{\rho }_{1}},{{\rho }_{2}},z} \right)}}} .$

Зaмечание. Изобарическое замыкание в настоящей работе используется по следующим причинам. Во-первых, во многих динамических процессах механическая релаксация по давлению и скорости происходит намного быстрее, чем температурная релаксация, например, взрывные процессы, ударные волны (см. также [11] для оценок времени релаксационных процессов). C изобарическим замыканием модель (8) допускает разные температуры фаз. Кроме того, как отмечалось в работе [9], изотермическое замыкание (равенство температур фаз) приводит к менее устойчивой модели, что проявляется в нефизичных осцилляциях в численных решениях.

3. МЕТОД РАЗРЕШЕНИЯ МЕЖФАЗНОЙ ГРАНИЦЫ

Как уже было сказано выше, для повышения точности разрешения контактной границы между компонентами, в системе определяющих уравнений (7) добавляются специальные члены в правую часть, задаваемые функцией $R\left( \alpha \right)$. Покажем теперь, как эта функция может быть интерпретирована в рамках термодинамической теории межфазной границы (уравнения Кана–Хилларда).

В этой теории параметр порядка $\phi $ задает распределение фаз и определяется следующим образом:

(13)

$\phi = {{m}_{1}} - {{m}_{2}},$

где m_i – массовая доля, ${{m}_{i}} = {{{{\alpha }_{i}}{{\rho }_{i}}} \mathord{\left/ {\vphantom {{{{\alpha }_{i}}{{\rho }_{i}}} \rho }} \right. \kern-0em} \rho }$. Его можно также рассматривать как функцию объемной доли,

(14)

$\phi \left( \alpha \right) = \frac{{\alpha \left( {{{\rho }_{1}} + {{\rho }_{2}}} \right) - {{\rho }_{2}}}}{{\alpha \left( {{{\rho }_{1}} - {{\rho }_{2}}} \right) + {{\rho }_{2}}}}.$

Уравнение для объемной доли в модели (8) расщепим на две части: конвективный перенос и численную регуляризацию для уточнения разрешения контактной границы, т.е.

(15)

$\frac{{\partial \alpha }}{{\partial t}} + u \cdot \operatorname{grad} \alpha = 0,$

(16)

$\frac{{\partial \alpha }}{{\partial t}} = R\left( \alpha \right).$

Основная идея рассматриваемой методики состоит в том, чтобы согласовать численную регуляризацию (16) с уравнением Кана–Хилларда (7), описывающим термодинамически согласованную модель диффузной границы. Подставив выражение (14) в уравнение (7), получим

(17)

$\frac{{\partial \alpha }}{{\partial t}} = r\left( \alpha \right)\Delta \mu \left( \phi \right),$

где

(18)

$r\left( \alpha \right) = \frac{{\partial \alpha }}{{\partial \phi }} = \frac{{{{\rho }^{2}}}}{{2{{\rho }_{1}}{{\rho }_{2}}}} = \frac{{{{{\left[ {\alpha \left( {{{\rho }_{1}} - {{\rho }_{2}}} \right) + {{\rho }_{2}}} \right]}}^{2}}}}{{2{{\rho }_{1}}{{\rho }_{2}}}}.$

Здесь предполагается, что фазовые плотности ${{\rho }_{1}}$ и ${{\rho }_{2}}$ не меняются на этапе численной регуляризации.

Сравнивая уравнения (16) и (17), получаем

(19)

$R\left( \alpha \right) = r\left( \alpha \right)\Delta \mu \left( \phi \right) = r\left( \alpha \right)\frac{{\partial \phi }}{{\partial t}},$

что замыкает определяющую систему уравнений (8). Таким образом, в предлагаемой модели течения двухфазной смеси несмешивающихся жидкостей, определяющие уравнения состоят из системы уравнений (8) и уравнения для функции порядка (7), через которую вычисляется регуляризирующая функция $R\left( \alpha \right)$.

4. ЧИСЛЕННЫЙ МЕТОД

При интегрировании системы уравнений (8) мы применяем принцип разделения по физическим процессам и разбиваем задачу на две подзадачи, одна из которых связана с решением основной гиперболической части, а вторая – с интегрированием регуляризирующей поправки:

(20а)

$\begin{gathered} \frac{{\partial {{\alpha }_{1}}{{\rho }_{1}}}}{{\partial t}} + {\text{div}}\left( {{{\alpha }_{1}}{{\rho }_{1}}u} \right) = 0,\quad \frac{{\partial {{\alpha }_{2}}{{\rho }_{2}}}}{{\partial t}} + {\text{div}}\left( {{{\alpha }_{2}}{{\rho }_{2}}u} \right) = 0,\quad \frac{{\partial \rho u}}{{\partial t}} + {\text{div}}\left( {\rho uu + PI} \right) = 0, \\ \frac{{\partial \rho e}}{{\partial t}} + {\text{div}}\left( {\rho Hu} \right) = 0,\quad \frac{{\partial \alpha }}{{\partial t}} + u \cdot \operatorname{grad} \alpha = 0, \\ \end{gathered} $

(20б)

$\begin{gathered} \frac{{\partial {{\alpha }_{1}}{{\rho }_{1}}}}{{\partial t}} = {{\rho }_{1}}R\left( \alpha \right),\quad \frac{{\partial {{\alpha }_{2}}{{\rho }_{2}}}}{{\partial t}} = - {{\rho }_{2}}R\left( \alpha \right),\quad \frac{{\partial \rho u}}{{\partial t}} = R\left( \alpha \right)\left( {{{\rho }_{1}} - {{\rho }_{2}}} \right)u, \\ \frac{{\partial \rho e}}{{\partial t}} = R\left( \alpha \right)\left[ {\left( {{{\rho }_{1}} - {{\rho }_{2}}} \right)k + \left( {{{\rho }_{1}}{{\varepsilon }_{1}} - {{\rho }_{2}}{{\varepsilon }_{2}}} \right)} \right],\quad \frac{{\partial \alpha }}{{\partial t}} = R\left( \alpha \right). \\ \end{gathered} $

Далее рассмотрим эти две задачи подробнее.

4.1. Гиперболическая система

Последнее уравнение в (20а) является уравнением адвекции для объемной доли, которое можно переписать в следующей квазиконсервативной форме:

(21)

$\frac{{\partial \alpha }}{{\partial t}} + {\text{div}}\left( {u\alpha } \right) = \alpha \operatorname{div} \left( u \right).$

Мы будем использовать уравнение (20) при разработке численной схемы, так как это позволит на дискретном уровне точно удовлетворить важному условию сбалансированности, когда диффузия контактной границы двух жидкостей с одинаковым давлением дает то же самое смесевое давление [6], [9].

Систему уравнений (20а) запишем в декартовой системе координат (x¹, x², x³) в векторном виде:

(22)

$\frac{{\partial {\mathbf{q}}}}{{\partial t}} + \frac{{\partial {\mathbf{f}}\left( {\mathbf{q}} \right)}}{{\partial {{x}^{1}}}} + \frac{{\partial {\mathbf{g}}\left( {\mathbf{q}} \right)}}{{\partial {{x}^{2}}}} + \frac{{\partial {\mathbf{h}}\left( {\mathbf{q}} \right)}}{{\partial {{x}^{3}}}} = {\mathbf{s}}\left( {\mathbf{q}} \right),$

где

${\mathbf{q}} = {{\left[ {\begin{array}{*{20}{c}} {{{\rho }_{1}}{{\alpha }_{1}}}&{{{\rho }_{2}}{{\alpha }_{2}}}&{\rho u}&{\rho v}&{\rho w}&{\rho e}&{{\text{ }}z} \end{array}} \right]}^{{\text{т}}}}$, ${\mathbf{s}}\left( {\mathbf{q}} \right) = {{\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0&{{\text{ }}\alpha \operatorname{div} \left( {\mathbf{u}} \right)} \end{array}} \right]}^{{\text{т}}}}$, f, g, h являются потоками по направлениям x¹, x², x³ соответственно.

Система уравнений (22) дискретизируется по пространству на декартовой сетке методом конечных объемов:

$\frac{{d{{{{\mathbf{\bar {q}}}}}_{{i,j,k}}}}}{{dt}} = \frac{1}{{\Delta x_{i}^{1}}}\left( {{{{\mathbf{f}}}_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}} - {{{\mathbf{f}}}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}}} \right) + \frac{1}{{\Delta x_{j}^{2}}}\left( {{{{\mathbf{g}}}_{{i,j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},k}}} - {{{\mathbf{g}}}_{{i,j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},k}}}} \right) + \frac{1}{{\Delta x_{k}^{3}}}\left( {{{{\mathbf{h}}}_{{i,j,k - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - {{{\mathbf{h}}}_{{i,j,k + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right){\text{ + }}{{{\mathbf{s}}}_{{i,j,k}}}.$

Правая часть уравнения (23) приближается следующим образом:

${{s}_{{i,j,k}}} = {{\alpha }_{{i,j,k}}}\left[ {\frac{1}{{\Delta x_{i}^{1}}}\left( {{{u}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}} - {{u}_{{i - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}}} \right)} \right. + \frac{1}{{\Delta x_{j}^{2}}}\left( {{{v}_{{i,j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},k}}} - {{v}_{{i,j - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},k}}}} \right) + \left. {\frac{1}{{\Delta x_{k}^{3}}}\left( {{{w}_{{i,j,k + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - {{w}_{{i,j,k - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right)} \right].$

Численные потоки на границах ячеек ${{{\mathbf{f}}}_{{i \pm {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}}$, ${{{\mathbf{g}}}_{{i \pm {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}}$, ${{{\mathbf{h}}}_{{i \pm {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}}$ и соответственно скорости на гранях ${{u}_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},j,k}}}$, ${{v}_{{i,j + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},k}}}$ и ${{w}_{{i,j,k + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ рассчитываются методом Годунова [19] с приближенным решателем задачи Римана HLLC [20].

Схема второго порядка реализуется с помощью схемы MUSCL. Производные примитивных переменных $\left( {\begin{array}{*{20}{c}} {{{\alpha }_{1}}{{\rho }_{1}}}&{{{\alpha }_{2}}{{\rho }_{2}}}&P&u&{{{\alpha }_{1}}} \end{array}} \right)$ вычисляются с ограничителями MINMOD. Интерполированные примитивные переменные слева и справа ребра ячеек определяется следующим образом:

$\begin{array}{*{20}{l}} {a_{{i + 1/2}}^{R} = {{a}_{{i + 1}}} - \frac{1}{2}\min \bmod \left( {\Delta {{a}_{{i + 3/2}}},\Delta {{a}_{{i + 1/2}}}} \right)} \end{array},$

$\begin{array}{*{20}{l}} {a_{{i + 1/2}}^{L} = {{a}_{i}} + \frac{1}{2}\min \bmod \left( {\Delta {{a}_{{i + 1/2}}},\Delta {{a}_{{i - 1/2}}}} \right)} \end{array},$

где $a = {{\alpha }_{1}}{{\rho }_{1}},\;{{\alpha }_{2}}{{\rho }_{2}},\;P,\;u,\;\alpha $, $\begin{array}{*{20}{l}} {a_{{i + 1/2}}^{L}} \end{array}$ и $\begin{array}{*{20}{l}} {a_{{i + 1/2}}^{R}} \end{array}$ – интерполированные значения слева и справа ребра $i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$, соответственно, $\Delta {{a}_{{i + 1/2}}} = {{a}_{{i + 1}}} - {{a}_{i}}$, $\min \bmod (x,y) = \operatorname{sign} (x)\max \left\{ {0,\min \left[ {\left| x \right|,y\operatorname{sign} (x)} \right]} \right\}$.

В схеме MUSCL при решении локальной задачи Римана в методе Годунова применяются следующие начальные данные:

$a = \left\{ \begin{gathered} a_{{i + 1/2}}^{L},\quad x < 0, \hfill \\ a_{{i + 1/2}}^{R},\quad x > 0. \hfill \\ \end{gathered} \right.$

Численный поток через ребро $i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ определяется приближенным решением (по схеме HLLC) задачи Римана.

4.2. Система уравнений межфазной границы

Система обыкновенных дифференциальных уравнений (20б) для каждой ячейки расчетной сетки решается методом Эйлера. Последнее уравнение должно решать совместно с уравнением (7).

Уравнение (7) содержит производную четвертого порядка по параметру порядка $\phi $, поэтому использование явной схемы может потребовать слишком жесткого ограничения на шаг по времени. По этой причине рассмотрим для этого уравнения следующую неявную схему:

(23)

$\begin{gathered} \frac{{\phi _{i}^{{n + 1}} - \phi _{i}^{n}}}{{\Delta t}} = \frac{{\mu _{{i + 1}}^{{n + 1}} - 2\mu _{i}^{{n + 1}} + \mu _{{i - 1}}^{{n + 1}}}}{{\Delta {{x}^{2}}}}, \\ \mu _{i}^{{n + 1}} - \ln (1 + \phi _{i}^{{n + 1}}) + \ln (1 - \phi _{i}^{{n + 1}}) + {{\chi }^{2}}\frac{{\phi _{{i + 1}}^{{n + 1}} - 2\phi _{i}^{{n + 1}} + \phi _{{i - 1}}^{{n + 1}}}}{{\Delta {{x}^{2}}}} + {{\theta }_{0}}\phi _{i}^{n} = 0. \\ \end{gathered} $

Это система нелинейных уравнений относительно ${\mathbf{Z}}_{i}^{{n + 1}} = (\phi _{i}^{{n + 1}},\mu _{i}^{{n + 1}})$. Для ее решения применяется метод Ньютона. Система линейных уравнений относительно итерационной невязки $\delta {\mathbf{Z}}_{i}^{{}} = {\mathbf{Z}}_{i}^{{\left( {k + 1} \right)}} - {\mathbf{Z}}_{i}^{{\left( k \right)}}$ (k – индекс итерации) решается методом сопряжeнных градиентов.

Вычислив $\phi _{i}^{{n + 1}}$ таким образом, $R\left( \alpha \right)$ можно определить затем по формуле

(24)

$R(\alpha _{i}^{n}) = r(\alpha _{i}^{n})\frac{{\phi _{i}^{{n + 1}} - \phi _{i}^{n}}}{{\Delta t}}.$

Возможен альтернативный подход, когда функция $R\left( \alpha \right)$ вычисляется по значению объемной доли из дискретизации последнего уравнения в системе (20б):

(25)

$R(\alpha _{i}^{n}) = \frac{{\alpha _{i}^{{n + 1}} - \alpha _{i}^{n}}}{{\Delta t}},$

где $\alpha _{i}^{{n + 1}}$ определяется уравнением (13) по значению $\phi _{i}^{{n + 1}}$,

$\alpha _{i}^{{n + 1}} = \frac{{(1 + \phi _{i}^{{n + 1}}){{\rho }_{2}}}}{{{{\rho }_{1}}(1 - \phi _{i}^{{n + 1}}) + {{\rho }_{2}}(1 + \phi _{i}^{{n + 1}})}}.$

Первые четыре уравнения в системе (20б) определяют изменение остальных параметров на стадии регуляризации. Как отмечалось выше, на этой стадии фазовые плотности не изменяются; фактически, решение системы (20б) корректирует значения скорости, давления и внутренней энергии в области диффузной границы. Соответствующие уравнения интегрируются по стандартной явной схеме первого порядка.

5. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Для верификации предложенного метода проводится серия расчетов, в которых тестируется зависимость разрешения области диффузного интерфейса от значения параметров модели Кана–Хилларда ${{\theta }_{0}}$ и $\chi $, а также показывается эффективность и точность метода в расчетах двухфазных течений с интерфейсом. Сравнение проводится с результатами расчетов без регуляризирующей поправки (стандартная модель 5 уравнений [9]).

5.1. Эволюция диффузной границы в модели Кана–Хилларда

Сначала мы рассматриваем модельную задачу релаксации диффузной границы в соответствии с уравнением Кана–Хилларда. Нестационарные одномерные уравнения (7) интегрируются по времени с начального распределения

$\phi = \tanh \left[ {2.0\left( {x - 0.5} \right)} \right],\quad x \in \left[ {0,1} \right],$

на сетке с 100 равномерно распределенными ячейками. На основе решения для функции порядка рассчитывается эволюция объемной доли α со времени. Используется неявная схема (23) . Шаг по времени составляет $\Delta t = 1.0$. Предполагается, что фазовые плотности равны, ${{\rho }_{1}} = {{\rho }_{2}}$.

На фиг. 1а показаны результаты расчета с параметрами χ = 2Δx и θ₀ = 7.0 для первых 5 шагов по времени. Видно, что численные значения объемной доли находятся в физически допустимой области между 0 и 1.

Фиг. 1.

Численные решения для распределения объемной доли α: (а) эволюция со временем, χ = 2Δx , θ₀ = 7.0; (б) зависимость от параметра χ, θ₀ = 7.0; (в) зависимость от параметра θ₀, χ = 5Δx.

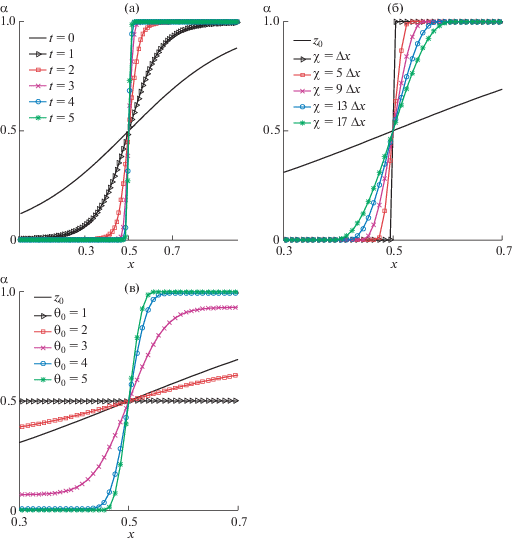
На фиг. 1б показаны результаты расчетов с параметром θ₀ = 7.0 на момент времени t = 5.0 при различных значениях параметра χ. Этот параметр контролирует ширину диффузной границы. Очевидно, чем меньше χ, тем меньше ширина диффузной границы. Параметр χ фактически определяет количество точек N_d в диффузионной зоне, ${{N}_{d}} \approx {\chi \mathord{\left/ {\vphantom {\chi {\Delta x}}} \right. \kern-0em} {\Delta x}}$.

На фиг. 1в представлены результаты расчетов с параметром χ = 5Δx на момент времени t = 5.0 при различных значениях параметра θ₀. Уменьшение значения этого параметра приводит к увеличению ширины размазывания диффузной границы. При этом видно, что при значениях ${{\theta }_{0}} \geqslant 5$ происходит насыщение, зависимость от параметра ослабевает и сходит на нет.

На основании этих результатов мы выбираем χ = 2Δx и θ₀ = 7.0 для расчетов течений двухфазных сред, которые будут рассмотрены ниже. При таких параметрах ширина диффузной границы должна контролироваться моделью в диапазоне 2–3 счетных ячеек.

5.2. Ударная труба

Рассмотрим один из стандартных тестов для течений двухфазных сред – одномерное течение в ударной трубе. Среда состоит из двух жидкостей с разными уравнениями состояния, параметры которых приведены в табл. 1. Длина расчетной области составляет 1 м. В начальный момент времени жидкость 1 расположена слева, а жидкость 2 – справа от межфазной границы, которая находится в точке x = 0.7 м.

Таблица 1.

Параметры уравнений состояний

Жидкость	γ	a ((Па м⁶)/кг)	b (м³/кг)	π (Па)
1	4.400	0	0	6 × 10⁸
2	1.400	5	10^–3	0

Начальные данные задаются в виде

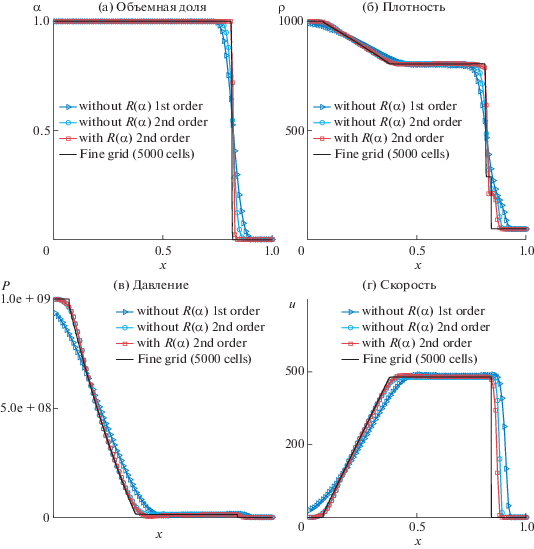
где α – объемная доля жидкости 1.

На фиг. 2 представлены численные результаты без контролирующей поправки, $R\left( \alpha \right) = 0$, на сетке из 100 и 5000 ячеек и результаты с контролирующей поправкой $R\left( \alpha \right)$ на сетке из 100 ячеек. Численные результаты на сетке 5000 ячеек получается по MUSCL схеме второго порядка. Видно, что в расчетах с $R\left( \alpha \right)$ численная диссипация оказывается намного меньше, чем в расчетах без $R\left( \alpha \right)$.

Фиг. 2.

Численные решения задачи об ударной трубе.

Штрафом за введение в модель регуляризирующей поправки является нарушение консервативности. Система определяющих уравнений, вообще говоря, не имеет более форму законов сохранения (только в предельном случае, когда ширина диффузной границы стягивается в точку). Поэтому вполне закономерен вопрос, насколько велика плата за введение этой поправки, т.е., как сильно изменяется полная масса и энергия системы.

Чтобы ответить на этот вопрос и оценить порядок неконсервативности схемы с $R\left( \alpha \right)$, определим следующие параметры: суммарная масса $M = \sum\nolimits_{i = 1}^n {{{\rho }_{i}}\Delta x} $, суммарная полная энергия $E = \sum\nolimits_{i = 1}^n {{{\rho }_{i}}{{e}_{i}}\Delta x} $, где i – индекс ячейки. Тогда погрешность, связанную с неконсервативностью, можно оценить величиной

${\text{err}}\left( W \right) = \frac{{\left| {{{W}_{{{\text{end}}}}} - {{W}_{0}}} \right|}}{{{{W}_{0}}}},\quad W = M,E,$

где W₀ и W_end – значения параметра в начале и в конце расчета соответственно. В табл. 2 показано изменение погрешности в зависимости от количества ячеек. Видно, что погрешность уменьшается с измельчением сетки.

Таблица 2.

Изменение погрешности в зависимости от количества ячеек

Количество ячеек	100	200	400
err(M)	1.72e–03	1.24e–03	8.40e–04
err(E)	6.08e–04	3.38e–04	1.78e–04

5.3. Взаимодействие ударной волной с газовым пузырьком

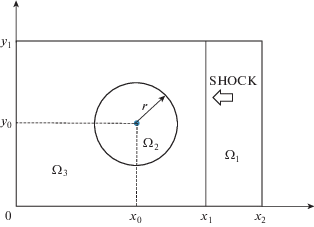
Рассматривается двумерная задача о взаимодействии ударной волны с пузырьком газа [9]. Похожие тесты рассматриваются также в работах [21], [22]. Двухфазная среда аналогична рассмотренной выше в п. 5.2. Жидкость 2 – это газ внутри пузырька, жидкость 1 – жидкость вне пузырька. Расчетная область показана на фиг. 3. Геометрические размеры области определяются следующими значениями: x₀ = 0.70 м, x₁ = 0.95 м, x₂ = 1.20 м, y₀ = 0.50 м, y₁ = 1.00 м, r₀ = 0.20 м.

Фиг. 3.

Схема расчета задачи о взаимодействии ударной волны с газовым пузырьком.

Задание начальных данных определяется следующими формулами:

где α – объемная доля материала 2.

Расчетная область дискретизируется по пространству декартовой равномерной сеткой из 120 × 100 счетных ячеек. Расчеты на этой сетке проводятся по стандартной модели без контролирующей поправки, $R\left( \alpha \right) = 0$, и по предложенной модели с контролируемой зоной диффузной границы.

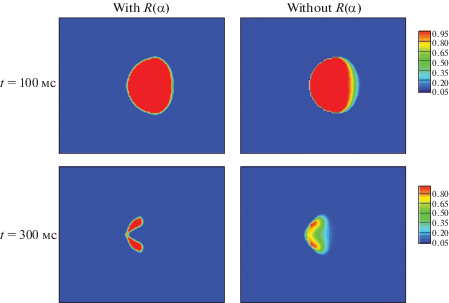
Результаты расчетов приведены на фиг. 4 и 5 , где изображены распределение объемной доли и поле градиента плотности (численный шлиерен), соответственно, на два характерных момента времени, t = 100 μs и t = 300 μс, которые отвечают моменту прохождения ударной волны по области пузырька и более позднему моменту времени, когда происходит фрагментация пузырька.

Фиг. 4.

Распределение объемной доли газа в задаче о взаимодействии ударной волны с пузырьком.

Фиг. 5.

Поле градиента плотности (численный шлиерен) в задаче о взаимодействии ударной волны с пузырьком.

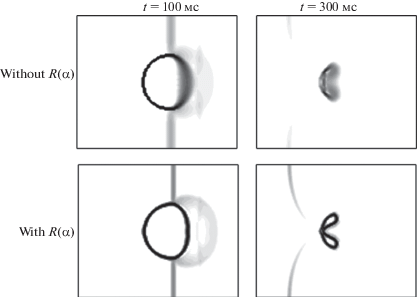
Видно, что основные характеристики течения, возникающего при дифракции ударной волны на деформируемом газовом пузырьке, хорошо воспроизводятся в обоих расчетах. Поверхность пузырька под воздействием ударной волны принимает характерную двулепестковую форму. Формируется волновая структура из падающей, отраженной и преломленной внутри пузырька ударных волн. Вместе с тем введение регуляризирующей поправки $R\left( \alpha \right)$ в соответствии с уравнением Кана–Хилларда показывает заметное улучшение в разрешении диффузионной границы между материалами. При этом характерная область диффузной границы (отмечена желтым цветом на фиг. 4) с течением времени фактически не нарастает, в отличие от стандартного случая без $R\left( \alpha \right)$.

ЗАКЛЮЧЕНИЕ

Разработан и реализован численный метод, обеспечивающий высокое и контролируемое пространственное разрешение межфазных границ при моделировании течений неоднородных двухфазных сжимаемых сред. В качестве модели двухфазной среды использовалась односкоростная модель пяти уравнений с регуляризирующей поправкой в правой части. Показано, что регуляризирующая поправка может быть определена в соответствии с термодинамической моделью Кана–Хилларда для описания зоны межфазной границы. В результате получена численная модель зоны диффузной границы с двумя контролирующими ширину зоны параметрами. Проведен анализ зависимости численных решений (размера зоны интерфейса) от контролирующих параметров. Проведены расчеты некоторых тестовых задач, которые показали заметное улучшение разрешения межфазных границ при использовании модели с уравнением Кана–Хилларда.

Благодарим рецензента за полезные замечания.

Список литературы

Hirt C.W., Amsden A.A., Cook J.L. An arbitrary Lagrangian-Eulerian computing method for all flow speeds // J. Comput. Phys. 1974. V. 14. P. 227–253.
Sussman M., Smereka P., Osher S. A Level Set Approach for Computing Solutions to Incompressible Two-Phase Flow // SIAM J. Sci. Comput. 2007. V. 29. P. 1781–1824.
Glimm J., Li X.L., Liu Y.J., Xu Z.L. Zhao N. Conservative front tracking with improved accuracy // SIAM J. Numer. Anal. 2003. V. 41. P. 1926–1947.
Terashima H., Tryggvason G. A front-tracking/ghost-fluid method for fluid interfaces in compressible flows // J. Comput. Phys. 2009. V. 228. P. 4012–4037.
Mulder W., Osher S., Sethian J.A. Computing interface motion in compressible gas dynamics // J. Comput. Phys. 1992. V. 100. P. 209–228.
Abgrall R. How to prevent pressure oscillations in multicomponent flow calculations: a quasi-conservative approach // J. Comput. Phys. 1996. V. 125. P. 150–160.
Saurel R., Abgrall R. A multiphase Godunov method for compressible multi-fluid and multiphase flows // J. Comput. Phys. 1999. V. 150. № 2. P. 425–467.
Menshov I., Zakharov P. On the composite Riemann problem for multi-material fluid flows // Int. J. Numer. Meth. Fluids. 2014. V. 76. P. 109–127.
Allaire G., Clerc S., Kokh S. A five-equation model for the simulation of interfaces between compressible fluids // J. Comput. Phys. 2002. V. 181. P. 577–616.
Tiwari A., Jonathan B.F., Pantano C. A diffuse interface model with immiscibility preservation // J. Comput. Phys. 2013. V. 252. P. 290–309.
Kapila A.K., Menikoff R., Bdzil J.B., Son S.F., Stewart D.S. Two-phase modeling of deflagration-to-detonation transition in granular materials: Reduced equations // Physics of Fluids. 2001. V. 13. P. 3002–3024.
Балашов В.А., Савенков Е.Б. Квазигидродинамическая система уравнений для описания течений многофазной жидкости с учетом поверхностных эффектов // Препринты ИПМ им. М.В. Келдыша. 2015. № 75. 37 с.
Балашов В.А., Савенков Е.Б. Многокомпонентная квазигидродинамическая модель для описания течений многофазной жидкости с учетом межфазного взаимодействия // Прикл. Механ. и техн. физ. 2018. № 3. С. 57–68.
Cahn J.W., Hilliard J.E. Free Energy of a Nonuniform System. I. Interfacial Free Energy // J. Chem. Phys. 1958. V. 28. P. 258–267.
Gurtin M.E. Generalized Ginzburg–Landau and Cahn-Hilliard equations based on a microforce balance // Physics of Fluids. 1996. V. 92. P. 178–192.
Copetti M.I.M., Elliott C.M. Numerical analysis of the Cahn-Hilliard equation with a logarithmic free energy // Numer. Math. 1992. V. 63. P. 39–65.
Chetverushkin B.N. Kinetically consistent schemes in gas dynamics // Mat. Mod. 1999. V. 11(5). P. 84–100.
Elizarova T.G., Sokolova M.E., Sheretov Yu. Quasi-gasdynamic equations and numerical modeling of the viscous gas flows // Comput. Math. and Math. Phys. 2005. V. 45. № 3. P. 524–534.
Godunov S.K. A Difference Scheme for Numerical Solution of Discontinuous Solution of Hydrodynamic Equations // Math. Sbornik. 1959. V. 47(89). P. 271–306.
Toro E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. Springer, 3^rd edition. 2009.
Coralic V., Colonius T. Finite-volume WENO scheme for viscous compressible multicomponent flows // J. Comput. Phys. 2014. V. 274. P. 95–121.
Franchina N., Savini M., Bassi F. Multicomponent gas flow computations by a discontinuous Galerkin scheme using L2-projection of perfect gas EOS // J. Comput. Phys. 2016. V. 315. P. 302–322.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал