Журнал вычислительной математики и математической физики, 2020, T. 60, № 5, стр. 884-899
О точности бикомпактных схем при расчете нестационарных ударных волн
М. Д. Брагин 1, 2, 3, *, Б. В. Рогов 1, 2, **
1 ИПМ РАН
125047 Москва, Миусская пл., 4, Россия
2 МФТИ
141700 Долгопрудный, М.o., Институтский пер., 9, Россия
3 ИГиЛ СО РАН
630090 Новосибирск, пр-т Лаврентьева, 15, Россия
* E-mail: michael@bragin.cс
** E-mail: rogov.boris@gmail.com
Поступила в редакцию 02.09.2019
После доработки 02.09.2019
Принята к публикации 14.01.2020
Аннотация
Рассмотрены бикомпактные схемы четвертого порядка классической аппроксимации по пространству и повышенного (не менее второго) по времени. Исследована их точность на разрывных решениях квазилинейной гиперболической системы законов сохранения, содержащих ударные волны с переменными скоростями распространения. В качестве примера такой системы взята система уравнений теории мелкой воды. Показано, что немонотонная бикомпактная схема имеет повышенный порядок сходимости в областях влияния нестационарных ударных волн. Если же подавлять схемные осцилляции посредством процедуры консервативной монотонизации, то бикомпактная схема, несмотря на высокую точность на гладких решениях, снижает свой порядок сходимости до первого порядка в областях влияния ударных волн. Библ. 46. Фиг. 18.
1. ВВЕДЕНИЕ
В классической работе [1] было показано, что среди линейных разностных схем для линейного уравнения переноса нет монотонных схем с минимальным порядком аппроксимации выше первого по всем независимым переменным (здесь и далее под “аппроксимацией” мы будем понимать классическую аппроксимацию на гладких решениях, если явно не указано иное). Вследствие этого “запрета Годунова” разностные схемы повышенного порядка аппроксимации для гиперболических систем законов сохранения при сквозном счете генерируют осцилляции в областях высоких градиентов искомых функций. В литературе предложены различные способы подавления этих осцилляций или, другими словами, монотонизации численного решения. Одним из распространенных способов монотонизации является нелинейная коррекция численных потоков. Такая коррекция используется в MUSCL-схемах [2], TVD-схемах [3], WENO-схемах [4], NED-схемах [5], DG-схемах [6], САВARET-схемах [7]. Далее эти схемы будем сокращенно называть NFC-схемами (Nonlinear Flux Correction). Наряду с ограничителями (limiters) численных потоков для уменьшения осцилляций около разрывов в схемах высокого порядка аппроксимации применяются искусственная диссипация [8]–[11], численные фильтры [12]–[15], а также различные процедуры гибридизации [16]–[20], в которых обычно комбинируются монотонизированная и немонотонная схемы.
Однако коррекция потоков около сильных разрывов решения в схемах высокого порядка приводит к нежелательным эффектам. В работах [21]–[23] было показано, что NFC-схемы имеют не более чем первый порядок локальной сходимости в областях влияния ударных волн. Также снижение порядка сходимости NFC-схем до первого имеет место и для интегралов от искомых функций, рассчитанных по квадратурной формуле повышенного порядка точности на интервалах, одна из границ которых находится в области влияния ударной волны [24]–[29]. Такую сходимость интегралов от сеточных функций авторы работ [24]–[29] называют интегральной сходимостью. Как указано в [24]–[29], причина падения порядка сходимости до первого связана с тем, что в NFC-схемах коррекция численных потоков приводит к снижению их гладкости и, как следствие, снижению порядка аппроксимации ε-условий Гюгонио на фронтах ударных волн [30]. О связи гладкости численных потоков и порядка сходимости разностных схем говорят также и результаты работ [24], [27], в которых установлено, что немонотонная схема Русанова [31] и немонотонная компактная схема из [23] с достаточно гладкими численными потоками имеют не менее чем второй порядок интегральной сходимости в областях, содержащих сильные разрывы. В отличие от монотонизированных NFC-схем указанные немонотонные схемы обладают повышенным порядком сходимости в областях влияния ударных волн. Отметим, что эти немонотонные схемы генерируют ложные осцилляции, локализованные около ударных волн.
В работах [32]–[34] были предложены центральные компактные схемы на неразнесенных декартовых сетках для решения квазилинейных гиперболических систем законов сохранения. Схемы получены методом прямых и имеют четвертый порядок пространственной аппроксимации. Шаблон вышеупомянутых компактных схем по каждой пространственной переменной состоит из двух целых узлов, по этой причине эти схемы стали называться бикомпактными. Для значений искомых функций в дополнительных полуцелых узлах шаблона выводятся специальные уравнения – следствия исходных гиперболических уравнений. В итоге дискретные уравнения схем имеют первый разностный порядок по пространственным переменным для искомых сеточных функций в целых узлах [35]. Поэтому решение этих уравнений требует обращения только блочно-двухдиагональных матриц, хотя компактные схемы [32]–[34] – неявные, абсолютно устойчивые и могут быть использованы в широком диапазоне локальных чисел Куранта. Особенностью этих схем является то, что они сохраняют порядок пространственной аппроксимации на произвольно неравномерных сетках из целых узлов. Кроме того, бикомпактные схемы имеют улучшенные дисперсионные свойства по сравнению с классическими трехточечными компактными схемами [35] того же порядка аппроксимации. Отметим, что полудискретные центральные бикомпактные схемы являются бездиссипативными. Диссипативные свойства полностью дискретных бикомпактных схем определяются диссипацией методов интегрирования по времени полудискретных схем. В качестве методов интегрирования по времени в [32]–[34] предлагается использовать экономичные неявные методы типа диагонально-неявных методов Рунге–Кутты (DIRK) [36]. В работах [37], [38] предложены обобщения этих схем на случай многомерных гиперболических уравнений, а в работе [39] – обобщения на случай произвольного четного (четвертого, шестого восьмого и так далее) порядка аппроксимации пространственных производных.
В настоящей работе, во-первых, рассмотрен вопрос о возможности построить численный метод на основе бикомпактной разностной аппроксимации пространственной производной [35], который сходится с повышенным (вторым) порядком в большей части области влияния нестационарной ударной волны. В качестве модельной задачи для такого метода рассмотрена задача Коши для гиперболической системы уравнений мелкой воды. Во-вторых, рассмотрен вопрос о порядке сходимости бикомпактной схемы высокого порядка аппроксимации в области влияния нестационарной ударной волны в случае, когда в процессе счета к схеме применяется процедура монотонизации для подавления ложных осцилляций около ударной волны.
2. БИКОМПАКТНЫЕ СХЕМЫ БЕЗ МОНОТОНИЗАЦИИ
Для квазилинейной гиперболической системы законов сохранения
рассмотрим задачу Коши на временном интервале $(0,T]$ с периодическими начальными условиями где символы ${{\partial }_{t}}$, ${{\partial }_{x}}$ обозначают операции частного дифференцирования по времени t и координате x соответственно; ${\mathbf{u}}(x,t)$ – искомая, а ${\mathbf{f}}({\mathbf{u}})$ – заданная вектор-функции из m компонент; $X > 0$ – период.Полудискретная бикомпактная схема четвертого порядка аппроксимации для системы уравнений (1) имеет вид [37]
(3)
$\begin{gathered} \frac{d}{{dt}}(A_{0}^{x}{{{\mathbf{u}}}_{{j + 1/2}}}) + \Lambda _{1}^{x}{{{\mathbf{f}}}_{{j + 1/2}}} = 0, \\ \frac{d}{{dt}}(\Lambda _{1}^{x}{{{\mathbf{u}}}_{{j + 1/2}}}) + \Lambda _{2}^{x}{{{\mathbf{f}}}_{{j + 1/2}}} = 0,\quad j = \overline {0,N - 1} , \\ \end{gathered} $Дисперсионные свойства бездиссипативной полудискретной схемы (3) в линейном приближении исследованы в работах [35], [41], где показано, что эта схема имеет улучшенные дисперсионные свойства по сравнению с известными компактными схемами того же порядка аппроксимации.
Начальные условия (2) для функций ${{{\mathbf{u}}}_{j}}(t)$ и ${{{\mathbf{u}}}_{{j + 1/2}}}(t)$ будут следующими:
Полностью дискретные бикомпактные схемы получаются путем применения какого-либо устойчивого численного метода интегрирования по времени системы ОДУ полудискретной схемы (3) . В данном разделе будут рассмотрены свойства разностных решений двух полностью дискретных бикомпактных схем на равномерных сетках с постоянным пространственным шагом ${{h}_{{x,j + 1/2}}} = h$ и постоянным временным шагом $\tau $.
Первая из двух схем, названная базовой в [32]–[34] и далее обозначаемая как DIRK1B4, получается путем интегрирования уравнений (3) по неявной схеме Эйлера. Она имеет погрешность аппроксимации $O(\tau ,{{h}^{4}})$ и является абсолютно устойчивой и консервативной [32]–[34]. В работах [33], [34] исследованы дисперсионные и диссипативные свойства, а также свойства монотонности базовой схемы. Аналитически показано, что базовая схема для линейного скалярного уравнения переноса является монотонной по Годунову, когда число Куранта κ не меньше, чем 0.25. Отметим, что коэффициент схемной вязкости у данной схемы положителен при числе Куранта $\kappa > 0$ и монотонно растет c его ростом. Численный эксперимент [33], [34] показал, что базовая схема для квазилинейного уравнения Хопфа является монотонной, когда локальное число Куранта $\kappa \geqslant 0.15.$
Разностные решения второй схемы, обозначаемой как Rich2B4, получаются уточнением разностных решений базовой бикомпактной схемы со вторым порядком точности по времени методом экстраполяции Ричардсона [42], [43]. Проводятся два расчета по базовой бикомпактной схеме на сетках с временными шагами $\tau $ и $\tau {\text{/}}2$. При этом пространственный шаг сетки h берется таким, чтобы вклад ошибки пространственной дискретизации в погрешность численного решения оказался малым по сравнению со вкладом ошибки дискретизации по времени. При сгущении пространственно-временной сетки поддерживается постоянство величины отношения шагов $r = {\tau \mathord{\left/ {\vphantom {\tau h}} \right. \kern-0em} h}$. Решение экстраполяционной бикомпактной схемы Rich2B4 в момент времени ${{t}^{n}} = n{\kern 1pt} \tau $ рассчитывается по следующей формуле:
(4)
${\mathbf{u}}_{k}^{n}({\text{Rich2B4;}}\;\tau ) = 2{\mathbf{u}}_{k}^{n}({\text{DIRK1B4;}}\;{\tau \mathord{\left/ {\vphantom {\tau 2}} \right. \kern-0em} 2}) - {\mathbf{u}}_{k}^{n}({\text{DIRK1B4;}}\;\tau ),\quad k = j,j + 1{\text{/}}2,$Важно уточнить, что экстраполяция (4) является пассивной, или глобальной: она выполняется после завершения расчета и лишь для тех слоев (и соответствующих им моментов времени), на которых требуется получить окончательное, высокоточное решение. Например, во многих задачах это только последний слой (финальный момент времени). Экстраполированное решение не вычисляется на каждом слое и не используется для переходов со слоя на слой, так как расчет ведется на двух вложенных сетках по монотонной схеме DIRK1B4. Следовательно, экстраполяция (4) не вызывает проблем для устойчивости счета в случае сильных ударных волн, а порождаемые ею немонотонности можно устранить какой-либо постобработкой.
В качестве конкретной гиперболической системы (1) возьмем систему уравнений первого приближения теории мелкой воды (см. [44]), для которой
(5)
${\mathbf{u}} = \left( {\begin{array}{*{20}{c}} H \\ Q \end{array}} \right),\quad {\mathbf{f}}({\mathbf{u}}) = \left( {\begin{array}{*{20}{c}} Q \\ {{{{{Q}^{2}}} \mathord{\left/ {\vphantom {{{{Q}^{2}}} {H + {{g{{H}^{2}}} \mathord{\left/ {\vphantom {{g{{H}^{2}}} 2}} \right. \kern-0em} 2}}}} \right. \kern-0em} {H + {{g{{H}^{2}}} \mathord{\left/ {\vphantom {{g{{H}^{2}}} 2}} \right. \kern-0em} 2}}}} \end{array}} \right),$(6)
$u(x,0) = a\sin \left( {\frac{{2\pi x}}{X} + \frac{\pi }{4}} \right),\quad H(x,0) = \frac{1}{{4g}}{{\left[ {a\sin \left( {\frac{{2\pi x}}{X} + \frac{\pi }{4}} \right) + b} \right]}^{2}},$Результаты расчета задачи Коши (1), (5), (6) для моментов времени $T = 0.5$ и $T = 1.0$ представлены на фиг. 1–4 и на фиг. 5–10 соответственно. Из данных на фиг. 1 и 5 видно, что при $t \approx 0.5$ и $x \approx 6$ формируется прерывная волна, которая движется в положительном направлении оси Ox и достигает положения $x \approx 9$ в момент времени $t = 1.0$.
Фиг. 1.
Результаты расчетов на момент времени $T = 0.5$. Сплошная линия – профиль глубины H, полученный по схеме DIRK1B4 на сетке с пространственным шагом $h = 0.001$, точки – порядки локальной сходимости схемы Rich2B4, найденные по формуле (8) при $N = 5000$.

Фиг. 2.
Абсолютные погрешности глубины H на момент времени $T = 0.5$ для схемы Rich2B4. Кривые: 1 – $N = 1250$, 2 – 2500, 3 – 5000, 4 – 10 000.
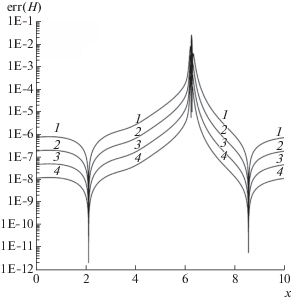
Фиг. 3.
Абсолютные погрешности инварианта w1 на момент времени $T = 0.5$ для схемы Rich2B4. Кривые: 1 – $N = 1250$, 2 – 2500, 3 – 5000, 4 – 10 000.

Фиг. 4.
Абсолютные погрешности инварианта w2 на момент времени $T = 0.5$ для схемы Rich2B4. Кривые: 1 – $N = 1250$, 2 – 2500, 3 – 5000, 4 – 10 000.

Фиг. 5.
Результаты расчетов на момент времени $T = 1.0$: сплошная линия – профиль глубины H, полученный по схеме DIRK1B4 на сетке с пространственным шагом $h = 0.001$, точки – порядки локальной сходимости схемы Rich2B4, найденные по формуле (8) при $N = 5000$.

Фиг. 6.
Профили глубины H вблизи ударной волны на момент времени $T = 1.0$, посчитанные по схеме Русанова и бикомпактным схемам Rich2B4, SDIRK3B4 (монотонизированной) и DIRK1B4.
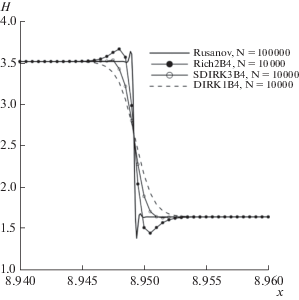
Фиг. 7.
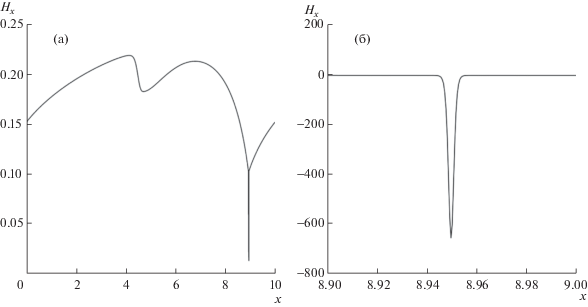
Профиль первой разностной производной ${{H}_{x}}$ глубины H на момент времени $T = 1.0$, построенный по результатам расчетов по схеме DIRK1B4 на сетке с пространственным шагом $h = 0.001$ (a) при $x \in [0,10]$ и (б) при $x \in [8.9,9.0]$
Фиг. 8.
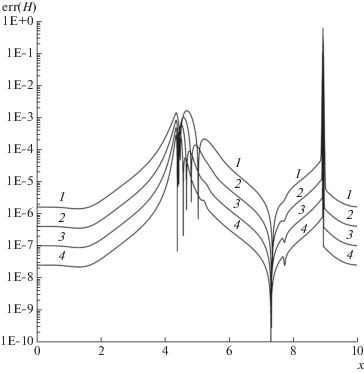
Абсолютные погрешности глубины H на момент времени $T = 1.0$ для схемы Rich2B4. Кривые: 1 – $N = 1250$, 2 – 2500, 3 – 5000, 4 – 10 000.
Фиг. 9.
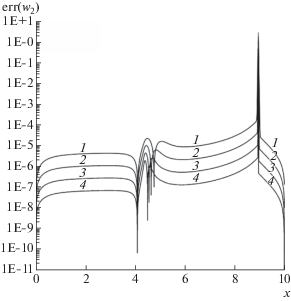
Абсолютные погрешности инварианта w1 на момент времени $T = 1.0$ для схемы Rich2B4. Кривые: 1 – $N = 1250$, 2 – 2500, 3 – 5000, 4 – 10 000.
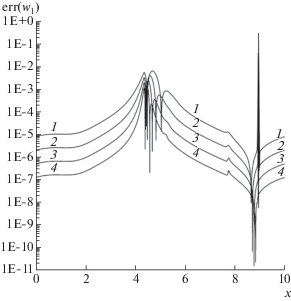
Фиг. 10.
Абсолютные погрешности инварианта w2 на момент времени $T = 1.0$ для схемы Rich2B4. Кривые: 1 – $N = 1250$, 2 – 2500, 3 – 5000, 4 – 10 000.
В согласии с анализом монотонности [33], [34] базовая бикомпактная схема DIRK1B4 при определенных шагах сетки не генерировала нефизические осцилляции при расчете профилей H, Q. На фиг. 1, 5 и 6 показаны профили глубины H, рассчитанные по схеме DIRK1B4. Также схема DIRK1B4 не генерирует нефизических осцилляций при расчете первых разностных производных величин H, Q. На фиг. 7a и 7б представлено распределение величины ${{\left( {{{H}_{x}}} \right)}_{k}} = 2{{\left( {{{H}_{{k + 1/2}}} - {{H}_{k}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{H}_{{k + 1/2}}} - {{H}_{k}}} \right)} h}} \right. \kern-0em} h}$ вдоль оси Oх как в целых $k = j$, так и полуцелых $k = j + 1{\text{/}}2$ узлах на момент времени $T = 1.0$. При этом на фиг. 7a показана верхняя часть данного распределения при значениях ${{\left( {{{H}_{x}}} \right)}_{k}} > 0$, а на фиг. 7б – распределение в окрестности ударной волны.
На фиг. 2–4, 6 и 8–10 представлены результаты расчетов по экстраполяционной бикомпактной схеме Rich2B4 на последовательности сгущающихся пространственных сеток с числом ячеек $N = 1250$, 2500, 5000 и 10 000 при отношении шагов $r = 0.05$. Расчеты показали, что схема Rich2B4 не генерирует нефизические осцилляции при $T = 0.5$, а при $T = 1.0$ эта схема генерирует нефизические осцилляции, локализованные около ударной волны, как это видно из фиг. 6. Для исследования вопроса о поведении погрешности решения схемы Rich2B4 при сгущении сетки желательно иметь аналитическое решение нелинейной задачи Коши (1), (5), (6). Поскольку такое решение не известно, в качестве него будем рассматривать решение, рассчитанное по схеме Русанова [31] на очень мелкой сетке с пространственным шагом h = 10–4 и отношением шагов $r = 0.05$. Схема Русанова позволяет получить решение задачи Коши (1), (5), (6) без ложных осцилляций для момента времени $T = 0.5$. Решение этой схемы для $T = 1.0$ содержит нефизические осцилляции, локализованные в малой окрестности ударной волны, как это видно из фиг. 6. Однако этот дефект решения схемы Русанова приемлем для оценки погрешности решений бикомпактных схем, рассчитанных на сетках с шагом $h \geqslant {{10}^{{ - 3}}}$. На фиг. 2–4 и 8–10 показаны распределения ошибок решений схемы Rich2B4 для глубины H, а также для инвариантов Римана ${{w}_{1}},\;{{w}_{2}}$ (см. [29])
гиперболической системы уравнений (1), (5). В формулах (7) величина $с = \sqrt {gH} $ есть скорость распространения малых возмущений. Из данных на фиг. 2–4 и 8–10 следует, что локальная ошибка численных решений для H, ${{w}_{1}},\;{{w}_{2}}$ при сгущении сетки убывает со вторым порядком везде за исключением тех областей, где ошибки резко возрастают или резко падают. Заметим, что ошибка численных решений резко возрастает в окрестности ударной волны. На фиг. 1 и 5 точками в каждом пятидесятом целом узле показаны порядки p локальной сходимости глубины H, определенные согласно формуле(8)
$p(2N) = {{\log }_{2}}\left( {\frac{{{\text{err}}\left( {H(N)} \right)}}{{{\text{err}}\left( {H(2N)} \right)}}} \right)$3. МОНОТОНИЗИРОВАННАЯ БИКОМПАКТНАЯ СХЕМА
Рассмотрим бикомпактную схему SDIRK3B4, получающуюся путем применения L-устойчивого однократно диагонально-неявного метода Рунге–Кутты третьего порядка точности с тремя неявными стадиями SDIRK3 [45] к интегрированию системы ОДУ полудискретной бикомпактной схемы (3) . Вследствие “запрета Годунова” схема SDIRK3B4 является немонотонной и порождает нефизические осцилляции в областях высоких градиентов решения. Мы будем применять процедуру консервативной монотонизации, предложенную в работе [46], в процессе счета по схеме SDIRK3B4 на каждом временном слое для уменьшения нефизических осцилляций.
На фиг. 11–14 и 15–18 представлены результаты расчетов задачи Коши (1), (5), (6) по монотонизированной бикомпактной схеме SDIRK3B4 для моментов времени $T = 0.5$ и $T = 1.0$ соответственно. Расчеты выполнены на последовательности сгущающихся сеток с числом ячеек $N = 1250$, 2500, 5000 и 10 000 при отношении шагов $r = 0.07$. Профили глубины H, вычисленные по монотонизированной схеме SDIRK3B4, не имеют заметных осцилляций и представлены на фиг. 6, 11 и 15.
Фиг. 11.
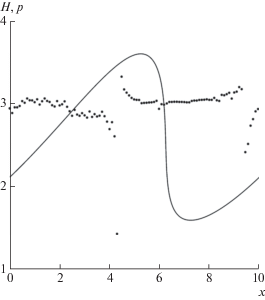
Результаты расчетов на момент времени $T = 0.5$. Сплошная линия – профиль глубины H, полученный по монотонизированной схеме SDIRK3B4 на сетке с $N = 1250$; точки – порядки локальной сходимости монотонизированной схемы SDIRK3B4, найденные по формуле (8) при $N = 5000$.
Фиг. 12.
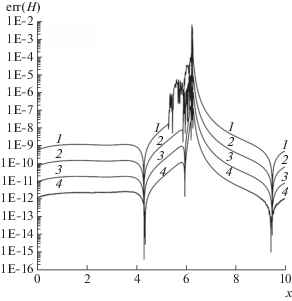
Абсолютные погрешности глубины H на момент времени $T = 0.5$ для монотонизированной схемы SDIRK3B4. Кривые: 1 – $N = 1250$, 2 – 2500, 3 – 5000, 4 – 10 000.
Фиг. 13.
Абсолютные погрешности инварианта w1 на момент времени $T = 0.5$ для монотонизированной схемы SDIRK3B4. Кривые: 1 – $N = 1250$, 2 – 2500, 3 – 5000, 4 – 10 000.
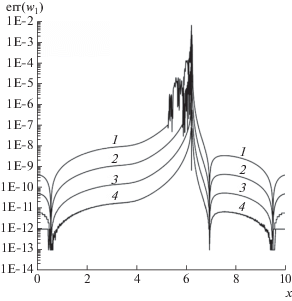
Фиг. 14.
Абсолютные погрешности инварианта w2 на момент времени $T = 0.5$ для монотонизированной схемы SDIRK3B4. Кривые: 1 – $N = 1250$, 2 – 2500, 3 – 5000, 4 – 10 000.
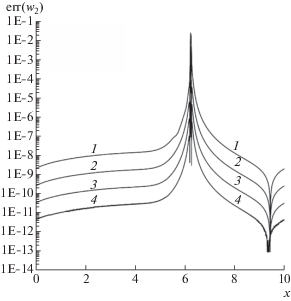
Фиг. 15.
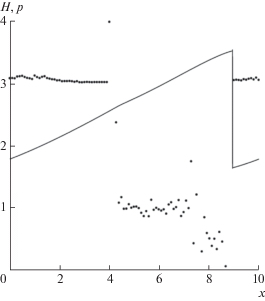
Результаты расчетов на момент времени $T = 1.0$. Сплошная линия – профиль глубины H, полученный по монотонизированной схеме SDIRK3B4 на сетке с $N = 1250$; точки – порядки локальной сходимости монотонизированной схемы SDIRK3B4, найденные по формуле (8) при $N = 5000$.
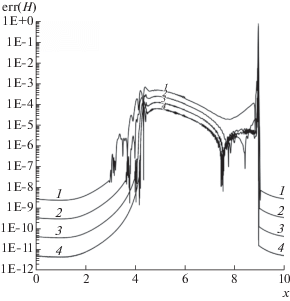
Фиг. 16.
Абсолютные погрешности глубины H на момент времени $T = 1.0$ для монотонизированной схемы SDIRK3B4. Кривые: 1 – $N = 1250$, 2 – 2500, 3 – 5000, 4 – 10 000.
Фиг. 17.
Абсолютные погрешности инварианта w1 на момент времени $T = 1.0$ для монотонизированной схемы SDIRK3B4. Кривые: 1 – $N = 1250$, 2 – 2500, 3 – 5000, 4 – 10 000.
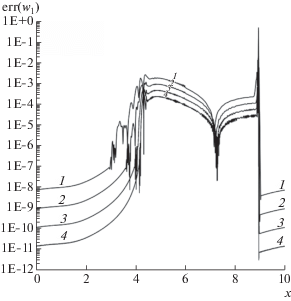
Фиг. 18.
Абсолютные погрешности инварианта w2 на момент времени $T = 1.0$ для монотонизированной схемы SDIRK3B4. Кривые: 1 – $N = 1250$, 2 – 2500, 3 – 5000, 4 – 10 000.

Важно отметить, что задача Коши для гиперболической системы уравнений (1), (5) с периодическими условиями (6) описывает докритическое течение жидкости c горизонтальной скоростью
для которой характеристические скорости ${{\lambda }_{1}} = u - c$, ${{\lambda }_{2}} = u + c$ [29] инвариантов Римана ${{w}_{1}},{{w}_{2}}$ удовлетворяют неравенствамНеравенства (9) указывают на то, что информация о величинах ${{w}_{1}}$ и ${{w}_{2}}$ распространяется в отрицательном и положительном направлениях оси Ox соответственно. Ниже будет показано, как неравенства (9) сказываются на профилях величин ${{w}_{1}}$ и ${{w}_{2}}$, а также на профиле величины
(10)
$H = {{{{{({{w}_{2}} - {{w}_{1}})}}^{2}}} \mathord{\left/ {\vphantom {{{{{({{w}_{2}} - {{w}_{1}})}}^{2}}} {(16g)}}} \right. \kern-0em} {(16g)}}.$Профили абсолютных ошибок расчета глубины H и инвариантов Римана ${{w}_{1}},{{w}_{2}}$ показаны на фиг. 12–14 на момент времени $T = 0.5$, когда формируется нестационарная ударная волна, движущаяся вправо. На ударной волне генерируются осцилляции величины ${{w}_{1}}$, которые переносятся за ее фронт в согласии с неравенством ${{\lambda }_{1}} < 0$. Из фиг. 13 видны области распространения осцилляций малой амплитуды для разных шагов сетки. Поскольку величина H зависит от величины ${{w}_{1}}$ согласно (10), то на фиг. 12 также можно наблюдать осцилляции за ударной волной. В то же время на фиг. 14 осцилляции за ударной волной отсутствуют, что согласуется с неравенством ${{\lambda }_{2}} > 0$. На фиг. 11 в каждом пятидесятом целом узле точками показаны порядки p локальной сходимости величины H, рассчитанные по формуле (8) при $N = 5000$. Видно, что порядок этой сходимости близок к трем везде, за исключением зон, где погрешность расчетов резко уменьшается. Подобный порядок сходимости имеет место и для инвариантов ${{w}_{1}},\;{{w}_{2}}$, что видно из фиг. 13–14.
На профилях абсолютных ошибок H и инвариантов Римана ${{w}_{1}},\;{{w}_{2}}$, рассчитанных по монотонизированной схеме SDIRK3B4 и соответствующих моменту времени $T = 1.0$, осцилляции малой амплитуды за ударной волной наблюдаются для H, ${{w}_{1}}$ и отсутствуют для ${{w}_{2}}$. Причем по сравнению со случаем $T = 0.5$ эти осцилляции имеют бóльшую амплитуду. Чтобы яснее видеть динамику убывания ошибок со сгущением сетки, разностные решения для H и ${{w}_{1}}$ были усреднены по пространству в области $x \in [6,8.9]$ за ударной волной. Для осреднения решения $U({{x}_{j}},T)$ использовалась следующая формула [29]:
Профили ошибок H и инвариантов Римана ${{w}_{1}},\;{{w}_{2}}$, представленные на фиг. 16–18, показывают следующую динамику при сгущении сетки. В области влияния $x \in [4,9]$ нестационарной ударной волны (то есть в следе волны [25]) убывание ошибок для монотонизированной схемы SDIRK3B4 при сгущении сетки соответствует не более чем первому порядку локальной сходимости. Вне области влияния порядок локальной сходимости близок к третьему порядку. На фиг. 15 в каждом пятидесятом целом узле точками показаны порядки p локальной сходимости величины H, рассчитанные по формуле (8) при $N = 5000$. Таким образом, процедура монотонизации [46] численного решения приводит к снижению порядка локальной сходимости схемы в следе нестационарной ударной волны.
4. ЗАКЛЮЧЕНИЕ
Исследована точность двух бикомпактных схем повышенного порядка классической аппроксимации по времени и четвертого по пространству при расчете разрывных решений квазилинейной гиперболической системы законов сохранения. Первая из изученных бикомпактных схем получена экстраполяцией по Ричардсону бикомпактной схемы первого порядка аппроксимации по времени и имеет второй порядок точности по времени на гладких решениях. Согласно “запрету Годунова”, она является немонотонной. Отметим, что экстраполяция в этой схеме реализуется пассивно, то есть после завершения расчетов по монотонной схеме первого порядка по времени на двух вложенных сетках и только для тех моментов времени, для которых требуется найти решение и исследовать его точность. В результате такой экстраполяции получается численное решение повышенной точности с локализованной немонотонностью небольшой амплитуды. Вторая схема получена путем применения процедуры консервативной монотонизации [46] к бикомпактной схеме третьего порядка аппроксимации по времени. В качестве разрывного решения рассмотрено решение задачи Коши с нестационарной ударной волной для гиперболической системы уравнений теории мелкой воды. В результате численных экспериментов показано, что первая бикомпактная схема имеет второй порядок сходимости в области влияния нестационарной ударной волны. Вторая бикомпактная схема, несмотря на высокую точность на гладких решениях, снижает свой порядок сходимости до первого порядка в области влияния ударной волны.
Таким образом, проведенное в настоящей работе исследование подтверждает вывод работ [23], [24], [29] о невозможности одновременно с высокой точностью монотонно локализовать двигающиеся с переменной скоростью сильные разрывы и сохранить повышенный порядок сходимости в областях их влияния.
Авторы выражают благодарность Н.А. Хандеевой за любезно предоставленные результаты расчетов по схеме Русанова.
Список литературы
Годунов С.К. Разностный метод численного расчета разрывных решений уравнений гидродинамики // Матем. сб. 1959. Т. 47. № 3. С. 271–306.
Van Leer B. Toward the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method // J. Comput. Phys. 1979. V. 32. № 1. P. 101–136.
Harten A. High resolution schemes for hyperbolic conservation laws // J. Comput. Phys. 1983. V. 49. № 3. P. 357–393.
Jiang G.S., Shu C.-W. Efficient implementation of weighted ENO schemes // J. Comput. Phys. 1996. V. 126. № 1. P. 202–228.
Liu X., Tadmor E. Third order nonoscillatory central scheme for hyperbolic conservation laws // Numer. Math. 1998. V. 79. № 3. P. 397–425.
Cockburn B. An introduction to the discontinuous Galerkin method for convection-dominated problems // Lecture Notes in Mathematics. 1998. V. 1697. P. 151–268.
Karabasov S.A., Goloviznin V.M. Compact accurately boundary-adjusting high-resolution technique for fluid dynamics // J. Comput. Phys. 2009. V. 228. № 19. P. 7426–7451.
Остапенко В.В. Симметричные компактные схемы с искусственными вязкостями повышенного порядка дивергентности // Ж. вычисл. матем. и матем. физ. 2002. Т. 42. № 7. С. 1019–1038.
Fiorina B., Lele S.K. An artificial nonlinear diffusivity method for supersonic reacting flows with shocks // J. Comput. Phys. 2006. V. 222. № 1. P. 246–264.
Kawai S., Lele S.K. Localized artificial diffusivity scheme for discontinuity capturing on curvilinear meshes // J. Comput. Phys. 2008. V. 227. № 22. P. 9498–9526.
Kurganov A., Liu Y. New adaptive artificial viscosity method for hyperbolic systems of conservation laws // J. Comput. Phys. 2012. V. 231. № 24. P. 8114–8132.
Ekaterinaris J.A. Implicit, high-resolution, compact schemes for gas dynamics and aeroacoustics // J. Comput. Phys. 1999. V. 156. № 2. P. 272–299.
Yee H.C., Sandham N.D., Djomehri M.J. Low-dissipative high-order shock-capturing methods using characteristic-based filters // J. Comput. Phys. 1999. V. 150. № 1. P. 199–238.
Yee H.C., Sjögreen B. Adaptive filtering and limiting in compact high order methods for multiscale gas dynamics and MHD systems // Comput. Fluids. 2008. V. 37. № 5. P. 593–619.
Darian H.M., Esfahanian V., Hejranfar K. A shock-detecting sensor for filtering of high-order compact finite difference schemes // J. Comput. Phys. 2011. V. 230. № 3. P. 494–514.
Adams N.A., Shariff K. A high-resolution hybrid compact-ENO scheme for shock-turbulence interaction problems // J. Comput. Phys. 1996. V. 127. № 1. P. 27–51.
Pirozzoli S. Conservative hybrid compact-WENO schemes for shock-turbulence interaction // J. Comput. Phys. 2002. V. 178. № 1. P. 81–117.
Ren Y.-X., Liu M., Zhang H. A characteristic-wise hybrid compact-WENO scheme for solving hyperbolic conservation laws // J. Comput. Phys. 2003. V. 192. № 2. P. 365–386.
Shen Y., Yang G. Hybrid finite compact-WENO schemes for shock calculation // Int. J. Numer. Meth. Fluids. 2007. V. 53. № 4. P. 531–560.
Брагин М.Д., Рогов Б. В. Гибридные бикомпактные схемы с минимальной диссипацией для уравнений гиперболического типа // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 6. С. 958–972.
Остапенко В.В. О сходимости разностных схем за фронтом нестационарной ударной волны // Ж. вычисл. матем. и матем. физ. 1997. Т. 37. № 10. С. 1201–1212.
Casper J., Carpenter M.H. Computational consideration for the simulation of shock-induced sound // SIAM J. Sci. Comput. 1998. V. 19. № 1. P. 813–828.
Остапенко В.В. О построении разностных схем повышенной точности для сквозного расчета нестационарных ударных волн // Ж. вычисл. матем. и матем. физ. 2000. Т. 40. № 12. С. 1857–1874.
Ковыркина О.А., Остапенко В.В. О сходимости разностных схем сквозного счeта // Докл. АН. 2010. Т. 433. № 5. С. 599–603.
Ковыркина О.А., Остапенко В.В. О реальной точности разностных схем сквозного счета // Матем. моделирование. 2013. Т. 25. № 9. С. 63–74.
Михайлов Н.А. О порядке сходимости разностных схем WENO за фронтом ударной волны // Матем. моделирование. 2015. Т. 27. № 2. С. 129–138.
Ковыркина О.А., Остапенко В.В. О построении комбинированных разностных схем повышенной точности // Докл. АН. 2018. Т. 478. № 5. С. 517–522.
Ладонкина М.Е., Неклюдова О.А., Остапенко В.В., Тишкин В.Ф. О точности разрывного метода Галеркина при расчете ударных волн // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 8. С. 148–156.
Ковыркина О.А., Остапенко В.В. О монотонности и точности схемы КАБАРЕ при расчете обобщенных решений с ударными волнами // Вычислительные технологии. 2018. Т. 23. № 2. С. 37–54.
Остапенко В.В. О конечно-разностной аппроксимации условий Гюгонио на фронте ударной волны, распространяющейся с переменной скоростью // Ж. вычисл. матем. и матем. физ. 1998. Т. 38. № 8. С. 1355–1367.
Русанов В.В. Разностные схемы третьего порядка точности для сквозного счета разрывных решений // Докл. АН СССР. 1968. Т. 180. № 6. С. 1303–1305.
Рогов Б.В., Михайловская М.Н. Монотонная высокоточная компактная схема бегущего счета для квазилинейных уравнений гиперболического типа // Докл. АН. 2011. Т. 440. № 2. С. 172–177.
Рогов Б.В., Михайловская М.Н. Монотонная высокоточная компактная схема бегущего счета для квазилинейных уравнений гиперболического типа // Матем. моделирование. 2011. Т. 23. № 12. С. 65–78.
Михайловская М.Н., Рогов Б.В. Монотонные компактные схемы бегущего счета для систем уравнений гиперболического типа // Ж. вычисл. матем. и матем. физ. 2012. Т. 52. № 4. С. 672–695.
Rogov B.V. Dispersive and dissipative properties of the fully discrete bicompact schemes of the fourth order of spatial approximation for hyperbolic equations // Appl. Numer. Math. 2019. V. 139. P. 136–155.
Kennedy C.A., Carpenter M.H. Diagonally implicit Runge–Kutta methods for stiff ODEs // Appl. Numer. Math. 2019. V. 146. P. 221–244.
Рогов Б.В. Высокоточная монотонная компактная схема бегущего счета для многомерных уравнений гиперболического типа // Ж. вычисл. матем. и матем. физ. 2013. Т. 53. № 2. С. 264–274.
Chikitkin A.V., Rogov B.V., Utyuzhnikov S.V. High-order accurate monotone compact running scheme for multidimensional hyperdolic equations // Appl. Numer. Math. 2015. V. 93. P. 150–163.
Chikitkin A.V., Rogov B.V., Family of central bicompact schemes with spectral resolution property for hyperbolic equations // Appl. Numer. Math. 2019. V. 142. P. 151–170.
Самарский А.А. Теория разностных схем. М.: Физматлит, 1989.
Рогов Б.В., Брагин М.Д. О свойствах спектрального разрешения симметричных бикомпактных схем четвертого порядка аппроксимации // Докл. АН. 2017. Т. 475. № 2. С. 140–144.
Марчук Г.И., Шайдуров В.В. Повышение точности решений разностных схем. М.: Наука, 1979.
Zlatev Z., Dimov I., Farago I., Havasi A. Richardson Extrapolation, Berlin: De Gruyter, 2018.
Стокер Дж. Дж. Волны на воде. Математическая теория и приложения. М.: Изд-во иностр. лит., 1959.
Alexander R. Diagonally implicit Runge–Kutta methods for stiff O.D.E.'s // SIAM J. Numer. Anal. 1977. V. 14. № 6. P. 1006–1021.
Брагин М.Д., Рогов Б.В. Консервативная монотонизация бикомпактных схем // Препринты ИПМ им. М.В. Келдыша. 2019. № 8. 26 с.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики


