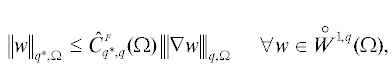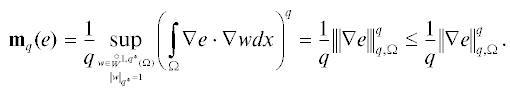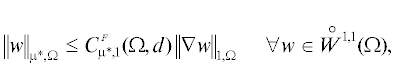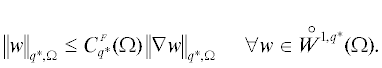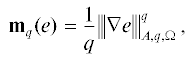Журнал вычислительной математики и математической физики, 2020, T. 60, № 5, стр. 767-783

Оценки отклонения от точных решений краевых задач в мерах более сильных, чем энергетическая норма

С. И. Репин^*

Санкт-Петербургское отделение Математического Института им. В.А. Стеклова РАН
191023 Санкт-Петербург, Фонтанка, 27, Россия

^* E-mail: repin@pdmi.ras.ru

Поступила в редакцию 28.10.2019
После доработки 28.10.2019
Принята к публикации 14.01.2020

DOI: 10.31857/S0044466920050142

Полный текст (PDF)

Аннотация

Изучаются оценки величины отклонения заданной функции от точного решения краевой задачи эллиптического типа. Для тех случаев, когда оценки строятся в терминах естественной энергетической нормы, такие оценки были получены ранее. В данной работе предлагается подход к получению более сильных мер отклонения и соответствующих оценок, которые применимы, если точное решение и аппроксимация имеют повышенную регулярность (в отношении порядка интегрируемости). Эти меры включают стандартную энергетическую норму как простой специальный случай. В статье предлагается общий подход к конструированию различных мер, основанный на использовании вспомогательной вариационной задачи. Более подробно исследуются два класса мер, близких по своим свойствам к нормам пространств ${{L}^{q}}$ и ${{L}^{\infty }}$. Устанавливаются их свойства и для них строятся двусторонние оценки (миноранты и мажоранты), которые содержат только известные функции и могут быть явно вычислены. Библ. 28.

Ключевые слова: уравнения эллиптического типа, оценки отклонения от точного решения, апостериорные оценки.

1. ВВЕДЕНИЕ

Проблема получения явно вычисляемых оценок отклонения от точного решения краевой (начально-краевой) задачи имеет важное значение для количественного анализа различных математических моделей, основанных на дифференциальных уравнениях. В общей форме постановка задачи состоит в следующем. Пусть $\mathcal{A}:V \to V{\text{'}}$ – дифференциальный оператор, областью определения которого является банахово пространство $V$, а областью значений – банахово пространство $V{\text{'}}$. Предположим, что задача

(1.1)

$\mathcal{A}u = f,\quad f \in V{\text{'}},$

корректна и имеет единственное решение $u$. Требуется оценить расстояние между $u$ и функцией ${v} \in V$ в норме пространства $V$ так, чтобы эта оценка была верна для любой функции ${v} \in V$, не содержала явно неизвестное точное решение $u$, и обеспечивала достаточно хорошую оценку. Другими словами, необходимо построить функционал ${{M}_{ \oplus }}:V \to {{\mathbb{R}}_{{ \geqslant 0}}}$ такой, что ${{M}_{ \oplus }}({v})$ зависит только от известных данных (геометрии области, коэффициентов уравнения, краевых условий и т.п.), ${{M}_{ \oplus }}(u) = 0$ и, кроме того,

(1.2)

${{\left\| {u - {v}} \right\|}_{V}} \leqslant {{M}_{ \oplus }}({v})\quad \forall {v} \in V,$

(1.3)

Для того, чтобы количественный анализ задачи соответствовал всем требованиям вычислений с гарантированной точностью (в зарубежной терминологии fully reliable computations), необходимо также построить вычисляемую миноранту ${{M}_{ \ominus }}({v})$ с аналогичными свойствами. Величина ${{I}_{{{\text{eff}}}}}: = {{M}_{ \oplus }}({v}){\text{/}}{{M}_{ \ominus }}({v})$ называется индексом эффективности и дает представление о качестве оценок и величине реальной погрешности.

Заметим, что как правило, ${v}$ рассматривается как численная аппроксимация $u$ и в этом случае речь идет об апостериорной оценке погрешности. При этом, в отличие от априорной оценки, нас интересует не скорость асимптотического убывания погрешности при увеличении размерности аппроксимирующего пространства, а возможность явно оценить погрешность конкретного приближенного решения. Однако есть и другие, не менее важные проблемы, когда функция $v$ является решением другой математической проблемы, или возникает как результат обработки экспериментальных данных. Задача построения функционалов (мажорант отклонения от точного решения), удовлетворяющих (1.2) и (1.3) для вариационных задач с выпуклыми коэрцитивными функционалами была поставлена и решена в [1], [2]. В настоящее время методы построения таких функционалов (мажорант отклонения от точного решения) для уравнений эллиптического и параболического типа в терминах энергетической нормы хорошо разработаны (см. монографию [3], а также статьи [4], [5]–[10] и другие публикации, упомянутые в этих работах). Существует два метода построения $M({v})$: первый основан на использовании теории двойственности вариационного исчисления, а второй (невариационный) использует специальные преобразования интегральных тождеств, определяющих обобщенное решение задачи. Первый метод подробно изложен в [2], а второй в [3]. Ниже мы рассмотрим некоторые оценки, полученные этими методами.

Однако есть и другой не менее важный вопрос:

В терминах какой меры оценивается отклонение от $u$?

Если $\mathcal{A}$ является линейным сильно эллиптическим оператором, то выбор в качестве меры энергетической нормы ${{\left\| {u - {v}} \right\|}_{V}}$ представляется вполне естественным. Обычно именно эту норму стараются оценить различными методами при анализе конечноэлементных аппроксимаций (см., например [11], [12]). Однако часто возникает потребность в других оценках. В последние годы широкое распространение получили оценки в терминах специально сконструированных линейных функционалов (в зарубежной литературе они называются goal oriented quantities, см., например, [13], [14]). В этом случае рассматриваются меры существенно более слабые, чем энергетическая. Более того, обычно меры такого рода не являются метриками и могут обращаться в ноль на функциях, не являющихся точным решением задачи. Тем не менее соответствующие оценки оказались востребованными, поскольку дают представление о качестве аппроксимации специально выбранных характеристик решения. В данной работе предлагается метод получения оценок отклонения от точного решения в терминах мер более сильных, чем энергетическая норма. Для того, чтобы яснее изложить основную идею этого метода, необходимо вначале кратко напомнить некоторые принципиальные факты, лежащие в основе анализа погрешности приближенных решений уравнений в частных производных (подробное изложение этих вопросов содержится в [3]).

Рассмотрим простейший пример уравнения Пуассона $\Delta u + f = 0$ в липшицевой области $\Omega $ с $f \in {{L}^{2}}(\Omega )$ и краевыми условиями Дирихле $u = {{u}_{0}}$ на границе $\partial \Omega $. Соответствующее обобщенное решение удовлетворяет интегральному тождеству

(1.4)

где $ \cdot $ обозначает скалярное произведение в пространстве векторов, а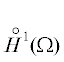

обозначает подпространство ${{H}^{1}}(\Omega )$, состоящее из функций, обращающихся в ноль на границе. В этом случае

(1.5)

$\int\limits_\Omega {\nabla e} \cdot \nabla wdx = {{\mathcal{F}}_{{v}}}(w)\quad \forall w \in {{V}_{0}},$

где $e: = u - {v}$, а

${{\mathcal{F}}_{{v}}}(w): = \int\limits_\Omega {(fw - \nabla {v} \times \nabla w)} dx$

это линейный непрерывный функционал, определенный на ${{V}_{0}}$ (здесь и далее символ := означает “равно по определению”). Нетрудно видеть, что функционал ${{\mathcal{F}}_{{v}}}$ тождественно равен нулю, если ${v}$ совпадает с точным решением $u$. Во всех остальных случаях его норма, задаваемая соотношением

(1.6)

$\left| {{{\mathcal{F}}_{{v}}}} \right|: = \mathop {sup}\limits_{w \in {{V}_{0}}{\backslash \{ }0\} } \frac{{\left| {{{\mathcal{F}}_{{v}}}(w)} \right|}}{{\left\| {\nabla w} \right\|}},$

будет больше нуля. Здесь и далее $\left\| {\, \cdot \,} \right\|$ (или ${{\left\| {\, \cdot \,} \right\|}_{{2,\Omega }}}$) обозначает норму в пространстве ${{L}^{2}}(\Omega )$ для скалярных и векторных функций. Из (1.3) следует, что

$\int\limits_\Omega {{{{\left| {\nabla (u - {v})} \right|}}^{2}}} dx = {{\mathcal{F}}_{{v}}}(u - {v}) \leqslant \left| {{{\mathcal{F}}_{{v}}}} \right|\left\| {\nabla (u - {v})} \right\|.$

Поэтому $\left\| {\nabla (u - {v})} \right\| \leqslant \left| {{{\mathcal{F}}_{{v}}}} \right|$ так, что $\left| {{{\mathcal{F}}_{{v}}}} \right|$ контролирует отклонение ${v}$ от $u$. Более того, так как $\left| {{{\mathcal{F}}_{{v}}}(w)} \right| \leqslant \left\| {\nabla (u - {v})} \right\|\left\| {\nabla w} \right\|$, то (1.6) влечет обратное неравенство. Таким образом, в данном простом случае энергетическая норма отклонения ${{\left\| {\nabla e} \right\|}_{\Omega }}$ совпадает с $\left| {{{\mathcal{F}}_{{v}}}} \right|$, определенной как супремум в (1.6). Во многих более сложных задачах удается доказать, что норма отклонения эквивалентна $\left| {{{\mathcal{F}}_{{v}}}} \right|$, так что с математической точки зрения проблема сводится к получению вычисляемых оценок этой величины. Поскольку норма $\left| {{{\mathcal{F}}_{{v}}}} \right|$ определяется как супремум по бесконечному множеству функций, на практике ее вряд ли возможно вычислить (за исключением некоторых специальных случаев, когда супремум можно найти аналитическими методами). Поэтому для построения функционала ${{M}_{ \oplus }}({v})$ (удовлетворяющего (1.2) и (1.3)) необходимо получить мажоранту $\left| {{{\mathcal{F}}_{{v}}}} \right|$ в терминах интегральных норм. Для этого существуют два различных подхода.

В 80-е годы прошлого века среди вычислителей, использующих метод конечных элементов, получил широкое распространение т.н. метод невязок (residual method). Он был предложен в статьях [15], [16] и изучен в многочисленных публикациях других авторов (см., например, [11], [17]–[21], [12] и цитируемые там работы). Основная идея этого метода заключается в том, чтобы использовать свойство ортогональности галеркинских аппроксимаций и оценить сверху $\left| {{{\mathcal{F}}_{{{{u}_{h}}}}}} \right|$ в том случае, когда ${v}$ совпадает с галеркинским решением ${{u}_{h}}$, полученным как точное решение конечномерной задачи на подпространстве ${{V}_{h}} \subset {{V}_{0}}$. Естественно, что при этом множество функций, сравниваемых с $u$, существенно ограничивается (так что важное свойство (1.2) не выполняется). У метода есть и ряд других недостатков, которые могут приводить к сильной переоценке величины ошибки (подробный сравнительный анализ различных апостериорных оценок погрешности в контексте метода конечных элементов содержится в монографии [22]). В вычислительной практике этот метод в основном используется для генерации индикаторов локальных ошибок, на основе которых производится адаптация сеток.

Для получения функционала ${{M}_{ \oplus }}({v})$, удовлетворяющего условиям (1.2), (1.3), надо использовать другой метод оценки $\left| {{{\mathcal{F}}_{{v}}}} \right|$, который основан на декомпозиции этого функционала при помощи вспомогательных интегральных тождеств. Этот метод был предложен в [6] (заметим, что для вариационных задач функционалы ${{M}_{ \oplus }}({v})$ были уже получены ранее в [1], [2] при помощи методов теории двойственности вариационного исчисления). В частности, для задачи (1.4) можно применить тождество

(1.7)

$\int\limits_\Omega {(\nabla w \cdot y + w\operatorname{div} y)} {\kern 1pt} dx = 0\quad \forall w \in {{V}_{0}},\quad \forall y \in H(\Omega ,{\text{div}}),$

где $H(\Omega ,{\text{div}}): = {\text{\{ }}y \in {{L}^{2}}(\Omega ,{{\mathbb{R}}^{d}})\,|\,\operatorname{div} y \in {{L}^{2}}(\Omega ){\text{\} }}$ обозначает гильбертово пространство со скалярным произведением ${{(y,z)}_{{{\text{div}}}}}: = \int_\Omega {(y \cdot z + \operatorname{div} y\operatorname{div} z)} \,dx$ и соответствующей нормой ${{\left\| y \right\|}_{{{\text{div}}}}}$. При помощи (1.7) мы получаем следующее представление функционала ${{\mathcal{F}}_{{v}}}$:

(1.8)

${{\mathcal{F}}_{{v}}}(w) = \int\limits_\Omega {\left( {(\nabla {v} - y) \cdot \nabla w + w(\operatorname{div} y + f)} \right)} {\kern 1pt} dx.$

Используя (1.5), (1.8), и неравенство Фридрихса, нетрудно получить оценку

(1.9)

$\left\| {\nabla e} \right\| \leqslant \left\| {\nabla {v} - y} \right\| + {{C}^{F}}(\Omega )\left\| {\operatorname{div} y + f} \right\|\quad \forall y \in H(\Omega ,{\text{div}}),$

где ${{C}^{F}}(\Omega )$ обозначает постоянную в неравенстве Фридрихса для области $\Omega $. Понятно, что вместо точного значения ${{C}^{F}}(\Omega )$ можно использовать любую оценку этой постоянной сверху (которую для случая однородных краевых условий легко построить).

Для общей задачи (1.1) с монотонным и положительно-определенным оператором $\mathcal{A}$ естественно определить меру (норму) отклонения от точного решения как

(1.10)

${{\left| {\left\| e \right\|} \right|}_{\mathcal{A}}}: = \mathop {sup}\limits_{w \in V{\backslash }\{ 0\} } \frac{{\left| {\left\langle {\mathcal{A}u - \mathcal{A}{v},w} \right\rangle } \right|}}{{{{{\left| w \right|}}_{\mathcal{A}}}}} = \mathop {sup}\limits_{w \in V{\backslash \{ }0\} } \frac{{\left| {{{\mathcal{F}}_{{v}}}(w)} \right|}}{{{{{\left| w \right|}}_{\mathcal{A}}}}},$

где $\left| w \right|_{\mathcal{A}}^{2}: = \left\langle {\mathcal{A}w,w} \right\rangle $, а скобки обозначают спаривание $V{\kern 1pt} {\text{'}}$ и $V$. Мера (1.10) характеризует величину функционала ${{\mathcal{F}}_{{v}}}(w): = \left\langle {f - \mathcal{A}{v},w} \right\rangle $. Легко видеть, что если ${{u}_{{v}}} \in V$ удовлетворяет уравнению

(1.11)

$\left\langle {\mathcal{A}{{u}_{{v}}},w} \right\rangle = {{\mathcal{F}}_{{v}}}(w)\quad \forall w \in V,$

то

${{\left| {\left\| e \right\|} \right|}_{\mathcal{A}}} \geqslant \frac{{\left| {{{\mathcal{F}}_{{v}}}({{u}_{{v}}})} \right|}}{{{{{\left| {{{u}_{{v}}}} \right|}}_{\mathcal{A}}}}} = {{\left| {{{u}_{{v}}}} \right|}_{\mathcal{A}}}.$

С другой стороны, $\left| {{{\mathcal{F}}_{{v}}}(w)} \right|| \leqslant {{\left\| {\mathcal{A}{{u}_{{v}}}} \right\|}_{{V{\kern 1pt} {\text{'}}}}}{{\left\| w \right\|}_{V}}$. Если норма ${{\left\| w \right\|}_{V}}$ подчинена ${{\left| w \right|}_{\mathcal{A}}}$, то можно оценить ${{\left| {\left\| e \right\|} \right|}_{\mathcal{A}}}$ сверху через ${{\left\| {\mathcal{A}{{u}_{{v}}}} \right\|}_{{V{\kern 1pt} {\text{'}}}}}$. Таким образом, величина ${{\left| {\left\| e \right\|} \right|}_{\mathcal{A}}}$ оценивается той или иной нормой решения задачи (1.11), в которой правая часть задается функционалом невязки ${{\mathcal{F}}_{{v}}}$ (заметим, что в случае уравнения Пуассона ${{u}_{{v}}}$ в (1.11) совпадает с $e$). Изложенную выше схему можно обобщить и построить различные меры отклонения от точного решения в нормах более сильных, чем энергетическая.

В общем виде основная идея заключается в следующем. Допустим, что мы имеем дополнительную информацию о точном решении: например, известно что $u$ принадлежит более узкому функциональному классу $\widehat V$. Кроме того, функция ${v}$ также принадлежит $\widehat V$. Мы можем использовать этот факт и получить оценку ошибки $e = u - {v}$ в терминах более сильной меры, если в (1.10) взять супремум по более широкому классу функций $w$, для которого можно корректно доопределить произведение $\left\langle { \cdot , \cdot } \right\rangle $.

В частности, предположим, что в задаче (1.4) 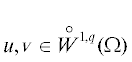, $q > 2$. При этом в качестве меры отклонения ${v}$ от $u$ можно взять

(1.12)

${{\left| {\left\| e \right\|} \right|}_{{q,\Omega }}}: = \mathop {sup}\limits_{w \in {{{\mathop W\limits^ \circ }}^{{1,q*}}}(\Omega ){\backslash \{ }0\} } \frac{{\left| {{{\mathcal{F}}_{{v}}}(w)} \right|}}{{{{{\left\| {\nabla w} \right\|}}_{{q*,\Omega }}}}} \leqslant {{\left\| {\nabla e} \right\|}_{{q,\Omega }}},$

где $q* = \tfrac{q}{{q - 1}}$. Пусть $2 \leqslant p < q$, тогда $q* < p{\text{*}}$. Поскольку

и для любой функции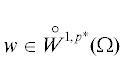

выполнено ${{\left\| {\nabla w} \right\|}_{{q*,\Omega }}} \leqslant {{\left| \Omega \right|}^{{\tfrac{1}{{q*}} - \tfrac{1}{{p*}}}}}{{\left\| {\nabla w} \right\|}_{{p*,\Omega }}}$, то

(1.13)

${{\left| {\left\| {\nabla e} \right\|} \right|}_{{q,\Omega }}} = \mathop {sup}\limits_{w \in {{{\mathop W\limits^ \circ }}^{{1,q*}}}(\Omega ){\backslash \{ }0{\text{\} }}} \frac{{\int\limits_\Omega {\nabla e \cdot \nabla wdx} }}{{{{{\left\| {\nabla w} \right\|}}_{{q*,\Omega }}}}} \geqslant {{\left| \Omega \right|}^{{\tfrac{1}{{p*}} - \tfrac{1}{{q*}}}}}\mathop {sup}\limits_{w \in {{{\mathop W\limits^ \circ }}^{{1,p*}}}(\Omega ){\backslash \{ }0{\text{\} }}} \frac{{\int\limits_\Omega {\nabla e} \cdot \nabla wdx}}{{{{{\left\| {\nabla w} \right\|}}_{{p*,\Omega }}}}} = {{\left| \Omega \right|}^{{\tfrac{1}{q} - \tfrac{1}{p}}}}{{\left| {\left\| {\nabla e} \right\|} \right|}_{{p,\Omega }}}.$

Таким образом, с ростом показателя эти нормы ведут себя точно так же, как и обычные ${{L}^{q}}$-нормы. Заметим, что ${{\left| {\left\| {\nabla w} \right\|} \right|}_{{2,\Omega }}} = {{\left\| {\nabla w} \right\|}_{{2,\Omega }}}$ и поэтому ${{\left| {\left\| {\nabla w} \right\|} \right|}_{{q,\Omega }}}$ оценивается снизу величиной ${{\left| \Omega \right|}^{{\tfrac{1}{2} - \tfrac{1}{q}}}}{{\left\| {\nabla e} \right\|}_{{2,\Omega }}}$. Нормы (1.12) обладают и другими сходными свойствами. Например, для $q \geqslant 2$ имеют место неравенства

(1.14)

(1.15)

${{\left\| w \right\|}_{{q*,\Omega }}} \leqslant \hat {C}_{{q*,q}}^{P}(\Omega ){{\left| {\left\| {\nabla w} \right\|} \right|}_{{q,\Omega }}}\quad \forall w \in {{W}^{{1,q}}}(\Omega ),\quad {{{\text{\{ }}{\kern 1pt} {\text{\{ }}w{\text{\} }}{\kern 1pt} {\text{\} }}}_{\Omega }} = 0,$

причем $\hat {C}_{{q*,q}}^{F}(\Omega ) \leqslant {{c}_{q}}(\Omega ){{C}^{F}}(\Omega )$ и $\hat {C}_{{q*,q}}^{P}(\Omega ) \leqslant {{c}_{q}}(\Omega ){{C}^{P}}(\Omega )$. Здесь ${{C}^{F}}(\Omega )$ и ${{C}^{F}}(\Omega )$ – это постоянные в соответствующих неравенствах Фридрихса и Пуанкаре, а ${{c}_{q}}(\Omega ) = {{\left| \Omega \right|}^{{\tfrac{1}{{q*}} - \tfrac{1}{q}}}}$. Доказательство (1.14) следует непосредственно из оценок

${{\left\| w \right\|}_{{q*,\Omega }}} \leqslant {{\left| \Omega \right|}^{{\tfrac{1}{{q*}} - \tfrac{1}{2}}}}{{\left\| {\hat {w}} \right\|}_{{2,\Omega }}} \leqslant {{C}^{F}}(\Omega ){{\left| \Omega \right|}^{{\tfrac{1}{{q*}} - \tfrac{1}{2}}}}{{\left\| {\nabla w} \right\|}_{{2,\Omega }}} \leqslant {{C}^{F}}(\Omega ){{c}_{q}}(\Omega ){{\left| {\left\| {\nabla w} \right\|} \right|}_{{q,\Omega }}}.$

Точно так же устанавливается (1.15).

В 2.4 показано, что для $d = 1$ нормы (1.13) эквивалентны стандартным нормам в пространствах Лебега с такими же показателями суммируемости. Вопрос об эквивалентности норм такого типа нормам градиента в соответствующем пространстве ${{L}^{q}}$ (для $d > 1$) рассматривался в [23], [24], где изучалась разрешимость задачи (1.4) в пространствах ${{L}^{q}}$ и соответствующие варианты разложения Гельмгольца для векторных полей. Однако в этих работах использовалось более широкое множество тест-функций, а явно вычисляемые оценки константы в соответствующем неравенстве эквивалентности не приводятся. Можно показать, что нормы (1.13) также эквивалентны нормам градиента в ${{L}^{q}}$, однако, вопрос о соответствующих константах эквивалентности требует дальнейшего исследования, которое выходит за рамки настоящей статьи.

Другое определение меры отклонения от точного решения можно ввести при помощи подходящей вариационной формулировки. В простейшем случае (1.4) мы определили меру погрешности как норму решения вспомогательной краевой задачи (1.5), в которой правая часть задается функционалом ${{\mathcal{F}}_{{v}}}$. Эта задача эквивалентна минимизации функционала

$\mathop {inf}\limits_{w \in {{V}_{0}}} {{J}_{{v}}}(w),\quad {{J}_{{v}}}(w): = \frac{1}{2}{{\left\| {\nabla w} \right\|}^{2}} - {{\mathcal{F}}_{{v}}}(w),$

причем $inf{{J}_{{v}}} = - \tfrac{1}{2}{{\left\| {\nabla e} \right\|}^{2}}$. Таким образом, норму отклонения можно определить при помощи равенства

(1.16)

$\mathop {sup}\limits_{w \in {{V}_{0}}} \left\{ {{{\mathcal{F}}_{{v}}}(w) - \frac{1}{2}{{{\left\| {\nabla w} \right\|}}^{2}}} \right\} = \frac{1}{2}{{\left\| {\nabla e} \right\|}^{2}}.$

Как будет показано далее, это определение допускает широкие обобщения, которые приводят к множеству различных мер отклонения от точного решения. В соответствии с принятыми в разд. 2 обозначениями (1.16) определяет меру ${{{\mathbf{m}}}_{2}}(e)$ (см. (2.3)). Там же показано, что норма ${{\left| {\left\| {\nabla e} \right\|} \right|}_{{q,\Omega }}}$ связана с мерой вариационного типа ${{{\mathbf{m}}}_{q}}(e)$, которая является обобщением (1.16). Аналогичная мера ${{\left| {\left\| {\nabla e} \right\|} \right|}_{{\infty ,\Omega }}}$ может быть построена и для случая $q = \infty $. Эти меры являются частными случаями обобщенной меры ${{{\mathbf{m}}}_{G}}$, определенной в (2.1).

В разд. 3 даны двусторонние оценки ${{{\mathbf{m}}}_{q}}(e)$ и показано, что эта величина оценивается сверху величиной, аналогичной (1.9), в которой слагаемые задаются нормами ${{\left\| {\nabla {v} - y} \right\|}_{{q,\Omega }}}$ и ${{\left\| {\operatorname{div} y + f} \right\|}_{{q,\Omega }}}$. Далее показано, что надлежащим образом взвешенная сумма этих слагаемых с показателем $q = \infty $ образует мажоранту меры ${{{\mathbf{m}}}_{\infty }}(e)$. Также показано, что в случае если $q = 2$, а $\Omega $ заменена на подобласть $\omega $, сумма этих слагаемых мажорирует некоторую локальную меру $e$. Основные идеи сначала подробно обсуждаются на самом простом примере задачи для уравнения Пуассона с краевыми условиями Дирихле. В разд. 4 мы кратко рассматриваем их обобщения для уравнений более общего вида.

2. МЕРЫ ОТКЛОНЕНИЯ ОТ ТОЧНОГО РЕШЕНИЯ

2.1. Обобщенная мера отклонения от точного решения

В определении (1.5) функционал ${{\mathcal{F}}_{{v}}}(w)$ был задан на функциях $w \in {{V}_{0}}$. Однако, если решение $u$ и функция ${v}$ принадлежат более узкому функциональному классу так, что $e = u - {v} \in {{\hat {V}}_{0}} \subset {{V}_{0}}$, то мы можем доопределить его на более широком множестве $\hat {V}_{0}^{'}$ тест-функций $w$ (предполагается, что эти функции обращаются в ноль на границе области), так что значение ${{\mathcal{F}}_{{v}}}(w) = \int_\Omega {\nabla e} \cdot \nabla wdx$ определено.

Пусть $G:\hat {V}_{0}^{'} \to {{\mathbb{R}}_{{ \geqslant 0}}}$ – выпуклый полунепрерывный снизу функционал, такой что $G(w) = 0$, если $w \equiv 0$ и $G$ коэрцитивен на функциях из $\hat {V}_{0}^{'}$. Для $e \in {{\hat {V}}_{0}}$ введем меру

(2.1)

${{{\mathbf{m}}}_{G}}(e): = \mathop {sup}\limits_{w \in \hat {V}_{0}^{'}} \left\{ {{{\mathcal{F}}_{{v}}}(w) - G(w)} \right\} \geqslant 0.$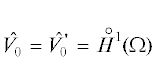

В зависимости от выбора функционала $G$, мы получаем различные меры для функции $e$. В частности, если задана неотрицательная выпуклая функция $g$ такая, что $g(0) = 0$, то функционал можно определить в интегральной форме

(2.2)

$G(w): = \int\limits_\Omega g (\left| {\nabla w} \right|)dx.$

При этом равенство (1.8) оказывается простейшей формой (2.1), соответствующей выбору $g(t) = \tfrac{1}{2}{{t}^{2}}$. В этом случае

Нетрудно видеть, что ${{{\mathbf{m}}}_{G}}(e) \geqslant 0$, причем если ${v} = u$, то ${{\mathcal{F}}_{{v}}}(w) \equiv 0$ и мера обращается в ноль. Если вариационная задача в (2.1) всегда имеет единственное решение (например для строго выпуклой функции $g$), то ${{{\mathbf{m}}}_{G}}(e) = 0$ означает $e = 0$.

Действительно, предположим что 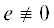и при этом ${{{\mathbf{m}}}_{G}}(e) = 0$. Супремум в (2.1) достигается на единственной функции и эта функция $w \equiv 0$. Заметим, что если , то всегда найдется функция $\bar {w} \in {{V}_{0}}$ такая, что

${{\mathcal{F}}_{{v}}}(w) = \int\limits_\Omega {\nabla e} \cdot \nabla \bar {w}dx > 0.$

Отсутствие такой функции означало бы, что тождество

$\int\limits_\Omega {\nabla {v}} \cdot \nabla wdx = \int\limits_\Omega {fw} dx$

выполняется для любой функции $w \in {{V}_{0}}$, но в этом случае ${v} = u$ и $e = 0$. Поскольку $g$ строго выпукла, то $g\left( {\left| {\nabla \bar {w}} \right|} \right) > g(0) = 0$, и мы заключаем, что

$\mathop {sup}\limits_{w \in \hat {V}_{0}^{'}} \int\limits_\Omega {(\nabla e \cdot \nabla w - g(\nabla w))} dx > \int\limits_\Omega {(\nabla e \cdot \nabla \bar {w})} {\kern 1pt} dx > 0.$

Следовательно, супремум больше нуля и $w \equiv 0$ не может быть решением вариационной задачи. Мы пришли к противоречию, которое доказывает, что ${{{\mathbf{m}}}_{G}}(e) = 0$ тогда и только тогда, когда $e = 0$.

Мера ${{{\mathbf{m}}}_{G}}(e)$ определяет множество

$\mathcal{N}_{u}^{\epsilon }: = \{ e \in {{\hat {V}}_{0}}\,|\,{{{\mathbf{m}}}_{G}}(e) < \epsilon \} ,$

которое является $\varepsilon $-окрестностью точного решения $u$. Нетрудно показать, что множество $\mathcal{N}_{u}^{\epsilon }$ является выпуклым. Пусть ${{e}_{1}} = {{{v}}_{1}} - u$ и ${{e}_{2}} = {{{v}}_{2}} - u$ принадлежат $\mathcal{N}_{u}^{\epsilon }$. Для любых ${{\lambda }_{1}},{{\lambda }_{2}} \geqslant 0$ таких, что ${{\lambda }_{1}} + {{\lambda }_{2}} = 1$ выполнено

$\begin{gathered} \mathop {sup}\limits_{w \in \hat {V}_{0}^{'}} \int\limits_\Omega {(\nabla ({{\lambda }_{1}}{{e}_{1}} + {{\lambda }_{2}}{{e}_{2}})} \cdot \nabla w - g(\nabla w)){\kern 1pt} dx \leqslant {{\lambda }_{1}}\mathop {sup}\limits_{w \in \hat {V}_{0}^{'}} \int\limits_\Omega {(\nabla {{e}_{1}} \cdot \nabla w - g(\nabla w))} {\kern 1pt} dx + \\ + \;{{\lambda }_{2}}\mathop {sup}\limits_{w \in \hat {V}_{0}^{'}} \int\limits_\Omega {(\nabla {{e}_{2}} \cdot \nabla w - g(\nabla w))} {\kern 1pt} dx = {{\lambda }_{1}}{{{\mathbf{m}}}_{g}}({{e}_{1}}) + {{\lambda }_{2}}{{{\mathbf{m}}}_{g}}({{e}_{2}}) \leqslant \epsilon . \\ \end{gathered} $

Таким образом, меняя функцию $g$, можно генерировать различные множества выпуклых окрестностей точного решения, т.е. задавать ту или иную локальную топологию в окрестности точного решения краевой задачи. Далее мы рассмотрим некоторые примеры, в которых (2.1) определяет меры, более сильные, чем энергетическая норма. При этом не исключаются такие ситуации, где мера может принимать бесконечные значения.

2.2. Мера ${{{\mathbf{m}}}_{q}}$

Пусть . В этом случае 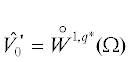, где $q*: = \tfrac{q}{{q - 1}}$, и мы можем определить следующую меру степенного типа:

(2.3)

${{{\mathbf{m}}}_{q}}(e): = \mathop {sup}\limits_{w \in \hat {V}_{0}^{'}} \int\limits_\Omega {\left( {\nabla e \cdot \nabla w - \frac{1}{{q{\text{*}}}}{{{\left| {\nabla w} \right|}}^{{q*}}}} \right)} dx.$

Формально все изложение ниже верно при любом $q > 1$, но поскольку нас интересуют меры более сильные, чем энергетическая норма, мы будем предполагать что $q \geqslant 2$. Максимайзер

в (2.3) существует и удовлетворяет уравнению

(2.4)

$\int\limits_\Omega {{{{\left| {\nabla {{w}_{{q*}}}} \right|}}^{{q* - 2}}}} (\nabla {{w}_{{q*}}} \cdot \nabla )dx = \int\limits_\Omega {\nabla e} \cdot \nabla wdx\quad \forall w \in \hat {V}_{0}^{'}.$

Таким образом, имеем

(2.5)

${{{\mathbf{m}}}_{q}}(e) = \int\limits_\Omega {\left( {\nabla e \cdot \nabla {{w}_{{q*}}} - \frac{1}{{q{\text{*}}}}{{{\left| {\nabla {{w}_{{q*}}}} \right|}}^{{q*}}}} \right)d} x = \left( {1 - \frac{1}{{q{\text{*}}}}} \right)\int\limits_\Omega {{{{\left| {\nabla {{w}_{{q*}}}} \right|}}^{{q*}}}} dx = \frac{1}{q}\left\| {\nabla {{w}_{{q*}}}} \right\|_{{q*,\Omega }}^{{q*}},$

т.е. мера отклонения от точного решения определяется нормой $\nabla {{w}_{{q*}}}$, где ${{w}_{{q*}}}$ – это решение нелинейной вспомогательной задачи (2.4), в которой правая часть задана функционалом ${{\mathcal{F}}_{{v}}}$.

Другое представление меры ${{{\mathbf{m}}}_{q}}(e)$ следует из равенства

(2.6)

${{{\mathbf{m}}}_{q}}(e) = \mathop {sup}\limits_{\begin{array}{*{20}{c}} {w \in {{{\mathop W\limits^ \circ }}^{{1,q*}}}(\Omega )} \\ {{{{\left\| w \right\|}}_{{q*}}} = 1} \end{array}} \mathop {sup}\limits_{\mu \geqslant 0} \mu \int\limits_\Omega {\nabla e} \cdot \nabla wdx - \frac{{{{\mu }^{{q*}}}}}{{q{\text{*}}}}.$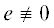

Если

, то супремум по $\mu $ достигается на $\bar {\mu } = \mathop {\left( {\int_\Omega ^{} {\nabla e} \cdot \nabla wdx} \right)}\nolimits^{\tfrac{1}{{q* - 1}}} $ (ясно, что при вычислении супремума в (2.6) те функции $w$, на которых интеграл отрицателен, можно исключить). Подставляя это значение $\bar {\mu }$ и проводя формальные преобразования, получаем (с учетом (1.12)), что

(2.7)

Чтобы оценить меру снизу, заметим, что для любого $\mu > 0$,

${{{\mathbf{m}}}_{g}}(e) \geqslant \int\limits_\Omega {\left( {\mu \nabla e \cdot \nabla e - \frac{{{{\mu }^{q}}}}{q}{{{\left| {\nabla e} \right|}}^{q}}} \right){\kern 1pt} } dx.$

Положим $\mu = \bar {\mu }: = \mathop {\left( {\tfrac{{{{{\left\| {\nabla e} \right\|}}^{2}}}}{{\left\| {\nabla e} \right\|_{{q,\Omega }}^{q}}}} \right)}\nolimits^{\tfrac{1}{{q - 1}}} .$ Тогда

(2.8)

${{{\mathbf{m}}}_{g}}(e) \geqslant \frac{1}{{q{\text{*}}}}\mathop {\left( {\frac{{{{{\left\| {\nabla e} \right\|}}^{2}}}}{{{{{\left\| {\nabla e} \right\|}}_{{q,\Omega }}}}}} \right)}\nolimits^{q*} .$

Эту оценку можно переписать в виде

(2.9)

${{{\mathbf{m}}}_{g}}(e) \geqslant \frac{1}{q}C(q,e)\left\| {\nabla e} \right\|_{{q,\Omega }}^{q},\quad {\text{где}}\quad C(q,e) = \frac{q}{{q{\text{*}}}}\frac{{{{{\left\| {\nabla e} \right\|}}^{{2q*}}}}}{{\left\| {\nabla e} \right\|_{{q,\Omega }}^{{q* + q}}}}.$

В некоторых случаях величину $C(q,e)$ можно оценить снизу. Например, если известно, что $u \in W_{0}^{{1,\infty }}(\Omega )$ и что аппроксимация ${v}$ также принадлежит $W_{0}^{{1,\infty }}(\Omega )$ (это условие обычно выполняется), то ${{\left\| {\nabla e} \right\|}_{\infty }} = {{\kappa }_{\infty }} < \infty $. Более того, имеется (грубая) оценка $\kappa \leqslant {{\left\| {\nabla u} \right\|}_{\infty }} + {{\left\| {\nabla {v}} \right\|}_{\infty }}$ и величину $C(q,e)$ можно оценить снизу величиной $\tfrac{q}{{q{\text{*}}}}{{\kappa }^{{q*(2 - q)}}}$ поскольку $\left\| {\nabla e} \right\|_{q}^{q} \leqslant {{\kappa }^{{q - 2}}}{{\left\| {\nabla e} \right\|}^{2}}$. Таким образом,

(2.10)

${{{\mathbf{m}}}_{g}}(e) \geqslant \frac{1}{{q{\text{*}}}}\kappa _{\infty }^{{q*(2 - q)}}\left\| {\nabla e} \right\|_{q}^{q}.$

Предположим, что известна более слабая априорная оценка точного решения ${{\left\| {\nabla {v}} \right\|}_{{t,\Omega }}} \leqslant {{\kappa }_{t}}$, где $q < t < \infty $. Используем интерполяционное неравенство (см., например, [25], [26])

и оценим правую часть (2.8). В этом случае мы приходим к оценке

(2.11)

${{{\mathbf{m}}}_{g}}(e) \geqslant \frac{1}{{q{\text{*}}}}\kappa _{t}^{{(1 - \theta )\mu q*}}\left\| {\nabla e} \right\|_{{q,\Omega }}^{\beta },$

где $\beta = (\mu - 1)q{\text{*}}$, $\theta = \tfrac{2}{q}\tfrac{{t - q}}{{t - 2}} < 1$ и $\mu = q\tfrac{{t - 2}}{{t - q}}$.

2.3. Мера ${{{\mathbf{m}}}_{\infty }}$

Мера, определенная (2.1), тем сильнее, чем шире пространство тест-функций $\hat {V}_{0}^{'}$. Если $u$ и функция ${v}$ принадлежат 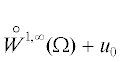, то $\hat {V}_{0}^{'}$ можно определить как . Положим в (2.1)

$g(\nabla w) = \kappa \left| {\nabla w} \right|,$

где $\kappa $ – это положительная постоянная (анализ нетрудно обобщить на случай, когда $\kappa $ – это функция $x$ такая, что $\kappa (x) \in [{{\kappa }_{ - }},{{\kappa }_{ + }}]$). В этом случае

(2.12)

${{{\mathbf{m}}}_{\infty }}(\nabla e) = \mathop {sup}\limits_{w \in \hat {V}_{0}^{'}{\backslash \{ }0{\text{\} }}} \int\limits_\Omega {\left( {\nabla e \cdot \nabla w - \kappa \left| {\nabla w} \right|} \right)} {\kern 1pt} dx.$

В отличие от предыдущего случая, максимайзер в (2.12) может не существовать (как функция из

), а сама мера может принимать бесконечное значение. Тем не менее ее можно использовать для определенной характеристики величины $e$. Нетрудно видеть, что если $\left| {\nabla e} \right| \leqslant \kappa $ почти везде в $\Omega $, то

${{{\mathbf{m}}}_{\infty }}(\nabla e) \leqslant \mathop {sup}\limits_{w \in \hat {V}_{0}^{'}{\backslash \{ }0{\text{\} }}} \int\limits_\Omega {\left( {\left| {\nabla e} \right| - \kappa } \right)} \left| {\nabla w} \right|dx = 0.$

Определим величину

(2.13)

${{\left\| {\left| {\nabla e} \right|} \right\|}_{\infty }}: = \mathop {sup}\limits_{w \in V_{0}^{'}{\backslash \{ }0{\text{\} }}} \frac{{\int\limits_\Omega {\nabla e} \cdot \nabla wdx}}{{{{{\left\| {\nabla w} \right\|}}_{{1,\Omega }}}}} \leqslant {{\left\| {\nabla w} \right\|}_{\infty }}.$

Эта норма является более сильной, чем ${{\left\| {\left| {\nabla e} \right|} \right\|}_{{q,\Omega }}}$ для любого $q < + \infty $. Действительно, так как ${{\left\| {\nabla w} \right\|}_{{1,\Omega }}} \leqslant {{\left| \Omega \right|}^{{1/q}}}{{\left\| {\nabla w} \right\|}_{{q*,\Omega }}}$, то

(2.14)

${{\left\| {\left| {\nabla e} \right|} \right\|}_{\infty }} \geqslant \frac{1}{{{{{\left| \Omega \right|}}^{{1/q}}}}}\mathop {sup}\limits_{w \in {{{\mathop W\limits^ \circ }}^{{1,q*}}}(\Omega )} \frac{{\int\limits_\Omega {\nabla {v}} \cdot \nabla wdx}}{{{{{\left\| {\nabla w} \right\|}}_{{q*,\Omega }}}}} = \frac{1}{{{{{\left| \Omega \right|}}^{{1/q}}}}}{{\left\| {\left| {\nabla e} \right|} \right\|}_{q}}.$

Теперь мы покажем, что

(2.15)

${{{\mathbf{m}}}_{\infty }}(\nabla e) = \left\{ \begin{gathered} 0,\quad {{\left\| {\left| {\nabla e} \right|} \right\|}_{{\infty ,\Omega }}} \leqslant \kappa , \hfill \\ + \infty ,\quad {{\left\| {\left| {\nabla e} \right|} \right\|}_{{\infty ,\Omega }}} \geqslant \kappa . \hfill \\ \end{gathered} \right.$

Для этого заметим, что любую функцию $\hat {V}_{0}^{'}$ можно представить в виде $\lambda \bar {w}$, где $\lambda \geqslant 0$, а $\bar {w} \in \hat {V}_{0}^{'}$ и ${{\left\| {\nabla \bar {w}} \right\|}_{{1,\Omega }}} = 1$. Поэтому

${{{\mathbf{m}}}_{\infty }}(\nabla e) = \mathop {sup}\limits_{\lambda \geqslant 0} \mathop {sup}\limits_{\begin{array}{*{20}{c}} {\bar {w} \in \mathop {\widehat V}\nolimits_0^\prime ,} \\ {\parallel \nabla \bar {w}{{\parallel }_{{1,\Omega }}} = 1} \end{array}} \left( {\int\limits_\Omega {\nabla e} \cdot \nabla \lambda \bar {w}dx - \kappa } \right) = \mathop {sup}\limits_{\lambda \geqslant 0} \lambda \left( {\mathop {sup}\limits_{\begin{array}{*{20}{c}} {\bar {w} \in \hat {V}_{0}^{'},} \\ {{{{\left\| {\nabla \bar {w}} \right\|}}_{{1,\Omega }}} = 1} \end{array}} \int\limits_\Omega {\nabla e} \cdot \nabla \bar {w}dx - \kappa } \right) = \mathop {sup}\limits_{\lambda \geqslant 0} \lambda \left( {{{{\left| {\left\| {\nabla e} \right\|} \right|}}_{\infty }} - \kappa } \right)$

и мы приходим к (2.15).

Рассмотрим некоторые другие свойства этой меры. Предположим, что ${{{\mathbf{m}}}_{\infty }}(\nabla e) = 0$. В этом случае

$0 = {{{\mathbf{m}}}_{\infty }}(\nabla e) \geqslant \mathop {sup}\limits_{\lambda > 0} \lambda \int\limits_\Omega {\left( {\left| {\nabla e} \right| - \kappa } \right)} \left| {\nabla e} \right|dx$

и, следовательно,

(2.16)

$\int\limits_\Omega {(\left| {\nabla e} \right| - \kappa )} \left| {\nabla e} \right|dx \leqslant 0.$

Эта оценка, конечно, не означает, что $\left| {\nabla e} \right| \leqslant \kappa $ почти всюду в $\Omega $. Однако мы можем достаточно просто оценить величину

${{{\text{\{ }}\left| {\nabla e} \right| - \kappa {\text{\} }}}_{ \oplus }}: = \mathop {max}\limits_{x \in \Omega } {\text{\{ }}\left| {\nabla e} \right| - \kappa ,0{\text{\} }}.$

Определим множества

$\Omega _{ - }^{\kappa }: = {\text{\{ }}x \in \Omega \,|\,\left| {\nabla e} \right| \leqslant \kappa {\text{\} }}\quad {\text{и}}\quad \Omega _{ + }^{\kappa } = \Omega {\backslash }\Omega _{ - }^{\kappa }.$

В соответствии с (2.16) имеем

$\kappa \int\limits_{\Omega _{ + }^{\kappa }} {\left( {\left| {\nabla e} \right| - \kappa } \right)} {\kern 1pt} dx \leqslant \int\limits_{\Omega _{ + }^{\kappa }} {\left( {\left| {\nabla e} \right| - \kappa } \right)} \left| {\nabla e} \right|dx \leqslant \int\limits_{\Omega _{ - }^{\kappa }} {\left( {\kappa - \left| {\nabla e} \right|} \right)} \left| {\nabla e} \right|dx \leqslant \int\limits_{\Omega _{ - }^{\kappa }} \kappa \left( {\kappa - \left| {\nabla e} \right|} \right)dx \leqslant {{\kappa }^{2}}\left| \Omega \right|.$

Отсюда мы заключаем, что если ${{{\mathbf{m}}}_{\infty }}(\nabla e) = 0$, то

(2.17)

$\int\limits_\Omega {\mathop {\left\{ {\left| {\nabla e} \right| - \kappa } \right\}}\nolimits_ \oplus } dx \leqslant \kappa \left| \Omega \right|.$

Далее будет построен критерий, позволяющий установить, что для функции $v$ действительно ${{{\mathbf{m}}}_{\infty }}(\nabla e) = 0$. В соответствии с (2.17) это дает определенную информацию о том, насколько существенно $\left| {\nabla e} \right|$ превышает $\kappa $.

2.4. Случай $d = 1$

В случае $d = 1$ можно установить простую зависимость между ${{\left| {\left\| {\, \cdot \,} \right\|} \right|}_{\infty }}$ и ${{\left| {\left\| {\, \cdot \,} \right\|} \right|}_{q}}$ и обычными нормами ${{\left\| {\, \cdot \,} \right\|}_{\infty }}$ и ${{\left\| {\, \cdot \,} \right\|}_{q}}$. Пусть $\Omega = (0,l)$, тогда

${{\left| {\left\| {e{\text{'}}{\kern 1pt} } \right\|} \right|}_{\infty }} = \mathop {sup}\limits_{w \in {{W}^{{1,1}}}(\Omega ){\backslash \{ }0\} } \frac{{\int\limits_0^l {e{\text{'}}} w{\text{'}}dx}}{{\int\limits_0^l {\left| {w{\text{'}}} \right|} dx}}.$

Рассмотрим функции вида

(2.18)

$w(x) = \int\limits_0^x \phi dx - x{{\left\{ {\left\{ \phi \right\}} \right\}}_{\Omega }},\quad w{\text{'}} = \phi - {{\left\{ {\left\{ \phi \right\}} \right\}}_{\Omega }},$

где $\phi \in {{L}^{1}}(\Omega )$, а ${{\left\{ {\left\{ \phi \right\}} \right\}}_{\Omega }}: = \tfrac{1}{l}\int_0^l \phi dx$. Нетрудно видеть, что $w(0) = w(l) = 0$ и

$\int\limits_0^l {\left| {w{\text{'}}} \right|} {\kern 1pt} dx \leqslant \int\limits_0^l {\left| \phi \right|dx} + \left| {\int\limits_0^l {\left| \varphi \right|} {\kern 1pt} dx} \right| \leqslant 2\int\limits_0^l {\left| \phi \right|} {\kern 1pt} dx.$

Так как

$\int\limits_0^l {e{\text{'}}} dx = 0,\quad {\text{то}}\quad \int\limits_0^l {e{\text{'}}} w{\text{'}}dx = \int\limits_0^l {e{\text{'}}} \phi dx$

и, следовательно,

(2.19)

${{\left\| {\left| {e{\text{'}}{\kern 1pt} } \right|} \right\|}_{\infty }} \geqslant \mathop {sup}\limits_{\phi \in {{L}^{1}}(\Omega ){\backslash \{ }0{\text{\} }}} \frac{{\int\limits_0^l {e{\text{'}}} \phi dx}}{{2\int\limits_0^l {\left| \phi \right|} {\kern 1pt} dx}} = \frac{1}{2}{{\left\| {e{\text{'}}{\kern 1pt} } \right\|}_{\infty }}.$

Пример ниже показывает, что в общем случае постоянную 1/2 увеличить нельзя. Пусть $l = 1$, $\xi \in [0.5,1)$ и

$e(x) = \left\{ \begin{gathered} \frac{x}{\xi },\quad x \in [0,\xi ), \hfill \\ \frac{{1 - x}}{{1 - \xi }},\quad x \in [\xi ,1],\quad {{\left\| {e{\text{'}}} \right\|}_{\infty }} = \frac{1}{{1 - \xi }}. \hfill \\ \end{gathered} \right.$

При этом $\int_0^l {e{\text{'}}} w{\text{'}}dx = \tfrac{{w(\xi )}}{{\xi (1 - \xi )}}$. Таким образом, при вычислении супремума в (2.19) мы приходим к задаче: найти непрерывную функцию $w$ такую, что $w(\xi ) = 1$ и $w(0) = w(1) = 0$ с минимальным интегралом $\int_0^1 \left| {w{\text{'}}} \right|dx$. Ясно, что эта функция должна быть монотонна на каждом из интервалов $(0,\xi )$ и $(\xi ,1)$ и должна сохранять знак. В этом случае $\int_0^1 \left| {w{\text{'}}} \right|dx = 2w(\xi )$, а супремум равен $\tfrac{1}{{2\xi (1 - \xi )}}$, так что ${{\left| {\left\| {e{\text{'}}} \right\|} \right|}_{\infty }} = \tfrac{1}{{2\xi (1 - \xi )}}$ и $\tfrac{{{{{\left\| {\left| {e{\text{'}}} \right|} \right\|}}_{\infty }}}}{{{{{\left\| {e{\text{'}}} \right\|}}_{\infty }}}} = \tfrac{1}{{2\xi }}$. При $\xi = \tfrac{1}{2}$ две нормы совпадают, но если $\xi $ стремится к $1$, то коэффициент пропорциональности между нормами стремится к 1/2.

Аналогичную оценку можно получить для ${{\left\| {\left| {\, \cdot \,} \right|} \right\|}_{q}}$ с $q \in (1, + \infty )$. Для этого используем представление (2.18) с $\phi \in {{L}^{{q*}}}(\Omega )$. Тогда

${{\left\| {\left| {e{\text{'}}} \right|} \right\|}_{{q,\Omega }}} = \mathop {sup}\limits_{w \in {{W}^{{1,q*}}}(\Omega ){\backslash \{ }0{\text{\} }}} \frac{{\int\limits_0^l {e{\text{'}}w{\text{'}}dx} }}{{{{{\left\| {w{\text{'}}} \right\|}}_{{q*,\Omega ,}}}}} \geqslant \mathop {sup}\limits_{\phi \in {{L}^{{q*}}}(\Omega ){\backslash \{ }0\} } \frac{{\int\limits_0^l {e{\text{'}}} \phi dx}}{{{{{\left\| \phi \right\|}}_{{q*\Omega }}} + \left| {{{{\left\{ {\left\{ \phi \right\}} \right\}}}_{\Omega }}} \right|{{l}^{{1/q*}}}}}.$

Поскольку

$\left| {\int\limits_0^l {\phi dx} } \right| \leqslant {{l}^{{1/q}}}{{\left\| \phi \right\|}_{{q*,\Omega }}}\quad {\text{и}}\quad \left| {{{{\left\{ {\left\{ \phi \right\}} \right\}}}_{\Omega }}} \right|{{l}^{{1/q*}}} \leqslant {{l}^{{1/q + 1/q* - 1}}}{{\left\| \phi \right\|}_{{q*,\Omega }}},$

то мы заключаем что ${{\left\| {\left| {e{\text{'}}} \right|} \right\|}_{{q,\Omega }}} \geqslant \tfrac{1}{2}{{\left\| {e{\text{'}}} \right\|}_{{q,\Omega }}}$.

3. МАЖОРАНТА ${{{\mathbf{m}}}_{G}}(e)$

3.1. Общий случай

Перейдем к двусторонним оценкам величины ${{{\mathbf{m}}}_{G}}(e)$. Оценка снизу вытекает непосредственно из определения (2.1). Действительно, для любого конечномерного пространства $W_{0}^{k}$ ($\dim W_{0}^{k} = k$) такого, что $W_{0}^{k} \subset \hat {V}_{0}^{'}$

(3.1)

${{{\mathbf{m}}}_{G}}(e) \geqslant \mathop {sup}\limits_{w \in W_{0}^{k}} \left\{ {{{\mathcal{F}}_{{v}}}(w) - G(w)} \right\} = M_{{G, \ominus }}^{k}({v}).$

Для получения этой миноранты надо решить конечномерную задачу, так что величина $M_{{G, \ominus }}^{k}(e)$ практически вычисляема. Более того, точное решение этой вспомогательной задачи не обязательно и можно использовать и любое приближенное решение при условии, что оно не сильно отличается по функционалу от точного. Если в совокупности подпространства $W_{0}^{k}$ предельно плотны в $\hat {V}_{0}^{'}$, то последовательность $M_{{G, \ominus }}^{k}({v})$ стремится (снизу) к ${{{\mathbf{m}}}_{G}}({v})$ при $k \to + \infty $. Таким образом, вычисление оценки снизу не сопряжено с какими-то принципиальными трудностями.

Ситуация с оценкой сверху сложнее. Вычислить супремум по бесконечному набору функций в общем случае не представляется возможным. Поэтому надо найти другой метод, позволяющий оценить этот супремум сверху. Рассмотрим случай, когда функционал $G$ задан соотношением (2.2). Используя тождество (1.7), мы получаем

(3.2)

${{{\mathbf{m}}}_{G}}(e) = \mathop {sup}\limits_{w \in \hat {V}_{0}^{'}} \int\limits_\Omega {(\nabla e \cdot \nabla w - g(\left| {\nabla w} \right|))dx} = \int\limits_\Omega {(\nabla {v} - y)} \cdot \nabla wdx + \int\limits_\Omega {(\operatorname{div} y + f)} wdx - \int\limits_\Omega g \left( {\left| {\nabla w} \right|} \right)dx,$

где $y \in {{Y}_{{{\text{div}}}}}: = \left\{ {y \in \nabla {{{\hat {V}}}_{0}},\operatorname{div} y \in {{L}^{\mu }}(\Omega )} \right\}.$ Здесь $\nabla {{\hat {V}}_{0}}$ обозначает векторнозначные функции, являющиеся градиентами функций из ${{\hat {V}}_{0}}$, а $\mu $ определяется регулярностью $f$ так, чтобы $(\operatorname{div} y + f)w \in {{L}^{1}}(\Omega )$ для любого $w$. В этом случае

(3.3)

$\int\limits_\Omega {(\operatorname{div} y + f)} {\kern 1pt} wdx \leqslant {{\left\| {\operatorname{div} y + f} \right\|}_{{\mu ,\Omega }}}{{\left\| w \right\|}_{{\mu *,\Omega }}}.$

Величина $\mu {\kern 1pt} *$ ограничивается условием вложения $W_{\Omega }^{{1,1}}$ ↪ ${{L}^{{\mu *}}}(\Omega )$ и определяется соотношением $\mu * \leqslant \tfrac{d}{{d - 1}}$ при $d \geqslant 2$ (для $d = 1$ можно взять любое конечное $\mu {\text{*}}$). При выполнении этих условий имеет место обобщенное неравенство Фридрихса

(3.4)

где $C_{{\mu *,1}}^{F}$ обозначает соответствующую константу. Оценив при помощи (3.2) и (3.3) правую часть (3.4), получим

(3.5)

$\begin{gathered} {{{\mathbf{m}}}_{G}}(e) \leqslant \mathop {sup}\limits_{w \in V_{0}^{'}} \left\{ {\int\limits_\Omega {\left| {\nabla {v} - y} \right|} } \right.\left| {\nabla w} \right|dx + C_{{\mu *,1}}^{F}{{\left\| {\operatorname{div} y + f} \right\|}_{{\mu ,\Omega }}}\int\limits_\Omega {\left| {\nabla w} \right|} {\kern 1pt} dx - \left. {\int\limits_\Omega g (\left| {\nabla w} \right|){\kern 1pt} dx} \right\} \leqslant \\ \leqslant \;\mathop {sup}\limits_{t \geqslant 0} \int\limits_\Omega {\left( {\left( {\left| {\nabla {v} - y} \right| + C_{{\mu *,1}}^{F}{{{\left\| {\operatorname{div} y + f} \right\|}}_{{\mu ,\Omega }}}} \right)t - g(t)} \right)} {\kern 1pt} dx \leqslant \\ \leqslant \;\int\limits_\Omega {g{\text{*}}} \left( {\left| {\nabla {v} - y} \right| + C_{{\mu *,1}}^{F}{{{\left\| {\operatorname{div} y + f} \right\|}}_{{\mu ,\Omega }}}} \right)dx = :M_{{G, \oplus }}^{1}({v}). \\ \end{gathered} $

В частности, если $\operatorname{div} y + f = 0$, то

(3.6)

${{{\mathbf{m}}}_{G}}(e) \leqslant \int\limits_\Omega {g{\text{*}}} \left( {\left| {\nabla {v} - y} \right|} \right)dx.$

Заметим, что если $g$ задается квадратичной функцией, то (3.6) переходит в известную оценку Прагера-Синга.

Использование (3.6) требует оценки постоянной $C_{{\mu *,1}}^{F}$, что в общем случае может вызвать затруднения. Поэтому имеет смысл модифицировать эту оценку, введя некоторые (незначительные) ограничения на вектор-функцию $y$, предположив, что $\bar {\Omega } = \bigcup\nolimits_{i = 1}^N {{{{\bar {\Omega }}}_{i}}} $, где ${{\Omega }_{i}}$ – выпуклые непересекающиеся подобласти и

(3.7)

$\int\limits_{{{\Omega }_{i}}} {(\operatorname{div} y + f)} {\kern 1pt} dx = 0,\quad i = 1,2,\; \ldots ,\;N.$

В этом случае при оценке интеграла (3.3) можно применить метод, предложенный в [3], в котором для подобластей вместо неравенства Фридрихса используются неравенства Пуанкаре

(3.8)

${{\left\| {w - {{{\left\{ {\left\{ w \right\}} \right\}}}_{{{{\Omega }_{i}}}}}} \right\|}_{{\mu *,{{\Omega }_{i}}}}} \leqslant C_{{\mu *,1}}^{P}{{\left\| {\nabla w} \right\|}_{{1,{{\Omega }_{i}}}}},$

где $\mu * < \tfrac{d}{{d - 1}}$, ${{\left\{ {\left\{ w \right\}} \right\}}_{{{{\Omega }_{i}}}}}$ обозначает среднее значение функции в ${{\Omega }_{i}}$, а постоянная $C_{{\mu *,1}}^{P}$ для выпуклых областей вычислена в [27]. Введем обозначение

${{\mathcal{R}}_{{{{\Omega }_{i}}}}}: = C_{{\mu *,1}}^{P}({{\Omega }_{i}}){{\left\| {\operatorname{div} y + f} \right\|}_{{\mu ,{{\Omega }_{i}}}}}.$

Тогда

$\int\limits_\Omega {(\operatorname{div} y + f)} wdx \leqslant \sum\limits_{i = 1}^N {{{\mathcal{R}}_{{{{\Omega }_{i}}}}}} {{\left\| {\nabla w} \right\|}_{{1,{{\Omega }_{i}}}}}$

и мы модифицируем (3.5) следующим образом:

(3.9)

$\begin{gathered} {{{\mathbf{m}}}_{G}}(e) \leqslant \mathop {sup}\limits_{w \in \hat {V}_{0}^{'}} \left\{ {\sum\limits_{i = 1}^N {\int\limits_{{{\Omega }_{i}}} {((\left| {\nabla {v} - y} \right| + {{R}_{{{{\Omega }_{i}}}}})} } \left| {\nabla w} \right| - g(\left| {\nabla w} \right|))dx} \right\} \leqslant \sum\limits_{i = 1}^N \mathop {sup}\limits_{{{t}_{i}} \geqslant 0} \int\limits_{{{\Omega }_{i}}} {((\left| {\nabla {v} - y} \right| + {{R}_{{{{\Omega }_{i}}}}}){{t}_{i}} - g({{t}_{i}}))} {\kern 1pt} dx \leqslant \\ \leqslant \;\sum\limits_{i = 1}^N \int\limits_{{{\Omega }_{i}}} {g{\text{*}}} (\left| {\nabla {v} - y} \right| + {{R}_{{{{\Omega }_{i}}}}}){\kern 1pt} dx = :M_{{G, \oplus }}^{N}({v}). \\ \end{gathered} $

3.2. Мажоранта ${{{\mathbf{m}}}_{q}}(e)$

Пусть $f \in {{L}^{q}}(\Omega )$ и известно, что точное решение обладает повышенной суммируемостью, так что

$u \in {{K}_{q}}(\Omega ): = {{W}^{{1,q}}}(\Omega ) \cap ({{V}_{0}} + {{u}_{0}}),\quad 2 < q < + \infty .$

Мы хотим получить явно вычисляемые оценки меры ${{{\mathbf{m}}}_{q}}(e)$, введенной в п. 2.2 . Естественно, мы должны потребовать, чтобы функция ${v}$ также принадлежала множеству ${{K}_{q}}(\Omega )$. Заметим, что последнее условие обычно выполняется автоматически, так как в большинстве численных методов аппроксимации строятся при помощи кусочно гладких функций (например полиномов). Введем множество вектор-функций

${{H}_{{{\text{div}},q}}}: = \{ y \in {{L}^{q}}(\Omega ,{{\mathbb{R}}^{d}})\,|\,\operatorname{div} y \in {{L}^{q}}(\Omega )\} .$

Учитывая (1.9), мы заключаем, что для любой функции

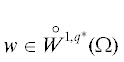и любой вектор-функции $y \in {{H}_{{{\text{div}},q}}}$ выполнено тождество

(3.10)

$\begin{gathered} \int\limits_\Omega {\left( {\nabla e \cdot \nabla w - \frac{1}{{q{\text{*}}}}{{{\left| {\nabla w} \right|}}^{{q*}}}} \right)dx} = \int\limits_\Omega {(y - \nabla {v})} \cdot \nabla wdx + \int\limits_\Omega {(f + \operatorname{div} y)} wdx - \frac{1}{{q{\text{*}}}}\left\| {\nabla w} \right\|_{{q*,\Omega }}^{{q*}} \leqslant \\ \leqslant \;\left( {{{{\left\| {\nabla {v} - y} \right\|}}_{{q,\Omega }}} + {{C}_{{q*}}}(\Omega ){{{\left\| {\operatorname{div} y + f} \right\|}}_{{q,\Omega }}}} \right){{\left\| {\nabla w} \right\|}_{{q*,\Omega }}} - \frac{1}{{q{\text{*}}}}\left\| {\nabla w} \right\|_{{q*,\Omega }}^{{q*}}, \\ \end{gathered} $

где $C_{{{{q}^{ * }}}}^{F}$ является постоянной в неравенстве

(3.11)

Оценивая супремум по $w$ сверху, получаем оценку

(3.12)

${{{\mathbf{m}}}_{q}}(e) \leqslant \frac{1}{q}{{\left( {{{{\left\| {\nabla {v} - y} \right\|}}_{{q,\Omega }}} + C_{{q*}}^{F}(\Omega ){{{\left\| {\operatorname{div} y + f} \right\|}}_{{q,\Omega }}}} \right)}^{q}}.$

С учетом (2.7) приходим к следующему результату.

Утверждение 1. Для любой функции ${v} \in {{K}_{q}}(\Omega )$ имеет место оценка

(3.13)

${{\left\| {\left| {\nabla e} \right|} \right\|}_{{q,\Omega }}} \leqslant {{\left\| {\nabla {v} - y} \right\|}_{{q,\Omega }}} + C_{{q*}}^{F}(\Omega ){{\left\| {\operatorname{div} y + f} \right\|}_{{q,\Omega }}},$

где $y$ – произвольная векторнозначная функция из ${{H}_{{{\text{div}},q}}}$.

При преобразовании (3.10) можно пойти несколько иным путем и использовать вариант неравенства Юнга (см., например, [25], [26])

$\zeta \zeta * \leqslant \frac{1}{q}{{\alpha }^{{\tfrac{q}{{q*}}}}}{{\zeta }^{q}} + \frac{1}{{\alpha q{\text{*}}}}\mathop {(\zeta {\text{*}})}\nolimits^{q*} ,$

которое выполняется для сопряженных чисел $\alpha $ и $\alpha {\text{*}}$ и любых неотрицательных $\zeta $ и $\zeta {\text{*}}$. Применив его, получаем оценки

$C_{{q*}}^{F}(\Omega ){{\left\| {\operatorname{div} y + f} \right\|}_{{q,\Omega }}}{{\left\| {\nabla w} \right\|}_{{q*,\Omega }}} \leqslant \frac{{{{{(\alpha {\text{*}})}}^{{\tfrac{q}{{q*}}}}}}}{q}\mathop {(C_{{q*}}^{F})}\nolimits^q \left\| {\operatorname{div} y + f} \right\|_{{q,\Omega }}^{q} + \frac{1}{{q{\text{*}}\alpha {\text{*}}}}\left\| {\nabla w} \right\|_{{q*,\Omega }}^{{q*}}.$

Применив их в (3.10), получаем следующую мажоранту:

(3.14)

${{{\mathbf{m}}}_{q}}(e) \leqslant {{M}_{{q, \oplus }}}(e): = \frac{1}{q}\left( {{{\alpha }^{{\tfrac{q}{{q*}}}}}\left\| {\nabla {v} - y} \right\|_{{q,\Omega }}^{q} + {{{(\alpha {\text{*}})}}^{{\tfrac{q}{{q*}}}}}\mathop {(C_{{q*}}^{F})}\nolimits^q \left\| {\operatorname{div} y + f} \right\|_{{q,\Omega }}^{q}} \right).$

Нетрудно видеть, что правые части оценок (3.13) и (3.14) не содержат неизвестных функций, а соответствующие нормы представлены интегралами и могут быть явно вычислены.

В частности, если $q = q* = 2$, то мы получаем известную оценку (см., [3], [2])

(3.15)

${{\left\| {\nabla (u - {v})} \right\|}^{2}} = 2{{{\mathbf{m}}}_{g}}(e) \leqslant \alpha {{\left\| {\nabla {v} - y} \right\|}^{2}} + \alpha {\text{*}}{{({{C}^{F}})}^{2}}{{\left\| {\operatorname{div} y + f} \right\|}^{2}},$

где ${{C}_{2}}$ совпадает с постоянной в неравенстве Фридрихса для функций из пространства

3.2. Мажоранта ${{{\mathbf{m}}}_{\infty }}(e)$

Теперь мы считаем, что $f \in {{L}^{\infty }}(\Omega )$ и что точное решение $u$, и аппроксимация ${v}$ принадлежат множеству

${{K}_{\infty }}(\Omega ): = {{W}^{{1,\infty }}}(\Omega ) \cap ({{V}_{0}} + {{u}_{0}}).$

В качестве $\hat {V}_{0}^{'}$ используем пространство

, а вместо ${{H}_{{{\text{div}},q}}}$ введем множество

$y \in {{H}_{{{\text{div}},\infty }}}(\Omega ): = \{ y \in {{L}^{\infty }}(\Omega ,{{\mathbb{R}}^{d}})\,|\,\operatorname{div} y \in {{L}^{\infty }}(\Omega )\} .$

Преобразуем выражение для меры следующим образом:

(3.16)

$\begin{gathered} {{{\mathbf{m}}}_{\infty }}(\nabla e) = \mathop {sup}\limits_{w \in \hat {V}_{0}^{'}} \int\limits_\Omega {\left( {f + \operatorname{div} y)w + (y - \nabla {v}) \cdot \nabla w - \kappa \left| {\nabla w} \right|} \right)} {\kern 1pt} dx \leqslant \\ \leqslant \;\mathop {sup}\limits_{w \in \hat {V}_{0}^{'}} \left\{ {{{{\left\| {f + \operatorname{div} y} \right\|}}_{{\infty ,\Omega }}}\int\limits_\Omega {\left| w \right|dx} + \int\limits_\Omega {\left( {(y - \nabla {v}) \cdot \nabla w - \kappa \left| {\nabla w} \right|} \right){\kern 1pt} } dx} \right\} \leqslant \\ \leqslant \;\mathop {sup}\limits_{w \in \hat {V}_{0}^{'}} \int\limits_\Omega {\left( {(C_{{1,1}}^{F}(\Omega ){{{\left\| {f + \operatorname{div} y} \right\|}}_{{\infty ,\Omega }}} - \kappa )\left| {\nabla w} \right| + (y - \nabla {v}) \cdot \nabla w} \right)} {\kern 1pt} dx. \\ \end{gathered} $

Здесь $C_{{1,1}}^{F}(\Omega )$ – постоянная в неравенстве Фридрихса ${{\left\| w \right\|}_{{1,\Omega }}} \leqslant C_{{1,1}}^{F}(\Omega {{\left\| {\nabla w} \right\|}_{{1,\Omega }}}$ для любого

. Подынтегральное выражение имеет вид

$({{\mathcal{R}}_{y}} - \kappa )\left| {\nabla w} \right| + (y - \nabla {v}) \cdot \nabla w,$

где ${{\mathcal{R}}_{y}}: = C_{{1,1}}^{F}(\Omega ){{\left\| {f + \operatorname{div} y} \right\|}_{{\infty ,\Omega }}}$ – это неотрицательная постоянная. Если на некотором открытом множестве $\omega $ с положительной мерой выполнено условие ${{\mathcal{R}}_{y}} - \kappa > \left| {y - \nabla {v}} \right|$, то выбрав функцию $w$ с носителем на этом множестве, получаем ${{{\mathbf{m}}}_{\infty }}(\nabla e) = + \infty $. Напротив, если для почти всех $x \in \Omega $ выполнено

$\kappa \geqslant {{\mathcal{R}}_{y}} + \left| {y - \nabla {v}} \right|,$

то подынтегральное выражение всегда неположительно и ${{{\mathbf{m}}}_{\infty }}(\nabla e) = 0$. С учетом (2.15) мы приходим к следующему результату: eсли для ${v} \in W_{0}^{{1,\infty }}(\Omega )$ существует функция $y \in {{H}_{{{\text{div}},\infty }}}(\Omega )$ такая, что почти везде в $\Omega $ выполняется условие

(3.17)

$C_{{1,1}}^{F}{{\left\| {f + \operatorname{div} y} \right\|}_{{\infty ,\Omega }}} + \left| {y - \nabla {v}} \right| \leqslant \kappa ,$

то ${{\left\| {\left| {\nabla (u - {v})} \right|} \right\|}_{{\infty ,\Omega }}} \leqslant \kappa $.

Пример. Рассмотрим простой пример, который иллюстрирует условие (3.17). Функция $u = \tfrac{1}{2}x(x + 1)$ является решением уравнения $u{\text{''}} = 1$ с условиями $u(0) = 0$ и $u(1) = 1$. Пусть ${v} = u + e(x)$, причем величина отклонения удовлетворяет условию

(3.18)

${{\left\| {e{\text{'}}} \right\|}_{\infty }} = \mathop {sup}\limits_{x \in (0,1)} \left| {e{\text{'}}(x)} \right| = {{\zeta }_{ \oplus }}\quad {\text{и}}\quad \mathop {inf}\limits_{x \in (0,1)} \left| {e{\text{'}}(x)} \right| = 0.$

Положим $y = x + b + \tfrac{1}{2}$, где $b$ – произвольная постоянная. В этом случае $\operatorname{div} y + f = y{\kern 1pt} {\text{'}} - 1 = 0$ и первое слагаемое в (3.17) обращается в ноль. Вычислим второе слагаемое

$\left| {y - \nabla {v}} \right| = \left| {x + b + \frac{1}{2} - u{\text{'}} - e{\text{'}}{\kern 1pt} } \right| = \left| {b - e{\text{'}}(x)} \right|.$

Учитывая (3.18), мы заключаем, что ${{\left\| {y - \nabla {v}} \right\|}_{\infty }} = max\left\{ {\left| b \right|,\left| {b - {{\zeta }_{ \oplus }}} \right|} \right\}$. Выбрав $b = \tfrac{{{{\zeta }_{ \oplus }}}}{2}$, получим

${{\left\| {y - \nabla {v}} \right\|}_{{\infty ,\Omega }}} = {{\left\| {y - {v}{\kern 1pt} {\text{'}}{\kern 1pt} } \right\|}_{{\infty ,(0,1)}}} = \frac{{{{\zeta }_{ \oplus }}}}{2}.$

Таким образом, в (3.17) $\kappa = \tfrac{{{{\zeta }_{ \oplus }}}}{2}$ и, следовательно, ${{\left\| {\left| {e{\text{'}}} \right|} \right\|}_{\infty }} \leqslant \tfrac{{{{\zeta }_{ \oplus }}}}{2}$. Учитывая (2.19), заключаем, что для ${{L}^{\infty }}$ нормы отклонения должно выполняться ${{\left\| {\left| {e{\text{'}}} \right|} \right\|}_{\infty }} \leqslant {{\zeta }_{ \oplus }}$. Эта оценка действительно выполняется (см. (3.18)).

Другие мажоранты величины ${{{\mathbf{m}}}_{\infty }}(e)$ можно получить, используя принцип декомпозиции области. При этом вместо постоянной $C_{{1,1}}^{F}(\Omega )$ используются локальные постоянные в неравенствах типа Пуанкаре. Пусть $\Omega $ разделена на выпуклые непересекающиеся подобласти ${{\Omega }_{i}}$, $i = 1,2,\; \ldots ,\;N$, так что $\bar {\Omega } = \bigcup\nolimits_{i = 1}^N {{{{\bar {\Omega }}}_{i}}} $ и

(3.19)

${{\left\{ {\left\{ {\operatorname{div} y + f} \right\}} \right\}}_{{{{\Omega }_{i}}}}} = 0,\quad i = 1,2,\; \ldots ,\;N.$

В соответствии с [28] для любой функции $w \in {{W}^{{1,1}}}(\Omega )$ с нулевым средним выполняется неравенство Пуанкаре

(3.20)

${{\left\| w \right\|}_{{1,{{\Omega }_{i}}}}} \leqslant C_{{1,1}}^{P}({{\Omega }_{i}}){{\left\| {\nabla w} \right\|}_{{1,{{\Omega }_{i}}}}}$

с постоянной $C_{{1,1}}^{P}({{\Omega }_{i}}) = \tfrac{{\operatorname{diam} {{\Omega }_{i}}}}{2}$. Заметим, что условия (3.19) не создают существенных технических трудностей, если только число подобластей не слишком велико. С учетом (3.20) мы преобразуем супремум в (3.16) несколько иным способом

$\begin{gathered} {{{\mathbf{m}}}_{\infty }}(\nabla e) = \mathop {sup}\limits_{w \in \hat {V}_{0}^{'}} \sum\limits_{i = 1}^N \int\limits_{{{\Omega }_{i}}} {\left( {(f + \operatorname{div} y)w + (y - \nabla {v}) \cdot \nabla w - \kappa \left| {\nabla w} \right|} \right)} {\kern 1pt} dx \leqslant \\ \leqslant \;\mathop {sup}\limits_{w \in \hat {V}_{0}^{'}} \int\limits_\Omega {(\mathcal{R}_{y}^{N}\left| {\nabla w} \right| + (y - \nabla {v}) \cdot \nabla w - \kappa \left| {\nabla w} \right|)dx} . \\ \end{gathered} $

Здесь $\mathcal{R}_{y}^{N}$ – это функция, определенная соотношением $\mathcal{R}_{y}^{N}(x) = {{\mathcal{R}}_{{{{\Omega }_{i}}}}}$, если $x \in {{\Omega }_{i}}$, где ${{\mathcal{R}}_{{{{\Omega }_{i}}}}} = C_{{1,1}}^{P}({{\Omega }_{i}}){{\left\| {f + \operatorname{div} y} \right\|}_{{\infty ,{{\Omega }_{i}}}}}$. Ясно, что ${{\mathcal{R}}_{{{{\Omega }_{i}}}}}$ является неотрицательной постоянной, ассоциированной с ${{\Omega }_{i}}$, так что $\mathcal{R}_{y}^{N}$ является кусочно-постоянной функцией. Мы приходим к следующей модификации условия (3.17): eсли для ${v} \in W_{0}^{{1,\infty }}(\Omega )$ существует функция $y$ такая, что почти везде в $\Omega $ выполняется условие

(3.21)

$\mathcal{R}_{y}^{N} + \left| {y - \nabla {v}} \right| \leqslant \kappa {\kern 1pt} ,$

то ${{\left\| {\left| {\nabla (u - {v})} \right|} \right\|}_{\infty }} \leqslant \kappa $.

3.3. Локальные меры расстояния до точного решения

Если множество пробных функций $w$ ограничить функциями, отличными от нуля только в подобласти $\omega \subset \Omega $, то мы получим меры расстояния локального типа. Пусть ${{\hat {V}}_{0}} = \{ w \in {{W}^{{1,2}}}(\Omega )\,|\,w = 0\;{\text{в}}\;\Omega {\kern 1pt} {\text{'}}: = \Omega {\backslash }\bar {\omega }\} $, а $\mathcal{H}(\omega )$ обозначает множество функций, гармонических в $\omega $, т.е.,

$\mathcal{H}(\omega ): = \left\{ {h(x) \in {{{\hat {V}}}_{0}}\,|\,\int\limits_\Omega {\nabla h \cdot \nabla wdx} = 0\;\;\forall w \in {{{\hat {V}}}_{0}}} \right\}.$

Границы областей $\omega $ и $\Omega {\text{'}}$ предполагаются липшицевыми. Определим величину

(3.22)

${{\left\| {\left| {\nabla e} \right|} \right\|}_{{2,\omega }}}: = \mathop {sup}\limits_{w \in {{{\hat {V}}}_{0}}{\backslash \{ }0{\text{\} }}} \frac{{\int\limits_\Omega {\nabla e} \cdot \nabla wdx}}{{{{{\left\| {\nabla w} \right\|}}_{{2,\omega }}}}},$

которая является лишь полунормой и превращается в норму только на фактор-пространстве функций, отличающихся на гармоническую функцию. Введем соответствующую фактор-норму ${{\left\| e \right\|}_{{{{{\hat {V}}}_{0}}{\backslash }\mathcal{H}}}}: = \mathop {inf}\limits_{h \in \mathcal{H}(\omega )} {{\left\| {\nabla (e - h)} \right\|}_{{2,\omega }}}$. Нетрудно видеть, что ${{\left\| {\left| {\nabla e} \right|} \right\|}_{{2,\omega }}} = {{\left\| e \right\|}_{{{{{\hat {V}}}_{0}}{\backslash }\mathcal{H}}}}$. Оценим эту величину сверху. Для любой функции $y \in H(\omega ,{\text{div}})$

$\int\limits_\Omega {\nabla e} \cdot \nabla wdx \leqslant {{\left\| {\operatorname{div} y + f} \right\|}_{{2,\omega }}}{{\left\| w \right\|}_{{2,\omega }}} + {{\left\| {\nabla {v} - y} \right\|}_{{2,\omega }}}{{\left\| {\nabla w} \right\|}_{{2,\omega }}}.$

Отсюда и из (3.22) вытекает, что

(3.23)

${{\left\| e \right\|}_{{{{{\hat {V}}}_{0}}{\backslash }\mathcal{H}}}} \leqslant {{\left\| {\nabla {v} - y} \right\|}_{{2,\omega }}} + {{C}^{F}}(\omega ){{\left\| {\operatorname{div} y + f} \right\|}_{{2,\omega }}},$

где ${{C}^{F}}(\omega )$ – постоянная в неравенстве Фридрихса для области $\omega $. Таким образом, сумма двух локальных норм в правой части (3.23) ограничивает только фактор-норму, которая показывает, насколько близко к ${v}$ расположена функция, точно удовлетворяющая дифференциальному уравнению.

Если ввести дополнительное условие на функцию $y$, а именно ${{\left\{ {\left\{ {\operatorname{div} y + f} \right\}} \right\}}_{\omega }} = 0$, то ${{C}^{F}}(\omega )$ можно заменить на постоянную в неравенстве Пуанкаре ${{C}^{F}}(\omega )$. В частности, для выпуклой области $\omega $ имеем оценку

(3.24)

${{\left\| e \right\|}_{{\mathop {{{{\hat {V}}}_{0}}}\nolimits_{} {\backslash }\mathcal{H}}}} \leqslant {{\left\| {\nabla {v} - y} \right\|}_{{2,\omega }}} + \frac{{\operatorname{diam} \omega }}{\pi }{{\left\| {\operatorname{div} y + f} \right\|}_{{2,\omega }}}.$

Оценки (3.23) и (3.24), конечно, не дают полного представления о величине локальной ошибки, но это вполне естественно. Мы не можем ожидать, что сумма локальных норм, составляющих их правые части, могла бы оценить полную норму ${{\left\| {\nabla (u - {v})} \right\|}_{{2,\omega }}}$ без учета краевых условий и поведения функций в $\Omega {\text{'}}$.

4. ОБОБЩЕНИЯ НА ДРУГИЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА

Рассмотренная выше схема переносится на другие уравнения эллиптического типа, если соответствующие точные решения обладают повышенной регулярностью (в смысле степени интегрируемости). Пусть, например, уравнение

(4.1)

$\operatorname{div} A\nabla u + f = 0,$

с краевым условием $u = {{u}_{0}}$ имеет решение в ${{K}_{q}}(\Omega )$ для $q > 2$, и функция ${v}$ также принадлежит этому множеству. Матрица $A$ считается симметричной и положительно-определенной с ограниченными коэффициентами, причем

${{\lambda }_{1}}{{\left| \zeta \right|}^{2}} \leqslant A(x)\zeta \cdot \zeta \leqslant {{\lambda }_{2}}{{\left| \zeta \right|}^{2}},\quad 0 < {{\lambda }_{1}} \leqslant {{\lambda }_{2}}.$

Для $\zeta \in {{\mathbb{R}}^{d}}$ определим ${{\left| \zeta \right|}_{A}}: = {{\left| {A\zeta \cdot \zeta } \right|}^{{1/2}}}$ и норму

${{\left\| {\nabla w{\kern 1pt} } \right\|}_{{A,\Omega ,q}}}: = \mathop {\left( {\int\limits_\Omega {\left| {\nabla w} \right|_{A}^{q}dx} } \right)}\nolimits^{1/q} .$

Аналогом меры (2.3) является

${{{\mathbf{m}}}_{q}}(e) = \mathop {sup}\limits_{w \in {{{\mathop W\limits^ \circ }}^{{1,q*}}}(\Omega )} \left( {\int\limits_\Omega {A\nabla e \cdot \nabla w} - \frac{1}{{q{\text{*}}}}\left\| {\nabla w} \right\|_{{A,q*,\Omega }}^{{q*}}} \right).$

При помощи рассуждений, аналогичных (2.6), (2.7), можно показать, что

где

${{\left\| {\left| {\nabla e} \right|} \right\|}_{{A,q,\Omega }}}: = \mathop {sup}\limits_{\begin{array}{*{20}{c}} {w \in {{{\mathop W\limits^ \circ }}^{{1,q*}}}(\Omega )} \\ {\parallel w{{\parallel }_{{A,q*,\Omega }}} = 1} \end{array}} \int\limits_\Omega {A\nabla e} \cdot \nabla wdx.$

Нетрудно видеть, что для любой функции $y \in {{H}_{{{\text{div}},q}}}$

(4.2)

$\int\limits_\Omega {A\nabla e \cdot \nabla wdx} - \frac{1}{{q{\text{*}}}}\left\| {\nabla w} \right\|_{{A,q*,\Omega }}^{{q*}} = \int\limits_\Omega {(\operatorname{div} y + f)} wdx + \int\limits_\Omega {(y - A\nabla {v})} \cdot \nabla wdx - \frac{1}{{q{\text{*}}}}\left\| {\nabla w} \right\|_{{A,q*,\Omega }}^{{q*}}{\kern 1pt} .$

Вследствие (4.2) получаем оценку

${{{\mathbf{m}}}_{q}}(e) \leqslant \mathop {sup}\limits_{w \in {{{\mathop W\limits^ \circ }}^{{1,q*}}}(\Omega )} \left\{ {({{\mathcal{R}}_{y}} + {{{\left\| {A\nabla {v} - y} \right\|}}_{{{{A}^{{ - 1}}},q,\Omega }}}){{{\left\| {\nabla w} \right\|}}_{{A,q*,\Omega }}} - \frac{1}{{q{\text{*}}}}\left\| {\nabla w} \right\|_{{A,q,\Omega }}^{{q*}}} \right\},$

где ${{\mathcal{R}}_{y}}: = {{C}_{{A,q*}}}(\Omega ){{\left\| {\operatorname{div} y + f} \right\|}_{{q,\Omega }}}$, а постоянная определяется неравенством

В качестве оценки этой постоянной можно взять ${{C}_{{A,q}}}(\Omega ) \leqslant \lambda _{1}^{{ - 1/2}}{{C}_{{q*}}}(\Omega )$ (см. (3.11)). Оценивая супремум, получаем мажоранту для меры отклонения от $u$, аналогичную (3.12)

${{{\mathbf{m}}}_{q}}(e) \leqslant \frac{1}{q}\mathop {({{\mathcal{R}}_{y}} + {{{\left\| {A\nabla {v} - y} \right\|}}_{{{{A}^{{ - 1}}},q,\Omega }}})}\nolimits^q .$

Соответствующие обобщения других, ранее полученных оценок для уравнений более общего, чем (4.1) вида (и других краевых условий), можно построить при помощи аналогичных рассуждений.

Список литературы

Repin S. A posteriori error estimation for nonlinear variational problems by duality theory // Zapiski Nauchnih Seminarov, V.A. Steklov Mathematical Institute (POMI). 1997. V. 243. P. 201–214.
Repin S. A posteriori error estimation for variational problems with uniformly convex functionals // Math. Comp. 2000. V. 69 (230). P. 481–500.
Repin S. A posteriori estimates for partial differential equations. Berlin: Walter de Gruyter GmbH & Co. KG, 2008.
Matculevich S., Repin S. Estimates of the distance to the exact solution of parabolic problems based on local Poincaré type inequalities // Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklova. 2014. V. 425. № 1. P. 7–34.
Repin S. Estimates of deviation from exact solutions of initial-boundary value problems for the heat equation // Rend. Mat. Acc. Lincei. 2002. V. 13. P. 121–133.
Репин C.И. Двусторонние оценки отклонения от точного решения для равномерно эллиптических уравнений // Труды С.-Петербургского математического общества. 2001. Т. 9. С. 148–179 (English translation: Repin S. Two-sided estimates of deviation from exact solutions of uniformly elliptic equations // Amer. Math. Soc. Transl. 2003. Series 2. V. 209. P. 143–171).
Repin S., Sauter S. Functional A Posteriori Estimates for the Reaction-Diffusion Problem // C. R. Acad. Sci. Paris. 2006. Ser. 1. V. 343. P. 349–354.
Репин С.И., Фролов М.Е. Апостериорные оценки погрешности приближенных решений краевых задач эллиптического типа // Ж. вычисл. матем. и матем. физ. 2002. Т. 42. № 12. С. 1704–1716.
Repin S., Sauter S., Smolianski A. Two-sided a posteriori error estimates for mixed formulations of elliptic problems // SIAM J. Num. Analysis. 2007. V. 45. P. 928–945.
Repin S., Tomar S. Guaranteed and robust error bounds for nonconforming approximations of elliptic problems // IMA J. Numer. Anal. 2011. V. 31. № 2. P. 597–615.
Ainsworth M., Oden J.T. A Posteriori Error Estimation in Finite Element Analysis. New York: John Wiley & Sons, 2000.
Verfürth R. A Review of A Posteriori Error Estimation and Adaptive Mesh-Refinement Techniques. Stuttgart: Wiley-Teubner, 1996.
Bangerth W., Rannacher R. Adaptive finite element methods for differential equations. Berlin: Birkhäuser, 2003.
Eriksson K., Estep D., Hansbo P., Johnson C. Introduction to adaptive methods for differential equations // Acta Numerica. 1995. P. 105–158.
Babuška I., Rheinboldt W.C. Error estimates for adaptive finite element computations // SIAM J. Numer. Anal. 1978. V. 15. P. 736–754.
Babuška I., Rheinboldt W.C. A-posteriori error estimates for the finite element method // Int. J. Numer. Meth. Engrg. 1978. V. 12. P. 1597–1615.
Ainsworth M., Oden J.T. A unified approach to a posteriori error estimation using element residual methods // Numer. Math. 1993. V. 65. P. 23–50.
Babuška I., Strouboulis T. The Finite Element Method and its Reliability. Oxford: Clarendon Press, 2001.
Carstensen C. A posteriori estimate for the mixed finite element method // Math. Comput. 1997. V. 66. № 218. P. 465–476.
Carstensen C. Quasi-interpolation and a posteriori error analysis of finite element methods // Mathematical Modelling in Numerical Analysis. 1999. V. 33. № 6. P. 1187–1202.
Carstensen C., Verfürth R. Edge residuals dominate a posteriori error estimates for low order finite element methods // SIAM J. Numer. Anal. 1999. V. 36. № 5. P. 1571–1587.
Mali O., Nettaanmäki P., Repin S. Accuracy verification methods. Theory and Algorithms Berlin: Springer, 2014.
Simader C.G., Sohr H. The Dirichlet Problem for the Laplacian in bounded and unbounded domains. Pitman Research Notes in Mathematical Series. V. 360. Harlow: Addison Wesley Longman Ltd., 1996.
Simader C.G., Sohr H., Varnhorn W. Necessary and sufficient conditions for the existence of Helmholtz decompositions in general domains // Ann Univ Ferrara. 2014. V. 60. P. 245–262.
Evans L. Partial differential equations. Providence, Rhode Island: American Mathematical Society, 1998.
Ladyzhenskaya O.A. The boundary value problems of mathematical physics. New York: Springer-Verlag, 1985.
Mizuguchi M., Tanaka K., Sekine K., Oishi S. Estimation of Sobolev embedding constant on a domain dividable into bounded convex domains // Journal of Inequalities and Applications. 2017. V. 299.
Acosta G., Durán R.G. An optimal Poincaré inequality in ${{L}_{1}}$ for convex domains //Proc. Amer. Math. Soc. 2004. V. 132. P. 195–202.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал