Журнал вычислительной математики и математической физики, 2020, T. 60, № 6, стр. 975-984

Асимптотическое решение коэффициентных обратных задач для уравнений типа Бюргерса

В. Т. Волков¹, Н. Н. Нефедов^1, *

¹ МГУ, физический факультет
119991 Москва, Ленинские горы, Россия

Поступила в редакцию 31.10.2019
После доработки 31.10.2019
Принята к публикации 11.02.2020

DOI: 10.31857/S0044466920060125

Аннотация

Для сингулярно возмущенного уравнения реакция-диффузия-адвекция, называемого в приложениях уравнением типа Бюргерса и имеющего периодическое по времени решение с внутренним переходным слоем, асимптотический анализ применен при решении некоторых обратных задач восстановления параметров модели (определения коэффициента линейного усиления и граничных условий) по известной информации о наблюдаемом решении прямой задачи на заданном временном отрезке (периоде). Проведены численные эксперименты, демонстрирующие эффективность предлагаемого подхода. Библ. 26. Фиг. 3.

Ключевые слова: сингулярно возмущенная задача, уравнение типа реакция-диффузия-адвекция, внутренний слой, коэффициентная обратная задача.

1. ВВЕДЕНИЕ

В работе показана возможность применения методов асимптотического анализа при решении обратных задач для нелинейного сингулярно возмущенного уравнения типа Бюргерса (уравнения реакция-диффузия-адвекция) с периодическими по времени коэффициентами. В частности, рассмотрены задачи о восстановлении коэффициента линейного усиления (коэффициента реакции), описывающего свойства среды, и граничных условий по известной информации о наблюдаемом решении прямой задачи на некотором временном интервале (периоде). Подобные задачи возникают в газовой динамике, в нелинейной теории волн, биофизике, химической кинетике и многих других практических приложениях и описываются нелинейными параболическими уравнениями с малыми параметрами при производных (см., например, [1] и ссылки в этой работе). Эти задачи интенсивно изучаются в связи с тем, что они выступают в качестве математических моделей, выявляющих основные механизмы, определяющие поведение и более сложных моделей нелинейной теории волн. К этому классу задач относятся уравнения Бюргерса [2]–[4] и уравнения типа Бюргерса [5]–[10].

Особенностью задач указанного типа является то, что их решения могут содержать узкие пограничные и/или внутренние слои (стационарные и/или движущиеся фронты). Как следствие, эти задачи чрезвычайно сложны для численного решения. Однако наличие малого параметра приводит к появлению двух противоположных эффектов: с одной стороны, чем меньше этот параметр, тем более неустойчивое численное решение будет получено; с другой стороны, чем меньше этот параметр, тем более точную априорную информацию о решении можно извлечь с помощью асимптотического анализа. Эти два факта дают возможность объединить асимптотический и численный подходы для построения эффективных методов решения как прямых, так и соответствующих обратных задач. Асимптотико-численный анализ сингулярно возмущенных задач типа реакция-диффузия-адвекция может быть найден, например, в работах [11]–[15]. Обратные коэффициентные задачи широко исследуются в связи с многими приложениями (см., например, [16]–[19] и ссылки в этих работах).

Идея использования асимптотического анализа при построении эффективных численных методов решения обратных задач для сингулярно возмущенных уравнений была впервые реализована в работе [20], где рассматривалась коэффициентная обратная задача для нелинейного сингулярно возмущенного уравнения типа реакция-диффузия-адвекция. В указанной работе использовался подход, основанный на строгом асимптотическом анализе и заключающийся в выделении априорной информации о положении движущегося фронта в решении прямой задачи и пограничных слоях в решении сопряженной задачи для построения специальной адаптированной сетки [21]–[23]. Предложенный метод позволил значительно оптимизировать численный счет и существенно повысить стабильность решения соответствующей обратной задачи. В то же время нужно отметить, что применение стандартных методов решения обратных коэффициентных задач, даже использующих эффективные численные методы и априорную информацию о структуре решения, с нашей точки зрения, не является достаточно эффективным подходом. В настоящей работе предлагается и иллюстрируется концепция асимптотического решения обратных коэффициентных задач для сингулярно возмущенных уравнений, решения которых содержат переходные слои.

Важной особенностью асимптотического подхода к исследованию нелинейных дифференциальных уравнений с малыми параметрами является то, что асимптотический анализ позволяет свести исходную нелинейную сингулярно возмущенную задачу к набору более простых задач, которые не содержат малых параметров и имеют меньшую пространственную размерность (а иногда и вовсе содержат не дифференциальные, а алгебраические уравнения), получив при этом достаточно точное качественное и количественное описание решения. Таким образом, кроме оптимизации численных расчетов, применение асимптотического анализа дает возможность установить более простые связи между входными данными и параметрами обратной задачи (коэффициенты в уравнении, граничные и начальные условия и т.п.), которые необходимо определить, что позволяет существенно упростить процедуру решения обратных задач.

Эти идеи были применены в работах [24], [25] и заключались в том, что если имеется экспериментальная возможность фиксировать параметры движущегося фронта (фронта ударной волны, фронта реакции или пламени и т.д.) в некоторый момент времени, то методы асимптотического анализа позволяют с заданной точностью свести исходную обратную задачу для уравнения в частных производных к существенно более простой задаче, связывающей измеренные параметры фронта с коэффициентом в уравнении, который необходимо восстановить. При этом вопрос об определении неизвестного коэффициента сводился к простому дифференцированию наблюдаемого решения прямой задачи в фиксированный момент времени.

Структура работы такова. В разд. 2 приведена постановка прямой коэффициентной задачи и сформулирована теорема существования решения и его асимптотическое приближение, в рамках условий которой решается обратная задача. В разд. 3 приводится и обсуждается ее асимптотическое решение. В разд. 4 описывается численный эксперимент, демонстрирующий эффективность предложенного подхода.

2. ОСНОВНЫЕ РЕЗУЛЬТАТЫ АСИМПТОТИЧЕСКОГО ИССЛЕДОВАНИЯ ПРЯМОЙ ЗАДАЧИ

Рассмотрим прямую задачу для нелинейного сингулярно возмущенного уравнения типа реакция-диффузия-адвекция, называемого в приложениях уравнением типа Бюргерса, и применяемого, например, в нелинейной теории волн для описания квадратично нелинейных волн в среде без дисперсии с линейным усилением (см. [8]–[10]). А именно,

(1)

$\begin{gathered} \varepsilon \left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} - \frac{{\partial u}}{{\partial t}}} \right) = - u \cdot \frac{{\partial u}}{{\partial x}} + q(t) \cdot u, \\ (x,t) \in D: = \{ x \in ( - 1,1);t \in \mathbb{R}\} , \\ u( - 1,t) = {{u}_{{{\text{left}}}}}(t),\quad u(1,t) = {{u}_{{{\text{right}}}}}(t),\quad t \in \mathbb{R}, \\ u(x,0) = u(x,t + T),\quad x \in [ - 1,1],\quad t \in \mathbb{R}, \\ \end{gathered} $

где $\varepsilon $ – малый параметр $(0 < \varepsilon \ll 1)$, а функции $q(t)$, ${{u}_{{{\text{left}}}}}(t)$ и ${{u}_{{{\text{right}}}}}(t)$ – достаточно гладкие и T-периодические по переменной $t$. Для этой задачи будет сформулирована теорема существования решения, в рамках которой будет поставлена обратная коэффициентная задача и получено ее асимптотическое решение.

Рассматриваемая нами прямая задача (1) является частным случаем рассмотренной в [11]:

(2)

$\begin{gathered} \varepsilon \left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} - \frac{{\partial u}}{{\partial t}}} \right) = A(u,x,t)\frac{{\partial u}}{{\partial x}} + B(u,x,t), \\ (x,t) \in \mathcal{D}: = \{ x \in ( - 1,1);t \in \mathbb{R}\} , \\ u( - 1,t) = {{u}_{{{\text{left}}}}}(t),\quad u(1,t) = {{u}_{{{\text{right}}}}}(t),\quad t \in \mathbb{R}, \\ u(x,0) = u(x,t + T),\quad x \in [ - 1,1],\quad t \in \mathbb{R}, \\ \end{gathered} $

где $\varepsilon $ – малый параметр $(0 < \varepsilon \ll 1)$, а функции $A(u,x,t)$, $B(u,x,t)$ (в (1) $A(u,x,t) = - u$, $B(u,x,t) = q(t) \cdot u$), ${{u}_{{{\text{left}}}}}(t)$ и ${{u}_{{{\text{right}}}}}(t)$ – достаточно гладкие и T-периодические по переменной $t$. В работе [11] при определенных условиях на входящие в задачу функции было доказано существование периодического решения, его устойчивость, а также получено асимптотическое приближение решения по параметру $\varepsilon $. Поэтому ниже мы приведем основной результат работы [11] для задачи (2), который будет применен при формулировке условий теоремы существования решения прямой задачи (1), а также использован для решения обратной задачи для (1).

2.1. Условия, теорема существования решения задачи (2)

Если положить $\varepsilon = 0$ в уравнении (2), получим так называемое вырожденное уравнение

(3)

$A(u,x,t)\frac{{\partial u}}{{\partial x}} + B(u,x,t) = 0,$

где $t$ – параметр. Уравнение (3) – обыкновенное дифференциальное уравнение первого порядка и рассматривается с одним из следующих начальных условий из задачи (2):

(4)

$u( - 1,t) = {{u}_{{{\text{left}}}}}(t)\quad {\text{для}}\quad t \in R,$

(5)

$u(1,t) = {{u}_{{{\text{right}}}}}(t)\quad {\text{для}}\quad t \in R.$

Относительно этих начальных задач мы предполагаем следующее.

Условие 1. Задачи (3),(4) и (3),(5) имеют решения $u = {{\varphi }^{l}}(x,t)$ и $u = {{\varphi }^{r}}(x,t)$, определенные при $(x,t) \in \bar {\mathcal{D}}$, $T$-периодические по $t$ и удовлетворяющие неравенствам

$\begin{gathered} {{\varphi }^{l}}(x,t) < {{\varphi }^{r}}(x,t)\quad {\text{для}}\quad (x,t) \in \bar {\mathcal{D}}, \\ A({{\varphi }^{r}}(x,t),x,t) < 0,\quad A({{\varphi }^{l}}(x,t),x,t) > 0\quad {\text{для}}\quad (x,t) \in \bar {\mathcal{D}}. \\ \end{gathered} $

Для формулировки следующего условия введем функцию $I(x,t)$:

$I(x,t): = \int\limits_{{{\varphi }^{l}}(x,t)}^{{{\varphi }^{r}}(x,t)} {A(u,x,t)du} .$

Условие 2. Пусть уравнение

(6)

$I(x,t) = 0$

имеет гладкое $T$-периодическое решение $x = {{x}_{0}}(t)$, удовлетворяющее следующим неравенствaм:

$ - 1 < {{x}_{0}}(t) < 1\quad {\text{при}}\quad t \in R,$

$\int\limits_{{{\varphi }^{l}}({{x}_{0}}(t),t)}^s {A(u,{{x}_{0}}(t),t)du > 0} \quad {\text{для}}\;{\text{любого}}\quad s \in ({{\varphi }^{l}}({{x}_{0}}(t),t),{{\varphi }^{r}}({{x}_{0}}(t),t))\quad {\text{и}}\quad t \in R.$

Условие 3. Корень ${{x}_{0}}(t)$ уравнения (6) удовлетворяет неравенству

$\frac{{\partial I}}{{\partial x}}({{x}_{0}}(t),t) < 0\quad {\text{при}}\quad t \in R.$

Из условия 3, в частности, следует, что ${{x}_{0}}(t)$ – простой корень уравнения (6) при $t \in R$.

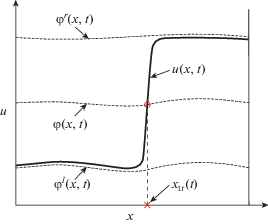
В работе [11] показано, что при сформулированных выше условиях задача (2) имеет T-периодическое по переменной $t$ решение вида периодически движущегося фронта: на интервале $( - 1,1)$ существует точка ${{x}_{{{\text{tr}}}}}(t;\varepsilon )$, движущаяся по периодическому во времени закону, в окрестности которой наблюдается узкий внутренний переходный слой. А именно, для всех $t$ слева от указанной точки (при $ - 1 < x < {{x}_{{{\text{tr}}}}}(t,\varepsilon )$) решение близко к ${{\varphi }^{l}}(x,t)$, а справа (при ${{x}_{{{\text{tr}}}}}(t,\varepsilon ) < x < 1$) – к ${{\varphi }^{r}}(x,t)$, определенных в условии 1. В окрестности ${{x}_{{{\text{tr}}}}}(t;\varepsilon )$ возникает область быстрого изменения решения – внутренний переходный слой, а такие решения называются контрастными структурами.

Заметим, что положение точки перехода заранее неизвестно, и его можно определить как точку пересечения решения и некоторого уровня ${{\varphi }^{{(0)}}}(x,t)$: ${{\varphi }^{l}}(x,t) < {{\varphi }^{{(0)}}}(x,t) < {{\varphi }^{r}}(x,t)$. Пример решения, имеющего внутренний слой, приведен на фиг. 1.

Фиг. 1.

Внутренний слой (движущийся фронт) в фиксированный момент времени $t$.

Обратная задача будет заключаться в определении неизвестного коэффициента $q(t)$, при котором фронт будет двигаться по заданному временному закону или этот коэффициент находится по наблюдению траектории движения фронта. Показано, что для рассматриваемого класса уравнений коэффициентная обратная задача сводится к существенно более простой задаче – линейному алгебраическому уравнению, связывающему наблюдаемое положение движущегося фронта с коэффициентами в уравнении и граничными условиями. Таким образом, если имеется возможность наблюдения траектории движения фронта на временном периоде, то вопрос об определении неизвестного коэффициента уравнения или граничного режима сводится к набору простых алгебраических операций.

Основным результатом работы [11] является следующий.

Теорема 1. Пусть выполнены условия 1–3. Тогда для достаточно малых $\varepsilon $ существует асимптотически устойчивое по Ляпунову решение $u(x,t,\varepsilon )$ задачи (2) такое, что для любого сколь угодно малого, но фиксированного $\nu $ имеют место предельные соотношения

$\mathop {lim}\limits_{\varepsilon \to 0} u(x,t,\varepsilon ) = \left\{ \begin{gathered} {{\varphi }^{l}}(x,t),\quad x \in [0,{{x}_{0}}(t) - \nu ],\quad t \in R, \hfill \\ {{\varphi }^{r}}(x,t),\quad x \in [{{x}_{0}}(t) + \nu ,1],\quad t \in R. \hfill \\ \end{gathered} \right.$

Более того, ${{x}_{{{\text{tr}}}}}(t;\varepsilon ) - {{x}_{0}}(t) = O(\varepsilon ),$ $t \in R$, $u(x,t,\varepsilon ) - {{\varphi }^{l}}(x,t) = O(\varepsilon )$ для $x \in [0,{{x}_{0}}(t) - \nu ],$ $t \in R$ и $u(x,t,\varepsilon ) - {{\varphi }^{r}}(x,t) = O(\varepsilon )$ для $x \in [{{x}_{0}}(t) + \nu ,1],$ $t \in R$.

Замечание 1. В работе [11] получено более подробное описание структуры переходного слоя и более точное асимптотическое приближение решения.

2.2. Теорема существования решения задачи (1)

Функции ${{\varphi }^{l}}(x,t)$ и ${{\varphi }^{r}}(x,t)$ в задаче (1) определяются как решения следующих задач Коши:

(7)

$\begin{gathered} {{\varphi }^{l}}(x,t){\kern 1pt} :\quad - {\kern 1pt} u\frac{{du}}{{dx}} + q(t) \cdot u = 0,\quad u( - 1,t) = {{u}_{{{\text{left}}}}}(t); \\ {{\varphi }^{r}}(x,t){\kern 1pt} :\quad - {\kern 1pt} u\frac{{du}}{{dx}} + q(t) \cdot u = 0,\quad u(1,t) = {{u}_{{{\text{right}}}}}(t), \\ \end{gathered} $

и находятся в явном виде:

(8)

$\begin{gathered} {{\varphi }^{l}}(x,t) = q(t) \cdot (x + 1) + {{u}_{{{\text{left}}}}}(t), \\ {{\varphi }^{r}}(x,t) = q(t) \cdot (x - 1) + {{u}_{{{\text{right}}}}}(t). \\ \end{gathered} $

В силу условия 1 потребуем выполнения неравенств

(9)

$\begin{gathered} {{\varphi }^{l}}(x,t) = q(t) \cdot (x + 1) + {{u}_{{{\text{left}}}}}(t) < 0, \\ {{\varphi }^{r}}(x,t) = q(t) \cdot (x - 1) + {{u}_{{{\text{right}}}}}(t) > 0 \\ \end{gathered} $

при $(x,t) \in \bar {D}: = \{ x \in [ - 1,1],t \in \mathbb{R}\} $. Несложные вычисления показывают, что эти неравенства выполняются при следующих условиях.

Условие 4. Пусть

${{u}_{{{\text{right}}}}}(t) > 0,\quad {{u}_{{{\text{left}}}}}(t) < 0,\quad 2q(t) + {{u}_{{{\text{left}}}}}(t) < 0,\quad - {\kern 1pt} 2q(t) + {{u}_{{{\text{right}}}}}(t) > 0,\quad t \in \mathbb{R}.$

Функция

(10)

$I(x,t) = \int\limits_{{{\varphi }^{l}}(x,t)}^{{{\varphi }^{r}}(x,t)} \,A(u,x,t)du,$

определенная в условии 2 теоремы 1 в случае задачи (1) принимает вид

(11)

$I(x,t) = \int\limits_{{{\varphi }^{l}}(x,t)}^{{{\varphi }^{r}}(x,t)} \, - {\kern 1pt} udu = \frac{1}{2}({{\varphi }^{l}}(x,t) + {{\varphi }^{r}}(x,t))({{\varphi }^{l}}(x,t) + {{\varphi }^{r}}(x,t)).$

Таким образом, уравнение

(12)

$I(x,t) = 0,$

определяющее главный член асимптотики положения фронта ${{x}_{0}}(t)$, с учетом формул (8) преобразуется к виду

$\frac{1}{2} \cdot (2q(t) + {{u}_{{{\text{left}}}}}(t) - {{u}_{{{\text{right}}}}}(t)) \cdot (2q(t) \cdot x + {{u}_{{{\text{left}}}}}(t) + {{u}_{{{\text{right}}}}}(t)) = 0.$

В силу условия 4 первая скобка отрицательна при всех $t \in R$, поэтому ${{x}_{0}}(t)$ определяется из уравнения

(13)

$2q(t) \cdot x + {{u}_{{{\text{left}}}}}(t) + {{u}_{{{\text{right}}}}}(t) = 0.$

Условие 5. Пусть также для всех $t \in \mathbb{R}$ имеет место неравенство $q(t) > 0$ и

$ - 1 < \frac{{{{u}_{{{\text{left}}}}}(t) + {{u}_{{{\text{right}}}}}(t)}}{{2q(t)}} < 1.$

Это требование обеспечит выполнение условий 2 и 3, в частности, обеспечивает существование T-периодического решения (13)

(14)

${{x}_{0}}(t) = - \frac{{{{u}_{{{\text{left}}}}}(t) + {{u}_{{{\text{right}}}}}(t)}}{{2q(t)}}$

при $ - 1 < {{x}_{0}}(t) < 1$ для всех $t \in \mathbb{R}$.

Кроме того,

(15)

$\frac{{\partial I}}{{\partial x}}({{x}_{0}}(t),t) = (2q(t) + {{u}_{{{\text{left}}}}}(t) - {{u}_{{{\text{right}}}}}(t))q(t) < 0\quad {\text{при}}\;{\text{всех}}\quad t \in \mathbb{R}.$

Потребуем также выполнения дополнительного условия, позволяющего избежать рассмотрения специальных ситуаций при решении обратной задачи.

Условие 6. Пусть также при всех $t \in \mathbb{R}$ выполнено неравенство

$\left| {{{u}_{{{\text{left}}}}}(t) + {{u}_{{{\text{right}}}}}(t)} \right| \ne 0.$

Таким образом, имеет место следующая теорема существования решения прямой задачи (1), являющаяся следствием теоремы 1 при перечисленных выше условиях.

Теорема 2. Пусть выполнены условия 4–6. Тогда для достаточно малых $\varepsilon $ существует асимптотически устойчивое по Ляпунову решение $u(x,t,\varepsilon )$ задачи (1) такое, что для любого сколь угодно малого, но фиксированного $\nu $ выполнены предельные соотношения

Более того, при всех $t \in R$ имеют место оценки ${{x}_{{{\text{tr}}}}}(t;\varepsilon ) - {{x}_{0}}(t) = O(\varepsilon ),$ а также $u(x,t,\varepsilon ) - {{\varphi }^{l}}(x,t) = O(\varepsilon )$ для $x \in [0,{{x}_{0}}(t) - \nu ]$ и $u(x,t,\varepsilon ) - {{\varphi }^{r}}(x,t) = O(\varepsilon )$ для $x \in [{{x}_{0}}(t) + \nu ,1]$.

Сделаем важное для формулировки основного результата обратной задачи замечание.

Замечание 2. Из доказательства теорем 1 и 2 также следует непрерывная зависимость решения задачи (1) от малых возмущений коэффициента $q(t)$, т.е. если в задаче (1) вместо $q(t)$ стоит зависящий гладким образом от малых параметров $\epsilon $ и $\delta $ коэффициент $\tilde {q}(t,\varepsilon ,\delta )$, причем $\tilde {q}(t,\varepsilon ,\delta ) - q(t) = O(\varepsilon + \delta )$, то имеет место следующий результат (аналог теоремы 2):

${{x}_{{{\text{tr}}}}}(t;\varepsilon ,\delta ) - {{x}_{0}}(t) = O(\varepsilon + \delta ),$ ${\text{а}}\;{\text{также}}$ $u(x,t,\varepsilon ,\delta ) - {{\varphi }^{{( - )}}}(x,t) = O(\varepsilon + \delta )$ для $x \in [0,{{x}_{0}}(t) - \nu ]$ и $u(x,t,\varepsilon ,\delta ) - {{\varphi }^{{( + )}}}(x,t) = O(\varepsilon + \delta )$ для $x \in [{{x}_{0}}(t) + \nu ,1]$ ${\text{при}}\;{\text{всех}}\;t \in R$.

Аналогичный результат имеет место и для малых возмущений граничных условий.

3. АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ

Продемонстрируем эффективность развиваемого подхода в определении характеристик математической модели, описываемой задачей (1). Постановку обратной задачи можно записать в операторном виде:

$A(q) = f,$

где $A$: $C(q(t):t \in R) \to C(f(t):t \in R)$.

В данной работе точный оператор $A$ задачи мы заменяем на приближенный оператор ${{A}_{\varepsilon }}$: $C \to C$, определяемый формулой (14). Из теоремы 2 следует, что ${{\left\| {A - {{A}_{\varepsilon }}} \right\|}_{C}} = O(\varepsilon )$. В результате решается следующая задача:

${{A}_{\varepsilon }}({{q}_{\varepsilon }}) = f.$

Мы предполагаем, что имеется возможность наблюдения положения фронта, т.е. $f(t) = {{x}_{{{\text{tr}}}}}(t;\varepsilon )$ на интервале времени, равном периоду $T$. При этом мы предполагаем, что условия существования решения задачи (1) выполнены.

3.1. Асимптотическое решение обратной коэффициентной задачи определения коэффициента линейного усиления

Одним из результатов асимптотического анализа, проведенного в [11], является равномерная по $t \in R$ оценка

(16)

$\left| {{{x}_{{{\text{tr}}}}}(t;\varepsilon ) - {{x}_{0}}(t)} \right| = O(\varepsilon ).$

Поэтому уравнение (13), определяющее ${{x}_{0}}(t)$, можно переписать в виде

(17)

$2q(t) \cdot {{x}_{{{\text{tr}}}}}(t;\varepsilon ) + {{u}_{{{\text{left}}}}}(t) + {{u}_{{{\text{right}}}}}(t) = O(\varepsilon ).$

Таким образом, если имеется возможность наблюдения положения фронта ${{x}_{{{\text{tr}}}}}(t;\varepsilon ) = f(t)$ на интервале времени, равном периоду $T$, то коэффициентная обратная задача для уравнения типа Бюргерса сводится к существенно более простой задаче – линейному алгебраическому уравнению, связывающему наблюдаемое положение движущегося фронта с коэффициентами в уравнении и граничными условиями. Решение этого уравнения относительно $q(t)$, в силу замечания 2, является асимптотическим решением обратной коэффициентной задачи для (1) с точностью $O(\varepsilon )$.

Так как наблюдаемое положение фронта известно, как правило, с некоторой ошибкой порядка $O(\delta )$

(18)

${{x}_{{{\text{tr}}}}}(t;\varepsilon ) = {{x}_{{{\text{obs}}}}}(t) + O(\delta ),\quad t \in [0,T],$

то (17) можно переписать в виде

(19)

$2q \cdot {{x}_{{{\text{obs}}}}}(t) + {{u}_{{{\text{left}}}}}(t) + {{u}_{{{\text{right}}}}}(t) = O(\varepsilon ) + O(\delta ).$

Таким образом, из этого уравнения имеем, что

(20)

$q(t,\varepsilon ,\delta ) = - \frac{{{{u}_{{{\text{left}}}}}(t) + {{u}_{{{\text{right}}}}}(t)}}{{2{{x}_{{{\text{obs}}}}}(t)}}$

в силу замечания 2 является асимптотическим решением обратной коэффициентной задачи (1) с точностью $O(\varepsilon + \delta )$.

Замечание 3. Уравнение (17) дает возможность асимптотического решения обратной задачи граничного управления: определения одной из граничных функций ${{u}_{{{\text{left}}}}}(t)$ или ${{u}_{{{\text{right}}}}}(t)$ при условии, что две другие $q$ и ${{x}_{{{\text{obs}}}}}$ известны или заданы (точно или приближенно).

4. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

В качестве модельной задачи, иллюстрирующей возможность и эффективность применения предложенного подхода при конечных значениях малого параметра и погрешностях входных данных, рассмотрим задачу (1) для следующего набора функций и параметров

(21)

${{q}^{{{\text{model}}}}}(t) = 5 + cost,\quad {{u}_{{{\text{left}}}}}(t) = - 20 + sint,\quad {{u}_{{{\text{right}}}}}(t) = 15 - cost,\quad T = 2\pi ,\quad \varepsilon = {{10}^{{ - 1}}}.$

Наш вычислительный эксперимент предполагает получение входных данных (симуляцию входных данных обратной задачи) – наблюдаемого положения внутреннего слоя ${{x}_{{{\text{obs}}}}}(t) = f(t)$ на основании решения прямой задачи (1) с набора функций и параметров (21). Задача (1) численно решается как начальная задача на стабилизацию к периодическому режиму. Возможность использования такого подхода следует из того, что при наших условиях теоремы 2 решение задачи (1) асимптотически устойчиво по Ляпунову. Подробно численный алгоритм решения периодической задачи (1), использующий данные асимптотического анализа, и применение его для симуляции данных рассматриваемой обратной задачи описан в работах [21] и [26], поэтому мы не приводим его здесь. Отметим, что для численного решения этим методом прямой задачи (1) нам необходимо знать решение $u(x,t)$ в начальный момент времени $u(x,0) \equiv {{u}_{{{\text{init}}}}}(x)$. В качестве начального условия ${{u}_{{{\text{init}}}}}(x,\varepsilon )$ можно, как решение следующей стационарной задачи:

$\begin{gathered} \varepsilon \frac{{{{\partial }^{2}}g}}{{\partial {{x}^{2}}}} = - g\frac{{\partial g}}{{\partial x}} + q(0)g,\quad x \in ( - 1,1), \\ g( - 1) = {{\left. {{{u}_{{{\text{left}}}}}(t)} \right|}_{{t = 0}}},\quad g(1) = {{\left. {{{u}_{{{\text{right}}}}}(t)} \right|}_{{t = 0}}}. \\ \end{gathered} $

Решение которой близко к решению задачи (1) и может быть найдено с помощью счета на установление. В качестве начального условия счета на установление была взята функция

Заметим, что функции ${{g}_{0}}(x)$ и начальное положение фронта реакции ${{x}_{{00}}}$ используются только для того, чтобы смоделировать входные данные обратной задачи ${{x}_{{t.p.}}}(t) \equiv {{f}_{\delta }}(t)$ и не влияют на решение соответствующей обратной задачи.

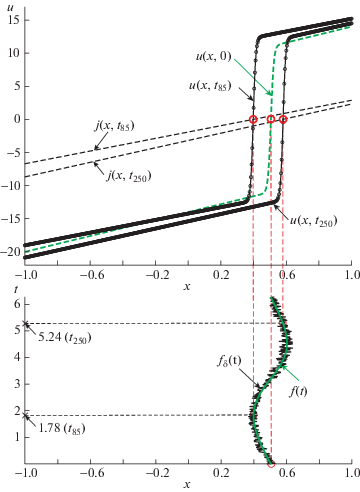
На фиг. 2 представлен результат симуляции входных данных обратной задачи, т.е. функции $f(t)$, для набора параметров (21).

Фиг. 2.

Пример симуляции данных $f(t)$ обратной задачи (1)–(18) для $t \in [{{t}_{0}},T] \equiv [0,2\pi ]$, $q(t) = 5 + cost$, ${{u}_{{{\text{left}}}}}(t) = - 20 + sint$, ${{u}_{{{\text{right}}}}}(t) = 15 - cost$, $\varepsilon = {{10}^{{ - 1.0}}}$, $\delta = 7\% $, с параметрами сеток: $N = 500$, $M = 300$.

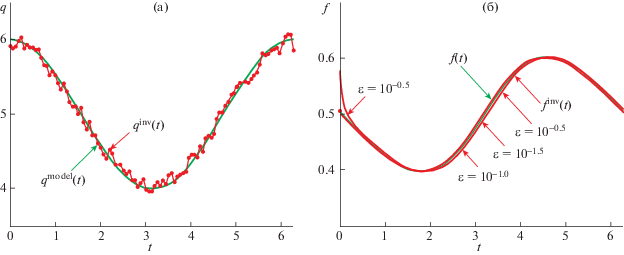
В предыдущем разделе было показано, как методы асимптотического анализа позволили свести постановку исходной обратной задачи для (1) к уравнению (20), которое непосредственно связывает искомый коэффициент $q(t)$ с данными обратной задачи $f(t)$. В результате алгоритм нахождения коэффициента ${{q}^{{{\text{inv}}}}}(t)$ из уравнения (20) для рассматриваемого набора функций (21) примет вид

(22)

${{q}^{{{\text{inv}}}}}(t) = - \frac{{{{u}_{{{\text{left}}}}}(t) + {{u}_{{{\text{right}}}}}(t)}}{{2f(t)}}.$

Результаты расчетов представлены на фиг. 3 и демонстрируют эффективность предложенного в работе подхода. Результаты расчетов показывают, что предложенный подход работает и для фиксированных значений малого параметра ($\varepsilon = {{10}^{{ - 0.5}}}$) и погрешностей входных данных.

Фиг. 3.

(a) – функция ${{q}^{{{\text{inv}}}}}(t)$ восстановлена для симулированных данных ${{f}_{\delta }}(t)$ ($\varepsilon = {{10}^{{ - 1.0}}}$, $\delta = 2\% $), (б) – сравнение функции ${{f}^{{{\text{inv}}}}}(t)$ как результат решения прямой задачи для функции $q(t) \equiv {{q}^{{{\text{inv}}}}}(t)$ (в случае симуляции входных данных ${{f}_{\delta }}(t)$, $\delta = 0\% $, для $\varepsilon = {{10}^{{ - 0.5}}}$, $\varepsilon = {{10}^{{ - 1.0}}}$, $\varepsilon = {{10}^{{ - 1.5}}}$ соответственно) с “точными” данными.

5. ЗАКЛЮЧЕНИЕ

В работе продемонстрировано дальнейшее развитие асимптотико-численных методов решения прямых и обратных задач с пограничными и внутренними слоями. Этот подход применен к новому классу периодических по времени задач типа реакция-диффузия-адвекция с внутренними переходными слоями. Введена концепция асимптотического решения обратных коэффициентных задач. Этот подход продемонстрирован на обратной коэффициентной задаче. Для этого уравнения задача сводится к существенно более простой задаче – линейному алгебраическому уравнению, связывающему наблюдаемое положение движущегося фронта с коэффициентами в уравнении и граничными условиями. Это позволяет классифицировать исходную задачу как корректно поставленную обратную задачу. Нам представляется, что предлагаемый нами подход может быть применен к достаточно широкому классу задач с пограничными и внутренними слоями.

Авторы благодарны А.Г. Яголе и Д.В. Лукьяненко за обсуждение этой работы, способствовавшему ее улучшению, кроме того, выражают благодарность Д.В. Лукьяненко за проведение вычислительных экспериментов, иллюстрирующих эффективность развиваемого подхода.

Список литературы

Nefedov N. Comparison Principle for Reaction-Diffusion-Advection Problems with Boundary and Internal Layers // Lect. Notes in Comput. Sci. 2013. 8236. P. 62–72.
Burgers J.M. A mathematical model illustrating the theory of turbulence // Advances in Applied Mechanics. 1948. V. 1. P. 171–199.
Parker A. On the periodic solution of the Burgers equation: a unified approach // Proc. R. Soc. Lond. A. 1992. V. 438. P. 113–132.
Cole J.D. On a quasilinear parabolic equation occurring in aerodynamics // Quart. Appl. Math. 1951. V. 9. P. 225–236.
Malfliet W. Approximate solution of the damped Burgers equation // J. Phys. A: Math. Gen. 1993. V. 26. P. 723–728.
Fahmy E.S., Raslan K.R., Abdusalam H.A. On the exact and numerical solution of the time-delayed Burgers equation // Int. J. Comput. Math. 2008. V. 85. № 11. P. 1637–1648.
Rudenko O.V., Gurbatov S.N., Hedberg C.M. Nonlinear Acoustics Through Problems and Examples // Victoria, BC, Canada: Trafford, 2011.
Руденко О.В. Линеаризуемое уравнение для волн в диссипативных средах с модульной, квадратичной и квадратично-кубичной нелинейностями // ДАН. 2016. Т. 471. № 1. С. 23–27.
Руденко О.В. Модульные солитоны // ДАН. 2016. Т. 471. № 6. С. 451–454.
Nefedov N.N., Rudenko O.V. On front motion in a Burgers-type equation with quadratic and modular nonlinearity and nonlinear amplification // Doklady Mathematics. 2018. V. 97. P. 99–103.
Nefedov N., Recke L., Schneider K. Existence and asymptotic stability of periodic solutions with an interior layer of reaction-advection-diffusion equations // J. of Math. Analysis and Appl. 2013. V. 405. № 1. P. 90–103.
Антипов Е.А., Волков В.Т., Левашова Н.Т., Нефедов Н.Н. Решение вида движущегося фронта двумерной задачи реакция–диффузия // Моделирование и анализ информационных систем. 2017. Т. 24. № 3. С. 259–279.
Lukyanenko D., Nefedov N., Nikulin E., Volkov V. Use of Asymptotics for New Dynamic Adapted Mesh Construction for Periodic Solutions with an Interior Layer of Reaction-Diffusion-Advection Equations // Lect. Notes in Comput. Sci. 2017. 10187. P. 107–118.
Антипов Е.А., Левашова Н.Т., Нефедов Н.Н. Асимптотика движущегося фронта в задаче “реакция–диффузия–адвекция” // ЖВМ и МФ. 2014. Т. 54. № 10. С. 1594–1607.
Volkov V., Lukyanenko D., Nefedov N. Asymptotic-numerical method for the location and dynamics of internal layers in singular perturbed parabolic problems // Lect. Notes in Comput. Sci. 2017. 10187. P. 721–729.
Kabanikhin S.I. Definitions and examples of inverse and ill-posed problems // J. Inverse and Ill-Posed Problems. 2008. V. 16. № 4. P. 317–357.
Belishev M.I. Boundary control in reconstruction of manifolds and metrics (the BC method) // Inverse Problems. 1997. V. 12. № 5. P. 1–45.
Beilina L., Klibanov M.V. A globally convergent numerical method for a coefficient inverse problem // SIAM J. on Scientific Computing. 2008. V. 31. № 1. P. 478–509.
Kabanikhin S.I., Sabelfeld K.K., Novikov N.S., Shishlenin M.A. Numerical solution of an inverse problem of coeffcient recovering for a wave equation by a stochastic projection methods // Monte Carlo Methods and Applications. 2015. V. 21. № 3. P. 189–203.
Lukyanenko D., Shishlenin M., Volkov V. Solving of the coefficient inverse problems for a nonlinear singularly perturbed reaction-diffusion-advection equation with the final time data // Communications in Nonlinear Science and Numerical Simulation. 2018. V. 54. P. 233–247.
Волков В.Т., Лукьянеко Д.В., Нефедов Н.Н. Аналитико-численный подход к описанию периодических по времени движущихся фронтов в сингулярно возмущенных моделях реакция–диффузия–адвекция // ЖВМ и МФ. 2019. Т. 59. № 1. С. 50–62.
Lukyanenko D.V., Volkov V.T., Nefedov N.N. Dynamically adapted mesh construction for the efficient numerical solution of a singular perturbed reaction–diffusion–advection equation // Modeling and Analysis of Information Systems. 2017. V. 24. №. 3. P. 322–338.
Lukyanenko D., Nefedov N., Nikulin E., Volkov V.T. Use of asymptotics for new dynamic adapted mesh construction for periodic solutions with an interior layer of reaction–diffusion–advection equations // Lecture Notes in Computer Science. 2017. 10187. P. 107–118.
Lukyanenko D.V., Grigorev V.B., Volkov V.T., Shishlenin M.A. Solving of the coefficient inverse problem for a nonlinear singularly perturbed two-dimensional reaction-diffusion equation with the location of moving front data // Computers and Mathematics with Applications. 2019. V. 77. № 5. P. 1245–1254.
Лукьянеко Д.В., Волков В.Т., Нефедов Н.Н., Ягола А.Г. Применение асимптотического анализа для решения обратной задачи определения коэффициента линейного усиления в уравнении типа Бюргерса // Вестник МГУ. Серия 3. Физика. Астрономия. 2019. №. 2. P. 38–43.
Lukyanenko D.V., Shishlenin M.A., Volkov V.T. Asymptotic analysis of solving an inverse boundary value problem for a nonlinear singularly perturbed time-periodic reaction–diffusion–advection equation // J. Inverse Ill-Posed Probl. 2019. V. 27. № 5. 745–758.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал