Журнал вычислительной математики и математической физики, 2020, T. 60, № 8, стр. 1291-1303
Функционально-дифференциальные уравнения точечного типа. Бифуркация
Л. А. Бекларян 1, *, А. Л. Бекларян 2, **
1 Центральный экономико-математический институт РАН
117418 Москва, Нахимовский пр-т, 47, Россия
2 Национальный исследовательский университет
“Высшая школа экономики”
119049 Москва, ул. Шаболовка, 26-28, Россия
* E-mail: beklar@cemi.rssi.ru
** E-mail: abeklaryan@hse.ru
Поступила в редакцию 15.02.2020
После доработки 15.02.2020
Принята к публикации 09.04.2020
Аннотация
Важность функционально-дифференциальных уравнений точечного типа определяется тем, что по решениям таких уравнений строятся решения типа бегущей волны для индуцированных бесконечномерных обыкновенных дифференциальных уравнений и наоборот. Для таких уравнений имеет место явление ветвления решения. Для линейного однородного функционально-дифференциального уравнения точечного типа получена теоремa о бифуркации типа ветвления решения. Библ. 15. Фиг. 6.
1. ВВЕДЕНИЕ
Для уравнений математической физики, являющихся уравнением Эйлера–Лагранжа соответствующих вариационных задач, важный класс решений – это солитонные решения [1], [2]. В ряде моделей такие решения хорошо приближаются солитонными решениями для конечно-разностных аналогов исходных уравнений, которые взамен непрерывной среды описывают взаимодействие сгустков среды, помещенных в вершинах решетки [2], [3]. Возникающие системы относятся к классу бесконечномерных динамических систем. К наиболее широко рассматриваемым классам подобных задач относятся бесконечномерные системы с потенциалами Френкеля–Конторовой (периодические и медленно растущие потенциалы) и Ферми–Паста–Улама (потенциалы экспоненциального роста), широкий обзор которых приведен в работе [4].
Изучение солитонных решений (решений типа бегущей волны) основано на существовании взаимно однозначного соответствия солитонных решений для бесконечномерных динамических систем с решениями индуцированных функционально-дифференциальных уравнений точечного типа [5]–[8]. Отмеченная связь между солитонными решениями бесконечномерной динамической системы и решениями индуцированного функционально-дифференциального уравнения является фрагментом более общей схемы, выходящей за рамки данной работы [9]. Важно, что исследование солитонных решений бесконечномерной динамической системы эквивалентно исследованию решений индуцированного функционально-дифференциального уравнения точечного типа. Теорема существования и единственности решения (теорема существования) для индуцированного функционально-дифференциального уравнения точечного типа гарантирует существование и единственность (существование) солитонного решения с заданными начальными значениями. Сами решения функционально-дифференциальных уравнений точечного типа с квазилинейной правой частью изучаются в рамках формализма, основанного на групповых особенностях таких уравнений и развиваемого в работах одного из авторов [10], [5], [6], [11], и представлены в монографии [8]. Для линейных систем получены критерии существования решения в форме аналога теоремы Нетер, а также точечной полноты решений [12]. Получены легко проверяемые достаточные условия существования решения [13].
В представленной работе для линейного однородного функционально-дифференциального уравнения точечного типа получена теорема о бифуркации типа ветвления решения.
2. ФУНКЦИОНАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ТОЧЕЧНОГО ТИПА
Функционально-дифференциальным уравнением точечного типа называется уравнение
где $f:\mathbb{R} \times {{\mathbb{R}}^{{ns}}} \to {{\mathbb{R}}^{n}}$ – отображение класса ${{C}^{{(0)}}}$; ${{q}_{j}}({\kern 1pt} \cdot {\kern 1pt} )$, $j = 1, \ldots ,s$ – диффеоморфизмы прямой, сохраняющие ориентацию; ${{B}_{R}}$ – замкнутый интервал $[{{t}_{0}},{{t}_{1}}]$, замкнутая числовая полупрямая $[{{t}_{0}}, + \infty [$, или числовая прямая $R$. Используя замену времени, для функций отклонения аргумента $[{{q}_{j}}(t) - t]$, $j = 1, \ldots ,s$, всегда можно добиться выполнения условияОсновная цель при изучении функционально-дифференциальных уравнений точечного типа – это исследование начально-краевой задачи
(3)
$\dot {x}(t) = \varphi (t),\quad t \in \mathbb{R}{\backslash }{{B}_{R}},\quad \varphi ({\kern 1pt} \cdot {\kern 1pt} ) \in {{L}_{\infty }}(\mathbb{R},{{\mathbb{R}}^{n}}),$Регуляризация Красовского. Идея преодоления этого недостатка восходит к Красовскому [14]. Для функционально-дифференциальных уравнений запаздывающего типа (${{q}_{j}}(t) \leqslant t,j = 1, \ldots ,s$) по решению $x({\kern 1pt} \cdot {\kern 1pt} )$ уравнения (1) строится кривая ${{x}_{t}}$ в пространстве $C([ - d,0],{{\mathbb{R}}^{n}})$, $d = ma{{x}_{{j \in \{ 1, \ldots ,s\} }}}{{h}_{j}}$ по правилу: ${{x}_{t}}(\theta ) = x(t + \theta )$, $\theta \in [ - d,0]$. Правая часть функционально-дифференциального уравнения индуцирует функционал на бесконечномерном пространстве $C([ - d,0],{{\mathbb{R}}^{n}})$ и определяет обыкновенное дифференциальное уравнение, которому удовлетворяет решение ${{x}_{t}}$. Фазовым пространством для такого уравнения выступает бесконечномерное пространство $C([ - d,0],{{\mathbb{R}}^{n}})$. Движение вдоль решений в таком фазовом пространстве удовлетворяет полугрупповому свойству и к таким системам применимы методы теории динамических систем. Такой подход позволяет рассматривать класс функционально-дифференциальных уравнений, значительно более широкий, чем представленные функционально-дифференциальные уравнения точечного типа. Вместе с тем при таком подходе теряется информация о поведении решений в исходном фазовом пространстве ${{\mathbb{R}}^{n}}$, а также связь с теорией решений обыкновенных дифференциальных уравнений.
Иной подход, предлагаемый для исследования таких уравнений, основан на формализме, центральным элементом которого являются конструкции, использующие некоторую конечно порожденную группу $Q$ диффеоморфизмов прямой (групповой операцией в такой группе является суперпозиция диффеоморфизмов) со свойством $\left\langle {{{q}_{1}}, \ldots ,{{q}_{s}}} \right\rangle \subseteq Q$. Суть подхода в том, что бесконечномерная вектор-функция ${{\{ x(q(t))\} }_{{q \in Q}}}$, построенная по решению $x({\kern 1pt} \cdot {\kern 1pt} )$ уравнения (1), будет решением некоторого индуцированного бесконечномерного обыкновенного дифференциального уравнения с фазовым пространством в виде полного прямого произведения
Отмеченный групповой подход позволяет рассматривать функционально-дифференциальные уравнения точечного типа как расширение класса обыкновенных дифференциальных уравнений в смысле сохранения: теоремы существования и единственности начально-краевой задачи, а также непрерывной зависимости от начально-краевых условий и правой части уравнения; точечной полноты решений краевой задачи и т.д. Важно, что при таком подходе мы имеем возможность изучать поведение траекторий в исходном фазовом пространстве ${{\mathbb{R}}^{n}}$, выявить препятствия, не позволяющие функционально-дифференциальному уравнению точечного типа наследовать свойства обыкновенных дифференциальных уравнений.
2.1. Теорема существования и единственности для функционально-дифференциального уравнения точечного типа
Определим банахово пространство функций $x({\kern 1pt} \cdot {\kern 1pt} )$ с весами
Сформулируем систему ограничений на правую часть функционально-дифференциальных уравнений точечного типа:
(а) $f({\kern 1pt} \cdot {\kern 1pt} ) \in {{C}^{{(0)}}}(\mathbb{R} \times {{\mathbb{R}}^{{n \times s}}},{{\mathbb{R}}^{n}})$ (здесь функцию $f({\kern 1pt} \cdot {\kern 1pt} )$ по переменной $t$ можно положить кусочно-непрерывной c разрывами I рода в точках дискретного множества);
(б) условие квазилинейного роста: для любых $t,{{z}_{j}},{{\bar {z}}_{j}},j = 1, \ldots ,s,$
(в) существует $\mu {\text{*}} \in {{\mathbb{R}}_{ + }}$ такое, что выражение
(г) величины
Правую часть $f({\kern 1pt} \cdot {\kern 1pt} )$ функционально-дифференциального уравнения точечного типа мы будем рассматривать как элемент банахового пространства ${{V}_{{\mu {\text{*}}}}}(\mathbb{R} \times {{\mathbb{R}}^{{ns}}},{{\mathbb{R}}^{n}})$
Теорема 1 (см. [10]). Если для некоторого $\mu \in (0,\mu {\text{*}}) \cap (0,1)$ выполняется неравенство
то при любых фиксированных начально-краевых условияхУсловие (5) является точным и неулучшаемым. Можно привести примеры уравнений, для которых при нарушении этого условия отсутствует либо существование решения, либо его единственность. Если неравенство (5) выполняется при каких-то значениях $\mu \in (0,\mu {\text{*}}) \cap (0,1)$, то оно будет справедливым на некотором максимальном интервале, которое обозначим через $({{\mu }_{1}}({{L}_{f}};h),{{\mu }_{2}}({{L}_{f}};h))$. Из теоремы существования и единственности решения функционально-дифференциального уравнения точечного типа следует, что в условиях теоремы 1 решение существует в более узких пространствах $\mathcal{L}_{{{{\mu }_{2}}({{L}_{f}};h) - \varepsilon }}^{n}{{C}^{{(0)}}}(\mathbb{R})$ со сколь угодно малыми $\varepsilon > 0$ и единственно в более широких пространствах $\mathcal{L}_{{{{\mu }_{1}}({{L}_{f}};h) + \varepsilon }}^{n}{{C}^{{(0)}}}(\mathbb{R})$ со сколь угодно малыми $\varepsilon > 0$.
Очевидно, что в случае обыкновенных дифференциальных уравнений неравенство (5) выполняется. Само неравенство (5) выделяет подкласс функционально-дифференциальных уравнений, для которых сохраняются такие свойства обыкновенных дифференциальных уравнений, как существование и единственность решения начально-краевой задачи, точечная полнота решений краевой задачи, а также непрерывная зависимость решений от начально-краевых условий и правой части уравнения (грубость уравнения). Условие, в виде неравенства (5), определяет регулярное расширение класса обыкновенных дифференциальных уравнений в классе функционально-дифференциальных уравнений точечного типа с сохранением вышеперечисленных свойств обыкновенных дифференциальных уравнений.
3. БИФУРКАЦИЯ
Рассмотрим задачу Коши (начальную задачу) для линейной однородной системы функционально-дифференциальных уравнений точечного типа, определенной на всей прямой
где ${{\tau }_{j}} \in \mathbb{Z},$ $j = 1 \ldots ,s$, ${{\tau }_{1}} < \ldots < {{\tau }_{s}}$. В соответствии с обозначениями для функционально-дифференциального уравнения точечного типа, правая часть уравнения (6) имеет вид где ${{q}_{j}}(t) = t + {{\tau }_{j}},$ $j = 1, \ldots ,s$. Очевидно, чтоДля такой системы характеристическое уравнение принимает вид квазиполинома:
(8)
$\left| {\lambda E - \sum\limits_{j = 1}^s \,{{A}_{j}}{{e}^{{\lambda {{\tau }_{j}}}}}} \right| = 0.$Будем рассматривать комплексификацию $n$-мерного пространства ${{\mathbb{R}}^{n}}$, т.е. комплексное пространство ${{\mathcal{Z}}^{n}} = {{\mathbb{R}}^{n}} + i{{\mathbb{R}}^{n}}$. Линейный оператор $A$, действующий в действительном пространстве ${{\mathbb{R}}^{n}}$, порождает линейный оператор в комплексифицированном пространстве ${{\mathcal{Z}}^{n}}$, действующий по правилу $Az = A(x + iy) = Ax + iAy$. Введем обозначение
(9)
$\mathbb{A}(\lambda ) = \sum\limits_{j = 1}^s \,{{A}_{j}}{{e}^{{\lambda {{\tau }_{j}}}}},\quad \lambda \in \mathbb{C}.$Для заданных $\lambda \in \mathbb{C}$ и $r \in \mathbb{R}$ определим
(11)
$\varrho (\lambda ) = \{ \bar {\lambda }:\bar {\lambda } = \lambda + i2\pi k,\;\bar {\lambda } \in \sigma (\mathbb{A}(\lambda )),\;k \in \mathbb{Z}\} ,\quad \rho (r) = \bigcup\limits_{{\text{Re}}\lambda = r} \,\varrho (\lambda ).$Лемма 1. Для любого $\mathcal{N} > 0$ множество $\bigcup\nolimits_{|r| \leqslant \mathcal{N}} \,\rho (r)$ либо конечно, либо пусто.
Доказательство. Пусть задано $r \in [ - \mathcal{N},\mathcal{N}]$. Для $z \in {{\mathcal{Z}}^{n}}$, ${{\left\| z \right\|}_{{{{\mathcal{Z}}^{n}}}}} = 1$, $\lambda \in \mathbb{C}$, $\operatorname{Re} \lambda = r$ рассмотрим равенство
Положим $\lambda = \tilde {\lambda } + i2\pi l$, где $\left| {\operatorname{Im} \tilde {\lambda }} \right| < 2\pi $. Так как ${{e}^{{(\lambda + i2\pi l){{\tau }_{j}}}}} = {{e}^{{\tilde {\lambda }{{\tau }_{j}}}}}$, то последнее равенство примет вид(13)
$(\tilde {\lambda } + i2\pi l)z - \sum\limits_{j = 1}^s \,{{A}_{j}}{{e}^{{\tilde {\lambda }{{\tau }_{j}}}}}z = 0.$Пусть $\lambda \in \sigma (\mathbb{A}(\lambda ))$. Тогда множество собственных векторов, соответствующих собственным числам $\bar {\lambda } \in \varrho (\lambda )$, линейно независимы.
Наряду с характеристическим уравнением (8) рассмотрим другое характеристическое уравнение:
(14)
$\left| {\nu E - {\text{exp}}\left( {\sum\limits_{j = 1}^s \,{{A}_{j}}{{\nu }^{{{{h}_{j}}}}}} \right)} \right| = 0.$Лемма 2. Для всякого собственного значения $\lambda $ характеристического уравнения (8) величина $\nu = {{e}^{\lambda }}$ является собственным значением характеристического уравнения (14) и соответственно для любого собственного значения $\bar {\lambda } \in \varrho (\lambda )$ также имеет место равенство $\nu = {{e}^{{\bar {\lambda }}}}$. Каждый собственный вектор $z \in {{\mathcal{Z}}^{n}}$ оператора $\sum\nolimits_{j = 1}^s \,{{A}_{j}}{{e}^{{\lambda {{\tau }_{j}}}}}$ с собственным значением $\bar {\lambda } \in \varrho (\lambda )$ является собственным вектором оператора $\exp \left( {\sum\nolimits_{j = 1}^s \,{{A}_{j}}{{\nu }^{{{{\tau }_{j}}}}}} \right)$ с собственным значением $\nu = {{e}^{\lambda }}$. Линейная оболочка собственных подпространств оператора $\sum\nolimits_{j = 1}^s \,{{A}_{j}}{{e}^{{\lambda {{\tau }_{j}}}}}$, соответствующих собственным значениям $\bar {\lambda } \in \varrho (\lambda )$, и только она является собственным подпространством оператора $\exp \left( {\sum\nolimits_{j = 1}^s \,{{A}_{j}}{{\nu }^{{{{\tau }_{j}}}}}} \right)$ с собственным значением $\nu = {{e}^{\lambda }}$. Более того, линейная оболочка подпространств присоединенных векторов оператора $\sum\nolimits_{j = 1}^s \,{{A}_{j}}{{e}^{{\lambda {{\tau }_{j}}}}}$, соответствующих собственным значениям из множества $\varrho (\lambda )$, совпадает с подпространством присоединенных векторов оператора $\exp \left( {\sum\nolimits_{j = 1}^s \,{{A}_{j}}{{\nu }^{{{{\tau }_{j}}}}}} \right)$, отвечающих собственному значению $\nu = {{e}^{\lambda }}$.
Доказательство. Пусть $\lambda $ является собственным значением характеристического уравнения (8). Тогда она является решением характеристического уравнения для матрицы $A(\lambda )$, т.е. решением уравнения
(15)
$\left| {\zeta E - \sum\limits_{j = 1}^s \,{{A}_{j}}{{e}^{{\lambda {{\tau }_{j}}}}}} \right| = 0$(16)
$({{e}^{\xi }} - \nu ) = v(\xi )(\xi - \lambda - i2\pi {{k}_{1}}) \ldots (\xi - \lambda - i2\pi {{k}_{r}}),$Всякий набор вещественных матриц $\mathcal{A} = ({{A}_{1}}, \ldots ,{{A}_{s}})$ и отклонений $\bar {\tau } = ({{\tau }_{1}}, \ldots ,{{\tau }_{s}})$ будем обозначать через $\Theta = ({{A}_{1}}, \ldots ,{{A}_{s}},{{\tau }_{1}}, \ldots ,{{\tau }_{s}})$. Очевидно, что пара $\Theta = (\mathcal{A},\bar {\tau })$ однозначно определяет правую часть линейного однородного функционально-дифференциального уравнения (6), а $\mathcal{A} = ({{A}_{1}}, \ldots ,{{A}_{s}})$ ее определяет как элемент банахова пространства $\mathcal{L}({{\mathbb{R}}^{{ns}}},{{\mathbb{R}}^{n}})$. Следуя прежним обозначениям, положим $h = \left( {\left| {{{\tau }_{1}}} \right|, \ldots ,\left| {{{\tau }_{s}}} \right|} \right)$. В дальнейшем для всех приведенных величин будем отмечать их зависимость от $\Theta $ или $\mathcal{A}$.
Пусть $\mathcal{T}(\Theta )$ – множество решений квазиполинома (8) (с учетом их кратности). При заданном $\Theta $ мы можем корректно определить величины
(17)
$\underline \delta (\Theta ) = {\text{inf}}\{ \delta :\sharp \{ \lambda :\lambda \in \mathcal{T}(\Theta ),\;\left| {\operatorname{Re} \lambda } \right| < \delta \} \geqslant n\} ,$(18)
$\overline \delta (\Theta ) = {\text{sup}}\{ \delta :\sharp \{ \lambda :\lambda \in \mathcal{T}(\Theta ),\;\left| {\operatorname{Re} \lambda } \right| < \delta \} \leqslant n\} ,$(19)
$\underline \mu (\Theta ) = {\text{exp}}( - \overline \delta (\Theta )),\quad \bar {\mu }(\Theta ) = {\text{exp}}( - \underline \delta (\Theta )),$Для обыкновенных дифференциальных уравнений, т.е. при $h = 0$, величина $\underline \delta (\Theta )$ совпадает с верхним ляпуновским показателем и $\overline \delta (\Theta ) = + \infty (\underline \mu (\Theta ) = 0)$.
Лемма 3. Для всякого набора $\Theta = (\mathcal{A},\bar {\tau }) = ({{A}_{1}}, \ldots ,{{A}_{s}},{{\tau }_{1}}, \ldots ,{{\tau }_{s}})$ имеет место оценка $\overline \delta (\Theta ) \geqslant \underline \delta (\Theta )$.
Доказательство. Оно непосредственно следует из определений величин $\overline \delta (\Theta )$ и $\underline \delta (\Theta )$.
В терминах величин $\overline \delta (\Theta )$ и $\underline \delta (\Theta )$ ($\underline \mu (\Theta )$ и $\bar {\mu }(\Theta )$) для начальной задачи (6), (7) можем сформулировать теорему существования и единственности решения из пространства $\mathcal{L}_{\mu }^{n}{{C}^{{(0)}}}(\mathbb{R})$ при соответствующих значениях параметра $\mu \in (0,1)$. Для решений из пространств $\mathcal{L}_{\mu }^{n}{{C}^{{(0)}}}(\mathbb{R})$ по параметру $\mu \in (0,1)$ будут описаны бифуркации как потери решений, так и их ветвления.
Теорема 2. Пусть задан набор $\Theta = (\mathcal{A},\bar {\tau }) = ({{A}_{1}}, \ldots ,{{A}_{s}},{{\tau }_{1}}, \ldots ,{{\tau }_{s}})$. Если имеет место оценка $\overline \delta (\Theta ) > \underline \delta (\Theta )$, то при каждом $\mu \in (\underline \mu (\Theta ),\bar {\mu }(\Theta )]$, для уравнения (6) в пространстве $\mathcal{L}_{\mu }^{n}{{C}^{{(0)}}}(\mathbb{R})$ существует $n$ линейно независимых решений. При значениях $\mu = \bar {\mu }(\Theta )$ и $\mu = \underline \mu (\Theta ) \ne 0$ происходит бифуркация. В пространстве $\mathcal{L}_{\mu }^{n}{{C}^{{(0)}}}(\mathbb{R}),$ $\mu > \bar {\mu }(\Theta )$, происходит потеря части из $n$ линейно независимых решений, а в пространстве $\mathcal{L}_{{\underline \mu (\Theta )}}^{n}{{C}^{{(0)}}}(\mathbb{R})$ происходит рождение (ветвление) новых линейно независимых решений.
Если имеет место равенство $\overline \delta (\Theta ) = \underline \delta (\Theta )$, то в пространстве $\mathcal{L}_{\mu }^{n}{{C}^{{(0)}}}(\mathbb{R}),$ $\mu = \bar {\mu }(\Theta ) = \underline \mu (\Theta )$, для уравнения (6) существует $m,m > n$, линейно независимых решений. При значении $\mu = \bar {\mu }(\Theta ) = \underline \mu (\Theta )$ происходит бифуркация. В пространстве $\mathcal{L}_{\mu }^{n}{{C}^{{(0)}}}(\mathbb{R})$, $\mu > \bar {\mu }(\Theta ) = \underline \mu (\Theta )$, происходит потеря решения и остается только лишь $m{\text{'}},\;m{\text{'}} < n$, линейно независимых решений.
Доказательство. Пусть выполняется неравенство $\overline \delta (\Theta ) > \underline \delta (\Theta )$. В силу определения величин $\overline \delta (\Theta )$ и $\underline \delta (\Theta )$ в открытом цилиндре $\left| {\operatorname{Re} \lambda } \right| < \overline \delta (\Theta )$ расположено $n$ решений квазиполинома (8) (с учетом их кратности) и эти решения локализуются в более меньшем замкнутом цилиндре $\left| {\operatorname{Re} \lambda } \right| \leqslant \underline \delta (\Theta )$. При этом в замкнутом цилиндре $\left| {\operatorname{Re} \lambda } \right| \leqslant \overline \delta (\Theta )$ расположено более $n$ решений, а в открытом цилиндре $\left| {\operatorname{Re} \lambda } \right| < \underline \delta (\Theta )$ расположено менее $n$ решений. В силу отмеченных спектральных свойств и следуют утверждения теоремы для этого случая.
Пусть выполняется равенство $\overline \delta (\Theta ) = \underline \delta (\Theta )$. В силу определения величин $\overline \delta (\Theta )$ и $\underline \delta (\Theta )$, в замкнутом цилиндре $\left| {\operatorname{Re} \lambda } \right| \leqslant \overline \delta (\Theta )$ расположено более чем $n$ решений квазиполинома (8) (с учетом их кратности), а в открытом цилиндре $\left| {\operatorname{Re} \lambda } \right| < \overline \delta (\Theta )$ расположено менее чем $n$ решений. В силу отмеченных спектральных свойств и следуют утверждения теоремы также и для этого случая.
Для линейного однородного функционально-дифференциального уравнения точечного типа, определяемого набором $\Theta = (\mathcal{A},\bar {\tau })$, основное неравенство теоремы 1, гарантирующее существование и единственность решения начальной задачи (6), (7), принимает вид
(20)
${{L}_{\mathcal{A}}}\sum\limits_{j = 1}^s \,{{\mu }^{{ - |{{\tau }_{j}}|}}} < ln{{\mu }^{{ - 1}}},\quad \mu \in (0,1),$Сформулируем условие, гарантирующее бифуркацию из первой части теоремы 2.
Теорема 3. Пусть задан набор $\Theta = (\mathcal{A},\bar {\tau }) = ({{A}_{1}}, \ldots ,{{A}_{s}},{{\tau }_{1}}, \ldots ,{{\tau }_{s}})$, для которого неравенство
(21)
${{L}_{\mathcal{A}}}\sum\limits_{j = 1}^s \,{{\mu }^{{ - |{{\tau }_{j}}|}}} < ln{{\mu }^{{ - 1}}},\quad \mu \in (0,1),$Доказательство. В силу теоремы 1, для начальной задачи (6), (7) при каждом $\mu \in ({{\mu }_{1}}({{L}_{\mathcal{A}}},h),{{\mu }_{2}}({{L}_{\mathcal{A}}},h))$ в пространстве $\mathcal{L}_{\mu }^{n}{{C}^{{(0)}}}(\mathbb{R})$ имеет место теорема существования и единственности решения. Поэтому квазиполином (8) в цилиндре
3.1. Пример бифуркации
Рассмотрим уравнение с запаздыванием в следующей форме:
В соответствии с обозначениями данного раздела рассматриваемому уравнению (22) соответствуют набор $\Theta = (\alpha , - 1)$ и константа Липшица ${{L}_{\mathcal{A}}} = \left| \alpha \right|$. Будем рассматривать задачи о бифуркации пространства решений из $\mathcal{L}_{\mu }^{n}{{C}^{{(k)}}}(\mathbb{R}),\;\mu \in (\underline \mu (\Theta ),\bar {\mu }(\Theta ))$, по параметрам $\mu $ и $\alpha $.Характеристический квазиполином такого уравнения принимает вид
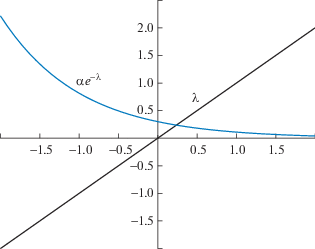
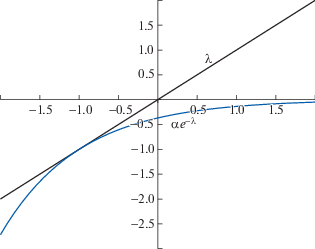
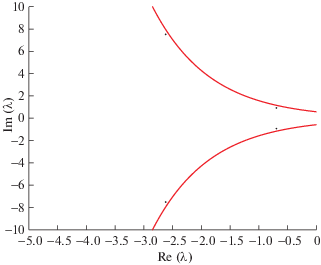
при $\alpha \geqslant 0$ имеет единственный действительный корень (см. фиг. 1), который мы обозначим через $\hat {\lambda }(\alpha )$. При этом функция $\hat {\lambda }(\alpha )$ монотонно возрастающая по $\alpha $. Действительные части комплексных корней ограничены сверху, сама верхняя грань монотонно возрастает по $\alpha $, и при малых $\alpha $ отрицательна.С другой стороны, характеристическое уравнение (23) при $ - {{e}^{{ - 1}}} < \alpha < 0$ имеет два действительных корня (см. фиг. 2 и 3), а при $\alpha = - {{e}^{{ - 1}}}$ имеем единственный действительный корень, равный $ - 1$ кратности $2$. Правый корень мы также обозначим через $\hat {\lambda }(\alpha )$ и функция $\hat {\lambda }(\alpha )$ будет монотонно возрастающая по $\alpha $ (см. фиг. 4). При $\alpha < 0$ действительные части комплексных корней ограничены сверху, сама верхняя грань монотонно убывает по $\alpha $. Более того, отмеченная верхняя грань меньше, чем левый действительный корень, который при $\alpha \to 0 - 0$ стремится к $ - \infty $.
Для рассматриваемого уравнения соответствующее основное неравенство теоремы существования и единственности имеет вид
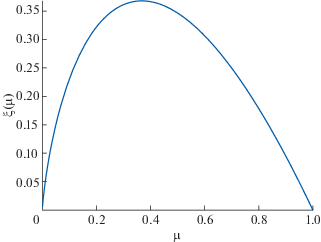
Рассматривая функцию $\xi (\mu ) = - \mu ln\mu $ (см. фиг. 5), несложно показать, что неравенство (24) имеет решение тогда и только тогда, когда $\left| \alpha \right| < {{e}^{{ - 1}}}$. Следовательно, при $\left| \alpha \right| < {{e}^{{ - 1}}}$ для любого $\mu \in ({{\mu }_{1}}(\left| \alpha \right|,1),{{\mu }_{2}}(\left| \alpha \right|,1))$ в пространстве $\mathcal{L}_{\mu }^{n}{{C}^{{(k)}}}(\mathbb{R})$ имеет место теорема 1 о существовании и единственности решения уравнения (22) при заданном начальном условии.Случай 1: $\left| \alpha \right| < {{e}^{{ - 1}}}$. Из теоремы существования и единственности решения будет следовать включение ${{e}^{{ - |\hat {\lambda }(\alpha )|}}} \in \left( {{{\mu }_{1}}\left( {\left| \alpha \right|,1} \right),{{\mu }_{2}}\left( {\left| \alpha \right|,1} \right)} \right)$ и других собственных значений $\tilde {\lambda }(\alpha )$ характеристического уравнения со свойством ${{e}^{{ - |{\text{Re}}\tilde {\lambda }(\alpha )|}}} \in \left( {{{\mu }_{1}}\left( {\left| \alpha \right|,1} \right),{{\mu }_{2}}\left( {\left| \alpha \right|,1} \right)} \right)$ нет. Для рассматриваемых $\Theta = (\alpha , - 1)$ выполняются условия теоремы 3, в частности $\overline \delta (\Theta ) > \underline \delta (\Theta )$, $\left( {{{\mu }_{1}}\left( {\left| \alpha \right|,1} \right),{{\mu }_{2}}\left( {\left| \alpha \right|,1} \right)} \right) \subseteq (\underline \mu (\Theta ),\bar {\mu }(\Theta ))$, и имеет место описанная там бифуркация пространства решений $\mathcal{L}_{\mu }^{n}{{C}^{{(k)}}}(\mathbb{R})$ по параметру $\mu $ при значениях $\mu = \underline \mu (\Theta )$ и $\mu = \bar {\mu }(\Theta ))$.
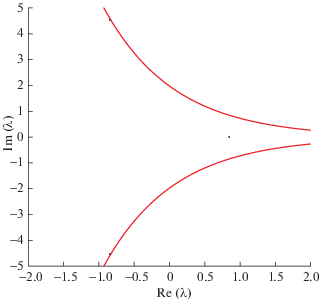
Случай 2: $\alpha \geqslant {{e}^{{ - 1}}}$. Выше было отмечено, что квазиполином всегда имеет единственный действительный корень $\hat {\lambda }(\alpha )$. Нас интересует такое минимальное значение ${{\alpha }_{{min}}} \geqslant {{e}^{{ - 1}}}$, при котором впервые появляется пара комплексно-сопряженных корней ${{\lambda }_{1}}({{\alpha }_{{min}}})$ и ${{\bar {\lambda }}_{1}}({{\alpha }_{{min}}})$ квазиполинома, таких что $\left| {\operatorname{Re} ({{\lambda }_{1}}({{\alpha }_{{min}}}))} \right| = \left| {\operatorname{Re} ({{{\bar {\lambda }}}_{1}}({{\alpha }_{{min}}}))} \right| = \left| {\hat {\lambda }({{\alpha }_{{min}}})} \right|$ (см. фиг. 4). После подстановки указанных условий в уравнение (23) получаем условие на $\hat {\lambda }({{\alpha }_{{min}}})$
(25)
${{e}^{{\hat {\lambda }({{\alpha }_{{min}}})}}}cos\left( {\hat {\lambda }({{\alpha }_{{min}}}){{e}^{{\hat {\lambda }({{\alpha }_{{min}}})}}}\sqrt {{{e}^{{2\hat {\lambda }({{\alpha }_{{min}}})}}} - 1} } \right) = - 1.$В таком случае, для $\Theta = (\alpha , - 1)$, ${{e}^{{ - 1}}} \leqslant \alpha < {{\alpha }_{{min}}}$ выполняется условие теоремы 2, а именно, $\overline \delta (\Theta ) > \underline \delta (\Theta )$. Тогда в пространстве $\mathcal{L}_{\mu }^{n}{{C}^{{(k)}}}(\mathbb{R}),\;\mu \in (\underline \mu (\Theta ),\bar {\mu }(\Theta ))$, справедлива теорема существования и единственности решения уравнения (22) при заданном начальном условии и имеет место описанная там бифуркация пространства решений по параметру $\mu $ при значениях $\mu = \underline \mu (\Theta )$ и $\mu = \bar {\mu }(\Theta ))$. Из теоремы существования и единственности решения будет следовать включение ${{e}^{{ - \hat {\lambda }(\alpha )}}} \in (\underline \mu (\Theta ),\bar {\mu }\Theta ))$ и соответственно в пространстве $\mathcal{L}_{\mu }^{n}{{C}^{{(k)}}}(\mathbb{R}),$ $\mu = {{e}^{{ - \hat {\lambda }(\alpha )}}}$, также справедлива теорема существования и единственности решения уравнения (22) при заданном начальном условии.
При значении ${{\alpha }_{{min}}}$ выполняется равенство $\overline \delta (\Theta ) = \underline \delta (\Theta )$ и соответственно $\underline \mu (\Theta ) = \bar {\mu }(\Theta )$. По теореме 2 имеет место описанная там бифуркация пространства решений по параметру $\mu $ при значении $\mu = \underline \mu (\Theta ) = \bar {\mu }(\Theta )$. Более того, $\underline \mu (\Theta ) = \bar {\mu }(\Theta ) = {{e}^{{ - \hat {\lambda }({{\alpha }_{{{\text{min}}}}})}}}$ и в пространстве $\mathcal{L}_{\mu }^{n}{{C}^{{(k)}}}(\mathbb{R}),$ $\mu = {{e}^{{ - \hat {\lambda }({{\alpha }_{{{\text{min}}}}})}}},$ возникает $3$-параметрическое семейство решений.
Случай 3: $\alpha \leqslant - {{e}^{{ - 1}}}$. Ранее мы отметили, что при $\alpha \in ( - {{e}^{{ - 1}}},0)$ для характеристического уравнения (23) имеем два действительных корня кратности $1$, а при $\alpha = - {{e}^{{ - 1}}}$ имеем единственный действительный корень $\hat {\lambda }( - {{e}^{{ - 1}}}) = - 1$ кратности $2$ (см. фиг. 2 и 3). В случае 1 было описано пространство решений, связанное с правым корнем $\hat {\lambda }(\alpha )$ характеристического уравнения. Показано, что в пространстве $\mathcal{L}_{\mu }^{n}{{C}^{{(k)}}}(\mathbb{R}),$ $\mu = {{e}^{{ - |\hat {\lambda }(\alpha )|}}}$, справедлива теорема существования и единственности решения уравнения (22) при заданном начальном условии.
При дальнейшем уменьшении значения $\alpha $ действительных корней нет (см. фиг. 6). При этом найдется $d > 0$ такое, что при $ - d < \alpha < - {{e}^{{ - 1}}}$ существует единственная пара сопряженных комплексных корней квазиполинома (23) с минимальным модулем действительной части.
При значении $\alpha = - {{e}^{{ - 1}}}$ выполняется равенство $\overline \delta (\Theta ) = \underline \delta (\Theta )$ и соответственно $\underline \mu (\Theta ) = \bar {\mu }(\Theta )$. По теореме 2 имеет место описанная там бифуркация пространства решений по параметру $\mu $ при значении $\mu = \underline \mu (\Theta ) = \bar {\mu }(\Theta )$. Более того, $\underline \mu (\Theta ) = \bar {\mu }(\Theta ) = {{e}^{{ - |\hat {\lambda }( - {{e}^{{ - 1}}})|}}}$ и в пространстве $\mathcal{L}_{\mu }^{n}{{C}^{{(k)}}}(\mathbb{R}),$ $\mu = {{e}^{{ - |\hat {\lambda }( - {{e}^{{ - 1}}})|}}}$, возникает $2$-параметрическое семейство решений.
Рассмотрим вопрос о поведении пространства решений по параметру $\alpha $ (бифуркация по параметру $\alpha $). При каждом $\Theta = (\alpha , - 1),$ $\alpha \in \mathbb{R}$, будем рассматривать решения функционально-дифференциального уравнения из пространства $\mathcal{L}_{\mu }^{n}{{C}^{{(k)}}}(\mathbb{R}),$ $\mu \in (\underline \mu (\Theta ),\bar {\mu }(\Theta ))$. Из случаев 1–3 следует, что для $\alpha \in ( - {{e}^{{ - 1}}},{{\alpha }_{{{\text{min}}}}})$ размерность пространства решений равна единице и имеет место теорема существования и единственности решения. При $\alpha = - {{e}^{{ - 1}}}$ размерность пространства решений равна двум, а при $\alpha = {{\alpha }_{{{\text{min}}}}}$ размерность пространства решений равна трем.
Список литературы
Miwa T., Jimbo M., Date E. Solitons: Differential Equations, Symmetries and Infinite Dimensional Algebras. UK: Cambridge University Press, 2000.
Toda M. Theory of Nonlinear Lattices. Berlin, Heidelberg: Springer, 1989.
Frenkel Ya.I., Contorova T.A. On the theory of plastic deformation and twinning // J. of Experimental and Theoretical Physics. 1938. V. 8. № 1. P. 89–95.
Pustyl'nikov L.D. Infinite-dimensional non-linear ordinary differential equations and the KAM theory // Russian Mathematical Surveys. 1997. V. 52. № 3. P. 551–604.
Beklaryan L.A. Group singularities of differential equations with deviating arguments and metric invariants related to them // J. of Mathematical Sciences. 2001. V. 105. № 1. P. 1799–1811.
Beklaryan L.A. Equations of advanced-retarded type and solutions of traveling-wave type for infinite-dimensional dynamic systems // J. of Mathematical Sciences. 2004. V. 124. № 4. P. 5098–5109.
Beklaryan L.A., Khachatryan N.K. Traveling wave type solutions in dynamic transport models // Functional Differential Equat. 2006. V. 13. № 2. P. 125–155.
Beklaryan L.A. Introduction to the theory of functional differential equations. Group approach. Moscow: Factorial Press, 2007 (in Russian).
Beklaryan L.A., Beklaryan A.L. Traveling waves and functional differential equations of pointwise type. What is common? // Proc. of the VIII International Conference on Optimization and Applications (OPTIMA-2017), Petrovac, Montenegro, October 2–7. 2017.
Beklaryan L.A. A method for the regularization of boundary value problems for differential equations with deviating argument // Soviet Math. Dokl. 1991. V. 43. № 2. P. 567–571.
Beklaryan L.A. Introduction to the theory of functional differential equations and their applications. Group approach // J. of Mathematical Sciences. 2006. V. 135. № 2. P. 2813–2954.
Beklaryan L.A. The linear theory of functional differential equations: existence theorems and the problem of pointwise completeness of the solutions // Sbornik: Mathematics. 2011. V. 202. № 3. P. 307–340.
Beklaryan L.A., Beklaryan A.L. Solvability problems for a linear homogeneous functional-differential equation of the pointwise type // Differential Equat. 2017. V. 53. № 2. P. 145–156.
Krasovsky N.N. Stability of Motion: Applications of Lyapunov’s Second Method to Differential Systems and Equations with Delay. Stanford, California: Stanford University Press, 1963.
Rudin W. Functional Analysis. New Delhi: McGraw Hill, 1974.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики