Журнал вычислительной математики и математической физики, 2022, T. 62, № 9, стр. 1564-1584
Регулярные аппроксимации наибыстрейшего движения мобильного робота при ограниченных фазовых координатах
А. Н. Дарьина 1, *, А. И. Дивеев 1, **, Д. Ю. Карамзин 1, ***, Ф. Л. Перейра 2, ****, Е. А. Софронова 1, *****, Р. А. Чертовских 2, ******
1 ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 40, Россия
2 Исследовательский центр систем и технологий (SYSTEC), Университет г. Порто
Порто, Португалия
* E-mail: daryina@ccas.ru
** E-mail: aidiveev@mail.ru
*** E-mail: dmitry_karamzin@mail.ru
**** E-mail: flp@fe.up.pt
***** E-mail: sofronova_ea@mail.ru
****** E-mail: roman.home@gmail.com
Поступила в редакцию 01.05.2021
После доработки 05.04.2022
Принята к публикации 11.05.2022
- EDN: PPOANY
- DOI: 10.31857/S0044466922090095
Аннотация
Исследована задача быстродействия для мобильного управляемого робота при фазовых ограничениях. Предложен численный метод решения, основанный на принципе максимума Понтрягина. Известно, что задача управления мобильным роботом, как и любое движение, согласно унициклической модели, принадлежит классу существенно нерегулярных задач относительно фазовых ограничений. Решение такой задачи с помощью принципа максимума затруднено тем, что нет формулы для меры-множителя Лагранжа. Неясно, как выразить эту меру через другие экстремальные значения, и тем самым непонятно, как свести условия принципа максимума к соответствующей краевой задаче. Чтобы обойти указанную трудность, в работе предложен один метод регуляризации задачи, основанный на $\varepsilon $-возмущении. Приведены результаты численного эксперимента. Результаты эксперимента демонстрируют непрерывность меры-множителя. Библ. 21. Фиг. 5.
1. ВВЕДЕНИЕ
В работе изучается движение мобильного робота при ограничениях, накладываемых на фазовые координаты. В качестве критерия оптимальности рассматривается быстродействие, т.е. время, затрачиваемое на движение из заданной точки $A$ в точку $B$. Задача о наибыстрейшем движении мобильного робота при фазовых ограничениях, или задача о наибыстрейшем обходе роботом препятствия, формулируется следующим образом:
(1)
$\begin{gathered} J(p,u,T): = T \to \min ,\quad {{{\dot {x}}}_{1}} = p\cos \alpha ,\quad {{{\dot {x}}}_{2}} = p\sin \alpha ,\quad \dot {\alpha } = u, \\ x(0) = A,\quad x(T) = B,\quad \alpha (0) = {{\alpha }_{0}},\quad p \in [ - 1,1],\quad u \in [ - 1,1],\quad x_{1}^{2} + x_{2}^{2} \geqslant 1. \\ \end{gathered} $В задаче (1) реализуется так называемая простейшая унициклическая модель движения, которая дополняется возможностью разворота робота на месте, т.е. движением при $p = 0$. Она отвечает, например, упрощенной модели трехколесного робота с передним приводом. Отметим, что продольная и угловая скорости в этой модели являются независимыми, что не является характерным для некоторых других мобильных роботов (например, для гусеничного робота). Тем не менее предлагаемый в этой работе подход применим и к другим моделям мобильных роботов. Общий метод исследования обсуждается в разд. 4.
Важно отметить существование решения задачи (1). Действительно, очевидно, что в этой задаче всегда найдется допустимый процесс, и, значит, существование решения в классе измеримых управлений $p,\;u$ следует из известной теоремы Филиппова (см. [1]) (поскольку правая часть динамической системы линейна по управлению, а множество значений управления – выпуклый компакт). Обозначим решение этой задачи (которых может быть много) через $(x{\kern 1pt} *,\alpha {\kern 1pt} *,p{\kern 1pt} *,u{\kern 1pt} *,T{\kern 1pt} *)$.
Итак, задача состоит в оптимальном (по быстродействию) обходе роботом препятствия, которое задано в виде единичного круга на плоскости. В нашей работе предлагается некоторый численный метод нахождения решения $(x{\kern 1pt} *,\alpha {\kern 1pt} *,p{\kern 1pt} *,u{\kern 1pt} *,T{\kern 1pt} *)$, основанный на принципе максимума Понтрягина (см. [2]).
Отметим, что решение задачи (1) с помощью принципа максимума осложнено рядом трудностей. Во-первых, любая допустимая траектория, соприкасающаяся с границей единичного круга, не будет регулярной по Р.В. Гамкрелидзе (см. [3], [2, гл. 6]). Действительно, в любой точке границы имеет место
а значит, градиент функции $\Gamma (x,p,u): = - 2p({{x}_{1}}\cos \alpha + {{x}_{2}}\sin \alpha )$ – скалярного произведения правой части динамической системы на градиент фазоограничения – по $(p,u)$ равен нулю. Более того, по этой же причине в задаче (1) заведомо не будут выполняться даже и более слабые, чем условия регулярности, известные условия управляемости относительно фазовых ограничений (см. [4]). (Такая ситуация весьма распространена в технических системах, где обычно количество фазовых переменных превышает количество переменных управления.) Поэтому мера-множитель Лагранжа, отвечающая за фазовое ограничение, может иметь сингулярную составляющую. В связи с этим, т.е. в связи с отсутствием регулярности и наличием сингулярной составляющей меры, не представляется возможным свести условия принципа максимума к соответствующей краевой задаче, решение которой привело бы к решению задачи управления. Здесь, в частности, возникает проблема нахождения точек выхода на границу и схода с границы фазового ограничения.Кроме того, применение принципа максимума затруднено наличием особого режима по угловой скорости $u$. Робот не всегда будет следовать с максимальной по модулю угловой скоростью, т.е. при ${\text{|}}u{\kern 1pt} {\text{|}} = 1$. Однако на участках, где ${\text{|}}u{\kern 1pt} {\text{|}} < 1$, условие максимума, очевидно, не информативно. Возникает проблема нахождения точек выхода на особый режим управления и схода с него.
Оба явления, т.е. отсутствие регулярности относительно фазового ограничения и особый режим управления по угловой скорости, имеют совершенно разную природу. Тем не менее одним из возможных решений и в первом, и во втором случаях является подходящая регуляризация исходной задачи. В работе предлагается с помощью малого параметра $\varepsilon > 0$ определенным образом возмутить исходную задачу (1), так чтобы возмущенная задача стала регулярной в упомянутом выше смысле. Для этого будут использованы дополнительные переменные управления.
2. ОБЩАЯ ТЕОРИЯ
В этом разделе приведем некоторые факты из теории принципа максимума для задач быстродействия с фазовыми ограничениями. Рассмотрим такую задачу в общем виде:
(2)
$\begin{gathered} T \to \min ,\quad \dot {x} = f(x,u),\quad x(0) = A,\quad x(T) = B, \\ u(t) \in U\quad {\text{для}}\;{\text{п}}{\text{.в}}{\text{.}}\;\;t \in [0,T], \\ g(x(t)) \leqslant 0\quad \forall {\kern 1pt} t \in [0,T]. \\ \end{gathered} $Отображения
Пусть $u({\kern 1pt} \cdot {\kern 1pt} )$ – управление, а $x({\kern 1pt} \cdot {\kern 1pt} )$ – отвечающая ему траектория на отрезке времени $[0,T]$. Тройка $(x,u,T)$ называется допустимым процессом, если выполнены концевые и фазовые ограничения. Допустимый процесс $(x{\kern 1pt} *,u{\kern 1pt} *,T{\kern 1pt} *)$ называется оптимальным, если конечное время $T$ в (2) принимает наименьшее возможное значение на множестве всех допустимых процессов (так называемый глобальный минимум). Ниже предположим, что в задаче (2) существует по крайней мере один оптимальный процесс $(x{\kern 1pt} *,u{\kern 1pt} *,T{\kern 1pt} *)$.
Для формулировки принципа максимума Понтрягина потребуются некоторые определения и обозначения. Назовем точку $u \in U$ регулярной, если градиенты $\nabla {{\varphi }^{i}}(u)$, $i \in I(u)$, линейно независимы. Здесь $I(u): = \{ i:{{\varphi }^{i}}(u) = 0\} $ – так называемое множество активных индексов (т.е. множество индексов активных ограничений); символ $\nabla $ означает классический градиент скалярной функции.
Пусть задана измеримая функция $u({\kern 1pt} \cdot {\kern 1pt} ):\mathbb{R} \to \mathbb{R}$.
Определение 1. Замыканием по мере функции $u( \cdot )$ в точке $\tau $ называется множество векторов $v \in {{\mathbb{R}}^{m}}$ таких, что
Многозначное отображение, ставящее в соответствие точке на прямой замыкание по мере функции в этой точке, обозначим как $\operatorname{Clos} u$. В контексте изучения задач оптимального управления понятие замыкания по мере измеримой функции было предложено в [5]. В [6] элементы множества $\operatorname{Clos} u(\tau )$ называются существенными значениями функции $u$ в точке $\tau $. Некоторые свойства замыкания по мере функции описаны также в [7].
Рассмотрим функцию
Сформулируем условие регулярности.
Определение 2. Процесс $(x{\kern 1pt} *,u{\kern 1pt} *,T{\kern 1pt} *)$ называется регулярным относительно фазовых ограничений, если для всех $t \in [0,T{\kern 1pt} *]$, и всех $u \in \operatorname{Clos} u{\kern 1pt} *{\kern 1pt} (t)$ таких, что $g(x{\kern 1pt} *{\kern 1pt} (t)) = \Gamma (x{\kern 1pt} *{\kern 1pt} (t),u) = 0$, точка $u$ регулярна, и выполнено условие
Рассмотрим расширенную функцию Гамильтона–Понтрягина
где $\psi ,\;\mu $ – переменные из ${{\mathbb{R}}^{n}}$ и $\mathbb{R}$ соответственно.Теорема 1. Предположим, что регулярный относительно фазовых ограничений процесс $(x{\kern 1pt} *,u{\kern 1pt} *,T{\kern 1pt} *)$ является оптимальным в задаче (2). Тогда существуют множители Лагранжа: число $\lambda \in [0,1]$, абсолютно непрерывная векторная функция $\psi \in {{\mathbb{W}}_{{1,\infty }}}([0,T{\kern 1pt} *];{{\mathbb{R}}^{n}})$, и непрерывная скалярная функция $\mu \in \mathbb{C}([0,T{\kern 1pt} *];\mathbb{R})$ такие, что
Теорема 1 была получена в [7] при некоторых дополнительных предположениях гладкости, а в [8] и [9] была доказана в полной общности. Краткая версия доказательства приведена в разд. 6. Отметим также, что теорема 1 является уточнением соответствующего результата из [2, гл. 6]. Уточнение касается непрерывности меры-множителя $\mu ({\kern 1pt} \cdot {\kern 1pt} )$.
Приведем несколько замечаний, которые будут использованы далее.
Замечание 1. Из условий принципа максимума вытекает известный закон сохранения вдоль экстремали (см. [2], [10])
Замечание 2. Из условий принципа максимума следует, что $\mu ({\kern 1pt} \cdot {\kern 1pt} )$ постоянна на любом отрезке времени $[a,b]$, на котором оптимальная траектория лежит во внутренности фазовых ограничений, т.е. когда $g(x{\kern 1pt} *{\kern 1pt} (t)) < 0$ $\forall {\kern 1pt} t \in [a,b]$.
Замечание 3. Ввиду правила множителей Лагранжа, условие максимума влечет
Замечание 4. Пусть набор множителей $(\lambda ,\psi ,\mu )$ удовлетворяет принципу максимума, и $a \in \mathbb{R}$ – произвольное число. Тогда набор множителей
снова удовлетворяет всем условиям принципа максимума (см. [2], [12]). Поэтому можно считать, что $\mu (T{\kern 1pt} *) = 0$ и тогда $\mu (t) \geqslant 0$, или, что эквивалентно, $\mu (0) = 0$ и тогда $\mu (t) \leqslant 0$.Принцип максимума из теоремы 1 предоставляет так называемую полную систему уравнений для нахождения оптимального процесса, в которой количество уравнений формально равно количеству неизвестных. Действительно, в условиях регулярности на границе фазового ограничения замечание 3 позволяет выразить $\mu $ через другие экстремальные значения. Вне границы фазового ограничения $\mu $ постоянна, согласно замечанию 2. Поэтому, используя свойство непрерывности, меру-множитель $\mu $ можно выразить через $x{\kern 1pt} *,\;\psi ,\;u{\kern 1pt} *$. Если одновременно с этим с помощью условия максимума получается выразить и экстремальное управление, то условия принципа максимума сводятся к решению соответствующей краевой задачи, которая может быть решена стандартными методами. Опираясь на эти соображения, можно предложить алгоритм вычисления экстремалей. Такой алгоритм будет описан ниже в вычислительной части работы (разд. 5) и применен для нахождения приближенного решения задачи о наибыстрейшем обходе препятствия мобильным роботом (1).
Отметим, что условие регулярности, сформулированное в определении 2, нельзя назвать удобным для предварительного анализа задачи, поскольку оно оперирует с заданным оптимальным процессом, который, вообще говоря, заранее неизвестен (его нам и следует вычислить). В связи с этим представляется более практичным иметь некоторое априорное условие регулярности в терминах функций $f,\;\varphi $ и $g$, которое бы гарантировало регулярность любого допустимого процесса, а значит, и заведомую применимость метода, основанного на теореме 1. Такое априорное условие регулярности несложно привести.
Условие Р). Для всех $x \in {{\mathbb{R}}^{n}}$, $u \in U$ таких, что $g(x) = \Gamma (x,u) = 0$, имеет место, что точка $u$ регулярна, и
Это априорное условие легко проверить для конкретной задачи. В контексте задач быстродействия, его естественно дополнить следующим замечанием.
Замечание 5. Пусть $0 \in \operatorname{int} f(x,U)$ $\forall {\kern 1pt} x$. Тогда условие Р) достаточно проверять на множестве
Это следует из леммы 1 в разд. 6. Тогда условие Р) гарантирует регулярность любого оптимального процесса задачи. Это модифицированное условие Р) используется ниже при анализе движения мобильного робота.3. РЕГУЛЯРИЗАЦИЯ ЗАДАЧИ
Любой допустимый процесс задачи (1) нерегулярен относительно фазовых ограничений, как только траектория касается границы допустимой области. Действительно, в любой точке границы области имеем ${{x}_{1}}\cos \alpha + {{x}_{2}}\sin \alpha = 0$, и, значит, градиент функции $\Gamma (x,p,u) = - 2p({{x}_{1}}\cos \alpha + {{x}_{2}}\sin \alpha )$ по $(p,u)$ равен нулю. Поэтому теорему 1 не удается применить для численного решения поставленной задачи, как это было сделано, например, в [9]. Однако предлагается рассмотреть некоторое возмущение исходной задачи такое, что в возмущенной задаче выполняется условие Р). Теорему 1 будем применять к возмущенной задаче.
Итак, зафиксируем малое число $\varepsilon > 0$ и рассмотрим $\varepsilon $-задачу
(3)
$\begin{gathered} J(p,u,v,w,T): = T \to \min ,\quad {{{\dot {x}}}_{1}} = p\cos \alpha + \varepsilon {{w}_{1}} + \varepsilon {{v}_{1}},\quad {{{\dot {x}}}_{2}} = p\sin \alpha + \varepsilon {{w}_{2}} + \varepsilon {{v}_{2}}, \\ \dot {\alpha } = u,\quad x(0) = A,\quad x(T) = B,\quad \alpha (0) = {{\alpha }_{0}}, \\ {{p}^{2}} + w_{1}^{2} + w_{2}^{2} \leqslant 1,\quad {{u}^{2}} + v_{1}^{2} + v_{2}^{2} \leqslant 1,\quad x_{1}^{2} + x_{2}^{2} \geqslant 1. \\ \end{gathered} $Покажем, что $\varepsilon $-задача регулярна. Имеет место следующее утверждение.
Предложение 1. Любое решение ${{\wp }_{\varepsilon }}$ задачи $(3)$ является регулярным относительно фазовых ограничений.
Доказательство. Имеем
Векторы ${{a}_{1}},\;{{a}_{2}},\;{{a}_{3}}$, очевидно, попарно линейно независимы при активных ограничениях на управление, так как ${\text{|}}x{\kern 1pt} {\text{|}} = 1$. Поэтому, как легко видеть, если три вектора линейно зависимы, то первый вектор (с точностью до знака) является линейной комбинацией двух других: ${{a}_{1}} = \alpha {{a}_{2}} + \beta {{a}_{3}}$, причем $\alpha \ne 0$ и $\beta \ne 0$. Тем самым $u = 0$, и
Несложно проверяется, что решения $\varepsilon $-задачи аппроксимируют решение задачи (1), а именно, имеет место следующее утверждение.
Лемма 1. Для любой числовой последовательности ${{\varepsilon }_{k}} \to 0$ существует решение $x{\kern 1pt} *,\;\alpha {\kern 1pt} *,\;T{\kern 1pt} *$ задачи $(1)$ и подпоследовательность ${{\varepsilon }_{{{{k}_{i}}}}}$ такие, что ${{x}_{{{{\varepsilon }_{{{{k}_{i}}}}}}}} \rightrightarrows x{\kern 1pt} *$, ${{\alpha }_{{{{\varepsilon }_{{{{k}_{i}}}}}}}} \rightrightarrows \alpha {\kern 1pt} *$, и ${{T}_{{{{\varepsilon }_{{{{k}_{i}}}}}}}} \to T{\kern 1pt} *$. Если решение задачи $(1)$ единственно, то ${{\varepsilon }_{{{{k}_{i}}}}} = {{\varepsilon }_{k}}$.
Утверждение является простым следствием слабой секвенциальной компактности шара в гильбертовом пространстве и того, что $\varepsilon $-задача является релаксацией линейно-выпуклой задачи (1).
Таким образом, установлено, что если требуется найти численно хотя бы одно (какое-либо) решение задачи (1), то при малом $\varepsilon > 0$ таким решением может быть решение $\varepsilon $-задачи (3), которое, в свою очередь, можно найти приближенно с помощью решения условий принципа максимума Понтрягина.
Перейдем к условиям принципа максимума для задачи (3). Фазовое ограничение ${\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}} \leqslant 1$ заменим на эквивалентное ему ${\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{\text{/}}2 \leqslant 1{\text{/}}2$, что, очевидно, не отразится на свойстве регулярности $\varepsilon $-задачи. Имеем
Согласно принципу максимума существуют (зависящие от $\varepsilon $) число $\lambda \geqslant 0$, абсолютно непрерывная вектор-функция $\psi (t)$ и непрерывная убывающая скалярная функция $\mu (t)$ такие, что
(4)
$\lambda + \left| {{{\psi }_{1}}(t) + \mu (t){{x}_{{\varepsilon 1}}}(t)} \right| + \left| {{{\psi }_{2}}(t) + \mu (t){{x}_{{\varepsilon 2}}}(t)} \right| + \left| {{{\psi }_{3}}(t)} \right| > 0\quad \forall {\kern 1pt} t \in [0,{{T}_{\varepsilon }}].$Уравнение для сопряженной переменной принимает вид
(5)
$\begin{gathered} {{{\dot {\psi }}}_{1}}(t) = - \mu (t)({{p}_{\varepsilon }}(t)\cos {{\alpha }_{\varepsilon }}(t) + \varepsilon {{w}_{{\varepsilon 1}}}(t) + \varepsilon {{v}_{{\varepsilon 1}}}(t)), \\ {{{\dot {\psi }}}_{2}}(t) = - \mu (t)({{p}_{\varepsilon }}(t)\sin {{\alpha }_{\varepsilon }}(t) + \varepsilon {{w}_{{\varepsilon 2}}}(t) + \varepsilon {{v}_{{\varepsilon 2}}}(t)), \\ {{{\dot {\psi }}}_{3}}(t) = {{p}_{\varepsilon }}(t)\sin {{\alpha }_{\varepsilon }}(t)({{\psi }_{1}}(t) + \mu (t){{x}_{{\varepsilon 1}}}(t)) - {{p}_{\varepsilon }}(t)\cos {{\alpha }_{\varepsilon }}(t)({{\psi }_{2}}(t) + \mu (t){{x}_{{\varepsilon 2}}}(t)), \\ \end{gathered} $Условие максимума распадается на два независимых условия
(6)
$\begin{gathered} \mathop {\max }\limits_{{{p}^{2}} + |w{{|}^{2}} \leqslant 1} (({{\psi }_{1}}(t) + \mu (t){{x}_{{\varepsilon 1}}}(t))(p\cos {{\alpha }_{\varepsilon }}(t) + \varepsilon {{w}_{1}}) + ({{\psi }_{2}}(t) + \mu (t){{x}_{{\varepsilon 2}}}(t))(p\sin {{\alpha }_{\varepsilon }}(t) + \varepsilon {{w}_{2}})) = \\ = ({{\psi }_{1}}(t) + \mu (t){{x}_{{\varepsilon 1}}}(t))({{p}_{\varepsilon }}(t)\cos {{\alpha }_{\varepsilon }}(t) + \varepsilon {{w}_{{\varepsilon 1}}}(t)) + ({{\psi }_{2}}(t) + \mu (t){{x}_{{\varepsilon 2}}}(t))({{p}_{\varepsilon }}(t)\sin {{\alpha }_{\varepsilon }}(t) + \varepsilon {{w}_{{\varepsilon 2}}}(t)), \\ \end{gathered} $(7)
$\begin{gathered} \mathop {\max }\limits_{{{u}^{2}} + |v{{|}^{2}} \leqslant 1} (({{\psi }_{1}}(t) + \mu (t){{x}_{{\varepsilon 1}}}(t))\varepsilon {{v}_{1}} + ({{\psi }_{2}}(t) + \mu (t){{x}_{{\varepsilon 2}}}(t))\varepsilon {{v}_{2}} + {{\psi }_{3}}(t)u) = \\ = ({{\psi }_{1}}(t) + \mu (t){{x}_{{\varepsilon 1}}}(t))\varepsilon {{v}_{{\varepsilon 1}}}(t) + ({{\psi }_{2}}(t) + \mu (t){{x}_{{\varepsilon 2}}}(t))\varepsilon {{v}_{{\varepsilon 2}}}(t) + {{\psi }_{3}}(t){{u}_{\varepsilon }}(t) \\ \end{gathered} $Закон сохранения и условие трансверсальности по времени дают
(8)
$\mathop {\max }\limits_{{{p}^{2}} + |w{{|}^{2}} \leqslant 1,{\kern 1pt} {{u}^{2}} + |v{{|}^{2}} \leqslant 1} \bar {H}({{x}_{\varepsilon }}(t),{{\alpha }_{\varepsilon }}(t),p,u,v,w,\psi (t),\mu (t)) = \lambda \quad \forall {\kern 1pt} t \in [0,{{T}_{\varepsilon }}].$Кроме того, функция $\mu (t)$ постоянна на тех отрезках времени, где оптимальная траектория целиком лежит внутри фазового ограничения ${\text{|}}{{x}_{\varepsilon }}(t){\kern 1pt} {\text{|}} > 1$. Также, не ограничивая общности, согласно замечанию 4 можно полагать, что $\mu ({{T}_{\varepsilon }}) = 0$. Таким образом, $\mu (t) \geqslant 0$.
Утверждение 1. Имеет место более сильное, чем $(4)$, условие нетривиальности
(9)
$\left| {{{\psi }_{1}}(t) + \mu (t){{x}_{{\varepsilon 1}}}(t)} \right| + \left| {{{\psi }_{2}}(t) + \mu (t){{x}_{{\varepsilon 2}}}(t)} \right| + \left| {{{\psi }_{3}}(t)} \right| > 0\quad \forall {\kern 1pt} t \in [0,{{T}_{\varepsilon }}].$Таким образом, множитель $\lambda $ далее не играет существенной роли, поскольку в выражениях ниже он не участвует, и можно считать после нормировки, что
Теперь найдем выражения для вычисления управлений ${{p}_{\varepsilon }},\;{{u}_{\varepsilon }},\;{{{v}}_{\varepsilon }},\;{{w}_{\varepsilon }}$ и меры-множителя Лагранжа $\mu $.
Из условия максимума (7) имеем
Утверждение 2. Имеет место более сильное, чем условие $(9)$, условие нетривиальности
(10)
$\left| {{{\psi }_{1}}(t) + \mu (t){{x}_{{\varepsilon 1}}}(t)} \right| + \left| {{{\psi }_{2}}(t) + \mu (t){{x}_{{\varepsilon 2}}}(t)} \right| > 0\quad \forall {\kern 1pt} t \in [0,{{T}_{\varepsilon }}].$Из условия максимума (6) имеем
Вычислим $\mu $. На границе фазового ограничения $\Gamma ({{x}_{\varepsilon }},{{\alpha }_{\varepsilon }},{{p}_{\varepsilon }},{{u}_{\varepsilon }},{{v}_{\varepsilon }},{{w}_{\varepsilon }}) = 0$, т.е. (зависимость от времени в дальнейшем для сокращения записи опускаем)
Решая его, после исключения приобретенных корней, получаем формулу
(11)
$\begin{array}{*{20}{l}} {\mu = - \frac{{{{r}_{3}}}}{{4{{r}_{4}}}} \pm \frac{{{{C}_{7}}}}{2} + \frac{1}{2}\sqrt {2{{C}_{5}} - {{C}_{6}} - \frac{{4{{r}_{2}}{{r}_{3}}{\text{/}}r_{4}^{2} - r_{3}^{3}{\text{/}}r_{4}^{3} - 8{{r}_{1}}{\text{/}}{{r}_{4}}}}{{4{{C}_{7}}}}} ,} \end{array}$Формула (11) используется для расчета $\mu (t)$ только на границе фазового ограничения, т.е. на тех участках траектории робота, где $x_{{\varepsilon 1}}^{2}(t) + x_{{\varepsilon 2}}^{2}(t) = 1$. Вне границы $\mu $ не изменяется со временем. Кроме того, $\mu $ непрерывна, что позволяет найти точки стыка (т.е. точки, в которых экстремаль выходит на границу или сходит с нее). Полученное значение для $\mu $ подставляется в выражения для ${{p}_{\varepsilon }},\;{{v}_{\varepsilon }},\;{{w}_{\varepsilon }}$ и в сопряженное уравнение. Таким образом, условия принципа максимума сводятся к решению соответствующей краевой задачи.
Итак, построена регулярная аппроксимация исходной задачи (1) и приведены нужные формулы для сведения к краевой задаче. При этом возмущенная задача (3), как и исходная, также является задачей быстродействия, что мы специально отмечаем. В общем случае, т.е. для задачи управления (2), регуляризация быстродействия быстродействием представляется нетривиальной задачей. По всей видимости, такой тип регуляризации осуществим лишь при некоторых дополнительных предположениях. Тем не менее, если пренебречь свойством быстродействия аппроксимирующей задачи и, тем самым, возмущать помимо динамики еще и минимизирующий функционал, то оказывается возможным предложить достаточно общую схему регуляризации задачи управления. Более того, можно добиться даже более сильного условия регулярности относительно фазового ограничения. Такую общую схему регуляризации обсуждаем в следующем разделе.
4. РЕГУЛЯРИЗАЦИЯ В ОБЩЕМ СЛУЧАЕ
Обратимся к регуляризации общей задачи быстродействия с фазовыми ограничениями. Существует множество различных подходов к регуляризации. Ниже мы рассмотрим лишь один из таких подходов.
Рассмотрим возмущенную задачу
(12)
$\begin{gathered} J(u,v,T): = T + \int\limits_0^T \,{\text{|}}v{\kern 1pt} {{{\text{|}}}^{2}}dt \to \min ,\quad \dot {x} = f(x,u) + \varepsilon v, \\ x(0) = A,\quad x(T) = B,\quad \varphi (u) \leqslant 0,\quad g(x) \leqslant 0. \\ \end{gathered} $Напомним, что фазовое ограничение называется регулярным, если $\nabla g(x) \ne 0$ $\forall {\kern 1pt} x:$ $g(x) = 0$. Ограничения на управление $\varphi (u) \leqslant 0$ регулярны, если регулярны все точки множества $U$. Эти предположения (которые естественны для ряда прикладных задач) ниже считаются a priori выполненными. В этих предположениях проверим для данных задачи (12) выполнение условия регулярности в смысле определения 2.
Для задачи (12) имеем
Предложение 1. Пусть фазовые ограничения регулярны, и регулярны все точки $u \in U$. Тогда любой допустимый процесс задачи $(12)$ регулярен относительно фазовых ограничений.
Исследуем вопрос о существовании решения в возмущенной задаче. Заметим, что никаких геометрических ограничений на управление ${v}$ не имеется, и, следовательно, исходя из вида функционала, можно считать, что управление ${v}$ ограничено лишь по норме ${{\left\| {\, \cdot \,} \right\|}_{{{{L}_{2}}}}}$. Однако при известных предположениях можно гарантировать, что решение задачи (12) принадлежит пространству ${{\mathbb{W}}_{{1,2}}}([0,T])$.
Теорема 2. Предположим, что
(a) множество $U$ компактно;
(b) множество $f(x,U)$ выпукло при всех $x$;
(c) имеет место оценка ${\text{|}}f(x,u){\kern 1pt} {\text{|}} \leqslant {\text{const}}(1 + \;{\text{|}}x{\kern 1pt} {\text{|}})$ $\forall {\kern 1pt} u \in U$;
(d) в исходной задаче $(2)$ существует допустимый процесс.
Тогда существует решение $({{x}_{\varepsilon }},{{u}_{\varepsilon }},{{v}_{\varepsilon }},{{T}_{\varepsilon }})$ задачи $(12)$ в классе траекторий $x \in {{\mathbb{W}}_{{1,2}}}([0,T])$ и управлений $u \in {{\mathbb{L}}_{\infty }}([0,T])$, $v \in {{\mathbb{L}}_{2}}([0,T])$ такое, что ${{x}_{\varepsilon }} \rightrightarrows {{x}_{0}}$, ${{\left\| {{{v}_{\varepsilon }}} \right\|}_{{{{\mathbb{L}}_{2}}}}} \to 0$ при $\varepsilon \to 0$, где ${{x}_{0}}$ – одно из решений исходной задачи $(2)$.
Доказательство. Прежде всего отметим существование решения в исходной задаче (2). Действительно, в силу сделанных предположений (a)–(d) это следует из теоремы Филиппова (см. [1]). Обозначим это решение через $(x{\kern 1pt} *,\;u{\kern 1pt} *,\;T{\kern 1pt} *)$.
Возьмем натуральное число $N$ и рассмотрим $\varepsilon ,N$-задачу, которая получается из задачи (12) путем добавления одного ограничения на управления: $\left| v \right| \leqslant N$. Процесс $(x{\kern 1pt} *,\;u{\kern 1pt} *,\;0,\;T{\kern 1pt} *)$ является допустимым в $\varepsilon ,N$-задаче, и, значит, в силу той же теоремы у нее существует решение, которое мы обозначим через $({{x}_{{\varepsilon ,N}}},{{u}_{{\varepsilon ,N}}},{{v}_{{\varepsilon ,N}}},{{T}_{{\varepsilon ,N}}})$. Устремим $N \to \infty $ и найдем искомый процесс $({{x}_{\varepsilon }},{{u}_{\varepsilon }},{{v}_{\varepsilon }},{{T}_{\varepsilon }})$.
Имеем
(13)
${{T}_{{\varepsilon ,N}}} + \left\| {{{v}_{{\varepsilon ,N}}}} \right\|_{{{{L}_{2}}}}^{2} = J({{x}_{{\varepsilon ,N}}},{{u}_{{\varepsilon ,N}}},{{v}_{{\varepsilon ,N}}},{{T}_{{\varepsilon ,N}}}) \leqslant J(x{\kern 1pt} *,u{\kern 1pt} *,0,T{\kern 1pt} *) = T{\kern 1pt} *.$Из условия (с) и из (13) с помощью стандартных оценок, включающих неравенство Гронуола, получаем, что последовательность функций ${{x}_{{\varepsilon ,N}}}$ ограничена в равномерной метрике ${{\left\| {{{x}_{{\varepsilon ,N}}}} \right\|}_{C}} \leqslant {\text{const}}$. Поэтому семейство функций
В классе траекторий из ${{\mathbb{W}}_{{1,2}}}([0,T])$ также справедлив принцип максимума. Его несложно вывести по аналогии с доказательством теоремы 2, применив к $\varepsilon ,N$-задаче принцип максимума для траекторий класса ${{\mathbb{W}}_{{1,\infty }}}([0,T])$ и перейдя в полученных условиях к пределу при $N \to \infty $. Для простоты изложения предположим, что $g(A) + g(B) < 0$, т.е. что концы траектории лежат строго во внутренности фазового ограничения. С одной стороны, такое предположение позволяет избежать в пределе эффекта вырождающегося принципа максимума (см. [4], [12]) – случая, который требует отдельного рассмотрения. С другой стороны, оно не является существенным для задачи об обходе препятствия мобильным роботом. Тогда, переходя стандартным образом к пределу при $N \to \infty $ в условиях принципа максимума, можно утверждать существование нетривиального набора множителей Лагранжа $({{\lambda }_{\varepsilon }},{{\psi }_{\varepsilon }},{{\mu }_{\varepsilon }})$, удовлетворяющего сопряженной системе, условию максимума и условию трансверсальности по времени. (Условие максимума выводится с помощью интегральной формы и слабой сходимости.) Условие нетривиальности
(14)
${{\lambda }_{\varepsilon }} + \left| {{{\psi }_{\varepsilon }}(t) - {{\mu }_{\varepsilon }}(t)\nabla g({{x}_{\varepsilon }}(t))} \right| > 0\quad \forall {\kern 1pt} t \in [0,{{T}_{\varepsilon }}]$Рассмотрим $\varepsilon $-условие максимума по $v$. Имеем
(15)
${{v}_{\varepsilon }}(t) = \frac{\varepsilon }{{2{{\lambda }_{\varepsilon }}}}({{\psi }_{\varepsilon }}(t) - {{\mu }_{\varepsilon }}(t)\nabla g({{x}_{\varepsilon }}(t))).$Заметим, что, добавив в функционал $J$ малый член $\varepsilon {{\left\| u \right\|}_{{{{L}_{2}}}}}$, наряду с регулярностью относительно фазовых ограничений, можно добиться и выполнения усиленного условия Лежандра. Тогда можно утверждать (см. [7]), что множитель ${{\mu }_{\varepsilon }}$ является даже липшицевой функцией (однако с константой Липшица, зависящей от $\varepsilon $).
Теперь применим описанную выше схему возмущения к задаче о движении мобильного робота (1). При этом понятно, что задача (12) представляет собой некоторую общую схему возмущения относительно фазового ограничения, но не учитывает возможных особых режимов. Однако, очевидно, что не все время в пути робот будет разворачиваться с максимальной по модулю угловой скоростью, и поэтому анализ особого режима по угловой скорости является критически важным для модели (1). Проблему особых режимов можно решить (по аналогии с разд. 3) с помощью дополнительной регуляризации задачи и введения дополнительных переменных управления. Другим подходом может служить возмущение минимизируемого функционала с помощью малой интегральной добавки. Ниже рассмотрим именно второй подход как альтернативу первому подходу, рассмотренному в разд. 3.
Рассмотрим возмущенную задачу
(16a)
$J(p,u,v,T): = T + \varepsilon \int\limits_0^T \,{\text{|}}p{\kern 1pt} {{{\text{|}}}^{2}}dt + \varepsilon \int\limits_0^T \,{\text{|}}u{\kern 1pt} {{{\text{|}}}^{2}}dt + \int\limits_0^T \,{\text{|}}v{\kern 1pt} {{{\text{|}}}^{2}}dt \to \min ,$(16b)
${{\dot {x}}_{1}} = p\cos \alpha + \varepsilon {{v}_{1}},\quad {{\dot {x}}_{2}} = p\sin \alpha + \varepsilon {{v}_{2}},\quad \dot {\alpha } = u,$Имеем
Рассмотрим зависящие от параметра $\varepsilon $ число $\lambda > 0$ (случай $\lambda = 0$, как несложно проверить, исключен), абсолютно непрерывную вектор-функцию $\psi (t)$ и непрерывную и убывающую скалярную функцию $\mu (t)$, которые удовлетворяют принципу максимума. Имеем
(17)
$\begin{gathered} {{{\dot {\psi }}}_{1}}(t) = - \mu (t)({{p}_{\varepsilon }}(t)\cos {{\alpha }_{\varepsilon }}(t) + \varepsilon {{v}_{{\varepsilon 1}}}(t)), \\ {{{\dot {\psi }}}_{2}}(t) = - \mu (t)({{p}_{\varepsilon }}(t)\sin {{\alpha }_{\varepsilon }}(t) + \varepsilon {{v}_{{\varepsilon 2}}}(t)), \\ {{{\dot {\psi }}}_{3}}(t) = {{p}_{\varepsilon }}(t)\left[ {\sin {{\alpha }_{\varepsilon }}(t)({{\psi }_{1}}(t) + \mu (t){{x}_{{\varepsilon 1}}}(t)) - \cos {{\alpha }_{\varepsilon }}(t)({{\psi }_{2}}(t) + \mu (t){{x}_{{\varepsilon 2}}}(t))} \right], \\ \end{gathered} $Анализ условия максимума по переменным ${{v}_{1}},\;{{v}_{2}}$ дает
(19)
${{v}_{{\varepsilon 1}}}(t) = \frac{\varepsilon }{{2\lambda }}({{\psi }_{1}}(t) + \mu (t){{x}_{{\varepsilon 1}}}(t)),\quad {{v}_{{\varepsilon 2}}}(t) = \frac{\varepsilon }{{2\lambda }}({{\psi }_{2}}(t) + \mu (t){{x}_{{\varepsilon 2}}}(t)).$Условие максимума по переменной $p$ влечет
(20)
${{p}_{\varepsilon }}(t) = \operatorname{sgn} {{a}_{\varepsilon }}(t)\min \left\{ {\frac{{{\text{|}}{{a}_{\varepsilon }}(t){\kern 1pt} {\text{|}}}}{{2\varepsilon \lambda }},1} \right\},$(21)
${{a}_{\varepsilon }}(t) = ({{\psi }_{1}}(t) + \mu (t){{x}_{{\varepsilon 1}}}(t))\cos {{\alpha }_{\varepsilon }}(t) + ({{\psi }_{2}}(t) + \mu (t){{x}_{{\varepsilon 2}}}(t))\sin {{\alpha }_{\varepsilon }}(t).$Из условия максимума по переменной $u$ следует, что
(22)
${{u}_{\varepsilon }}(t) = \operatorname{sgn} {{\psi }_{3}}(t)\min \left\{ {\frac{{{\text{|}}{{\psi }_{3}}(t){\kern 1pt} {\text{|}}}}{{2\varepsilon \lambda }},1} \right\}.$Заметим, что $\left| {{{\psi }_{1}}({{T}_{\varepsilon }})} \right| + \left| {{{\psi }_{2}}({{T}_{\varepsilon }})} \right| > 0$. Действительно, иначе, учитывая, что $\mu ({{T}_{\varepsilon }}) = 0$ и ${{\psi }_{3}}({{T}_{\varepsilon }}) = 0$ ввиду условия трансверсальности по времени получаем $\lambda = 0$. Таким образом, после нормировки можно считать, что
(23)
${{({{\psi }_{1}}({{T}_{\varepsilon }}))}^{2}} + {{({{\psi }_{2}}({{T}_{\varepsilon }}))}^{2}} = 1.$Найдем формулы для множителей $\lambda $ и $\mu $. Используя условие трансверсальности по времени, учитывая, что $\mu ({{T}_{\varepsilon }}) = 0$, ${{\psi }_{3}}({{T}_{\varepsilon }}) = 0$ и (23), решая соответствующее квадратное уравнение и отбрасывая лишние корни, приходим к следующим выражениям для $\lambda $:
Случай 1. Пусть ${{a}_{\varepsilon }}({{T}_{\varepsilon }}) \leqslant - {{\varepsilon }^{2}}{\text{/}}\sqrt {1 - \varepsilon } $. Тогда
(24)
$\lambda = {{\lambda }_{1}} = \frac{{ - {{a}_{\varepsilon }}({{T}_{\varepsilon }}) + \sqrt {a_{\varepsilon }^{2}({{T}_{\varepsilon }}) + {{\varepsilon }^{2}}(\varepsilon + 1)} }}{{2(\varepsilon + 1)}}.$Случай 2. Пусть ${{a}_{\varepsilon }}({{T}_{\varepsilon }}) \in ( - {{\varepsilon }^{2}}{\text{/}}\sqrt {1 - \varepsilon } ,{{\varepsilon }^{2}}{\text{/}}\sqrt {1 - \varepsilon } )$. Тогда
(25)
$\lambda = {{\lambda }_{2}} = \sqrt {\frac{{a_{\varepsilon }^{2}({{T}_{\varepsilon }}) + {{\varepsilon }^{3}}}}{{4\varepsilon }}} .$Случай 3. Пусть ${{a}_{\varepsilon }}({{T}_{\varepsilon }}) \geqslant {{\varepsilon }^{2}}{\text{/}}\sqrt {1 - \varepsilon } $. Тогда
(26)
$\lambda = {{\lambda }_{3}} = \frac{{{{a}_{\varepsilon }}({{T}_{\varepsilon }}) + \sqrt {a_{\varepsilon }^{2}({{T}_{\varepsilon }}) + {{\varepsilon }^{2}}(\varepsilon + 1)} }}{{2(\varepsilon + 1)}}.$На границе фазового ограничения имеем
Случай A. Пусть ${{a}_{\varepsilon }}(t) \leqslant - 2\varepsilon \lambda $. Тогда
(27)
$\mu = \frac{{2\lambda }}{{{{\varepsilon }^{2}}}}({{x}_{{\varepsilon 1}}}\cos {{\alpha }_{\varepsilon }} + {{x}_{{\varepsilon 2}}}\sin {{\alpha }_{\varepsilon }}) - ({{\psi }_{1}}{{x}_{{\varepsilon 1}}} + {{\psi }_{2}}{{x}_{{\varepsilon 2}}}).$Случай Б. Пусть ${{a}_{\varepsilon }}(t) \in ( - 2\varepsilon \lambda ,2\varepsilon \lambda )$. Тогда
(28)
$\mu = - \frac{{({{\psi }_{1}}\cos {{\alpha }_{\varepsilon }} + {{\psi }_{2}}\sin {{\alpha }_{\varepsilon }})({{x}_{{\varepsilon 1}}}\cos {{\alpha }_{\varepsilon }} + {{x}_{{\varepsilon 2}}}\sin {{\alpha }_{\varepsilon }}) + {{\varepsilon }^{3}}({{\psi }_{1}}{{x}_{{\varepsilon 1}}} + {{\psi }_{2}}{{x}_{{\varepsilon 2}}})}}{{{{{({{x}_{{\varepsilon 1}}}\cos {{\alpha }_{\varepsilon }} + {{x}_{{\varepsilon 2}}}\sin {{\alpha }_{\varepsilon }})}}^{2}} + {{\varepsilon }^{3}}}}.$Случай В. Пусть ${{a}_{\varepsilon }}(t) \geqslant 2\varepsilon \lambda $. Тогда
(29)
$\mu = - \frac{{2\lambda }}{{{{\varepsilon }^{2}}}}({{x}_{{\varepsilon 1}}}\cos {{\alpha }_{\varepsilon }} + {{x}_{{\varepsilon 2}}}\sin {{\alpha }_{\varepsilon }}) - ({{\psi }_{1}}{{x}_{{\varepsilon 1}}} + {{\psi }_{2}}{{x}_{{\varepsilon 2}}}).$Заметим, что каждого ${{\lambda }_{1}},\;{{\lambda }_{2}}$ и ${{\lambda }_{3}}$ реализуются свои случаи А, Б и В (итак, всего имеется 9 разных случаев).
Вне границы фазового ограничения $\mu $ не изменяется со временем. Кроме того, $\mu $ непрерывна, что позволяет найти точки стыка (т.е. точки, в которых экстремаль выходит на границу или сходит с нее). Полученное значение для $\mu $ подставляется в выражения для ${{p}_{\varepsilon }},\;{{{v}}_{\varepsilon }}$ и в сопряженное уравнение. Таким образом, условия принципа максимума сводятся к решению соответствующей краевой задачи.
Теперь, считая выполненным (23), $\mu ({{T}_{\varepsilon }}) = 0$ и ${{\psi }_{3}}({{T}_{\varepsilon }}) = 0$, получим необходимые оценки сверху на ${\text{|}}\psi {\kern 1pt} {\text{|}}$ и $\mu $ в зависимости от $\varepsilon $. Поскольку из формул для $\lambda $ в общем случае имеем $\lambda = O({{\varepsilon }^{{ - 1}}})$, то из формул для ${{v}_{\varepsilon }}$ находим
В завершение теоретической части отметим, что радиус окружности, задающей фазовое ограничение, может быть выбран произвольным образом, т.е. не обязательно быть единичным. В таком случае немного меняется формула для $\mu $, где появляется радиус окружности $r$. Тем не менее, с точки зрения вычислений случай именно единичной окружности интересен тем, что он является пограничным в следующем смысле: ясно, что робот может двигаться одновременно с максимальными угловой и продольной скоростями только по единичной окружности. Если как-либо изменить радиус, то это уже не так: при $r > 1$ угловая скорость не максимальна, а при $r < 1$ – продольная.
5. ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
Рассмотрим следующую схему приближенного решения исходной задачи (1). Фиксируем некоторое $\varepsilon \in (0,1)$ и переходим к возмущенной задаче (16), которая регуляризована. К возмущенной задаче применяем численный метод, предложенный в [9], [15]. Используем решение этой задачи для заданного $\varepsilon $ в качестве начального приближения к решению задачи (16) с меньшим значением $\varepsilon $. Решение этой задачи для наименьшего из рассмотренных значений $\varepsilon $ считаем приближением к решению исходной задачи (1).
5.1. Алгоритм решения задачи (16)
Принцип максимума для этой задачи сводится к краевой задаче с помощью выражений, приведенных в предыдущем разделе. Краевая задача принципа максимума решается методом стрельбы в обратном времени (т.е. перебор значений параметров, определяющих решение краевой задачи, проводится при $t = T$).
Итак, рассматривается краевая задача для системы обыкновенных дифференциальных уравнений (16b) и (17) и краевых условий (16c) и (18). При $t = T$ имеем следующие условия на решение: мобильный робот находится в точке $B$ (16c) и третья компонента сопряженной переменной равна нулю (18). Используя (23), считаем, что ${{\psi }_{1}}(T) = \cos (\theta )$ и ${{\psi }_{2}}(T) = \sin (\theta )$, где $\theta \in [0,2\pi )$. Также положим $\alpha (T) = \beta $, где $\beta \in [0,2\pi )$. Если значения $\theta $ и $\beta $ заданы, то при $t = T$ заданы все функции, входящие в рассматриваемую систему дифференциальных уравнений. Суть метода стрельбы состоит в том, чтобы численно найти значения параметров $\theta $ и $\beta $, чтобы решение $(x(t),\psi (t))$ системы дифференциальных уравнений (16b) и (17), удовлетворяющее указанным краевым условиям при $t = T$, также удовлетворяло бы (в заданной точностью) краевым условиям при $t = 0$ (значения всех параметров, определяющих точность численного решения задачи, приведены в следующем пункте.). Такая траектория является решением краевой задачи, полученной из принципа максимума Понтрягина, и, следовательно, является экстремалью рассматриваемой задачи оптимального управления.
При заданном наборе значений величин $\theta $ и $\beta $ система уравнений (16b) и (17) численно интегрируется в обратном времени классическим методом Рунге–Кутты четвертого порядка с постоянным шагом. Перед началом интегрирования вычисляется значение $\lambda $ по формулам (24)–(26). Считая, что исходная точка $B$ не принадлежит границе, полагаем $\mu (t) = 0$, пока траектория не достигнет границы фазового ограничения (16e). При вычислении правых частей дифференциальных уравнений функции управления $p(t)$, $u(t)$, ${{v}_{1}}(t)$ и ${{v}_{2}}(t)$ вычисляются по формулам (20), (22) и (19) соответственно.
Правые части интегрируемых дифференциальных уравнений, вообще говоря, негладкие, ввиду возможных переключений режимов управления $p(t)$ и $u(t)$, т.е. при $t$, когда выполнено ${\text{|}}{{a}_{\varepsilon }}(t){\kern 1pt} {\text{|}} = 2\varepsilon \lambda $ (переключение $p(t)$, ${{a}_{\varepsilon }}(t)$ задано выражением (21)) и ${\text{|}}{{\psi }_{3}}(t){\kern 1pt} {\text{|}} = 2\varepsilon \lambda $ (переключение $u(t)$). В эти моменты времени соответствующее управление становится или перестает быть максимальным (равным 1 по абсолютной величине). Чтобы избежать потерю точности в окрестности таких точек, при расчете правых частей в методе Рунге–Кутты считаем шаг неуспешным, если при его вычислении происходит такое переключение для одного из управлений. В таком случае уменьшаем шаг интегрирования вдвое и повторяем попытку выполнения шага. Уменьшение шага прекращается после семикратного уменьшения начального шага (что отвечает уменьшению начального шага примерно на два порядка), после чего продолжаем интегрирование с начальным шагом по времени с новым режимом по рассмотренному управлению.
Если траектория пересекает границу фазового ограничения (16e), то в точке пересечения вычисляем значение меры-множителя Лагранжа $\mu $, используя выражения (27)–(29). Если его абсолютное значение не превосходит заданной (малой) величины, считаем, что в этой точке $\mu (t)$ непрерывно, в этот момент времени происходит заход на границу фазового ограничения, дальше траектория следует по этой границе, расчет меры-множителя на каждом шаге по времени происходит по формулам (27)–(29). Если же его значение больше заданной величины, то, ввиду разрыва $\mu (t)$ в этой точке, построенная траектория не является частью экстремали и, следовательно, не представляет интереса.
Для траекторий, проходящих по границе фазового ограничения, осуществляем следующую процедуру. На каждом шаге по времени фиксируем $\mu $ и продолжаем интегрирование системы дифференциальных уравнений с этим фиксированным значением меры-множителя Лагранжа. Такая траектория сходит с границы и может являться частью экстремали, соединяющей границу с точкой $A$ или снова заходящей на границу.
На каждом шаге по времени измеряется расстояние от текущей позиции робота до краевого условия при $t = 0$ в (16c), и если оно меньше заданного значения, то построенная траектория считается решением краевой задачи. Если таких траекторий найдено несколько, то выбираем ту из них, которая отвечает меньшему значению функционала (16a).
Были использованы следующие условия, по которым траектория отвергалась из кандидатов в экстремали рассмотренной задачи:
– время движения робота больше заданного (достаточно большого) значения,
– при следовании по границе нарушение монотонности $\mu $,
– при сходе с границы нарушение фазового ограничения.
Для наибольшего значения $\varepsilon $ начальный выбор значений параметров $\theta $ и $\beta $ проводили на равномерной сетке в квадрате ${{[0,2\pi )}^{2}}$, локальные минимумы соответствующих невязок уточнялись методом деления пополам. Для бóльших значений $\varepsilon $ в качестве начального значения указанных параметров брали их “оптимальное” значение, найденное для меньшего значения $\varepsilon $.
5.2. Результаты расчетов
Программой, реализующей указанный алгоритм, была численно решена задача оптимального управления (0) для следующих исходных данных:
Фиг. 1.
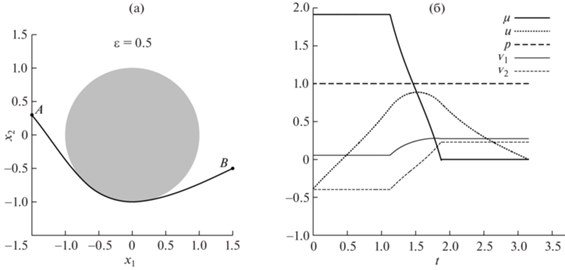
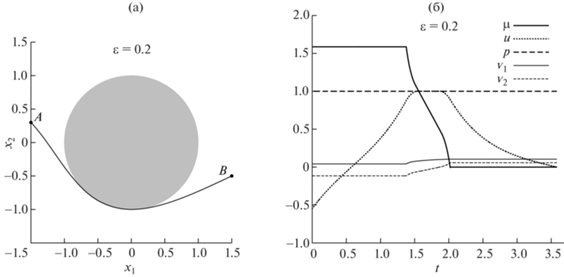
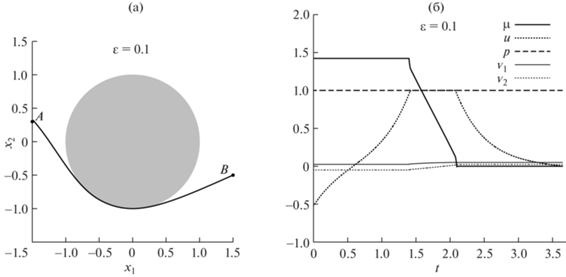
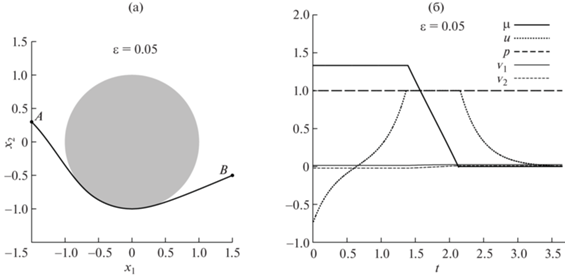
Вычисленное решение регуляризованной задачи (0) при $\varepsilon = 0.9$: (а) – оптимальная траектория робота, (б) – эволюция вдоль этой траектории меры-множителя Лагранжа $\mu (t)$ и управлений $u(t),\;p(t),\;{{{v}}_{1}}(t)$ и ${{{v}}_{2}}(t)$. Препятствие показано на (а) серым цветом.
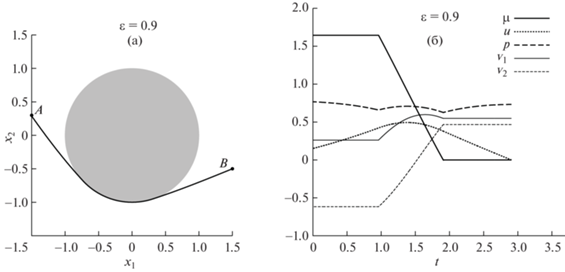
Шаг интегрирования системы дифференциальных уравнений брали равным 10–3. Если траектория пересекала границу фазового ограничения (16e), точку пересечения находили линейной интерполяцией, в этой точке вычисляли $\mu $ и считали ее непрерывной (т.е. в этой точке происходит заход на границу), если абсолютная величина этого значения не превосходила 10–2. Решение краевой задачи считалось построенным, если расстояние от траектории до начального условия (т.е. в (16c) при $t = 0$) не превосходило 10–2. Построение траектории останавливалось, если время следования по траектории превосходило 20 единиц времени.
Хотя, как описано выше, решение задачи строилось в обратном времени, т.е. от $\tilde {t} = 0$ до $\tilde {t} = - T$, для построения фигур все функции преобразованы и показаны в прямом времени: $t = \tilde {t} + T$. Чтобы упростить сравнение, для всех значений $\varepsilon $ на вертикальных и горизонтальных осях всех фигур, приведенных ниже, показаны одинаковые интервалы значений.
Были проведены расчеты для $\varepsilon = 0.9$, 0.5, 0.2, 0.1 и 0.05, вычисленные оптимальные траектории и соответствующие управления показаны на фиг. 1–5 соответственно.
На первый взгляд, траектории робота, отвечающие решениям задачи оптимального управления при разных значениях $\varepsilon $, отличаются друг от друга мало (ср. фиг. 1а–5a). Каждая из этих траекторий состоит из трех частей – части заходящей на границу фазового ограничения, движению по границе и части, сходящей с границы. Однако режимы управления, обеспечивающие такое движение, различаются существенно. Так, при $\varepsilon = 0.9$ ни скорость поворота робота $u(t)$, ни его продольная скорость $p(t)$, не являются максимальными ни в какой точке траектории (фиг. 1б). При $\varepsilon = 0.5$ (фиг. 2б) скорость поворота снова нигде не достигает максимального значения, но его продольная скорость становится максимальной на всем участке движения, т.е. $p(t) = 1$ $\forall {\kern 1pt} t \in [0,T]$. При $\varepsilon = 0.2$ (фиг. 3б) продольная скорость остается всегда максимальной, а скорость поворота достигает максимального значения на некотором участке движения вдоль границы. При $\varepsilon = 0.1$ и 0.05 качественного изменения в сравнении с предыдущим случаем нет, но скорость поворота достигает максимального значения на большем участке границы (фиг. 4б и 5б), чем для траектории при $\varepsilon = 0.2$.
Время следования по оптимальным траекториям ${{T}_{\varepsilon }}$ растет с уменьшением $\varepsilon $: ${{T}_{{0.9}}} = 2.91$, ${{T}_{{0.5}}} = 3.16$, ${{T}_{{0.2}}} = 3.58$, ${{T}_{{0.1}}} = 3.64$ и ${{T}_{{0.05}}} = 3.65$. Мы не рассматривали меньших значений $\varepsilon $, поскольку разница между двумя последними, ${{T}_{{0.05}}}$ и ${{T}_{{0.1}}}$, мала – порядка 10–2. Кроме того, отметим поведение регуляризаторов, т.е. функций ${{{v}}_{1}}$ и ${{{v}}_{2}}$ (тонкие линии на фиг. 1б–5б). Видно, что они стремятся к нулю в равномерной метрике при $\varepsilon \to 0$, причем с линейной относительно $\varepsilon $ скоростью, что также свидетельствует о сходимости метода.
Следует отметить характер изменения $\mu $ при уменьшении $\varepsilon $ (при движении по границе, так как при движении вне границы величина меры-множителя Лагранжа не меняется). При $\varepsilon = 0.9$ фиг. 1б между точкой входа и схода с границы $\mu (t)$ – практически линейная функция. При $\varepsilon = 0.5$ и 0.2 (фиг. 2б и 3б) заметно характерное нелинейное поведение – вблизи точки захода и схода с границы функция быстро меняется, оставаясь близкой к линейной при удалении от этих точек. Такая нелинейность (рост градиента) особенно заметна при $\varepsilon = 0.1$ (фиг. 4б). Однако при $\varepsilon = 0.05$ линейность уже полностью восстанавливается. Это означает, что предельная мера-множитель Лагранжа, которая отвечает принципу максимума в исходной задаче (1), по всей вероятности непрерывна. В этой связи отметим, что в известной литературе существует совсем немного примеров, которые демонстрируют наличие сингулярной составляющей меры и, в частности, атомов (см., например, [16], [17]). Представляется любопытным, что в такой существенно нерегулярной задаче, как движение мобильного робота относительно препятствия, мера-множитель все же сохраняет свойство непрерывности. Заметим, что такое свойство не гарантируется никакой существующей теорией и установлено пока лишь эмпирически.
6. ПРИЛОЖЕНИЕ
Приведем доказательство теоремы 1. Напомним следующее понятие (см. [4]).
Определение 3. В концевых точках выполняются условия управляемости относительно фазовых ограничений, если найдутся векторы ${{u}_{A}},{{u}_{B}} \in U$ такие, что
Относительно этих условий и условия регулярности имеет место следующее простое утверждение.
Предложение 2. Пусть допустимый процесс $(x,u,T)$ регулярен относительно фазовых ограничений. Тогда в концевых точках выполнены условия управляемости относительно фазовых ограничений.
Доказательство очевидно следует из определений. Перейдем к доказательству теоремы.
Доказательство теоремы 1. Рассмотрим заданный оптимальный процесс управления $(x{\kern 1pt} *,u{\kern 1pt} *,T{\kern 1pt} *)$, регулярный относительно фазовых ограничений. В силу предложения 2 в концевых точках выполнены условия управляемости относительно фазовых ограничений. Тогда ввиду результатов, полученных в [4], [7], [13], а также уточнений, сделанных в [8, лемма 4.1], существует невырождающий набор множителей Лагранжа $(\lambda ,\psi ,\mu )$ такой, что функция $\mu (t)$ непрерывна на $(0,T{\kern 1pt} *)$, и который удовлетворяет всем условиям принципа максимума, кроме условия нетривиальности, которое слабее, чем в теореме:
(30)
$\lambda + \ell \left( {\left\{ {t \in [0,T{\kern 1pt} *]:\;\psi (t) - \mu (t)\nabla g(x{\kern 1pt} *{\kern 1pt} (t)) \ne 0} \right\}} \right) > 0.$Ясно, что ввиду (30) и замечания 1 можно считать, что функция $\mu $ непрерывна на всем отрезке времени $[0,T{\kern 1pt} *]$.
Необходимо показать, что в условиях регулярности, сформулированных в этой работе, условие (30) влечет
(31)
$\lambda + \left| {\psi (t) - \mu (t)\nabla g(x{\kern 1pt} *{\kern 1pt} (t))} \right| > 0\quad \forall {\kern 1pt} t \in [0,T{\kern 1pt} *].$Для простоты изложения предположим, что $u{\kern 1pt} *{\kern 1pt} (t) \in \operatorname{int} U$ для п.в. $t$. (Общий случай рассматривается в полной аналогии.) При этом предположении из условия максимума следует, что
(32)
$H_{u}^{'}(x{\kern 1pt} *{\kern 1pt} (t),u,\psi (t),\lambda ) = \mu (t)\Gamma _{u}^{'}(x{\kern 1pt} *{\kern 1pt} (t),u)\quad \forall {\kern 1pt} u \in \mathcal{U}(t),\quad t \in [0,T{\kern 1pt} *],$Рассмотрим произвольную точку $t \in \mathcal{T}$. В силу регулярности $\Gamma _{u}^{'}(x{\kern 1pt} *{\kern 1pt} (t),{{u}_{0}}) \ne 0$ для некоторого ${{u}_{0}} = {{u}_{0}}(t) \in \mathcal{U}(t)$. Поэтому, взяв скалярное произведение (32) с $\Gamma _{u}^{'}(x{\kern 1pt} *{\kern 1pt} (t),{{u}_{0}})$, учитывая, что ${\text{|}}\Gamma _{u}^{'}(x{\kern 1pt} *{\kern 1pt} (t),{{u}_{0}}){\kern 1pt} {{{\text{|}}}^{2}} > 0$, получаем, что
(33)
$\mu (t) = \frac{{\left\langle {H_{u}^{'}(x{\kern 1pt} *{\kern 1pt} (t),{{u}_{0}}(t),\psi (t),\lambda ),\Gamma _{u}^{'}(x{\kern 1pt} *{\kern 1pt} (t),{{u}_{0}}(t))} \right\rangle }}{{{\text{|}}\Gamma _{u}^{'}(x{\kern 1pt} *{\kern 1pt} (t),{{u}_{0}}){\kern 1pt} {{{\text{|}}}^{2}}}}\quad \forall {\kern 1pt} t \in \mathcal{T}.$(34)
$\mu (t) \leqslant {\text{const}}(\lambda \; + \;{\text{|}}\psi (t){\kern 1pt} {\text{|}}{\kern 1pt} )\quad \forall {\kern 1pt} t \in \mathcal{T}.$Предположим, что условие (31) нарушено. Тогда $\lambda = 0$, и существует точка ${{t}_{0}} \in [0,T{\kern 1pt} *]$ такая, что $\psi ({{t}_{0}}) = \mu ({{t}_{0}})\nabla g(x{\kern 1pt} *{\kern 1pt} ({{t}_{0}}))$. Для $t \in [0,T{\kern 1pt} *]$ положим
Сначала рассмотрим случай ${{t}_{0}} \in \mathcal{T}$. После переобозначений оценка (34) принимает следующий вид
(35)
${\text{|}}\mu (t){\kern 1pt} {\text{|}} \leqslant {{C}_{1}}{\text{|}}\psi (t){\kern 1pt} {\text{|}}\quad \forall {\kern 1pt} t \in \mathcal{T}.$В силу свойства Липшиц-непрерывности сопряженной функции $\psi $ имеем
(36)
${\text{|}}\psi (t){\kern 1pt} {\text{|}} \leqslant K{\text{|}}t - {{t}_{{0{\kern 1pt} }}}{\text{|}}\quad \forall {\kern 1pt} t \in [0,T{\kern 1pt} *],$Докажем оценку
(37)
${\text{|}}\mu (t){\kern 1pt} {\text{|}} \leqslant {{C}_{1}}K{\text{|}}t - {{t}_{0}}{\kern 1pt} {\text{|}}\quad \forall {\kern 1pt} t \in [0,T{\kern 1pt} *].$Действительно, при $t \in \mathcal{T}$ эта оценка вытекает из (35) и (36). Рассмотрим точку $t \in [0,T{\kern 1pt} *]$, $t > {{t}_{0}}$, такую, что $t \notin \mathcal{T}$. Поскольку множество $\mathcal{T}$ замкнуто, а ${{t}_{0}} \in \mathcal{T}$, существует точка ${{t}_{*}} \in \mathcal{T}$, ${{t}_{0}} \leqslant {{t}_{*}} < t$, такая, что $\mathcal{T} \cap ({{t}_{*}},t] = \emptyset $. Для точки ${{t}_{*}}$ оценка (37) уже доказана. В то же время из [7, предложение 4.8] вытекает постоянство функции $\mu $ на $[{{t}_{*}},t]$. Эти рассуждения доказывают (37) справа от ${{t}_{0}}$. Точно такие же рассуждения проводятся и слева от точки ${{t}_{0}}$. Оценка (37) установлена.
Используя полученную оценку и (36), из сопряженного уравнения имеем
Отсюда
(38)
${\text{|}}\psi (t){\kern 1pt} {\text{|}} \leqslant K{{C}_{2}}({{C}_{1}} + 1)\frac{{{{{(t - {{t}_{0}})}}^{2}}}}{2}\quad \forall {\kern 1pt} t \in [0,T{\kern 1pt} *].$Переход к пределу при $n \to \infty $ показывает, что $\psi = 0$, $\mu = 0$. Значит, все множители равны нулю, что противоречит условию нетривиальности (30).
Случай ${{t}_{0}} \notin T$ легко свести к уже рассмотренному случаю из [7, предложение 4.8]. Условие (30) доказано.
Лемма 2. Пусть $(x{\kern 1pt} *,u{\kern 1pt} *,T{\kern 1pt} *)$ – оптимальный процесс в задаче $(2)$. Предположим, что выполнено условие: $0 \in \operatorname{int} f(x,U)$ $\forall {\kern 1pt} x \in {{\mathbb{R}}^{n}}$. Тогда $\exists {\kern 1pt} \delta > 0{\text{:}}$
Доказательство проводится стандартными рассуждениями от противного.
7. ЗАКЛЮЧЕНИЕ
В работе изучена задача управления мобильным роботом при наличии фазовых ограничений. В качестве критерия оптимальности рассмотрено быстродействие. На основе принципа максимума Понтрягина предложен алгоритм для вычисления решения. Однако прямое приложение принципа максимума не приводит к нужному результату, что обусловлено существенной нерегулярностью задачи относительно фазовых ограничений. Поэтому был предложен метод регуляризации задачи, который позволяет решить задачу приближенно с помощью $\varepsilon $-аппроксимаций. Этот метод применен к тестовой задаче о безынерционном движении трехколесного мобильного робота с передним приводом. Приведены результаты численного эксперимента. Настоящее исследование является завершением цикла работ [18]–[21] авторского коллектива по тематике задач быстродействия для мобильного робота при фазовых ограничениях.
Авторы выражают признательность рецензенту за сделанные замечания и интересный комментарий.
Список литературы
Filippov A.F. On certain problems of optimal regulation // Bull. Moscow State Univer., ser. Math. and Mech. 1959. V. 2. P. 25–38.
Pontryagin L.S., Boltyanskii V.G., Gamkrelidze R.V., Mishchenko E.F. The Mathematical Theory of Optimal Processes, Interscience, New York, 1962.
Gamkrelidze R.V. Optimal control processes with restricted phase coordinates // Izv. Akad. Nauk SSSR Ser. Mat. 1960. V. 24, P. 315–356.
Arutyunov A.V. Optimality conditions: Abnormal and Degenerate Problems. Mathematics and Its Application. Kluwer Acad. Publ., 2000.
Дубовицкий А.Я., Милютин А.А. Необходимые условия слабого экстремума в задачах оптимального управления со смешанными ограничениями типа неравенства // Ж. вычисл. матем. и матем. физ. 1968. Т. 8. № 4. С. 725–779.
Clarke F.H., Vinter R.B. Optimal multiprocesses // SIAM J. Control Optim. 1989. V. 27. № 5. P. 1072–1091.
Arutyunov A.V., Karamzin D.Yu. On some continuity properties of the measure lagrange multiplier from the maximum principle for state constrained problems // SIAM J. Control Optim. 2015. V. 53. № 4. P. 2514–2540.
Karamzin D., Pereira F.L. On a few questions regarding the study of state-constrained problems in optimal control // J. Optim. Theor. Appl. 2019. V. 180. № 1.
Chertovskih R., Karamzin D., Khalil N.T., Pereira F.L. An indirect method for regular state-constrained optimal control problems in flow fields // IEEE Transact. Automat. Control. 2021. V. 66. № 2. P. 787–793.
Арутюнов А.В., Карамзин Д.Ю. Свойства экстремалей в задачах оптимального управления с фазовыми ограничениями // Дифференц. ур-ния. 2016. Т. 52. № 11. С. 1464–1476.
Mordukhovich B.S. Variational Analysis and Generalized Differentiation. Vol. I. Basic Theory. Springer-Verlag, 2006, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Berlin.
Arutyunov A., Karamzin D. A survey on regularity conditions for state-constrained optimal control problems and the non-degenerate maximum principle // J. Optim. Theor. Appl. 2020. V. 184. № 3. P. 697–723.
Arutyunov A.V., Karamzin D.Yu., Pereira F.L. The maximum principle for optimal control problems with state constraints by R.V. Gamkrelidze: Revisited // J. Optim. Theory Appl. 2011. V. 149.
Arutyunov A.V., Karamzin D.Yu., Pereira F.L. Optimal Impulsive Control. The Extension Approach. Springer, 2011.
Chertovskih R., Karamzin D., Khalil N.T., Lobo Pereira F. Regular path-constrained time-optimal control problems in three-dimensional flow fields // Europ. J. Control. 2020. V. 56. P. 98–106.
Афанасьев А.П., Дикусар В.В., Милютин А.А., Чуканов С.А. Необходимое условие в оптимальном управлении. М.: Наука, 1990. 318 с.
Захаров Е.В., Карамзин Д.Ю. К исследованию условий непрерывности меры-множителя Лагранжа в задачах с фазовыми ограничениями // Дифференц. ур-ния. 2015. Т. 51. № 3. С. 395–401.
Дарьина А.Н., Дивеев А.И., Карамзин Д.Ю., Перейра Ф.Л., Софронова Е.А., Чертовских Р.А. Исследование метода возмущений для решения нерегулярных задач оптимального управления с фазовыми ограничениями // Вопросы теории безопасности и устойчивости систем. 2020. № 22. С. 25–51.
Дарьина А.Н., Дивеев А.И., Карамзин Д.Ю., Перейра Ф.Л., Софронова Е.А., Чертовских Р.А. Регулярные возмущения оптимального движения трехколесного мобильного робота с передним приводом при ограниченных фазовых переменных // Вопросы теории безопасности и устойчивости систем. 2020. № 22. С. 52–77.
Chertovskih R., Daryina A., Diveev A., Karamzin D., Pereira F.L., Sofronova E. Regular perturbations to the motion of a three-wheeled mobile robot with the front-wheel drive under restricted state variables // Europ. Control Conf. (ECC 2020), St-Petersburg, May 2020. P. 1210–1215. article 9143809.
Chertovskih R., Daryina A., Diveev A., Karamzin D., Pereira F.L., Sofronova E. Investigation of a perturbation method to solve essentially non-regular time-optimal control problems with state constraints // Europ. Control Conf. (ECC 2020), St-Petersburg, May 2020. P. 849–854. article 9143703.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики