Химия высоких энергий, 2019, T. 53, № 4, стр. 255-266
Кинетика радикально-цепной полимеризации. I. Зависящие от времени распределения макрорадикалов и олигомеров
И. П. Ким a, Е. И. Кац b, В. А. Бендерский a, *
a Институт проблем химической физики РАН
142432 Московская обл, Черноголовка, просп. Академика Семенова 1, Россия
b Институт Теоретической Физики им. Л.Д. Ландау РАН
142432 Московская обл, Черноголовка, просп. Академика Семенова 1, Россия
* E-mail: bender@icp.ac.ru
Поступила в редакцию 05.02.2019
После доработки 22.02.2019
Принята к публикации 25.02.2019
Аннотация
Представлено численное и аналитическое решение кинетических уравнений и соответствующих уравнений для моментов распределений макрорадикалов и олигомеров в процессе радикально-цепной полимеризации. Показано, что начальный рост цепи происходит в баллистическом режиме с участием первичных радикалов первого поколения. Передача цепи, в которой макрорадикал, реагируя с растворителем, образует олигомер и первичный радикал следующего поколения, вызывает переход от баллистического режима к диффузионному, в котором перемешиваются цепи различных поколений. Зависящие от времени распределения найдены при константах скорости роста и передачи цепи, не зависящих от ее длины.
I. ВВЕДЕНИЕ
Кинетические уравнения Смолуховского (УС) и Беккера–Деринга (УБД), первоначально предложенные в теории коагуляции бимолекулярно объединяющихся частиц и затем широко применяемые в физике конденсированных сред (например в теории зародышеобразования при фазовых переходах 1-го рода), относятся к двум различным сценариям агрегации и фрагментации растущих кластеров [1–13].
УС описывают необратимую агрегацию как систему связанных кинетических уравнений, учитывающих образование $n$-мера из $n{\text{'}}$- и $(n - n{\text{'}})$-меров и его гибель в последующих актах присоединения к нему любого $n$-мера
(1.1)
${\frac{{d{{P}_{n}}}}{{dt}} = \frac{{\text{1}}}{{\text{2}}}\sum\limits_{n{\text{'}} = {\text{1}}}^n {{{W}_{{n{\text{',}}n - n{\text{'}}}}}{{P}_{{n{\text{'}}}}}{{P}_{{n - n{\text{'}}}}}} - {{P}_{n}}\sum\limits_{n{\text{'}} = {\text{1}}}^\infty {{{W}_{{nn{\text{'}}}}}{{P}_{{n{\text{'}}}}}} },$(1.2)
${{{M}_{{\text{1}}}}(t) = \sum\limits_{n = {\text{1}}}^\infty {n{{P}_{n}}(t) = {{M}_{1}}} (0) = {{M}_{0}}}.$При не зависящих от $n$ и $n{\text{'}}$ константах скорости (все ${{W}_{{nn{\text{'}}}}} = W,$ масштаб измерения времени равен ${{\text{1/}}W}$) решение имеет вид
(1.3)
${{{{{P}_{n}}(t)} \mathord{\left/ {\vphantom {{{{P}_{n}}(t)} {{{M}_{0}}}}} \right. \kern-0em} {{{M}_{0}}}} = {{{\left( {t{\text{/2}}} \right)}}^{{n - {\text{1}}}}}{{{\left( {{\text{1}} + {t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}} \right)}}^{{ - {\text{(}}n + {\text{1)}}}}}}.$Зависящие от времени моменты распределения (1.3) равны
(1.4)
$\begin{gathered} {{M}_{{\text{0}}}}(t) = \sum\limits_{n = {\text{0}}}^\infty {{{P}_{n}}(t)} = {{M}_{0}}{{\left( {{\text{1}} + t{\text{/2}}} \right)}^{{ - 1}}}, \\ {{M}_{{\text{2}}}}(t) = \sum\limits_{n = 0}^\infty {{{n}^{{\text{2}}}}} {{P}_{n}}(t) = {{M}_{0}}\left( {{\text{1}} + t} \right). \\ \end{gathered} $Формулы (1.4) означают линейный рост размера агрегата (числа в нем мономерных единиц и его массы, определяемых как отношения M1/M0 и M2/M1). При больших n и t одного порядка (1.3) преобразуется в соотношение подобия
(1.5)
${{P}_{n}}(t) \approx {{\left( {{t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}} \right)}^{{ - {\text{2}}}}}{\text{exp}}\left( { - {{2n} \mathord{\left/ {\vphantom {{2n} t}} \right. \kern-0em} t}} \right),\,\,\,\,n,\,t \gg {\text{1,}}\,\,\,\,{t \mathord{\left/ {\vphantom {t n}} \right. \kern-0em} n} \sim 1.$Из (1.5) следует, что в асимптотической области (1.5) ММР не зависит от начальных условий.
УБД описывают совокупность последовательных присоединений и отщеплений от существующего агрегата одного мономера, приводящих к равновесному распределению размеров. Изменение концентрации $n$-меров ${{P}_{n}}(t),$ вызывает разность входящего и уходящего потоков в это состояние, обусловленных присоединением мономера к (n – 1)- и $n$-мерам и обратного перехода (n + 1) - в $n$- и $n$- в (n – 1)-меры при мономолекулярном отщеплении мономера с константами скорости ${{{V}_{{n + {\text{1}}}}}}$ и ${{{V}_{n}}}$
(1.6)
$\begin{gathered} \frac{{d{{P}_{n}}}}{{dt}} = {{J}_{{n - 1}}} - {{J}_{n}}, \\ {{J}_{n}} = {{W}_{{n,1}}}{{P}_{n}}{{P}_{{\text{1}}}} - {{V}_{{n + {\text{1}}}}}{{P}_{{n + {\text{1}}}}},\,\,\,n \geqslant {\text{2}}{\text{.}} \\ \end{gathered} $Зависящее от времени ММР, описываемое УБД, также удовлетворяет условию сохранения массы (1.2), которое, в отличие от УС, относится к процессу при динамическом равновесии. Когда все потоки равны нулю, устанавливаются равновесные концентрации $n$-меров ${{\tilde {P}}_{n}},$ равные
(1.7)
$\begin{gathered} {{{\tilde {P}}}_{n}} = \frac{{{{W}_{{n - {\text{1,1}}}}}}}{{{{V}_{n}}}}{{{\tilde {P}}}_{{\text{1}}}}{{{\tilde {P}}}_{{n - {\text{1}}}}} = ... = {{{\tilde {P}}}_{{\text{1}}}}\prod\limits_{j = {\text{1}}}^{n - {\text{1}}} {\frac{{{{W}_{{j,{\text{1}}}}}}}{{{{V}_{{j + {\text{1}}}}}}}} = {{{\tilde {P}}}_{{\text{1}}}}Q_{n}^{{\text{0}}}, \\ Q_{{\text{1}}}^{{\text{0}}} = {\text{1,}} \\ \end{gathered} $(1.8)
${{{W}_{{n,{\text{1}}}}}Q_{n}^{{\text{0}}} = {{V}_{{n + 1}}}Q_{{n + {\text{1}}}}^{{\text{0}}}}.$Квазистационарные состояния являются обобщением равновесных для открытых систем с постоянным потоком, и их концентрации определены условиями равенства нулю производных всех концентраций ${{d{{{\bar {P}}}_{n}}} \mathord{\left/ {\vphantom {{d{{{\bar {P}}}_{n}}} {dt}}} \right. \kern-0em} {dt}} = 0{\text{',}}$ когда потоки для всех кластеров одинаковы (все ${{{J}_{n}} = J}'$ независимо от $t$ и $n$), т.е. в системе в целом действует единый постоянный поток. Равновесное состояние является частным случаем квазистационарного, в котором $J$ = 0. Из этого определения и (1.6) следует, что квазистационарные концентрации зависят от постоянного потока, как параметра
(1.9)
${{\bar {P}}_{n}} = Q_{n}^{0}{{\left( {{{P}_{{\text{1}}}}} \right)}^{n}}\left( {1 - J\sum\limits_{j = 1}^{n - 1} {{1 \mathord{\left/ {\vphantom {1 {\left( {{{W}_{{j,1}}}Q_{j}^{0}{{{\left( {{{P}_{1}}} \right)}}^{{j - 1}}}} \right)}}} \right. \kern-0em} {\left( {{{W}_{{j,1}}}Q_{j}^{0}{{{\left( {{{P}_{1}}} \right)}}^{{j - 1}}}} \right)}}} } \right).$Область значений этого параметра J покрывает доступную область кинетических режимов от баллистического (все ${{{V}_{n}} = {\text{0}}}$) до равновесного. Когда обе константы скорости не зависят от $n,$ отношение скоростей агрегации и фрагментации определяет единственный параметр
При постоянной концентрации мономера, поддерживаемой внешним источником [6], и $\theta < 1,$ когда доминирует фрагментация, процесс заканчивается образованием равновесного распределения малых агрегатов
Когда $\theta > 1$ возникает квазистационарное состояние с ненулевым потоком и близким к равномерному распределением $n$-меров
Удивительной особенностью УС и УБД является появление при увеличивающихся с длиной цепи константах роста метастабильных состояний, о появлении которых сигнализирует нарушение условия сохранения первого момента распределения агрегатов по степени полимеризации (1.2). Это происходит при некотором характеристическом времени, называемым временем коагуляции. Именно поэтому эти уравнения широко используются не только для описания процессов образования неоднородных и фрактальных структур и кинетики фазовых переходов [10–12].
В отличие от поликонденсации, для которой выполнен детальный анализ УС и УБД [6, 9, 10] при различных зависимостях констант скоростей от длины цепи, для радикально-цепной полимеризации (РП) анализ этих уравнений, как правило, ограничивался широко известным решением в квазистационарном приближении (КСП) [14, 15]. Интерес к изучению зависящих от времени характеристик РП появился сравнительно недавно [16–18] и связан с двумя причинами. Во-первых, КСП, основанное на приближении среднего поля, применимо только для высокомолекулярных полимеров, когда скорость полимеризации усредняется по большому числу актов присоединения и флуктуации на масштабе числа звеньев, много меньшего длины цепи, подавляются, усредняясь по большому числу событий. Очевидно, что справедливость такого описания нарушается при рассмотрении олигомеров, т.е. агрегатов с более короткими (обычно наноразмерными) цепями. Во-вторых, ставшее актуальным получение полимеров со специальной архитектурой в наноразмерных масштабах длины фрагментов связано с полимеризацией, когда константы скорости отдельных процессов отличаются на несколько порядков (рассматривались константы ${{\sim }n}$ и ${{{n}^{{\text{2}}}}}$ [1, 8, 12]), и усреднение связано с учетом пространственно-временных распределений констант скорости. Отметим, что для разработки новых перспективных в приложениях материалов, актуально решение обратной задачи: каким должно быть распределение констант скорости, чтобы получить структуры с заданным пространственным молекулярно-массовым распределением (ММР). Прежде чем приступить к решению этой задачи, нужно изучить свойства кинетических уравнений, описывающих РП, и связанных с ними уравнений моментов распределений (УМР) для более простых задач. Этому малоизученному вопросу и посвящена настоящая работа, в которой кинетические уравнения РП с постоянными константами скорости рассмотрены на основе формализма, разработанного для УС и УБД [10–13].
Следует также отметить аналогию между получением олигомеров с управляемой структурой и распространением нелинейных волн превращения в реакционно-способных средах [19]. В обоих процессах возникают интересные явления, определяемые зависимостью констант скоростей от длины растущей цепи и степени превращения и вызывающие золь-гель переходы [14, 15]. Эти переходы рассматривались ранее как результат критического роста вязкости флюида, подавляющего диффузионно-ограниченный рост цепи. Кинетический механизм золь-гель переходов, инициируемых РП, ранее не рассматривался. По нашему мнению, интересно рассмотреть полимеризацию под этим углом зрения. Именно в этом и заключается цель нашей работы. Наш анализ основан на численном и аналитическом решении УС и УБД, модифицированных для описания кинетики РП в жидкой фазе. Особое внимание уделено зависящим от времени распределениям концентраций макрорадикалов и олигомеров.
Дальнейший план статьи таков. В разделе II из кинетических уравнений, описывающих общепринятую схему РП, выведены уравнения для зависящих от времени моментов распределений и найдено их аналитическое решение. Приведено также численное решение этих уравнений, иллюстрирующее особенности РП по сравнению с процессами коагуляции. В разделе III выводится уравнение для производящей функции, которое позволяет найти зависящие от времени концентрации макрорадикалов с заданной длиной цепи. Как любые задачи о случайных процессах, РП может иметь дуальное представление, в пространстве конформаций, меняющихся согласно соответствующим реакциям, или во времени, вводя характерное время для каждого шага превращения. Соответственно этому дуализму, в разделе IV полученные результаты формулируются в терминах волн возбуждения и превращения радикалов и цепей. В заключительном разделе V мы резюмируем полученные результаты и обсуждаем возможности их обобщения для решения более сложных задач. Некоторые технические детали вычислений представлены в Приложении.
II. КИНЕТИЧЕСКИЕ УРАВНЕНИЯ И УРАВНЕНИЯ МОМЕНТОВ ДЛЯ ПРОЦЕССА РП
Кинетическая схема цепного процесса РП включает: инициирование (создание начальной концентрации первичных радикалов ${R(0) = {{R}_{0}}}$ внешним воздействием, в частности, УФ или $\gamma $‑облучением), рост цепи (присоединение мономера с начальной концентрацией ${{{M}_{{\text{0}}}}}$ к первичному радикалу с образованием радикала ${{{R}_{{\text{1}}}}},$ который присоединяет мономер, превращаясь в ${{{R}_{{\text{2}}}}},$ и т.д. до макрорадикалов с растущей длиной цепи ${{{R}_{n}}}$),
(2.1)
$\begin{gathered} R + M\xrightarrow{{{{k}_{{g1}}}}}{{R}_{{\text{1}}}}, \\ {{R}_{{\text{1}}}} + M\xrightarrow{{{{k}_{{g2}}}}}{{R}_{{\text{2}}}}, \ldots , \\ {{R}_{{n - {\text{1}}}}} + M\xrightarrow{{{{k}_{{gn}}}}}{{R}_{n}} \\ \end{gathered} $и так называемую передачу цепи, при которой макрорадикал ${{{R}_{n}}}$ взаимодействует с молекулой флюида F, образуя полимер с тем же числом мономерных единиц ${{{P}_{n}}}$ и регенерируя первичный радикал
В однородной среде, вязкость которой не зависит от протекающего в ней превращения, можно ограничиться упрощенной схемой, в которой константы скорости роста и передачи цепи не зависят от степени полимеризации (длины цепи), и кинетика РП в масштабе времен ${1 \mathord{\left/ {\vphantom {1 {{{k}_{g}}M}}} \right. \kern-0em} {{{k}_{g}}M}}$ определяется одним параметром, равным отношению скоростей роста и передачи цепи
(2.3)
${k = {{{{k}_{t}}} \mathord{\left/ {\vphantom {{{{k}_{t}}} {{{k}_{g}}}}} \right. \kern-0em} {{{k}_{g}}}}{{M}_{{\text{0}}}}}.$Обе реакции предполагаются необратимыми. Схема РП отличается от моделей Смолуховского и Беккера–Деринга наличием двух подсистем. В подсистеме радикалов первичные радикалы превращаются в макрорадикалы в реакции (2.1) и регенерируются в реакции (2.2) с характерной концентрацией ${R(t)}.$ С другой стороны, полимеризация в подсистеме мономер–олигомер характеризуется концентрацией мономеров, которая на несколько порядков больше концентрации радикалов, ${{{M}_{{\text{0}}}} \gg {{R}_{{\text{0}}}}}.$ Этим двум масштабам концентраций соответствуют два масштаба времен, рост цепи радикалов происходит с характерным временем ${1 \mathord{\left/ {\vphantom {1 {{{k}_{g}}{{M}_{0}},}}} \right. \kern-0em} {{{k}_{g}}{{M}_{0}},}}$ а образование полимера происходит значительно медленнее в масштабе времен ${1 \mathord{\left/ {\vphantom {1 {{{k}_{t}}}}} \right. \kern-0em} {{{k}_{t}}}}.$ Отношение масштабов характеризует средняя длина цепи, т.е. число актов роста цепи ~${{{{{M}_{{\text{0}}}}} \mathord{\left/ {\vphantom {{{{M}_{{\text{0}}}}} {{{R}_{{\text{0}}}}}}} \right. \kern-0em} {{{R}_{{\text{0}}}}}},}$ после которых происходит передача цепи и регенерируется первичный радикал. Поскольку после полного превращения всех мономеров в олигомеры восстанавливается начальная концентрация первичных радикалов, РП можно рассматривать как автокаталитический процесс типа рассмотренных в [19].
Перечисленные особенности кинетики РП иллюстрирует рис. 1, на котором приведены зависящие от времени концентрации макрорадикалов с различной длиной цепи. Для коротких олигомеров $n \leqslant 20$ (при ${{R}_{{\text{0}}}},$ ${k \sim {\text{1}}{{{\text{0}}}^{{ - {\text{2}}}}}}$) кинетика ${{{R}_{n}}}$ включает две составляющие, из которых быстрая с максимумом при ${t_{m}^{{\left( 1 \right)}} \approx n}$ соответствует баллистическому росту цепи первого поколения, а медленная с максимумом при ${t_{m}^{{\left( 2 \right)}} \sim {{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} k}} \right. \kern-0em} k}}$ относится к последующим поколениям. С ростом $n$ эти компоненты смешиваются, образуя широкую область почти постоянных концентраций макрорадикалов. Таким образом, первоначальный баллистический рост коротких цепей с узким ММР, максимум которого смещается во времени, характерный для УС (см. (1.3)), переходит в диффузионный рост, присущий УБД и приводящий к широкому ММР. Особенность РП состоит в том, что между баллиститическим и диффузионным ростом расположена широкая промежуточная область, не описываемая ни УС, ни УБД.
Рис. 1.
Зависящие от времени концентрации макрорадикалов nRn, n = 2, 4, 7, 10, 15, 22, 31, кривые 1–7 соответственно. R0/M0 = 0.02, kt/kg M0 = 0.05.

Двум подсистемам соответствуют два закона сохранения, относящиеся к полному числу радикалов и суммарному числу мономеров в составе изолированных мономеров и в составе макрорадикалов и олигомеров
где введены безразмерные концентрации, отнесенные к начальной концентрации мономеров и(2.5)
${a = {{{{R}_{0}}} \mathord{\left/ {\vphantom {{{{R}_{0}}} {{{M}_{{\text{0}}}}}}} \right. \kern-0em} {{{M}_{{\text{0}}}}}}}.$Два условия сохранения относятся к первичным радикалам и нулевому моменту распределения макрорадикалов ${{{S}_{{\text{0}}}}}$ (с характерными величинами ${a \ll {\text{1}}}$) и первым моментам распределений макрорадикалов ${{{S}_{{\text{1}}}}}$ и олигомеров ${{{P}_{{\text{1}}}}}$ (порядка 1)
(2.6)
$\begin{gathered} {{S}_{k}}(t) = \sum\limits_{n = 1}^\infty {{{n}^{k}}} {{R}_{n}}(t),\,\,\,\,{{P}_{1}}(t) = \sum\limits_{n = 1}^\infty n {{P}_{n}}(t), \\ k = 0,1,2,.... \\ \end{gathered} $Кинетические уравнения имеют вид
(2.7)
$\begin{gathered} \dot {M} = - MR - M{{S}_{0}},\,\,\,\,\dot {R} = - MR + k{{S}_{0}}, \\ {{{\dot {R}}}_{n}} = M{{R}_{{n - 1}}} - \left( {M + k} \right){{R}_{n}},\,\,\,\,n \geqslant {\text{1,}} \\ {{{\dot {P}}}_{n}} = k{{R}_{n}},\,\,\,\,n \geqslant {\text{2,}} \\ \end{gathered} $а $R(t)$ подчиняется линейному уравнению
решение которого представлено в Приложении и при ${{\text{0}} < v < {\text{1}}}$ имеет вид
Численное решение уравнений (2.7)–(2.9) выполнено в кодах MATLAB по программе ODE113 для двух значений N = 100 и 200. Результаты совпадают при $k > 0.01.$
Кинетика $R\left( t \right)$ включает быстрый экспоненциальный спад (П3) с характерным временем ${{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {\left( {{{k}_{g}}{{M}_{{\text{0}}}} + {{k}_{t}}} \right)}}} \right. \kern-0em} {\left( {{{k}_{g}}{{M}_{{\text{0}}}} + {{k}_{t}}} \right)}}}$ от начального значения ${{{R}_{{\text{0}}}}}$ до ${{{{{R}_{{\text{0}}}}k} \mathord{\left/ {\vphantom {{{{R}_{{\text{0}}}}k} {(1 + k)}}} \right. \kern-0em} {(1 + k)}}},$ широкую область, в которой концентрация первичных радикалов мала и приблизительно постоянна, и последующее восстановление начальной концентрации в масштабе времени ${1 \mathord{\left/ {\vphantom {1 {{{k}_{t}}.}}} \right. \kern-0em} {{{k}_{t}}.}}$ Суммарная концентрация макроради-калов ${{{S}_{{\text{0}}}}}$ подчиняется уравнению
(2.10)
${{\dot {S}}_{{\text{0}}}} + \left( {k + \exp (--at)} \right){{S}_{{\text{0}}}} = \exp (--at)$и равна ${{{S}_{{\text{0}}}} \approx {{R}_{{\text{0}}}}{{{({\text{1}} + k)}}^{{ - {\text{1}}}}}}$ в широкой области t, так что при ${k \ll {\text{1}}}$ основная часть полимеризации происходит при суммарной концентрации макрорадикалов, близкой к ${{R}_{0}}.$ Макроскопические характеристики РП приведены на рис. 2. Широкая промежуточная область в кинетике связанной с радикалами подсиcтемы (кривые 1 и 2) соответствует КСП. Полимеризация включает промежуточное образование макрорадикалов, первый момент распределения которых имеет максимум, когда средние скорости роста и передачи цепи сравниваются по мере расхода мономера.
Рис. 2.
Макроскопические характеристики РП: расход мономеров $M(t)$, относительные изменения концентрации первичных радикалов ${{{{R}_{0}}(t)} \mathord{\left/ {\vphantom {{{{R}_{0}}(t)} {{{R}_{0}}(0)}}} \right. \kern-0em} {{{R}_{0}}(0)}}$ и суммарной концентрации макрорадикалов ${{{{S}_{0}}(t)} \mathord{\left/ {\vphantom {{{{S}_{0}}(t)} {{{R}_{0}}(0)}}} \right. \kern-0em} {{{R}_{0}}(0)}},$ концентрации мономерных звеньев в составе всех макрорадикалов ${{S}_{1}}(t)$ и олигомеров ${{P}_{1}}(t),$ кривые 1–5 соответственно. ${{{{R}_{0}}} \mathord{\left/ {\vphantom {{{{R}_{0}}} {{{M}_{0}}}}} \right. \kern-0em} {{{M}_{0}}}}$ = 0.03, ${{{{k}_{t}}} \mathord{\left/ {\vphantom {{{{k}_{t}}} {{{k}_{g}}{{M}_{0}}}}} \right. \kern-0em} {{{k}_{g}}{{M}_{0}}}}$ = 0.02.

Суммируя уравнения для макрорадикалов и учитывая (2.4), находим уравнения для моментов следующих порядков
(2.11)
$\begin{gathered} {{{\dot {S}}}_{{\text{1}}}} = MR + M{{S}_{0}} - k{{S}_{1}}, \\ {{{\dot {S}}}_{{\text{2}}}} = MR + M{{S}_{{\text{0}}}} + {\text{2}}M{{S}_{1}} - k{{S}_{2}}, \\ {{{\dot {S}}}_{{\text{3}}}} = MR + M{{S}_{0}} + {\text{3}}M{{S}_{1}} + {\text{3}}M{{S}_{2}} - k{{S}_{{\text{3}}}}, \\ {{{\dot {S}}}_{{\text{4}}}} = MR + M{{S}_{0}} + {\text{4}}M{{S}_{1}} + {\text{6}}M{{S}_{2}} + {\text{4}}M{{S}_{{\text{3}}}} - k{{S}_{{\text{4}}}}. \\ \end{gathered} $В отличие от УС и УБД, уравнения (2.11) линейны. Их решения – линейная комбинация экспонент с амплитудами и показателями, зависящими от $a$ и $k$
(2.12)
$\begin{gathered} {{S}_{1}} = \frac{a}{{a - k}}\left( {{{e}^{{ - kt}}} - {{e}^{{ - at}}}} \right), \\ {{S}_{2}} = {{S}_{1}} + \frac{2}{{(a - k)(2a - k)}} \times \\ \times \,\,\left( {(a - k){{e}^{{ - kt}}} - (2a - k){{e}^{{ - (a + k)t}}} + a{{e}^{{ - 2at}}}} \right). \\ \end{gathered} $Из (2.12) следует начальный рост моментов: ${{S}_{{\text{1}}}} \approx at,$ ${{S}_{{\text{2}}}} \approx {{S}_{{\text{1}}}} + a{{t}^{2}},$ $at < 1,$ $kt < {\text{1,}}$так что их отношение, определяющее среднюю массо-взвешенную длину цепи, линейно растет со временем
(2.13)
${{\left\langle {{{n}_{R}}} \right\rangle }_{{{\text{12}}}}} = {{{{S}_{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{S}_{{\text{2}}}}} {{{S}_{{\text{1}}}}}}} \right. \kern-0em} {{{S}_{{\text{1}}}}}} \approx {\text{1}} + t.$Формула (2.13) показывает, что, как и в модели Смолуховского, баллистический рост цепи пропорционален времени. Зависящие от времени средне-числовая ${{n}_{{01}}} > \,\,\,{{{{S}_{{\text{1}}}}} \mathord{\left/ {\vphantom {{{{S}_{{\text{1}}}}} {{{S}_{{\text{0}}}}}}} \right. \kern-0em} {{{S}_{{\text{0}}}}}}$ и массо-взвешенная длина цепи макрорадикалов приведены на рис. 3, вместе с отношениями моментов ${{\left( {{{{{S}_{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{S}_{{\text{2}}}}} {{{S}_{{\text{0}}}}}}} \right. \kern-0em} {{{S}_{{\text{0}}}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ и ${{\left( {{{{{S}_{{\text{4}}}}} \mathord{\left/ {\vphantom {{{{S}_{{\text{4}}}}} S}} \right. \kern-0em} S}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}$ и при малых t удовлетворяют (2.13). Наименьшей среди указанных отношений является средне-числовая длина, а наибольшей – средне-массовая. Как следует из (2.12), длина цепи макрорадикалов максимальна при v = 0 (в отсутствие передачи цепи) и уменьшается с ростом v (рис. 4), стремясь к нулю (в радикалах нет мономерных звеньев), когда полный расход мономера прекращает рост цепи.
Рис. 3.
Зависящая от времени средняя длина цепи макрорадикалов, найденная как отношения моментов ${{S}_{1}}{\text{/}}S,$ ${{\left( {{{{{S}_{2}}} \mathord{\left/ {\vphantom {{{{S}_{2}}} S}} \right. \kern-0em} S}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ ${{{{S}_{2}}} \mathord{\left/ {\vphantom {{{{S}_{2}}} {{{S}_{1}}}}} \right. \kern-0em} {{{S}_{1}}}},\,\,{{\left( {{{{{S}_{4}}} \mathord{\left/ {\vphantom {{{{S}_{4}}} S}} \right. \kern-0em} S}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}},$ кривые 1–4 соответственно. ${{{{R}_{0}}} \mathord{\left/ {\vphantom {{{{R}_{0}}} {{{M}_{0}}}}} \right. \kern-0em} {{{M}_{0}}}}$ = 0.01, ${{{{k}_{t}}} \mathord{\left/ {\vphantom {{{{k}_{t}}} {{{k}_{g}}{{M}_{0}}}}} \right. \kern-0em} {{{k}_{g}}{{M}_{0}}}}$ = 0.02.
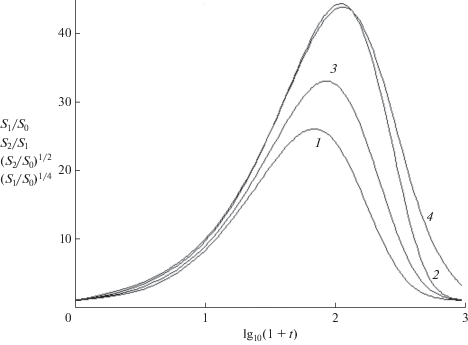
Рис. 4.
Зависимость средней длины цепи макрорадикалов ${{\left\langle {{{n}_{R}}} \right\rangle }_{{12}}}$от времени при различном отношении скоростей передачи и роста цепи. ${{{{k}_{t}}} \mathord{\left/ {\vphantom {{{{k}_{t}}} {{{k}_{g}}{{R}_{0}}}}} \right. \kern-0em} {{{k}_{g}}{{R}_{0}}}}$ = 0, 0.5, 1, 2, 3, кривые 1–5 соответственно. ${{{{M}_{{\text{0}}}}} \mathord{\left/ {\vphantom {{{{M}_{{\text{0}}}}} {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}}$ = 25.

Зависящая от времени средняя длина цепи олигомеров, найденная как отношения моментов ${{{{P}_{{\text{1}}}}} \mathord{\left/ {\vphantom {{{{P}_{{\text{1}}}}} P}} \right. \kern-0em} P},$ ${{\left( {{{{{P}_{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{P}_{{\text{2}}}}} P}} \right. \kern-0em} P}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ ${{{{P}_{2}}} \mathord{\left/ {\vphantom {{{{P}_{2}}} {{{P}_{1}}}}} \right. \kern-0em} {{{P}_{1}}}},$ ${{\left( {{{{{P}_{{\text{4}}}}} \mathord{\left/ {\vphantom {{{{P}_{{\text{4}}}}} P}} \right. \kern-0em} P}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}},$ представлена на рис. 5. Как и для макрорадикалов, массо-взвешенная и средне-числовая длина цепи соответствует границам полосы, в которой изменяются указанные моменты. Их начальный квадратичный рост относится к баллистическому режиму. Уменьшение длины цепи происходит при переходе к диффузионному росту.
Рис. 5.
Зависящая от времени средняя длина цепи олигомеров, найденная как отношения моментов ${{{{P}_{1}}} \mathord{\left/ {\vphantom {{{{P}_{1}}} P}} \right. \kern-0em} P},$ ${{\left( {{{{{P}_{2}}} \mathord{\left/ {\vphantom {{{{P}_{2}}} P}} \right. \kern-0em} P}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ ${{{{P}_{2}}} \mathord{\left/ {\vphantom {{{{P}_{2}}} {{{P}_{1}}}}} \right. \kern-0em} {{{P}_{1}}}},\,{{\left( {{{{{P}_{4}}} \mathord{\left/ {\vphantom {{{{P}_{4}}} P}} \right. \kern-0em} P}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}},$ кривые 1–4 соответственно. ${{{{R}_{0}}} \mathord{\left/ {\vphantom {{{{R}_{0}}} {{{M}_{0}}}}} \right. \kern-0em} {{{M}_{0}}}}$ = 0.01, ${{{{k}_{t}}} \mathord{\left/ {\vphantom {{{{k}_{t}}} {{{k}_{g}}{{M}_{0}}}}} \right. \kern-0em} {{{k}_{g}}{{M}_{0}}}}$ = 0.02.

III. УРАВНЕНИЕ ДЛЯ ПРОИЗВОДЯЩЕЙ ФУНКЦИИ
Чтобы найти зависящие от времени концентрации макрорадикалов ${{{R}_{n}}{\text{(}}t{\text{)}}}$, введем следующую производящую функцию
(3.1)
$\begin{gathered} G\left( {t,z} \right) = \sum\limits_{n = {\text{1}}}^N {{{R}_{n}}\left( t \right){\text{exp}}\left( { - nz} \right)} ,\,\,\,\,G\left( {{\text{0,}}z} \right) = {\text{0,}} \\ G{\text{(}}t,z{\text{)}} = {{S}_{0}}{\text{(}}t{\text{)}}{\text{.}} \\ \end{gathered} $Уравнение для производящей функции следует из суммы кинетических уравнений для РП, а граничные и начальные условия учитывают законы сохранения (2.4)
(3.2)
$\begin{gathered} \frac{{\partial G}}{{\partial t}} + {\text{(}}k + {\text{exp(}} - {\text{(}}at{\text{))(1}} - {\text{exp(}} - z{\text{))}}G{\text{(}}z,t{\text{)}} = \\ = {\text{exp(}} - {\text{(}}at{\text{))(1}} - {\text{exp(}} - z{\text{))}}R{\text{(}}t{\text{)}}. \\ \end{gathered} $Уравнение (3.2) совпадает с уравнением (2.10) с заменой ${{{e}^{{ - at}}}}$ на ${{e}^{{ - at}}}\left( {{\text{1}} - {{e}^{{ - z}}}} \right),$ так что решение можно найти тем же методом, что и уравнений (2.9) и (2.10), введя в (П9) вместо переменной (П4) новую переменную
Разлагая производящую функцию в ряд по степеням ${{e}^{{ - z}}},$ находим
(3.4)
${{R}_{n}}{\text{(}}t{\text{)}} = {{{\text{(}} - {\text{1)}}}^{n}}{{\left. {\frac{{{{\partial }^{n}}G}}{{\partial {{z}^{n}}}}} \right|}_{{z = 0}}},$как коэффициенты этого ряда. Формулы производных неполных гамма-функций (П12) взяты из [31]. Хотя такое решение полезно для проверки приближенных и численных решений, оно, как и аналогичные решения УС и УБД [10, 11], слишком громоздко и неудобно для анализа. Поэтому ограничимся описанием результатов численных расчетов. ММР макрорадикалов (рис. 6) изменяются во времени. При ${t < {\text{50}}}$ образуются узкие ММР с зависящим от $t$ максимумом, обусловленные баллистическим ростом. В интервале $0.5 < at < 2$ при ${{k \mathord{\left/ {\vphantom {k a}} \right. \kern-0em} a} \leqslant {\text{1}}}$ ММР уширяется, охватывая интервал длин цепи от 1 до ${1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a},$ что соответствует диффузионному росту, когда концентрация макрорадикалов квазистационарна. При $t \gg {1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}$ преимущественно образуются короткие цепи из-за уменьшающейся концентрации мономера. Зависящие от времени ММР олигомеров (рис. 7) также демонстрируют изменение распределения в трех указанных временных интервалах. При ${at \gg 1}$ полимеризация заканчивается образованием ММР, в котором доминируют короткие олигомеры.
Рис. 6.
Массо-взвешенное распределение макрорадикалов в моменты времени t = 10, 20, 50, 100, 150 , кривые 1–5 соответственно. ${{{{R}_{0}}} \mathord{\left/ {\vphantom {{{{R}_{0}}} {{{M}_{0}}}}} \right. \kern-0em} {{{M}_{0}}}}$ = 0.03. ${{{{k}_{t}}} \mathord{\left/ {\vphantom {{{{k}_{t}}} {{{k}_{g}}{{M}_{0}}}}} \right. \kern-0em} {{{k}_{g}}{{M}_{0}}}}$ = 0.04.

Рис. 7.
Массо-взвешенное распределение олигомеров в моменты времени t = 10, 20, 50, 100, 150, кривые 1–5 соответственно. ${{{{R}_{0}}} \mathord{\left/ {\vphantom {{{{R}_{0}}} {{{M}_{0}}}}} \right. \kern-0em} {{{M}_{0}}}}$ = 0.03. ${{{{k}_{t}}} \mathord{\left/ {\vphantom {{{{k}_{t}}} {{{k}_{g}}{{M}_{0}}}}} \right. \kern-0em} {{{k}_{g}}{{M}_{0}}}}$ = 0.04.

Фрактальную структуру определяет степенная зависимость линейного размера и объема агрегата от числа мономеров в его составе
(3.5)
$R(n) = {{R}_{0}}{{n}^{{{1 \mathord{\left/ {\vphantom {1 {{{d}_{f}}}}} \right. \kern-0em} {{{d}_{f}}}}}}},\,\,\,V(n) = \frac{{4\pi }}{3}R_{0}^{3}{{n}^{{{3 \mathord{\left/ {\vphantom {3 {{{d}_{f}}}}} \right. \kern-0em} {{{d}_{f}}}}}}},$Аномальный дробный порядок реакций в неоднородных средах возникает при усреднении скорости по совокупности пространственных конфигураций [23–26]. Появление подобного эффекта следует ожидать и для РП с широким ММР, когда концентрация определяет рост цепей многих поколений. Дробный порядок РП проявляется в зависимости средней длины цепи макрорадикалов и олигомеров от константы скорости передачи цепи ${{k}_{t}}$
(3.6)
$\left\langle {{{n}_{R}}} \right\rangle ,\,\,\,\left\langle {{{n}_{P}}} \right\rangle \sim k_{t}^{h},$IV. ВОЛНЫ ВОЗБУЖДЕНИЯ И ПРЕВРАЩЕНИЯ
Кинетическим аналогом баллистического роста цепи при малых скоростях передачи цепи (${{{{k}_{g}}{{M}_{0}}} \mathord{\left/ {\vphantom {{{{k}_{g}}{{M}_{0}}} {{{k}_{t}} \gg 1}}} \right. \kern-0em} {{{k}_{t}} \gg 1}}$) является превращение реагента А в последовательность интермедиатов ${{X}_{n}}$ в результате необратимых мономолекулярных реакций, заканчивающихся образованием конечного продукта $B$
(4.1)
$\begin{gathered} A\xrightarrow{{{{k}_{1}}}}{{X}_{1}}\xrightarrow{{{{k}_{1}}}}{{X}_{2}} \cdots {{X}_{N}}\xrightarrow{{{{k}_{1}}}}B, \\ A(0) = {{A}_{0}},\,\,\,\,{{X}_{n}}(0) = B(0) = 0, \\ \end{gathered} $которая описывается распределением Пуассона для неравновесных концентраций
(4.2)
$X\left( {n,u} \right) = {{A}_{0}}\exp \left( { - u} \right)\frac{{{{u}^{n}}}}{{n!}},\,\,\,\,u = {{k}_{1}}t.$В окрестности максимума зависящего от времени распределения, в котором ${{n}_{m}}(t) = {{k}_{1}}t,$ концентрации преобразуются в нормальное распределение
(4.3)
$\begin{gathered} X\left( {n,u} \right) \approx X\left( {{{n}_{m}},u} \right)\exp \left( { - \frac{{{{{\left( {n - {{n}_{m}}} \right)}}^{2}}}}{{2{{n}_{m}}}}} \right), \\ 1 \ll {{n}_{m}} \leqslant N. \\ \end{gathered} $Формулы (4.3) показывают, что в достаточно длинной последовательности необратимых мономолекулярных реакций изменение распределения во времени соответствует движению волнового пакета с постоянной скоростью по оси n, которое сопровождается его расплыванием. Кинетическая схема (1.1) описывает наиболее простую модель волны возбуждения (концентрации ${{X}_{n}}$ последовательно возрастают, а затем уменьшаются после прохождения фронта), в которой роль пространственной координаты выполняет число актов превращения n . Если последовательно вступающие в реакции интермедиаты образуют пространственную молекулярную цепочку узлов, кинетическая схема (1.1) описывает концентрационные волны в такой цепочке. Последовательно происходят превращения соседних узлов. В зависимости от отношения констант скорости прямой и обратной реакций возникают волны возбуждения (переход реагента в продукт, расположенный на концах цепочки, интермедиаты, расположенные во внутренних узлах цепочки, остаются в начальном состоянии) и превращения (фронт волны разделяет реагенты и продукты, на фронте волны степень превращения изменяется от 0 до 1). Когда превращения в соседних узлах являются реакциями первого порядка, волны возбуждения и превращения обладают широкими фронтами. Параметры фронтов незначительно изменяются при бимолекулярных превращениях элементов. Существенное изменение картины распространения, вплоть до остановки фронтов и возникновения автоколебаний концентраций интермедиатов, происходит в реакциях более высокого порядка и под действием внешних потоков реагентов [19, 27–30]. Как следует из (1.3), (1.5) и (1.8), эти общие свойства сложных химических систем можно описать с помощью обобщенных УС и УБД. В волне возбуждения образуются цепи с узким ММР и средней длиной цепи, пропорциональной времени роста $\bar {n} \approx t.$ ММР в волне превращения содержит цепи с длинами от 0 до $n\sim t.$ В отличие от моделей, описываемых УС и УСБ, в которых возникают волны только одного типа, в кинетике РП существуют и волны возбуждения и волны превращения, которые переходят одни в другие.
V. ВЫВОДЫ
1. В общепринятом механизме РП, кинетика роста цепей макрорадикалов и олигомеров не описывается с помощью УС и УБД.
2. Квазистационарное приближение, широко используемое для описания РП, не позволяет найти многообразие кинетических характеристик.
3. Основной особенностью РП является наличие двух связанных подсистем – радикальной, где первичные радикалы превращаются в макрорадикалы и обратно, и полимерной, в которой мономеры необратимо превращаются в олигомеры.
4. Основными характеристиками процесса является баллистический и диффузионный рост цепей с широкой промежуточной областью, в которой происходит резкое изменение ММР. Баллистический рост цепи первого поколения аналогичен распространению волны возбуждения (волнового пакета, в котором цепь увеличивается на одно мономерное звено). При диффузионном росте смешиваются цепи многих поколений, создаваемых многократной регенераций первичных радикалов.
5. Основная особенность РП – зависимость распределений от кинетических параметров и времени – обеспечивает принципиальную возможность получить полимеры с управляемым многомодовым ММР. Переход от одно- к двухмодовому ММР наблюдается в сопровождающейся золь-гель переходом РП тетрафторэтилена [14, 15] и виниловых мономеров [17].
Работа выполнена при финансовой поддержке Программы Фундаментальных Исследований Президиума РАН ПФИ I.55П и по теме Государственного задания № 0089-2014-0025.
Список литературы
Ziff R.M., Stell G. // J. Chem. Phys. 1980. V. 73. P. 3492.
Leyvraz F., Tschudi H.R. // J. Phys. A. 1982. V. 15. P. 1951.
Ziff R.M., Ernst M.H., Hendriks E.M. // J. Phys. A. 1983. V. 16. P. 2293.
Kuchanov S.I. // Adv. Polym. Sci. 1992. V. 103. P. 3.
Blackman J.A., Marshall A. // J. Phys. A. 1994. V. 27. P. 725.
Davies S.C., King J.R., Wattis J.A.D. // J. Phys. A. 1999. V. 32. P. 7745.
Duncan D.B., Soheili A.R. // Appl. Numer. Math. 2001. V. 37. P. 1.
Leyvraz F. // Phys. Reps. 2003. V. 383. P. 95.
Kuchanov S.I., Slot H., Stroeks A. // Progr. Polym. Sci. 2004. V. 29. P. 513.
Wattis J.A.D., Bolton C.D., Coveney P.V. // J. Phys. A. 2004. V. 37. P. 2895.
Wattis J.A.D. // J. Phys. A. 2006. V. 39. P. 7283.
Wattis J.A.D. // Physica D. 2006. V. 222. P. 1.
Leyvraz F. // Phys. Reps. 2003. V. 383. P. 95.
Kim I.P., Benderskii V.A. // High Energy Chem. 2011. V. 45. P. 372.
Kim I.P., Benderskii V.A. // High Energy Chem. 2015. V. 49. P. 1.
Lynd N.A., Hillmyer M.A. // Macromolecules 2007. V. 40. P. 8050.
Zhao T., Zheng Y., Poly J., Wang W. // Nature Comm. 2013. V. 4. P. 1873.
Gentekos D.T., Dupuis L.N., Fors B.P. // J. Am. Chem. Soc. 2016. V. 138. P. 1848.
Лоскутов А.Ю., Михайлов А.С. Введение в синергетику. М.: Наука. 1990.
Mandelbrot B.B. The Fractal Geometry of Nature. N.Y.: Freeman. 1983.
Zilman A., Kiefer J., Molino F., porte G., Safran S.A. // Phys. Rev. Lett. 2003. V. 91. P. 015901.
Kim I.P., Benderskii V.A. // High Energy Chem. 2010. V. 44. P. 357.
Ben-Avrahan D., Halvin S. // Diffusion and Reactions in Fractal and Disordered Systems. Cambridge. : Cambridge Univ. Press. Cambridge. 2000.
CamposD., Mendez V., Fort J. // Phys. Rev. E. 2002. V. 69. P. 031115.
Kopelman R. // J. Statist. Phys. 1986. V. 42. P. 185.
Kopelman R. // Science. 1988. V. 241. P. 1620.
Ouellette N.T., Gollub J.P. // Phys. Fluids. 2008. V. 20. P. 064104.
Mikhailov A.S., Ertl G. // Phys. Chem. Chem. Phys. 2009. V. 10. P. 86.
Engineering of Chemical Complexity. Lecture Notes in Complex Systems. V. 11. Mikhailov S.A. (Eds). Singapore. World Scientific. 2013.
Halvin S., Ben-Avraham D. // Advan. Phys. 2002. V. 51. P. 187.
Бейтмен Г., Эрдейи А. // Высшие трансцендентные функции. М.: Наука. 1965. Т. 2.
Дополнительные материалы отсутствуют.
Инструменты
Химия высоких энергий


