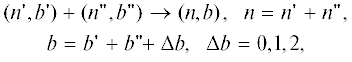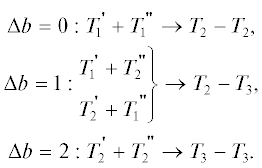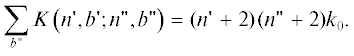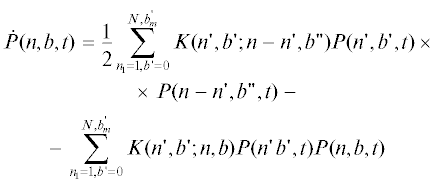Химия высоких энергий, 2021, T. 55, № 3, стр. 171-180
Кинетика поликонденсации IV. Рост ациклических случайно разветвленных цепей
И. П. Ким a, А. С. Коткин a, В. А. Бендерский a, *
a Федеральное государственное бюджетное учреждение науки Институт проблем химической физики
Российской академии наук
142432 Московская обл., Черноголовка, просп. акад. Семенова, 1, Россия
* E-mail: bender@icp.ac.ru
Поступила в редакцию 10.12.2020
После доработки 24.12.2020
Принята к публикации 10.01.2021
Аннотация
Кинетические уравнения для концентраций $nb$-меров ($n$ – число звеньев, $b$ – число случайно расположенных среди них разветвлений) в процессе поликонденсации трифункциональных мономеров (ПК-3), учитывают совокупность необратимых последовательно-параллельных реакций между функциональными группами $(n,b)$ и $(n{\kern 1pt} ',b{\kern 1pt} ')$-меров с константами скорости $\chi (b,b{\kern 1pt} ')$. Стехиометрические коэффициенты равны числу перестановок групп, образующих связь, при $\Delta (b + b{\kern 1pt} ') = $ 0, 1, 2. Координаты реакций объединяются в сеть неоднородного марковского процесса. Показано, что гипотеза Флори (все $\chi (b,b{\kern 1pt} ')$ одинаковы) приводит к не зависящему явно от времени гауссову распределению ${{W}_{n}}(b)$ с максимумом ${{b}_{{\max }}}$, линейно растущим с длиной цепи $n$.
I. ВВЕДЕНИЕ
В предыдущей статье [1], на примере поликонденсации трифункциональных метоксисиланов (ПК-3), показано, что рост цепей сопровождается ростом числа образующихся в них разветвлений. Чтобы описать кинетику такого роста, недостаточно обычно используемых кинетических уравнений для суммарных концентраций всех конформеров с заданной длиной цепи $n$ [2–5] и необходимо разделить совокупность $n$-меров на подгруппы по числу разветвлений $b$, максимальное число которых равно
где ${{[n} \mathord{\left/ {\vphantom {{[n} 2}} \right. \kern-0em} 2}]$ – целая часть числа ${n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0em} 2}$. Разделение не только увеличивает число переменных, которое квадратично растет ($\sim {{[{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0em} 2}]}^{2}}$), но и число путей роста, в которых образуются $n$-меры с изменяющимся числом разветвлений где первое из условий – длина цепи продукта реакции (2) равна сумме длин цепи партнеров, – означает отсутствие обратных реакций расщепления продуктов, а изменение числа разветвлений обусловлено реакциями между звеньями с различным числом связей с партнерами. Если $\Delta b$ = 0, в реакции (2) участвуют концевые звенья партнеров $T_{1}^{'}$ и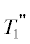 (с одной связью с ближайшим соседом в цепи), которые превращаются в два линейных
звена (с двумя связями) $n$-мера ${{T}_{2}} - {{T}_{2}}$. $\Delta b$ = 1, когда линейное звено партнера образует связь с концевым звеном другого и в цепи
$n$-мера появляются линейное звено и разветвление (с тремя связями) ${{T}_{2}} - {{T}_{3}}$. $\Delta b$ = 2 в реакции между линейными звеньями, превращающимися в два разветвления в $n$-мере
(с одной связью с ближайшим соседом в цепи), которые превращаются в два линейных
звена (с двумя связями) $n$-мера ${{T}_{2}} - {{T}_{2}}$. $\Delta b$ = 1, когда линейное звено партнера образует связь с концевым звеном другого и в цепи
$n$-мера появляются линейное звено и разветвление (с тремя связями) ${{T}_{2}} - {{T}_{3}}$. $\Delta b$ = 2 в реакции между линейными звеньями, превращающимися в два разветвления в $n$-мере
Дополнив реакции (3) реакциями с участием мономеров
(4)
$\begin{gathered} {{T}_{0}} + {{T}_{0}} \to 2{{T}_{1}},\,\,\,\,{{T}_{0}} + {{T}_{1}} \to {{T}_{1}} + {{T}_{2}}, \\ {{T}_{0}} + {{T}_{2}} \to {{T}_{2}} + {{T}_{3}} \\ \end{gathered} $получим кинетическую схему для описания ПК-3, в которой $(nb)$-меры характеризуются тремя целыми числами ${{T}_{k}}$, зависящими от $n$ и $b$
и константы скорости реакций (2) связаны с константами скоростей реакций (3) и (4) $\chi (k{\kern 1pt} ',k)$ стехиометрическими коэффициентами ${{C}_{{kk'}}}$, равными, согласно закону действующих масс, произведению чисел этих групп в партнерах:
(6)
$\begin{gathered} K({{T}_{k}},{{T}_{{k{\kern 1pt} '}}}) = {{C}_{{kk{\kern 1pt} '}}}T{}_{k}{{T}_{{k{\kern 1pt} '}}}, \\ {{C}_{{kk'}}} = (f - k)(f - k{\kern 1pt} '){{T}_{k}}{{T}_{{k{\kern 1pt} '}}}\chi (k,k{\kern 1pt} '). \\ \end{gathered} $Отметим, что кинетическая схема с шестью константами скорости
справедлива при дополнительном предположении, что “элементарные” константы (7) не зависят от длины цепи и числа разветвлений в партнерах, т.е. одинаковы во всех стереоизомерах, образующихся при перестановках ${{T}_{k}}$ с сохранением $n$ и $b$. Представление $nb$-мера (5) соответствует условиям изучения структуры полиалкоксисиланов методом ЯМР 29Si, в котором измеряются зависящие от времени концентрации атомов кремния с различным числом связей Si–O–Si [1, 6–11], что позволяет описать ПК-3 кинетическими уравнениями для измеряемых концентраций nb-меров. Дальнейшее общепринятое упрощение кинетической задачи связано с уменьшением числа констант (7). Гипотеза Флори [12–14] предполагает, что для идеально гибкой цепи, состоящей из одинаковых звеньев с равновероятным угловым распределением образующихся связей, все 6 констант $\chi (k,k{\kern 1pt} ')$ одинаковы и равны единственной константе ${{k}_{0}}$, определяющей масштаб времени превращения
которую можно исключить, перейдя от лабораторного времени $t$ к безразмерному времени ${{k}_{0}}Nt$, где $N$ − начальная концентрация мономеров.
В приближении Флори вместо концентраций nb-меров можно ввести суммарные концентрации $n$-меров со всеми возможными разветвлениями
для которых кинетические уравнения Смолуховского описывают необратимые последовательные реакции и не зависят от числа разветвлений
(10)
${{\dot {P}}_{n}} = \frac{1}{2}\sum\limits_{n' = 1}^{n - 1} {K\left( {n{\kern 1pt} ',n - n{\kern 1pt} '} \right){{P}_{{n{\kern 1pt} '}}}{{P}_{{n - n{\kern 1pt} '}}}} - \sum\limits_{n' = 1}^N {K(n,n{\kern 1pt} '){{P}_{n}}{{P}_{{n{\kern 1pt} '}}}} ,$определяется произведением чисел функциональных групп в партнерах.
Первоначальное обоснование гипотезы Флори, справедливость которой для органических полимеров многократно подтверждалась [11–17], состояло в том, что рост цепи происходит в обратимых квазистационарных условиях, близких к термодинамическому равновесию по схеме Беккера–Деринга [4–6], когда отношение концентраций реагентов и продуктов, в согласие с условием детального баланса, однозначно определяется разностью их свободных энергий
(12)
$\begin{gathered} \Delta G_{{nn'}}^{0} = \Delta H_{{nn{\kern 1pt} '}}^{0} - T\Delta S_{{nn{\kern 1pt} '}}^{0}, \\ \Delta S_{{nn{\kern 1pt} '}}^{0} = \Delta {{S}_{\chi }} + {{k}_{B}}\ln {{C}_{{nn{\kern 1pt} '}}} \\ \end{gathered} $и не зависит от пути перехода $n$ в $n{\kern 1pt} '$. Это объяснение нельзя считать обоснованным, поскольку изменения свободных энергий стереоизомеров (например, углеводородов) в зависимости от числа разветвлений достигают 5–7 Ккал/моль [18, 19], что изменяет константы равновесия более чем на два порядка. Согласно теории переходного состояния (ТПС), константа скорости термически активированного перехода равна [20–23]
(13)
$\begin{gathered} K(n,n{\kern 1pt} ') = \frac{{{{k}_{B}}T}}{{2\pi \hbar }}\exp ({{\alpha }_{{nn{\kern 1pt} '}}}{{\Delta {{S}_{{nn{\kern 1pt} '}}}} \mathord{\left/ {\vphantom {{\Delta {{S}_{{nn{\kern 1pt} '}}}} {{{k}_{B}}}}} \right. \kern-0em} {{{k}_{B}}}}) \times \\ \times \,\,\exp (--\alpha \Delta {{H}_{{nn{\kern 1pt} '}}}{\text{/}}{{k}_{B}}T),\,\,\,\,\Delta {{H}_{{nn}}} = H_{n}^{0} - H_{{n{\kern 1pt} '}}^{0}, \\ \Delta {{S}_{{inn{\kern 1pt} '}}} = S_{n}^{0} - S_{{n{\kern 1pt} '}}^{0} \\ \end{gathered} $(14)
${{\alpha }_{{nn{\kern 1pt} '}}} = \partial G_{{nn{\kern 1pt} '}}^{\# }{\text{/}}\partial \Delta {{G}_{{nn{\kern 1pt} '}}},\,\,\,\,0 < {{\alpha }_{{nn{\kern 1pt} '}}} < 1$связывает свободную энергию активации $\Delta G_{{nn'}}^{\# }$ и свободную энергию реакции. Энтропия реакции $\Delta {{S}_{{nn'}}}$ является суммой изменения энтропии элементарной реакции и изменения конфигурационной энтропии, определяемого стехиометрическими коэффициентами в (6) и (11), так что гипотеза Флори означает равенство элементарных констант (8) для всех переходов между nb- и $n{\kern 1pt} 'b{\kern 1pt} '$-мерами, т.е. свободных энергий и коэффициентов переноса в реакциях (3) и (4). Равенство коэффициентов переноса требует также одинаковых энергий реорганизации в переходном состоянии для всех реакций. Отметим, что кинетическая модель (10) и (11) относится к необратимым реакциям, в противоречие с предположением Флори. Даже перечисление указанных аргументов дает основание считать причину равенства элементарных констант до сих пор не установленной. По-видимому, ее следует искать в свойствах самой кинетической задачи, которая не сводится к уравнениям (11), допускающим простое аналитическое решение [3, 4, 13–16]. Учет разветвлений заменяет последовательный рост $n$-меров множеством разветвляющихся параллельно-последовательных путей, которые формируют изменяющийся со временем канал реакции вокруг криволинейного пути наиболее вероятного роста и одновременного разветвления nb-меров. В таком описании процесс ПК-3 становится подобным рассматриваемому в ТПС наиболее вероятному пути реакции, вдоль которого свободная энергия минимальна, а ширина окружающего этот путь канала определяется распределением плотности траекторий с растущими энергиями [20–24]. Подобные модели на основе ТПС начали разрабатываться недавно для сетей сложных биохимических процессов матричной репликации [25–30]. Наши поиски в текущей литературе не обнаружили статей, посвященных подобному рассмотрению ПК-3.
В настоящей статье, в качестве первого шага в исследовании этой еще нерешенной задачи, мы рассмотрим кинетику необратимого роста цепей со случайными разветвлениями, в которой константы скорости реакций (2) различны даже в приближении Флори из-за различия стехиометрических коэффициентов (6), и представим более богатую картину роста цепи по сравнению с (10) и (11), когда рост цепи изменяет число и распределение в ней разветвлений. Статья состоит из следующих разделов. Во втором разделе построена древовидная разветвляющаяся с ростом $n$ сеть координат реакций, в которой $nb$-меры являются вершинами, а кратность соединяющих их ребер, обозначающих переходы между вершинами, равна коэффициентам (6). Пользуясь этой сетью, найдены константы скорости реакций образования и аннигиляции nb-меров и выявлена скрытая симметрия констант скорости переходов (2) в приближении Флори (8). В третьем разделе рассмотрены кинетические уравнения для концентраций и найдены их численные решения в том же приближении (8). В четвертом разделе описаны функции распределения по числу разветвлений, которые явно не зависят от времени (постоянны при постоянных $n$), но зависят от длины цепи. Их моменты характеризуют изменения структуры цепи в процессе ПК-3 и наиболее вероятный путь в nb-плоскости. Обсуждения результатов, в том числе причин выполнения гипотезы Флори (8), связанных с перемешиванием путей в сети, собраны в пятом разделе.
II. СЕТЬ КООРДИНАТ РЕАКЦИЙ ПОЛИКОНДЕНСАЦИИ
Представим рост цепи графически. Каждый nb-мер в представлении (5) считаем вершиной. Вершины с заданными значениями n расположим в одном ряду. Соединяющими вершины направленными ребрами (стрелками) изобразим переходы (2) с фиксированным значением $\Delta n$ и кратностью, равной стехиометрическому числу перехода (6). Получившаяся структура для присоединения мономеров ($\Delta n$ = 1) показана на рис. 1а и имеет вид дерева с корнем (100) и растущим числом вершин в последовательных рядах. Аналогичное построение для присоединения димеров ($\Delta n$ = 2) изображают два дерева с корнями (100) и (200) и удвоенными номерами рядов (рис. 1б). Для мономеров и димеров, в которых ${{T}_{2}}$ = 0, возможны два перехода $\Delta b$ = 0, 1. Начиная с присоединения тримеров, возникают также переходы $\Delta b$ = 2 (рис. 1в, 1г). Продолжив аналогичное построение, получим сеть координат для всей совокупности параллельно-последовательных реакций в процессе ПК-3. Следует указать, что эта сеть координат реакций отличается от обычно используемого графического представления полимеров [32, 33], в котором химический граф, состоящий из вершин (звеньев) и ребер (связей между ними) схематически представляет структуру одного полимера, а не путь его образования. В рассматриваемых нами деревьях ребра определяют не химические связи, а потоки реагентов, т.е. скорости превращений.
Рис. 1.
Деревья, отображающие присоединения мономеров (а), димеров (б), тримеров (в, г) к растущим $nb$-мерам.
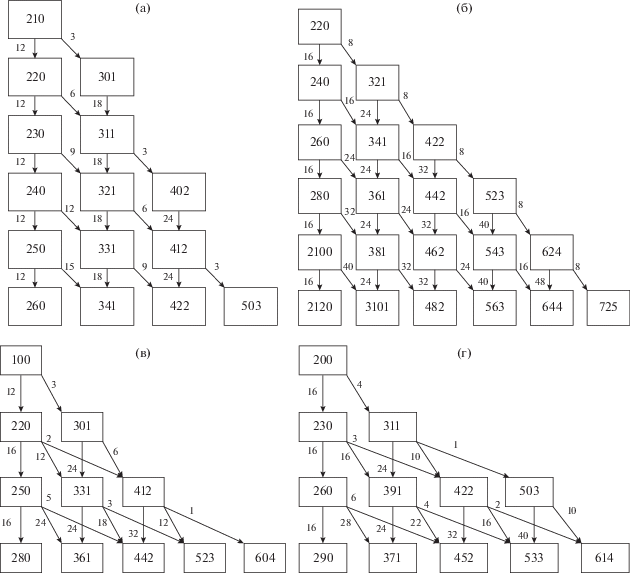
Стехиометрические коэффициенты, указанные на рис. 1, непосредственно следуют из (3)–(6) и показывают, что суммарная скорость перехода (2) для всех $n{\kern 1pt} 'b{\kern 1pt} '$-меров одинаковой длины (одного ряда) во все доступные состояния nb-меров одинакова, не зависит от $b'$,$b$ и равна константе скорости перехода (11) в уравнениях (10)
Свойство симметрии (15) следует из сохранения числа звеньев при переходе, когда одновременно с образованием разветвления ($\Delta {{T}_{3}} = 1$) образуется концевая группа $\Delta {{T}_{1}} = 1$ и $\Delta {{T}_{2}} = - 2$.
ПК-3, как разветвленный цепной процесс, образует сеть, составленную из цепей Маркова, описывающих стохастические процессы с отсутствием памяти о предыдущих событиях. Росту цепи с $n \leqslant N$ за счет присоединения одного и того же $n{\kern 1pt} 'b{\kern 1pt} '$-мера (рис. 1), соответствует дерево, вершинами которого являются состояния конечной цепи Маркова. Согласно их классификации [31, 32], необратимым реакциям (2) соответствуют переходы между невозвратными состояниями с поглощающей границей $n = N$, на которой для всех $n$ вероятности переходов ${{C}_{{N,n > N}}} = 0$. Поскольку вероятности переходов зависят от $(nb),(n{\kern 1pt} 'b{\kern 1pt} ')$, цепь Маркова является неоднородной. Эргодические цепи Маркова описывают последовательности обратимых реакций, когда возможны переходы между всеми состояниями (в том числе и через другие состояния), так что пробная частица, попавшая в эргодическое множество, никогда его не покидает. Переходы в эргодических цепях образуют циклы возврата с конечным периодом. Вероятность посещения любого состояния в эргодическом множестве стремится к 1 при $t = \infty $. Объединив все эргодические $(r - s)$ и невозвратные ($s)$ состояния в группы, матрицу перехода можно представить в канонической форме
где $Q$ – матрица переходов в множестве невозвратных состояний, $R$ – матрица переходов из невозвратных состояний в эргодические, $S$ – матрица переходов в эргодической цепи. Нулевая матрица (верхняя правая клетка) обозначает отсутствие переходов из эргодического множества в не принадлежащие к нему состояния. Эргодическое множество, состоящее из одного элемента, является поглощающим. Множеству поглощающих состояний из $q$ элементов соответствует единичная матрица $I$ ($q \times q$). Матрица для переходов (2), т.е. из невозвратных состояний в поглощающие, имеет вид где $R$ ($q \times s$) – прямоугольная матрица переходов из $s$ невозвратных в $q$ поглощающие состояния.III. КИНЕТИЧЕСКИЕ УРАВНЕНИЯ
Чтобы применить кинетическую модель к росту случайно разветвленных ациклических цепей, разделим все $n$-меры с концентрацией ${{P}_{n}}(t)$ на подгруппы с постоянным числом разветвлений и концентрациями ${{P}_{{nb}}}(t)$. Уравнения Смолуховского для концентраций $(nb)$-меров имеют вид
с начальными условиями
Граничное условие при $n = N$ определяет поток вещества, уходящего из системы: этот поток равен нулю, если число звеньев в процессе ПК-3 сохраняется.
Численное решение кинетических уравнений (18) выполнено в кодах MATLAB по программе ODE113, дополненной подпрограммой расчета стехиометрических коэффициентов (6) по формулам (3)–(5). Значения коэффициентов для коротких цепей приведены на рис. 1. Расчеты проведены на персональном компьютере с рабочей частотой процессора 4 Ггц и оперативной памятью 16 Гб. При $N$ = 50 время расчета составляло 15 мин.
Если справедлива гипотеза Флори (8), разветвления ${{T}_{3}}$ образуются с одинаковой вероятностью при рекомбинации свободных функциональных групп во всех парах ${{T}_{1}} + {{T}_{2}} \to {{T}_{2}} + {{T}_{3}}$ и ${{T}_{2}} + {{T}_{2}} \to 2{{T}_{3}}$, так что равновесное распределение $n$-меров по числу случайно расположенных разветвлений $b$ определяется вероятностью разместить $b$ звеньев ${{T}_{3}}$ среди ($n - b - 2$) звеньев с двумя связями ${{T}_{2}}$
(20)
$W_{{nb}}^{*} = {{B}_{n}}\frac{{(n - b - 2)!}}{{b!(n - 2b - 2)!}},\,\,\,B_{n}^{{ - 1}} = \sum\limits_{b = 0}^{[{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0em} 2}]} {W_{{nb}}^{*}} ,$Стокмайер, впервые рассмотревший уравнения (10) [13] (см. также [14]), показал, что равновесная функция распределения $n$-меров, учитывающая конфигурационную энтропию, воспроизводит константы скорости в этих уравнениях, справедливых для необратимых реакций. Однако, как показано выше, это свойство кинетических уравнений не связано с установлением равновесия между прямой и обратной реакцией, а следует из закона действующих масс. По аналогии с (21), введем функцию распределения ${{W}_{{nb}}}$ для неравновесных концентраций nb-меров, представив их относительные концентрации в $n$-мере в виде
и найдем ${{W}_{{nb}}}$ из решения (18) с константами скоростей, пропорциональными стехиометрическим коэффициентам. Численное решение показывает (рис. 2), что отношения ${{{{P}_{{nb}}}(t)} \mathord{\left/ {\vphantom {{{{P}_{{nb}}}(t)} {{{P}_{n}}}}} \right. \kern-0em} {{{P}_{n}}}}$ не зависят от времени в изученной широкой области изменения переменных: 0 $ \leqslant {{k}_{0}}t \leqslant $ 10, 1 $ \leqslant n \leqslant N$, $0 \leqslant b \leqslant [n{\text{/}}2]$, где максимальная длина цепи $N$ изменялась от 6 до 50. Значения ${{W}_{{nb}}}$ приведены в табл. 1. В согласии с (20) зависимости ${{W}_{n}}(b)$, приведенные на рис. 2 и 3, имеют вид гауссианов, у которых максимум ${{b}_{{\max }}}$ линейно, а полуширина $\sigma $ сублинейно растут с ростом длины цепи
(23)
$\begin{gathered} {{W}_{{nb}}} = {{\pi }^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{\sigma }^{{ - 1}}}\exp ( - (b - {{b}_{{\max }}}){\text{/}}{{\sigma }^{2}}), \\ {{b}_{{\max }}} \cong 0.253n - 1.001, \\ \sigma \cong (0.461 + 0.086n){\text{/}}(1 + 0.018n). \\ \end{gathered} $Рис. 2.
Не зависящее от времени распределение nb-меров по числу разветвлений, равное (22), ${{W}_{{nb}}} = {{{{P}_{{nb}}}(t)} \mathord{\left/ {\vphantom {{{{P}_{{nb}}}(t)} {{{P}_{n}}(t)}}} \right. \kern-0em} {{{P}_{n}}(t)}}$. На панелях слева показано, что ${{W}_{{nb}}}$ постоянны в широком интервале $t$. Нормированные распределение ${{W}_{n}}(b)$, показанные на панелях справа, имеют форму гауссианов (23). Значения $n$ равны 10,20,30 на панелях сверху вниз соответственно. Значения $b$ указаны на горизонтальных прямых слева.
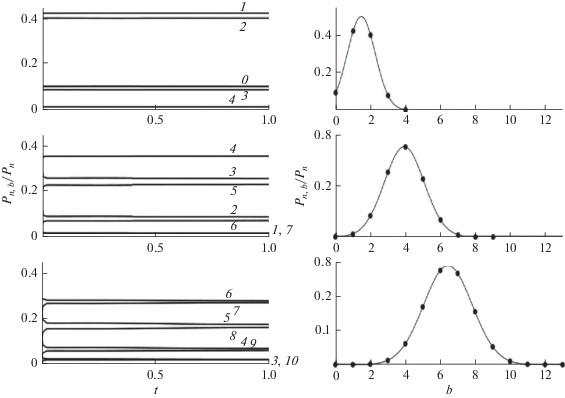
Таблица 1.
Нормированное распределение $n$-меров по числу разветвлений $b$
| n\b | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 0.857 | 0.143 | |||||||||||
| 6 | 0.503 | 0.470 | 0.027 | ||||||||||
| 8 | 0.231 | 0.552 | 0.211 | 0.007 | |||||||||
| 10 | 0.094 | 0.424 | 0.402 | 0.079 | 0.002 | ||||||||
| 12 | 0.035 | 0.257 | 0.454 | 0.225 | 0.028 | 0.001 | |||||||
| 15 | 0.007 | 0.093 | 0.321 | 0.385 | 0.169 | 0.024 | 0.001 | ||||||
| 18 | 0.001 | 0.027 | 0.155 | 0.342 | 0.324 | 0.129 | 0.020 | 0.001 | |||||
| 21 | 0.007 | 0.059 | 0.207 | 0.339 | 0.269 | 0.101 | 0.017 | 0.001 | |||||
| 24 | 0.002 | 0.019 | 0.096 | 0.244 | 0.321 | 0.223 | 0.080 | 0.014 | 0.001 | ||||
| 27 | 0.005 | 0.037 | 0.134 | 0.265 | 0.295 | 0.185 | 0.064 | 0.012 | 0.001 | ||||
| 36 | 0.001 | 0.008 | 0.038 | 0.114 | 0.216 | 0.264 | 0.209 | 0.107 | 0.035 | 0.007 |
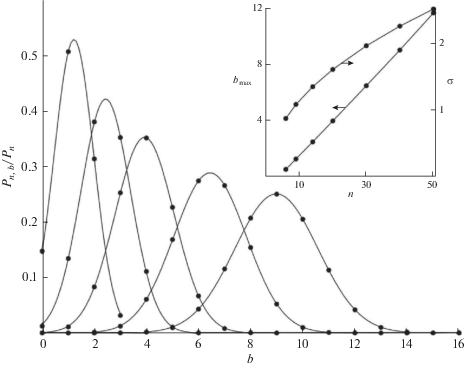
Рис. 3.
Нормированное распределение nb-меров по числу разветвлений (23). Зависимости ${{b}_{{\max }}}(n)$ и $\sigma (n)$ показаны на вставке. Значения n на кривых слева направо равны 9, 14, 20, 30, 40.
Найденная зависимость близка к комбинаторному соотношению (18), аппроксимируемому гауссианом с заменой факториалов по формуле Стирлинга
Это совпадение показывает, что зависящее от времени распределение $nb$-меров в процессе ПК-3 можно приближенно представить произведением аналитического решения (10), найденного в [13, 14], и не зависящего от времени распределения (21)
(25)
$\begin{gathered} {{P}_{{nb}}}(t) = {{W}_{{nb}}}{{P}_{n}}(t), \\ {{P}_{n}}(t) = \frac{{3(2n)!}}{{(n - 1)!(n + 2)!}}{{\alpha }^{{n - 1}}}{{(1 - \alpha )}^{{n + 2}}}, \\ \alpha = 3t{{(1 + 3t)}^{{ - 1}}}. \\ \end{gathered} $Выражения (25) справедливы для неограниченных систем ($N = \infty $) в области времен, меньших критического $t \leqslant {{t}_{c}}$ = 1/3. При $t = {{t}_{c}}$ второй момент расходится, а первый начинает уменьшаться. Оба эти свойства решения
(25) показывают, что в критической точке возникает новая фаза – гель, т.е. бесконечный
кластер (БК), в который направлен поток образующихся $n$-меров с длиной цепи $n \to \infty $. В замкнутой конечной системе ($n \leqslant N$) бимолекулярные реакции роста цепи (2) возможны только при 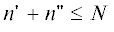 , так что гель не образуется: первый момент сохраняется при всех $t$, ${{M}_{1}}(\infty ) = 1$, а второй момент монотонно растет до ${{M}_{2}}(\infty ) = N$. Поликонденсация заканчивается образованием $N$-меров при $t = \infty $. Чтобы воспроизвести появление критической точки в конечной системе, необходимо учесть
в правых частях кинетических уравнений потоки с образованием $n$-меров с $n > N$, т.е. сделать систему открытой. Если сохранить число уравнений равным $N$ и учесть бимолекулярные реакции между всеми $n{\kern 1pt} '$- и
, так что гель не образуется: первый момент сохраняется при всех $t$, ${{M}_{1}}(\infty ) = 1$, а второй момент монотонно растет до ${{M}_{2}}(\infty ) = N$. Поликонденсация заканчивается образованием $N$-меров при $t = \infty $. Чтобы воспроизвести появление критической точки в конечной системе, необходимо учесть
в правых частях кинетических уравнений потоки с образованием $n$-меров с $n > N$, т.е. сделать систему открытой. Если сохранить число уравнений равным $N$ и учесть бимолекулярные реакции между всеми $n{\kern 1pt} '$- и 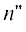 -мерами (
-мерами (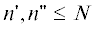 ), максимальная длина цепи в продуктах ПК-3 равна $2N$. В такой открытой системе (с удвоением длины цепи) кинетика ПК-3 воспроизводит появление
критической точки ${{t}_{c}} = 1{\text{/}}3$, но максимальное значение второго момента остается конечным: ${{M}_{2}}({{t}_{c}}) \approx $ 10 при $N$= 50. Кинетику в пост-гелевой области характеризуют монотонный рост массы в геле,
при слабо изменяющейся длине цепи в обеих фазах.
), максимальная длина цепи в продуктах ПК-3 равна $2N$. В такой открытой системе (с удвоением длины цепи) кинетика ПК-3 воспроизводит появление
критической точки ${{t}_{c}} = 1{\text{/}}3$, но максимальное значение второго момента остается конечным: ${{M}_{2}}({{t}_{c}}) \approx $ 10 при $N$= 50. Кинетику в пост-гелевой области характеризуют монотонный рост массы в геле,
при слабо изменяющейся длине цепи в обеих фазах.
IV. РАСПРЕДЕЛЕНИЕ n-МЕРОВ ПО ЧИСЛУ РАЗВЕТВЛЕНИЙ
Поскольку распределение (23) зависит от изменяющейся во времени длины цепи, моменты распределения $nb$-меров
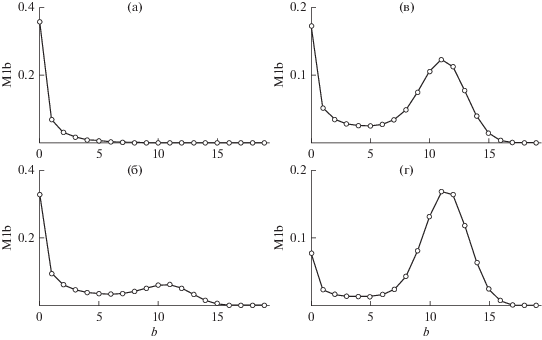
дают возможность найти изменение распределения по числу разветвлений в процессе ПК-3. Распределение первого момента ($s$ = 1) представлено на рис. 4. Верхняя панель слева ($t$ = 0.2) показывает начальный рост $nb$-меров с $n \leqslant 5$ (см. табл. 1), среди которых доминируют неразветвленные. Нижняя панель слева (t = 0.4) показывает, что уменьшение концентрации коротких $n$-меров сопровождается появлением и ростом дополнительного максимума распределения сильно разветвленных $nb$-меров. На панелях справа ($t$ = 0.6 сверху и 1.0 снизу) вклад сильно разветвленных $nb$-меров становится основным и соответствует образованию сильно разветвленных $Nb$-меров. Интервал длин цепи, в котором структура $nb$-меров изменяется от слабо к сильно разветвленной, определяют средне-числовая и средне-массовая длина цепи, равные отношениям соответствующих моментов
(27)
${{\left\langle n \right\rangle }_{{10}}} = {{{{M}_{1}}(b)} \mathord{\left/ {\vphantom {{{{M}_{1}}(b)} {{{M}_{0}}(b)}}} \right. \kern-0em} {{{M}_{0}}(b)}},\,\,\,{{\left\langle n \right\rangle }_{{21}}} = {{{{M}_{2}}(b)} \mathord{\left/ {\vphantom {{{{M}_{2}}(b)} {{{M}_{1}}(b)}}} \right. \kern-0em} {{{M}_{1}}(b)}}.$Рис. 4.
Первый момент распределения (26) в зависимости от времени $t = $.0.2, 0.4, 0.6, 1.0 на панелях а–г соответственно.
Среднее число разветвлений в растущих цепях равно
(28)
$\left\langle {b(t)} \right\rangle = \sum\limits_{n = 1}^N {n{{P}_{n}}(t)\sum\limits_{b = 0}^{[n/2]} {b{{B}_{n}}(b)} } .$Благодаря линейному смещению максимума гауссиана ${{B}_{n}}(b)$ с ростом $n$ (23) и (24)
среднее число разветвлений пропорционально второму моменту ${{P}_{n}}(t)$, который для $N = \infty $ расходится в критической области ${{t}_{c}} \approx {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}$, где начинается гелеобразование, обусловленное образованием цепей с длиной $N$.
Переходы между состояниями (5) можно сопоставить с динамической системой, в которой движение может быть эргодическим и движением с перемешиванием [34–38]. При эргодическом движении траектории последовательно заполняют объем с периодичностью движения сложного маятника с медленно изменяющейся частотой. Напротив, при перемешивании сразу образуется рыхлая сетка, заполняющая весь объем, а затем перемешивание траекторий создает более плотную сетку, изменяя ее структуру [35, 36]. Начальный рост концентраций n-меров, когда доминирует один путь, напоминает эргодическое движение. Первоначально присоединяются мономеры по вертикали на схеме рис. 1а ($\Delta n = 1,\,\,\Delta b = 0$), затем появляются слабо разветвленные nb-меры, растущие быстрее линейных, вследствие больших стехиометрических коэффициентов. По мере расхода мономеров, доминирующим становится присоединение димеров с $\Delta b = 0$, а затем и с $\Delta b = 1$ (по схеме рис. 1б). После уменьшения концентрации димеров, основной рост обусловлен присоединением тримеров и т.д. Однако последующий рост цепи изменяется, в него вовлекается множество $nb$-меров с различной длиной цепи и числом разветвлений, создавая множество пересекающихся траекторий с разными скоростями переходов (см. рис. 1в и г), что соответствует движению с перемешиванием. Это изменение характера движения иллюстрирует рис. 5, на котором представлены зависящие от времени первые моменты nb-меров с различным числом разветвлений. На начальном участке ($t < $ 0.3) доминирует медленный рост коротких линейных цепей. В интервале (0.3 $ \leqslant t \leqslant $ 0.5) происходит перемешивание, а затем рост сильно разветвленных $nb$-меров с длиной цепи, близкой к $N$.
Рис. 5.
Зависящие от времени первые моменты распределения nb-меров с числом разветвлений, указанным на кривых. $N$ = 50.
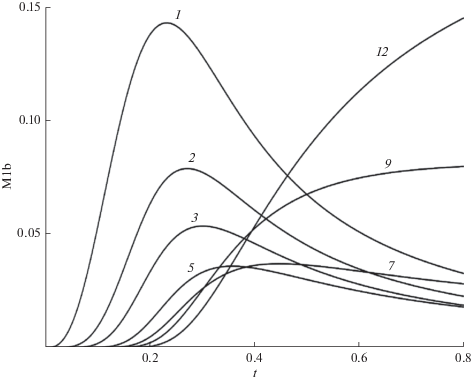
В теории динамических систем [34–38] показано, что именно перемешивание вызывает переход от регулярного движения к стохастическому. Его отличия от эргодического движения – разбегание траекторий, подавление парных корреляций и появления энтропии перемешивания, обусловлены тем, что состояния системы связаны с локальной неустойчивостью состояний, населенности которых определяются множеством проходящих через них траекторий. Эти отличия являются общими для разветвляющихся процессов, в том числе ПК-3. Введенная Колмогоровым энтропия перемешивания (см. [34–36]) обусловлена ростом огрубленного фазового объема, ограниченного огибающей множества разбегающихся траекторий
Выражение (30) означает, что, при сохранении начального фазового объема, следующего из теоремы Лиувилля, огрубленный фазовый объем увеличивается. Связанная с увеличением этого объема энтропия перемешивания линейно возрастает со временем
и ее инкремент $h$ не зависит от способа разбиения фазового пространства и огрубления. Характеристикой перемешивания в целом является предел ${{\Delta {{S}_{{mix}}}} \mathord{\left/ {\vphantom {{\Delta {{S}_{{mix}}}} t}} \right. \kern-0em} t}$ при ${{\Gamma }_{0}} \to 0,\,\,t \to \infty $, равный $h$. Статистические закономерности движения в системах с одинаковыми значениями $h$ одинаковы.
В применении этих свойств систем с перемешиванием к рассматриваемой нами модели отметим, что в огрубленной модели роста $n$-меров (10), (11) число траекторий ~N/2, а при росте $nb$‑меров (18) оно ~N2/4, так что движение в огрубленной модели близко к эргодическому, а при росте разветвленных $nb$-меров становится перемешивающимся с $h\sim {{k}_{B}}\ln (N{\text{/}}2)$. Этой энтропии соответствует изменение свободной энергии, превышающее возможный разброс значений элементарных констант (7). Возникающее в рассмотренной нами кинетической модели перемешивание, как универсальное явление, приводит к эффективным значениям констант (7), усредненным по совокупности траекторий, вне зависимости от справедливости гипотезы Флори (8).
V. ВЫВОДЫ
1. Вместо модели Флори–Стокмайера, являющейся огрубленным представлением ациклических полимеров только длинной цепи и не учитывающей изменение их структуры в процессе ПК-3, предложена расширенная кинетическая модель, в которой полимер характеризуют длина цепи $n$ и число ее разветвлений b.
2. Показано, что в расширенной модели распределение по числу разветвлений является универсальным (не зависит от времени и пути образования nb-меров) и имеет вид гауссиана (23) с зависящими от $n$ максимальным значением и дисперсией. Рост цепи сопровождается увеличением наиболее вероятного числа разветвлений $\sim \,{n \mathord{\left/ {\vphantom {n 4}} \right. \kern-0em} 4}$.
3. Показано, что предложенная модель ПК-3 изоморфна моделям статистических динамических систем, в которых огрубление вызывает перемешивание большого числа траекторий и создает дополнительную энтропию перемешивания, логарифмически растущую с максимальной длиной цепи.
4. Перемешивание усредняет константы скорости элементарных бимолекулярных реакций (2) между функциональными группами nb-меров по множеству путей, проходящих через заданное состояние, что обеспечивает статистическое равенство констант (7), не связанное с гипотезой Флори (8).
5. Универсальность найденного распределения (23) и явления перемешивания путей дают основание предположить, что на основе предложенной модели роста nb-меров можно построить кинетическую модель гелеобразования, в котором рост цепей сопровождается увеличением числа разветвлений и найти их характеристики как в до-гелевой, так и пост-гелевой областях.
Список литературы
Ким И.П., Черняк А.В., Бендерский В.А. // Химия высоких энергий. 2021. Т. 55. № 2.С. 128−138.
Wattis J.A.D. // J. Phys. A. 2006. V. 39. P. 7283.
Leyvraz F. // Phys. Rep. 2003. V. 383. P. 95.
Wattis J.A.D. // Physica D. 2006. V. 222. P. 1.
Duderstadt F., Dreyer W. // J. Stat. Phys.2006. V.123. P. 55.
Brinker C.J., Scherer G.W./ / Sol-Gel Science. Physics and Chemistry of Sol-Gel Processing. 1990. Academic Press. Boston.
Ng L.V., Thompson P., Sanchez J., Macosko W., McCormick A.V. // Macromolecules 1995. V. 28. P. 6471.
Brunet F. // J.Non-Crystal.Solids. 1998. V.231. P.58.
Rankin S.E., Kasehagen L.J., McCormick A.V., Macosko C.W. // Macromolecules. 2000. V. 33. P. 7639.
Matejka L., Dukh O., Hlavata D., Meissner B., Brus J. // Macromolecules 2001. V. 34. P. 6904.
Dong H., Zhang Z., lee M-H., Mueller D.W., Reidy R.F. // J. Sol-Gel Sci. 2007. V. 41. P.11.
Flory P.J. // Principles of Polymer Chemistry. 1979. Cornell University Press. Ithaca. N.Y.
Stockmayer W.H. // J. Chem. Phys. 1943. V. 11. P. 45.
Ziff R.M., Stell G. // J. Chem. Phys. 1980. V.73. P. 3492.
Ерухимович И.Я. // ЖЭТФ. 1995. Т. 108. С. 1004.
Tamm M.V., Nechaev S.K., Erukhimovich I.Y. // Eur. Phys. J. E. 2005. V. 17. P. 209.
Everaers R., Grosberg A.Y., Rubinstein M., Rosa A. // Soft Matter. 2017. V. 13. P. 1223.
Tatevskii V.M., Benderskii V.A., Jarovoi S.S. // Rules and Methoda for calculation of physic0-chemical properties of paraffinic hydrocarbons. 1961. Pergamon Press. Oxford.
Lyman W.J., Reehl W.F. // Handbook of Chemical Property Estimation Methods. 1990. ACS. Washington.
Miller W.H. // J. Phys. Chem. 1983.M. 87. V.87. P. 3811.
Truhlar D.G., Garrett B.C.// J. Chem. Phys. 1987. V. 84. P. 365.
Hanggi P., Talkner P., Borkovec M. // Rev. Mod. Phys. 1990. V. 62. P. 251.
Benderskii V.A., Makarov D.E., Wight C.A. // Chemical Dynamics at Low Temperatures. 1994. Wiley. N.Y.
Benderskii V.A., Veytoshkin E.V., Irgibaeva I.S., Trommsdorff H.-P. // Chem. Phys. 2000. V. 262. P. 393.
Krivov S.V., Karplus M.// J. Phys. Chem. B. 2006. V. 141. P. 12689.
Andrieux D., Gaspard P. // Proc. Nat. Acad. Sci. USA 2008. V. 105. P. 2516.
Peters B., Bolhuis P.G., Mullen G.G., Shea J-E. // J. Chem. Phys. 2013. V. 138. № 054106.
Lu J., Vanden-Eijnden E. // J. Chem. Phys. 2014. V. 141. № 044109.
Sartori P., Pigolotti S. // Phys. Rev. X. 2015. V. 5. № 041039.
Chiuchi D., Ferrare J., Pigolotti S. // Phys. Rev. E. 2019. V. 100. № 062502.
Kemeny J.G., Snell J.L.,Knapp A.W. Denurable Markov chains. 1976. Springer. N.Y.
Levin D.A., Peres Y., Wilmer E.L. (2009). Markov Chains and Mixing Times. Providence, RI: Amer. Math. Soc. MR2466937.
Goutsias J., Jenkinson G. // Phys. Rep. 2013. V. 529. P. 199.
Sinai Ya.G. Introducrionto Ergodic Theory. Princeton Univ. Press. Guilford. 1977.
Chirikov B.V. // Phys. Rep. 1979. V. 52. P. 263.
Zaslavsky G.M. Chaos in Dynamical Systems. Harwood. N.Y. 1985.
Gutzwiller M.C. Chaos in classical and quantum dynamics. 1990. Springer. Berlin.
Nakamura K. Quantum versus chaos. 1997. Kluver Acad. Publ. Dordrecht.
Дополнительные материалы отсутствуют.
Инструменты
Химия высоких энергий