Химия высоких энергий, 2021, T. 55, № 4, стр. 255-265
Кинетика поликонденсации: V. Зависящий от времени состав золь- и гель-фаз
В. А. Бендерский a, *, Е. И. Кац b, И. П. Ким a, А. С. Коткин a
a Федеральное государственное бюджетное учреждение науки Институт проблем химической физики
Российской академии наук
142432 Московская обл., Черноголовка, просп. Академика Семенова, 1, Россия
b Институт Теоретической Физики им. Л.Д. Ландау РАН
142432 Московская обл., Черноголовка, просп. Академика Семенова 1, Россия
* E-mail: bender@icp.ac.ru
Поступила в редакцию 24.02.2021
После доработки 05.03.2021
Принята к публикации 12.03.2021
Аннотация
Зависящие от времени концентрации $n$-меров $P(n,t)$ найдены из численного решения кинетических уравнений для системы, содержащей в начальный момент времени $t = 0$ конечное число мономеров $N$ от 32 до 1024, где рост цепи ограничен, $n \leqslant N$, и суммарная масса фаз сохраняется до и после гель-точки ${{T}_{0}}$. Показано, что из свойства динамического самоподобия кластеров с различными $N$ следует, что в золе ${{P}_{s}}(n,N,t > {{T}_{0}})$ = $P(n,N,{{T}_{0}}){{{{T}_{0}}} \mathord{\left/ {\vphantom {{{{T}_{0}}} t}} \right. \kern-0em} t}$, а в геле ${{P}_{g}}(n,N,t > {{T}_{0}})$ = $P(n,N,{{T}_{0}})$ – ‒ ${{P}_{s}}(n,N,t)$. Рост массы геля обусловлен потоком поликонденсации из золя с образованием рыхлых кластеров и последующим созреванием, когда гель переходит в плотную глобулу со средней длиной $\left\langle n \right\rangle \sim N$ и рыхлой опушкой $\left\langle n \right\rangle \sim {{N}^{{1/2}}}$. Найдены времена этих превращений.
I. ВВЕДЕНИЕ
Начиная с классических работ Флори и Стокмайера [1–5], описание разветвляющегося процесса поликонденсации мономеров с числом функциональных групп в каждом мономере $f = $ 3 (ПК-3) тесно связано с фазовым переходом исходного раствора мономеров (золя) в гель. Первоначальные представления о переходе состояло в том, что в конечный момент времени, называемый гель-точкой ${{T}_{0}}$, образуется бесконечно длинная полимерная цепь, которая в дальнейшем присоединяет к себе мономеры и образовавшиеся ранее $n$-меры, уменьшая их массу в золе. Кинетическая модель, основанная на уравнениях Смолуховского (УС), приводит к тем же зависимостям концентраций от времени и длины цепи, что и статистическая модель, подтверждая существование гель-точки и зависимость степени превращения от времени в окрестности ${{T}_{0}}$. Основанная на УС модель ПК-3 была предметом многочисленных последующих исследований [6–13] (более подробную библиографию см. в [9, 10]), в которых найдено аналитическое решение системы кинетических уравнений, описывающих необратимый рост полимерных цепей в системе, состоящей в начальный момент времени из бесконечного числа мономеров, $N = \infty $. Такую систему ниже будем называть открытой, поскольку выходящий из нее поток массы не равен нулю. Для ПК-3 кинетические уравнения открытой системы имеют вид
(1)
$\frac{{d{{P}_{n}}}}{{dt}} = \frac{1}{2}\sum\limits_{n{\kern 1pt} ' = 1}^{n - 1} {{{K}_{{n{\kern 1pt} ',n - n{\kern 1pt} '}}}{{P}_{{n{\kern 1pt} '}}}{{P}_{{n - n{\kern 1pt} '}}} - {{P}_{n}}} \sum\limits_{n{\kern 1pt} ' = 1}^\infty {{{K}_{{nn{\kern 1pt} '}}}{{P}_{{n{\kern 1pt} '}}}} $(2)
$\begin{gathered} K(n,n{\kern 1pt} ') = \theta \left( n \right)\theta (n{\kern 1pt} '),\,\,\,\,\theta = \alpha + \beta n, \\ \begin{array}{*{20}{c}} {{\text{A}}:\alpha = 2,\,\,\beta = 1} \\ {{\text{B}}:\alpha = 0,\,\,\beta = 1} \end{array}. \\ \end{gathered} $Случай А учитывает, что каждый мономер способен образовать от одной до трех связей ($f$ = 3), так что концевые группы $n$-мера сохраняют две функциональных группы, звенья линейной цепи – одну, а разветвления – ни одной. Случай $B$ описывает $n$-мер, в котором все звенья линейной цепи сохраняют одну функциональную группу, что, в частности, соответствует циклическим $n$-мерам [2, 14]. Уравнение (1) можно переписать в форме уравнений непрерывности входящих и уходящих массовых потоков для всех $n$-меров
где входящий поток учитывает, что $n$-мер образуется из всех $n{\kern 1pt} '$- и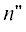 -меров, если
-меров, если 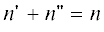 , а уходящий обусловлен рекомбинацией $n$-мера со всеми $n'$-мерами с образованием более длинной цепи $(n + n{\kern 1pt} ')$. Изменение массы золя (первый момент распределения ${{M}_{1}}(t)$) определяет поток в гель, т.е. в бесконечный ${\text{N}}$-мер
, а уходящий обусловлен рекомбинацией $n$-мера со всеми $n'$-мерами с образованием более длинной цепи $(n + n{\kern 1pt} ')$. Изменение массы золя (первый момент распределения ${{M}_{1}}(t)$) определяет поток в гель, т.е. в бесконечный ${\text{N}}$-мер
(4)
${{M}_{1}}(t) = \sum\limits_{n = 1}^\infty {nP(n,t)} ,\,\,\,\,\frac{{d{{M}_{1}}}}{{dt}} = - {{J}_{\infty }}.$Из (4) следует, что полная масса сохраняется при экспоненциально быстром спаде концентраций n-меров, когда ${{J}_{\infty }}$ = 0, и остается конечной при степенном спаде $P(n,t)\sim {{n}^{{ - s}}},\,\,s > 2$. В силу сохранения массы первый момент в обоих случаях постоянен вплоть до гель-точки ${{T}_{0}}$
Масса золя начинает уменьшаться при $t \geqslant {{T}_{0}}$ пропорционально ${{({t \mathord{\left/ {\vphantom {t {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}})}^{{ - 1}}}$, поскольку часть массы переходит из золя в гель, в котором длина цепи предполагается бесконечной. Характеристики открытой модели $N = \infty $, найденные в [6–13], собраны ниже
| $\alpha = 2,\,\,\beta = 1$ | $\alpha = 0,\,\,\beta = 1$ | (6) | |
| ${{T}_{0}}$ | 1/3 | 1 | |
| ${{M}_{1}}(t),\,\,t \geqslant {{T}_{0}}$ | $\frac{{2{{T}_{0}}}}{{3t}}{{\left( {1 - \frac{{{{T}_{0}}}}{{3t}}} \right)}^{{ - 1}}}$ | $\frac{{{{T}_{0}}}}{t}$ | |
| $(\alpha + \beta n){{P}_{n}}(t),\,\,t \leqslant {{T}_{0}}$ | $3{{\pi }^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{e}^{{ - 1}}}{{2}^{{ - 2n}}}{{n}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}{{t}^{{n - 1}}}{{\left( {1 + 3t} \right)}^{{ - (2n + 1)}}}$ | ${{(2\pi )}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{n}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}{{t}^{{n - 1}}}{{e}^{{n(1 - t)}}}$ | |
| $(\alpha + \beta n){{P}_{n}}(t)\;,\;t \geqslant {{T}_{0}}$ | $3{{\pi }^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{e}^{{ - 1}}}{{2}^{{ - 1}}}{{n}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}{{t}^{{ - 1}}}$ | ${{(2\pi )}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{n}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}{{t}^{{ - 1}}}$ |
Отличие А от В только в значении ${{T}_{0}}$. Шкалу времени в А и В можно совместить: t → → $\left( {1 + {\alpha \mathord{\left/ {\vphantom {\alpha \beta }} \right. \kern-0em} \beta }} \right)t = 3t$. При $t = {{T}_{0}}$ ${{P}_{n}}(t)$ совпадают с точностью до численного коэффициента, равного 0.311 (А) и 0.399 (В). В обоих случаях при $t \leqslant {{T}_{0}}$ ${{P}_{n}}(t)$ экспоненциально уменьшаются с ростом $n$, а после гель-точки молекулярно-массовое распределение (ММР) в золь-фазе остается постоянным, концентрации всех $n$-меров изменяются одинаково
(7)
${{P}_{n}}(t) = {{P}_{n}}({{T}_{0}})({{{{T}_{0}}} \mathord{\left/ {\vphantom {{{{T}_{0}}} t}} \right. \kern-0em} t}),\,\,\,t > {{T}_{0}}.$Второй момент расходится в гель-точке, чему соответствует бесконечная длина цепи $N$-мера в открытой системе. Как доказано в [7–10], из симметрии ядра (2), $K(n,n{\kern 1pt} ') = K(n{\kern 1pt} ',n)$ следуют соотношения подобия
(8)
$K(sn,sn{\kern 1pt} ') = {{s}^{\gamma }}K(n,n{\kern 1pt} '),\,\,\,K(n,n{\kern 1pt} ') = {{n}^{\gamma }}K(1,{{n{\kern 1pt} '} \mathord{\left/ {\vphantom {{n{\kern 1pt} '} n}} \right. \kern-0em} n})$из которых, учитывая кинетическое уравнение для мономеров ($n = 1$), следует, что решения (1) для открытой системы имеют сепарабельную форму, удовлетворяющую условиям динамического скейлинга
(9)
${{P}_{\infty }}(n,t) = \varphi (t)\chi (\eta ),\,\,\,\,\eta (n,t) = {n \mathord{\left/ {\vphantom {n {h(t)}}} \right. \kern-0em} {h(t)}}$(10)
$p = (1 + {\alpha \mathord{\left/ {\vphantom {\alpha \beta }} \right. \kern-0em} \beta })t{{\left( {1 + (1 + {\alpha \mathord{\left/ {\vphantom {\alpha \beta }} \right. \kern-0em} \beta })t} \right)}^{{ - 1}}}$устанавливающим взаимно однозначное соответствие статистических и кинетических характеристик.
Подводя итог этой части обзора, отметим, что модель [1–10] не описывает структуру геля, информация о котором ограничивается расчетом гель-точки и потока (4).
Изменение свойств геля и, в частности, распределения в нем $n$-меров, в открытых системах не рассматриваются. Это ограничение преодолено в теории Лифшица, Гросберга и Хохлова (ЛГХ) [15–17], где введена универсальная модель полимерной цепи, построенная не на феноменологических гипотезах Флори, а на постулатах статистической физики. Поскольку химические (продольные) связи между звеньями идеально гибкой цепи не накладывают ограничений на направления звеньев, их радиальное распределение на расстояниях $r \gg {{a}_{0}}$ (${{a}_{0}}$– расстояние между соседними звеньями в цепи) остается таким же, как при отсутствии продольных связей. Это позволяет ввести плотность $n$-мера, сглаженную в масштабе ${{R}_{n}}\sim {{a}_{0}}\sqrt n $ и не зависящую от химических связей между звеньями. Внутренняя энергия такой системы, названной идеальной, зависит только от длины цепи, а ее термодинамические характеристики обусловлены отклонениями от идеальной системы. Такой выбор нулевого приближения важен тем, что отклонения исчезают в обоих предельных случаях, как при $r \ll {{R}_{n}}$, когда преобладает взаимодействие с постоянным числом ближайших соседей, и при $r \gg {{R}_{n}}$, когда объемные взаимодействия экспоненциально малы. Конформационная энтропия максимальна в области ${r \mathord{\left/ {\vphantom {r {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}\sim \sqrt n $, где объемные взаимодействия охватывают наибольшее число звеньев. В идеальной модели $n$-мер сворачивается в гауссов клубок с линейным размером ${{R}_{n}}$ и объемом ${{V}_{n}}\sim a_{0}^{3}{{n}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}$, так что концентрация мономеров в $n$-мере
оказывается такой же, как и в решении кинетической задачи (6). Введенное ЛГХ состояние частичного химического равновесия основано на том, что времена разрыва химических связей на много порядков больше времен конформационных переходов. Последние происходят при фиксированной последовательности звеньев и фиксированной сглаженной радиальной плотности. Связь между универсальной моделью ЛГХ и решением кинетических уравнений можно проследить, сравнив скорость ПК-3 и бинарную корреляционную функцию
(12)
$\begin{gathered} {{\rho }_{2}}({{u}_{1}},{{u}_{2}}) = {{(4\pi )}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}\int\limits_0^1 {z_{1}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}{{{\left| {{{z}_{1}} - {{z}_{2}}} \right|}}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}} \times \\ \times \,\,\exp \left( { - \frac{{u_{1}^{2}}}{{4z{}_{1}}} - \frac{{{{{({{u}_{1}} - {{u}_{2}})}}^{2}}}}{{4\left| {{{z}_{1}} - {{z}_{2}}} \right|}}} \right)d{{z}_{1}}d{{z}_{2}}, \\ {{u}_{{1(2)}}} = {{{{r}_{{1(2)}}}} \mathord{\left/ {\vphantom {{{{r}_{{1(2)}}}} {{{R}_{n}}}}} \right. \kern-0em} {{{R}_{n}}}} \\ \end{gathered} $которая при $\left| {{{u}_{1}} - {{u}_{2}}} \right|\sim $1 также является гауссианом
(13)
${{\rho }_{2}}(\left| {{{u}_{1}} - {{u}_{2}}} \right|)\sim {{({{2\pi na_{0}^{2}} \mathord{\left/ {\vphantom {{2\pi na_{0}^{2}} 3}} \right. \kern-0em} 3})}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}\exp \left( {{{ - 3{{{({{u}_{1}} - {{u}_{2}})}}^{2}}} \mathord{\left/ {\vphantom {{ - 3{{{({{u}_{1}} - {{u}_{2}})}}^{2}}} 4}} \right. \kern-0em} 4}} \right).$Из (13) следует, что функция (12) не изменяется при изменениях масштаба $\left| {{{u}_{1}} - {{u}_{2}}} \right|$ кратных $n$. Это свойство масштабной вариантности, называемое самоподобием,справедливо и для скорости роста цепи. Химическая связь между $n$- и $n{\kern 1pt} '$-мерами образуется, когда функциональные группы входящих в их состав звеньев находятся на расстоянии реактивного диаметра $D\sim {{a}_{0}}$. Размерная константа скорости, определяющая масштаб времени в (1), пропорциональна вероятности реализации конфигурации, в которой расстояние между произвольными парами звеньев в $n$- и $n{\kern 1pt} '$-мерах $D\sim \left| {{{u}_{1}} - {{u}_{2}}} \right|$, т.е. функции (13) для универсальной модели ЛГХ. Следует отметить, что это утверждение не зависит от механизма ПК-3 и следует из стохастической теории бимолекулярных реакций [18, 1, 9 ]. Согласно ЛГХ, полимерная цепь может существовать не только в форме гауссова клубка, но и глобулы, либо имеющей рыхлую оболочку, состоящую из более коротких цепей, либо резкую границу плотной фазы. Переходы между этими состояниями, а также переход глобулы в рыхлый статистический клубок являются фазовыми переходами первого рода. На границе плотной глобулы и рыхлой опушки происходит разрыв плотности. Более короткие цепи способны образовать глобулу без опушки непосредственно из клубка. Таким образом, полимерная цепь может находиться в трех фазовых состояниях: клубок, глобула с опушкой с конечным скачком радиальной плотности на границе раздела и глобула без опушки, когда возникает резкая граница между клубком и плотной глобулой.
Свойства самоподобия широко используются в теории протекания [20–24], фундаментальная задача которой рассматривает движение по узлам решетки, в которой часть узлов уже заполнена. Эта задача во многом сходна с описанием роста цепей ПК-3, если считать $n$-мер кластером, состоящим из связанных узлов. Если ни один из кластеров не простирается по всей решетке, его заполнение не распространяется по всей решетке. Такой кластер называется конечным (внутренним), тогда как кластер, который простирается по всей решетке, называется перколяционным. Перколяционный кластер возникает при критическом значении $p = {{p}_{c}}$, тогда как при $p < {{p}_{c}}$ вероятность протекания уменьшается до нуля в малой окрестности ${{p}_{c}}$. Вероятность протекания $P(p)$ определяется как вероятность того, что жидкость, первоначально заполнившая один из случайно выбранных узлов, способна побывать в любом другом. Кинетическая вероятность равна наибольшему значению $p$, при котором возникает протекание в бесконечной решетке. Масса или число узлов $M(L)$ наибольшего кластера растет с увеличением размера решетки $L \to \infty $
(14)
$M(L)\sim \left\{ \begin{gathered} \ln L,\,\,\,\,p < {{p}_{c}} \hfill \\ {{L}^{D}},\,\,\,\,p = {{p}_{c}} \hfill \\ {{L}^{E}},\,\,\,\,\,p > {{p}_{c}} \hfill \\ \end{gathered} \right..$Ниже ${{p}_{c}}$ кластер, простирающийся по всей решетке, не существует, т.е. размер наибольшего кластера намного порядков меньше ${{L}^{E}}$. На пороге протекания размер растет $\sim {{L}^{D}},D < E$ – фрактальная размерность. Значение ${{p}_{c}}$ = 1/2 для треугольной решетки равно критическому значению степени превращения в ПК-3. Статистическое самоподобие кластеров состоит в том, что кластер в целом остается подобным себе при увеличении его размера. Самоподобие обусловлено постоянством фрактальной размерности и сохраняется при пространственной ренормировке. Для треугольной решетки ее масштаб можно изменить в $b = \sqrt 3 $, группируя занятые узлы и заменяя исходные ячейки размером ${{b}^{2}} = 3$, в которых занято большинство узлов, одним занятым узлом. Такое преобразование подобия означает, что исходный кластер, содержащий две или три поры, превращается в огрубленной решетке в занятый, а кластер без занятых и с одним занятым узлом преобразуются в пустой. В результате ренормировки образуется новая решетка с концентрацией занятых узлов $p{\kern 1pt} '$. Поскольку узлы в исходной решетке заполняются независимо, вероятности найти ячейку с тремя и двумя заполненными узлами равна ${{p}^{3}}$ и $3{{p}^{2}}(1 - p)$ соответственно, так что заполнение огрубленной решетки равно
Огрубление можно проводить многократно, причем при каждом шаге ренормировки значения $p$ и $p{\kern 1pt} '$ связаны (15). При $p = {{p}_{c}} = $ 1/2 ренормировка не изменяет условия протекания, (${{p}_{c}}$ – неподвижная точка ренормировки). Две другие неподвижные точки соответствуют пустой и полностью заполненной решетке ($p{\kern 1pt} ' = 0$ и $p{\kern 1pt} ' = 1$). Если $0 < p < {{p}_{c}}$, концентрация занятых узлов уменьшается, а при ${{p}_{c}} < p < 1$ растет после каждого шага, так что достаточное число шагов описывает переходы в $p{\kern 1pt} ' \to 0$ и $p{\kern 1pt} ' \to 1$ при $p < p{\kern 1pt} '$ и $p > p{\kern 1pt} '$ соответственно. Эту процедуру можно применить и к ПК-3, чтобы получить золь с низкой плотностью ($p{\kern 1pt} '\sim {1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-0em} N}$) и плотный гель ($p{\kern 1pt} '\sim 1$).
Статистическое самоподобие внутреннего кластера при $p = {{p}_{c}}$ означает, что его масса удовлетворяет при больших ${L \mathord{\left/ {\vphantom {L b}} \right. \kern-0em} b}$ скейлинговому соотношению
Поскольку левая часть в (16) не зависит от $b$, масса кластера – однородная функция, и ее единственной формой является степенная функция
Распределение конечных кластеров не имеет характерного масштаба, т.е. является степенным. Если на кластер, состоящий из $n$-узлов, наложить квадрат со стороной $L$, то масса внутри квадрата зависит от отношения размера квадрата и радиуса инерции кластера ${{R}_{g}}$
(18)
${{M}_{n}}(L)\sim \left\{ \begin{gathered} A{{({L \mathord{\left/ {\vphantom {L {R{}_{g}}}} \right. \kern-0em} {R{}_{g}}})}^{D}},\,\,\,L \ll {{R}_{g}}(s) \hfill \\ s,\,\,\,\,L \gg {{R}_{g}}(s). \hfill \\ \end{gathered} \right.$(18) позволяет найти распределение кластеров по размерам в точке $p = {{p}_{c}}$. Если $\left\langle {n(s)} \right\rangle $ – среднее число кластеров, состоящих из $s$-узлов, то число кластеров из $s$ узлов в $L \times L$ решетке равно $\left\langle {n(s)} \right\rangle {{L}^{2}}$, и вероятность того, что случайно выбранный узел принадлежит $s$-кластеру равна
(19)
$W(s) = {{s\left\langle {n(s)} \right\rangle } \mathord{\left/ {\vphantom {{s\left\langle {n(s)} \right\rangle } {\sum\limits_{s = 1}^N {s\left\langle {n(s)} \right\rangle } }}} \right. \kern-0em} {\sum\limits_{s = 1}^N {s\left\langle {n(s)} \right\rangle } }},$(20)
$\left\langle s \right\rangle = \sum\limits_{s = 1}^{{{L}^{D}}} {{{{{s}^{2}}\left\langle {n(s,L)} \right\rangle } \mathord{\left/ {\vphantom {{{{s}^{2}}\left\langle {n(s,L)} \right\rangle } {\sum\limits_{s = 1}^{{{L}^{D}}} {s\left\langle {n(s)} \right\rangle } }}} \right. \kern-0em} {\sum\limits_{s = 1}^{{{L}^{D}}} {s\left\langle {n(s)} \right\rangle } }}} .$Поскольку преобразование подобия с коэффициентом $b$ переводит $L \times L$ в $({L \mathord{\left/ {\vphantom {L b}} \right. \kern-0em} b}) \times ({L \mathord{\left/ {\vphantom {L b}} \right. \kern-0em} b})$, которое не изменяет значение ${{p}_{c}}$, для $s\left\langle {n(s)} \right\rangle $ справедливо соотношение подобия
(21)
$s\left\langle {n(s)} \right\rangle = {{b}^{{ - 2}}}s{\kern 1pt} '\left\langle {n(s{\kern 1pt} ')} \right\rangle ,\,\,\,\,s{\kern 1pt} ' = {s \mathord{\left/ {\vphantom {s {{{b}^{D}}}}} \right. \kern-0em} {{{b}^{D}}}}$(22)
$\left\langle {n(s)} \right\rangle = {{s}^{{ - \eta }}}f({s \mathord{\left/ {\vphantom {s {{{L}^{D}}}}} \right. \kern-0em} {{{L}^{D}}}})$(23)
$\left\langle {n(s)} \right\rangle \sim {{s}^{{ - \eta }}},\,\,\,\,\eta = 1 + {E \mathord{\left/ {\vphantom {E D}} \right. \kern-0em} D}.$Средняя длина и средняя масса кластера зависят от размера решетки
(24)
$\begin{gathered} \left\langle {n(s)} \right\rangle = {{s}^{{ - \eta }}}f({s \mathord{\left/ {\vphantom {s {{{L}^{D}}}}} \right. \kern-0em} {{{L}^{D}}}}) = {{L}^{{ - \eta D}}}g({s \mathord{\left/ {\vphantom {s {{{L}^{D}}}}} \right. \kern-0em} {{{L}^{D}}}}) = {{L}^{{ - (D + E)}}}g({s \mathord{\left/ {\vphantom {s {{{L}^{D}}}}} \right. \kern-0em} {{{L}^{D}}}}), \\ \left\langle s \right\rangle = \sum\limits_{s = 1}^{{{L}^{D}}} {{{s}^{2}}{{\left\langle {n(s,L)} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {n(s,L)} \right\rangle } {\sum\limits_{s = 1}^{{{L}^{D}}} {s\left\langle {n(s)} \right\rangle } }}} \right. \kern-0em} {\sum\limits_{s = 1}^{{{L}^{D}}} {s\left\langle {n(s)} \right\rangle } }}} \sim \\ \sim {{L}^{{2D - E}}}\int\limits_{{{{{1 \mathord{\left/ {\vphantom {1 L}} \right. \kern-0em} L}}}^{D}}}^1 {{{{\left( {\frac{s}{{{{L}^{D}}}}} \right)}}^{2}}g({s \mathord{\left/ {\vphantom {s {{{L}^{D}}}}} \right. \kern-0em} {{{L}^{D}}}}){{ds} \mathord{\left/ {\vphantom {{ds} {{{L}^{D}}}}} \right. \kern-0em} {{{L}^{D}}}}\sim {{L}^{{2D - E}}}} , \\ \end{gathered} $Корреляционная длина определяется квадратом среднего расстояния между узлами конечного кластера и для гауссова распределения пропорциональна радиусу инерции
(26)
${{\xi }^{2}} = 2\sum\limits_s {R_{g}^{2}} (s){{s}^{2}}{{\left\langle {n(s,p)} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {n(s,p)} \right\rangle } {\sum\limits_s {{{{(s)}}^{2}}\left\langle {n(s,p)} \right\rangle } }}} \right. \kern-0em} {\sum\limits_s {{{{(s)}}^{2}}\left\langle {n(s,p)} \right\rangle } }}$имеет степенную особенность в критической точке и для треугольной решетки подчиняется условию самоподобия (4)
(27)
$\begin{gathered} \xi (p)\sim {{\left| {p - {{p}_{c}}} \right|}^{{ - \nu }}},\,\,\,\,\xi (p{\kern 1pt} ') = {{b}^{{ - 1}}}\xi (p), \\ p{\kern 1pt} ' = {{p}_{c}} + {{3(p - {{p}_{c}})} \mathord{\left/ {\vphantom {{3(p - {{p}_{c}})} 2}} \right. \kern-0em} 2},\,\,\,\,{{p}_{c}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},\,\,\,\,b = \sqrt 3 \\ \end{gathered} $так что критический индекс равен v = 4/3 ≈ ≈ ${{\ln (\sqrt 3 )} \mathord{\left/ {\vphantom {{\ln (\sqrt 3 )} {\ln ({3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2})}}} \right. \kern-0em} {\ln ({3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2})}}$. При$p > {{p}_{c}}$ все узлы можно разделить на входящие в состав всех конечных кластеров и только бесконечного кластера (БК)
(28)
$p = {{p}_{\infty }} + \sum\limits_n {s\left\langle {n(s)} \right\rangle \sim {{{(p - {{p}_{c}})}}^{{D - E}}}} .$Из (25) и (28) следует, что доля конечных кластеров уменьшается с ростом степени превращения до нуля, чему в теории ЛГХ соответствует переход рыхлого геля в плотный. Когда корреляционная длина приближается к размеру решетки ($\xi \approx L$) на зависимости $p(L)$ в области ${{p}_{\infty }}$ появляется плато $\xi \leqslant L \leqslant 2\xi $, разделяющее два участка степенного роста (22) и (27). Многочисленные примеры применения теории протекания приведены в [24]. Заканчивая сопоставление теорий ФС, ЛГХ и протекания в применении к кинетике ПК-3, следует указать, что для описания перехода золя в гель решение УС для открытой системы оказывается недостаточным и его необходимо дополнить анализом не только пространственного роста конечных кластеров, но и кинетики этого роста с образованием гелей с различной плотностью. Как показывает современное состояние теории протекания, решение этой задачи связано с кинетической задачей для конечных систем. Мы не нашли решение этой задачи в текущей литературе, посвященной теории поликонденсации, хотя недавнее рассмотрение кинетики роста сетей полимеров и биополимеров, связанное с бимолекулярными реакциями $n$-меров с мономерами [25–28], указывает на ее актуальность.
В этой статье, исходя из поставленной задачи, мы заменим открытую систему замкнутой, содержащей при $t = 0$$N$ мономеров, и рассмотрим свойства замкнутых систем с различными значениями $N$, когда при всех $N$ и $t$ суммарная масса фаз сохраняется и выходяший поток ${{J}_{N}} = 0$. Во втором разделе рассмотрен рост $n$-меров конечной длины, переходящий от кинетики, близкой к открытой системе при $n < N$, к образованию $N$-кластеров. В третьем разделе предложен метод разделения концентраций $n$-меров в трех фазах и описана кинетика перехода золя в рыхлый и плотный гель. В четверном разделе рассмотрено последующее созревание геля, обусловленное превращением рыхлого геля в плотный. Выводы собраны в пятом разделе.
II. РОСТ ЦЕПЕЙ В ЗАМКНУТОЙ СИСТЕМЕ
Кинетику ПК-3 в замкнутой системе описывают $N$ уравнений УС, в правых частях которых учитываются бимолекулярные реакции с участием $n$ и $n{\kern 1pt} '$-меров, если $n + n{\kern 1pt} ' \leqslant N$. Моменты зависящего от времени распределения концентраций $n$-меров в замкнутой системе имеют вид
(29)
${{M}_{s}}(t) = {{N}^{{ - 1}}}\sum\limits_{n = 1}^N {{{n}^{s}}{{P}_{N}}(n,t),} \,\,\,\,s = 0,1,2...\,,$(30)
$\begin{gathered} M_{{nn{\kern 1pt} '}}^{s}(t) = \frac{1}{2}( - {{n}^{s}} - {{(n{\kern 1pt} ')}^{s}} + \\ + \,\,{{(n + n{\kern 1pt} ')}^{s}})K(n,n{\kern 1pt} '){{P}_{n}}(t){{P}_{{n{\kern 1pt} '}}}(t). \\ \end{gathered} $Из (30) непосредственно следует, что матрица ${{\hat {M}}_{1}}$ – нулевая, в согласие с условием сохранения массы. Элементы матрицы ${{\hat {M}}_{0}}$ отрицательны и пропорциональны значениям ядра (2), а ${{\hat {M}}_{2}}$ положительны
(31)
$M_{{nn{\kern 1pt} '}}^{s}(t) = \left\{ \begin{gathered} - \frac{1}{2}K(n,n{\kern 1pt} '){{P}_{n}}(t){{P}_{{n{\kern 1pt} '}}}(t),\,\,\,\,s = 0 \hfill \\ 0,\,\,\,\,s = 1 \hfill \\ nn{\kern 1pt} 'K(n,n{\kern 1pt} '){{P}_{n}}(t){{P}_{{n{\kern 1pt} '}}}(t),\,\,\,\,s = 2 \hfill \\ \end{gathered} \right..$Складывая столбцы матриц с элементами (30), находим уравнения для зависящих от времени моментов распределения $n$-меров
в виде сумм $M_{{nn'}}^{s}(t)`$
(33)
$\begin{gathered} \frac{{d{{{\rm M}}_{0}}}}{{dt}} = - \frac{1}{2}\sum\limits_{n,n' = 1}^N {K(n,n{\kern 1pt} '){{P}_{n}}(t){{P}_{{n{\kern 1pt} '}}}(t),} \\ \frac{{d{{{\rm M}}_{1}}}}{{dt}} = 0,\,\,\,\frac{{d{{{\rm M}}_{2}}}}{{dt}} = \sum\limits_{n,n{\kern 1pt} ' = 1}^N {nn{\kern 1pt} 'K(n,n{\kern 1pt} '){{P}_{n}}(t){{P}_{{n{\kern 1pt} '}}}(t)} . \\ \end{gathered} $Для ядер (2) суммирования по $n$ и $n{\kern 1pt} '$ в (32) независимы
(34)
$\begin{gathered} \frac{{d{{{\rm M}}_{0}}}}{{dt}} = - \frac{1}{2}{{\left( {\sum\limits_{n = 1}^N {\theta (n){{P}_{n}}(t)} } \right)}^{2}}, \\ \frac{{d{{{\rm M}}_{2}}}}{{dt}} = {{\left( {\sum\limits_{n, = 1}^N {n\theta (n){{P}_{n}}(t)} } \right)}^{2}}. \\ \end{gathered} $Численное решение кинетических уравнений выполнено в кодах MATLAB по программе ODE113. Расчеты проведены на персональном компьютере с рабочей частотой процессора 4 Ггц и оперативной памятью 16 Гб. При $N$ = 1024 время расчета составляло ~5 мин. Пользуясь аналитическим решением при $N = \infty $ и численным решением при конечных $N$, находим зависящие от времени моменты в до- и пост-гелевой области. В отличие от открытой системы, в которой гель-точку определяет первый момент, в замкнутых системах такой точки нет. В достаточно больших замкнутых системах ($N \geqslant {{10}^{2}}$) кинетические кривые состоят из трех временных интервалов, относящихся к последовательным переходам из начального состояния $N$ мономеров в промежуточные состояния с широким распределением $n$-меров, близким к распределению в открытой системе, и переходу из промежуточного в конечное состояние, где основная масса переходит в $N$-мер. Промежуточное состояние существует в сравнительно узком интервале времени $t \approx t* > {{T}_{0}}$, а переход в $N$-мер происходит при $t\sim {{T}_{N}} \gg t*$. Моменты в этих состояниях равны
(35)
$\begin{array}{*{20}{c}} {{{M}_{0}}(0) = 1,\,\,\,\,{{M}_{2}}(0) = 1} \\ {{{M}_{0}}(t*)\sim 2{{N}^{{ - 1/2}}},\,\,\,\,{{M}_{2}}(t*)\sim 2\sqrt N } \\ {{{M}_{0}}({{T}_{N}}) \approx {{N}^{{ - 1}}},\,\,\,\,{{M}_{2}}({{T}_{N}}) \approx N\delta (N - n).} \end{array}$Моменты при $t\sim t*$ находятся из значений сумм, из которых две первых определяются нижним пределом
(36)
$\begin{gathered} \sum\limits_{n = 1}^N {{{n}^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 2}} \right. \kern-0em} 2}}}} \approx } \sum\limits_{n = 1}^\infty {{{n}^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 2}} \right. \kern-0em} 2}}}} = \varsigma ({5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2})} = 1.341, \\ \sum\limits_{n = 1}^N {{{n}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}} \approx } \sum\limits_{n = 1}^\infty {{{n}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}} = \varsigma ({5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2})} = 2.612, \\ \sum\limits_{n = 1}^N {{{n}^{{ - 1/2}}}} \approx 2{{N}^{{1/2}}}. \\ \end{gathered} $Отличие ${{M}_{2}}(t),\,\,t < {{T}_{N}}$ в замкнутых системах с различными $N$ от открытой системы показано на рис. 1. Скачок второго момента в окрестности ${{T}_{0}}$ становится более резким с ростом $N$, интервал $t{\text{*}} - {{T}_{0}}$ сокращается. Изменение кинетики ПК-3 при $t\sim {{T}_{N}}$ и $t\sim t{\text{*}}$ характеризуют ${{M}_{0}}(t)$ и ${{M}_{2}}(t)$, приведенные на рис. 2 в двойном логарифмическом масштабе. Уменьшение нулевого момента (верхняя панель) почти не отличается от открытой системы при $t \leqslant t{\text{*}}$, а затем стремится к постоянному значению $\sim {1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-0em} N}$. ${{{{M}_{2}}(t)} \mathord{\left/ {\vphantom {{{{M}_{2}}(t)} N}} \right. \kern-0em} N}$ после скачка при $t\sim {{T}_{N}}$ слабо зависит от $N$, увеличиваясь до 1. Из (35), (36) и рис. 2 следует, что можно принять в качестве оценки зависящих от $N$ характеристических времен $t{\text{*}}$ и ${{T}_{N}}$ точки пересечения ${{M}_{0}}(t)$ с постоянными значениями ${{M}_{0}}(t*) = 2{{N}^{{ - 1/2}}}$ и ${{M}_{0}}({{T}_{N}}) \approx {{N}^{{ - 1}}}$.
(37)
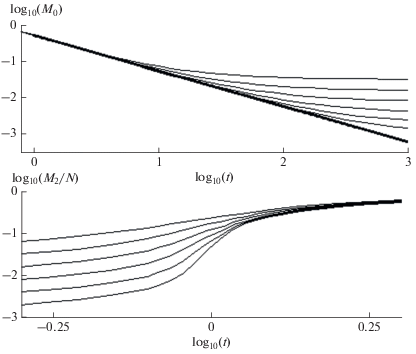
$t* \approx {{\sqrt N } \mathord{\left/ {\vphantom {{\sqrt N } 2}} \right. \kern-0em} 2},\,\,\,{{T}_{N}} \approx N.$Рис. 1.
Изменение со временем второго момента распределения $n$-меров в фазовом переходе в открытой (пунктир) и закрытых системах с начальным числом мономеров $N$ = 32, 64, 128, 256, 512, 1024 (кривые 1–6 соответственно).
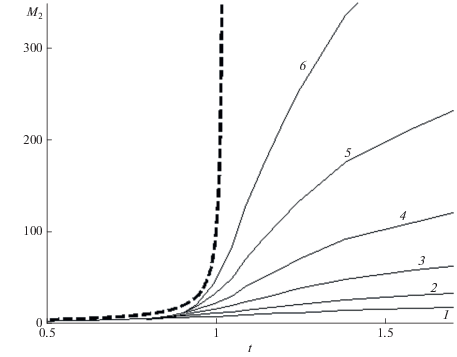
Рис. 2.
Зависящие от времени нулевой и первый моменты распределения $n$-меров в двойном логарифмическом масштабе (верхняя и нижняя панели). Жирная кривая на верхней панели относится к открытой системе, а кривые сверху вниз на обеих панелях – к закрытым системам с начальным числом мономеров $N$ = 32, 64, 128, 256, 512, 1024.
Хотя константа скорости роста цепи $K(n,n{\kern 1pt} ')$ квадратично увеличивается с ростом длины цепи, сама скорость уменьшается $\sim nn{\kern 1pt} 'P(n)P(n{\kern 1pt} ')$. Подобно открытой системе, масса геля, образующегося за время $t{\text{*}}$, мала (образуется ${{\sqrt N } \mathord{\left/ {\vphantom {{\sqrt N } 2}} \right. \kern-0em} 2}$ связей из $N$необходимых в геле). Основная масса геля образуется в интервале $[t*,{{T}_{N}}]$. Начальный участок почти совпадает с зависимостью ${{M}_{0}}(t)$ в открытой системе, а конечный близок к постоянному значению ${{M}_{0}}\left( \infty \right) = {1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-0em} N}$, соответствующему $N$-меру. Между ними расположена широкая область с промежуточной асимптотикой, которую по аналогии с (9), (15) и (17) можно представить в виде
(38)
${{M}_{0}}(t,{N \mathord{\left/ {\vphantom {N {\left\langle {n(t)} \right\rangle }}} \right. \kern-0em} {\left\langle {n(t)} \right\rangle }})\sim \varphi (t)\chi ({N \mathord{\left/ {\vphantom {N {\left\langle {n(t)} \right\rangle }}} \right. \kern-0em} {\left\langle {n(t)} \right\rangle }})\sim {{t}^{{ - \gamma }}}{{N}^{{ - \tau }}}.$Для открытой системы $\gamma $ = 1, $\tau $ = 0, для $N$-мера $\gamma $ = 0, $\tau $ = 1.
Аналогичная зависимость для второго момента (нижняя панель рис. 2) также состоит из двух медленных участков, разделенных скачком в области гель-точки, где в открытой системе ${{M}_{2}}({{T}_{0}}) = \infty $. Начальный интервал, как и в открытой системе, относится к медленному росту коротких цепей в золе, а рост после скачка к превращениям в геле.
Зависящие от времени молекулярно-массовые распределения представлены на рис. 3. Верхняя панель относится к моменту времени $t$ = 1.01, близкому к гель-точке открытой системы ${{T}_{0}} = 1$, когда отклонения массовых концентраций $n$-меров от предсказываемых (6) для золя в сумме не превышают ${{10}^{{ - 2}}}$. Эти отклонения относятся к $n$‑мерам, образующимся в геле и включают не только $N$-меры, но и широкое распределение $n$‑меров с длиной цепи $n < N$, суммарная масса которых одного порядка с массой $N$-меров. В согласие с предсказанием теории ЛГХ, обе составляющие распределения одновременно появляются в окрестности ${{T}_{0}}$. Средняя панель ($t$ = 1.1) показывает, что масса $n$-меров в золе уменьшаются, а обе составляющие отклонений в замкнутых системах от открытой растут. Нижняя панель ($t = 2 > t{\text{*}}$), показывает, что в интервале $t* < t < {{T}_{N}}$ концентрации $n$-меров $n < N$ не растут, а уменьшаются, а концентрация $N$-меров возрастает. Отношение масс $n$-меров $n < N$ и N‑меров уменьшается с ростом $N$, что также согласуется с представлениями ЛГХ о переходе рыхлого геля в плотный.
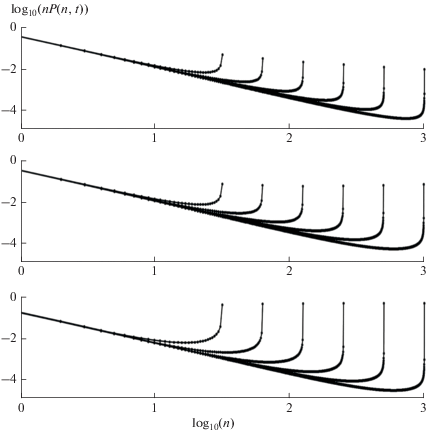
Рис. 3.
Зависящие от времени молекулярно-массовые распределения $n$-меров в пост-гелевой области $t > {{T}_{0}}$ = 1. Панели сверху вниз относятся к моментам времени $t = $ 1.01, 1.1, 2.0. Кривые слева направо соответствуют закрытым системам с начальным числом мономеров 32, 64, 128, 256, 512, 1024. Точки на кривых соответствуют целым числам $n$.
III. ПЕРЕХОД ЗОЛЯ В РЫХЛЫЙ И ПЛОТНЫЙ ГЕЛЬ
Поскольку кинетический расчет показал, что распределения массовых концентраций $n$-меров состоят из трех хорошо разрешенных по времени интервалов $t$ и $n$, схематически показанных на рис. 4, появляется возможность разделить концентрации $n$-меров в трех фазах – золе, рыхлом и плотном геле, предположив, в согласие с первоначальной гипотезой Флори, что ПК-3 в золе соответствует открытой системе, а ПК в рыхлом и плотном геле описываются отклонениями концентраций $n$-меров $n < N$ и $N$-меров в замкнутых системах от открытой, в согласие с представлениями теории протекания. Как схематически показано на рис. 4, сравнивая распределения в моменты времени ${{T}_{0}}$ и $t$, ввести длину цепи ${{N}_{1}}$, такую, что концентрации цепей с длиной $n \leqslant {{N}_{1}}$ незначительно отличаются от распределения в открытой системе ($N = \infty )$ и уменьшаются, достигая минимума в точке $n = {{N}_{1}}$. Очевидно, что этот интервал относится к распределению в золе, масса которого постоянна вплоть до гель-точки и уменьшается при $t > {{T}_{0}}$. В массе золя доминирует вклад коротких $n$-меров, поскольку первый момент их распределения определяется нижним пределом суммы (36). Минимум $n{{P}_{s}}(n,t)$ при $n = {{N}_{1}}$ появляется в пост-гелевой области при фиксированном значении $t$, когда уменьшение массы золя компенсирует рост массы геля. Следует отметить, что значение ${{N}_{1}}P({{N}_{1}},t)$, по крайней мере на порядок меньше растущих массовых концентраций более длинных $n$-меров в рыхлом геле, так что точность определения $N{}_{1}$ мало влияет на результаты расчета. Из рис. 3 и 4 следует, что масса геля имеет две составляющих − монотонный рост концентраций $n$-меров в интервале ${{N}_{1}} \leqslant n \leqslant N - 1$ и увеличение концентрации $N$-меров. В согласие с моделью ЛГХ, две этих составляющих относятся к рыхлому и плотному гелю соответственно. Из условия сохранения массы в замкнутой системе следует, что массы этих составляющих равны уменьшению массы золя по сравнению c его массой в гель-точке
где(40)
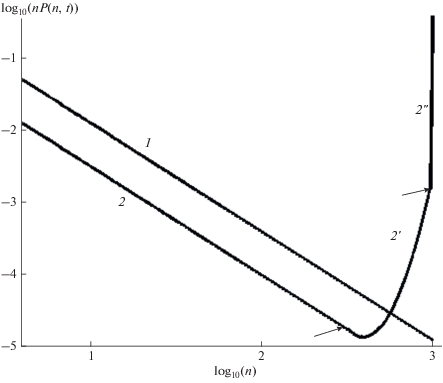
$\begin{gathered} {{M}_{s}}(t) = \sum\limits_{n = 1}^{N{}_{1}} {nP\left( {n,t} \right)} , \\ {{M}_{{gs}}}(t) = \sum\limits_{n = {{N}_{1}} + 1}^{N - 1} {nP(n,{{T}_{0}})} \left( {1 - {{{{T}_{0}}} \mathord{\left/ {\vphantom {{{{T}_{0}}} t}} \right. \kern-0em} t})} \right), \\ {{M}_{N}}(t) = N\left( {P(N,t} \right) - P(N,{{T}_{0}})). \\ \end{gathered} $Рис. 4.
Схема разделения масс золя (2), рыхлого (2') и плотного геля (2"). Кривая 1– молекулярно-массовое распределение в гель-точке.
Поскольку все значения непосредственно вычисляются, (40) позволяет разделить суммарную массу на массы трех фаз в произвольный момент времени. Результаты расчета представлены на рис. 5. На панели слева показано изменение масс золя и плотного геля ($N$-мера), которые незначительно изменяются в исследованном интервале $N$. На панели справа показано изменение массы рыхлого геля, которое имеет максимум в окрестности скачка ${{M}_{2}},\,\,t \approx t{\text{*}}$ и быстро уменьшается при $t > t{\text{*}}$, когда ${{M}_{N}} > {{M}_{S}}$. Даже $\max ({{M}_{{gs}}}) < $ 0.2 при $N \geqslant $ 32. С ростом $N$ максимальная масса рыхлого геля быстро падает, так что его промежуточное образование в переходе золь-плотный гель существенно только в малых агрегатах.
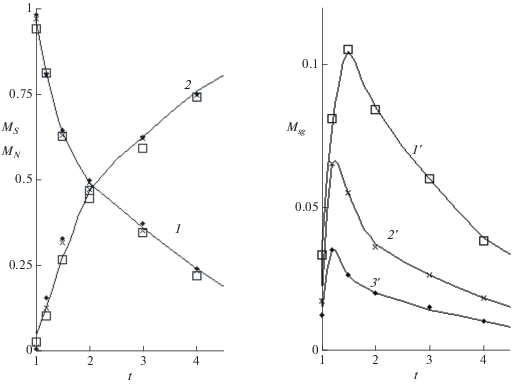
Рис. 5.
Зависящие от времени массовые доли золя (${{M}_{s}}$) и плотного геля (${{M}_{N}}$) – кривые 1 и 2 на панели слева и рыхлого геля ${{M}_{{sg}}}$ (панель справа). Кривые 1', 2', 3' относятся к $N = $ 64, 256, 1024, для которых рассчитанные значения показаны квадратами, крестами и точками соответственно.
IV. СОЗРЕВАНИЕ ГЕЛЯ
Из рис. 3 следует, что рост $N$-меров при $t\sim {{T}_{N}}$ происходит, по крайней мере, на порядок быстрее, чем более коротких кластеров. Причина этого эффекта заключена в самой выбранной модели. Поскольку в золе и в рыхлом геле молекулярно-массовое распределение имеет два максимума при малых ($n\sim 1$) и больших ($n\sim N$) длинах цепи, разделенных широкой областью с минимумом при $n\sim {{N}_{1}}$, в правых частях кинетических уравнений доминируют произведения $nn{\kern 1pt} '{{P}_{n}}{{P}_{{n{\kern 1pt} '}}}\sim N{{P}_{1}}{{P}_{N}}$, приводящие к образованию $N$-меров, которые не способны к рекомбинации. Этот механизм медленного образования (созревания) плотного геля идейно связан с механизмом поверхностного роста агрегатов, ограниченного диффузией мономеров к растущей поверхности [20, 29–31].
Согласно (28), переход рыхлого геля в плотный в теории протекания определяет разность евклидовой и фрактальной размерности. Степенную зависимость средней длины конечных кластеров от степени превращения можно преобразовать в зависимость от времени с помощью соотношения (10). Построенная зависимость ${{P}_{N}}(p)$ согласуется с (28) при $E - D \approx $ 0.15–0.20, что согласуется с предсказываемым значением для треугольной решетки, как модели ПК-3.
В заключение этого раздела укажем, что метод определения зависящего от времени состава золь и гель фаз, предложенный в этой статье, применимы и к более сложным процессам ПК-3, в которых образуются случайно разветвленные полимерные сети и сети, содержащие малые циклические фрагменты, рассмотренные в предыдущих статьях настоящей серии [32, 33], если одну замкнутую систему заменить распределением систем с различными $N$.
V. ВЫВОДЫ
1. Представлен сравнительный обзор результатов феноменологической теории Флори–Стокмайера (ТФС), последовательной статистической теории Лифшица–Гросберга–Хохлова (ТЛГХ) и теории протекания (ТП) в применении к кинетике фазового перехода золь-гель в процессе поликонденсации трифункциональных мономеров (ПК-3).
2. Показано, что замена открытой системы с бесконечным начальным числом мономеров ($N = \infty $) замкнутой системой с конечным значением $N$ позволяет построить кинетическую модель, которая воспроизводит кинетику фазовых переходов золя в рыхлый и плотный гель.
3. Численное решение системы кинетических уравнений баланса для концентраций $n$-меров с длиной цепи $n \leqslant N$ демонстрирует наличие трех интервалов времени: начального, в течение которого распределение незначительно отличается от открытой системы, промежуточного с наиболее широким распределением $n$-меров и средней длиной цепи $\sim {{N}^{{1/2}}}$, в котором концентрации минимальны, и конечного интервала созревания геля, в котором доминирует рекомбинация коротких ($n\sim 1)$ и длинных ($n\sim N$) $n$-меров с обра-зованием $N$-меров.
4. Предложен метод разделения масс золя, рыхлого и плотного геля, основанный на сохранении суммарной массы и свойствах динамического самоподобия.
5. Показано, что в согласие с ТП, свойства самоподобия позволяют установить связь между масштабом времени роста цепей и степенью превращения.
6. Показано, что рыхлый гель образуется в промежуточном интервале времени в окрестности гель-точки и затем исчезает в процессе созревания геля. С ростом $N$ максимальная концентрация рыхлого геля уменьшается, так что доминирующим становится переход золь – плотный гель без промежуточной стадии.
7. Предложенный метод применим к более сложным процессам ПК-3, включающим рост случайно разветвленных полимерных сетей и образование сетей с малыми циклическими фрагментами.
Список литературы
Flory P.J. // Principlesof Polymer Chemistry. 1979. Cornell University Press. Ithaca. N.Y.
Stockmayer W.H.J. // Chem. Phys. 1943. V. 11. P. 45.
Stockmayer W.H.J. // Chem. Phys. 1944. V. 12. P. 125.
Zimm B.H., Stockmayer W.H. // J. Chem. Phys. 1949. V. 17. P. 1301.
Jacobson H., Stockmayer W.H. // J. Chem. Phys. 1950.
Ziff R.M., Stell G.J.// Chem. Phys. 1980. V. 73. P. 3492.
Hendricks E.M., Ernst M.H., Ziff R.M. // J. Stat. Phys. 1983. V. 31. P. 519.
Davies S.C., King J.R., Wattis J.A.D. // J. Eng. Math. 1999. V. 36. P. 57.
van Roessel H.J., Shirvani M. // Physica D. 2006. V. 222. P. 29.
Leyvraz F. Phys. Rep. 2003. V. 383. P. 95.
Menon G., Pego R.L. SIAM J. // Math. Anal. 2005. V. 36. P. 1629.
Wattis J.A.D. // Physica D. 2006. V. 222. P. 1.
Laurencot P. // Phycica D. 2006. V.222. P. 80.
Ерухимович И.Я. // ЖЭТФ 1995. Т. 108. С. 1004.
Lifshitz I.M., Grosberg A.Y., Khokhlov A.R. // Rev. Mod.Phys. 1978. V. 50. P. 683.
Гросберг А.Ю., Хохлов А.Р. Статистическая физика макромолекул. М.: Наука, 1989.
Лифшиц И.М. Избранные труды. Электронная теория металлов. Полимеры и биополимеры. 1994. Наука. Москва. № 26, 29.
Gillespie D.T. // Annu.Rev. Phys. Chem. 2007. V.58. P. 35.
Laurenzi I.J . // J.Chem.Phys. 2000. V. 113. P. 3315.
Фракталы в физике. Труды 6-огомеждународного симпозиума. Триест. Под ред. Пьетронеро Л., Тозатти Э. 1988. Мир. Москва.
Федер Е. Фракталы. М.: Мир,1991.
Ben-Avraham D., Halvin S. Diffusion and reactions in fractals and disordered systems. 2000. Cambridge Univ. Press. Cambridge.
Cohen R., Halvin S. Complex networks. Structure, robustness and function. 2010. Cambridge Univ. Press. Cambridge.
Stauffer D., Aharony A. Introduction to percolation theory.2018. Taylor-Francis. Philadelphia.
Peters B., Bolhus P.G., Mullen R.G., Shea J-E. // J. Chem. Phys. 2013. V. 138. № 054106.
Lu J., Vanden-Eijhden E. // J. Chem.Phys. 2014. V.141. № 041109.
Krivov S.V. // J. Chem. TheoryComput. 2018. V. 14. P. 3418.
Chiuchiu D., Ferrare E., Pigolotti S. // Phys. Rev. E. 2019. V. 100. № 062502.
Voorhees P.W. // Annu. Rev. Mater. Sci. 1992. V. 22. P. 197.
Meerson B., Sasorov P.V. // Phys. Rev. E. 1996. V. 53. P. 3491.
Niethammer B., Pego R.L. // J. Stat. Phys. 1999. V. 95. P. 867.
Ким И.П., Черняк А.В., Бендерский В.А. // Химия высоких энергий. 2021. Т. 55. № 2. С. 128.
Ким И.П., Коткин А.С., Бендерский В.А. // Химия высоких энергий. 2021. Т. 55. № 3.
Дополнительные материалы отсутствуют.
Инструменты
Химия высоких энергий