Химия высоких энергий, 2021, T. 55, № 5, стр. 400-403
Молекулярно-динамическое моделирование самосборки медной нанопленки на кремниевой подложке в условиях газоразрядной плазмы
И. И. Файрушин a, b, c, *, А. Ю. Шемахин a, А. А. Хабирьянова d
a Казанский (Приволжский) федеральный университет
420008 г. Казань, ул. Кремлевская, 18, Россия
b Объединенный институт высоких температур
125412 г. Москва, ул. Ижорская, д. 13, стр. 2, Россия
c Казанский национальный исследовательский технический университет им. А.Н. Туполева-КАИ
420111 г. Казань, ул. Карла Маркса, 10, Россия
d Национальный исследовательский университет Высшая школа экономики
119048 г. Москва, ул. Усачева, 6, Россия
* E-mail: fairushin_ilnaz@mail.ru
Поступила в редакцию 05.02.2021
После доработки 28.04.2021
Принята к публикации 11.05.2021
Аннотация
С применением метода молекулярной динамики смоделирован процесс распыления медной мишени и последующего формирования на кремниевой подложке нанопленки меди. Параметры процесса соответствовали условиям в газоразрядной плазме пониженного давления. Полученные значения коэффициента распыления соответствуют экспериментальным данным. Определена скорость роста нанопленки.
Наноструктуры на основе меди могут служить альтернативой благородным металлам для использования их в качестве катализаторов в ряде химических процессов [1]. Один из способов получения наноструктур металлов – воздействие на массивный образец высокоэнергетичных ионов газоразрядной плазмы с последующим распылением и осаждением отдельных атомов и (или) кластеров металла на подложку [2, 3]. Данный способ может быть усовершенствован при помощи компьютерного моделирования [2–8], позволяющий выявлять оптимальные параметры без натурных экспериментов.
В работе разработана молекулярно-динамическая модель процесса распыления и осаждения атомов меди на кремниевую подложку при температурах, концентрациях и энергиях частиц, соответствующих условиям в газоразрядной плазме [2–6]. Для моделирования использовалась схема масштабирования параметров, разработанная P. Brault в [9]. Данная схема основана на том, что частота столкновений атомов газа в условиях лабораторной установки приравнивается к частоте столкновений в ячейке моделирования. В этом случае пересчет давления в экспериментальной установке через параметры моделирования выполняется согласно следующему соотношению
где N – число частиц в ячейке моделирования, kB – постоянная Больцмана, S – площадь поперечного сечения ячейки моделирования, dexp – характерный линейный размер экспериментального реактора. Для пересчета времени симуляции tsim в реальное время эксперимента texp будем основываться на допущении, что атомы между столкновениями движутся равномерно, а значение скорости в эксперименте и в модели должны быть равны [9]. Тогда время эксперимента рассчитывается как:Здесь важно заметить, что при таком рассмотрении скорость распыления атомов металла в моделировании оказывается очень большим и связано это с тем, что металлический образец в модели рассматривается с реальными значениями плотности упаковки атомов. Таким образом, плотность потока ионов в расчете на единицу площади поверхности металла становится более чем на три порядка выше, чем это происходит в натурном эксперименте. Указанный недостаток является неустранимым и может быть минимизирован увеличением размеров симуляционной ячейки, но полностью избавиться от него при современном уровне развития вычислительной техники не удается.
Рассматривалась прямоугольная элементарная ячейка моделирования. Использовались свободные граничные условия для продольного направления и периодические граничные условия в поперечном (рис. 1). Расчеты выполнялись с использованием программного пакета LAMMPS [10]. Составляющими модели являлись медная мишень и кремниевая подложка, пространство между ними заполнялось атомами аргона (рис. 1). Вся система состоит из 21448 частиц. Из них 16 184 атомов Cu, 4624 атомов Si, 640 атомов Ar. Взаимное размещение атомов в элементарной ячейке Cu эквивалентно ГЦК-решетке. При обычных условиях медь имеет ГЦК-решетку с а = 3.615 Å, где а – постоянная решетки. В модели медная мишень делится на 3 зоны. Нижний слой, толщины 0.3 нм, поддерживался при температуре 0 К для предотвращения движения мишени при воздействии высокоэнергетических ионов. Зона толщиной 3.3 нм термостатировалась для распределения энергии, выделяющейся при ударе ионов Ar+. Оставшаяся зона, толщиной 1.2 нм, состоит из свободно движущихся атомов. Она не термостатировалась для обеспечения корректного распыления атомов меди. Подготовительным этапом было плавление и нагревание медной мишени до температуры близкой к температуре парообразования. Кремниевая подложка так же делится на зоны: нижняя часть, толщиной 0.5 нм, с неподвижными атомами кремния для предотвращения движения кремниевой подложки при ударе атомов Cu, и оставшаяся часть, термостатируемая при 300 К. Элементарная ячейка кремния представляла собой кубическую решетку с параметром решетки а = 5.431 Å. Между мишенью и подложкой находится частично ионизированный газ Ar. Температура газа поддерживается при 300 К с помощью термостата Берендсона. 10% от всех частиц газа случайно выбирается в качестве ионов. Затем, ионам аргона задавалась скорость в направлении медной мишени, соответствующая кинетической энергии в 300 эВ. Большая часть атомов медной мишени, принявших участие в каскаде столкновений, остаются связанными в твердом теле, но один или несколько покидают поверхность и осаждаются на подложку.
Для взаимодействия ускоренных атомов (ионов) аргона с медью был выбран потенциал Зиглера–Бирсака–Литмарка (ЗБЛ) [11]. Необходимо отметить, что в недавней работе [12] было показано, что применение потенциала ЗБЛ позволяет моделировать образование полостей в наноструктурах из платины. Взаимодействие атомов кремния осуществлялось через потенциал Стилинджера–Вебера, а атомов меди – потенциал погруженного атома [2, 13]. Взаимодействие атомов меди и атомов кремния задавалось потенциалом Морзе, с параметрами взятыми из работы [14]. Реальное давление, соответствующее модели, согласно формуле (1), составило Pexp = 1.25 Па. В нашем случае, реальное время эксперимента составило texp = 15 мкс.
Проведенные численные эксперименты по распылению и осаждению атомов меди на кремниевую подложку показали, что модель медной мишени устойчива, атомы меди осаждаются на кремниевую подложку.
Эффективность распыления характеризуется коэффициентом распыления γ, который определяется как среднее число атомов, удаляемых с поверхности твердого тела одним бомбардирующим ионом. Для характеристики распыления многокомпонентных материалов используется парциальные коэффициенты распыления отдельных компонентов. Величина коэффициента распыления зависит от многих факторов: энергии иона, типа бомбардирующих атомов, распыляемого материала, давления рабочего газа, угла падения ионов, температуры мишени и т.д. При малых энергиях существует порог возникновения распыления. Далее коэффициент возрастает и достигает максимума. При очень высоких энергиях он снова падает, так как энергия иона выделяется глубоко и получивший ее ион мишени не может выйти наружу.
Рассмотрим полученную в результате моделирования зависимость коэффициента распыления меди от энергии падающих ионов, для того чтобы показать, что развитая в этой работе модель позволяет проводить расчеты распыления. Качественное, а по возможности и количественное согласие с экспериментальными данными выступит критерием корректности модели.
Коэффициент рассчитывается как отношение числа выбитых атомов к числу упавших на мишень ионов. Он может варьироваться в зависимости от структуры и состава мишени, от ее шероховатости, от энергии ионов, от угла падения и других факторов. Коэффициент распыления меньше для веществ с большой энергией связи, которая равна работе, затрачиваемой на отрыв атома от поверхности. Коэффициент распыления больше при большем атомном номере падающего иона – ион с большим атомным номером имеет большие размеры, соответственно, взаимодействует с большим числом атомов мишени.
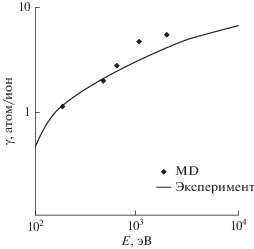
Зависимость коэффициента от энергии падающего иона представлена на рис. 2. Расчет коэффициента распыления по результатам численного эксперимента показал (рис. 2), что атомы меди распыляются с коэффициентом распыления соответствующим экспериментальным данным из литературы [15].
Рис. 2.
Зависимость коэффициента распыления атомов меди от энергии падающего иона Ar+ (MD – результат расчетов по данным моделирования, Эксперимент – результат экспериментальных исследований [15]).
Характер перемещения распыленных частиц в пространстве после выхода из твердого тела определяется расстоянием до подложки и давления рабочего газа. При высоких давлениях и больших расстояниях до подложки возможно значительное рассеяние частиц. При малых давлениях и расстояниях распыленные частицы движутся почти прямолинейно.
Толщина образованной медной нанопленки за время распыления в 12 пс составила ~2 нм (рис. 3). Скорость напыления рассчитывалась как отношение толщины пленки ко времени распыления. По результатам моделирования скорость напыления составила 0.6 мкм/с.
Рис. 3.
Изображение медной нанопленки, полученной в моделировании (светлые сферы – атомы меди, темные – атомы кремния).

В заключении можно сказать, что разработана молекулярно-динамическая модель процесса распыления и осаждения атомов меди на кремниевую подложку при температурах, концентрациях и энергиях частиц, полученных из литературы, посвященных исследованиям газоразрядной плазмы. Проведены численные эксперименты по распылению и осаждению атомов меди на кремниевую подложку. Эксперименты показали, что модель медной мишени устойчива, атомы меди осаждаются на кремниевую подложку. Расчeт коэффициента распыления по результатам численного эксперимента показал, что атомы меди распыляются с коэффициентом распыления соответствующим экспериментальным данным из литературы. Разработанная модель может служить удобным инструментом для подбора оптимальных параметров плазмохимического синтеза наноструктур меди.
Список литературы
Sun Y., Yu J., Ma Q. // Science Advances. 2018. V. 4. eaau3275.
Файрушин И.И., Сайфутдинов А.И., Софроницкий А.О. // Химия высоких энергий. 2020. Т. 54. № 2. С. 164.
Сайфутдинов А.И., Файрушин И.И., Кашапов Н.Ф. // Письма в ЖЭТФ. 2016. Т. 104. № 3. С. 178.
Shemakhin A.Yu., Zheltukhin V.S. // Advances in Materials Science and Engineering. 2019. V. 2019. 7120217.
Shemakhin A.Y., Zheltukhin V.S., Khubatkhuzin A.A. // Journal of Physics: Conference Series. 2016. V. 774. P. 012167.
Shemakhin A.Y., Zheltukhin V.S. // Journal of Physics: Conference Series. 2017. V. 927. P. 012055.
Galimzyanov B.N., Yarullin D.T., Mokshin A.V. // Acta Materialia. 2019. V. 169. P. 184.
Fairushin I.I., Saifutdinov A.I., Sofronitskiy A.O., Timerkaev B.A., Dautov G.Yu. // J. Physics: Conference Series. 2019. V. 1328. P. 012088.
Brault P. // Front. Phys. 2018. V. 6. 59.
Plimpton S. // J. Comput. Phys. 1995. V. 117. № 1. P. 1.
Корнич Г.В., Бетц Г., Бажин А.И. // Физика твердого тела. 2001. Т. 43. № 1. С. 30.
Orozco-Montes V., Caillard A., Brault P., Chamorro-Coral W., Bigarre J., Sauldubois A., Andreazza P., Cuynet S., Baranton S., Coutanceau C. // J. Phys. Chem. C. 2021. 125, 5, 3169–3179.
Foiles S.M., Baskes M.I., Daw M.S. // Phys. Rev. B. 1986. V. 33. P. 7983.
Hwang S.-F., Li Y.-H., Hong Z.-H. // Computational Materials Science. 2012. V. 56. P. 85.
Физика тонких пленок. Под ред. Хасса Г. и Туна Р.Э., Т. 3. М. 1968.
Дополнительные материалы отсутствуют.
Инструменты
Химия высоких энергий



