Физикохимия поверхности и защита материалов, 2019, T. 55, № 3, стр. 273-281
Избыточная и абсолютная адсорбция бинарного жидкого раствора микропористыми кристаллическими адсорбентами: кумол + н-октан/цеолит NaX
Э. С. Якубов *
Федеральное государственное бюджетное учреждение науки Институт физической химии и электрохимии
им. А.Н. Фрумкина РАН,
119071 Москва, Ленинский просп., 31, корп. 4, Россия
* E-mail: edjakub@mail.ru
Поступила в редакцию 18.12.2018
После доработки 21.01.2019
Принята к публикации 22.01.2019
Аннотация
Изотермы избыточной адсорбции кумола из растворов в н-октане на цеолите NaX измерены при температурах 303.15, 338.15 и 363.15 К с использованием общепринятого статического метода. Предельные (абсолютные) величины адсорбции чистых компонентов измерены пикнометрическим методом. Изотермы абсолютной адсорбции для указанной системы рассчитаны по модифицированному уравнению Дубинина–Радушкевича с тремя неподгоночными параметрами. Приводится подробный вывод расчетных формул. Данные по абсолютной адсорбции далее используются для оценки средней плотности адсорбата и других характеристик адсорбционной фазы.
ВВЕДЕНИЕ
С теоретической и практической точек зрения особенно важно иметь более глубокое понимание поведения жидких растворов в адсорбционном состоянии в микропористых адсорбентах, таких как цеолиты. Такое понимание требует помимо других вещей знание величин абсолютной адсорбции. Следует отметить, что изотерма абсолютной адсорбции является необходимой функцией при изучении явления адсорбции. Источником ценной информации, получаемой с помощью адсорбционной калориметрии, методов ИК-, ЯМР-, ЭПР-спектроскопии являются все адсорбированные молекулы, а не только избыточные. При физических переходах в адсорбционной фазе участвуют все молекулы, подобная же ситуация имеет место при вызванной адсорбцией деформации твердых адсорбентов. Отметим также, что модели, описывающие адсорбцию в рамках статистической термодинамики, основываются также на предположении о включенности всех адсорбированных молекул в процесс.
Тогда как в случае микропористых адсорбентов изотерму избыточной адсорбции можно измерить относительно легко, для точного определения изотермы абсолютной адсорбции требуется проведение тщательных и трудоемких экспериментов. Действительно, избыточная адсорбция, определяемая как избыток одного из компонентов, например компонента 1, в адсорбированном растворе по сравнению с его содержанием в равной порции объемного раствора, определяется обычно экспериментально измерением изменения концентрации в объемной фазе в результате адсорбции. В то время как измерение абсолютной адсорбции, определяемой как полное количество молекул адсорбата в адсорбционной фазе, предполагает знание объема пор адсорбента, которое, как правило, не известно.
Поэтому возникает основная проблема конвертации данных по избыточной адсорбции в абсолютную адсорбцию. В наших предыдущих работах [1, 2] мы предложили метод определения изотерм абсолютной адсорбции бинарных растворов в микропористых кристаллических адсорбентах. Метод был опробован на имеющихся экспериментальных изотермах абсолютной адсорбции для следующих систем: п-ксилол + н-октан + + NaX [3], этанол + бензол + NaX [4], бензол + + циклогексан + NaX [5], этанол + вода + силикалит [6] и тетрадецен-1 + н-додекан + NaX [7]. Рассчитанные значения довольно хорошо согласуются с экспериментальными данными.
Целью данной статьи является представление экспериментальных данных по избыточной адсорбции и рассчитанных изотерм абсолютной адсорбции для адсорбционной системы кумол + + н-октан + NaX.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Анализ экспериментальных данных по изотермам абсолютной адсорбции указанных выше адсорбционных систем позволяет предположить, что производные D1 и D в пределах экспериментальных ошибок связаны с величинами предельной адсорбции следующими соотношениями
(1)
${{D}_{1}} = {{\left( {\frac{{dw_{1}^{s}}}{{d{{c}_{1}}}}} \right)}_{{{{C}_{1}} = {{C}_{{1m}}}}}} = {{m}_{1}}$(2)
$D = {{\left( {\frac{{d{{w}^{s}}}}{{d{{c}_{1}}}}} \right)}_{{{{C}_{1}} = {{C}_{{1m}}}}}} = {{m}_{1}} - {{m}_{2}}.$Здесь и в выражениях ниже $w_{1}^{s}$ и ${{w}^{s}}$ – изотермы абсолютной адсорбции предпочтительно адсорбированного компонента 1 и раствора (в г/г) соответственно; ${{m}_{1}}$ и ${{m}_{2}}$ – предельные (абсолютные) величины адсорбции чистых компонентов (в г/г); ${{c}_{1}}$ и $c_{1}^{s}$ – равновесные концентрации 1-го компонента в объемной и адсорбционной фазах соответственно (в массовых долях); $w_{1}^{e}$ – изотерма избыточной адсорбции (в г/г), а через ${{c}_{{1m}}}$ обозначена концентрация, соответствующая максимальной избыточной адсорбции.
Ниже приводится вывод расчетных формул предлагаемого метода. Рассмотрим прежде всего хорошо известное соотношение, связывающее избыточную адсорбцию с абсолютной и составом адсорбционной фазы
(3)
$w_{1}^{{e\quad}} = {{w}^{s}}\left( {c_{1}^{s} - {{c}_{1}}} \right) = w_{1}^{s} - {{w}^{s}}{{c}_{1}}.$Дифференцирование (3) по с1 дает
(3а)
$\frac{{dw_{1}^{e}}}{{d{{c}_{1}}}} = \frac{{dw_{1}^{s}}}{{d{{c}_{1}}}} - \frac{{d{{w}^{s}}}}{{d{{c}_{1}}}}{{c}_{1}} - {{w}^{s}}.$Учитывая соотношения (1) и (2), а также тот факт, что при концентрации ${{c}_{{1m}}}$ производная $\frac{{dw_{1}^{e}}}{{d{{c}_{1}}}}$ равна нулю, получаем следующее выражение
где $w_{m}^{s}$ – значение абсолютной адсорбции раствора в точке ${{c}_{{1m}}}$ и, как следует из формулы (4), для его расчета достаточно знание предельных величин адсорбции.Итак, на кривой ${{w}^{s}}({{c}_{1}})$ нам известны три точки: ${{m}_{2}}\,,\,w_{m}^{s}\,$ и ${{m}_{1}}$, с помощью которых можно аппроксимировать всю кривую. С этой целью можно использовать эмпирическое уравнение, которое должно удовлетворять двум условиям: минимальному числу статистически значимых подгоночных параметров и высокой описательной способностью. С этой точки зрения уравнение Дубинина–Радушкевича более подходящее, чем любое другое уравнение. Таким образом, мы предлагаем использовать уравнение типа Дубинина–Радушкевича, модифицированное применительно к адсорбции из растворов,
(5)
${{w}^{s}} = {{m}_{2}} + ({{m}_{1}} - {{m}_{2}})\exp ( - k{{\left| {\ln {{c}_{1}}} \right|}^{n}}),$Действительно, эти константы могут быть определены следующим образом. Дифференцируя уравнение (5) по ${{c}_{1}}$, получаем
Отсюда имеем
(6)
$k = \frac{{{{c}_{{1m}}}}}{{n{{{( - \ln {{c}_{{1m}}})}}^{{n - 1}}}\exp \left\{ { - k{{{( - \ln {{c}_{{1m}}})}}^{n}}} \right\}}}.$Для того чтобы избавиться от константы k в правой части уравнения (6), воспользуемся уравнением (5), из которого следует, что в точке ${{c}_{{1m}}}$ имеем
С учетом этого уравнение (6) принимает вид
(7)
$k = \frac{{{{c}_{{1m}}}({{m}_{1}} - {{m}_{2}})}}{{n{{{( - \ln {{c}_{{1m}}})}}^{{n - 1}}}(w_{m}^{s} - {{m}_{2}})}}.$Далее, вычитая из обеих частей уравнения (4) m2, имеем
(8)
$\begin{gathered} w_{m}^{s} - {{m}_{2}} = {{m}_{1}} - {{m}_{2}} - ({{m}_{1}} - {{m}_{2}}){{c}_{{1m}}}, \\ \frac{{w_{m}^{s} - {{m}_{2}}}}{{{{m}_{1}} - {{m}_{2}}}} = 1 - {{c}_{{1m}}}. \\ \end{gathered} $Подстановка (8) в (7) дает
Следующий шаг – вывод выражения для константы n. Для этого подставим формулу (9) в исходное уравнение (5). Тогда в точке ${{c}_{{1m}}}$ имеем
С учетом соотношения (8) последнее выражение принимает вид
(10)
$(1 - {{c}_{{1m}}}) = \exp \left\{ { - \frac{{{{c}_{{1m}}}( - \ln {{c}_{{1m}}})}}{{n(1 - {{c}_{{1m}}})}}} \right\}.$Логарифмирование уравнения (10) дает
Отсюда окончательно получаем для константы n следующую формулу
Подстановка выражения (11) в соотношение (9) дает
Таким образом, константы k и n выражаются только через концентрацию ${{c}_{{1m}}}$, и для расчета изотермы абсолютной адсорбции $w_{1}^{s}$ по предлагаемому методу прежде всего необходимо определить величину ${{c}_{{1m}}}$ из изотермы избыточной адсорбции $w_{1}^{e}$, затем рассчитать константы n и k по формулам (11) и (12), далее рассчитать изотерму абсолютной адсорбции бинарного раствора ${{w}^{s}}$ по формуле (5) и, наконец, по уравнению (3) рассчитать $w_{1}^{s}$.
Следует отметить, что принятые при выводе уравнения (4) предположения относятся только к изотермам адсорбции II типа по классификации Шая и Надя [8], поскольку мы располагаем экспериментальными изотермами абсолютной адсорбции только для систем, цитированных выше [3–7]. Изотермы избыточной адсорбции всех этих систем относятся к типу II по классификации Шая и Надя. Мы не исключаем справедливость уравнений (1) и (2) и для других типов изотерм, но, насколько нам известно, соответствующие экспериментальные данные по изотермам абсолютной адсорбции в литературе отсутствуют. Здесь стоит напомнить форму изотермы избыточной адсорбции типа II: максимум изотермы смещен в сторону малых равновесных концентраций, а нисходящая часть изотермы почти линейна.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
В качестве адсорбента использовали исходный коммерческий цеолит NaX/ГОБ-партия 21/производства ВНИИНП (г. Н. Новгород). Цеолит активизировали нагреванием при 450°С в течение 8–10 ч в вакууме. Кумол и н-октан квалификации “ч. д. а.” перед использованием сушили цеолитом NaA.
Изотермы избыточной адсорбции измеряли по модифицированному статическому методу [9]. Основной чертой этого метода заключается в том, что эксперимент можно проводить на одном образце адсорбента во всей области концентраций без доступа воздуха. Равновесная концентрация в массовых долях предпочтительно адсорбируемого компонента измеряли на дифференциальном рефрактометре, кюветы которой образуют один узел с адсорбционной камерой.
Предельные величины адсорбции измеряли пикнометрическим методом [2 , 10].
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Удельные изотермы избыточной адсорбции $w_{1}^{e}$ (в г/г) для системы были измерены при трех температурах: 303.15, 338.15 и 363.15 K. Численные данные представлены в табл. 1 для дальнейшего использования. Экспериментальные результаты для 303.15 K показаны на рис. 1a и рис. 1б как функция концентрации кумола c1 и квадратного корня концентрации $\surd {{с }_{1}}$ соответственно, где c1 – массовая доля. Вследствие того, что изотермы избыточной адсорбции для системы кумол + н-октан + NaX принадлежат типу II, данные представлены в этой форме для удобства восприятия, так как в начальной области концентрации кривые очень крутые, что указывает на сильную адсорбцию.
Таблица 1.
Изотермы избыточной адсорбции для системы кумол (компонент 1)+ н-октан + NaX (${{c}_{1}}$, массовые доли; $w_{1}^{e}$, г/г)
| 303.15 K | 338.15 K | 363.15 K | |||
|---|---|---|---|---|---|
| ${{c}_{1}}$ | $w_{1}^{e}$ | ${{c}_{1}}$ | $w_{1}^{e}$ | ${{c}_{1}}$ | $w_{1}^{e}$ |
| 0 0.00059 0.00101 0.00252 0.00439 0.00807 0.01427 0.01843 0.02517 0.04069 0.07015 0.09917 0.15217 0.20051 0.30441 0.50121 0.70762 1 |
0 0.09278 0.11883 0.14525 0.16933 0.18554 0.18899 0.19678 0.19593 0.20372 0.19601 0.19335 0.18254 0.17395 0.15474 0.11338 0.06838 0 |
0 0.00104 0.00212 0.00402 0.00666 0.01178 0.01622 0.02165 0.02801 0.04300 0.07198 0.10087 0.15395 0.15677 0.20170 0.30491 0.50311 0.70869 1 |
0 0.09070 0.11368 0.13822 0.15866 0.16794 0.17967 0.18129 0.18218 0.19239 0.18678 0.18443 0.17277 0.17122 0.16697 0.15138 0.10668 0.06213 0 |
0 0.00129 0.00284 0.00518 0.00882 0.01356 0.01842 0.02395 0.02996 0.04477 0.07356 0.10243 0.15471 0.20304 0.30574 0.50529 0.70970 1 |
0 0.89570 0.11035 0.13283 0.14849 0.15948 0.16914 0.17022 0.17269 0.18376 0.17885 0.17643 0.16862 0.15917 0.14586 0.09904 0.05622 0 |
Рис. 1.
(а) Изотерма избыточной адсорбции $w_{1}^{e}$ (г/г) как функция с1 (мас. доля) исследованной адсорбционной системы при 303.15 K. (б) Изотерма избыточной адсорбции $w_{1}^{e}$ (г/г) как функция $\surd {{с }_{1}}$ (мас. доля) исследованной адсорбционной системы при 303.15 K.

Величина предельной адсорбции является важным параметром, необходимым при рассмотрении различных проблем адсорбционной теории, в особенности при выборе моделей адсорбционных систем. Обычный способ определения этой величины заключается в измерении адсорбции чистого пара вплоть до давления насыщенного пара. Недостатком этого метода является то, что невозможно избежать капиллярной конденсации. Поэтому мы выбрали пикнометрический метод определения предельных (абсолютных) величин адсорбции чистых компонентов m1 и m2. В табл. 2 приведены значения m1 и m2 в г/г при трех температурах.
Таблица 2.
Предельные (абсолютные) значения адсорбции чистого кумола (компонент 1) и н-октана в цеолите NaX
| T, K | m1, г/г | m2, г/г |
|---|---|---|
| 303.15 338.15 363.15 |
0.25054 0.23999 0.23245 |
0.18298 0.17647 0.17190 |
Основываясь на этих экспериментальных данных, мы можем далее вычислить изотермы абсолютной адсорбции по уравнению (5).
Рассмотрим систему кумол + н-октан + NaX при температуре 303.15 K более подробно. Самого начала следует отметить, что для обработки исходных данных мы использовали компьютерную программу “CurveExpert”. Прежде всего, изотерма сглаживалась, затем численным дифференцированием $w_{1}^{e}$ по c1 находилась ее производная. Приравниванием последней к нулю определялась концентрация c1m, при которой $w_{1}^{e}$ достигает максимального значения. Численное значение искомой концентрации составляет c1m = 0.039998, а соответствующая максимальная избыточная адсорбция равна $w_{{1m}}^{e}$ = 0.201603. Далее по формулам (11) и (12) вычислялись константы n и k: n = = 3.28552, k = 8.76559 × 10–4. Как можно видеть из табл. 2, предельные адсорбции для кумола и н-октана принимают следующие значения: m1 = = 0.25054 г/г и m2 =0.18298 г/г. Используя эти данные, мы можем рассчитать изотерму абсолютной адсорбции ws(c1) по формуле (5) и изотерму абсолютной адсорбции предпочтительно адсорбируемого компонента $w_{1}^{s}$ по формуле (3). Отметим, что в формуле (3) мы использовали фиттированные (сглаженные) значения $w_{1}^{e}$ для исходных экспериментальных концентраций. Все рассчитанные величины сведены в табл. 3.
Таблица 3.
Изотерма избыточной адсорбции $w_{1}^{e}$ (сглаженные значения), изотерма абсолютной адсорбции раствора ${{w}^{s}}$, изотерма абсолютной адсорбции компонента 1 $w_{1}^{s}$ и равновесная концентрация компонента 1 в адсорбционной фазе $c_{1}^{s}$ при 303.15 K для системы кумол + н-октан + NaX
| ${{c}_{1}}$, мас. доля | $w_{1}^{e}$, г/г | ${{w}^{s}}$, г/г | $w_{1}^{s}$, г/г | $c_{1}^{s}$, мас. доля |
|---|---|---|---|---|
| 0 0.00059 0.00101 0.00252 0.00439 0.00807 0.01427 0.01843 0.02517 0.04069 0.07015 0.09917 0.15217 0.20051 0.30441 0.50121 0.70762 1 |
0 0.09874 0.11633 0.14692 0.16429 0.18075 0.19250 0.19634 0.19968 0.20160 0.19853 0.19331 0.18279 0.17315 0.15282 0.11383 0.06960 0 |
0.18298 0.21864 0.22398 0.23239 0.23680 0.24091 0.24401 0.24516 0.24638 0.24788 0.24909 0.24962 0.25007 0.25026 0.25044 0.25052 0.25054 0.25054 |
0 0.09887 0.11655 0.14750 0.16533 0.18269 0.19598 0.20086 0.20588 0.21169 0.21600 0.21807 0.22084 0.22333 0.22905 0.23939 0.24688 0.25054 |
0 0.45222 0.52037 0.63473 0.69819 0.75833 0.80316 0.81930 0.83560 0.85397 0.86717 0.87360 0.88313 0.89240 0.91461 0.95557 0.98540 1 |
Следующий шаг – подтверждение обоснованности принятых допущений, выраженных зависимостями (1) и (2). Функцию $w_{1}^{s}$ = ${{f}_{1}}\left( {\surd {{c}_{1}}} \right)$ аппроксимировали кубическим сплайном, и было найдено, что производная df1/$d\left( {\surd {{c}_{1}}} \right)$ в точке $\surd {{c}_{{1m}}}$ равна 0.100092. Отсюда
Отклонение расчетного значения от экспериментального, характеризуемое относительной ошибкой в процентах δ, рассчитывали по следующей формуле
(13)
$\delta (y) = ({{\left| {{{y}^{{{\text{cal}}}}} - {{y}^{{{\text{exp}}}}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{y}^{{{\text{cal}}}}} - {{y}^{{{\text{exp}}}}}} \right|} {{{y}^{{{\text{exp}}}}}}}} \right. \kern-0em} {{{y}^{{{\text{exp}}}}}}}) \times 100.$Ошибка составляет
Аналогично, функцию ws = ${{f}_{2}}\left( {\surd {{c}_{1}}} \right)$ также аппроксимировали кубическим сплайном, и было найдено, что производная df2/$d\left( {\surd {{c}_{1}}} \right)$ в точке $\sqrt {{{c}_{{1m}}}} $ равна 0.0269866, что дает
Таким образом, в обоих случаях значение ошибки меньше, чем 0.15%, что вполне приемлемо.
Далее делением $w_{1}^{s}$ на ${{w}^{s}}$ находили концентрацию кумола в адсорбционной фазе в массовых долях $c_{1}^{s}$. На рис. 2 представлена зависимость состава адсорбционной фазы $c_{1}^{s}$ от равновесного состава объемного раствора $\sqrt {{{c}_{1}}} $. Также рассчитывали величину S, известную как коэффициент избирательности и определяемую для бинарного раствора формулой (14),
(14)
$S = {{(c_{1}^{s}{{c}_{2}})} \mathord{\left/ {\vphantom {{(c_{1}^{s}{{c}_{2}})} {({{c}_{1}}c_{2}^{s}}}} \right. \kern-0em} {({{c}_{1}}c_{2}^{s}}}) = {{(c_{1}^{s}(1 - {{c}_{1}}))} \mathord{\left/ {\vphantom {{(c_{1}^{s}(1 - {{c}_{1}}))} {(c_{1}^{{}}(1 - c_{1}^{s}))}}} \right. \kern-0em} {(c_{1}^{{}}(1 - c_{1}^{s}))}}.$Рис. 2.
Изотерма состава адсорбированного раствора $c_{1}^{s}$как функция $\surd {{с }_{1}}$ (мас. доля) для исследованной адсорбционной системы при 303.15 K.

На рис. 3 представлена величина S как функция $\sqrt {{{c}_{1}}} $.
Рис. 3.
Коэффициент селективности S как функция $\surd {{с }_{1}}$ (мас. доля) для исследованной адсорбционной системы при 303.15 K.

Особый интерес представляет избыточный объем смешения адсорбированного раствора VEs, поскольку он весьма чувствителен к перегруппировкам молекул в адсорбционном растворе. Изотермы абсолютной адсорбции позволяют определить эту величину согласно формуле:
(15)
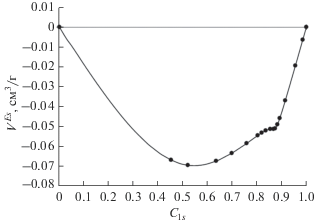
${{V}^{{Es}}} = \left( {{{{{{{{W}_{0}}} \mathord{\left/ {\vphantom {{{{W}_{0}}} w}} \right. \kern-0em} w}}}^{s}}} \right)\left[ {1 - \left( {{{w_{1}^{s}} \mathord{\left/ {\vphantom {{w_{1}^{s}} {{{m}_{1}}}}} \right. \kern-0em} {{{m}_{1}}}} + {{w_{2}^{s}} \mathord{\left/ {\vphantom {{w_{2}^{s}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} \right)} \right],$Рис. 4.
Зависимость избыточного объема смешения адсорбированного раствора ${{V}^{{Es}}}$ от состава $c_{1}^{s}$ при 303.15 K.
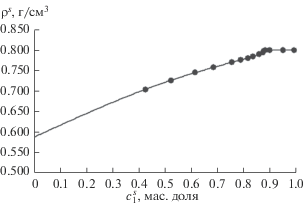
В качестве отступления заметим, что формула для оценки адсорбционного объема твердых адсорбентов, предложенная в нашей статье [12], дает значение, очень близкое к 0.3 см3/г. Эта формула имеет вид:
(16)
${{W}_{0}} = {{\left( {w_{1}^{e}{{\rho }_{{01}}}} \right)} \mathord{\left/ {\vphantom {{\left( {w_{1}^{e}{{\rho }_{{01}}}} \right)} {[{{\rho }_{{02}}}\left( {1 - {{c}_{{1m}}}} \right)\left( {{{\rho }_{{01}}} + \left( {{{\rho }_{{01}}} - {{\rho }_{{02}}}} \right){{c}_{{1m}}}} \right)],}}} \right. \kern-0em} {[{{\rho }_{{02}}}\left( {1 - {{c}_{{1m}}}} \right)\left( {{{\rho }_{{01}}} + \left( {{{\rho }_{{01}}} - {{\rho }_{{02}}}} \right){{c}_{{1m}}}} \right)],}}$Кроме того, мы рассчитали плотность адсорбционного раствора по следующему соотношению ρs = ws/W0. На рис. 5 представлена концентрационная зависимость ρs.
Теперь рассмотрим кратко результаты при двух других температурах. Исходные данные для расчета изотерм абсолютной адсорбции представлены ниже:
(i) T =338.15 K, c1m= 0.04683, √c1m = 0.2164, n = = 3.13586, k = 1.43606 × 10–3, $w_{{1m}}^{e}$ = 0.19365 г/г.
(ii) T = 363.15 K, c1m= 0.05531, √c1m = 0.2352, n = = 2.97866, k = 2.39980 × 10–3, $w_{{1m}}^{e}$ = 0.18377 г/г.
Результаты расчетов суммированы в табл. 4 и 5. Обоснованность зависимостей (1) и (2) также была подтверждена, причем относительные ошибки в процентах находились в интервале 0.18–0.57. На рис. 6 и 7 для 338.15 K представлены плотность ρs и избыточный объем смешения VEs адсорбированного раствора соответственно. Аналогичные величины для 363.15 K представлены на рис. 8 и 9.
Таблица 4.
Изотерма избыточной адсорбции $w_{1}^{e}$ (сглаженные значения), изотерма абсолютной адсорбции раствора ${{w}^{s}}$, изотерма абсолютной адсорбции компонента 1 $w_{1}^{s}$ и равновесная концентрация компонента 1 в адсорбционной фазе $c_{1}^{s}$ при 338.15 K для системы кумол + н-октан + NaX
| ${{c}_{1}}$, мас. доля | $w_{1}^{e}$, г/г | ${{w}^{s}}$, г/г | $w_{1}^{s}$, г/г | $c_{1}^{s}$, мас. доля |
|---|---|---|---|---|
| 0 0.00104 0.00212 0.00402 0.00666 0.01178 0.01622 0.02165 0.02801 0.04300 0.07198 0.10087 0.15395 0.15677 0.20170 0.30491 0.50311 0.70869 1 |
0 0.08948 0.11357 0.13653 0.15421 0.17203 0.18030 0.18632 0.19030 0.19355 0.19111 0.18542 0.17357 0.17294 0.16324 0.14302 0.10788 0.06854 0 |
0.17647 0.21117 0.21784 0.22334 0.22719 0.23092 0.23270 0.23412 0.23522 0.23675 0.23812 0.23877 0.23934 0.23936 0.23959 0.23983 0.23996 0.23999 0.23999 |
0 0.08970 0.11403 0.13743 0.15572 0.17475 0.18408 0.19139 0.19689 0.20373 0.20825 0.20950 0.21041 0.21047 0.21157 0.21614 0.22861 0.23861 0.23999 |
0 0.42475 0.52349 0.61533 0.68542 0.75676 0.79104 0.81749 0.83703 0.86053 0.87455 0.87742 0.87914 0.87928 0.88304 0.90123 0.95268 0.99428 1 |
Таблица 5.
Изотерма избыточной адсорбции $w_{1}^{e}$ (сглаженные значения), изотерма абсолютной адсорбции раствора $\quad{{w}^{s}}$, изотерма абсолютной адсорбции компонента 1 $w_{1}^{s}$ и равновесная концентрация компонента 1 в адсорбционной фазе $c_{1}^{s}$ при 363.15 K для системы кумол + н-октан + NaX
| ${{c}_{1}}$, мас. доля | $w_{1}^{e}$, г/г | $\quad{{w}^{s}}$, г/г | $w_{1}^{s}$, г/г | $c_{1}^{s}$, мас. доля |
|---|---|---|---|---|
| 0 0.00129 0.00284 0.00518 0.00882 0.01356 0.01842 0.02395 0.02996 0.04477 0.07356 0.10243 0.15471 0.20304 0.30574 0.50529 0.70970 1 |
0 0.08570 0.11124 0.13173 0.14926 0.16200 0.16979 0.17534 0.17910 0.18318 0.18264 0.17830 0.16786 0.15759 0.13627 0.09731 0.05780 0 |
0.17190 0.20262 0.20990 0.21510 0.21926 0.22222 0.22410 0.22554 0.22664 0.22834 0.22997 0.23078 0.23153 0.23187 0.23221 0.23240 0.23244 0.23245 |
0 0.08596 0.11183 0.13285 0.15119 0.16501 0.17391 0.18074 0.18589 0.19340 0.19955 0.20194 0.20368 0.20467 0.20727 0.21474 0.22276 0.23245 |
0 0.42428 0.53279 0.61760 0.68958 0.74254 0.77607 0.80139 0.82019 0.84698 0.86773 0.87500 0.87971 0.88269 0.89260 0.92398 0.95835 1 |
Рис. 7.
Зависимость избыточного объема смешения адсорбированного раствора ${{V}^{{Es}}}$ от состава $c_{1}^{s}$ при 338.15 K.
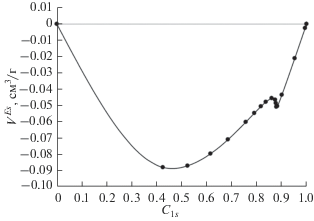
Рис. 9.
Зависимость избыточного объема смешения адсорбированного раствора ${{V}^{{Es}}}$ от состава $c_{1}^{s}$ при 363.15 K.

Как можно видеть из рис. 4, 7 и 9, на кривых VEs наблюдаются особенности в очень узком концентрационном интервале 0.86–0.90. Это, по-видимому, обусловлено упаковкой молекул и их конформационным состоянием при указанных составах.
В заключение следует отметить, что существуют косвенные указания [13, 14], а также прямые экспериментальные данные [10, 15, 16] о том, что плотности чистых адсорбатов при насыщении в микропористых адсорбентах меньше, чем соответствующие плотности объемных жидкостей (единственное исключение – вода). Аналогичное поведение плотностей адсорбированных растворов мы также наблюдаем и в нашей адсорбционной системе (см. рис. 5, 6 и 8). Это справедливо в широком интервале температур ниже критической точки. Такое поведение плотностей в адсорбционных системах можно связать со следующими факторами: упаковкой молекул в полостях с размером такого же порядка, стерическими эффектами, влиянием потенциального поля твердого адсорбента на конформации молекул. Эксперименты с одиннадцатью адсорбатами в цеолите NaX [10, 15, 16] показали, что плотности адсорбатов и объемных жидкостей становятся равными при приведенной температуре τ = T/Tc = 0.85 ± ± 0.08, а затем плотности адсорбатов принимают значения выше плотности объемной фазы. Из этого факта следует, что критическая температура объемной фазы не является особой точкой для адсорбционной фазы. Наши экспериментальные пикнометрические измерения подтверждают эти закономерности, как показано на рис. 10 и 11.
ЗАКЛЮЧЕНИЕ
Предложенный метод представляет собой простой и надежный способ расчета изотерм абсолютной адсорбции бинарных жидких растворов на микропористых кристаллических адсорбентах на основе экспериментальных изотерм избыточной адсорбции и предельных величин адсорбции чистых компонентов.
На основе изотерм абсолютной адсорбции для системы кумол + н-октан + NaX при температурах 303.15, 338.15 and 363.15 K рассчитаны основные физико-химические характеристики адсорбционной фазы, а именно, плотности и избыточные объемы смешения адсорбированных растворов. Показано, что критическая температура объемной фазы не является особой точкой адсорбционной фазы.
Полученные результаты показывают, что изотерма избыточной адсорбции в сочетании с изотермой абсолютной адсорбции и их температурная зависимость являются более информативными, чем только избыточная изотерма. Такие данные способствуют лучшему пониманию свойств жидких растворов в микропорах.
Список литературы
Ларионов О.Г., Якубов Э.С. // Журн. физ. хим .1995. Т. 69. № 7. С. 1327.
Якубов Э.С. // Сорбционные и хроматографические процессы. 2017. Т. 17. № 4. С. 564.
Larionov O.G., Jakubov E.S. // Langmuir. 1988. V. 4. № 6. P. 1223.
Larionov O.G., Jakubov E.S. // In: Proceedings of the 3d International Conference on Fundamentals of Adsorption. Eds. Mersmann A.B., Scholl S.E. UET. Inc. N.Y. 1991. P. 475.
Ларионов О.Г., Якубов Э.С. // Журн. физ. хим. 1995. Т. 69. № 11. С. 1998
Farhadpour F.A., Bono A. // J. Colloid and Interface Science. 1988. V. 124. № 1. P. 209.
Jakubov E.S., Larionov O.G. // Adsorption Science and Technology. 1998. V. 16. № 7. P. 547.
Ościk J. // Adsorption. PWN – Polish Scientific Publishers – Warszawa. Ellis Horwood Limited. Publishers – Chichester. 1982. P. 119–120.
Якубов Э.С. // Дис. … канд. хим.наук. М.: ИФХ РАН 2001.
Рахмуков Б.Х., Селиверстова И.И., Серпинский В.В., Фомкин А.А. // Изв. АН СССР. Сер. хим. 1979. Т. 28. № 11. С. 2419.
Брек Д. // Цеолитовые молекулярные сита. М.: Мир. 1976. С. 440.
Якубов Э.С., Якубов Т.С., Ларионов О.Г. // Коллоидный журнал. 2007. Т. 69. № 5. С. 714.
Фомкин А.А., Серпинский В.В., Беринг Б.П. // Изв. АН СССР. Сер. хим. 1975. Т. 24. № 6. С. 1244.
Чхаидзе Э.В., Фомкин А.А., Серпинский В.В., Цицишвили Г.В. // Изв. АН СССР. Сер. хим. 1985. Т. 34. № 5. С. 974.
Селиверстова И.И., Фомкин А.А., Серпинский В.В., Дубинин М.М. // Изв. АН СССР. Сер. хим. 1983. Т. 32 № 3. С. 493.
Селиверстова И.И., Фомкин А.А., Серпинский В.В. // Изв. АН СССР. Сер. хим. 1986. Т. 35. № 6. С. 1231.
Дополнительные материалы отсутствуют.
Инструменты
Физикохимия поверхности и защита материалов