1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 59, № 8, 2019

Журнал вычислительной математики и математической физики, 2019, T. 59, № 8, стр. 1420-1430

Обратная задача для уравнений сложного теплообмена

Г. В. Гренкин 1, 2, А. Ю. Чеботарев 1, 2, *

1 Дальневосточный федеральный ун-т
690950 Владивосток, ул. Суханова, 8, Россия

2 Ин-т прикл. матем. ДВО РАН
690041 Владивосток, ул. Радио, 7, Россия

* E-mail: chebotarev.ayu@dvfu.ru

Поступила в редакцию 07.03.2019
После доработки 07.03.2019
Принята к публикации 10.04.2019

Полный текст (PDF)

Аннотация

Рассматривается обратная задача с интегральным переопределением для уравнений сложного теплообмена, включающих ${{P}_{1}}$ приближение для стационарного уравнения переноса излучения. Найдены достаточные условия нелокальной однозначной разрешимости обратной задачи. Теоретический анализ проиллюстрирован численными примерами. Библ. 37. Фиг. 3.

Ключевые слова: квази-стационарные уравнения радиационного теплообмена, обратная задача, нелокальная однозначная разрешимость, численное моделирование.

1. ВВЕДЕНИЕ

Задачи сложного (радиационно-кондуктивного) теплообмена представляют значительный интерес для инженерных приложений [1]–[5]. Процесс сложного теплообмена моделируется системой, состоящей из дифференциального уравнения теплопроводности и интегро-дифференциального уравнения переноса излучения. В работах [6]–[20] выполнен анализ краевых задач и задач оптимального управления для уравнений сложного теплообмена с диффузионным ${{P}_{1}}$ приближением уравнения переноса излучения. Анализ различных краевых задач, связанных с радиационным теплообменом, представлен в [21]–[26].

Настоящая работа посвящена анализу обратной задачи для квази-стационарных нелинейных уравнений сложного теплообмена [6], [10], где требуется определить неизвестную интенсивность тепловых источников по интегральному переопределению. Близкие обратные задачи для стационарных уравнений сложного теплообмена рассмотрены в [27] и для квазистационарных уравнений в [28].

Обратные задачи восстановления неизвестных функций источников в линейных параболических уравнениях и системах с интегральными условиями переопределения рассматривались в работах С.Г. Пяткова и др. [29]–[32]. Анализ обратных задач с конечномерным переопределением для уравнений Навье-Стокса, уравнений тепловой конвекции и других моделей сплошных сред представлен в [33]–[37].

Сформулируем постановку обратной задачи для квази-стационарной модели сложного теплообмена в ограниченной трехмерной области $\Omega $ с отражающей границей $\Gamma = \partial \Omega $. Рассмотрим следующую начально-краевую задачу:

(1)
$\frac{{\partial \theta }}{{\partial t}} - a\Delta \theta + b{{\kappa }_{a}}({\text{|}}\theta {\text{|}}{{\theta }^{3}} - \varphi ) = q(t)f(x),\quad - {\kern 1pt} \alpha \Delta \varphi + {{\kappa }_{a}}(\varphi \; - \;{\text{|}}\theta {\text{|}}{{\theta }^{3}}) = 0\quad {\text{в }}\quad \Omega ,\quad 0 < t < T,$
(2)
$a{{\partial }_{n}}\theta + \beta (\theta - {{\theta }_{b}}) = 0,\quad \alpha {{\partial }_{n}}\varphi + \gamma (\varphi - \theta _{b}^{4}) = 0\quad {\text{н а }}\quad \Gamma ,$
(3)
${{\left. \theta \right|}_{{t = 0}}} = {{\theta }_{0}}.$
Здесь $\theta $ – нормализованная температура, $\varphi $ – нормализованная интенсивность излучения, усредненная по всем направлениям. Положительные физические параметры $a$, $b$, ${{\kappa }_{a}}$ и $\alpha $, описывающие свойства среды, определяются стандартным образом [16]. Через ${{\partial }_{n}}$ обозначаем производную в направлении внешней нормали ${\mathbf{n}}$ к границе $\Gamma $. Неотрицательные функции ${{\theta }_{b}}$, $\beta $ и $\gamma $ являются заданными. Функция $f$ описывает распределение тепловых источников, а неизвестная функция времени $q(t),t \in (0,T)$ описывает их интенсивность.

Обратная задача состоит в нахождении интенсивности источников $q(t),t \in (0,T)$, функций $\theta ,\varphi $, удовлетворяющих (1)–(3) и условию переопределения

(4)
$\int\limits_\Omega \,g(x)\theta (x,t)dx = r(t),\quad t \in (0,T),$
где $g = g(x),\;x \in \Omega $, $r = r(t),\;t \in (0,T)$ – заданные функции.

Статья организована следующим образом. В разд. 2 вводятся необходимые пространства и операторы, обратная задача формулируется в виде задачи Коши для уравнения с операторными коэффициентами. Разрешимость обратной задачи доказана в разд. 3. В разд. 4 выводятся априорные оценки, на основе которых доказывается единственность решения. Наконец, в разд. 5 представлен алгоритм решения обратной задачи для слоя с отражающими границами и приведены численные примеры.

2. ФОРМАЛИЗАЦИЯ ЗАДАЧИ

В дальнейшем считаем, что $\Omega $ – липшицева ограниченная область, $\Gamma = \partial \Omega $; $Q = \Omega \times (0,T)$, $\Sigma = \Gamma \times (0,T)$. Через ${{L}^{p}}$, $1 \leqslant p \leqslant \infty $, обозначаем пространство Лебега, через ${{H}^{m}}$ – пространство Соболева $W_{2}^{m}$, а через ${{L}^{p}}(0,T;X)$ – пространство Лебега функций класса ${{L}^{p}}$, определенных на $(0,T)$, со значениями в банаховом пространстве $X$.

Пусть $H = {{L}^{2}}(\Omega ),\;V = {{H}^{1}}(\Omega )$, через $V{\kern 1pt} '$ обозначаем пространство, сопряженное с пространством $V$. Пространство $H$ отождествляем с пространством $H{\kern 1pt} '$, так что $V \subset H = H{\kern 1pt} ' \subset V{\kern 1pt} '$. Обозначим через $\left\| {\, \cdot \,} \right\|$ стандартную норму в $H$, а через $(h,v)$ – значение функционала $h \in V{\kern 1pt} '$ на элементе $v \in V$, совпадающее со скалярным произведением в $H$, если $h \in H$.

Будем предполагать, что исходные данные удовлетворяют условиям:

(i) $\beta ,\gamma \in {{L}^{\infty }}(\Gamma ),$ $\beta \geqslant {{\beta }_{0}} > 0,$ $\gamma \geqslant {{\gamma }_{0}} > 0,$ ${{\beta }_{0}},{{\gamma }_{0}} = {\text{Const}},$ $0 \leqslant {{\theta }_{b}} \in {{L}^{\infty }}(\Sigma ).$

(ii) ${{\theta }_{0}} \in H,$ $f \in H,$ $g \in V,$ $\left\| f \right\| = \left\| g \right\| = 1,$ ${{(f,g)}^{2}} = 1 - {{\mu }^{2}},$ $0 \leqslant \mu < 1.$

(iii) $r \in {{H}^{1}}(0,T),$ $r(0) = (g,{{\theta }_{0}}).$

Отметим, что условие $\left\| f \right\| = \left\| g \right\| = 1$ не является ограничительным, поскольку всегда можно сделать переобозначение: $f: = f{\text{/}}\left\| f \right\|$, $q(t): = \left\| f \right\|q(t)$, $g: = g{\text{/}}\left\| g \right\|$, $r(t): = \left\| g \right\|r(t).$

Определим операторы и функционалы ${{A}_{{1,2}}}V \to V{\kern 1pt} '$, ${{g}_{{1,2}}} \in {{L}^{\infty }}(0,T;V{\kern 1pt} ')$, используя следующие равенства, справедливые для любых $\theta ,\varphi ,v \in V$:

$({{A}_{1}}\theta ,v) = a(\nabla \theta ,\nabla v) + \int\limits_\Gamma \,\beta \theta vd\Gamma ,\quad ({{A}_{2}}\varphi ,v) = \alpha (\nabla \varphi ,\nabla v) + \int\limits_\Gamma \,\gamma \varphi vd\Gamma ,$
$({{g}_{1}},v) = \int\limits_\Gamma \,\beta {{\theta }_{b}}vd\Gamma ,\quad ({{g}_{2}},v) = \int\limits_\Gamma \,\gamma \theta _{b}^{4}vd\Gamma .$
Билинейные формы $({{A}_{1}}u,v)$, $({{A}_{2}}u,v)$ определяют скалярные произведения в пространстве $V$, а соответствующие им нормы эквивалентны стандартной норме $V$. Поэтому определены непрерывные обратные операторы $A_{1}^{{ - 1}},A_{2}^{{ - 1}}:V{\kern 1pt} ' \mapsto V$ и оператор $B:V{\kern 1pt} ' \mapsto V{\kern 1pt} '$, $B = {{A}_{2}}{{({{A}_{2}} + {{\kappa }_{a}}I)}^{{ - 1}}}.$

Будем использовать следующее обозначение: ${{[s]}^{p}}: = {\text{|}}s{{{\text{|}}}^{p}}\operatorname{sign} s$, $p > 0$, $s \in \mathbb{R}$, для монотонной степенной функции.

Определение. Тройка $\{ q,\theta ,\varphi \} \in {{L}^{{5/4}}}(0,T) \times {{L}^{2}}(0,T;V) \times {{L}^{{5/4}}}(0,T;V)$ называется решением задачи (1)–(4), если $\theta {\kern 1pt} ' \in {{L}^{{5/4}}}(0,T;V{\kern 1pt} ')$ и почти всюду на $(0,T)$ справедливы равенства

(5)
$\theta {\kern 1pt} {\text{'}} + {{A}_{1}}\theta + b{{\kappa }_{a}}({{[\theta ]}^{4}} - \varphi ) = {{g}_{1}} + q(t)f,\quad {{A}_{2}}\varphi + {{\kappa }_{a}}(\varphi - {{[\theta ]}^{4}}) = {{g}_{2}},\quad (g,\theta (t)) = r(t),$
а также выполняется начальное условие ${{\left. \theta \right|}_{{t = 0}}} = {{\theta }_{0}}.$ Здесь и далее $\theta {\kern 1pt} ' = d\theta {\text{/}}dt$.

Нетрудно проверить, что уравнения (5) эквивалентны равенствам

(6)
$\theta {\kern 1pt} {\text{'}} + {{A}_{1}}\theta + b{{\kappa }_{a}}B{{[\theta ]}^{4}} = h + q(t)f,\quad \varphi = {{({{A}_{2}} + {{\kappa }_{a}}I)}^{{ - 1}}}({{g}_{2}} + {{\kappa }_{a}}{{[\theta ]}^{4}}),$
где $h = {{g}_{1}} + b{{\kappa }_{a}}{{({{A}_{2}} + {{\kappa }_{a}}I)}^{{ - 1}}}{{g}_{2}}.$ Отметим, что $B{{[\theta ]}^{4}} = ({{[\theta ]}^{4}} - \varphi ) + {{({{A}_{2}} + {{\kappa }_{a}}I)}^{{ - 1}}}{{g}_{2}}$, где $\varphi $ определяется по формуле (6), поскольку $B = I - {{\kappa }_{a}}{{({{A}_{2}} + {{\kappa }_{a}}I)}^{{ - 1}}} = {{A}_{2}}{{({{A}_{2}} + {{\kappa }_{a}}I)}^{{ - 1}}}$. Из условия интегрального переопределения следует представление для интенсивности источника,
(7)
$q(t) = \frac{1}{{(f,g)}}({{A}_{1}}\theta + b{{\kappa }_{a}}B{{[\theta ]}^{4}},g) + s(t),\quad {\text{г д е }}\quad s(t) = \frac{1}{{(f,g)}}\left( {r{\kern 1pt} '(t) - (h,g)} \right).$
В силу условия $({\text{iii}})$ справедливо и обратное: из (6), (7) следует, что $(g,\theta (t)) = r(t)$, $t \in (0,T).$ Таким образом, задача (1)–(4) сводится к задаче Коши для уравнения с операторными коэффициентами:
(8)
$\theta {\kern 1pt} {\text{'}} + {{A}_{1}}\theta + b{{\kappa }_{a}}B{{[\theta ]}^{4}} = \frac{1}{{(f,g)}}({{A}_{1}}\theta + b{{\kappa }_{a}}B{{[\theta ]}^{4}},g)f + {{h}_{0}},\quad {{\left. \theta \right|}_{{t = 0}}} = {{\theta }_{0}}.$
Здесь ${{h}_{0}} = h + s(t)f.$

3. РАЗРЕШИМОСТЬ ОБРАТНОЙ ЗАДАЧИ

Для вывода условий разрешимости нам потребуются следующие вспомогательные результаты, доказательство которых приводится в конце статьи.

Лемма 1. Пусть $u \in {{L}^{5}}(\Omega ),\eta \in V$, ${{A}_{2}}\eta + {{\kappa }_{a}}\eta = {{\kappa }_{a}}u.$ Тогда

(9)
${{\left\| \eta \right\|}_{{{{L}^{5}}(\Omega )}}} \leqslant \frac{{{{\kappa }_{a}}}}{{\sigma + {{\kappa }_{a}}}}{{\left\| u \right\|}_{{{{L}^{5}}(\Omega )}}}.$
Здесь

$\sigma = inf\left\{ {\tfrac{{16}}{{25}}{{{\left\| {\nabla v} \right\|}}^{2}} + \int\limits_\Gamma \,\gamma {{v}^{2}}d\Gamma ;\;v \in V,\;\left\| v \right\| = 1} \right\}.$

Лемма 2. Пусть $B:V{\kern 1pt} ' \mapsto V{\kern 1pt} '$, $B = {{A}_{2}}{{({{A}_{2}} + {{\kappa }_{a}}I)}^{{ - 1}}}.$ Тогда для произвольных $u,v \in V$ справедливы неравенства

(10)
$(B{{[u]}^{4}},u) \geqslant \frac{\sigma }{{\sigma + {{\kappa }_{a}}}}\left\| u \right\|_{{{{L}^{5}}(\Omega )}}^{5},\quad (B{{[u]}^{4}},v) \leqslant \frac{{\sigma + 2{{\kappa }_{a}}}}{{\sigma + {{\kappa }_{a}}}}\left\| u \right\|_{{{{L}^{5}}(\Omega )}}^{4}{{\left\| v \right\|}_{{{{L}^{5}}(\Omega )}}}.$

Достаточным условием существования решения нелинейной обратной задачи является ограничение на параметр $\mu $ в $({\text{ii}})$, которое выполняется, если угол между векторами $f$ и $g$ из ${{L}^{2}}(\Omega )$ достаточно мал.

Теорема 1. Пусть выполняются условия (i)–(iii) и справедливо неравенство

(11)
${{p}_{0}} = \frac{{\sigma + 2{{\kappa }_{a}}}}{\sigma }{\text{|}}\Omega {\kern 1pt} {{{\text{|}}}^{{3/10}}}{{\left\| g \right\|}_{{{{L}^{5}}(\Omega )}}}\frac{\mu }{{\sqrt {1 - {{\mu }^{2}}} }} < 1.$
Тогда задача (1)–(4) имеет решение и при этом $\theta \in {{L}^{5}}(Q)$.

Доказательство. Определим галеркинские приближения ${{\theta }_{m}}$ решения задачи (8) и выведем необходимые для доказательства разрешимости априорные оценки. В пространстве $V$ рассмотрим ортонормированный в $H$ базис ${{w}_{1}},{{w}_{2}},\; \ldots $, ${{V}_{m}} = {\text{span}}\{ {{w}_{1}}, \ldots ,{{w}_{m}}\} .$ Пусть ${{\theta }_{m}}(t) \in {{V}_{m}},\;t \in (0,T)$, является решением следующей задачи Коши:

(12)
$(\theta _{m}^{'} + {{A}_{1}}{{\theta }_{m}} + b{{\kappa }_{a}}B{{[{{\theta }_{m}}]}^{4}} - {{q}_{m}}f,\zeta ) = ({{h}_{0}},\zeta )\quad \forall \zeta \in {{V}_{m}},\quad {{\left. {{{\theta }_{m}}} \right|}_{{t = 0}}} = {{\theta }_{{0m}}}.$
Здесь
${{q}_{m}} = \frac{1}{{(f,{{g}_{m}})}}({{A}_{1}}{{\theta }_{m}} + b{{\kappa }_{a}}B{{[{{\theta }_{m}}]}^{4}},{{g}_{m}}),$
${{g}_{m}},\;{{\theta }_{{0m}}}$ – ортогональные проекции в $H$ функций $g,\;{{\theta }_{0}}$ на подпространство ${{V}_{m}}.$ Отметим сразу, что
(13)
${{g}_{m}} \to g\;{\text{в }}\;{\text{п р о с т р а н с т в е }}\;V,\quad {{\theta }_{{0m}}} \to \theta \;{\text{в }}\;{\text{п р о с т р а н с т в е }}\;H.$
Полагая $\zeta = {{g}_{m}}$ в (12), получаем равенство
$(\theta _{m}^{'},{{g}_{m}}) = (h,{{g}_{m}}) - \frac{{(f,{{g}_{m}})}}{{(f,g)}}(h,g) + \frac{{(f,{{g}_{m}})}}{{(f,g)}}r{\kern 1pt} '(t),$
проинтегрировав которое, заключаем в силу (13), что $({{\theta }_{m}},{{g}_{m}}) \in C[0,T]$ и при этом $({{\theta }_{m}},{{g}_{m}}) \to r$ в $C[0,T].$

Выведем необходимые для доказательства разрешимости априорные оценки. В пространстве $V$ будем использовать скалярное произведение ${{(u,v)}_{V}} = ({{A}_{1}}u,v)$ и соответствующую ему норму. Полагая $\zeta = {{\theta }_{m}}$ в (12) и используя лемму 2, получаем неравенство

(14)
$\frac{1}{2}\frac{d}{{dt}}{{\left\| {{{\theta }_{m}}} \right\|}^{2}} + \left\| {{{\theta }_{m}}} \right\|_{V}^{2} + \frac{{b{{\kappa }_{a}}\sigma }}{{\sigma + {{\kappa }_{a}}}}\left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{5} \leqslant {{q}_{m}}(f,{{\theta }_{m}}) + ({{h}_{0}},{{\theta }_{m}}).$
Оценим первое слагаемое в правой части (14):
(15)
${\text{|}}{{q}_{m}}(f,{{\theta }_{m}}){\text{|}} \leqslant \left( {{{{\left\| {{{\theta }_{m}}} \right\|}}_{V}}\left\| {{{g}_{m}}} \right\|{{{\left\| {{{g}_{m}}} \right\|}}_{V}} + b{{\kappa }_{a}}\frac{{\sigma + 2{{\kappa }_{a}}}}{{\sigma + {{\kappa }_{a}}}}\left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{4}{{{\left\| {{{g}_{m}}} \right\|}}_{{{{L}^{5}}(\Omega )}}}} \right)\frac{{{\text{|}}(f,{{\theta }_{m}}){\text{|}}}}{{{\text{|}}(f,{{g}_{m}}){\text{|}}}}.$
Заметим, что
(16)
${{\left\| {{{\theta }_{m}}} \right\|}_{V}}{{\left\| {{{g}_{m}}} \right\|}_{V}}\frac{{|(f,{{\theta }_{m}})|}}{{|(f,{{g}_{m}})|}} \leqslant \frac{1}{4}\left\| {{{\theta }_{m}}} \right\|_{V}^{2} + \frac{{\left\| {{{g}_{m}}} \right\|_{V}^{2}}}{{{{{(f,{{g}_{m}})}}^{2}}}}{{\left\| {{{\theta }_{m}}} \right\|}^{2}} \leqslant \frac{1}{4}\left\| {{{\theta }_{m}}} \right\|_{V}^{2} + C{{\left\| {{{\theta }_{m}}} \right\|}^{2}}.$
Здесь и далее при доказательстве теоремы через $C$ обозначаем постоянные, не зависящие от $m.$

Далее,

$\frac{{{\text{|}}(f,{{\theta }_{m}}){\text{|}}}}{{{\text{|}}(f,{{g}_{m}}){\text{|}}}} \leqslant \frac{{{\text{|}}({{h}_{m}},{{\theta }_{m}}){\text{|}}}}{{{\text{|}}(f,{{g}_{m}}){\text{|}}}} + \frac{{{\text{|}}({{g}_{m}},{{\theta }_{m}}){\text{|}}}}{{{{{\left\| {{{g}_{m}}} \right\|}}^{2}}}},$
где ${{h}_{m}} = f - (f,{{g}_{m}}){{g}_{m}}{\text{/}}{{\left\| {{{g}_{m}}} \right\|}^{2}}$ и при этом
$\left\| {{{h}_{m}}} \right\| \to \mu ,{\text{|}}(f,{{g}_{m}}){\text{|}} \to {\text{|}}(f,g){\text{|}} = \sqrt {1 - {{\mu }^{2}}} ,\quad \frac{{{\text{|}}({{g}_{m}},{{\theta }_{m}}){\text{|}}}}{{{{{\left\| {{{g}_{m}}} \right\|}}^{2}}}} \to {\text{|}}r{\text{|}}\quad {\text{в }}\quad C[0,T]\quad {\text{п р и }}\quad m \to \infty .$
Поэтому
$\left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{4}\frac{{{\text{|}}(f,{{\theta }_{m}}){\text{|}}}}{{{\text{|}}(f,{{g}_{m}}){\text{|}}}} \leqslant \frac{{\left\| {{{h}_{m}}} \right\|}}{{{\text{|}}(f,{{g}_{m}}){\text{|}}}}{\text{|}}\Omega {{{\text{|}}}^{{3/10}}}\left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{5} + \frac{{{\text{|}}({{g}_{m}},{{\theta }_{m}}){\text{|}}}}{{{{{\left\| {{{g}_{m}}} \right\|}}^{2}}}}\left\| {{{g}_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{4}.$
Следовательно, учитывая неравенство Юнга
$\left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{4} \leqslant \frac{{4{{\varepsilon }^{{5/4}}}}}{5}\left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{5} + \frac{1}{{5{{\varepsilon }^{5}}}},$
выводим при достаточно больших $m$ и малом $\varepsilon > 0$ следующую оценку для слагаемого в правой части (15):
(17)
$\frac{{\sigma + 2{{\kappa }_{a}}}}{{\sigma + {{\kappa }_{a}}}}\left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{4}{{\left\| {{{g}_{m}}} \right\|}_{{{{L}^{5}}(\Omega )}}}\frac{{\left| {(f,{{\theta }_{m}})} \right|}}{{\left| {(f,{{g}_{m}})} \right|}} \leqslant \frac{{1 + {{p}_{0}}}}{2}\frac{\sigma }{{\sigma + {{\kappa }_{a}}}}\left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{5} + C.$
Неравенства (16), (17), а также оценка $({{h}_{0}},{{\theta }_{m}}) \leqslant \tfrac{1}{4}\left\| {{{\theta }_{m}}} \right\|_{V}^{2} + \left\| {{{h}_{0}}} \right\|_{{V'}}^{2}$, позволяют оценить правую часть (14). В результате получаем неравенство
(18)
$\frac{1}{2}\frac{d}{{dt}}{{\left\| {{{\theta }_{m}}} \right\|}^{2}} + \frac{1}{2}\left\| {{{\theta }_{m}}} \right\|_{V}^{2} + p\left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{5} \leqslant \left\| {{{h}_{0}}} \right\|_{{V'}}^{2} + C(1 + {{\left\| {{{\theta }_{m}}} \right\|}^{2}}).$
Здесь $p = (1 - {{p}_{0}}){\text{/}}2.$ Интегрируя дифференциальное неравенство (18) и применяя лемму Гронуолла, выводим, что
(19)
${\text{п о с л е д о в а т е л ь н о с т ь }}\;{{\theta }_{m}}\;{\text{о г р а н и ч е н а }}\;{\text{в }}\;{{L}^{\infty }}(0,T;H),\;{{L}^{2}}(0,T;V),\;{{L}^{5}}(Q).$
Получим теперь оценку, гарантирующую компактность последовательности ${{\theta }_{m}}$ в ${{L}^{2}}(Q)$. В системе (12) положим $\zeta = {{\theta }_{m}}(t) - {{\theta }_{m}}(s)$ и проинтегрируем по $t$ на промежутке $(s,s + h)$ и по $s$ на $(0,T - h)$, считая $h > 0$ достаточно малым. Тогда
$\frac{1}{2}\int\limits_0^{T - h} {{\left\| {{{\theta }_{m}}(s + h) - {{\theta }_{m}}(s)} \right\|}^{2}}ds = \int\limits_0^{T - h} \,\int\limits_s^{s + h} \,{{c}_{m}}(t,s)dtds,$
где
${{c}_{m}}(t,s) = ({{A}_{1}}{{\theta }_{m}}(t) + b{{\kappa }_{a}}B{{[{{\theta }_{m}}(t)]}^{4}} - {{q}_{m}}(t)f - {{h}_{0}}(t),{{\theta }_{m}}(s) - {{\theta }_{m}}(t)).$
Учитывая неотрицательность слагаемых $({{A}_{1}}{{\theta }_{m}}(t),{{\theta }_{m}}(t))$ и $(B{{[{{\theta }_{m}}(t)]}^{4}},{{\theta }_{m}}(t))$, получаем неравенство
${{c}_{m}}(t,s) \leqslant ({{A}_{1}}{{\theta }_{m}}(t),{{\theta }_{m}}(s) + b{{\kappa }_{a}}(B{{[{{\theta }_{m}}(t)]}^{4}},{{\theta }_{m}}(s)) - ({{q}_{m}}(t)f - {{h}_{0}}(t),{{\theta }_{m}}(s) - {{\theta }_{m}}(t)).$
Заметим, что с учетом ограниченности последовательности ${{\theta }_{m}}$ в ${{L}^{\infty }}(0,T;H)$, справедлива оценка
${\text{|}}({{q}_{m}}(t)f,{{\theta }_{m}}(s) - {{\theta }_{m}}(t)){\text{|}} \leqslant C\left( {{{{\left\| {{{\theta }_{m}}(t)} \right\|}}_{V}} + \left\| {{{\theta }_{m}}(t)} \right\|_{{{{L}^{5}}(\Omega )}}^{4}} \right).$
Следовательно,
${{c}_{m}}(t,s) \leqslant C\left( {1 + \left\| {{{h}_{0}}(t)} \right\|_{V}^{2} + \left\| {{{\theta }_{m}}(t)} \right\|_{V}^{2} + \left\| {{{\theta }_{m}}(s)} \right\|_{V}^{2} + \left\| {{{\theta }_{m}}(t)} \right\|_{{{{L}^{5}}(\Omega )}}^{4} + \left\| {{{\theta }_{m}}(s)} \right\|_{{{{L}^{5}}(\Omega )}}^{4}} \right).$
Для оценки интегралов от слагаемых, зависящих от $t$, достаточно поменять порядок интегрирования. Используя ограниченность (19) последовательности ${{\theta }_{m}}$, получаем оценку равностепенной непрерывности,
(20)
$\int\limits_0^{T - h} {{\left\| {{{\theta }_{m}}(s + h) - {{\theta }_{m}}(s)} \right\|}^{2}}ds \leqslant Ch.$
Полученные оценки (19), (20) позволяют утверждать, переходя при необходимости к подпоследовательности, что существует функция $\theta $,
(21)
${{\theta }_{m}} \to \theta \;{\text{с л а б о }}\;{\text{в }}\;{{L}^{2}}(0,T;V),\;{{L}^{5}}(Q),\quad * \; - \;{\text{с л а б о }}\;{\text{в }}\;{{L}^{\infty }}(0,T;H),\;{\text{с и л ь н о }}\;{\text{в }}\;{{L}^{2}}(Q).$
Результатов о сходимости (21) достаточно для предельного перехода при $m \to \infty $ в системе (12) и доказательства того, что предельная функция $\theta $ удовлетворяет уравнению в (8) в смысле теории распределений и выполняется начальное условие. Отметим также, что поскольку из полученных оценок следуют включения $q \in {{L}^{{5/4}}}(0,T)$, $A\theta \in {{L}^{2}}(0,T;V{\kern 1pt} ')$, $B{{[\theta ]}^{4}} \in {{L}^{{5/4}}}(0,T;V{\kern 1pt} ')$, то функция $\theta {\kern 1pt} '$ также принадлежит ${{L}^{{5/4}}}(0,T;V{\kern 1pt} ')$ и дифференциальное уравнение в (6) выполняется почти всюду на $(0,T)$. Кроме того, $\varphi = {{({{A}_{2}} + {{\kappa }_{a}}I)}^{{ - 1}}}({{\kappa }_{a}}{{[\theta ]}^{4}} + {{g}_{2}}) \in {{L}^{{5/4}}}(0,T;V).$ Отметим, что в случае $g = f$ условие (11) заведомо выполняется, поскольку $\mu = 0.$ Именно этот случай рассмотрен в [28].

4. РЕГУЛЯРНОСТЬ И ЕДИНСТВЕННОСТЬ РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ

Получим дополнительные оценки решения задачи (1)–(4), существование которого гарантируется теоремой 1.

Теорема 2. Пусть выполняются условия (i)–(iii), (11) и дополнительно ${{\theta }_{0}} \in V,$ $f \in V$, ${{\theta }_{b}} = 0$. Тогда решение задачи (1)–(4) единственно и обладает свойствами

$\theta {\kern 1pt} ' \in {{L}^{2}}(0,T;V{\kern 1pt} '),\quad \theta \in {{L}^{\infty }}(0,T;V) \cap {{L}^{5}}(0,T;{{L}^{{15}}}(\Omega )),\quad {{A}_{1}}\theta \in {{L}^{2}}(Q),$
$\varphi \in {{L}^{2}}(0,T;V),\quad q \in {{L}^{2}}(0,T).$

Доказательство. Рассмотрим опять галеркинское приближение, использовавшееся при доказательстве теоремы 1. В качестве базисных функций ${{w}_{1}},\;{{w}_{2}},\; \ldots $ выберем собственные функции оператора ${{A}_{1}}$, ${{A}_{1}}{{w}_{j}} = {{\lambda }_{j}}{{w}_{j}}.$ В этом случае ${{A}_{1}}{{\theta }_{m}} \in {{V}_{m}}.$ Полагая $\zeta = {{A}_{1}}{{\theta }_{m}}$ в (12), получаем равенство

(22)
$\frac{1}{2}\frac{d}{{dt}}\left\| {{{\theta }_{m}}} \right\|_{V}^{2} + {{\left\| {{{A}_{1}}{{\theta }_{m}}} \right\|}^{2}} + (b{{\kappa }_{a}}B{{[{{\theta }_{m}}]}^{4}} - {{q}_{m}}f,{{A}_{1}}{{\theta }_{m}}) = ({{h}_{0}},{{A}_{1}}{{\theta }_{m}}).$
Здесь
${{q}_{m}} = \frac{1}{{(f,{{g}_{m}})}}({{A}_{1}}{{\theta }_{m}} + b{{\kappa }_{a}}B{{[{{\theta }_{m}}]}^{4}},{{g}_{m}}),\quad {{h}_{0}} = \frac{1}{{(f,g)}}r{\kern 1pt} '(t)f.$
Заметим, что
$(B{{[{{\theta }_{m}}]}^{4}},{{A}_{1}}{{\theta }_{m}}) = ({{[{{\theta }_{m}}]}^{4}},{{A}_{1}}{{\theta }_{m}}) - {{\kappa }_{a}}({{[{{\theta }_{m}}]}^{4}},{{\eta }_{m}}),$
где ${{\eta }_{m}} = {{({{A}_{2}} + {{\kappa }_{a}}I)}^{{ - 1}}}{{A}_{1}}{{\theta }_{m}}.$ Пусть ${{\psi }_{m}} = {{[{{\theta }_{m}}]}^{{5/2}}}.$ Тогда
$({{[{{\theta }_{m}}]}^{4}},{{A}_{1}}{{\theta }_{m}}) = \frac{{16}}{{25}}{{\left\| {\nabla {{\psi }_{m}}} \right\|}^{2}} + \int\limits_\Gamma \,\beta \psi _{m}^{2}d\Gamma \geqslant C\left\| {{{\psi }_{m}}} \right\|_{V}^{2}.$
Здесь снова через $C,\;{{C}_{1}},\;{{C}_{2}},\;...$ обозначаем различные постоянные, не зависящие от $m.$ Далее, в силу леммы 2, непрерывности оператора ${{({{A}_{2}} + {{\kappa }_{a}}I)}^{{ - 1}}}{{A}_{1}}:V \to V$, а также непрерывности вложения $V \to {{L}^{5}}(\Omega )$ получаем оценку
${\text{|}}({{[{{\theta }_{m}}]}^{4}},{{\eta }_{m}}){\text{|}} \leqslant \left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{4}{{\left\| {{{\eta }_{m}}} \right\|}_{{{{L}^{5}}(\Omega )}}} \leqslant C\left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{4}{{\left\| {{{\eta }_{m}}} \right\|}_{V}} \leqslant {{C}_{1}}\left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{3}\left\| {{{\theta }_{m}}} \right\|_{V}^{2}.$
Аналогичным образом выводим оценки
${\text{|}}(B{{[{{\theta }_{m}}]}^{4}},{{g}_{m}})(f,{{A}_{1}}{{\theta }_{m}}){\text{|}} \leqslant {{C}_{2}}\left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{3}\left\| {{{\theta }_{m}}} \right\|_{V}^{2},\quad {\text{|}}({{A}_{1}}{{\theta }_{m}},{{g}_{m}})(f,{{A}_{1}}{{\theta }_{m}}){\text{|}} \leqslant {{C}_{3}}\left\| {{{\theta }_{m}}} \right\|_{V}^{2}.$
Кроме того,
$({{h}_{0}},{{A}_{1}}{{\theta }_{m}}) = \frac{1}{{(f,g)}}r{\kern 1pt} '(t)(f,{{A}_{1}}{{\theta }_{m}}) \leqslant {\text{|}}r{\kern 1pt} '(t){{{\text{|}}}^{2}} + {{C}_{4}}\left\| {{{\theta }_{m}}} \right\|_{V}^{2}.$
Таким образом, из (22) следует неравенство
(23)
$\frac{1}{2}\frac{d}{{dt}}\left\| {{{\theta }_{m}}} \right\|_{V}^{2} + {{\left\| {{{A}_{1}}{{\theta }_{m}}} \right\|}^{2}} + C\left\| {{{\psi }_{m}}} \right\|_{V}^{2} \leqslant {{C}_{5}}\left( {1 + \left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{3}} \right)\left\| {{{\theta }_{m}}} \right\|_{V}^{2} + {\text{|}}r{\kern 1pt} '(t){{{\text{|}}}^{2}}.$
Из оценок (19) следует, что $\int_0^T \left\| {{{\theta }_{m}}} \right\|_{{{{L}^{5}}(\Omega )}}^{3}dt \leqslant C$ и поэтому, применяя неравенство Гронуолла, выводим из (23):
(24)
${\text{п о с л е д о в а т е л ь н о с т ь }}\;{{\theta }_{m}}\;{\text{о г р а н и ч е н а }}\;{\text{в }}\;{{L}^{\infty }}(0,T;V),\quad {{A}_{1}}{{\theta }_{m}}\;{\text{о г р а н и ч е н а }}\;{\text{в }}\;{{L}^{2}}(Q).$
Заметим также, что
$\int\limits_0^T \left\| {{{\theta }_{m}}} \right\|_{{{{L}^{{15}}}(\Omega )}}^{5}dt = \int\limits_0^T \left\| {{{\psi }_{m}}} \right\|_{{{{L}^{6}}(\Omega )}}^{2}dt \leqslant {{C}_{6}}\int\limits_0^T \left\| {{{\psi }_{m}}} \right\|_{V}^{2}dt \leqslant C.$
Следовательно,
(25)
${\text{п о с л е д о в а т е л ь н о с т ь }}\;{{\theta }_{m}}\;{\text{о г р а н и ч е н а }}\;{\text{в }}\;{{L}^{5}}(0,T;{{L}^{{15}}}(\Omega )).$
Из оценок (24), (25) вытекает, что для решения задачи (1)–(4) справедливы включения $\theta \in {{L}^{\infty }}(0,T;V) \cap {{L}^{5}}(0,T;{{L}^{{15}}}(\Omega )),$ ${{A}_{1}}\theta \in {{L}^{2}}(Q).$ Далее из равенств
$\varphi = {{({{A}_{2}} + {{\kappa }_{a}}I)}^{{ - 1}}}({{g}_{2}} + {{\kappa }_{a}}{{[\theta ]}^{4}}),\quad q(t) = \frac{1}{{(f,g)}}({{A}_{1}}\theta + b{{\kappa }_{a}}B{{[\theta ]}^{4}},g) + s(t),$
$\theta {\kern 1pt} ' = - {{A}_{1}}\theta - b{{\kappa }_{a}}B{{[\theta ]}^{4}} + h + q(t)f,$
на основании полученных свойств регулярности $\theta $, следуют включения $\varphi \in {{L}^{2}}(0,T;V),$ $q \in {{L}^{2}}(0,T),$ $\theta {\kern 1pt} ' \in {{L}^{2}}(0,T;V').$

Заметим также, что функция $t \mapsto \left\| {{{\theta }^{3}}} \right\|_{{{{L}^{3}}(\Omega )}}^{2}$ интегрируема на $(0,T)$, что важно для доказательства единственности решения обратной задачи. Интегрируемость следует из того, что $\theta \in {{L}^{2}}(0,T;{{L}^{6}}(\Omega )) \cap {{L}^{5}}(0,T;{{L}^{{15}}}(\Omega ))$, и неравенства Гёльдера

$\mathop {\left( {\int\limits_\Omega {\text{|}}\theta {{{\text{|}}}^{9}}dx} \right)}\nolimits^{2/3} \leqslant \mathop {\left( {\int\limits_\Omega {\text{|}}\theta {{{\text{|}}}^{6}}dx} \right)}\nolimits^{4/9} \mathop {\left( {\int\limits_\Omega {\text{|}}\theta {{{\text{|}}}^{{15}}}dx} \right)}\nolimits^{2/9} \leqslant C\left( {\frac{1}{3} + \mathop {\left( {\int\limits_\Omega {\text{|}}\theta {{{\text{|}}}^{{15}}}dx} \right)}\nolimits^{1/3} } \right).$
Докажем единственность решения. Пусть ${{\theta }_{1}},\;{{\theta }_{2}}$ – температурные поля, соответствующие двум решениям обратной задачи, $\theta = {{\theta }_{1}} - {{\theta }_{2}}.$ Тогда
(26)
$\theta {\kern 1pt} {\text{'}} + {{A}_{1}}\theta + b{{\kappa }_{a}}B({{[{{\theta }_{1}}]}^{4}} - {{[{{\theta }_{2}}]}^{4}}) = \frac{1}{{(f,g)}}({{A}_{1}}\theta + b{{\kappa }_{a}}B({{[{{\theta }_{1}}]}^{4}} - {{[{{\theta }_{2}}]}^{4}}),g)f,\quad {{\left. \theta \right|}_{{t = 0}}} = 0.$
Умножим скалярно (26) на $\theta $ и воспользуемся следующей оценкой:
${\text{|}}(B({{[{{\theta }_{1}}]}^{4}} - {{[{{\theta }_{2}}]}^{4}}),v){\text{|}} = {\text{|}}({{[{{\theta }_{1}}]}^{4}} - {{[{{\theta }_{2}}]}^{4}},Bv){\text{|}} \leqslant 2{{\left\| {{\kern 1pt} {\text{|}}{{\theta }_{1}}{{{\text{|}}}^{3}} + {\text{|}}{{\theta }_{2}}{{{\text{|}}}^{3}}} \right\|}_{{{{L}^{3}}(\Omega )}}}{{\left\| \theta \right\|}_{{{{L}^{6}}(\Omega )}}}\left\| v \right\|,$
которая справедлива, поскольку $\left\| {Bv} \right\| \leqslant \left\| v \right\|.$ Следовательно, с учетом непрерывности вложения $V \subset {{L}^{6}}(\Omega )$ и условия $\left\| f \right\| = \left\| g \right\| = 1$,
$b{{\kappa }_{a}}{\text{|}}(B({{[{{\theta }_{1}}]}^{4}} - {{[{{\theta }_{2}}]}^{4}}),\theta ){\text{|}} \leqslant 2{{\left\| {{\kern 1pt} {\text{|}}{{\theta }_{1}}{{{\text{|}}}^{3}} + {\text{|}}{{\theta }_{2}}{{{\text{|}}}^{3}}{\kern 1pt} } \right\|}_{{{{L}^{3}}(\Omega )}}}{{\left\| \theta \right\|}_{{{{L}^{6}}(\Omega )}}}\left\| \theta \right\| \leqslant \frac{1}{3}\left\| \theta \right\|_{V}^{2} + C\eta (t){{\left\| \theta \right\|}^{2}},$
$\frac{1}{{(f,g)}}b{{\kappa }_{a}}(B({{[{{\theta }_{1}}]}^{4}} - {{[{{\theta }_{2}}]}^{4}}),g)(f,\theta ) \leqslant \frac{1}{3}\left\| \theta \right\|_{V}^{2} + C\eta (t){{\left\| \theta \right\|}^{2}}.$
Здесь функция $\eta (t) = \left\| {{\kern 1pt} {\text{|}}{{\theta }_{1}}{{{\text{|}}}^{3}}\; + \;{\text{|}}{{\theta }_{2}}{{{\text{|}}}^{3}}} \right\|_{{{{L}^{3}}(\Omega )}}^{2}$ интегрируема на $(0,T).$ Через $C > 0$ обозначена постоянная, зависящая только от $b,{{\kappa }_{a}},f,g$ и $\Omega .$ Учтем также, что
$\frac{1}{{(f,g)}}({{A}_{1}}\theta ,g)(f,\theta ) \leqslant \frac{1}{3}\left\| \theta \right\|_{V}^{2} + C{{\left\| \theta \right\|}^{2}}.$
Так как $({{A}_{1}}\theta ,\theta ) = \left\| \theta \right\|_{V}^{2}$, в результате получаем оценку
$\frac{d}{{2dt}}{{\left\| \theta \right\|}^{2}} \leqslant C(1 + \eta (t)){{\left\| \theta \right\|}^{2}},$
из которой, в силу неравенства Гронуолла, следует, что $\theta = 0.$

5. ЧИСЛЕННЫЕ ПРИМЕРЫ

Представим алгоритм решения обратной задачи для одномерной модели, описывающей сложный теплообмен в плоскопараллельном слое толщиной $L$ с отражающими границами.

Неизвестную интенсивность источников $q(t),t \in (0,T)$, аппроксимируем постоянной на каждом интервале сетки по времени, $q(t) = {{q}_{m}}$, $t \in ({{t}_{{m - 1}}},{{t}_{m}})$, и последовательно подбираем ${{q}_{m}}$, $m = 1,2,\; \ldots $, таким образом, чтобы выполнялось равенство $I({{q}_{m}}) \equiv \int_0^L \,g(x)\theta (x,{{t}_{m}})dx = r({{t}_{m}})$. Отметим, что в случае, когда функции $f$ и $g$ не меняют знак, естественно ожидать монотонности функции $I(q)$. Действительно, если, например, $f,g \geqslant 0$, то при увеличении интенсивности $q$ источника тепла поле температуры и соответственно величина $I(q)$ должны увеличиваться. С учетом монотонности функции $I(q)$ для решения уравнения $I(q) = r$ можно использовать метод бисекций. Вначале выбираются числа ${{q}_{1}}$ и ${{q}_{2}}$ такие, что $I({{q}_{1}}) < r$, $I({{q}_{2}}) > r$. В качестве начального выбора этих чисел берутся значения ${{q}_{1}} = {{q}_{0}} - {{l}_{1}}$, ${{q}_{2}} = {{q}_{0}} + {{l}_{2}}$, где ${{q}_{0}}$ – значение $q(t)$, найденное на предыдущем временном слое, а ${{l}_{1}}$ и ${{l}_{2}}$ равны удвоенной разнице между значениями ${{q}_{m}}$, найденными на предыдущих двух временных слоях. Затем число ${{l}_{1}}$ увеличивается в 2 раза до тех пор, пока $I({{q}_{1}})$ не станет меньше $r$, а ${{l}_{2}}$ увеличивается в 2 раза до тех пор, пока $I({{q}_{2}})$ не станет больше $r$. Далее вычисляется значение $I(q)$ в точке ${{q}_{ * }} = ({{q}_{1}} + {{q}_{2}}){\text{/}}2$, и если $I({{q}_{ * }}) < r$, то ${{q}_{1}}$ становится равным ${{q}_{ * }}$, иначе ${{q}_{2}}$ становится равным ${{q}_{ * }}$. Этот процесс повторяется до тех пор, пока ${{q}_{2}} - {{q}_{1}}$ не станет меньше заданной величины $lon$, определяющей точность вычислений.

Для численного решения прямой задачи используется разностная схема неявного метода Эйлера с линеаризацией методом Ньютона на равномерной сетке. Исходный код программы доступен по ссылке https://github.com/grenkin/inverse_heat.

Примеры, рассмотренные ниже, иллюстрируют эффективность предложенного алгоритма даже в том случае, когда не выполнены достаточные условия однозначной разрешимости, представленные в предыдущих разделах. Пусть $L = 50$ см. Физические параметры среды соответствуют данным из [16]. Термодинамические характеристики соответствуют воздуху при нормальном атмосферном давлении и температуре 400°C, $a = 0.92$ см$^{2}$/с, $b = 18.7$ см/с. Положим $T = 20$ с, ${{\kappa }_{a}} = 0.01$ см$^{{ - 1}}$, $\alpha = 3.3...$ см, $\beta = 10$ см/с, $\gamma = 0.3$, ${{\theta }_{b}} = 0.4$. Начальная температура ${{\theta }_{0}}(x) = 0.8$, $x \in [0,L]$. В дальнейшем $f(x) = 1$, если $x \in [0,20]$, и $f(x) = 0$ иначе, т.е. источники локализованы в левой части интервала $\Omega = (0,L)$. В качестве весовой функции в условии переопределения (4) выбираем следующую гладкую функцию с носителем $[{{x}_{1}},{{x}_{2}}] \subset [0,L]$:

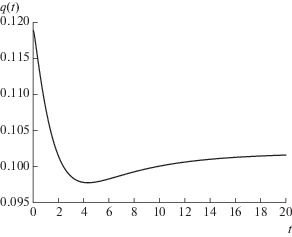
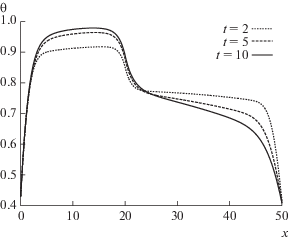
$g(x;{{x}_{1}},{{x}_{2}}) = \frac{1}{2}\left( {1 - cos\left( {\frac{{2\pi (x - {{x}_{1}})}}{{{{x}_{2}} - {{x}_{1}}}}} \right)} \right),\quad {\text{е с л и }}\quad x \in ({{x}_{1}},{{x}_{2}}),\quad {\text{и }}\quad g(x;{{x}_{1}},{{x}_{2}}) = 0\quad {\text{и н а ч е }}.$

Пример 1. Положим $g(x): = g(x;10,40),\;x \in (0,50)$, $r(t) = 12,\;t \in (0,T)$. Носители функций $f$ и $g$ пересекаются на отрезке $[10,20].$ На фиг. 1 представлен график найденной интенсивности источников $q(t),\;t \in (0,T),$ а на фиг. 2 – график поля температуры в моменты времени $t = 2,5,10$.

Фиг. 1.

Интенсивность источников.

Фиг. 2.

Поле температуры при $t = 2,5,10$.

Используемый метод теоретического анализа обратной задачи предполагает, что пересечение носителей функций $f$ и $g$ имеет положительную меру, а также, что $g \in {{H}^{1}}(\Omega ).$ Однако постановка обратной задачи (1)–(4) имеет смысл и при не выполнении указанных условий. Представленный алгоритм численного решения работает и в этом случае. Приведем пример, когда носители функций $f$ и $g$ не пересекаются.

Пример 2. Положим $g(x): = g(x;30,50),\;x \in (0,50)$, $r(t) = 8,\;t \in (0,T)$. График вычисленной интенсивности $q(t)$ представлен на фиг. 3.

Фиг. 3.

Решение обратной задачи.

Отметим следующую особенность численного решения обратной задачи в случае непересекающихся носителей функций $f$ и $g$. В примере 2 величина $q(t)$ достигает сравнительно большого значения (порядка ${{10}^{1}}$) на первом временном слое, а значения $q(t)$ на последующих временных слоях имеют порядок ${{10}^{{ - 1}}}$.

Отметим, что при постоянной функции $r(t) = {\text{Const}}$ решение обратной задачи $q(t)$, начиная с некоторого момента времени, мало изменяется, что иллюстрирует стабилизацию решения обратной задачи.

6. ДОКАЗАТЕЛЬСТВО ЛЕММ 1, 2

Лемма 1. Пусть $u \in {{L}^{5}}(\Omega ),\;\eta \in V$, ${{A}_{2}}\eta + {{\kappa }_{a}}\eta = {{\kappa }_{a}}u.$ Тогда

(27)
${{\left\| \eta \right\|}_{{{{L}^{5}}(\Omega )}}} \leqslant \frac{{{{\kappa }_{a}}}}{{\sigma + {{\kappa }_{a}}}}{{\left\| u \right\|}_{{{{L}^{5}}(\Omega )}}}.$
Здесь

$\sigma = inf\left\{ {\tfrac{{16}}{{25}}{{{\left\| {\nabla v} \right\|}}^{2}} + \int\limits_\Gamma \gamma {{v}^{2}}d\Gamma ;\;v \in V,\;\left\| v \right\| = 1} \right\}.$

Доказательство. Умножим скалярно уравнение для $\eta $ на срезку ${{[{{(\eta )}_{n}}]}^{4}},\;n > 0$,

$\alpha (\nabla \eta ,\nabla {{[{{(\eta )}_{n}}]}^{4}}) + \int\limits_\Gamma \,\gamma \eta {{[{{(\eta )}_{n}}]}^{4}}d\Gamma + {{\kappa }_{a}}(\eta ,{{[{{(\eta )}_{n}}]}^{4}}) = {{\kappa }_{a}}(u,{{[{{(\eta )}_{n}}]}^{4}}) \leqslant {{\kappa }_{a}}{{\left\| u \right\|}_{{{{L}^{5}}(\Omega )}}}{{\left\| \eta \right\|}_{{{{L}^{5}}(\Omega )}}}.$
Тогда для функции ${{\psi }_{n}} = {{[{{(\eta )}_{n}}]}^{{5/2}}}$ получаем оценку
$(\sigma + {{\kappa }_{a}}){{\left\| {{{\psi }_{n}}} \right\|}^{2}} \leqslant \frac{{16}}{{25}}\alpha {{\left\| {\nabla {{\psi }_{n}}} \right\|}^{2}} + \int\limits_\Gamma \,\gamma \psi _{n}^{2}d\Gamma + {{\kappa }_{a}}{{\left\| {{{\psi }_{n}}} \right\|}^{2}} \leqslant {{\kappa }_{a}}{{\left\| u \right\|}_{{{{L}^{5}}(\Omega )}}}{{\left\| \eta \right\|}_{{{{L}^{5}}(\Omega )}}}.$
Поэтому последовательность ${{\psi }_{n}},n = 1,2,\; \ldots $, ограничена в пространстве $V$ и ${{\psi }_{n}} \to \psi $ в $H$, где $\psi = {{[\eta ]}^{{5/2}}}.$ В пределе при $n \to + \infty $ получаем
$(\sigma + {{\kappa }_{a}}){{\left\| {{{\psi }_{n}}} \right\|}^{2}} \leqslant {{\kappa }_{a}}{{\left\| u \right\|}_{{{{L}^{5}}(\Omega )}}}{{\left\| \eta \right\|}_{{{{L}^{5}}(\Omega )}}},$
откуда следует оценка (27).

Лемма 2. Пусть $B:V{\kern 1pt} ' \mapsto V{\kern 1pt} '$, $B = {{A}_{2}}{{({{A}_{2}} + {{\kappa }_{a}}I)}^{{ - 1}}}.$ Тогда для произвольных $u,v \in V$ справедливы неравенства

(28)
$(B{{[u]}^{4}},u) \geqslant \frac{\sigma }{{\sigma + {{\kappa }_{a}}}}\left\| u \right\|_{{{{L}^{5}}(\Omega )}}^{5},\quad (B{{[u]}^{4}},v) \leqslant \frac{{\sigma + 2{{\kappa }_{a}}}}{{\sigma + {{\kappa }_{a}}}}\left\| u \right\|_{{{{L}^{5}}(\Omega )}}^{4}{{\left\| v \right\|}_{{{{L}^{5}}(\Omega )}}}.$

Доказательство. Заметим, что

$(B{{[u]}^{4}},u) = ({{[u]}^{4}} - {{\kappa }_{a}}{{({{A}_{2}} + {{\kappa }_{a}}I)}^{{ - 1}}}{{[u]}^{4}},u) = \left\| u \right\|_{{{{L}^{5}}(\Omega )}}^{5} - ({{[u]}^{4}},\eta ),$
где ${{A}_{2}}\eta + {{\kappa }_{a}}\eta = {{\kappa }_{a}}u.$ Поэтому, в силу леммы 1,
$(B{{[u]}^{4}},u) \geqslant \left\| u \right\|_{{{{L}^{5}}(\Omega )}}^{5} - \left\| u \right\|_{{{{L}^{5}}(\Omega )}}^{4}{{\left\| \eta \right\|}_{{{{L}^{5}}(\Omega )}}} \geqslant \left( {1 - \frac{{{{\kappa }_{a}}}}{{\sigma + {{\kappa }_{a}}}}} \right)\left\| u \right\|_{{{{L}^{5}}(\Omega )}}^{5}\frac{\sigma }{{\sigma + {{\kappa }_{a}}}}\left\| u \right\|_{{{{L}^{5}}(\Omega )}}^{5}.$
Далее, $(B{{[u]}^{4}},v) = ({{[u]}^{4}},v - \xi ),$ где ${{A}_{2}}\xi + {{\kappa }_{a}}\xi = {{\kappa }_{a}}v.$ Следовательно,

$(B{{[u]}^{4}},v) \leqslant \left\| u \right\|_{{{{L}^{5}}(\Omega )}}^{4}\left( {{{{\left\| v \right\|}}_{{{{L}^{5}}(\Omega )}}} + {{{\left\| \xi \right\|}}_{{{{L}^{5}}(\Omega )}}}} \right) \leqslant \frac{{\sigma + 2{{\kappa }_{a}}}}{{\sigma + {{\kappa }_{a}}}}\left\| u \right\|_{{{{L}^{5}}(\Omega )}}^{4}{{\left\| v \right\|}_{{{{L}^{5}}(\Omega )}}}.$

Список литературы

  1. Larsen E.W., Thömmes G., Klar A., Seaïd M., Götz M. Simplified ${{P}_{N}}$ approximations to the equations of radiative heat transfer and applications // J. Comput. Phys. 2002. V. 183. № 2. P. 652–675.

  2. Modest M.F. Radiative Heat Transfer. New York: Academic Press, 2003.

  3. Thömmes G., Pinnau R., Seaïd M., Götz M., Klar A. Numerical methods and optimal control for glass cooling processes // Transport Theory and Statistical Physics. 2002. V. 31. № 4–6. P. 513–529.

  4. Tse O., Pinnau R., Siedow N. Identification of temperature-dependent parameters in laser-interstitial thermo therapy // Math. Models Methods Appl. Sci. 2012. V. 22. № 9. P. 1250019.

  5. Tse O., Pinnau R. Optimal control of a simplified natural convection-radiation model // Commun. Math. Sci. 2013. V. 11. № 3. P. 679–707.

  6. Pinnau R. Analysis of optimal boundary control for radiative heat transfer modeled by $S{{P}_{1}}$-system // Commun. Math. Sci. 2007. V. 5. № 4. P. 951–969.

  7. Гренкин Г.В., Чеботарев А.Ю. Нестационарная задача сложного теплообмена // Ж. вычисл. матем. и матем. физ. 2014. Т. 54. № 11. С. 1806–1816.

  8. Гренкин Г.В., Чеботарев А.Ю. Неоднородная нестационарная задача сложного теплообмена // Сиб. электрон. матем. изв. 2015. Т. 12. С. 562–576.

  9. Гренкин Г.В., Чеботарев А.Ю. Нестационарная задача свободной конвекции с радиационным теплообменом // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 2. С. 275–282.

  10. Grenkin G.V., Chebotarev A.Yu., Kovtanyuk A.E., Botkin N.D., Hoffmann K.-H. Boundary optimal control problem of complex heat transfer model // J. Math. Anal. Appl. 2016. V. 433. № 2. P. 1243–1260.

  11. Kovtanyuk A.E., Chebotarev A.Yu. An iterative method for solving a complex heat transfer problem // Appl. Math. Comput. 2013. V. 219. № 17. P. 9356–9362.

  12. Kovtanyuk A.E., Chebotarev A.Yu., Botkin N.D., Hoffmann K.-H. The unique solvability of a complex 3D heat transfer problem // J. Math. Anal. Appl. 2014. V. 409. № 2. P. 808–815.

  13. Ковтанюк А.Е., Чеботарев А.Ю. Стационарная задача сложного теплообмена // Ж. вычисл. матем. и матем. физ. 2014. Т. 54. № 4. С. 711–719.

  14. Ковтанюк А.Е., Чеботарев А.Ю. Стационарная задача свободной конвекции с радиационным теплообменом // Дифференц. ур-ния. 2014. Т. 50. № 12. С. 1590–1597.

  15. Kovtanyuk A.E., Chebotarev A.Yu., Botkin N.D., Hoffmann K.-H. Theoretical analysis of an optimal control problem of conductive-convective-radiative heat transfer // J. Math. Anal. Appl. 2014. V. 412. № 1. P. 520–528.

  16. Kovtanyuk A.E., Chebotarev A.Yu., Botkin N.D., Hoffmann K.-H. Unique solvability of a steady-state complex heat transfer model // Commun. Nonlinear Sci. Numer. Simul. 2015. V. 20. № 3. P. 776–784.

  17. Kovtanyuk A.E., Chebotarev A.Yu., Botkin N.D., Hoffmann K.-H. Optimal boundary control of a steady-state heat transfer model accounting for radiative effects // J. Math. Anal. Appl. 2016. V. 439. № 2. P. 678–689.

  18. Chebotarev A.Yu., Kovtanyuk A.E., Grenkin G.V., Botkin N.D., Hoffmann K.-H. Nondegeneracy of optimality conditions in control problems for a radiative-conductive heat transfer model // Appl. Math. Comput. 2016. V. 289. P. 371–380.

  19. Ковтанюк А.Е., Чеботарев А.Ю. Нелокальная однозначная разрешимость стационарной задачи сложного теплообмена // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 5. С. 816–823.

  20. Chebotarev A.Yu., Grenkin G.V., Kovtanyuk A.E. Inhomogeneous steady-state problem of complex heat transfer // ESAIM Math. Model. Numer. Anal. 2017. V. 51. № 6. P. 2511–2519.

  21. Амосов А.А. Глобальная разрешимость одной нелинейной нестационарной задачи с нелокальным краевым условием типа теплообмена излучением // Дифференц. ур-ния. Т. 41. № 1. 2005. С. 93–104.

  22. Amosov A.A. Stationary nonlinear nonlocal problem of radiative-conductive heat transfer in a system of opaque bodies with properties depending on the radiation frequency // J. Math. Sc. 2010. V. 164. № 3. P. 309–344.

  23. Amosov A. Unique Solvability of a Nonstationary Problem of Radiative – Conductive Heat Exchange in a System of Semitransparent Bodies // Russian J. of Math. Phys. 2016. V. 23. № 3. P. 309–334.

  24. Амосов А.А. Стационарная задача сложного теплообмена в системе полупрозрачных тел с краевыми условиями диффузного отражения и преломления излучения // Ж. вычисл. матем. и матем. физ. 2017. Т. 57. № 3. С. 510–535.

  25. Amosov A.A. Unique Solvability of Stationary Radiative – Conductive Heat Transfer Problem in a System of Semitransparent Bodies // J. of Math. Sc. (United States). 2017. V. 224. № 5. P. 618–646.

  26. Amosov A.A. Nonstationary problem of complex heat transfer in a system of semitransparent bodies with boundary-value conditions of diffuse reflection and refraction of radiation // J. of Math. Sc.(United States). 2018. V. 233. № 6. P. 777–806.

  27. Chebotarev A.Yu., Grenkin G.V., Kovtanyuk A.E., Botkin N.D., Hoffmann K.-H. Inverse problem with finite overdetermination for steady-state equations of radiative heat exchange // J. Math. Anal. Appl. 2018. V. 460. № 2. P. 737–744.

  28. Chebotarev A.Yu., Pinnau R. An inverse problem for a quasi-static approximate model of radiative heat transfer // J. Math. Anal. Appl. 2019. V. 472. № 1. P. 314–327.

  29. Пятков С.Г., Сафонов Е.И. О некоторых классах линейных обратных задач для параболических систем уравнений // Научные ведомости Белгородского государственного университета. Серия: Математика. Физика. 2014. Т. 35. № 12(183). С. 61–75.

  30. Пятков С.Г., Сафонов Е.И. О некоторых классах линейных обратных задач для параболических систем уравнений // Сиб. электрон. матем. изв. 2014. Т. 11. С. 777–799.

  31. Пятков С.Г., Уварова М.В. Об определении функции источника в задачах тепломассопереноса по интегральным условиям переопределения // Сиб. журн. индустр. матем. 2016. Т. 19. № 4. С. 93–100.

  32. Пятков С.Г. О некоторых классах обратных задач об определении функции источника в системах конвекции-диффузии // Дифференц. ур-ния. 2017. Т. 53. № 10. С. 1385.

  33. Chebotarev A.Yu. Subdifferential inverse problems for stationary systems of Navier-Stokes type // J. Inverse Ill-Posed Probl. 1995. V. 3. № 4. P. 268–277.

  34. Чеботарев А.Ю. Определение правой части системы Навье-Стокса и обратные задачи для уравнений тепловой конвекции // Ж. вычисл. матем. и матем. физ. 2011. Т. 51. № 12. С. 2279–2287.

  35. Чеботарев А.Ю. Стабилизация сторонними токами равновесных МГД конфигураций // Ж. вычисл. матем. и матем. физ. 2012. Т. 52. № 12. С. 2238–2246.

  36. Чеботарев А.Ю. Обратная задача для систем Навье–Стокса с конечномерным переопределением // Дифференц. ур-ния. 2012. Т. 48. № 8. С. 1166.

  37. Чеботарев А.Ю. Обратные задачи для стационарных систем Навье–Стокса // Ж. вычисл. матем. и матем. физ. 2014. Т. 54. № 3. С. 519–528.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал