Журнал вычислительной математики и математической физики, 2021, T. 61, № 1, стр. 47-56

Выбор параметра регуляризации на основе реконструкции регуляризированного решения в задаче адаптивной коррекции сигналов

М. Л. Маслаков^*

АО “Российский институт мощного радиостроения”
199178 Санкт-Петербург, 11-я линия В.О., 66, Россия

Поступила в редакцию 23.01.2020
После доработки 10.07.2020
Принята к публикации 18.09.2020

DOI: 10.31857/S0044466921010063

Аннотация

Рассматривается адаптивная коррекция сигналов как решение обратной некорректной задачи. Данная задача сводится к интегральному уравнению типа свертки, а для его решения используется метод регуляризации. Для выбора параметра регуляризации предлагается осуществить реконструкцию регуляризированного решения. Представлены результаты численных экспериментов. Библ. 18. Фиг. 3.

Ключевые слова: некорректная задача, интегральное уравнение типа свертки, регуляризация, параметр регуляризации.

1. ВВЕДЕНИЕ

В статье рассматривается задача адаптивной коррекции частотно ограниченных информационных сигналов, передаваемых через нестационарные замирающие каналы связи (см. [1]). Данная задача сводится к решению интегрального уравнения типа свертки I рода (см. [2]), которое запишем в операторном виде

(1.1)

$HS = {{U}_{\delta }},$

где $H \in {{R}^{{k \times m}}}$, $k \geqslant m$, – матрица коэффициентов импульсной характеристики канала, $S \in {{R}^{m}}$ – вектор отсчетов передаваемого сигнала, ${{U}_{\delta }} \in {{R}^{k}}$ – вектор отсчетов принятого сигнала.

Вектор ${{U}_{\delta }}$ представляет собой результат измерений на фоне белого гауссовского шума, т.е.

(1.2)

${{U}_{\delta }} = \bar {U} + \xi ,$

где $\bar {U}$ – точные значения вектора отсчетов принятого сигнала, $\xi $ – аддитивный белый гауссовский шум с нулевым средним и дисперсией $\sigma _{\xi }^{2}$.

Матрица $H$ состоит из коэффициентов импульсной характеристики канала $h(t)$ (см. [3]), причем

(1.3)

$h(t) \equiv 0,\quad t \leqslant 0,$

(1.4)

$\int\limits_{ - \infty }^\infty {\left| {h(t)} \right|dt} < \infty .$

Матрица $H$ представляет собой циркулянтную матрицу k × m вида

(1.5)

$H = \left[ {\begin{array}{*{20}{c}} {h({{t}_{1}})}&0& \cdots &0 \\ {h({{t}_{2}})}&{h({{t}_{1}})}& \cdots &0 \\ \vdots & \ddots & \ddots & \vdots \\ {h({{t}_{k}})}&{}& \ddots &{h({{t}_{1}})} \\ 0& \ddots &{}&{h({{t}_{2}})} \\ \vdots &{}& \ddots & \vdots \\ 0& \cdots & \cdots &{h({{t}_{k}})} \end{array}} \right],$

где $h({{t}_{k}})$ – отсчеты импульсной характеристики $h(t)$.

Отметим, что на практике коэффициенты матрицы $H$ получают из решения уравнения (1.1) путем передачи тестового сигнала и получении отклика на него (см. [4], [5]). Таким образом, $H$ в общем случае является регуляризированным решением, а значит, $H \equiv {{H}_{\alpha }}$. В рамках рассматриваемой задачи полагаем

(1.6)

$\max \left| {\bar {H} - H} \right| \leqslant {{\delta }_{H}},$

где $\bar {H}$ – точные значения коэффициентов импульсной характеристики канала.

Точные оценки $\sigma _{\xi }^{2}$ и ${{\delta }_{H}}$ отсутствуют.

Для выбора параметра регуляризации применяют различные эвристические методы, описание и сравнительный анализ некоторых из них приводится, например, в [6]–[13]. Применение конкретного метода определяется особенностью постановки решаемой задачи.

В данной работе автором предлагается метод выбора параметра регуляризации путем реконструкции получаемого решения. Для этого предполагается осуществить поэлементную оценку регуляризированного решения и формирование опорных функций.

Статья организована следующим образом. В разд. 2 даны определение реконструированного регуляризированного решения и его свойства. В разд. 3 приведен метод выбора параметра регуляризации на основе реконструированного регуляризированного решения. При этом рассмотрены случаи точно известной и приближенной матрицы $H$. Результаты численного эксперимента представлены в разд. 4. Выводы по работе сформулированы в разд. 5.

2. РЕКОНСТРУКЦИЯ РЕГУЛЯРИЗИРОВАННОГО РЕШЕНИЯ

2.1. Получение реконструированного регуляризированного решения

Вектор передаваемого информационного сигнала $S$ представляет собой отсчеты фазоманипулированного одночастотного сигнала вида (см. [14], [15])

(2.1)

$s(t) = A\sum\limits_{n = 1}^N {\cos \left( {{{\omega }_{0}}t + \varphi (n)} \right)p(t - (n - 1){{T}_{{{\text{sym}}}}})} ,\quad t \in [0;N{{T}_{{{\text{sym}}}}}],$

где $N$ – количество передаваемых символов, $A$ – амплитуда передаваемого сигнала, ${{\omega }_{0}} = 2\pi {{f}_{0}}$ – несущая частота, $\varphi (n)$, $n = 1,2,\; \ldots ,\;N$ – фазы передаваемых символов, ${{T}_{{{\text{sym}}}}}$ – длительность символа,$p(t)$ – импульсная функция вида

$p(t) = \left\{ \begin{gathered} 1,\quad t \in [0;N{{T}_{{{\text{sym}}}}}], \hfill \\ 0,\quad t \notin [0;N{{T}_{{{\text{sym}}}}}]. \hfill \\ \end{gathered} \right.$

Введем оператор $Y$, осуществляющий операцию модуляции, т.е. формирующий сигнал (2.1) в соответствии с входным вектором $B = \left\{ {b(n)} \right\},n = 1,2,\; \ldots ,\;N$, состоящим из последовательности передаваемых информационных бит, т.е.

(2.2)

$S = YB.$

Последовательность фаз $\varphi (n)$, $n = 1,2,\; \ldots ,\;N$, однозначно соответствует вектору $B$. При этом для различной позиционности фазовой модуляции (ФМ) определенному набору бит соответствуют строго определенные значения фаз (см. [15]):

$b = \left\{ {0;1} \right\} \Leftrightarrow \varphi = \left\{ {0;\pi } \right\}~--{\text{ для двухпозиционной ФМ }}\left( {{\text{BPSK}}} \right){\text{;}}$

$b = \left\{ {00;01;11;10} \right\} \Leftrightarrow \varphi = \left\{ {0;\frac{\pi }{2};\pi ;\frac{{3\pi }}{2} \equiv - \frac{\pi }{2}} \right\}~--{\text{ для четырехпозиционной ФМ }}\left( {{\text{QPSK}}} \right){\text{;}}$

и т.д. с учетом кода Грея (см. [16]).

Также, для удобства, будем полагать, что

(2.3)

${{T}_{{{\text{sym}}}}}{{F}_{s}} \in \mathbb{N},$

где ${{F}_{s}}$ – частота дискретизации.

Решение уравнения (1.1) осуществляется методом регуляризации (в работе использован метод регуляризации Тихонова из [12]). Соответствующее численное решение этого уравнения обозначим вектором $S(\alpha )$, зависящим от параметра регуляризации $\alpha $.

Далее введем оператор ${{Y}^{ - }}$, осуществляющий оптимальный когерентный прием, т.е. демодуляцию (см. [15], [16]). Данный оператор введен лишь для удобства последующей записи математических выражений. Описание (реализация) ${{Y}^{ - }}$ приведено в [5]. Тогда, осуществив демодуляцию регуляризированного решения уравнения (1.1), определяемого вектором $S(\alpha )$, получим последовательность бит $B(\alpha ) = \left\{ {b(n,\alpha )} \right\}$, $n = 1,\;2,\; \ldots ,\;N$, которая также будет зависеть от параметра $\alpha $, т.е.

(2.4)

$B(\alpha ) = {{Y}^{ - }}S(\alpha ).$

Тогда решение

(2.5)

${{S}_{Y}}(\alpha ) = Y({{Y}^{ - }}S(\alpha ))$

будем называть реконструированным регуляризированным решением уравнения (1.1).

2.2. Свойства реконструированного регуляризированного решения

Рассмотрим квадратичные нормы исходного вектора $S$, а также регуляризированных решений уравнения (1.1) – $S(\alpha )$ и ${{S}_{Y}}(\alpha )$:

(2.6)

$E = {{\left\| S \right\|}^{2}},$

(2.7)

$E(\alpha ) = {{\left\| {S(\alpha )} \right\|}^{2}},$

(2.8)

${{E}_{Y}}(\alpha ) = {{\left\| {{{S}_{Y}}(\alpha )} \right\|}^{2}}.$

При этом для (2.7) и (2.8) имеют место следующие предельные соотношения:

(2.9)

$\mathop {\lim }\limits_{\alpha \to + \infty } E(\alpha ) = 0\quad \left( {{\text{см}}{\text{., например, }}[{\text{11}}]{\text{, }}[{\text{12}}]} \right),$

(2.10)

$\mathop {\lim }\limits_{\alpha \to + \infty } {{E}_{Y}}(\alpha ) = E.$

Последнее следует из выражения (2.1) с учетом допущения (2.3). Вообще говоря, для любого вектора $B$ имеем

(2.11)

${{\left\| {YB} \right\|}^{2}} = E.$

Иными словами

(2.12)

${{E}_{Y}}(\alpha ) \equiv {\text{const}} = E.$

Отметим, что в случае сигналов BPSK соотношение (2.11) справедливо и без допущения (2.3).

Оптимальное значение параметра регуляризации, согласно [5], соответствует минимуму функционала, представляющего собой количество битовых (символьных) ошибок

(2.13)

$q(\alpha ) = \sum\limits_{n = 1}^N {\left( {b(n) \oplus b(n,\alpha )} \right)} ,$

где $ \oplus $ – знак сложения по модулю два.

При этом отметим, что информационная последовательность бит $b(n)$, $n = 1,\;2,\; \ldots ,\;N$, на практике неизвестна.

Очевидно, что в случае, когда существует такое $\alpha * > 0$, при котором достигается минимум функционала (2.13)

(2.14)

$q(\alpha *) = 0,$

имеет место

(2.15)

${{S}_{Y}}(\alpha *) \equiv S.$

Однако из [5] следует, что (2.14) не всегда выполняется, т.е. для $\forall \alpha > 0$ может быть, что

(2.16)

$\mathop {\min }\limits_\alpha q(\alpha ) > 0.$

В этом случае (2.15) выполняется только лишь на некоторых отрезках (интервалах) из $\left[ {0;N{{T}_{{{\text{sym}}}}}} \right]$, т.е.

(2.17)

${{s}_{Y}}(t,\alpha ) \equiv s(t),\quad [{{t}_{1}};{{t}_{2}}] \cup [{{t}_{3}};{{t}_{4}}] \cup [{{t}_{5}};{{t}_{6}}] \ldots \in [0;N{{T}_{{{\text{sym}}}}}].$

Здесь ${{s}_{Y}}(t,\alpha )$ – фазоманипулированный сигнал, аналогичный (2.1), значения фаз которого соответствуют вектору $B(\alpha )$. Вектор ${{S}_{Y}}(\alpha )$ определяется отсчетами сигнала ${{s}_{Y}}(t,\alpha )$. Отметим, что интервалы $\left[ {{{t}_{k}};{{t}_{{k + 1}}}} \right]$ кратны длительности символа ${{T}_{{{\text{sym}}}}}$.

3. ВЫБОР ПАРАМЕТРА РЕГУЛЯРИЗАЦИИ

3.1. Случай точно известных коэффициентов матрицы $H$

Пусть матрица коэффициентов импульсной характеристики канала известна точно, т.е. ${{\delta }_{H}} = 0$.

Обозначим приближенное представление реконструированного решения в форме

(3.1)

${{U}_{Y}}(\alpha ) = H{{S}_{Y}}(\alpha ),$

при этом

(3.2)

${{\left\| {{{U}_{Y}}(\alpha )} \right\|}^{2}} = {{E}_{{{{U}_{Y}}}}}(\alpha ) > 0\quad (\forall \alpha > 0).$

Отметим, что в общем случае ${{E}_{{{{U}_{Y}}}}}(\alpha ) \ne {\text{const}}$, в отличие от (2.12).

Рассмотрим соотношение

(3.3)

$\begin{gathered} r(\alpha ) = {{\left\| {{{U}_{Y}}(\alpha ) - {{U}_{\delta }}} \right\|}^{2}} = {{\left\| {{{U}_{Y}}(\alpha ) - \bar {U} + \bar {U} - {{U}_{\delta }}} \right\|}^{2}} = \\ = \;{{\left\| {{{U}_{Y}}(\alpha ) - \bar {U}} \right\|}^{2}} + {{\left\| {\bar {U} - {{U}_{\delta }}} \right\|}^{2}} + 2\left\| {{{U}_{Y}}(\alpha ) - \bar {U}} \right\|\left\| {\bar {U} - {{U}_{\delta }}} \right\|. \\ \end{gathered} $

С учетом (1.2) данное выражение примет вид

(3.4)

$r(\alpha ) = {{\left\| {{{U}_{Y}}(\alpha ) - \bar {U}} \right\|}^{2}} + {{\left\| \xi \right\|}^{2}} + 2\left\| {{{U}_{Y}}(\alpha ) - \bar {U}} \right\|\left\| \xi \right\|.$

Допустим, что (2.14) и, следовательно, (2.15) выполняется. В этом случае ${{U}_{Y}}(\alpha *) \equiv \bar {U}$ и тогда выражение (3.5) преобразуется к виду

(3.5)

$r(\alpha *) = {{\left\| \xi \right\|}^{2}} = \sigma _{\xi }^{2}.$

Допустим, что выполняется условие (2.16) и, следовательно, имеет место (2.17). Значит, существуют такие интервалы $[t_{1}^{'};t_{2}^{'}] \cup [t_{3}^{'};t_{4}^{'}] \cup [t_{5}^{'};t_{6}^{'}]$, на которых выполняется

(3.6)

${{U}_{Y}}(\alpha ) \equiv \bar {U}.$

Отметим, что данные интервалы, вообще говоря, не равны интервалам из (2.17).

Обозначим объединение всех интервалов, на которых выполняется (3.6), как ${{T}_{0}}$, а где не выполняется – ${{T}_{e}}$. При этом

(3.7)

${{T}_{0}} \cup {{T}_{e}} \equiv [0;k].$

Тогда $\forall \alpha > 0$ имеют место следующие утверждения:

(3.8)

$\left\| {{{U}_{Y}}(\alpha ) - \bar {U}} \right\|_{{{{T}_{0}}}}^{2} = 0,$

(3.9)

$0 < \left\| {{{U}_{Y}}(\alpha ) - \bar {U}} \right\|_{{{{T}_{e}}}}^{2} \leqslant \left\| {2\bar {U}} \right\|_{{{{T}_{e}}}}^{2}.$

Утверждение (3.8) очевидно и следует из (3.6). Утверждение (3.9) следует из того, что в худшем случае

(3.10)

${{U}_{Y}}(\alpha ) = - \bar {U}.$

В результате выражение (3.4) преобразуется к виду

(3.11)

$\begin{gathered} r(\alpha ) = \left\| {{{U}_{Y}}(\alpha ) - \bar {U}} \right\|_{{{{T}_{0}} \cup {{T}_{e}}}}^{2} + \left\| \xi \right\|_{{{{T}_{0}} \cup {{T}_{e}}}}^{2} + 2{{\left\| {{{U}_{Y}}(\alpha ) - \bar {U}} \right\|}_{{{{T}_{0}} \cup {{T}_{e}}}}}{{\left\| \xi \right\|}_{{{{T}_{0}} \cup {{T}_{e}}}}} = \\ = \;\left\| {{{U}_{Y}}(\alpha ) - \bar {U}} \right\|_{{{{T}_{e}}}}^{2} + {{\left\| \xi \right\|}^{2}} + 2{{\left\| {{{U}_{Y}}(\alpha ) - \bar {U}} \right\|}_{{{{T}_{e}}}}}\left\| \xi \right\| = \left\| {{{U}_{Y}}(\alpha ) - \bar {U}} \right\|_{{{{T}_{e}}}}^{2} + \sigma _{\xi }^{2} + 2{{\left\| {{{U}_{Y}}(\alpha ) - \bar {U}} \right\|}_{{{{T}_{e}}}}}{{\sigma }_{\xi }}. \\ \end{gathered} $

Пусть для некоторого ${{\alpha }_{1}} > 0$ $T_{e}^{1} = [t_{1}^{'};t_{2}^{'}]$, а для ${{\alpha }_{2}} > 0$ $T_{e}^{2} = [t_{1}^{'};t_{3}^{'}]$. При этом $t_{2}^{'} < t_{3}^{'}$. Очевидно, что в этом случае

(3.12)

$\left\| {{{U}_{Y}}({{\alpha }_{1}}) - \bar {U}} \right\|_{{T_{e}^{1}}}^{2} < \left\| {{{U}_{Y}}({{\alpha }_{2}}) - \bar {U}} \right\|_{{T_{e}^{2}}}^{2}$

и, следовательно,

(3.13)

$r({{\alpha }_{1}}) < r({{\alpha }_{2}}),$

а значит, $\min r(\alpha )$ соответствует лучшему приближению ${{U}_{Y}}(\alpha )$ к $\bar {U}$ и в качестве оптимального значения параметра регуляризации можно взять

(3.14)

${{\alpha }_{{{\text{opt}}}}} = \arg \left( {\mathop {\min }\limits_\alpha r(\alpha )} \right),$

что также обеспечивает минимум функционала (2.13).

3.2. Случай приближенной матрицы $H$

Пусть матрица коэффициентов импульсной характеристики канала является регуляризированным приближенным решением ${{H}_{\alpha }}$ таким, что (1.6), ${{\delta }_{H}} > 0$ (${{\delta }_{H}}$ – неизвестно). Как показано в [4], оптимальное значение параметра регуляризации для матрицы ${{H}_{\alpha }}$ (т.е. обеспечивающее лучшее приближение ${{H}_{\alpha }}$ к $\bar {H}$) равно оптимальному значению параметра регуляризации для решения исходного уравнения (1.1). При этом

(3.15)

$\mathop {\lim }\limits_{\alpha \to + \infty } \left\| {{{H}_{\alpha }}} \right\| = 0,$

а значит,

(3.16)

$\mathop {\lim }\limits_{\alpha \to + \infty } \left\| {{{U}_{Y}}(\alpha )} \right\| = 0.$

Допустим выполнение (2.14) и (2.15). Тогда

(3.17)

$r(\alpha {\text{*}}) = {{\left\| {{{U}_{Y}}(\alpha {\text{*}}) - {{U}_{\delta }}} \right\|}^{2}} = {{\left\| {{{H}_{{\alpha {\text{*}}}}}{{S}_{Y}}(\alpha {\text{*}}) - {{U}_{\delta }}} \right\|}^{2}} = {{\left\| {{{H}_{{\alpha {\text{*}}}}}\bar {S} - {{U}_{\delta }}} \right\|}^{2}}.$

В этом случае (3.17) представляет собой невязку для регуляризированных коэффициентов матрицы ${{H}_{\alpha }}$, свойства которой приведены в [11], [12]. Отличительной особенностью выражения (3.17) является то, что коэффициенты матрицы ${{H}_{\alpha }}$ получены при решении уравнения (1.1) в условиях другой реализации шумовой составляющей в ${{U}_{\delta }}$.

Выражение (3.17) можно также представить в виде

(3.18)

$\begin{gathered} r(\alpha {\text{*}}) = {{\left\| {{{H}_{{\alpha {\text{*}}}}}\bar {S} - \bar {U} + \bar {U} - {{U}_{\delta }}} \right\|}^{2}} = {{\left\| {{{H}_{{\alpha {\text{*}}}}}\bar {S} - \bar {U}} \right\|}^{2}} + {{\left\| {\bar {U} - {{U}_{\delta }}} \right\|}^{2}} - 2\left\| {{{H}_{{\alpha {\text{*}}}}}\bar {S} - \bar {U}} \right\|\left\| {\bar {U} - {{U}_{\delta }}} \right\| = \\ = \;{{\left\| {\vartheta (\alpha {\text{*}})} \right\|}^{2}} + {{\left\| \xi \right\|}^{2}} - 2\left\| {\vartheta (\alpha {\text{*}})} \right\|\left\| \xi \right\|, \\ \end{gathered} $

где $\vartheta (\alpha {\text{*}})$ – представляет собой “отбеленный” шум.

Причем $\vartheta (\alpha )$ и $\xi $ – независимы. Рассмотрим подробнее ${{\left\| {\vartheta (\alpha {\text{*}})} \right\|}^{2}}$:

(3.19)

${{\left\| {\vartheta (\alpha {\text{*}})} \right\|}^{2}} = {{\left\| {{{H}_{{\alpha {\text{*}}}}}\bar {S} - \bar {U}} \right\|}^{2}} = {{\left\| {{{H}_{{\alpha {\text{*}}}}}\bar {S} - \bar {H}\bar {S}} \right\|}^{2}} \leqslant E{{\left\| {{{H}_{{\alpha {\text{*}}}}} - \bar {H}} \right\|}^{2}}.$

Лучшее приближение ${{H}_{{\alpha *}}}$ обеспечит минимум $\left\| {\vartheta (\alpha {\text{*}})} \right\|$. При этом в [5] доказано, что условие (2.14) выполняется лишь в ограниченной области возможных значений $\left\{ {\alpha {\text{*}}} \right\}$, любое из которых будет являться оптимальным с точки зрения минимума функционала (2.13).

Пусть выполняется условие (2.16) и, следовательно, имеет место (2.17). При этом существуют интервалы ${{T}_{0}}$, на которых имеет место (3.19), т.е.

(3.20)

$\left\| {\vartheta (\alpha )} \right\|_{{{{T}_{0}}}}^{2} = \left\| {{{H}_{\alpha }}{{S}_{Y}}(\alpha ) - \bar {U}} \right\|_{{{{T}_{0}}}}^{2} = \left\| {{{H}_{\alpha }}\bar {S} - \bar {U}} \right\|_{{{{T}_{0}}}}^{2},$

а также интервалы ${{T}_{e}}$, на которых

(3.21)

$\left\| {\vartheta (\alpha )} \right\|_{{{{T}_{e}}}}^{2} = \left\| {{{H}_{\alpha }}{{S}_{Y}}(\alpha ) - \bar {U}} \right\|_{{{{T}_{e}}}}^{2}.$

С учетом (3.16) имеют место следующие предельные соотношения:

(3.22)

$\mathop {\lim }\limits_{\alpha \to + \infty } \left\| {\vartheta (\alpha )} \right\|_{{{{T}_{0}}}}^{2} = \left\| {\bar {U}} \right\|_{{{{T}_{0}}}}^{2},$

(3.23)

$\mathop {\lim }\limits_{\alpha \to + \infty } \left\| {\vartheta (\alpha )} \right\|_{{{{T}_{e}}}}^{2} = \left\| {\bar {U}} \right\|_{{{{T}_{e}}}}^{2},$

(3.24)

$\mathop {\lim }\limits_{\alpha \to + \infty } {{\left\| {\vartheta (\alpha )} \right\|}^{2}} = {{\left\| {\bar {U}} \right\|}^{2}} = {{E}_{U}}.$

Свойства невязки $r(\alpha )$ приведены в [12], в частности,

(3.25)

$\mathop {\lim }\limits_{\alpha \to + \infty } r(\alpha ) = {{\left\| {{{U}_{\delta }}} \right\|}^{2}} = {{E}_{{{{U}_{\delta }}}}},$

(3.26)

$\mathop {\lim }\limits_{\alpha \to 0 + } r(\alpha ) = {{\mu }^{2}},$

где ${{\mu }^{2}}$ – мера несовместности.

Кроме того, в рамках рассматриваемой задачи имеет место очевидное неравенство

(3.27)

$\mathop {\lim }\limits_{\alpha \to 0 + } \left\| {r(\alpha )} \right\|_{{{{T}_{0}}}}^{2} < \mathop {\lim }\limits_{\alpha \to 0 + } \left\| {r(\alpha )} \right\|_{{{{T}_{e}}}}^{2}.$

Таким образом, с учетом неравенства (3.12), из выражения ${{\left\| {\bar {U} - {{U}_{\delta }}} \right\|}^{2}} = {{\left\| \xi \right\|}^{2}} = {\text{const}}$ следует, что минимуму ${{\left\| {\vartheta (\alpha )} \right\|}^{2}} = {{\left\| {{{H}_{\alpha }}{{S}_{Y}}(\alpha ) - \bar {U}} \right\|}^{2}}$ соответствует минимум невязки $r(\alpha )$. А выбор ${{\alpha }_{{{\text{opt}}}}}$ из (3.14) обеспечивает минимум функционала (2.13).

3.3. Некоторые дополнительные замечания

Рассмотрим выбор параметра регуляризации по невязке для решения уравнения (1.1) в форме $S(\alpha )$ (см. [17]). С учетом принятых обозначений невязка есть

(3.28)

$\hat {r}(\alpha ) = {{\left\| {HS(\alpha ) - {{U}_{\delta }}} \right\|}^{2}}$.

Различные модификации данного подхода рассмотрены, например, в [13], как для случая ${{\delta }_{H}} = 0$, так и для случая ${{\delta }_{H}} \ne 0$ (но не в случае $H \equiv {{H}_{\alpha }}$).

Рассмотрим подробнее этот случай ($H \equiv {{H}_{\alpha }}$), имеющий место в рассматриваемой задаче коррекции сигналов. Тогда вместо (3.26) выражение для невязки примет вид

(3.29)

$\tilde {r}(\alpha ) = {{\left\| {{{H}_{\alpha }}S(\alpha ) - {{U}_{\delta }}} \right\|}^{2}}.$

В основном свойства невязки $\tilde {r}(\alpha )$ и ее предельные значения не отличаются от случаев $r(\alpha )$ и $\hat {r}(\alpha )$. Тем не менее имеются определенные различия.

1. $\exists {{\alpha }_{0}}:\forall \alpha > {{\alpha }_{0}}$ выполняется неравенство

(3.30)

${{\left\| {{{H}_{\alpha }}S(\alpha )} \right\|}^{2}} < {{\left\| {{{H}_{\alpha }}{{S}_{Y}}(\alpha )} \right\|}^{2}}$.

Доказательство следует из того, что ${{\left\| {{{H}_{\alpha }}} \right\|}^{2}}$ и ${{\left\| {S(\alpha )} \right\|}^{2}}$ – монотонно не возрастающие функции (см. [12]). Однако для ${{\left\| {{{S}_{Y}}(\alpha )} \right\|}^{2}}$ при $\forall \alpha $ выполняется (2.12).

Тогда имеем

(3.31)

${{\left\| {{{H}_{\alpha }}S(\alpha )} \right\|}^{2}} \leqslant {{\left\| {{{H}_{\alpha }}} \right\|}^{2}}{{\left\| {S(\alpha )} \right\|}^{2}},$

(3.32)

${{\left\| {{{H}_{\alpha }}{{S}_{Y}}(\alpha )} \right\|}^{2}} \leqslant {{\left\| {{{H}_{\alpha }}} \right\|}^{2}}E.$

С учетом (2.9) приходим к выводу, что найдется такое ${{\alpha }_{0}}:\forall \alpha > {{\alpha }_{0}}$ имеет место неравенство

(3.33)

${{\left\| {S(\alpha )} \right\|}^{2}} < E,$

а значит, неравенство (3.30) также выполняется.

Аналогично можно доказать выполнение неравенства

(3.34)

${{\left\| {\bar {H}S(\alpha )} \right\|}^{2}} < {{\left\| {\bar {H}{{S}_{Y}}(\alpha )} \right\|}^{2}}.$

При этом отметим, что ${{\alpha }_{0}}$ может быть $ \geqslant {\kern 1pt} 0$.

2. Функция ${{\left\| {{{H}_{\alpha }}S(\alpha )} \right\|}^{2}}$ монотонно не возрастающая $\forall \alpha > 0$, однако функция ${{\left\| {{{H}_{\alpha }}{{S}_{Y}}(\alpha )} \right\|}^{2}}$ не является монотонной на интервале $\left[ {0;\alpha {\text{'}}} \right]$. Данное свойство менее очевидно и следует из того, что в общем случае для различных векторов ${{B}_{1}}$ и ${{B}_{2}}$: ${{B}_{1}} \ne {{B}_{2}}$ имеет место

(3.35)

${{\left\| {\bar {H}Y{{B}_{1}}} \right\|}^{2}} \ne {{\left\| {\bar {H}Y{{B}_{2}}} \right\|}^{2}}.$

Следовательно, $\exists {{\alpha }_{1}},{{\alpha }_{2}} \in \left[ {0;\alpha {\text{'}}} \right]:{{\alpha }_{1}} < {{\alpha }_{2}}$, при которых

(3.36)

${{\left\| {\bar {H}{{S}_{Y}}({{\alpha }_{1}})} \right\|}^{2}} < {{\left\| {\bar {H}{{S}_{Y}}({{\alpha }_{2}})} \right\|}^{2}},$

и, как следствие, имеем

(3.37)

${{\left\| {{{H}_{{{{\alpha }_{1}}}}}{{S}_{Y}}({{\alpha }_{1}})} \right\|}^{2}} < {{\left\| {{{H}_{{{{\alpha }_{2}}}}}{{S}_{Y}}({{\alpha }_{2}})} \right\|}^{2}}.$

Это приводит к тому, что зависимость невязки от параметра регуляризации может иметь несколько локальных минимумов.

4. ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ

В данном разделе представлены результаты численного моделирования, демонстрирующие характерные свойства невязки при использовании реконструированного регуляризированного решения, а также эффективность предложенного метода выбора параметра регуляризации применительно к задаче адаптивной коррекции сигналов.

В качестве модели канала (функции $h(t)$) использована модель Ваттерсона (см. [18]), применяемая при моделировании коротковолновых каналов связи. При моделировании выбраны следующие параметры модели канала: 2 луча, интервал между лучами 2 мс, замирания каждого луча по закону Рэлея, используемая полоса частот 0/3–3/4 кГц. Параметры передаваемого сигнала: несущая частота сигнала ${{\omega }_{0}} = 2\pi {{f}_{0}}$ при ${{f}_{0}} = 1.8$ Гц; длительность символа ${{T}_{{{\text{sym}}}}} = 0.625$ мс. Частота дискретизации 16 кГц.

На фиг. 1 представлены характерные зависимости функционала $q(\alpha )$, невязок $r(\alpha )$, $\tilde {r}(\alpha )$, а также $\bar {r}(\alpha )$, определяемой из выражения

(4.1)

$\bar {r}(\alpha ) = {{\left\| {\bar {H}S(\alpha ) - {{U}_{\delta }}} \right\|}^{2}}.$

Фиг. 1.

Характерный вид зависимостей, полученных при ОСШ 5 дБ: $q(\alpha )$ (черная 1); $r(\alpha )$ (синяя 2); $\tilde {r}(\alpha )$ (красная 3); $\bar {r}(\alpha )$ (зеленая 4).

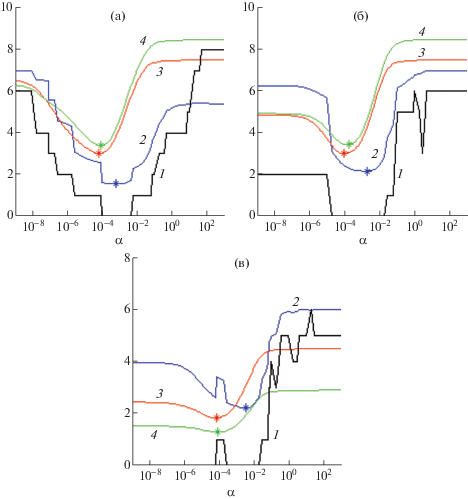
Отметим, что представленные на фиг. 1 зависимости $r(\alpha )$, $\tilde {r}(\alpha )$ и $\bar {r}(\alpha )$ для наглядности были нормированы.

Значения минимумов для зависимостей на фиг. 1а, б отмечены знаком *.

Дополнительно для демонстрации свойств 1, 2 на фиг. 2 приведены соответствующие зависимости ${{\left\| {{{H}_{\alpha }}{{S}_{Y}}(\alpha )} \right\|}^{2}}$, ${{\left\| {{{H}_{\alpha }}S(\alpha )} \right\|}^{2}}$ и ${{\left\| {\bar {H}S(\alpha )} \right\|}^{2}}$.

Фиг. 2.

Зависимости ${{\left\| {{{H}_{\alpha }}{{S}_{Y}}(\alpha )} \right\|}^{2}}$ (синяя 1), ${{\left\| {{{H}_{\alpha }}S(\alpha )} \right\|}^{2}}$ (красная 2), ${{\left\| {\bar {H}S(\alpha )} \right\|}^{2}}$ (зеленая 3).

Для демонстрации эффективности применения предложенного метода выбора параметра регуляризации проведен эксперимент и получены зависимости вероятности ошибки на бит от ОСШ. Вероятность ошибки на бит определяется из выражения

(4.2)

$P = \frac{1}{{LN}}\sum\limits_{l = 1}^L {q(l,{{{\hat {\alpha }}}_{l}})} ,$

где $L$ – объем выборки, $q(l,{{\hat {\alpha }}_{l}})$ – число ошибок в $l$-м эксперименте, ${{\hat {\alpha }}_{l}}$ – выбранное значение параметра регуляризации.

При моделировании были заданы параметры $L = 20\,000$, $N = 15$. Обозначим вероятности ошибки на бит следующим образом: $P$ – при выборе параметра регуляризации предлагаемым методом; $\tilde {P}$ – при выборе параметра регуляризации по невязке, определяемой из выражения (3.29).

Нижняя граница на фиг. 3 получена экспериментально при условии, что последовательность ${{b}_{m}}(n)$, $n = 1,\;2,,\; \ldots ,\;N$, известна точно в каждом из $M$ опытов.

Фиг. 3.

Зависимости вероятности ошибки на бит от ОСШ (SNR): $P$ (синяя 1), $\tilde {P}$ (красная 2), нижняя граница (черная 3).

Эффективность предложенного метода обусловлена следующим. Представим регуляризированное решение уравнения (1.1) в форме

(4.3)

$S(\alpha ) = \bar {S} + \eta (\alpha ),$

где $\eta (\alpha )$ назовем погрешностью (или ошибкой) вычисления, при этом

(4.4)

${{\left\| {\eta (\alpha )} \right\|}^{2}} > 0.$

Аналогично, для реконструированного регуляризированного решения

(4.5)

${{S}_{Y}}(\alpha ) = \bar {S} + {{\eta }_{Y}}(\alpha ).$

При этом из свойства (2.17) следует, что существуют такие интервалы ${{\hat {T}}_{0}}$, на которых

(4.6)

$\left\| {{{\eta }_{Y}}(\alpha )} \right\|_{{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} }}_{0}}}}^{2} \equiv 0,$

а значение нормы ошибки вычисления $\left\| {{{\eta }_{Y}}(\alpha )} \right\|_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} e}}^{2}$ тем меньше, чем меньше суммарная длительность интервала $\left| {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} }}_{e}}} \right|$, что и соответствует минимуму функционала (2.13). При этом в ряде случаев может быть, что $\left| {{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} }}_{e}}} \right| = 0$, и соответственно ${{\left\| {{{\eta }_{Y}}(\alpha )} \right\|}^{2}} \equiv 0$ на всей длительности сигнала, т.е. ${{\hat {T}}_{0}}$ = $\left[ {0;N{{T}_{{{\text{sym}}}}}} \right]$.

5. ЗАКЛЮЧЕНИЕ

Вычислительные эксперименты подтвердили применимость и эффективность предложенного метода выбора параметра регуляризации на основе реконструкции регуляризированного решения в задаче адаптивной коррекции сигналов. Данный метод не требует знания или получения оценок о погрешности правой части уравнения (1.1) и оценки ошибки вычисления матрицы ${{H}_{\alpha }}$. Однако требуется априорное знание определенных характеристик искомого решения $S$ для получения оценок элементов функции $s(t)$, необходимых для формирования опорных функций.

Список литературы

Eleftheriou E., Falconer D. Adaptive equalization techniques for HF channels // IEEE J.l on Selected Areas in Communicat. 1987. V. 5. I. 2. P. 238–247.
Santamarina J.C., Fratta D. Discrete Signals and Inverse Problems. John Wiley & Sons, Ltd, 2005.
Haykin S. Adaptive Filter Theory. 5-th ed. Boston: Pearson, 2014.
Маслаков М.Л. Применение двухпараметрических стабилизирующих функций при решении интегрального уравнения типа свертки методом регуляризации // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 4. С. 541–549.
Маслаков М.Л. Выбор параметра регуляризации в задачах адаптивной фильтрации // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 6. С. 951–560.
Bauer F., Lukas M.A. Comparing parameter choice methods for regularization of ill-posed problem // Math. Comput. Simul. 2011. V. 81. I. 9. P. 1795–1841.
Hansen P.C. Rank-Deficient and Discrete Ill-Posed Problems, SIAM, Philadelphia, 1998.
Lu S., Pereverzev S.V. Regularization Theory for Ill-posed Problems. De Gruyter, Berlin, 2013.
Hochstenbach M.E., Reichel L., Rodriguez G. Regularization parameter determination for discrete ill-posed problems // J. Comput. Appl. Math. 2015. V. 273. P. 132–149.
Hamarik U., Palm R., Raus T. A family of rules for parameter choice in Tikhonov regularization of ill-posed problems with inexact noise level // J. Comput. Appl. Math. 2012. V. 236. P. 2146–2157.
Гончарский А.В., Леонов А.С., Ягола А.Г. Обобщенный принцип невязки // Ж. вычисл. матем. и матем. физ. 1973. Т. 13. № 2. С. 294–302.
Тихонов А.Н., Гончарсикй А.В., Степанов В.В., Ягола А.Г. Численные методы решения некорректных задач. М.: Наука, 1990.
Сизиков В.С. О способах невязки при решении некорректных задач // Ж. вычисл. матем. и матем. физ. 2003. Т. 43. № 9. С. 1294–1312.
Johnson E.E., Koski E., Furman W.N., Jorgenson M., Nieto J. Third-Generation and Wideband HF Radio Communications. Artech House, Inc, Boston, 2013.
Xiong F. Digital Modulation Techniques, Second Edition. Artech House, Inc, Boston, 2006.
Proakis J.G., Salehi M. Digital Communications, Fifth Edition. New York: McGraw-Hill, 2008.
Морозов В.А. О принципе невязки при решении операторных уравнений методом регуляризации // Ж. вычисл. матем. и матем. физ. 1968. Т. 8. № 2. С. 295–309.
Watteson C.C., Juroshek J.R., Bensema W.D. Experimental Confirmation of an HF Channel Model // IEEE Transact. Communicat. Technology. 1970. V. COM-18. № 6. P. 792–803.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал